ЖИ көмекші
параллеграмм ауданы
Тақырып бойынша 26 материал табылды
параллеграмм ауданы
Материал туралы қысқаша түсінік
параллелограмм және ромб ауданы
Материалдың қысқаша нұсқасы
1 / 17
Жүктеу
Бөлісу
ЖИ арқылы жасау
Слайдтың жеке беттері
#1 слайд
Параллелограмн ың ауданы
1 слайд
Параллелограмн ың ауданы
#2 слайд
Оқу мақсаты:
8.1.3.11 параллелограммның, ромбтың
ауданы формулаларын қорытып шығару
және қолдану;
Сабақ мақсаты:
параллелограммның, ромбтың ауданы
формулаларын білу және есептер
шығаруда қолдану
Сабақ мақсаттары
2 слайд
Оқу мақсаты: 8.1.3.11 параллелограммның, ромбтың ауданы формулаларын қорытып шығару және қолдану; Сабақ мақсаты: параллелограммның, ромбтың ауданы формулаларын білу және есептер шығаруда қолдану Сабақ мақсаттары
#3 слайд
Фигура ауданын
табыңыз
3 слайд
Фигура ауданын табыңыз
#4 слайд
24 – теорема. Парaллелограмның
ауданы оның табаны мен биіктігінің
көбейтіндісіне тең.
Параллелограмның
ауданын табу
теоремасы
А
В
С
D
а
h
S
ABCD
= ah
4 слайд
24 – теорема. Парaллелограмның ауданы оның табаны мен биіктігінің көбейтіндісіне тең. Параллелограмның ауданын табу теоремасы А В С D а h S ABCD = ah
#5 слайд
ABCD параллелограмы берілсін.
Енді, параллелограмның табанына биіктік жүргізейік.
Осыдан, S
ABCD = ah екенін дәлелдейік.
Дәлелдеуі:
А
В
С
D Е
а
h
Бірінші, С төбесінен табанына
биіктік жүргізейік.
Сонда, EBCF тіктөртбұрыш және
оның ауданы S
EBCF
= ah
AB = CD және BE = CF, ABE мен
DCF үшбұрыштары тікбұрышты.
Тікбұрышты үшбұрыштардың
теңдік қасиеті бойынша бұл екі
үшбұрыш тең.
Тең фигуралардың аудандары да
тең, яғни бұл фигуралардың
аудандары тең.
F
5 слайд
ABCD параллелограмы берілсін. Енді, параллелограмның табанына биіктік жүргізейік. Осыдан, S ABCD = ah екенін дәлелдейік. Дәлелдеуі: А В С D Е а h Бірінші, С төбесінен табанына биіктік жүргізейік. Сонда, EBCF тіктөртбұрыш және оның ауданы S EBCF = ah AB = CD және BE = CF, ABE мен DCF үшбұрыштары тікбұрышты. Тікбұрышты үшбұрыштардың теңдік қасиеті бойынша бұл екі үшбұрыш тең. Тең фигуралардың аудандары да тең, яғни бұл фигуралардың аудандары тең. F
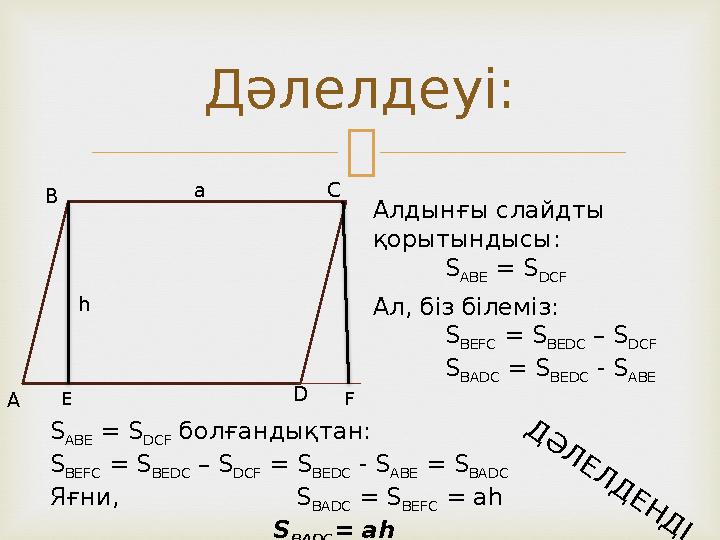
#6 слайд
Дәлелдеуі:
А
В
С
D Е
а
h
F
Алдынғы слайдты
қорытындысы:
S
ABE
= S
DCF
Ал, біз білеміз:
S
BEFC
= S
BEDC
– S
DCF
S
BADC
= S
BEDC
- S
ABE
S
ABE
= S
DCF
болғандықтан:
S
BEFC
= S
BEDC
– S
DCF
= S
BEDC
- S
ABE
= S
BADC
Яғни, S
BADC
= S
BEFC
= ah
S
BADC
= ah
Д
Ә
Л
Е
Л
Д
Е
Н
Д
І
6 слайд
Дәлелдеуі: А В С D Е а h F Алдынғы слайдты қорытындысы: S ABE = S DCF Ал, біз білеміз: S BEFC = S BEDC – S DCF S BADC = S BEDC - S ABE S ABE = S DCF болғандықтан: S BEFC = S BEDC – S DCF = S BEDC - S ABE = S BADC Яғни, S BADC = S BEFC = ah S BADC = ah Д Ә Л Е Л Д Е Н Д І
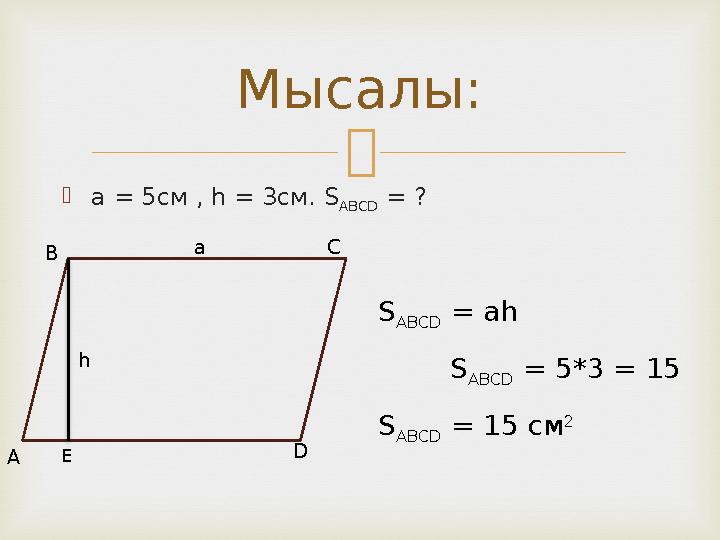
#7 слайд
а = 5см , h = 3см. S
ABCD
= ?
Мысалы:
А
В
С
D Е
а
h
S
ABCD
= ah
S
ABCD
= 5*3 = 15
S
ABCD = 15 см
2
7 слайд
а = 5см , h = 3см. S ABCD = ? Мысалы: А В С D Е а h S ABCD = ah S ABCD = 5*3 = 15 S ABCD = 15 см 2
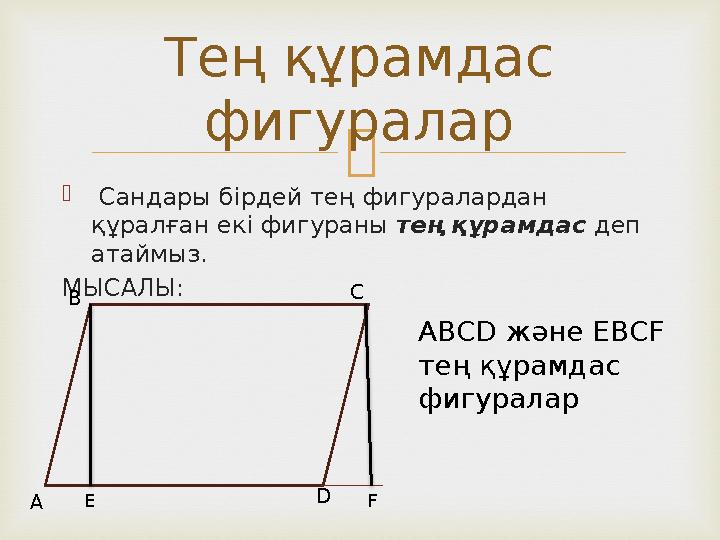
#8 слайд
Сандары бірдей тең фигуралардан
құралған екі фигураны тең құрамдас деп
атаймыз.
МЫСАЛЫ:
Тең құрамдас
фигуралар
А
В
С
D Е F
ABCD және EBCF
тең құрамдас
фигуралар
8 слайд
Сандары бірдей тең фигуралардан құралған екі фигураны тең құрамдас деп атаймыз. МЫСАЛЫ: Тең құрамдас фигуралар А В С D Е F ABCD және EBCF тең құрамдас фигуралар
#9 слайд
Параллелограмның
ауданын табу
теоремасы
25 – теорема. Парaллелограмның
ауданы оның екі сыбайлас
қабырғаларының және сүйір
бұрышының (негізі кез – келген
бұрышының) синусының
көбейтіндісіне тең
А
В
С
D
а
S
ABCD
= absinβ
β
b
9 слайд
Параллелограмның ауданын табу теоремасы 25 – теорема. Парaллелограмның ауданы оның екі сыбайлас қабырғаларының және сүйір бұрышының (негізі кез – келген бұрышының) синусының көбейтіндісіне тең А В С D а S ABCD = absinβ β b
#10 слайд
a = 5см, b = 8см, β = 30
o
.
S
ABCD
= ?
Мысал:
В
С
D
а
β
b
А
S
ABCD
= absinβ
S
ABCD
= 5*8*sin30
o
=
20
S
ABCD
= 20 см
2
10 слайд
a = 5см, b = 8см, β = 30 o . S ABCD = ? Мысал: В С D а β b А S ABCD = absinβ S ABCD = 5*8*sin30 o = 20 S ABCD = 20 см 2
#11 слайд
Параллелограмның
ауданын табу
формуласы
11 слайд
Параллелограмның ауданын табу формуласы
#12 слайд
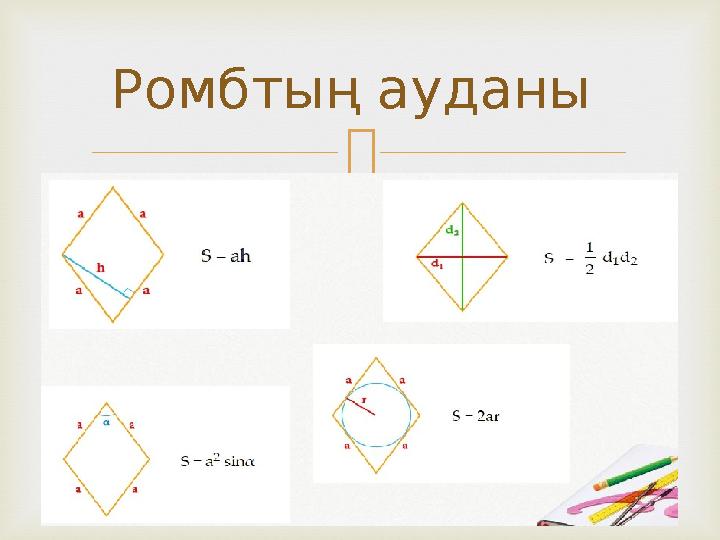
Ромбтың ауданы
12 слайд
Ромбтың ауданы
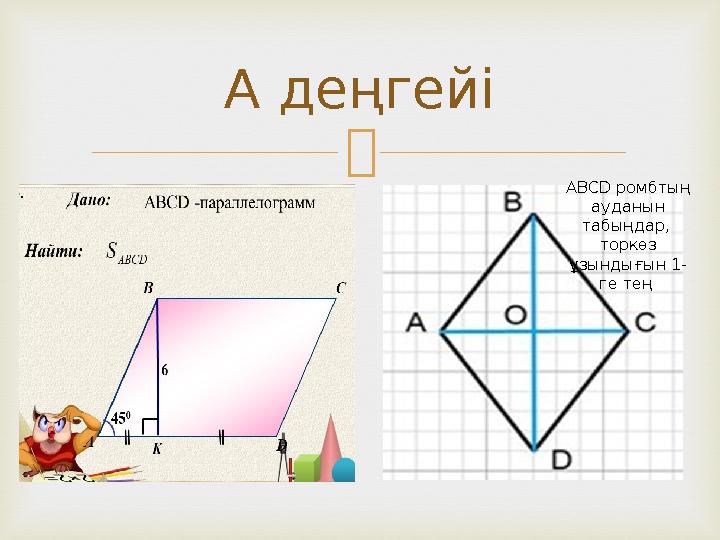
#13 слайд
А деңгейі
ABCD ромбтың
ауданын
табыңдар,
торкөз
ұзындығын 1-
ге тең
13 слайд
А деңгейі ABCD ромбтың ауданын табыңдар, торкөз ұзындығын 1- ге тең
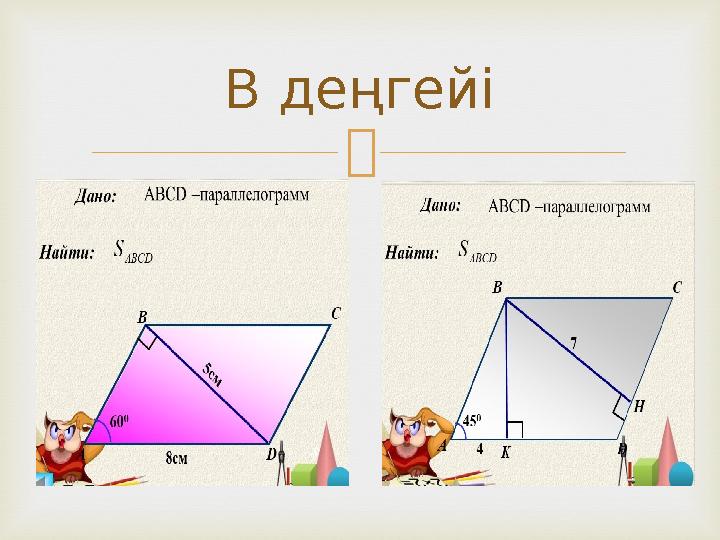
#14 слайд
В деңгейі
14 слайд
В деңгейі
#15 слайд
С деңгейі
Ромбтың диагональдарының қатынасы
3:4, ал ауданы 24 шаршы см. Ромб
қабырғаларының ұзындығын табыңдар
15 слайд
С деңгейі Ромбтың диагональдарының қатынасы 3:4, ал ауданы 24 шаршы см. Ромб қабырғаларының ұзындығын табыңдар
#16 слайд
https://wordwall.net/resource/27867250
Өзіңді тексер!
16 слайд
https://wordwall.net/resource/27867250 Өзіңді тексер!
Файл форматы:
pptx
16.01.2025
284
Жүктеу
ЖИ арқылы жасау
Жариялаған:
Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз,
шағым қалдыра аласыз
шағым қалдыра аласыз
