#1 слайд
ПАРАЛЛЕЛОГРАММ ЖӘНЕ ОНЫҢ ҚАСИЕТТЕРІ

1 слайд

#2 слайд
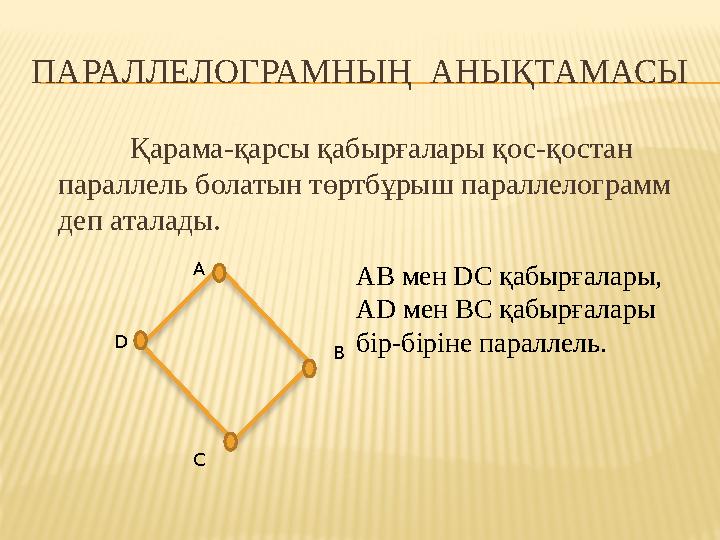
ПАРАЛЛЕЛОГРАМНЫҢ АНЫҚТАМАСЫ Қарама-қарсы қабырғалары қос-қостан параллель болатын төртбұрыш параллелограмм деп аталады. D A B C AB мен DC қабырғалары, AD мен BC қабырғалары бір-біріне параллель.

2 слайд

#3 слайд
ПАРАЛЛЕЛОГРАМНЫҢ БИІКТІГІ Параллелограмның бір төбесінен қарсы жатқан қабырғасына түсірілген перпдикуляр оның биіктігі деп аталады. D B C А К Н Мысалы, сол жақтағы көрсетілген параллелограмның D төбесінен түскен биіктіктер DK және DH , олар сәйкесінше АВ және ВС қабырғаларына түсіп тұр.

3 слайд

#4 слайд
ПАРАЛЛЕЛОГРАМНЫҢ БИІКТІГІ Параллелограмның қабырғасына биіктік түсірілсе, сол биіктік түсірілген қабырға табан деп аталады. D B C А Мысалы, сол жақтағы суреттегі биіктіктердің табандары АВ және ВС қабырғалары.

4 слайд

#5 слайд
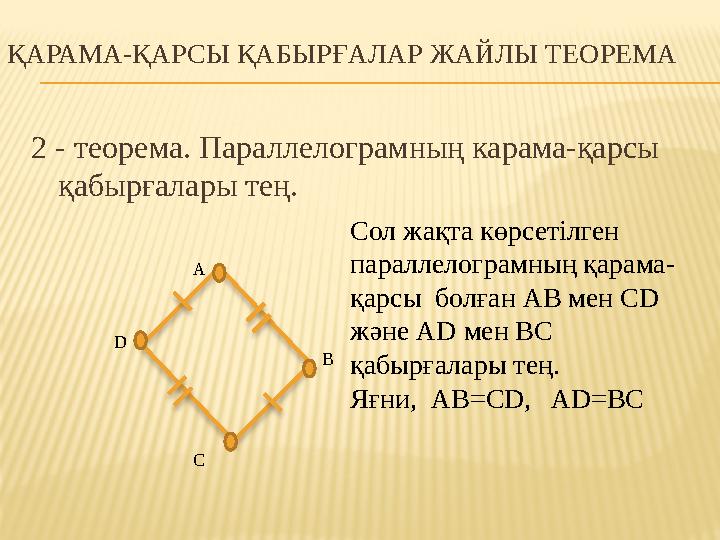
ҚАРАМА-ҚАРСЫ ҚАБЫРҒАЛАР ЖАЙЛЫ ТЕОРЕМА 2 - теорема. Параллелограмның карама-қарсы қабырғалары тең. D A B C Сол жақта көрсетілген параллелограмның қарама- қарсы болған АВ мен СD және АD мен ВС қабырғалары тең. Яғни, АВ=СD, AD=BC

5 слайд

#6 слайд
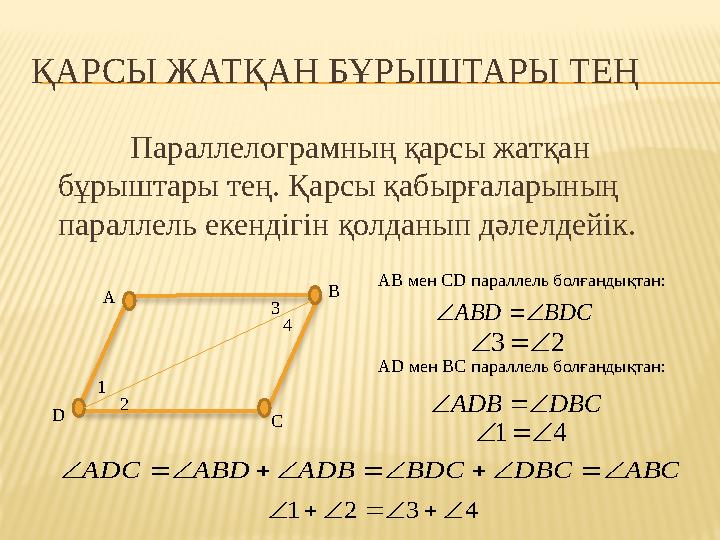
ҚАРСЫ ЖАТҚАН БҰРЫШТАРЫ ТЕҢ Параллелограмның қарсы жатқан бұрыштары тең. Қарсы қабырғаларының параллель екендігін қолданып дәлелдейік. D A B C 1 4 3 2 АВ мен СD параллель болғандықтан: AD мен BC параллель болғандықтан: ABD BDC  ADB DBC  ADC ABD ADB BDC DBC ABC      3 2  1 4  1 2 3 4   

6 слайд

#7 слайд
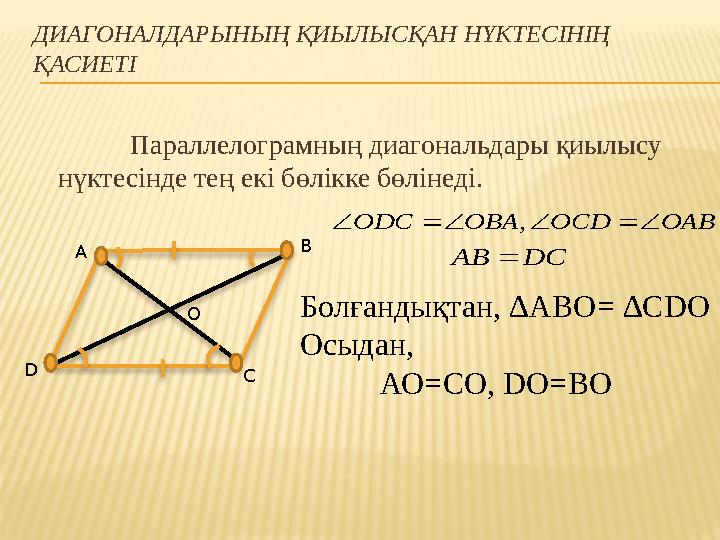
ДИАГОНАЛДАРЫНЫҢ ҚИЫЛЫСҚАН НҮКТЕСІНІҢ ҚАСИЕТІ Параллелограмның диагональдары қиылысу нүктесінде тең екі бөлікке бөлінеді. D A B C О Болғандықтан, ∆АВО= ∆CDO Осыдан, АО=СО, DO=ВO ,ODC OBA OCD OAB    AB DC

7 слайд

#8 слайд
МЫСАЛ AC=? BD=? D A B C О Берілгені: ВО=6см, ОС=4см Теорема бойынша: АС=2*ОС, BD=2*BO Осыдан, AC= 2*6=12см BD=2*4=8см

8 слайд

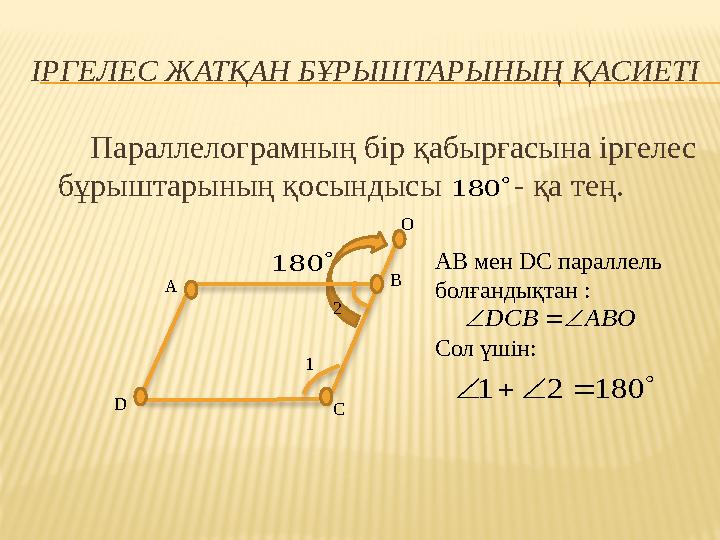
#9 слайд
ІРГЕЛЕС ЖАТҚАН БҰРЫШТАРЫНЫҢ ҚАСИЕТІ Параллелограмның бір қабырғасына іргелес бұрыштарының қосындысы - қа тең.180 D A B C 2 1 O 180 AB мен DC параллель болғандықтан : Сол үшін: DCB ABO  1 2 180   

9 слайд

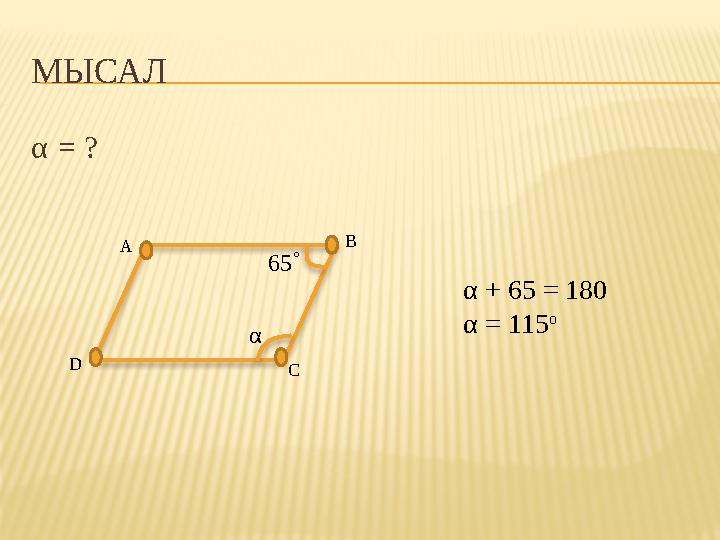
#10 слайд
МЫСАЛ α = ? D A B C α 65 α + 65 = 180 α = 115 o

10 слайд