Материалдар / Пікірлер алгебрасы

Пікірлер алгебрасы

Материал туралы қысқаша түсінік

Пікірлер алгебрасы

Әбдімәлік Ғаны Әбдіжәлилұлы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

29 Қазан 2024

0 рет жүктелген

Барлық пәндер Презентация Барлық сыныптар

450 ₸

Бүгін алсаңыз
+23 бонус беріледі
Бұл не?

Бүгін алсаңыз +23 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 11

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Пікірлер алгебрасы Пікірлер алгебрасы - логикалық байланыстар мен күрделі пікірлерді зерттейтін сала. Ол ақиқат немесе жалған мәндерді қабылдайтын хабарлы сөйлемдерді қарастырады. GA by Gani Abdumalik

1 слайд

Пікірлер алгебрасы Пікірлер алгебрасы - логикалық байланыстар мен күрделі пікірлерді зерттейтін сала. Ол ақиқат немесе жалған мәндерді қабылдайтын хабарлы сөйлемдерді қарастырады. GA by Gani Abdumalik

2 слайд
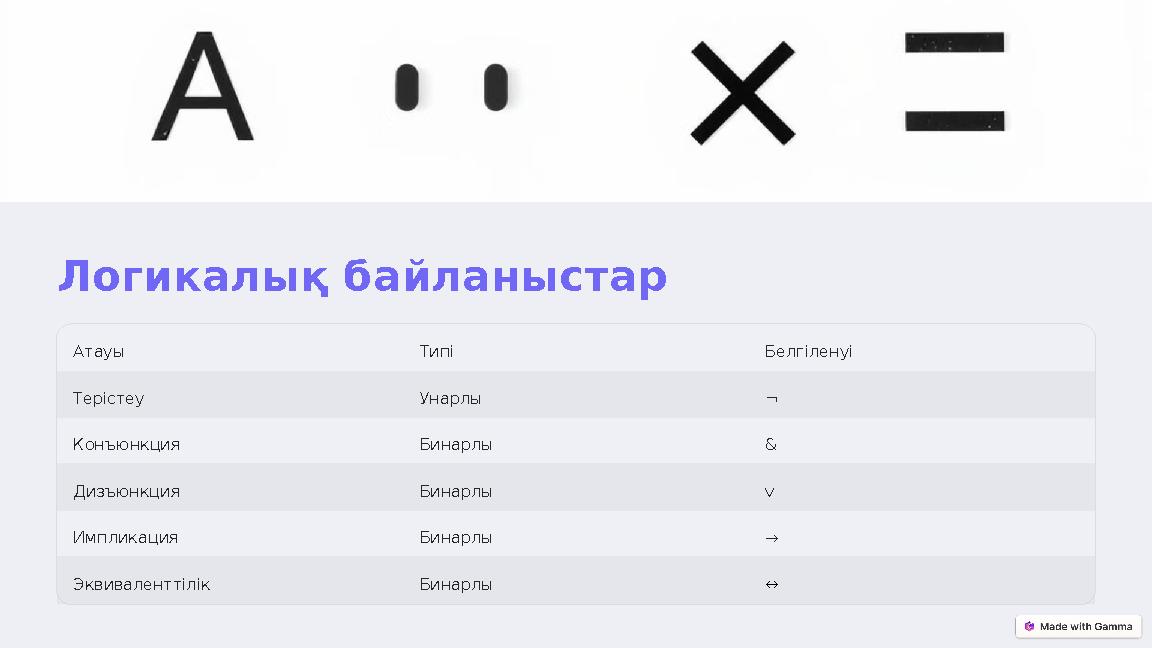
Логикалық байланыстар Атауы Типі Белгіленуі Терістеу Унарлы ¬ Конъюнкция Бинарлы & Дизъюнкция Бинарлы v Импликация Бинарлы → Эквиваленттілік Бинарлы ↔

2 слайд

Логикалық байланыстар Атауы Типі Белгіленуі Терістеу Унарлы ¬ Конъюнкция Бинарлы & Дизъюнкция Бинарлы v Импликация Бинарлы → Эквиваленттілік Бинарлы ↔

3 слайд
Күрделі пікірлер 1Анықтама Күрделі пікірлер - логикалық байланыстар арқылы құрылған құрама пікірлер. 2Мысал (A & B) → (⎯A v В) формуласы күрделі пікірге мысал бола алады. 3Мәні Күрделі пікірлер де қарапайым пікірлер сияқты ақиқат немесе жалған мәнін қабылдайды.

3 слайд

Күрделі пікірлер 1Анықтама Күрделі пікірлер - логикалық байланыстар арқылы құрылған құрама пікірлер. 2Мысал (A & B) → (⎯A v В) формуласы күрделі пікірге мысал бола алады. 3Мәні Күрделі пікірлер де қарапайым пікірлер сияқты ақиқат немесе жалған мәнін қабылдайды.

4 слайд
Бинарлық қатынастар 1 Анықтама Бинарлық қатынас - A2 жиынының R ішкі жиыны. 2 Графтық көрініс Бинарлық қатынасты граф түрінде бейнелеуге болады. 3 Жазылуы (ai, aj) R орнына ai R aj деп жазуға болады.

4 слайд

Бинарлық қатынастар 1 Анықтама Бинарлық қатынас - A2 жиынының R ішкі жиыны. 2 Графтық көрініс Бинарлық қатынасты граф түрінде бейнелеуге болады. 3 Жазылуы (ai, aj) R орнына ai R aj деп жазуға болады.

5 слайд
Бинарлық қатынас түрлері (1) Толық Кез келген екі элемент R қатынасымен байланысқан. Рефлексивті aRa барлық a үшін орындалады. Симметриялық a1Ra2 болса, a2Ra1 да орындалады.

5 слайд

Бинарлық қатынас түрлері (1) Толық Кез келген екі элемент R қатынасымен байланысқан. Рефлексивті aRa барлық a үшін орындалады. Симметриялық a1Ra2 болса, a2Ra1 да орындалады.

6 слайд
Бинарлық қатынас түрлері (2) Антирефлексивті a1Ra2 болса, a1 ≠ a2. Антисимметриялық a1Ra2 және a2Ra1 болса, a1 = a2. Асимметриялық a1Ra2 болса, a2Ra1 орындалмайды.

6 слайд

Бинарлық қатынас түрлері (2) Антирефлексивті a1Ra2 болса, a1 ≠ a2. Антисимметриялық a1Ra2 және a2Ra1 болса, a1 = a2. Асимметриялық a1Ra2 болса, a2Ra1 орындалмайды.

7 слайд
Бинарлық қатынас түрлері (3) Транзитивті a1Ra2 және a2Ra3 болса, a1Ra3 орындалады. Эквивалентті Транзитивті, рефлексивті және симметриялық қатынас. Квазитәртіпті Транзитивті және рефлексивті қатынас. Тәртіп Транзитивті және антисимметриялық қатынас.

7 слайд

Бинарлық қатынас түрлері (3) Транзитивті a1Ra2 және a2Ra3 болса, a1Ra3 орындалады. Эквивалентті Транзитивті, рефлексивті және симметриялық қатынас. Квазитәртіпті Транзитивті және рефлексивті қатынас. Тәртіп Транзитивті және антисимметриялық қатынас.

8 слайд
N-арлық қатынастар Анықтама N-арлық қатынас - n элементтен тұратын жиындардың бөлігі. Унарлық Бір жатысты қатынас, белгі деп те аталады. Бинарлық Екі жатысты қатынас, екі элементтен тұрады. Тернарлық Үш жатысты қатынас, үш элементтен тұрады.

8 слайд

N-арлық қатынастар Анықтама N-арлық қатынас - n элементтен тұратын жиындардың бөлігі. Унарлық Бір жатысты қатынас, белгі деп те аталады. Бинарлық Екі жатысты қатынас, екі элементтен тұрады. Тернарлық Үш жатысты қатынас, үш элементтен тұрады.

9 слайд
Булеан 1Анықтама Булеан - E жиынының барлық бөліктерінен құралған жиын. 2Белгіленуі Булеан B(E) = 2^E деп белгіленеді. 3Қасиеті M ⊆ N ⇔ M ∩ N = M бинарлық қатынасы B(E) жиынында жатады.

9 слайд

Булеан 1Анықтама Булеан - E жиынының барлық бөліктерінен құралған жиын. 2Белгіленуі Булеан B(E) = 2^E деп белгіленеді. 3Қасиеті M ⊆ N ⇔ M ∩ N = M бинарлық қатынасы B(E) жиынында жатады.

10 слайд
Қатынас мысалдары Теңдік Рефлексивті және симметриялы қатынас. Үлкен/кіші Рефлексивке қарсы және симметрияға қарсы қатынас. Параллельдік Рефлексивті және симметриялы қатынас.

10 слайд

Қатынас мысалдары Теңдік Рефлексивті және симметриялы қатынас. Үлкен/кіші Рефлексивке қарсы және симметрияға қарсы қатынас. Параллельдік Рефлексивті және симметриялы қатынас.