Сандар туралы

1 слайд
№23 Алатау орта мектебі Пәні: Математика Тақырыбы: Сандар туралы

1 слайд

2 слайд
№23 Алатау орта мектебі 8 сынып оқушысы Ахмет Азамат

2 слайд

3 слайд
“Математика – ақыл-ойды тәртіпке келтіретін ғылым” /Ломоносов/ “Математика – ғылымның патшасы”

3 слайд

4 слайд
Жоспар: Кіріспе. Анықтамасы. Тану. 2.1. Жазылуы. 2.2. Оқылуы. 2.3. Шығу тарихы. 2.3.1. Үнді математкиасы. 2.3.2. Мысыр математикасы. 2.3.3. Вавилон математикасы. 2.3.4. Ежелгі грек математикасы. Маңызды түйін. 3.1. Сандарды санау. Мағынасы. 3.2. Сандарды таңбалаудың қазіргі түрі. 3.2.1. Рим цифры. 3.2.2. Араб цифры. 4. Сандарды салыстыру. 4.1. Үлкен. 4.2. Кіші. 4.3. Тең. Түрге айыру. 5.1. Натурал сандар туралы ұғым. 5.1.1. Натурал сандарды жай көбейткіштерге жіктеу. 5.1.2. Санның бөлінгіштік белгілері. 5.2. Бүтін сандар. 5.2.1. Жұп және тақ сандар. 5.2.2. Сандар тізбегі. 5.3. Рационал сандар. 5.3.1. Оң және теріс сандар. 5.3.2. Қарама-қарсы сандар. 5.3.3. Рационал санның модулі. 5.3.4. Рационал сандарды салыстыру.

4 слайд

5 слайд
Кіріспе. • Дүние жүзі халқы ғасырлар бойы сандарды әр ел өз бетінше нөмірлей отырып, күнделікті өмірде пайдалана білді. Сөйтіп, есептеу барысында түрлі қиындықтарға кездесіп, ол сандарды үнемі өзгертіп отырды. • Сандарды пайдалану жер бетіндегі түрлі ұлттар ілгері заманда санның атқаратын қызметін өте жоғары бағалаған. Өйткені олар санды пайдаланбаса, өмір сүрулері қиындады. Себебі, күнделікті тіршілікте сауда да болсын, аңшылық та болсын, тұрмыс та болсын санға өте мұқтаж болған. Дүние жүзі математикасында сандарды пайдалану түрліше болды: біріншісі сандарды таңба, қиғаш жазу арқылы жазса, екіншісі жіпті түю арқылы, ал үшіншісі болса, иероглифтер арқылы жаза білген. Бұл сандарды таңбалау арқылы осы сандардың стандарт түрін ойлап таба білді. •Үндістан ғұламаларының жетістіктерінің арқасында қазіргі күнделікті өмірде пайдаланып жүрген сандарды ойлап тапқан болатын. Сонау шығыстан пайда болған сандарды жаугершілік замандарда, сауда-саттық арқылы бүкіл дүние жүзіне тарай отырып, түрлі халықтар өз математикасын дамытты. Сөйтіп, дүние жүзі бойынша ортақ сан пайда болды. •Дүние жүзі халықтарында математика әлемі әр түрлі деңгейде болған. Олар өз есептерін өздерінше есептеп, үнемі ескіден жаңаға ұмтылу арқылы математикаға өз үлестерін қосты. Орта ғасырларда өмір сүрген Еуропа ғұламалары математикада үлкен жаңалықтар ашып, математика ғылымына енгізді. Дүние жүзінде санды пайдаланудың жылпы екі түрін қалыптастырды. Олардың бірі –Рим цифры болса, екіншісі –араб цифры болып табылады. Осындай үлкен қиыншылықтардың арқасында біз қазір күнделікті өмірдегі сандарды пайдалана аламыз.

5 слайд

6 слайд
Анықтама. •Математикада ең алғаш ұғымдардың бірі ол –сан. Сандар –шындық дүниедегі нақты заттардың таза шамасын, мөлшерін көрсетеді. Мысалы: тоғыз оқушы (9 оқушы), жеті кітап (7 кітап), жүз жылқы (100 жылқы). •2. Тану. –2.1. Жазылуы. •Қазіргі кезде күнделікті қолданылып жүрген сандарды біз былай жазамыз: 0,1,2,3,4,5,6,7,8,9,...,100,...10000,...,10000000... тағы басқа сандар. –2.2. Оқылуы. •Өмірде пайдаланып жүрген сандарды былай оқимыз: 0 (нөл), 1 (бір), 2 (екі), 3 (үш), 4 (төрт), 5 (бес), 6 (алты), 7 (жеті), 8 (сегіз), 9 (тоғыз), 20 (жиырма),... т.б. –2.3. Шығу тарихы. •2.3.1. Үнді математикасы. 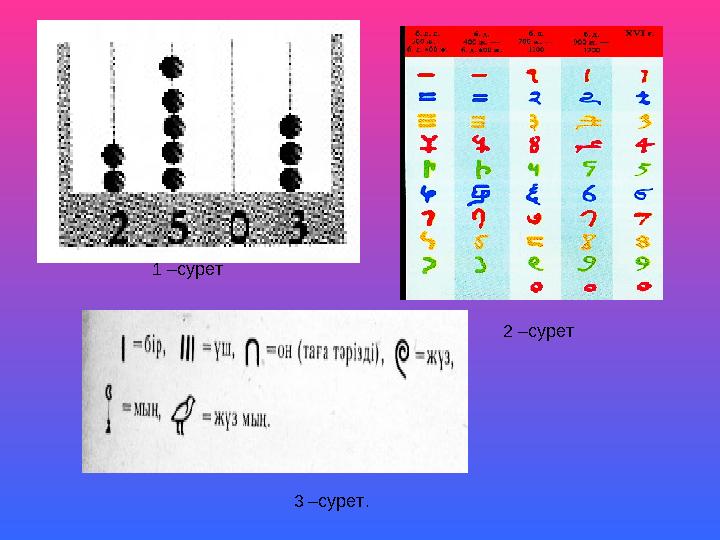• Көне замандарда арифметикалық амалдарды орындаудың ең озық тәсілі шоттарды пайдалану болды.

6 слайд

7 слайд
1 –сурет 2 –сурет 3 –сурет.

7 слайд

8 слайд
Осы шотты үнділер ойлап тапты. Бос қатар үшін таңба қажет болды. Сондықтан олар 0 (нөл) санын ойлап тапты. Басқа есептеу жүйелерінен айырмашылығы –үнділер тек 10 (он) символды ғана пайдаланған, бұл амал жүйені оңайлатқан. Символдар бүкіл әлемге тарай отырып, ғасырлардан ғасырға қарай өзгеріп отырады да, біртіндеп біз пайдаланып жүрген қазіргі заманғы сандарға айналды. Бастапқы кезде санаудың нәтижесі туралы мағлұматтарды ағашта, сүйекте таңба салу арқылы, жіпте түйін түю арқылы сақтап отырған. Жас қасқырдың жілігіндегі жазба (18 см, 55 таңба) соның дәлелі болып табылады. Ол жазба Моравиядан (Чехословакия) 1937 жылы табылған. Үнді жерінде сандарды былай таңбалаған: Мысырда ең алғашқы күнтізбе календары пайда болған. Календарь 12 айдан, 1 ай, 30 күн күн енгізілген. Мысырлықтар сандарды иероглиф арқылы белгілеген. Кейін мысырлықтар иератикалық жазуға көшті.

8 слайд

9 слайд
4 –сурет. 2.3.3. Вавилон математикасы. Вавилон елінде б.э.д. 300 ғасырында қиғаш жазу болған. Вавилондық 60-қа дейінгі барлық сандарды сына тәріздес белгімен белгілеген. 5 –сурет.

9 слайд

10 слайд
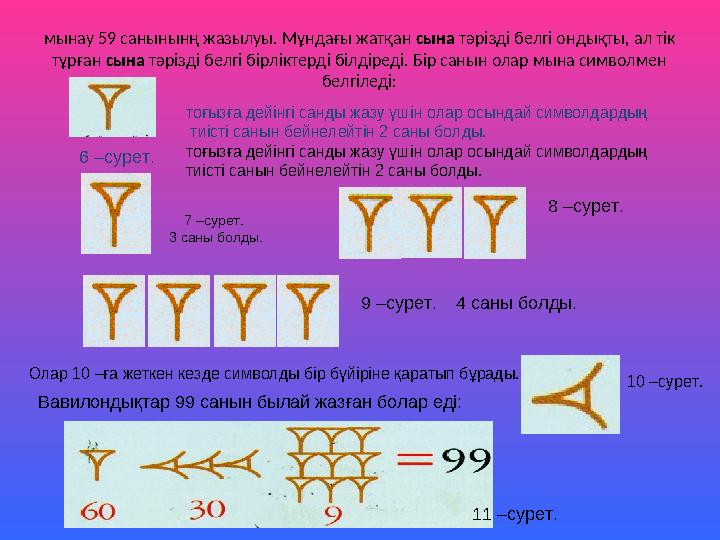
мынау 59 санынынң жазылуы. Мұндағы жатқан сына тәрізді белгі ондықты, ал тік тұрған сына тәрізді белгі бірліктерді білдіреді. Бір санын олар мына символмен белгіледі: тоғызға дейінгі санды жазу үшін олар осындай символдардың тиісті санын бейнелейтін 2 саны болды. тоғызға дейінгі санды жазу үшін олар осындай символдардың тиісті санын бейнелейтін 2 саны болды. 6 –сурет. 7 –сурет. 3 саны болды. 8 –сурет. 9 –сурет. 4 саны болды. Олар 10 –ға жеткен кезде символды бір бүйіріне қаратып бұрады. 10 –сурет. Вавилондықтар 99 санын былай жазған болар еді: 11 –сурет.

10 слайд

11 слайд
Вавилонда алғаш рет позициялық принципке негізделген санау жүйесі пайда болды. Кейін нөл (0) таңбасы қолданыла бастады. Сол жерде алғаш рет квадратты сызықты теңдеулердің алгебрасы жасалды. Кейде жоғары ретті теңдеулер де қарастырылды. Вавилон жерінде шумерлер өмір сүрді. Оларда 60-тық санау жүйесі болған. Б.э.д. 4000 жылы қиғаш жазу хаты сақталған. Б.э.д. Кир (538 жыл), А.Македонский (336 жыл) жылдары Вавилонды жаулап алған болатын. Кейін Македонский өлгеннен кейін Вавилонда Селеркиттер Эллиния елін құрды. Тексттері қыш тақташаларға жазылған. Мысыр, Вавилон елдері (жер шаруашылығымен шұғылданған) математикалық тексттері есептегіш мәселе болды. Мысырға қарағанда Вавилон математикасы есептегіш техникасы жетілген болып, ғылым абстракциялы болды. Нөмірлеу –позициялық сипатта болып есептеуді жеңілдетті. Екі таңба (1 немесе 60), (10 немесе 600) деген сияқты кестелер болды. Олар есептеулерді жеңілдетті. Вавилон математикасы Мысырға қарағанда жоғары деңгейде болды. Бірақ дедуктивті ғылымнан алыс еді. Санау жүйесі позициялық принципте болды. Яғни әріптер арқылы болды. Вавилон алгебрасын дамытқан ұлы тұлғалар: Герон (1- ғасыр), Диофант (3-ғасыр), Аль-Хорезми (IX ғасыр), Виет (XV ғасыр) болатын. 2.3.4. Ежелгі грек математикасы. Ертедегі гректерде ғылым Мысырдан және Вавилоннан ауысқан. Ежелгі Мысыр, Вавилон елдері құлдилаған кездері жаңа халық –гректер пайда болды. Яғни б.э.д. VIII-VII ғасырлар аралығында математикасы баяу дамып, прогресс болған болған жоқ. Бірақ б.э.д. VI ғасырда жағдай күрт абстрактылы –дедуктивті ғылымға айналды. Қатаң дәлелденген ғылым туды. Б.э.д. VI ғасырда гректерді парсылар шабуыл жасады. Бірақ, гректер жеңіске жетіп, орталық қаласы ретінде –Афина қаласын жариялады. Гректер Аттикалық нөмірлеуді қолданды (б.э.д. II ғасыр). Бұл нөмірлеу Рим нөмірлеуіне негізделген аддитивтік принципте болды. Кейін гректер абакты қолданумен байланысты Аттикалық нөмірлеуден әріптік нөмірлеуге ауысты. Гректер сандарды таңбалау үшін цифрлар қолданбай, әріптерді қолданды.

11 слайд

12 слайд
Осы келтірілген 27 таңбаның көмегімен 999-ға дейінгі барлық сандарды кескіндеуге болады. Мыңды белгілеу үшін алдынан үтір қойып бірліктер сияқты белгілейтін болды, мысалы, 13 –сурет. 8432 былай кескінделеді: 14 –сурет. 10 000 былай белгіленетін болды М. Сонда 48523 былай кескінделеді.: 15 –сурет. Грек математикасы өзінің гүлдену дәуіріне геометрия жөнінде Фалес, Пифагор, Евклид, Архимед, Апполоний арифметикасымен алгебра жөнінде Птоломей, механика жөнінде Архимед, Герон еңбектері арқасында жетті деуге болады. 12 –сурет.

12 слайд

13 слайд
3. Маңызды түйін. 3.1. Сандарды санау. Оның мағынасы. Математикалық теорияның бастапқы формасы түрлі халықтарда затты санау нәтижесінде пайда болған. Яғни б.э.д. X-VI ғасырларда. Сол кездері символдар пайда болды. Одан жүйе құрылды. Нөмірлеудің позициялық жүйесі бойынша Түрлі иероглифті логикалық емес жүйе. Алфавитті жүйе (әріп-сан). Ондық емес позициялық жүйе (позициялық жүйе Индияда б.э.500 жылы қолданылған). Санаудың алғашқы қадамы затпен басқа жиын арасында «өзара бірмәнді сәйкестіктен» басталды. Ай, көз, саусақтар -1,2,5 деген сандарды білдіреді. Еуропа, Азия халықтарында санның жалпы ұғымының пайда болуы туралы былай деуге болады: «один» -орысша, «eins»-немісше, «one»-ағылшынша, «un»-французша, «unus»-латынша бір (1) деген мағынаны білдіреді. «два»-орысша, «zwei»-немісше, «two»-ағылшынша екі (2) деген мағынаны білдіреді. «три», «deuh», «duo», «drey», «trous», «tres» деген сөздерден шыққан. Көптеген халықтарда ондық жүйе схема бойынша оның негізінде саусақты есептеу жатыр. Аристотель де солай ұйғарған. Лебег: «Егер адамда 11 саусақ болса, онда 11-лік сандар жүйесі болар еді» -деген болатын. 3.2. Сандарды таңбалаудың қазіргі түрі. Қазіргі таңда сандарды таңбалаудың, яғни жазылуының екі түрі бар. Олар: Рим цифры, Араб цифры түрінде таңбаланады. 3.2.1. Рим цифры. Рим цифрында (1) I, (5) V, (10) X, (50) L, (100) C, (1000) D, (500) M –деген мағынаны білдіреді. Рим цифрымен сандарды бізге жазу оңай болғанымен, есептеу өте қолайсыз болып табылады. Рим цифрын біз көбінесе мына жағдайларда ғана пайдалана аламыз, олар көбінесе: кітап бетін, сағат, тарау, ғасырларды жазу кезінде. Көп жағдайларда бәрімізге мәлім, күнделікті қолданылып жүрген өзіміздің (0,1,2,3,4,5,6,7,8,9,...,1000 т.б.) араб-цифрымен жазамыз. 3.2.2. Араб цифры. Араб цифры: 1,2,3,4,5,6,7,8,9,0 сандары араб цифрлары деп аталады. Яғни бұл сандар дүние жүзінің мәдениетінде кеңінен қолданылып жүрген сандар болып табылады. Үндістер жасаған бұл сандар арабтар арқылы Еуропаға тараған. Сонымен Еуропалықтар бұл сандапрды –үндістер емес, арабтардың цифры деп атап кеткен. Міне, содан бері бұл цифрлар –араб цифры деп аталып кеткен. Араб цифрларын қолданып жүрген екілік, төрттік, сегіздік, ондық жүйеде жазуға болады. Қазіргі таңда дүние жүзінде кеңінен қолданылып жүрген ол –ондық жүйе болып табылады. Яғни кез келген санды ондық жүйеде жазуға болады. Мысалы: натурал сан -9653 –ті разрядтық қосылғыштарға жіктеп көрелік: деп жазамыз.

13 слайд

14 слайд
Сандарды салыстыру. 4.1. Үлкен. Сандарды салыстырудан бұрын өткен ғасырларға көз жүгіртейік. Жалпы «салыстыру» деген ұғым, яғни «үлкен», «кіші» немесе «тең» деген ұғымдар бағзы заманнан келе жатқан дүние. Кез келген зат болсын, мейлі мал, жан-жануар болсын, ғимараттар немесе мемлекеттер болсын тағы басқа осы сияқты дүниелерді ата- бабаларымыз салыстыра білген. Яғни бір заттың көлеміне, мөлшеріне қарап оларды салыстыра білген. Мысалы: Жамбыл деген бай мырзаның 1000 жылқысы болсын, ал, Шыңғыс деген бай мырзаның 2500 жылқысы бар. Демек, екеуінің жылқысын санына қарай салыстырсақ, қай мырзаның жылқысының саны көп, сол адам бай деп есептелген. Демек, Шыңғыс мырза Жамбыл мырзадан бай тұрады деп есептеген. Енді кез келген бір екі санды салыстырып, көрелік. Ол сандар: 7 (жеті) және 9 (тоғыз) сандары болсын. Бұл жерде 9 (тоғыз) саны 7 (жеті) санынан үлкен. Мысалы: Бір қорада 9 тауық, екінші қорада 7 тауық бар деп алайық. Енді бізден сұрайды қай қорада тауық көп деп. Әрине, бірінші қорадағы тауықтар саны екінші қорадаға тауықтар санынан көп деп есептеледі. Енді осы жағдайға көз жеткізу үшін осы берілген сандарды кооординаталық түзу бойына салып көрелік. Мұндағы 7 (жеті) санын А нүктесінің координатасы деп, 9 (тоғыз) санын В нүктесінің координатасы, ал санақ басын 0(нөл) санын О –нүктесінің координатасы деп алайық. Сонда шығады. О А В 1 2 3 4 5 6 7 8 9 16 –сурет. Координаталық түзуден көріп тұрғанымыздай 9 (саны) 7 (санына) қарағанда санақ басы нүктесінен алшақ орналасқан. Демек, санақ басынан қай сан оң бағытта тысқарыда жатса, ол сан үлкен деп есептеледі. болады. Осыдан ұйғаратынымыз: болады. Демек, белгісі болады. Мысалы: Енді 1,6 және 0,9 деген сандарды салыстырып көрелік: Бұл жерде 1,6 (бір бүтін оннан алты) саны 0,9 (нөл бүтін оннан тоғыз) санынан үлкен. Себебі, біз ондық бөлшектерді салыстырғанда ең алдымен, оның бүтініне, кейін ондық, жүздік, мыңдық үлестеріне қарап салыстырамыз.

14 слайд

15 слайд
Бұл сандарды координаталық түзуге кескіндеп көрейік: Бұл жерде санақ басын әдеттегідей О нүктесі етіп аламыз. Берілген екі санның бөлшек бөлігіне қараймыз. Бірлік кесіндіміз 10 бөлікке бөлінген. және деп белгіледік. Көріп тұрғанымыздай нүктесі нүктесінің оң жағында, әрі санақ басынан алшақ жатыр. Сондықтан бұл сан үлкен болады деп ұйғарамыз. Яғни болады. 4.2. Кіші. Сандарды салыстырудың екінші белгісі –ол «кіші» деген ұғым. «Кіші» сөзі «үлкен» сөзіне қарама-қарсы бағытта болады. Мысалы: Кеше ауаның температурасы болған, бүгін ауаның температурасы төмендеп, болды. Термометрдегі сұйық төмендесе, ауа температурасы суитыны белгілі. Демек, бүгін кешегіге қарағанда суығырақ. Сондықтан, « саны санынан кіші» деп есептеледі.

15 слайд

16 слайд
Жазылуы: Мысалы: 100 (жүз) және 1000 (мың) сандарын салыстыратын болсақ, мұнда әрине болады. Себебі, 100 (жүз) саны 1000 (мың) санынан кіші болып табылады. Бұл сандарды да координаталық түзуге белгілейік: 18 –сурет. Мұндағы деп белгілейік. Енді, координаталық түзу бойында жатқан сандардың қайсысы екін...

16 слайд