Шеңберге жүргізілген жанама. Шеңберге жүргізілген жанамалардың қасиеттері.

1 слайд

2 слайд

3 слайд

4 слайд

5 слайд
Шеңбермен бір ғана ортақ нүктесі бар түзу  шеңберге жүргізілген жанама  деп аталады. Ортақ нүкте  жанасу нүктесі  деп аталады. a   түзуі – центрі  O   нүктесіндегі шеңберге жүргізілген жанама,  A  – жанасу нүктесі .

6 слайд
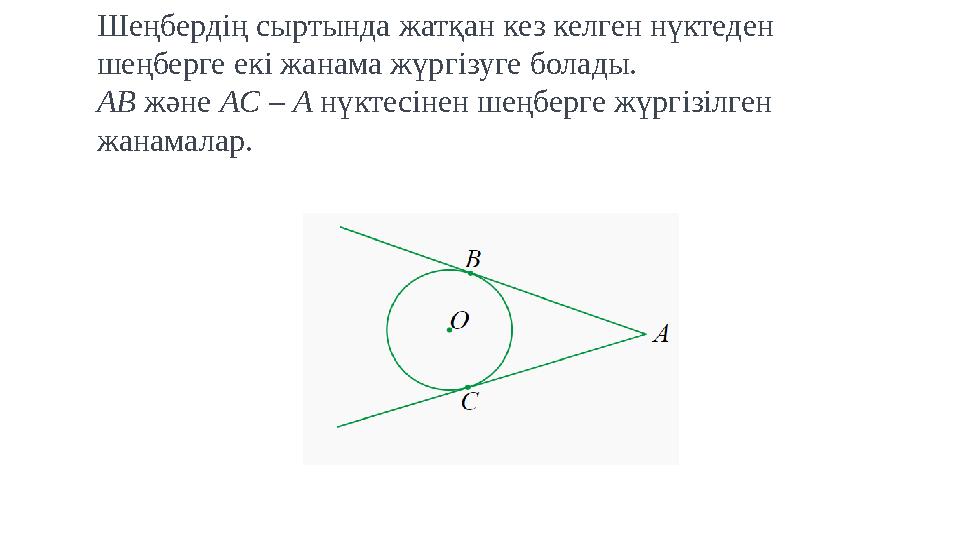
Шеңбердің сыртында жатқан кез келген нүктеден шеңберге екі жанама жүргізуге болады. AB   және  AC  –  A   нүктесінен шеңберге жүргізілген жанамалар.

7 слайд
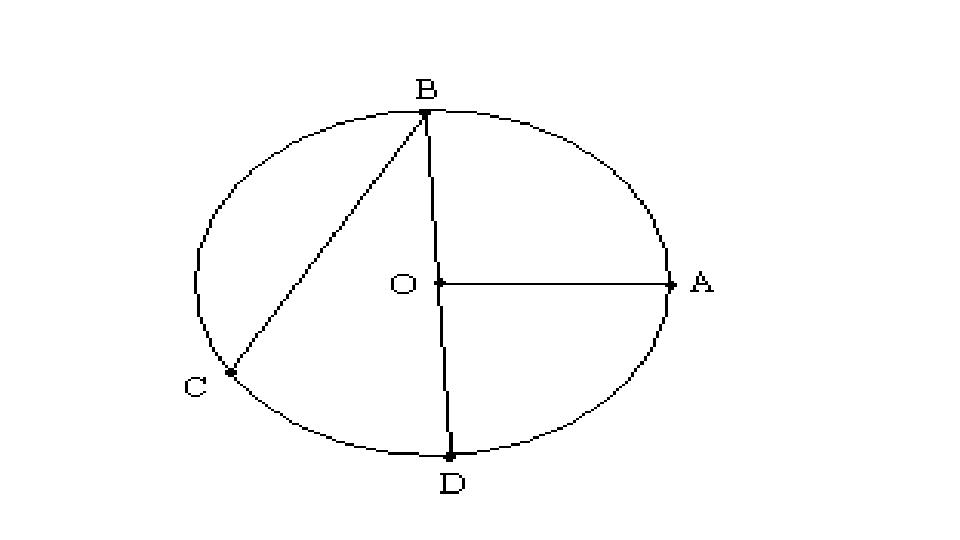
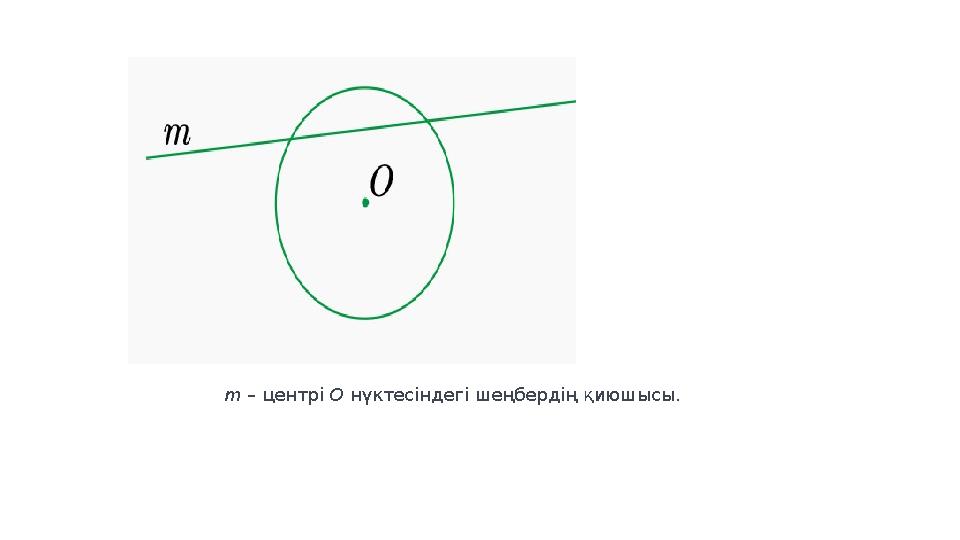
Шеңберді әртүрлі екі нүктеден қиып өтетін түзу  шеңбердің қиюшысы  деп аталады. AB  – центрі  O   нүктесіндегі шеңбердің қиюшысы.

8 слайд
m  – центрі  O   нүктесіндегі шеңбердің қиюшысы.

9 слайд
Теорема.   Шеңбердің жанамасы жанасу нүктесіне жүргізілген радиусқа перпендикуляр . Дәлелдеуі.   A  – жанасу нүктесі,  O  – шеңбер центрі болса, онда  OA  – радиусы. a   түзуі  OA   радиусына перпендикуляр емес болсын. Онда  OA   радиусы –  a   түзуіне көлбеу. Онда  O   нүктесінен  а  түзуіне жүргізілген перпендикуляр  OA   көлбеуінен кіші болады, яғни шеңбер центріне дейінгі арақашықтық радиустан кіші. Ендеше  a   түзуі мен шеңбердің екі ортақ нүктесі болады, бұл шартқа қайшы:  a   түзуі – шеңбермен тек бір ғана ортақ нүктесі бар жанама түзу. Бұдан  a   түзуі  OA - ға перпендикуляр емес деп жоруымыз қайшылыққа әкеледі. Ендеше  a  ⊥  OA . Теорема дәлелденді.

10 слайд
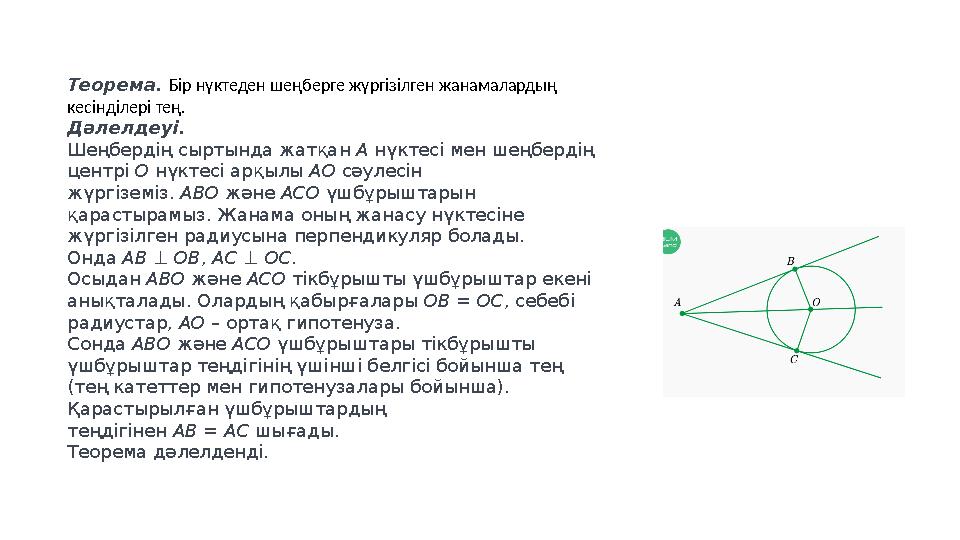
Теорема.   Бір нүктеден шеңберге жүргізілген жанамалардың кесінділері тең. Дәлелдеуі. Шеңбердің сыртында жатқан  A   нүктесі мен шеңбердің центрі  O   нүктесі арқылы  AO   сәулесін жүргіземіз.  ABO   және  ACO   үшбұрыштарын қарастырамыз. Жанама оның жанасу нүктесіне жүргізілген радиусына перпендикуляр болады. Онда  AB  ⊥  OB ,  AC  ⊥  OC . Осыдан  ABO   және  ACO   тікбұрышты үшбұрыштар екені анықталады. Олардың қабырғалары  OB  =  OC , себебі радиустар,  AO  – ортақ гипотенуза. Сонда  ABO   және  ACO   үшбұрыштары тікбұрышты үшбұрыштар теңдігінің үшінші белгісі бойынша тең (тең катеттер мен гипотенузалары бойынша). Қарастырылған үшбұрыштардың теңдігінен  AB  =  AC   шығады. Теорема дәлелденді.

11 слайд

12 слайд

13 слайд

14 слайд

15 слайд

16 слайд

17 слайд

18 слайд

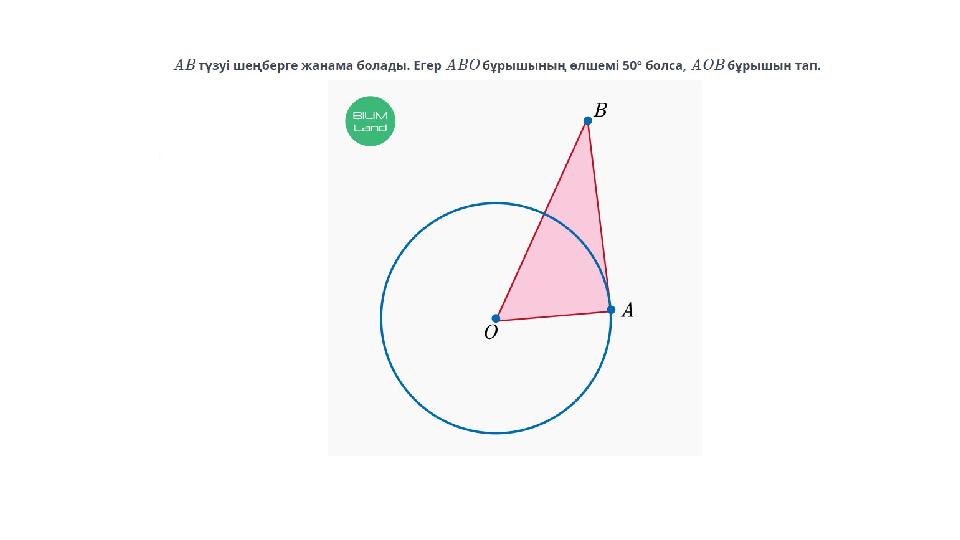
19 слайд

20 слайд

21 слайд
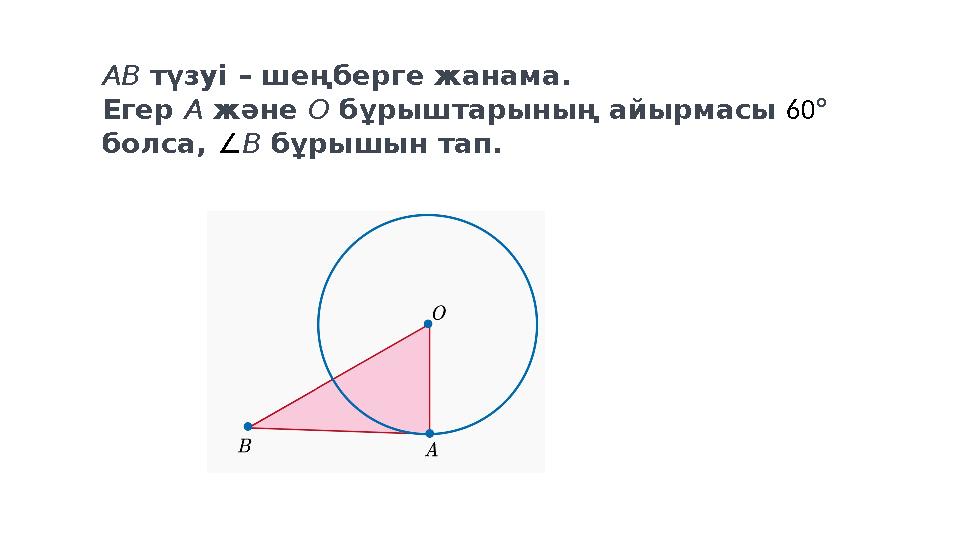
AB   түзуі – шеңберге жанама. Егер  A   және  O   бұрыштарының айырмасы  60 ° болса,  ∠ B   бұрышын тап.

22 слайд

23 слайд