Скалярное произведение векторов
Скалярное произведение векторов


#1 слайд
Преподаватель математики ОГАПОУ
«Белгородский техникум промышленности
и сферы услуг»
1 слайд
Преподаватель математики ОГАПОУ «Белгородский техникум промышленности и сферы услуг»

#2 слайд
Цели урока:
•
Ввести понятия угла между
векторами и скалярного произведения
векторов.
•
Рассмотреть формулу
скалярного произведения в координатах.
•
Показать применение скалярного произведения
векторов при решении задач.
2 слайд
Цели урока: • Ввести понятия угла между векторами и скалярного произведения векторов. • Рассмотреть формулу скалярного произведения в координатах. • Показать применение скалярного произведения векторов при решении задач.
#3 слайд
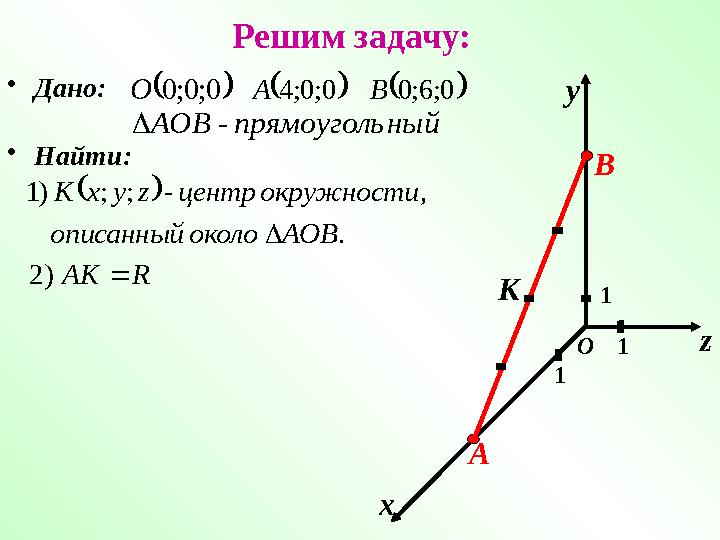
Решим задачу:
•
Дано: 0; 0; 0 О 0; 0; 4 А 0; 6; 0 В
ный прямоуголь АОВ -
х у
z
1 1
1О•
Найти:
А В
.
, - ; ; ) 1
АОВ около описанный
окружности центр z у х К
К
R АК ) 2
3 слайд
Решим задачу: • Дано: 0; 0; 0 О 0; 0; 4 А 0; 6; 0 В ный прямоуголь АОВ - х у z 1 1 1О• Найти: А В . , - ; ; ) 1 АОВ около описанный окружности центр z у х К К R АК ) 2
#4 слайд
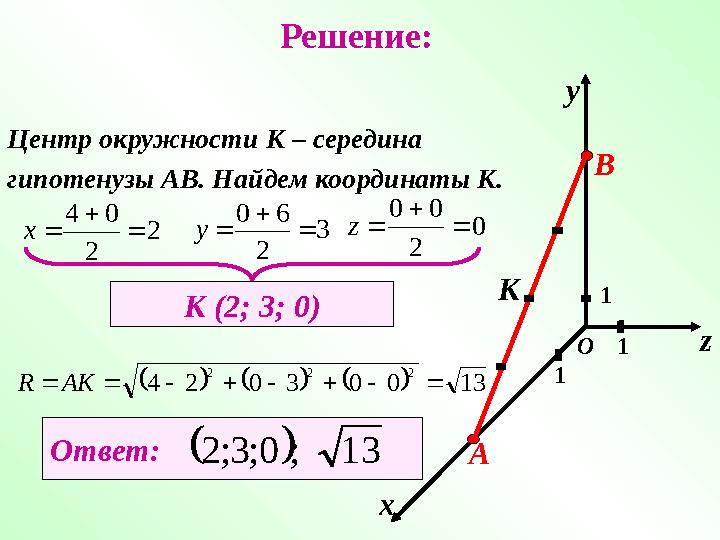
Решение:
х у
z
1 1
1О
А В
КЦентр окружности К – середина
гипотенузы АВ. Найдем координаты К.2
2
0 4
х 3
2
6 0
у 0
2
0 0
z
К (2; 3; 0)
13 0 0 3 0 2 4
2 2 2
АК R
Ответ:
13 ; 0 ; 3 ; 2
4 слайд
Решение: х у z 1 1 1О А В КЦентр окружности К – середина гипотенузы АВ. Найдем координаты К.2 2 0 4 х 3 2 6 0 у 0 2 0 0 z К (2; 3; 0) 13 0 0 3 0 2 4 2 2 2 АК R Ответ: 13 ; 0 ; 3 ; 2

#5 слайд
Вспомним:
•
Какие векторы называются равными?а
b
b а b a если b a ; ,
•
Как найти длину вектора по координатам его
начала и конца?
А В
2 2
А В А В у у х х АВ
•
Какие векторы называются коллинеарными?
или
b а b а
b а
2 1
2 1
2 1
z z
y y
x x
а
b
5 слайд
Вспомним: • Какие векторы называются равными?а b b а b a если b a ; , • Как найти длину вектора по координатам его начала и конца? А В 2 2 А В А В у у х х АВ • Какие векторы называются коллинеарными? или b а b а b а 2 1 2 1 2 1 z z y y x x а b

#6 слайд
Устно:
1) Дано: 4; 2 ; 3 А 2; 3; 4 В
Найти:
АВ
2) Дано:
1; 3 ; 2 А 0; 5 ; 4 В 4 ; 0; 5 С 3 ; 2 ; 7 D
Равны ли векторы и ?
АВ CD
1 ; 2 ; 2 АВ 1; 2 ; 2 CD
3) Дано:
4; 3 ; 1 А
2 ; 1; 5 В
1; 0; 2 С
2; 2 ; 4 D
Коллинеарны ли векторы и ?
АВ CD
6 ; 4; 8 АВ 1; 2 ; 2 CD Ответ:
30
Ответ: Нет, т.к.равные векторы имеют равные координаты.
Ответ: Нет
6 слайд
Устно: 1) Дано: 4; 2 ; 3 А 2; 3; 4 В Найти: АВ 2) Дано: 1; 3 ; 2 А 0; 5 ; 4 В 4 ; 0; 5 С 3 ; 2 ; 7 D Равны ли векторы и ? АВ CD 1 ; 2 ; 2 АВ 1; 2 ; 2 CD 3) Дано: 4; 3 ; 1 А 2 ; 1; 5 В 1; 0; 2 С 2; 2 ; 4 D Коллинеарны ли векторы и ? АВ CD 6 ; 4; 8 АВ 1; 2 ; 2 CD Ответ: 30 Ответ: Нет, т.к.равные векторы имеют равные координаты. Ответ: Нет

#7 слайд
Угол между векторами.
b a
0
0
b а
0
180
b a
а
b
О А
В α
а ОА b ОВ
0
90
b a Если то
, b а
Если то
b а Если то
b а
7 слайд
Угол между векторами. b a 0 0 b а 0 180 b a а b О А В α а ОА b ОВ 0 90 b a Если то , b а Если то b а Если то b а
#8 слайд
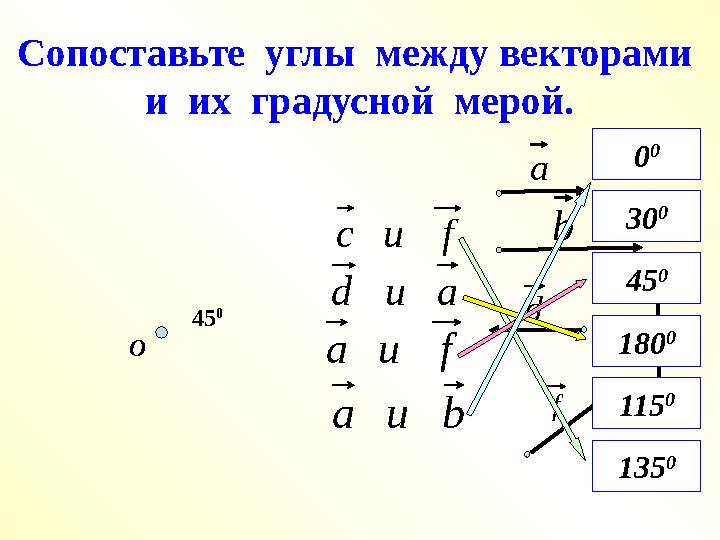
Сопоставьте углы между векторами
и их градусной мерой.а
b
с
d
f
О 45 0
f и c
a и d
f и a
b и a
135 045 0
180 00 0
30 0
115 0
8 слайд
Сопоставьте углы между векторами и их градусной мерой.а b с d f О 45 0 f и c a и d f и a b и a 135 045 0 180 00 0 30 0 115 0
#9 слайд
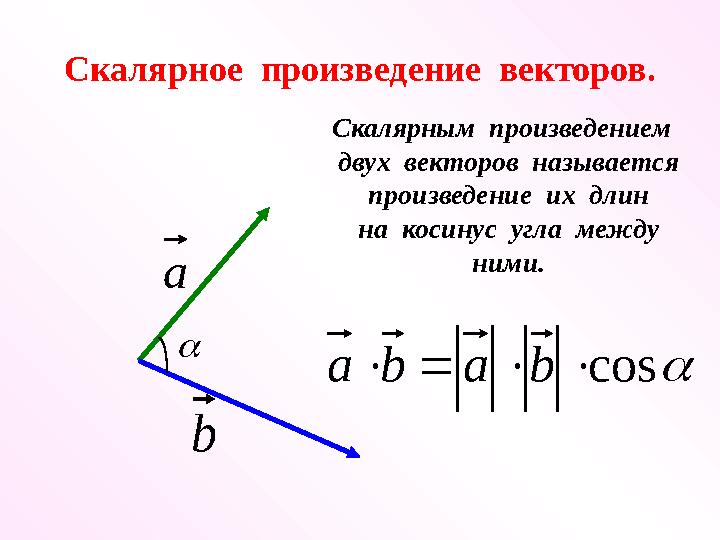
Скалярное произведение векторов.b
а
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
cos b a b a
9 слайд
Скалярное произведение векторов.b а Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. cos b a b a

#10 слайд
Если , то b a 0 90 cos
0
0 b a
Если
b а , то
1 180 cos
0
b a b a
Если b a , то
1 0 cos
0
b a b a
Если
b a , то
2 2
a a a a a a b a
cos b a b aВспомним планиметрию…
10 слайд
Если , то b a 0 90 cos 0 0 b a Если b а , то 1 180 cos 0 b a b a Если b a , то 1 0 cos 0 b a b a Если b a , то 2 2 a a a a a a b a cos b a b aВспомним планиметрию…
#11 слайд
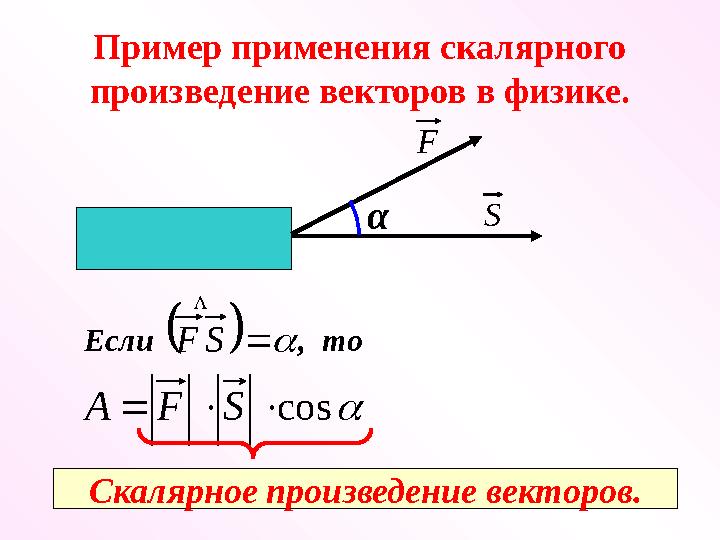
Пример применения скалярного
произведение векторов в физике.S
F
α
Если , то
S F
cos S F A
Скалярное произведение векторов.
11 слайд
Пример применения скалярного произведение векторов в физике.S F α Если , то S F cos S F A Скалярное произведение векторов.

#12 слайд
Формула скалярного произведения
векторов в пространстве.
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов. 1 1 1 ; ; z y x а 2 2 2 ; ; z y x b
2 1 2 1 2 1 z z y y x x b a
12 слайд
Формула скалярного произведения векторов в пространстве. Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов. 1 1 1 ; ; z y x а 2 2 2 ; ; z y x b 2 1 2 1 2 1 z z y y x x b a
#13 слайд
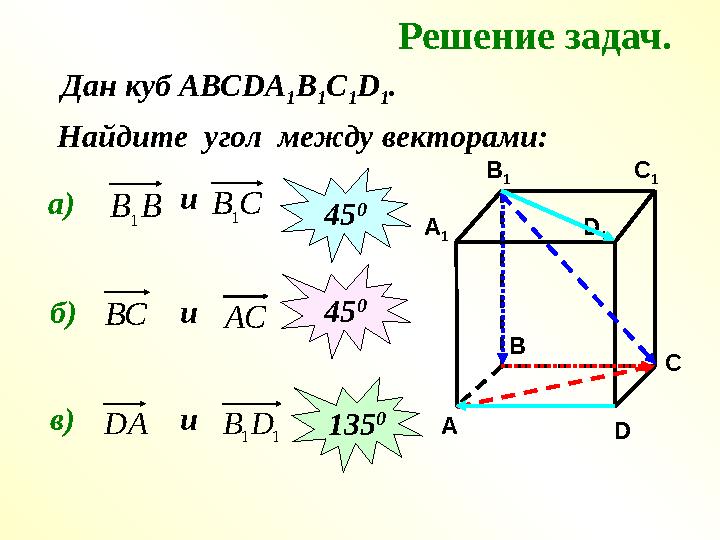
Решение задач.
Найдите угол между векторами:
CC
1
A
1 B
1
D
1
A B
Dа)В В 1
С В 1 и
45 0
б)
ВС АС и 45 0
в) Дан куб АВС DA
1 B
1 C
1 D
1 .
DA 1 1D B
и
135 0
13 слайд
Решение задач. Найдите угол между векторами: CC 1 A 1 B 1 D 1 A B Dа)В В 1 С В 1 и 45 0 б) ВС АС и 45 0 в) Дан куб АВС DA 1 B 1 C 1 D 1 . DA 1 1D B и 135 0
#14 слайд
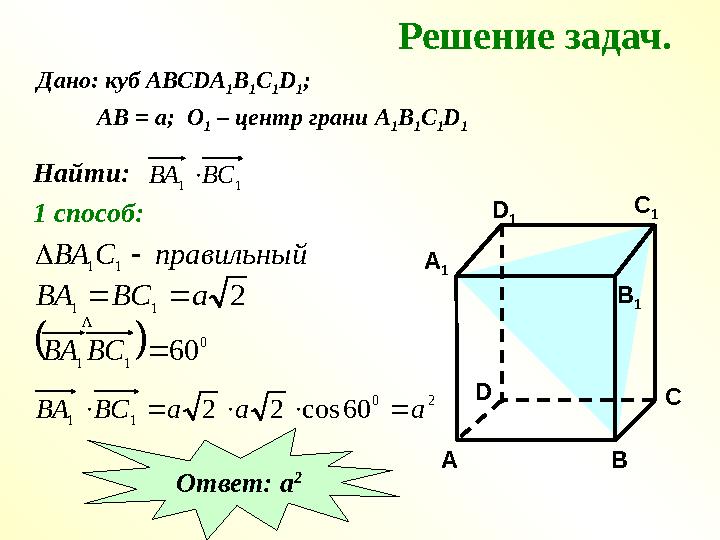
Дано: куб АВС DA
1 B
1 C
1 D
1 ;
АВ = а; О
1 – центр грани А
1 В
1 С
1 D
1
Найти:1 1 ВС ВА
1 способ:
CC
1
A
1
B
1D
1
A BD
правильный С ВА 1 1
2 1 1 а ВС ВА
0
1 1 60
ВС ВА
2 0
1 1 60 cos 2 2 а а а ВС ВА
Ответ: а 2 Решение задач.
14 слайд
Дано: куб АВС DA 1 B 1 C 1 D 1 ; АВ = а; О 1 – центр грани А 1 В 1 С 1 D 1 Найти:1 1 ВС ВА 1 способ: CC 1 A 1 B 1D 1 A BD правильный С ВА 1 1 2 1 1 а ВС ВА 0 1 1 60 ВС ВА 2 0 1 1 60 cos 2 2 а а а ВС ВА Ответ: а 2 Решение задач.
#15 слайд
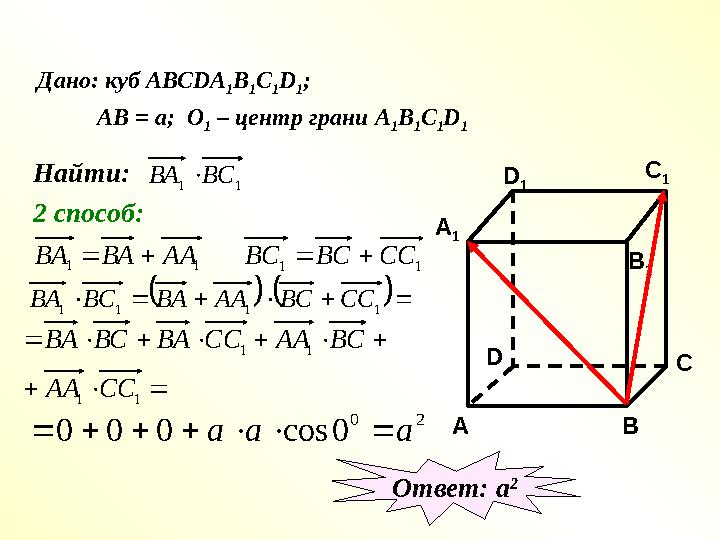
Дано: куб АВС DA
1 B
1 C
1 D
1 ;
АВ = а; О
1 – центр грани А
1 В
1 С
1 D
1
Найти:1 1 ВС ВА
2 способ:
CC
1
A
1
B
1D
1
A BD
1 1 СС ВС ВС 1 1 АА ВА ВА
1 1 1 1 СС ВС АА ВА ВС ВА
1 1
1 1
СС АА
ВС АА СС ВА ВС ВА
2 0
0 cos 0 0 0 a а а
Ответ: а 2
15 слайд
Дано: куб АВС DA 1 B 1 C 1 D 1 ; АВ = а; О 1 – центр грани А 1 В 1 С 1 D 1 Найти:1 1 ВС ВА 2 способ: CC 1 A 1 B 1D 1 A BD 1 1 СС ВС ВС 1 1 АА ВА ВА 1 1 1 1 СС ВС АА ВА ВС ВА 1 1 1 1 СС АА ВС АА СС ВА ВС ВА 2 0 0 cos 0 0 0 a а а Ответ: а 2
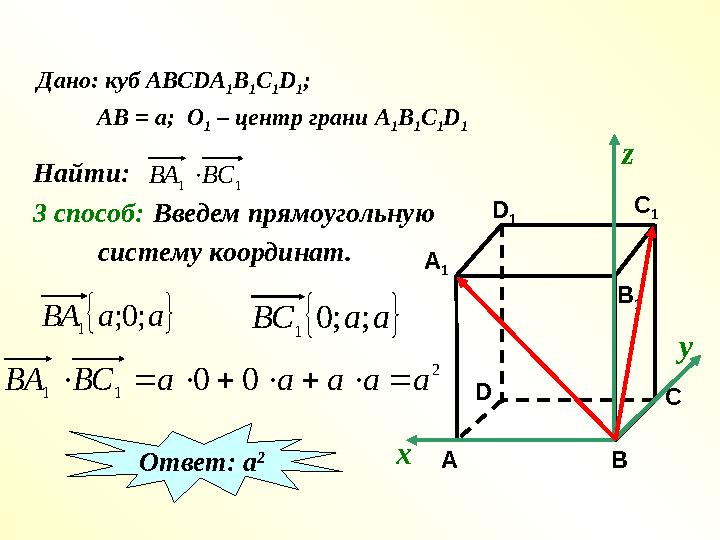
#16 слайд
Дано: куб АВС DA
1 B
1 C
1 D
1 ;
АВ = а; О
1 – центр грани А
1 В
1 С
1 D
1
Найти:1 1 ВС ВА
3 способ:
CC
1
A
1
B
1D
1
A BD Введем прямоугольную
систему координат.
х уz
а а ВС ; ; 0 1
а а ВА ; 0; 1
2
1 1 0 0 а а а а а ВС ВА
Ответ: а 2
16 слайд
Дано: куб АВС DA 1 B 1 C 1 D 1 ; АВ = а; О 1 – центр грани А 1 В 1 С 1 D 1 Найти:1 1 ВС ВА 3 способ: CC 1 A 1 B 1D 1 A BD Введем прямоугольную систему координат. х уz а а ВС ; ; 0 1 а а ВА ; 0; 1 2 1 1 0 0 а а а а а ВС ВА Ответ: а 2

#17 слайд
Решаем по группам:
Дополнительная задача:Вычислите угол
между вектором а
и координатным
вектором i. 2; 1; 2 а
Докажите, что четырехугольник ABCD –
квадрат, если вершины имеют координаты
A (-3;5;6), B (1;-5;7), C (8;-3;-1), D (4;7;-2).Вычислите угол
между вектором а
и координатным
вектором k. 1; 2; 2 а
+
1 ; 0 ; 0
0 ; 0 ; 1
k
iОтвет: а rccos(2/3)
Ответ: а rccos(1/3)
17 слайд
Решаем по группам: Дополнительная задача:Вычислите угол между вектором а и координатным вектором i. 2; 1; 2 а Докажите, что четырехугольник ABCD – квадрат, если вершины имеют координаты A (-3;5;6), B (1;-5;7), C (8;-3;-1), D (4;7;-2).Вычислите угол между вектором а и координатным вектором k. 1; 2; 2 а + 1 ; 0 ; 0 0 ; 0 ; 1 k iОтвет: а rccos(2/3) Ответ: а rccos(1/3)

#18 слайд
Дома : вывести формулу
М.И. Башмаков «Математика. Задачник»,
стр. 115 , № 5.51.2
2
2
2
2
2
2
1
2
1
2
1
2 1 2 1 2 1
cos
z y x z y x
z z y y x x
+
18 слайд
Дома : вывести формулу М.И. Башмаков «Математика. Задачник», стр. 115 , № 5.51.2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 cos z y x z y x z z y y x x +

#19 слайд
19 слайд

шағым қалдыра аласыз
















