ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Төртбұрыштар және көпбұрыштарға байланысты есептер шығару, 8 сынып
25 Қараша 2020
876
0 рет жүктелгенберіледі
Дипломдар мен сертификаттарды алып үлгеріңіз!
сертификат алыңыз!
1 слайд
Төртбұрыштар және
шеңберлер
1 слайд
Төртбұрыштар және шеңберлер
2 слайд
Презентация мазмұны
Төртбұрыштар, көпбұрыштар
Төртбұрыш түрлері. Олардың белгілері және қасиеттері.
Төртбұрыштар тақырыбына орай мысал есептер
Шеңбер, дөңгелек, хорда, қиюшы, сегмент, сектор.
Шеңберлер тақырыбына орай мысал есептер
2 слайд
Презентация мазмұны Төртбұрыштар, көпбұрыштар Төртбұрыш түрлері. Олардың белгілері және қасиеттері. Төртбұрыштар тақырыбына орай мысал есептер Шеңбер, дөңгелек, хорда, қиюшы, сегмент, сектор. Шеңберлер тақырыбына орай мысал есептер
3 слайд
Төртбұрыштар және
көпбұрыштар
3 слайд
Төртбұрыштар және көпбұрыштар
4 слайд
Төртбұрыштар. Көпбұрыштар.
Әрбір үшеуі бір түзуде жатпайтын төрт нүктені тізбектей қосатын
қиылыспайтын төрт кесіндіден және сол кесінділермен шектелген
жазықтықтың бөлігінен тұратын фигура төртбұрыш деп аталады.
Қарама-қарсы қабырғалары қос-қостан параллель болатын төртбұрыш
параллелограмм деп аталады.
Барлық бұрыштары тік болатын параллелограмм тіктөртбұрыш деп
аталады.
Барлық қабырғалары тең болатын параллелограмм ромб деп аталады.
Барлық қабырғалары тең тіктөртбұрыш квадрат (шаршы) деп аталады.
Екі қабырғасы ғана параллель болатын дөңес төртбұрыш трапеция деп
аталады.
4 слайд
Төртбұрыштар. Көпбұрыштар. Әрбір үшеуі бір түзуде жатпайтын төрт нүктені тізбектей қосатын қиылыспайтын төрт кесіндіден және сол кесінділермен шектелген жазықтықтың бөлігінен тұратын фигура төртбұрыш деп аталады. Қарама-қарсы қабырғалары қос-қостан параллель болатын төртбұрыш параллелограмм деп аталады. Барлық бұрыштары тік болатын параллелограмм тіктөртбұрыш деп аталады. Барлық қабырғалары тең болатын параллелограмм ромб деп аталады. Барлық қабырғалары тең тіктөртбұрыш квадрат (шаршы) деп аталады. Екі қабырғасы ғана параллель болатын дөңес төртбұрыш трапеция деп аталады.
5 слайд
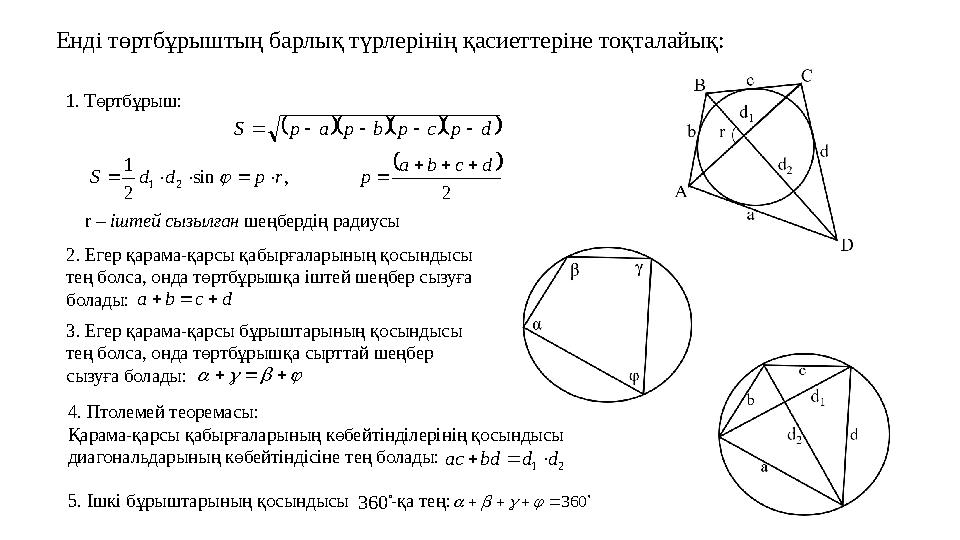
1. Төртбұрыш: d p c p b p a p S
2
, sin
2
1
2 1
d c b a
p r p d d S
r – іштей сызылған шеңбердің радиусы
2. Егер қарама-қарсы қабырғаларының қосындысы
тең болса, онда төртбұрышқа іштей шеңбер сызуға
болады:
d c b a
3. Егер қарама-қарсы бұрыштарының қосындысы
тең болса, онда төртбұрышқа сырттай шеңбер
сызуға болады:
4. Птолемей теоремасы:
Қарама-қарсы қабырғаларының көбейтінділерінің қосындысы
диагональдарының көбейтіндісіне тең болады:
2 1 d d bd ac
360 360
5. Ішкі бұрыштарының қосындысы -қа тең: Енді төртбұрыштың барлық түрлерінің қасиеттеріне тоқталайық:
5 слайд
1. Төртбұрыш: d p c p b p a p S 2 , sin 2 1 2 1 d c b a p r p d d S r – іштей сызылған шеңбердің радиусы 2. Егер қарама-қарсы қабырғаларының қосындысы тең болса, онда төртбұрышқа іштей шеңбер сызуға болады: d c b a 3. Егер қарама-қарсы бұрыштарының қосындысы тең болса, онда төртбұрышқа сырттай шеңбер сызуға болады: 4. Птолемей теоремасы: Қарама-қарсы қабырғаларының көбейтінділерінің қосындысы диагональдарының көбейтіндісіне тең болады: 2 1 d d bd ac 360 360 5. Ішкі бұрыштарының қосындысы -қа тең: Енді төртбұрыштың барлық түрлерінің қасиеттеріне тоқталайық:
6 слайд
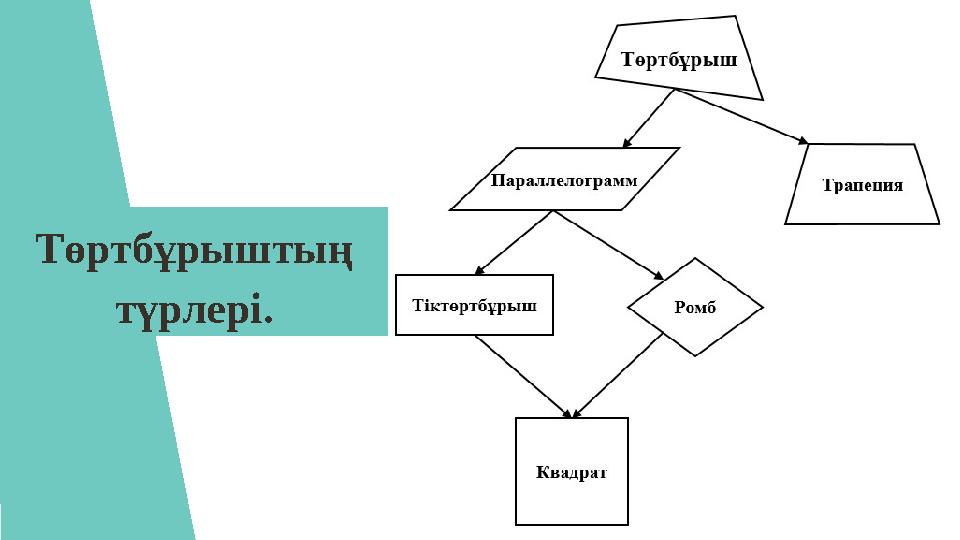
Төртбұрыштың
түрлері.
6 слайд
Төртбұрыштың түрлері.
7 слайд
Параллелограмм.d b c da b c a || , || ,
180 180
2 2 2
2
2
1 2 2 b а d d
AOD COD BOC AOB S S S S
2
sin , sin , 2 1 d d S ab S bh ah S b a
Белгілері және қасиеттері:
1) Қарама-қарсы қабырғалары тең және параллель:
2) Қарама-қарсы бұрыштары қос-қостан тең.
3) Кез-келген қабырғасына іргелес жатқан бұрыштарының қосындысы
-қа тең:
4) Диагональдары қиылысу нүктесінде қақ бөлінеді.
5) Диагональдарының квадраттарының қосындысы оның барлық
қабырғаларының квадраттарының қосындысына тең:
6) Әрбір диагоналы төртбұрышты екі тең үшбұрышқа бөледі:
7) O – диагоналдарының қиылысу нүктесі симметрия центрі болып табылады.
8) Ауданы:
9) Кез келген төртбұрыштың жатқан қабырғаларының ортасын кесінділермен қосатын болсақ, онда
параллелограмм шығады.
7 слайд
Параллелограмм.d b c da b c a || , || , 180 180 2 2 2 2 2 1 2 2 b а d d AOD COD BOC AOB S S S S 2 sin , sin , 2 1 d d S ab S bh ah S b a Белгілері және қасиеттері: 1) Қарама-қарсы қабырғалары тең және параллель: 2) Қарама-қарсы бұрыштары қос-қостан тең. 3) Кез-келген қабырғасына іргелес жатқан бұрыштарының қосындысы -қа тең: 4) Диагональдары қиылысу нүктесінде қақ бөлінеді. 5) Диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең: 6) Әрбір диагоналы төртбұрышты екі тең үшбұрышқа бөледі: 7) O – диагоналдарының қиылысу нүктесі симметрия центрі болып табылады. 8) Ауданы: 9) Кез келген төртбұрыштың жатқан қабырғаларының ортасын кесінділермен қосатын болсақ, онда параллелограмм шығады.
8 слайд
Тіктөртбұрыш2 2 ;
2
b a d
d
R
2
sin2 d
ab S
Белгілері және қасиеттері:
1) Тіктөртбұрыш параллелограмға жататындықтан, ол үшін параллелограмның
барлық қасиеттері орындалады.
2) Диагоналары тең.
3) Қарама-қарсы қабырғаларының орталары арқылы жүргізілген перпендикулярлар
оның симметрия осі болып табылады.
4) Кез келген тіктөртбұрышқа сырттай шеңбер сызуға болады:
5) Ауданы:
7) Кез келген тіктөртбұрыштың көршілес қабырғаларының ортасын кесінділермен
қоссақ – тіктөртбұрыш шығады.
8) Кез келген ромбының көршілес жатқан қабырғаларының ортасын кесінділермен
қоссақ – тіктөртбұрыш шығады.
8 слайд
Тіктөртбұрыш2 2 ; 2 b a d d R 2 sin2 d ab S Белгілері және қасиеттері: 1) Тіктөртбұрыш параллелограмға жататындықтан, ол үшін параллелограмның барлық қасиеттері орындалады. 2) Диагоналары тең. 3) Қарама-қарсы қабырғаларының орталары арқылы жүргізілген перпендикулярлар оның симметрия осі болып табылады. 4) Кез келген тіктөртбұрышқа сырттай шеңбер сызуға болады: 5) Ауданы: 7) Кез келген тіктөртбұрыштың көршілес қабырғаларының ортасын кесінділермен қоссақ – тіктөртбұрыш шығады. 8) Кез келген ромбының көршілес жатқан қабырғаларының ортасын кесінділермен қоссақ – тіктөртбұрыш шығады.
9 слайд
РОМБAB AH r AB BH d AB AH d , 2 , 2 2 1
2
, sin 2 2 1 2 d d
S a ar ah S a
Белгілері және қасиеттері:
1) Ромб параллелограмға жатады, сондықтан параллелограмның барлық
қасиеттері ол үшін жатады.
2) Барлық қабырғалары тең.
3) Екі диагоналы да бұрыштарының биссектрисасы болып табылады.
4) Диагоналдарын қамтитын түзулер оның симметрия осі болып табылады.
5) Кез келген ромбыға іштей шеңбер сызуға болады:
6) Диагональдары өзара перпендикуляр.
7) Ромбының ауданы:
9 слайд
РОМБAB AH r AB BH d AB AH d , 2 , 2 2 1 2 , sin 2 2 1 2 d d S a ar ah S a Белгілері және қасиеттері: 1) Ромб параллелограмға жатады, сондықтан параллелограмның барлық қасиеттері ол үшін жатады. 2) Барлық қабырғалары тең. 3) Екі диагоналы да бұрыштарының биссектрисасы болып табылады. 4) Диагоналдарын қамтитын түзулер оның симметрия осі болып табылады. 5) Кез келген ромбыға іштей шеңбер сызуға болады: 6) Диагональдары өзара перпендикуляр. 7) Ромбының ауданы:
10 слайд
КВАДРАТ
.
2
2
2
;
2
a d
R
a
r
.
2
2
2 d
a S
Белгілері және қасиеттері:
1) Квадрат әрі тіктөртбұрышқа, әрі ромбыға жататындықтан ол
үшін тіктөртбұрыштың да, ромбының да қасиеттері орындалады.
2) Квадраттың 4 симметрия осі бар: қабырғаларына , немесе
олардың орталары арқылы өтетін түзулер, диагональдарын
қамтитын түзулер.
3) Квадратқа іштей де, сырттай да сызуға болады:
4) Квадраттың ауданы:
10 слайд
КВАДРАТ . 2 2 2 ; 2 a d R a r . 2 2 2 d a S Белгілері және қасиеттері: 1) Квадрат әрі тіктөртбұрышқа, әрі ромбыға жататындықтан ол үшін тіктөртбұрыштың да, ромбының да қасиеттері орындалады. 2) Квадраттың 4 симметрия осі бар: қабырғаларына , немесе олардың орталары арқылы өтетін түзулер, диагональдарын қамтитын түзулер. 3) Квадратқа іштей де, сырттай да сызуға болады: 4) Квадраттың ауданы:
11 слайд
ТРАПЕЦИЯb а ||
2
b a
MN
180 v
BC
AD
k AOD BOC S S COD AOB , ~ ,
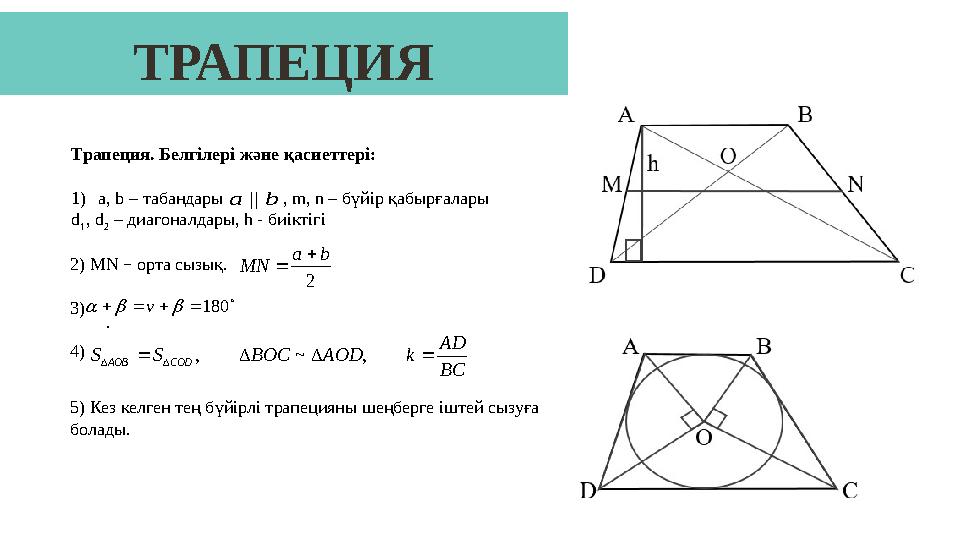
Трапеция . Белгілері және қасиеттері:
1) a, b – табандары , m, n – бүйір қабырғалары
d
1 , d
2 – диагоналдары, h - биіктігі
2) MN – орта сызық.
3)
4) .
5) Кез келген тең бүйірлі трапецияны шеңберге іштей сызуға
болады.
11 слайд
ТРАПЕЦИЯb а || 2 b a MN 180 v BC AD k AOD BOC S S COD AOB , ~ , Трапеция . Белгілері және қасиеттері: 1) a, b – табандары , m, n – бүйір қабырғалары d 1 , d 2 – диагоналдары, h - биіктігі 2) MN – орта сызық. 3) 4) . 5) Кез келген тең бүйірлі трапецияны шеңберге іштей сызуға болады.
12 слайд
2
h S
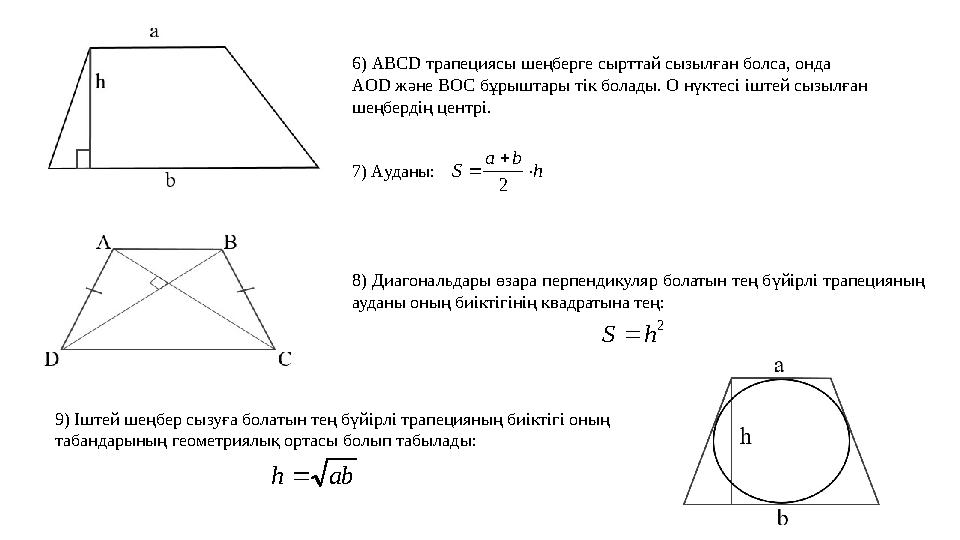
ab h 8) Диагональдары өзара перпендикуляр болатын тең бүйірлі трапецияның
ауданы оның биіктігінің квадратына тең:
9) Іштей шеңбер сызуға болатын тең бүйірлі трапецияның биіктігі оның
табандарының геометриялық ортасы болып табылады :
h
b a
S
26) ABCD трапециясы шеңберге сырттай сызылған болса , онда
A О D және ВОС бұрыштары тік болады . О нүктесі іштей сызылған
шеңбердің центрі.
7) Ауданы:
12 слайд
2 h S ab h 8) Диагональдары өзара перпендикуляр болатын тең бүйірлі трапецияның ауданы оның биіктігінің квадратына тең: 9) Іштей шеңбер сызуға болатын тең бүйірлі трапецияның биіктігі оның табандарының геометриялық ортасы болып табылады : h b a S 26) ABCD трапециясы шеңберге сырттай сызылған болса , онда A О D және ВОС бұрыштары тік болады . О нүктесі іштей сызылған шеңбердің центрі. 7) Ауданы:
13 слайд
ФАЛЕС теоремасы
Егер бұрыштың қабырғаларын қиятын параллель
түзулер бір қабырғасында бір - біріне тең кесінділер қиса , онда
олар екінші қабырғасынанда бір - біріне тең кесінділер қияды .
Сырттай сызылған көпбұрыш
Р – жарты периметр ,
r – іштей сызылған шеңбердің радиусы r p S
13 слайд
ФАЛЕС теоремасы Егер бұрыштың қабырғаларын қиятын параллель түзулер бір қабырғасында бір - біріне тең кесінділер қиса , онда олар екінші қабырғасынанда бір - біріне тең кесінділер қияды . Сырттай сызылған көпбұрыш Р – жарты периметр , r – іштей сызылған шеңбердің радиусы r p S
14 слайд
Дұрыс көпбұрышn a
3
2
, 2 , 3 2
,2 ,3
6 4 3
6 4 3
r
a r a r a
R a R a R a
.
180 2
,
180 sin2
n
tg
a
r
n
a
R n n
. 360 sin
2
1 180
180 sin2
2 2
2
n
n R
n
tg n r
n
n a R n
2 180 n
360
3 n d
Белгілері және қасиеттері:
1) – дұрыс n – бұрыштың қабырғасы, R – сырттай, r – іштей сызылған шеңбердің
радиустары, S – оның ауданы:
2)
3)
4) n – бұрыштың ішкі бұрыштарының қосындысы:
5) n – бұрыштың сыртқы бұрыштарының қосындысы:
6) n – бұрыштың бі р төбесінен шығатын диагональдарының саны:
7) n – бұрыштың диагональдарының саны:
2
)3 (
n n
N
14 слайд
Дұрыс көпбұрышn a 3 2 , 2 , 3 2 ,2 ,3 6 4 3 6 4 3 r a r a r a R a R a R a . 180 2 , 180 sin2 n tg a r n a R n n . 360 sin 2 1 180 180 sin2 2 2 2 n n R n tg n r n n a R n 2 180 n 360 3 n d Белгілері және қасиеттері: 1) – дұрыс n – бұрыштың қабырғасы, R – сырттай, r – іштей сызылған шеңбердің радиустары, S – оның ауданы: 2) 3) 4) n – бұрыштың ішкі бұрыштарының қосындысы: 5) n – бұрыштың сыртқы бұрыштарының қосындысы: 6) n – бұрыштың бі р төбесінен шығатын диагональдарының саны: 7) n – бұрыштың диагональдарының саны: 2 )3 ( n n N
15 слайд
Төртбұрыштар
бөліміне қатысты
мысал есептер
15 слайд
Төртбұрыштар бөліміне қатысты мысал есептер
16 слайд
16 слайд
17 слайд
17 слайд
18 слайд
18 слайд
19 слайд
19 слайд
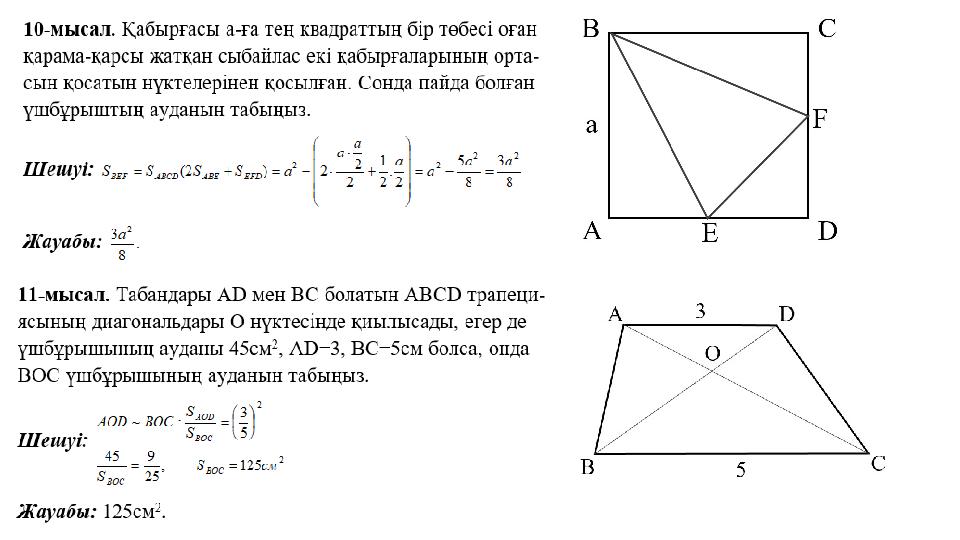
20 слайд
20 слайд
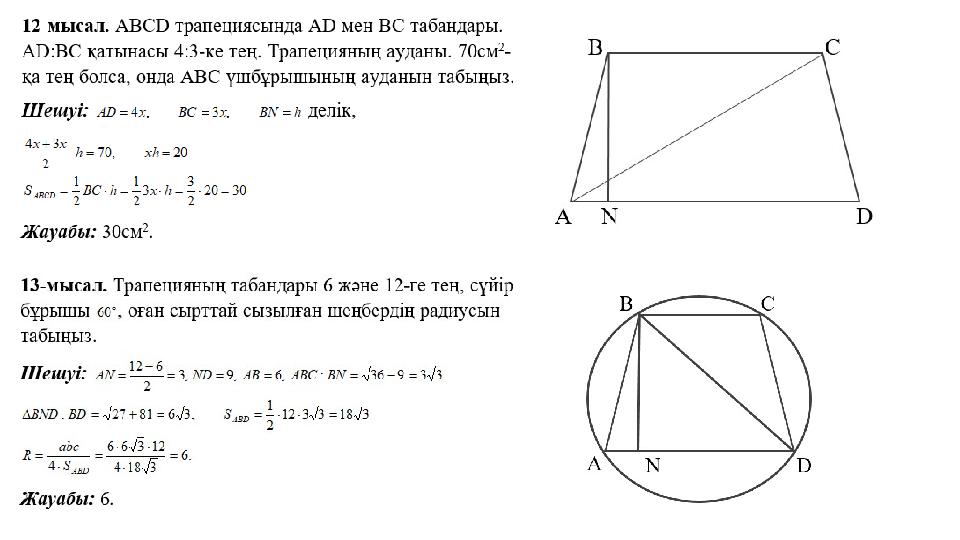
21 слайд
21 слайд
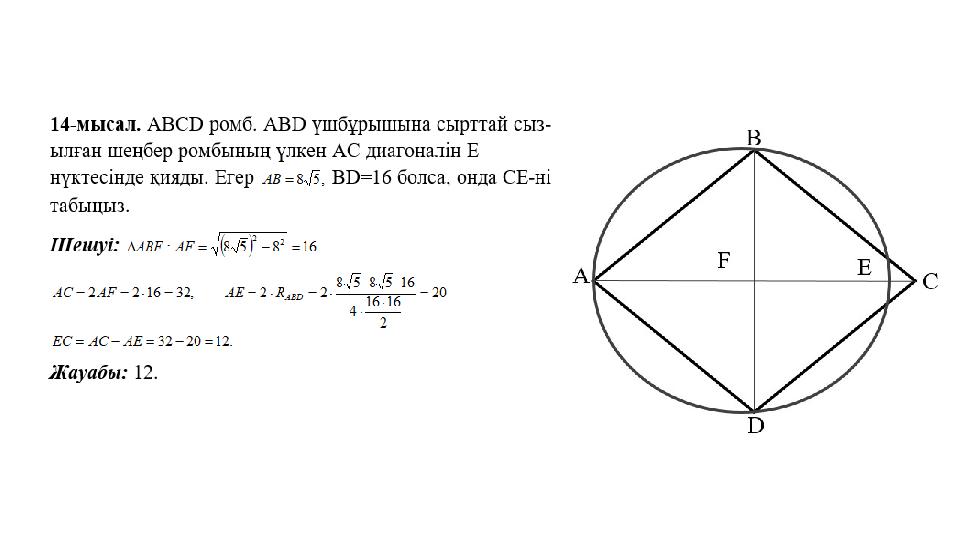
22 слайд
22 слайд
23 слайд
THANK YOU
Назар аударып қарағандарыңыз үшін рахмет!
23 слайд
THANK YOU Назар аударып қарағандарыңыз үшін рахмет!
