Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап
2 млн. ₸ табыс табыңыз!
МИНИСТРЛІКПЕН КЕЛІСІЛГЕН КУРСҚА ҚАТЫСЫП, АТТЕСТАЦИЯҒА ЖАРАМДЫ СЕРТИФИКАТ АЛЫҢЫЗ!
Сертификат Аттестацияға 100% жарамды
ТОЛЫҚ АҚПАРАТ АЛУ 
Үшбұрыш медианасының қасиеттері
Материал туралы қысқаша түсінік
Мұғалімдерге арналған
Авторы:
Автор материалды ақылы түрде жариялады.
Сатылымнан түскен қаражат авторға автоматты түрде аударылады.
Толығырақ
11 Ақпан 2019
769
0 рет жүктелгенТегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!
Дипломдар мен сертификаттарды алып үлгеріңіз!
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 10
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Үшбұрыштың медианаларының
қасиеттері
9.3.3.7
үшбұрыштың медианаларының
қасиеттерін дәлелдейді және қолданады;
1 слайд
Үшбұрыштың медианаларының қасиеттері 9.3.3.7 үшбұрыштың медианаларының қасиеттерін дәлелдейді және қолданады;
2 слайд
Үшбұрыштың медианаларының қасиеттері
1. Үшбұрыштың медианасы оны екі
теңшамалас (аудандары тең) үшбұрыштарға
бөледі.
2. Үшбұрыштың үш медианасы оны алты
теңшамалы үшбұрыштарға бөледі.
3. Медианалардың қиылысу нүктесін үшбұрыш
төбелерімен қосатын кесінділер осы
үшбұрышты тең шамалы үш үшбұрышқа
бөледі.
4. Медианалар бір нүктеде қиылысып,
қиылысу нүктесінде 2 : 1 қатынасында бөлінеді.
2 слайд
Үшбұрыштың медианаларының қасиеттері 1. Үшбұрыштың медианасы оны екі теңшамалас (аудандары тең) үшбұрыштарға бөледі. 2. Үшбұрыштың үш медианасы оны алты теңшамалы үшбұрыштарға бөледі. 3. Медианалардың қиылысу нүктесін үшбұрыш төбелерімен қосатын кесінділер осы үшбұрышты тең шамалы үш үшбұрышқа бөледі. 4. Медианалар бір нүктеде қиылысып, қиылысу нүктесінде 2 : 1 қатынасында бөлінеді.
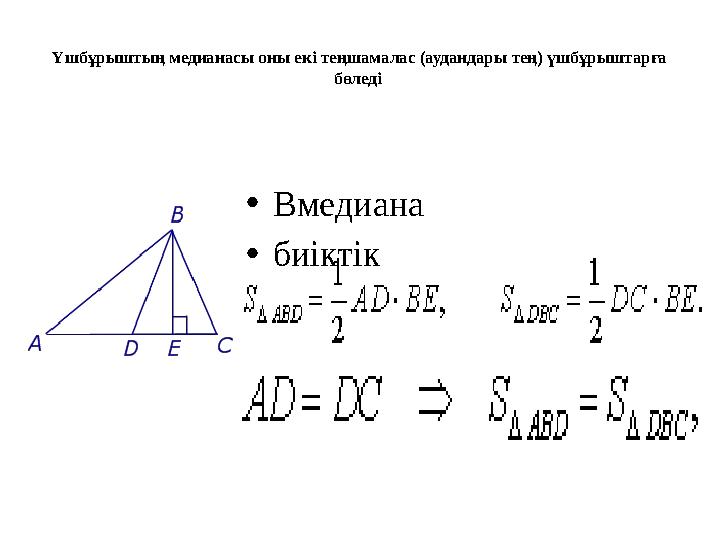
3 слайд
Үшбұрыштың медианасы оны екі теңшамалас (аудандары тең) үшбұрыштарға
бөледі
•
B медиана
•
биіктік
3 слайд
Үшбұрыштың медианасы оны екі теңшамалас (аудандары тең) үшбұрыштарға бөледі • B медиана • биіктік
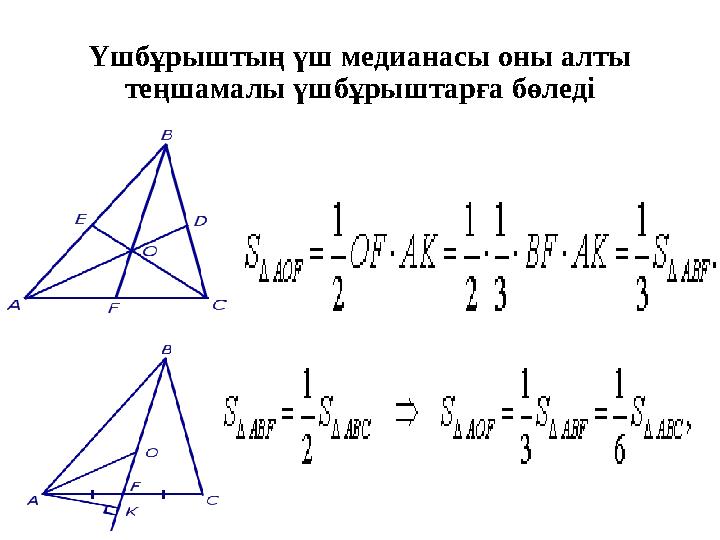
4 слайд
Үшбұрыштың үш медианасы оны алты
теңшамалы үшбұрыштарға бөледі
4 слайд
Үшбұрыштың үш медианасы оны алты теңшамалы үшбұрыштарға бөледі
5 слайд
Медианалардың қиылысу нүктесін үшбұрыш төбелерімен қосатын кесінділер осы
үшбұрышты теңшамалы үш үшбұрышқа бөледі
5 слайд
Медианалардың қиылысу нүктесін үшбұрыш төбелерімен қосатын кесінділер осы үшбұрышты теңшамалы үш үшбұрышқа бөледі
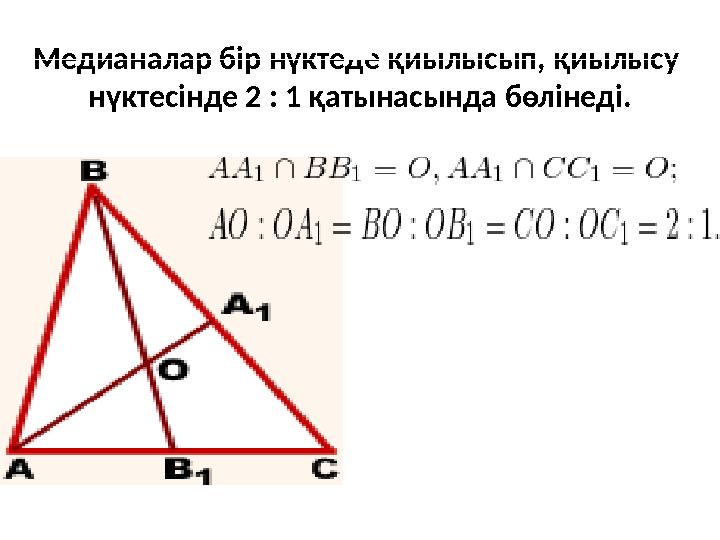
6 слайд
Медианалар бір нүктеде қиылысып, қиылысу
нүктесінде 2 : 1 қатынасында бөлінеді.
6 слайд
Медианалар бір нүктеде қиылысып, қиылысу нүктесінде 2 : 1 қатынасында бөлінеді.
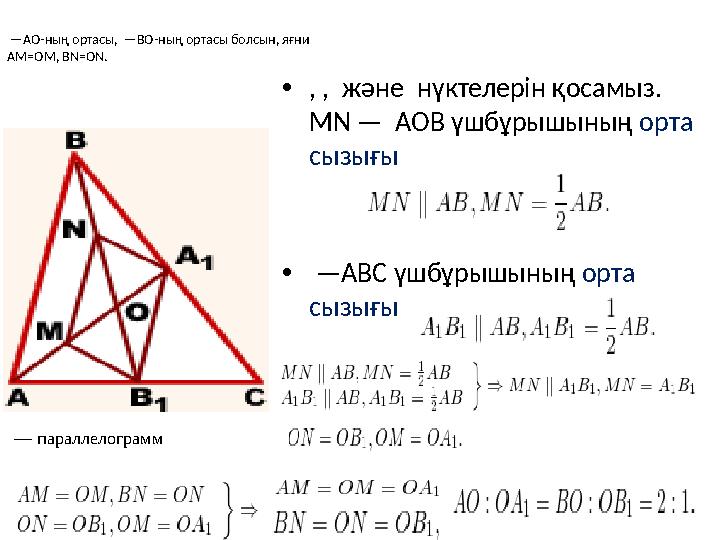
7 слайд
— AO-ның ортасы, —BO-ның ортасы болсын, яғни
AM=OM, BN=ON.
•
, , және нүктелерін қосамыз.
MN — AOB үшбұрышының орта
сызығы
•
— ABC үшбұрышының орта
сызығы
— параллелограмм
7 слайд
— AO-ның ортасы, —BO-ның ортасы болсын, яғни AM=OM, BN=ON. • , , және нүктелерін қосамыз. MN — AOB үшбұрышының орта сызығы • — ABC үшбұрышының орта сызығы — параллелограмм
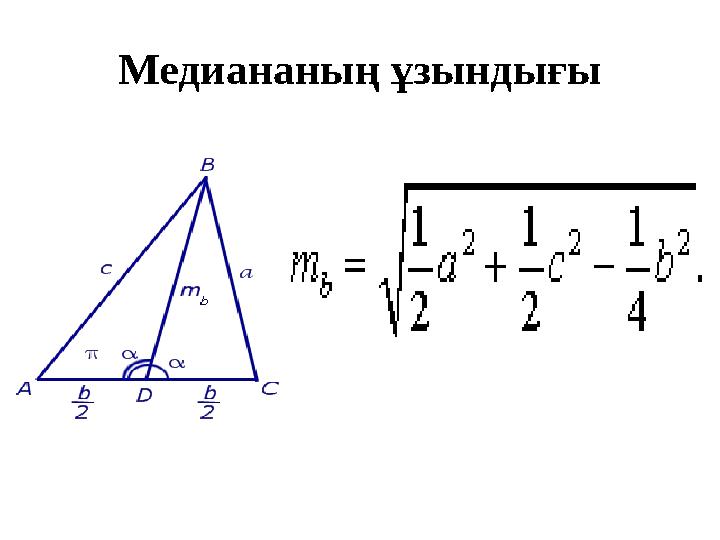
8 слайд
Медиананың ұзындығы
8 слайд
Медиананың ұзындығы
9 слайд
Салдар . Үшбұрыштың медианалары мен
қабырғаларының ұзындықтарының арасындағы
байланыс:
9 слайд
Салдар . Үшбұрыштың медианалары мен қабырғаларының ұзындықтарының арасындағы байланыс:
