Материалдар / Үшбұрышқа іштей және сырттай сызылған шеңберлер

Үшбұрышқа іштей және сырттай сызылған шеңберлер

Материал туралы қысқаша түсінік

Үшбұрышқа іштей және сырттай сызылған шеңберлер атты ашық сабақ презентациясы математика пәнінен сабақ беретін ұстаздарға әдістемелік көмек ретінде ұсынылып отыр.

Тілесқызы Тоғжан

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

14 Қазан 2018

819

1 рет жүктелген

Геометрия Презентация 7 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 8

Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз!

Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі.

Оқу-ағарту министірлігінің ресми жауабы

Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз!

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Үшбұрышқа іштей және сырттай сызылған шеңберлер Жамбыл облысы, Шу ауданы, Шоқпар ауылы, О.Жандосов орта мектебінің математика пәнінің мұғалімі Тілесқызы Тоғжан

1 слайд

Үшбұрышқа іштей және сырттай сызылған шеңберлер Жамбыл облысы, Шу ауданы, Шоқпар ауылы, О.Жандосов орта мектебінің математика пәнінің мұғалімі Тілесқызы Тоғжан

2 слайд
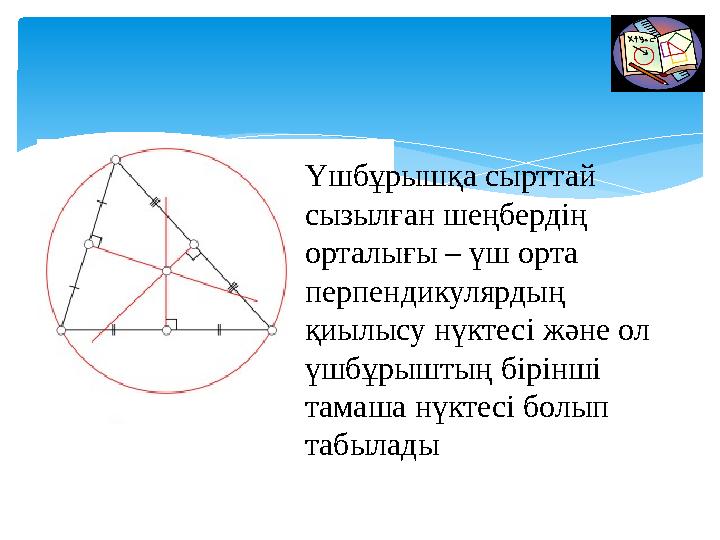
Үшбұрышқа сырттай сызылған шеңбердің орталығы – үш орта перпендикулярдың қиылысу нүктесі және ол үшбұрыштың бірінші тамаша нүктесі болып табылады

2 слайд

Үшбұрышқа сырттай сызылған шеңбердің орталығы – үш орта перпендикулярдың қиылысу нүктесі және ол үшбұрыштың бірінші тамаша нүктесі болып табылады

3 слайд
Үш орта перпендикулядың бір нүктеде қиылысатынын дәлелдеу үшін төмендегі теорема қолданылады. Теорема: Кесіндінің орта перпендикулярында жататын кез-келген нүкте берілген кесіндінің ұштарынан бірдей қашықтықта жатады.

3 слайд

Үш орта перпендикулядың бір нүктеде қиылысатынын дәлелдеу үшін төмендегі теорема қолданылады. Теорема: Кесіндінің орта перпендикулярында жататын кез-келген нүкте берілген кесіндінің ұштарынан бірдей қашықтықта жатады.

4 слайд
m ─ АВ кесіндісіне жүргізілген орта перпендикуляр, ал О нүктесі ─ осы кесіндінің ортасы болсын (2- сурет). m түзуінің бойынан кез-келген бірақ О нүктесінен басқа бір Р нүктесі алынсын. Р нүктесі мен АВ кесіндісінің ұштары қосылды. Дәлелдеу керек: АР = ВР Дәлелдеуі: АРВ үшбұрышын қарастырса, m түзуінде жатқан РО кесіндісі үшбұрыштың АВ табанына жүргізілген әрі медианасы, әрі биіктігі болып табылады. Осыдан, бұл үшбұрыш тең бүйірлі үшбұрыш және АВ ─ оның табаны. Демек, АР мен РВ үшбұрыштың бүйір қабырғалары, және олар тең, яғни АР = ВР. Дәлелденді. Теореманы тағы басқа жолмен де дәлелдеуге болады: ОАР және ОВР тікбұрыштары екі катеті бойынша тең (ОА = ОВ, ОР ─ ортақ катет). Сондықтан, АР = ВР. Дәлелденді.

4 слайд

m ─ АВ кесіндісіне жүргізілген орта перпендикуляр, ал О нүктесі ─ осы кесіндінің ортасы болсын (2- сурет). m түзуінің бойынан кез-келген бірақ О нүктесінен басқа бір Р нүктесі алынсын. Р нүктесі мен АВ кесіндісінің ұштары қосылды. Дәлелдеу керек: АР = ВР Дәлелдеуі: АРВ үшбұрышын қарастырса, m түзуінде жатқан РО кесіндісі үшбұрыштың АВ табанына жүргізілген әрі медианасы, әрі биіктігі болып табылады. Осыдан, бұл үшбұрыш тең бүйірлі үшбұрыш және АВ ─ оның табаны. Демек, АР мен РВ үшбұрыштың бүйір қабырғалары, және олар тең, яғни АР = ВР. Дәлелденді. Теореманы тағы басқа жолмен де дәлелдеуге болады: ОАР және ОВР тікбұрыштары екі катеті бойынша тең (ОА = ОВ, ОР ─ ортақ катет). Сондықтан, АР = ВР. Дәлелденді.

5 слайд
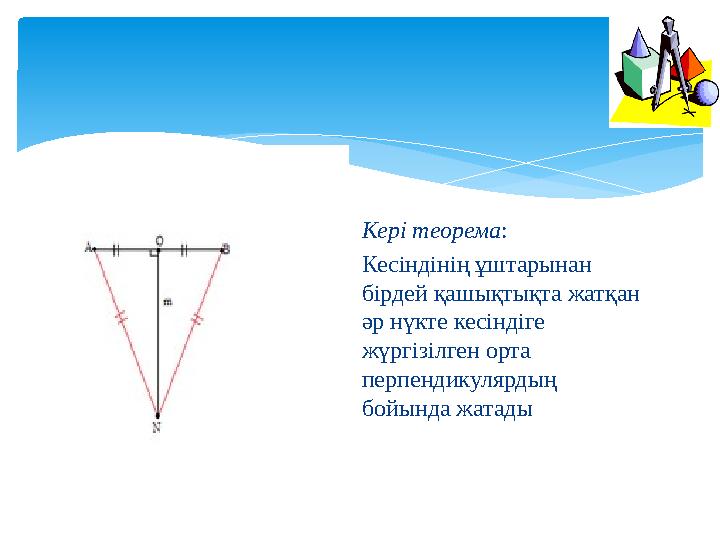
Кері теорема: Кесіндінің ұштарынан бірдей қашықтықта жатқан әр нүкте кесіндіге жүргізілген орта перпендикулярдың бойында жатады

5 слайд

Кері теорема: Кесіндінің ұштарынан бірдей қашықтықта жатқан әр нүкте кесіндіге жүргізілген орта перпендикулярдың бойында жатады

6 слайд
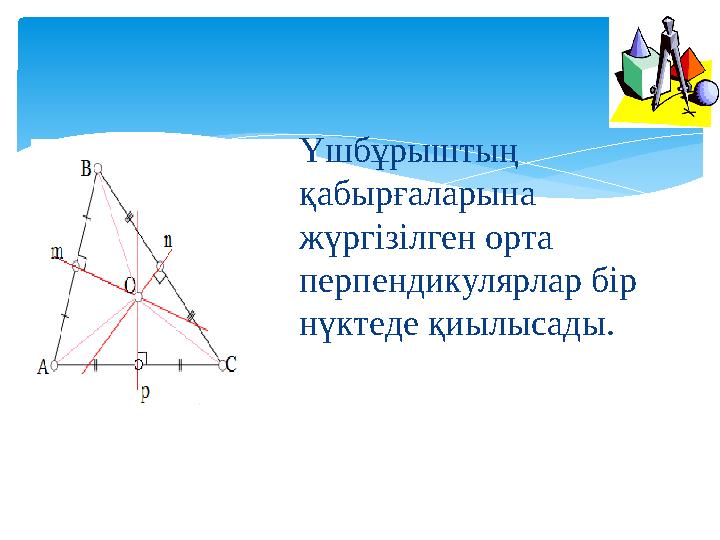
Үшбұрыштың қабырғаларына жүргізілген орта перпендикулярлар бір нүктеде қиылысады.

6 слайд

Үшбұрыштың қабырғаларына жүргізілген орта перпендикулярлар бір нүктеде қиылысады.

7 слайд
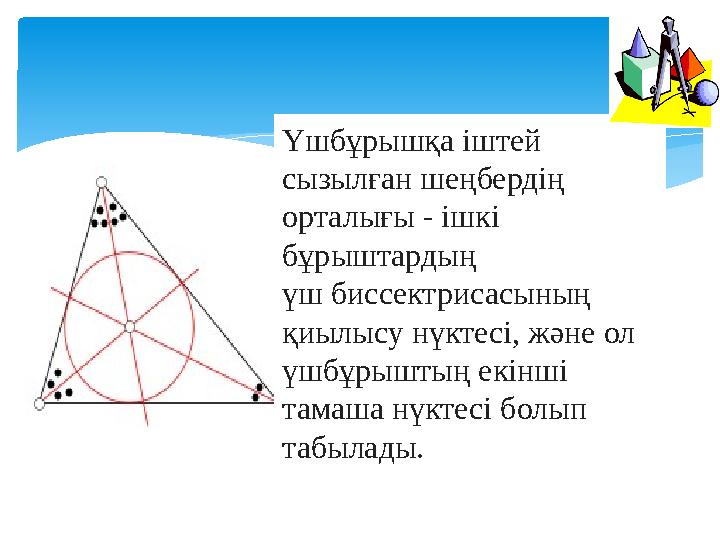
Үшбұрышқа іштей сызылған шеңбердің орталығы - ішкі бұрыштардың үш биссектрисасының қиылысу нүктесі, және ол үшбұрыштың екінші тамаша нүктесі болып табылады.

7 слайд

Үшбұрышқа іштей сызылған шеңбердің орталығы - ішкі бұрыштардың үш биссектрисасының қиылысу нүктесі, және ол үшбұрыштың екінші тамаша нүктесі болып табылады.