Материалдар / Вектор ұғымы

Вектор ұғымы

Материал туралы қысқаша түсінік

Вектор ұғымы дайын презентация 9 сынып

Тулешова Назерке Ерболаткызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

07 Қазан 2024

171

0 рет жүктелген

Геометрия Презентация 9 сынып

250 ₸

Бүгін алсаңыз
+13 бонус беріледі
Бұл не?

Бүгін алсаңыз +13 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 20

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Вектор ұғымы Сабақтың тақырыбы:

1 слайд

Вектор ұғымы Сабақтың тақырыбы:

2 слайд
екі векторлардың арасындағы бұрыштың анықтамасын біледі; векторлардың скалярлық көбейтіндісін табады; Сабақ мақсаты:

2 слайд

екі векторлардың арасындағы бұрыштың анықтамасын біледі; векторлардың скалярлық көбейтіндісін табады; Сабақ мақсаты:

3 слайд
cos bаba     cos bаba     теорема. Векторлардың скаляр көбейтіндісі олардың модульдерін сол векторлар арасындағы бұрыштың косинусына көбейткенде шығатын санға тең болады, яғни Бұдан, .0 baba   .0 baba  

3 слайд

cos bаba     cos bаba     теорема. Векторлардың скаляр көбейтіндісі олардың модульдерін сол векторлар арасындағы бұрыштың косинусына көбейткенде шығатын санға тең болады, яғни Бұдан, .0 baba   .0 baba  

4 слайд
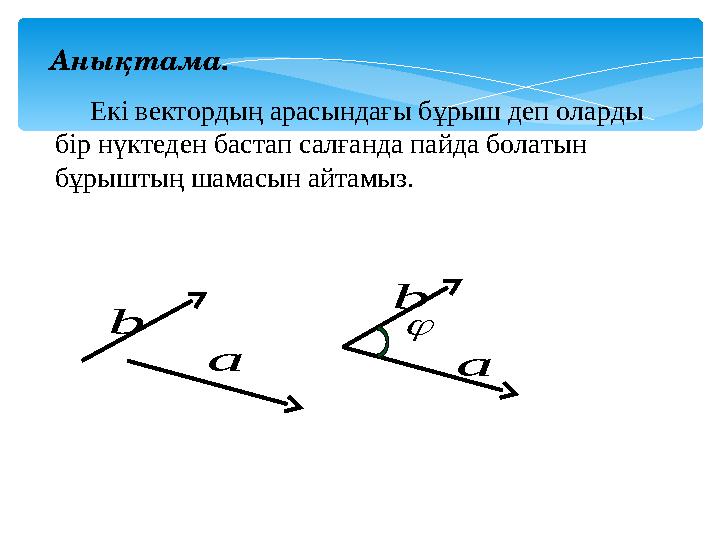
 b  Анықтама. Екі вектордың арасындағы бұрыш деп оларды бір нүктеден бастап салғанда пайда болатын бұрыштың шамасын айтамыз. b  а  а 

4 слайд

 b  Анықтама. Екі вектордың арасындағы бұрыш деп оларды бір нүктеден бастап салғанда пайда болатын бұрыштың шамасын айтамыз. b  а  а 

5 слайд
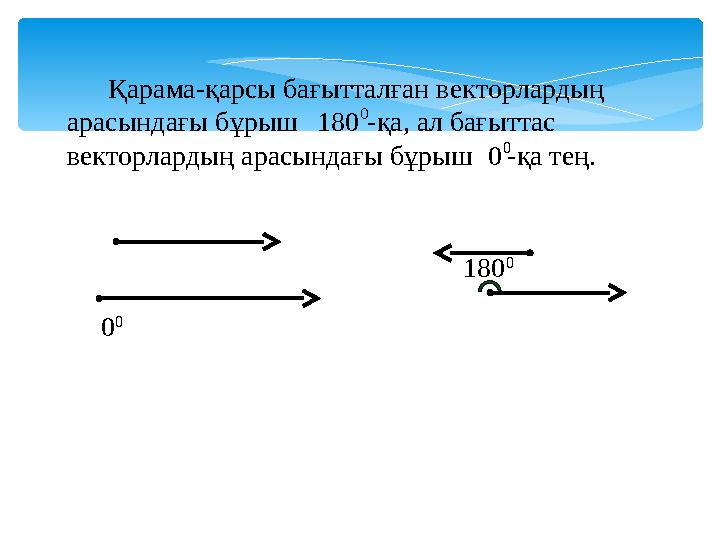
Қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа, ал бағыттас векторлардың арасындағы бұрыш -қа тең. 0 180 0 0 180 0 0 0

5 слайд

Қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа, ал бағыттас векторлардың арасындағы бұрыш -қа тең. 0 180 0 0 180 0 0 0

6 слайд
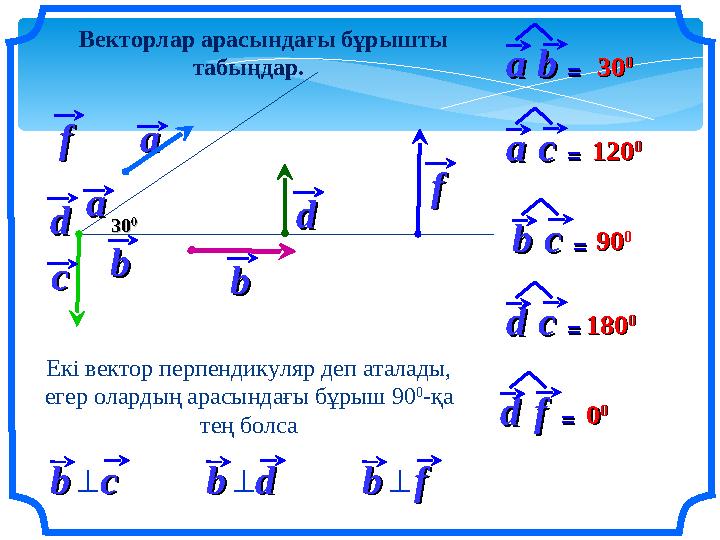
aa dd Векторлар арасындағы бұрышты табыңдар. bb 3030 00 aabb == cc ff 3030 00 aacc == bbcc == ddff == ddcc == 120120 00 9090 00 180180 00 00 00 aa bb dd ff Екі вектор перпендикуляр деп аталады, егер олардың арасындағы бұрыш 90 0 -қа тең болса bbcc  bbdd  bbff 

6 слайд

aa dd Векторлар арасындағы бұрышты табыңдар. bb 3030 00 aabb == cc ff 3030 00 aacc == bbcc == ddff == ddcc == 120120 00 9090 00 180180 00 00 00 aa bb dd ff Екі вектор перпендикуляр деп аталады, егер олардың арасындағы бұрыш 90 0 -қа тең болса bbcc  bbdd  bbff 

7 слайд
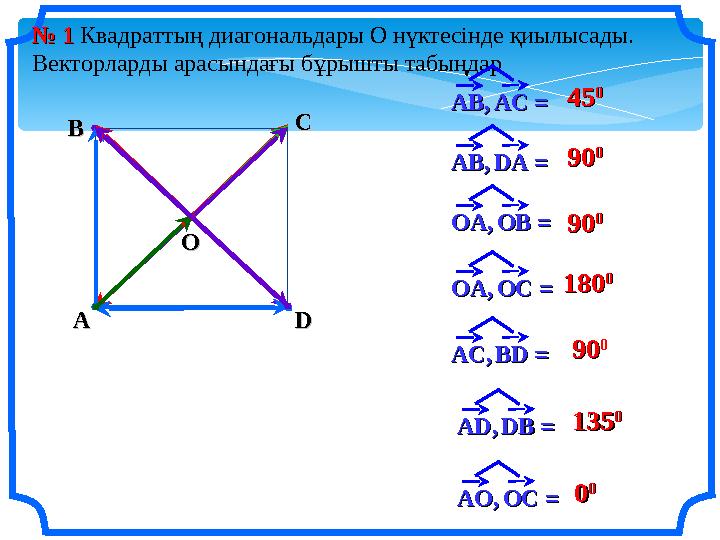
№ № 1 1 Квадраттың диагональдары О нүктесінде қиылысады. Векторларды арасындағы бұрышты табыңдар 4545 00 АВ,АВ, АС = АС = АА ВВ СС DD ОО АВ,АВ, DDА = А = OOА,А, OBOB = = ААOO,, OCOC = = OOА,А, OOС = С = ААCC,, BDBD = = ААDD,, DBDB = = 9090 00 9090 00 180180 00 9090 00 135135 00 00 00

7 слайд

№ № 1 1 Квадраттың диагональдары О нүктесінде қиылысады. Векторларды арасындағы бұрышты табыңдар 4545 00 АВ,АВ, АС = АС = АА ВВ СС DD ОО АВ,АВ, DDА = А = OOА,А, OBOB = = ААOO,, OCOC = = OOА,А, OOС = С = ААCC,, BDBD = = ААDD,, DBDB = = 9090 00 9090 00 180180 00 9090 00 135135 00 00 00

8 слайд
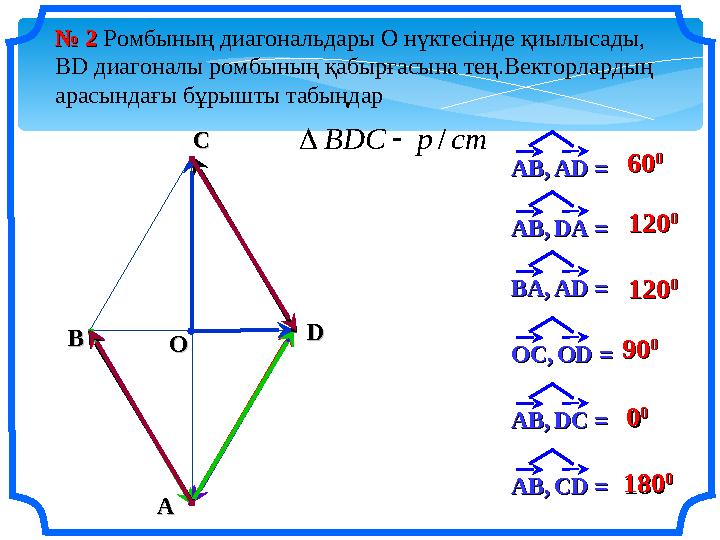
№ № 2 2 Ромбының диагональдары О нүктесінде қиылысады, ВD диагоналы ромбының қабырғасына тең.Векторлардың арасындағы бұрышты табыңдар 6060 00 АВ,АВ, ААDD = = АА ВВ СС DD ОО АВ,АВ, DDА = А = BBА,А, ADAD = = OCOC,, ODOD = = ААBB,, DCDC = = 121200 00 121200 00 9900 00 00 00 ААBB,, CDCD = = стрВDC / 181800 00

8 слайд

№ № 2 2 Ромбының диагональдары О нүктесінде қиылысады, ВD диагоналы ромбының қабырғасына тең.Векторлардың арасындағы бұрышты табыңдар 6060 00 АВ,АВ, ААDD = = АА ВВ СС DD ОО АВ,АВ, DDА = А = BBА,А, ADAD = = OCOC,, ODOD = = ААBB,, DCDC = = 121200 00 121200 00 9900 00 00 00 ААBB,, CDCD = = стрВDC / 181800 00

9 слайд
Скаляр көбейтіндінің төрт қасиеті: 1) 2) 3) 4) );( 21aaa  );;( 321bbbb  ;0 2 аaa  мен векторларының скаляр көбейтіндісі деп санын айтамыз. 2211 bababa    2211 bababa    2211 baba Анықтама. );( 21 bbb  ;abba     ;)( cbсaсba       )()( baba      

9 слайд

Скаляр көбейтіндінің төрт қасиеті: 1) 2) 3) 4) );( 21aaa  );;( 321bbbb  ;0 2 аaa  мен векторларының скаляр көбейтіндісі деп санын айтамыз. 2211 bababa    2211 bababa    2211 baba Анықтама. );( 21 bbb  ;abba     ;)( cbсaсba       )()( baba      

10 слайд
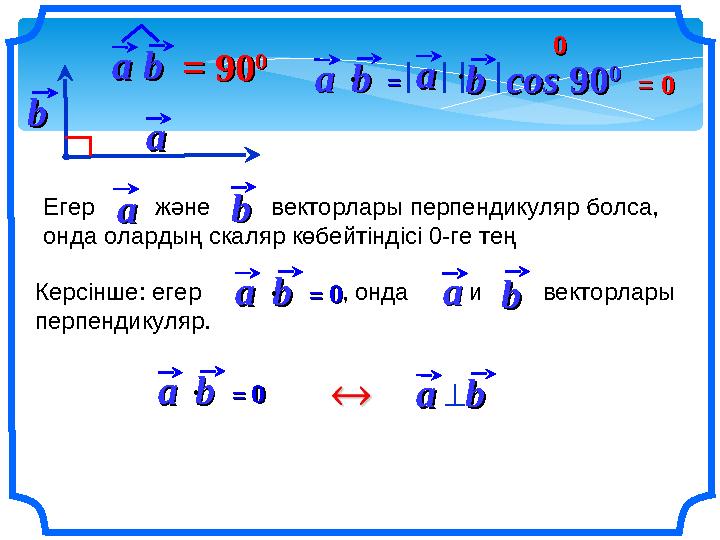
aabb ==aabb cos cos 9090 00 aa bb = 0 = 0 0 0 Егер және векторлары перпендикуляр болса, онда олардың скаляр көбейтіндісі 0-ге тең aa bb Керсінше: егер , онда и векторлары перпендикуляр. aabb == 00 aabb aabb == 00 aabb  aabb = 90= 90 00

10 слайд

aabb ==aabb cos cos 9090 00 aa bb = 0 = 0 0 0 Егер және векторлары перпендикуляр болса, онда олардың скаляр көбейтіндісі 0-ге тең aa bb Керсінше: егер , онда и векторлары перпендикуляр. aabb == 00 aabb aabb == 00 aabb  aabb = 90= 90 00

11 слайд
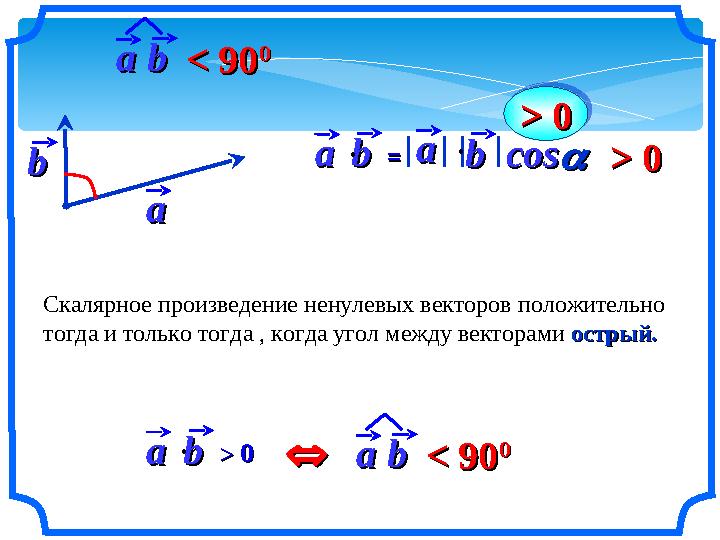
aabb ==aabb coscos aa bb Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда угол между векторами острый.острый. aabb >> 00 > 0> 0 > 0> 0 > 0> 0 aabb < 90< 90 00 aabb < 90< 90 00

11 слайд

aabb ==aabb coscos aa bb Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда угол между векторами острый.острый. aabb >> 00 > 0> 0 > 0> 0 > 0> 0 aabb < 90< 90 00 aabb < 90< 90 00

12 слайд
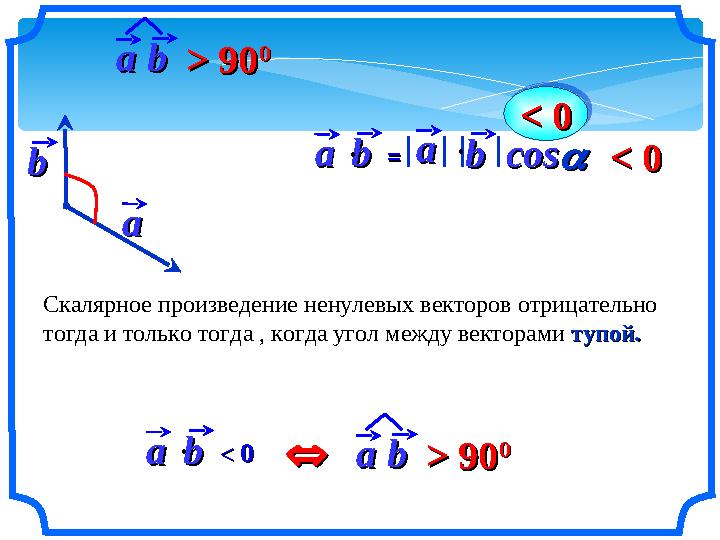
aabb ==aabb coscos aa bb Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой.тупой. aabb << 00 < 0< 0 < 0< 0 < 0< 0 aabb > 90> 90 00 aabb > 90> 90 00

12 слайд

aabb ==aabb coscos aa bb Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой.тупой. aabb << 00 < 0< 0 < 0< 0 < 0< 0 aabb > 90> 90 00 aabb > 90> 90 00

13 слайд
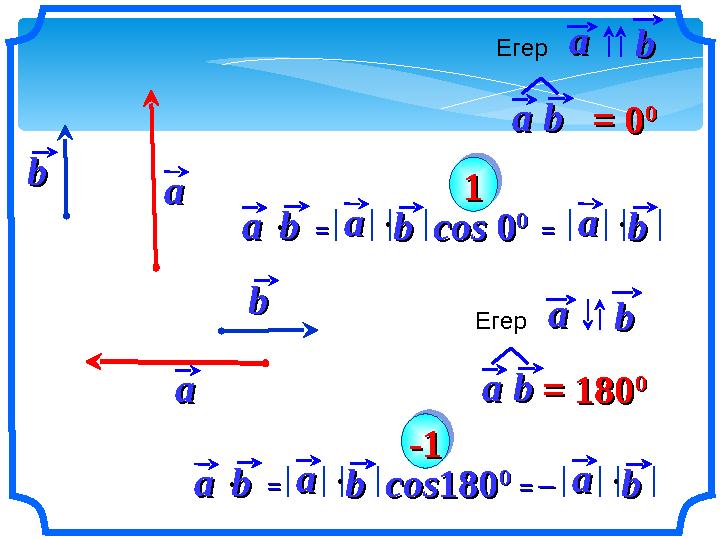
aabb ==aabb ==aabb cos cos 00 00 aa bb 11 11 aabb = 0= 0 00 Егер aabb aabb ==aabb coscos180180 00 aa bb -1-1 -1-1 aabb = 180= 180 00 Егер aabb = = –– aabb 

13 слайд

aabb ==aabb ==aabb cos cos 00 00 aa bb 11 11 aabb = 0= 0 00 Егер aabb aabb ==aabb coscos180180 00 aa bb -1-1 -1-1 aabb = 180= 180 00 Егер aabb = = –– aabb 

14 слайд
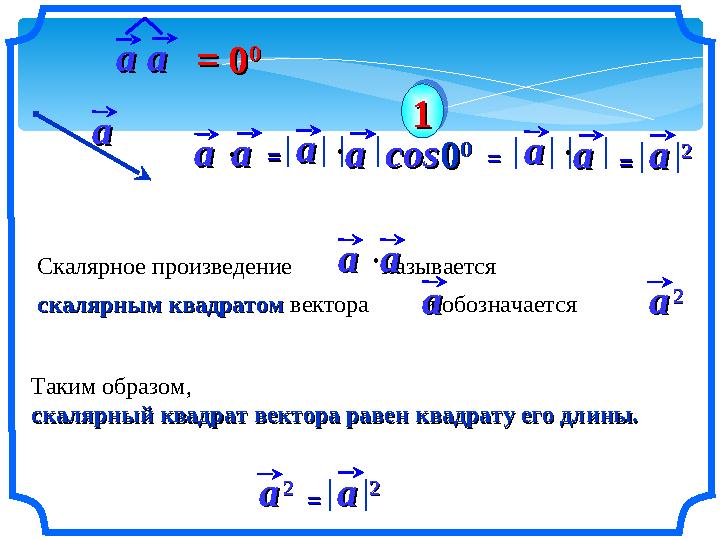
aaaa ==aaaa coscos aa 00 00 11 11 aaaa = 0= 0 00 aaaa == ==aa 22 Скалярное произведение называется скалярным квадратом скалярным квадратом вектора и обозначается aaaa aa aa 22 Таким образом, скалярный квадрат вектора равен квадрату его длины. скалярный квадрат вектора равен квадрату его длины. aa 22 ==aa 22

14 слайд

aaaa ==aaaa coscos aa 00 00 11 11 aaaa = 0= 0 00 aaaa == ==aa 22 Скалярное произведение называется скалярным квадратом скалярным квадратом вектора и обозначается aaaa aa aa 22 Таким образом, скалярный квадрат вектора равен квадрату его длины. скалярный квадрат вектора равен квадрату его длины. aa 22 ==aa 22

15 слайд
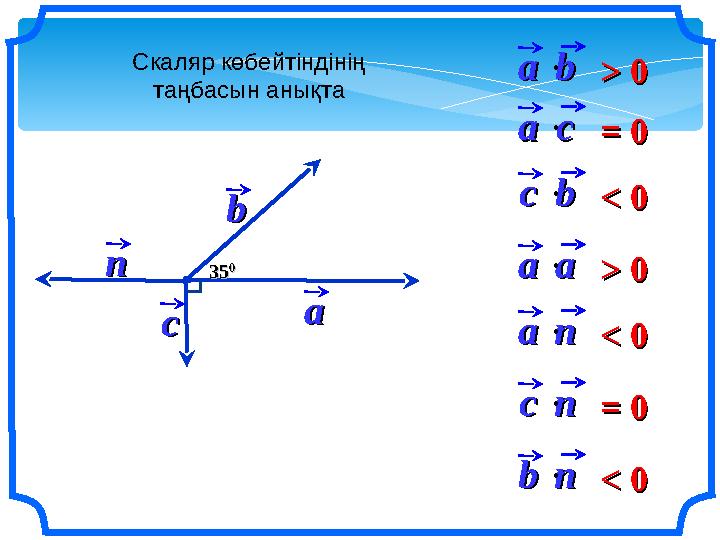
bb aa cc aabb  < 0< 0 3535 00 aacc  ccbb  = 0= 0 > 0> 0 aaaa nn aann  > 0> 0 < 0< 0 ccnn = 0= 0 bbnn < 0< 0 Скаляр көбейтіндінің таңбасын анықта

15 слайд

bb aa cc aabb  < 0< 0 3535 00 aacc  ccbb  = 0= 0 > 0> 0 aaaa nn aann  > 0> 0 < 0< 0 ccnn = 0= 0 bbnn < 0< 0 Скаляр көбейтіндінің таңбасын анықта

16 слайд
Есеп №1 Векторлардың скаляр көбейтіндісін табыңдар a=(3;5) и b=(-2;7). 2211 bababa    2211 bababa   

16 слайд

Есеп №1 Векторлардың скаляр көбейтіндісін табыңдар a=(3;5) и b=(-2;7). 2211 bababa    2211 bababa   

17 слайд
Есеп №2 Векторлар арасындағы бұрышты табыңдар: a)a=(4;0) и b=(2;-2); b)a=(5;-3) и b=(3;5). , , а)

17 слайд

Есеп №2 Векторлар арасындағы бұрышты табыңдар: a)a=(4;0) и b=(2;-2); b)a=(5;-3) и b=(3;5). , , а)

18 слайд
б)

18 слайд

б)

19 слайд
1) Қандай векторларды бағыттас векторлар деп атаймыз? 2) Қандай векторларды қарама – қарсы бағытталған векторлар деп атаймыз? 3)Қай кезде екі вектор арасындағы бұрыш 180 °-қа тең болады? 4) Қай кезде екі вектор арасындағы бұрыш 0°-қа тең болады? 5) Қай кезде екі вектор арасындағы бұрыш тік болады? 6) Қай кезде екі вектор арасындағы бұрыш сүйір болады? 7) Қай кезде екі вектор арасындағы бұрыш доғал болады? 8)Екі вектордың скалярлық көбейтіндісін қалай табамыз?

19 слайд

1) Қандай векторларды бағыттас векторлар деп атаймыз? 2) Қандай векторларды қарама – қарсы бағытталған векторлар деп атаймыз? 3)Қай кезде екі вектор арасындағы бұрыш 180 °-қа тең болады? 4) Қай кезде екі вектор арасындағы бұрыш 0°-қа тең болады? 5) Қай кезде екі вектор арасындағы бұрыш тік болады? 6) Қай кезде екі вектор арасындағы бұрыш сүйір болады? 7) Қай кезде екі вектор арасындағы бұрыш доғал болады? 8)Екі вектордың скалярлық көбейтіндісін қалай табамыз?