Материалдар / Векторларды көбейту

Векторларды көбейту

Материал туралы қысқаша түсінік

9 сынып оқушыларына вектор тақырыбын сызба арқылы түсіндіріп, геометрияға қызығушылығын ояту.

Ибрагимова Гулшат Муратбековна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

28 Желтоқсан 2017

926

0 рет жүктелген

Геометрия Сабақ жоспары 9 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 38

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Екі векторды векторлық көбейтуСабақ тақырыбы: № 28 орта мектептің математика пәнінің мұғалімі Ибрагимова Г.М.Қолданбалы курс “Сызықтық алгебра және аналитикалық геометрия”

1 слайд

Екі векторды векторлық көбейтуСабақ тақырыбы: № 28 орта мектептің математика пәнінің мұғалімі Ибрагимова Г.М.Қолданбалы курс “Сызықтық алгебра және аналитикалық геометрия”

2 слайд
Сабақ мақсаты: Оқушыларға екі вектордың векторлық көбейтіндісі туралы түсінік беру, олардың геометриялық және алгебралық қасиеттерімен таныстыру. Оқушыларға екі вектордың векторлық көбейтіндісі көмегімен кейбір геометриялық есептерді шығаруды үйрету. Оқушыларды өз білімдерін жүйелеуге және векторларға берілген есептерді шығаруға бейімдеу.

2 слайд

Сабақ мақсаты: Оқушыларға екі вектордың векторлық көбейтіндісі туралы түсінік беру, олардың геометриялық және алгебралық қасиеттерімен таныстыру. Оқушыларға екі вектордың векторлық көбейтіндісі көмегімен кейбір геометриялық есептерді шығаруды үйрету. Оқушыларды өз білімдерін жүйелеуге және векторларға берілген есептерді шығаруға бейімдеу.

3 слайд
Қайталау сұрақтары: 1. Вектор деген не? Векторды қалай белгілейді? 2. Вектордың абсолют шамасы деген не? 3. Нөлдік вектор деген не? 4. Қандай векторлар тең деп аталады? 5. Векторларды қосудың «үшбұрыш ережесін» тұжырымдап беріңдер. 6. Векторларды қосудың «параллелограмм ережесін» тұжырымдап беріңдер. 7. Қандай векторлар коллинеар векторлар деп аталады? Қоллинеар векторлардың қасиеті. 8. Векторлар арасындағы бұрыш қалай анықталады? 9. Векторлардың скаляр көбейтіндісі дегенге анықтама беріңдер. 10. Бірлік векторлар. Векторды үш оське жіктеу.

3 слайд

Қайталау сұрақтары: 1. Вектор деген не? Векторды қалай белгілейді? 2. Вектордың абсолют шамасы деген не? 3. Нөлдік вектор деген не? 4. Қандай векторлар тең деп аталады? 5. Векторларды қосудың «үшбұрыш ережесін» тұжырымдап беріңдер. 6. Векторларды қосудың «параллелограмм ережесін» тұжырымдап беріңдер. 7. Қандай векторлар коллинеар векторлар деп аталады? Қоллинеар векторлардың қасиеті. 8. Векторлар арасындағы бұрыш қалай анықталады? 9. Векторлардың скаляр көбейтіндісі дегенге анықтама беріңдер. 10. Бірлік векторлар. Векторды үш оське жіктеу.

4 слайд
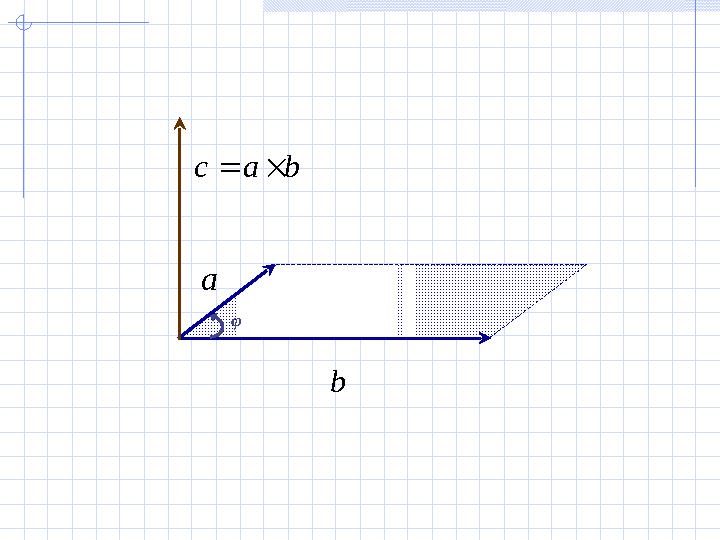
Анықтама. Нөлдік емес және векторларының векторлық көбейтіндісі деп символымен белгіленген мына үш шартты қанағаттандыратын векторын атайды: 1. векторының ұзындығы және векторла- рының ұзындықтарын олардың арасындағы бұрыш- тың синусына көбейткенге тең, яғни , мұндағы - және векторларының арасындағы бұрыш. 2. векторы және векторларының әрқайсысына перпендикуляр орналасқан. 3. векторының бағыты , , векторлары оң жақты үштік болатындай бағытта бағытталған.а  b  b а с      c  c  а  b   sin   b a c     а  b  c  а  b  c  а  b  c 

4 слайд

Анықтама. Нөлдік емес және векторларының векторлық көбейтіндісі деп символымен белгіленген мына үш шартты қанағаттандыратын векторын атайды: 1. векторының ұзындығы және векторла- рының ұзындықтарын олардың арасындағы бұрыш- тың синусына көбейткенге тең, яғни , мұндағы - және векторларының арасындағы бұрыш. 2. векторы және векторларының әрқайсысына перпендикуляр орналасқан. 3. векторының бағыты , , векторлары оң жақты үштік болатындай бағытта бағытталған.а  b  b а с      c  c  а  b   sin   b a c     а  b  c  а  b  c  а  b  c 

5 слайд
φb а с      а  b 

5 слайд

φb а с      а  b 

6 слайд
Егер және векторларының кемінде біреуі нөлдік вектор болса, онда олардың векторлық көбейтіндісі нөлдік векторға тең деп алынады. а  b 

6 слайд

Егер және векторларының кемінде біреуі нөлдік вектор болса, онда олардың векторлық көбейтіндісі нөлдік векторға тең деп алынады. а  b 

7 слайд
Екі вектордың векторлық көбейтіндісі туралы түсінік механикадан алынған. Егер векторы қандай болса да бір М нүктесіне түсірілген күшті бейнелесе, ал векторы болып О нүктесіне түсірілсе, онда векторы О нүктесіне қатысты күшінің моментіне тең болады. b  а  а ОМ   b а с      b 

7 слайд

Екі вектордың векторлық көбейтіндісі туралы түсінік механикадан алынған. Егер векторы қандай болса да бір М нүктесіне түсірілген күшті бейнелесе, ал векторы болып О нүктесіне түсірілсе, онда векторы О нүктесіне қатысты күшінің моментіне тең болады. b  а  а ОМ   b а с      b 

8 слайд
II. Векторлық көбейтіндінің геометриялық қасиеттері. 1 - Теорема. Нөлдік емес екі және векторлары коллинеар болуы үшін, олардың векторлық көбейтіндісінің нөлге тең болуы қажетті және жеткілікті: , а   0  b  ║  0  а  b  а  b    0   а  b 

8 слайд

II. Векторлық көбейтіндінің геометриялық қасиеттері. 1 - Теорема. Нөлдік емес екі және векторлары коллинеар болуы үшін, олардың векторлық көбейтіндісінің нөлге тең болуы қажетті және жеткілікті: , а   0  b  ║  0  а  b  а  b    0   а  b 

9 слайд
Қажеттілік. және векторлары коллинеар болсын. Мына жағдайлар болуы мүмкін: 1. , яғни және векторлары бағыттас болсын, сонда олардың арасындағы бұрыш -қа тең болады. Сондықтан, , бұдан болады; 2. , яғни және қарама-қарсы бағытталған векторлар болсын. Сонда олардың арасындағы бұрыш -қа тең болады. Сондықтан, , бұдан , яғни, екі жағдайда да .b  а  b a    а  b  0 0 0 0 sin 0       b a b а с      0   b а   b a    а  b  0 180 0 180 sin 0       b a b а с      0   b а   0   b а  

9 слайд

Қажеттілік. және векторлары коллинеар болсын. Мына жағдайлар болуы мүмкін: 1. , яғни және векторлары бағыттас болсын, сонда олардың арасындағы бұрыш -қа тең болады. Сондықтан, , бұдан болады; 2. , яғни және қарама-қарсы бағытталған векторлар болсын. Сонда олардың арасындағы бұрыш -қа тең болады. Сондықтан, , бұдан , яғни, екі жағдайда да .b  а  b a    а  b  0 0 0 0 sin 0       b a b а с      0   b а   b a    а  b  0 180 0 180 sin 0       b a b а с      0   b а   0   b а  

10 слайд
Жеткіліктілік. болсын. Сонда . болғандықтан, бұдан теңдігі шығады, яғни немесе . Ал бұл және векторларының коллинеар векторлар екенін көрсетеді.b a     sin 0      b a b a     0 , 0   b а   0 sin   0 0   0 180   а  b 

10 слайд

Жеткіліктілік. болсын. Сонда . болғандықтан, бұдан теңдігі шығады, яғни немесе . Ал бұл және векторларының коллинеар векторлар екенін көрсетеді.b a     sin 0      b a b a     0 , 0   b а   0 sin   0 0   0 180   а  b 

11 слайд
2-теорема. және векторларының векторлық көбейтіндісінің ұзындығы ортақ бас нүктеден шыққан және векторларына салынған параллелограмның ауданына тең. Анықтама бойынша а  b  а  b   sin     b a b a     φ b а с      а  b  S

11 слайд

2-теорема. және векторларының векторлық көбейтіндісінің ұзындығы ортақ бас нүктеден шыққан және векторларына салынған параллелограмның ауданына тең. Анықтама бойынша а  b  а  b   sin     b a b a     φ b а с      а  b  S

12 слайд
Параллелограмның ауданы: Үшбұрыштың ауданы:b a S     b a S     2 1 а  b  S

12 слайд

Параллелограмның ауданы: Үшбұрыштың ауданы:b a S     b a S     2 1 а  b  S

13 слайд
Бірлік векторлардың векторлық көбейтіндісі:k j i      i k j      j i k      k i j       i j k       j k i      

13 слайд

Бірлік векторлардың векторлық көбейтіндісі:k j i      i k j      j i k      k i j       i j k       j k i      

14 слайд
Екі вектордың векторлық көбейтіндісінің алгебралық қасиеттері: 1-қасиет. қарсы ауыстырымдылық қасиет 2-қасиет. сан көбейткішіне қатысты терімділік қасиет 3-қасиет. үлестірімділік қасиет 4-қасиет. Кез келген векторы үшінa b b a         ) ( ) ( b a b a          c b c a c b a              ) ( a  0   a a  

14 слайд

Екі вектордың векторлық көбейтіндісінің алгебралық қасиеттері: 1-қасиет. қарсы ауыстырымдылық қасиет 2-қасиет. сан көбейткішіне қатысты терімділік қасиет 3-қасиет. үлестірімділік қасиет 4-қасиет. Кез келген векторы үшінa b b a         ) ( ) ( b a b a          c b c a c b a              ) ( a  0   a a  

15 слайд
2 2 2 1 1 1 z y x z y x k j i b a        ) ; ; ( , ) ; ; ( 2 2 2 1 1 1 z y x b z y x a  Декарттық тік бұрышты координаталарымен берілген векторлардың векторлық көбейтіндісінің өрнегі.

15 слайд

2 2 2 1 1 1 z y x z y x k j i b a        ) ; ; ( , ) ; ; ( 2 2 2 1 1 1 z y x b z y x a  Декарттық тік бұрышты координаталарымен берілген векторлардың векторлық көбейтіндісінің өрнегі.

16 слайд
Есеп №1. Параллелограмның қабырғаларындағы векторлар берілген: Осы параллелограмның ауданын табайық.k j i а        3 k j i b     3 2      1; 3 ; 1   а    3 ; 1 ; 2   b    10 3 10 9 90 25 1 64 5;1 ;8 5 8 1 2 3 1 2 3 1 1 3 1 1 3 3 1 2 1 3 1 ,                              b a S k j i k j i k j i b a b a S                Шешуі : , Параллелограмның ауданы: Жауабы: 10 3

16 слайд

Есеп №1. Параллелограмның қабырғаларындағы векторлар берілген: Осы параллелограмның ауданын табайық.k j i а        3 k j i b     3 2      1; 3 ; 1   а    3 ; 1 ; 2   b    10 3 10 9 90 25 1 64 5;1 ;8 5 8 1 2 3 1 2 3 1 1 3 1 1 3 3 1 2 1 3 1 ,                              b a S k j i k j i k j i b a b a S                Шешуі : , Параллелограмның ауданы: Жауабы: 10 3

17 слайд
A( - 1;0;-1 ) B( 0;2;-3 ) C( 4;4;1 )Есеп №2 . Төбелері А(-1;0;-1), В(0;2;-3), С(4;4;1) нүктелерінде жатқан үшбұрыш ауданын тап. Шешу і: ) 2; 4; 5 ( ) 2 ; 2; 1( 2 1       АС АВ АС АВ S . 9 ;9 18 2 1 2 1 18 324 36 144 144 ) 6 ( ) 12 ( 12 ) 6 ; 12 ; 12( ) 6 ; 12 ; 12( 6 12 12 4 5 2 1 5 2 1 2 2 4 2 2 2 4 5 2 2 1 2 2 2                                      S АС АВ S АС АВ AC AB k j i k j i k j i            АС АВ

17 слайд

A( - 1;0;-1 ) B( 0;2;-3 ) C( 4;4;1 )Есеп №2 . Төбелері А(-1;0;-1), В(0;2;-3), С(4;4;1) нүктелерінде жатқан үшбұрыш ауданын тап. Шешу і: ) 2; 4; 5 ( ) 2 ; 2; 1( 2 1       АС АВ АС АВ S . 9 ;9 18 2 1 2 1 18 324 36 144 144 ) 6 ( ) 12 ( 12 ) 6 ; 12 ; 12( ) 6 ; 12 ; 12( 6 12 12 4 5 2 1 5 2 1 2 2 4 2 2 2 4 5 2 2 1 2 2 2                                      S АС АВ S АС АВ AC AB k j i k j i k j i            АС АВ

18 слайд
Есеп №3. Жақшаларды ашып өрнектерді ықшамда: 1 – тапсырма:       i k i k i j i k j k k k j k i k k j i j k i j i k j i k k i j k j i                                                                      2 2 2 0       c a b a b a c b c b c a a c a b b c b b b a c c c b c a a c b b c b a c c b а                                          2 0 0 2 2 – тапсырма:       k j i k k i j k j i                          a c b b c b a c c b а          

18 слайд

Есеп №3. Жақшаларды ашып өрнектерді ықшамда: 1 – тапсырма:       i k i k i j i k j k k k j k i k k j i j k i j i k j i k k i j k j i                                                                      2 2 2 0       c a b a b a c b c b c a a c a b b c b b b a c c c b c a a c b b c b a c c b а                                          2 0 0 2 2 – тапсырма:       k j i k k i j k j i                          a c b b c b a c c b а          

19 слайд
Есеп №4. Диагональдары және болып табылатын, мұнда - бірлік векторлар және олардың арасындағы бұрыш , параллелограмның ауданын табыңдар.n m    2 n m   5 4  n m   , 0 45 Шешуі: бір-біріне көбейтсек n m b a n m b a         5 4 , 2       2 5, 1 2 2 3 , 2 3 2 2 6 6 6 0 2 0 5 4 10 8                              S a b m n n m a b n n m n n m m m b b a b b a a a                         а  b 

19 слайд

Есеп №4. Диагональдары және болып табылатын, мұнда - бірлік векторлар және олардың арасындағы бұрыш , параллелограмның ауданын табыңдар.n m    2 n m   5 4  n m   , 0 45 Шешуі: бір-біріне көбейтсек n m b a n m b a         5 4 , 2       2 5, 1 2 2 3 , 2 3 2 2 6 6 6 0 2 0 5 4 10 8                              S a b m n n m a b n n m n n m m m b b a b b a a a                         а  b 

20 слайд
Есеп №5. және векторларына салынған параллелограмның диагональдары мен ауданын табыңдар. Ш ешуі: ) 1; 1 ; 0 (  а  j k a      k j i b        ) 1 ; 1 ; 1 ( b  а  b  ) 2 ; 0 ; 1 (   b а   ) 0; 2 ; 1 (     b а   5   b а   5   b а  

20 слайд

Есеп №5. және векторларына салынған параллелограмның диагональдары мен ауданын табыңдар. Ш ешуі: ) 1; 1 ; 0 (  а  j k a      k j i b        ) 1 ; 1 ; 1 ( b  а  b  ) 2 ; 0 ; 1 (   b а   ) 0; 2 ; 1 (     b а   5   b а   5   b а  

21 слайд
6 1 1 4 ) 1; 1; 2 ( 2 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 0 ,                        b a S k j i k j i k j i b a b a S               Жауабы: 6

21 слайд

6 1 1 4 ) 1; 1; 2 ( 2 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 0 ,                        b a S k j i k j i k j i b a b a S               Жауабы: 6

22 слайд
Тест сұрақтары: 1. А (-1;-2;4), В(-4;-2;0), С(3;-2;1) үшбұрышының төбелері болса, А төбесіндегі үшбұрыштың бұрышын табыңыз. А ) B) C) D) E) 2. векторлары өзара перпендикуляр. 0 60 0 30 0 45 0 180 c b a    , , у а      c a b а       3 2 болса, скаляр көбейтіндісін анықтаңыз. А ) B) C) D) E) y 0 90 2 yy3 2 3 y 3 3. Төбелері А(7;3;4), В(1;0;6), С(4;5;-2) нүктелерінде жатқан үшбұрыш ауданын тап. А ) 24 B) 23 C) 24,5 D) 23,5 E) 21

22 слайд

Тест сұрақтары: 1. А (-1;-2;4), В(-4;-2;0), С(3;-2;1) үшбұрышының төбелері болса, А төбесіндегі үшбұрыштың бұрышын табыңыз. А ) B) C) D) E) 2. векторлары өзара перпендикуляр. 0 60 0 30 0 45 0 180 c b a    , , у а      c a b а       3 2 болса, скаляр көбейтіндісін анықтаңыз. А ) B) C) D) E) y 0 90 2 yy3 2 3 y 3 3. Төбелері А(7;3;4), В(1;0;6), С(4;5;-2) нүктелерінде жатқан үшбұрыш ауданын тап. А ) 24 B) 23 C) 24,5 D) 23,5 E) 21

23 слайд
4. Егер 17 , 2 4    b a b    және 15   b a   болса, онда табыңыз. a  А ) 15 B) 13 C) 16 D) 14 E) 12 5. Егер және векторлар арасындағы бұрыш , әрі скаляр көбейтіндісі болса, онда осы векторлар арқылы салынған параллелограмның ауданы қаншаға тең болады? a  0 30 b  3   b a   А ) B) 2 C) D) 1 E) 2 1 2 3 3

23 слайд

4. Егер 17 , 2 4    b a b    және 15   b a   болса, онда табыңыз. a  А ) 15 B) 13 C) 16 D) 14 E) 12 5. Егер және векторлар арасындағы бұрыш , әрі скаляр көбейтіндісі болса, онда осы векторлар арқылы салынған параллелограмның ауданы қаншаға тең болады? a  0 30 b  3   b a   А ) B) 2 C) D) 1 E) 2 1 2 3 3

24 слайд
Тест сұрақтары: 1. А (-1;-2;4), В(-4;-2;0), С(3;-2;1) үшбұрышының төбелері болса, А төбесіндегі үшбұрыштың бұрышын табыңыз. А ) B) C) D) E) 2. векторлары өзара перпендикуляр. 0 60 0 30 0 45 0 180 c b a    , , у а      c a b а       3 2 болса, скаляр көбейтіндісін анықтаңыз. А ) B) C) D) E) y 0 90 2 yy3 2 3 y 3 3. Төбелері А(7;3;4), В(1;0;6), С(4;5;-2) нүктелерінде жатқан үшбұрыш ауданын тап. А ) 24 B) 23 C) 24,5 D) 23,5 E) 21

24 слайд

25 слайд
4. Егер 17 , 2 4    b a b    және 15   b a   болса, онда табыңыз. a  А ) 15 B) 13 C) 16 D) 14 E) 12 5. Егер және векторлар арасындағы бұрыш , әрі скаляр көбейтіндісі болса, онда осы векторлар арқылы салынған параллелограмның ауданы қаншаға тең болады? a  0 30 b  3   b a   А ) B) 2 C) D) 1 E) 2 1 2 3 3

25 слайд

26 слайд
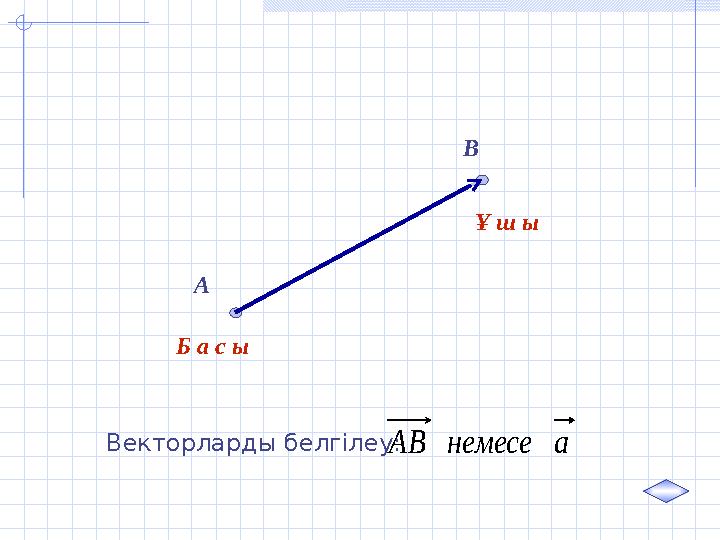
А В Б а с ы Ұ ш ы Векторларды белгілеу:а немесе АВ

26 слайд

А В Б а с ы Ұ ш ы Векторларды белгілеу:а немесе АВ

27 слайд
Вектордың абсолют шамасы немесе модулі деп векторды кескіндейтін кесіндінің ұзындығын атайды және деп белгілейді. АВ а ,  ) ; ; ( 2 2 2 z у х В ) ; ; ( 1 1 1 z у х А ) ; ; ( 3 2 1 а а а а  2 3 2 2 2 1 а а а а     2 1 2 2 1 2 2 1 2 ) ( ) ( ) ( z z у у х х АВ      

27 слайд

Вектордың абсолют шамасы немесе модулі деп векторды кескіндейтін кесіндінің ұзындығын атайды және деп белгілейді. АВ а ,  ) ; ; ( 2 2 2 z у х В ) ; ; ( 1 1 1 z у х А ) ; ; ( 3 2 1 а а а а  2 3 2 2 2 1 а а а а     2 1 2 2 1 2 2 1 2 ) ( ) ( ) ( z z у у х х АВ      

28 слайд
Егер в ектордың бас нүктесі оның ұшымен дәл келіп беттесіп жатса, онда ол векторды нөлдік вектор деп атайды және деп белгілейді. Нөлдік вектордың абсолют шамасы нөлге тең.0  0 0  

28 слайд

Егер в ектордың бас нүктесі оның ұшымен дәл келіп беттесіп жатса, онда ол векторды нөлдік вектор деп атайды және деп белгілейді. Нөлдік вектордың абсолют шамасы нөлге тең.0  0 0  

29 слайд
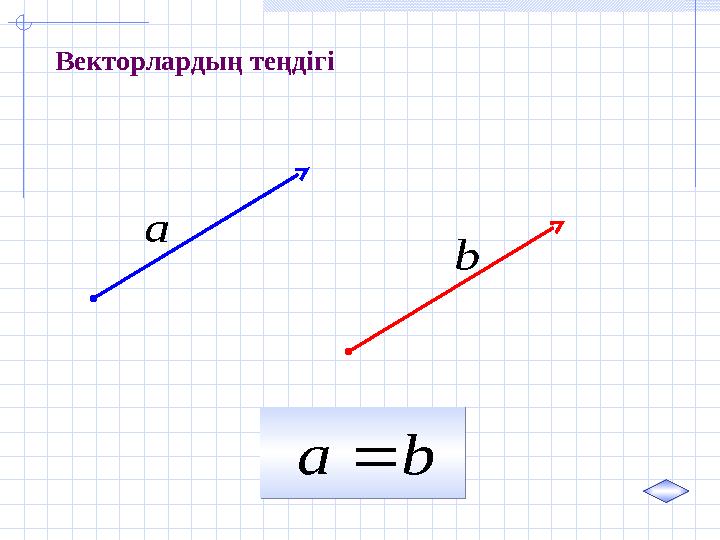
b а    b а    а  b Векторлардың теңдігі

29 слайд

b а    b а    а  b Векторлардың теңдігі

30 слайд
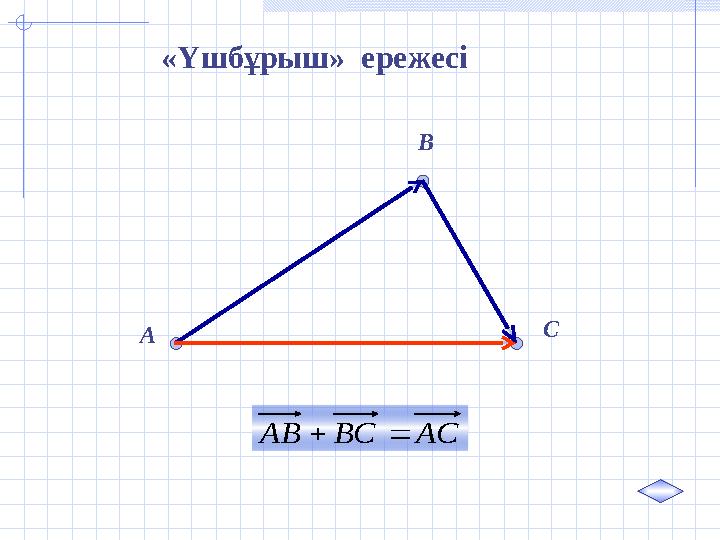
A B CАС ВС АВ  «Үшбұрыш» ережесіАС ВС АВ  

30 слайд

A B CАС ВС АВ  «Үшбұрыш» ережесіАС ВС АВ  

31 слайд
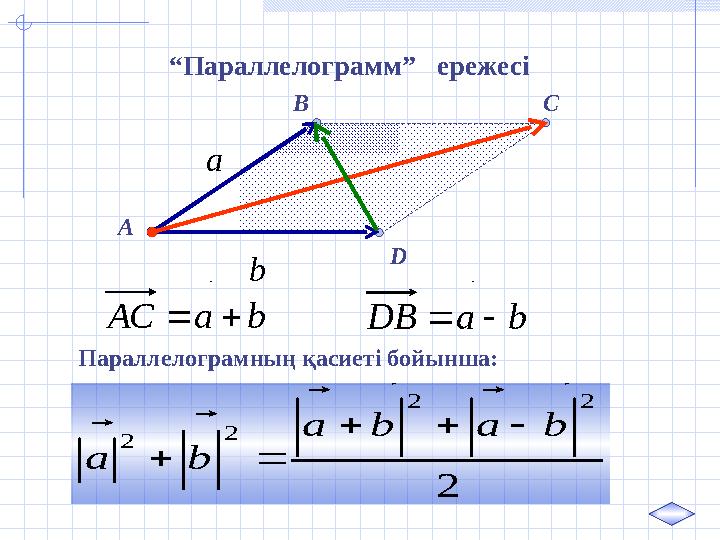
C A B D“ Параллелограмм” ережесіа  b  b а АС     b а DВ     Параллелограмның қасиеті бойынша: 2 2 2 2 2 b a b a b а           

31 слайд

C A B D“ Параллелограмм” ережесіа  b  b а АС     b а DВ     Параллелограмның қасиеті бойынша: 2 2 2 2 2 b a b a b а           

32 слайд

33 слайд
Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталады. Коллинер векторлардың сәйкес координаталары пропорционал болады. Белгілеуі: а  b  ) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b  3 3 2 2 1 1 b a b a b a  

33 слайд

Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталады. Коллинер векторлардың сәйкес координаталары пропорционал болады. Белгілеуі: а  b  ) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b  3 3 2 2 1 1 b a b a b a  

34 слайд
Нөлдік емес мен векторларының арасындағы бұрыш деп ВАС бұрышын атайды. Кез келген мен екі вектордың арасындағы бұрыш деп бас нүктесі ортақ әрі олармен тең векторлардың арасындағы бұрышты айтады. Бірдей бағытталған векторлардың арасындағы бұрыш нөлге тең деп есептеледі, ал қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа тең.АВ а  0 180 b  АC 0 0 180 0

34 слайд

Нөлдік емес мен векторларының арасындағы бұрыш деп ВАС бұрышын атайды. Кез келген мен екі вектордың арасындағы бұрыш деп бас нүктесі ортақ әрі олармен тең векторлардың арасындағы бұрышты айтады. Бірдей бағытталған векторлардың арасындағы бұрыш нөлге тең деп есептеледі, ал қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа тең.АВ а  0 180 b  АC 0 0 180 0

35 слайд
) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b мен векторларының скаляр көбейтіндісі деп санын атайды. 3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a    а  b   cos     b а b a     cos     b а b a    

35 слайд

) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b мен векторларының скаляр көбейтіндісі деп санын атайды. 3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a    а  b   cos     b а b a     cos     b а b a    

36 слайд
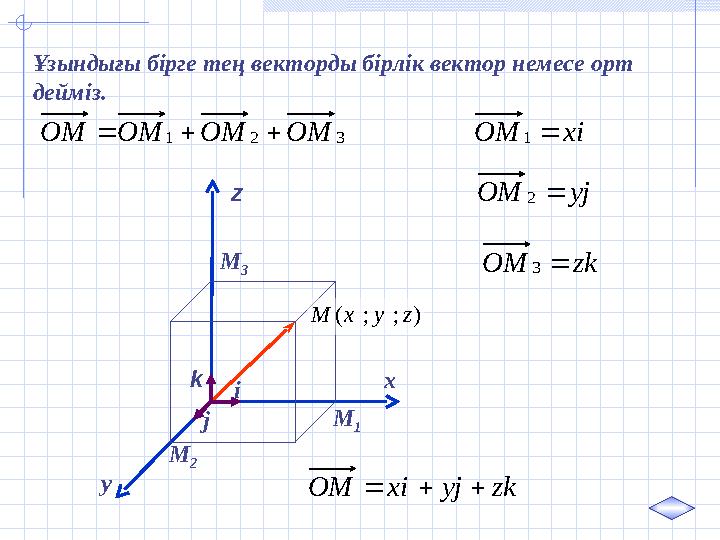
) ; ; ( z y x Mi jk x y z M 1 M 2 M 3Ұзындығы бірге тең векторды бірлік вектор немесе орт дейміз. 3 2 1 ОМ ОМ ОМ ОМ    i x ОМ   1 j y ОМ   2 k z ОМ   3 k z j y i x ОМ      

36 слайд

) ; ; ( z y x Mi jk x y z M 1 M 2 M 3Ұзындығы бірге тең векторды бірлік вектор немесе орт дейміз. 3 2 1 ОМ ОМ ОМ ОМ    i x ОМ   1 j y ОМ   2 k z ОМ   3 k z j y i x ОМ      

37 слайд
Үйге тапсырма: № 421, №427 есептер ( В.П.Минорский)

37 слайд

Үйге тапсырма: № 421, №427 есептер ( В.П.Минорский)