Виды движений

Материал туралы қысқаша түсінік

Виды движений 9.3.4.18 знать виды движений и их свойства; 9.3.4.19 уметь строить образы и прообразы фигур при симметриях, параллельном переносе, повороте, в том числе с использованием программного обеспечения;

Толегенов Олжас Шонайұлы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

07 Маусым 2022

492

0 рет жүктелген

Геометрия Презентация 9 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 56

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Виды движений 9.3.4.18 знать виды движений и их свойства; 9.3.4.19 уметь строить образы и прообразы фигур при симметриях, параллельном переносе, повороте, в том числе с использованием программного обеспечения;

1 слайд

2 слайд
Цели урока: изучить виды движений и их свойства; - различать центральную и осевую симметрию, поворот и параллельный перенос. Критерии оценивания: - распознает виды преобразования фигур; - различает виды движений и их свойства; - строит образы и прообразы фигур.

2 слайд

Цели урока: изучить виды движений и их свойства; - различать центральную и осевую симметрию, поворот и параллельный перенос. Критерии оценивания: - распознает виды преобразования фигур; - различает виды движений и их свойства; - строит образы и прообразы фигур.

3 слайд
Основные виды движений : 1. Осевая и центральная симметрии 2. Поворот 3. Параллельный перенос

3 слайд

Основные виды движений : 1. Осевая и центральная симметрии 2. Поворот 3. Параллельный перенос

4 слайд
Точки X и X ' называются симметричными относительно прямой a , и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка XX ' . Осевая симметрия.

4 слайд

Точки X и X ' называются симметричными относительно прямой a , и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка XX ' . Осевая симметрия.

5 слайд
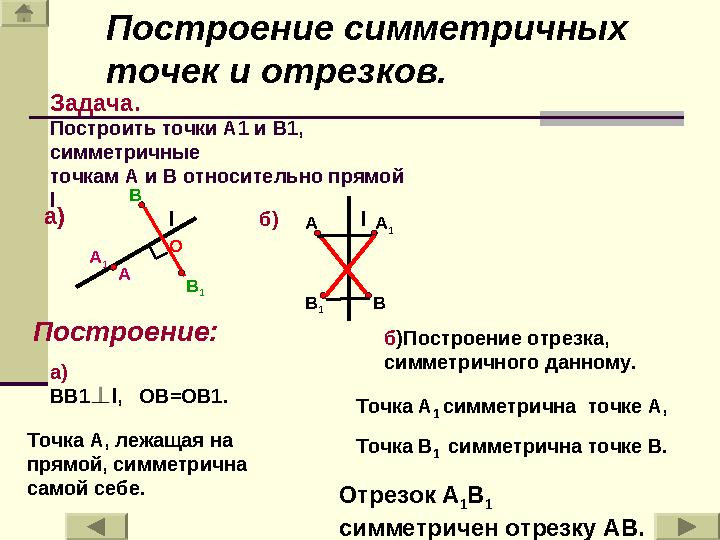
B A lа) A 1 B 1O A Blб) А 1 В 1Задача. Построить точки А1 и B 1, симметричные точкам А и В относительно прямой l Построение : а) ВВ1 l , ОВ=ОВ1. Точка А, лежащая на прямой, симметрична самой себе. б )Построение отрезка, симметричного данному. Точка А 1 симметрична точке А, Точка В 1 симметрична точке В. Отрезок А 1 В 1 симметричен отрезку АВ.Построение симметричных точек и отрезков.

5 слайд

B A lа) A 1 B 1O A Blб) А 1 В 1Задача. Построить точки А1 и B 1, симметричные точкам А и В относительно прямой l Построение : а) ВВ1 l , ОВ=ОВ1. Точка А, лежащая на прямой, симметрична самой себе. б )Построение отрезка, симметричного данному. Точка А 1 симметрична точке А, Точка В 1 симметрична точке В. Отрезок А 1 В 1 симметричен отрезку АВ.Построение симметричных точек и отрезков.

6 слайд
Осевой симметрией с осью a называется такое преобразование фигуры ,при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a .

6 слайд

Осевой симметрией с осью a называется такое преобразование фигуры ,при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a .

7 слайд
Осевая симметрия является движением . Почему отображение, сохраняющее расстояния, называется движением ? Это можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 180 0 вокруг оси а.

7 слайд

Осевая симметрия является движением . Почему отображение, сохраняющее расстояния, называется движением ? Это можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 180 0 вокруг оси а.

8 слайд
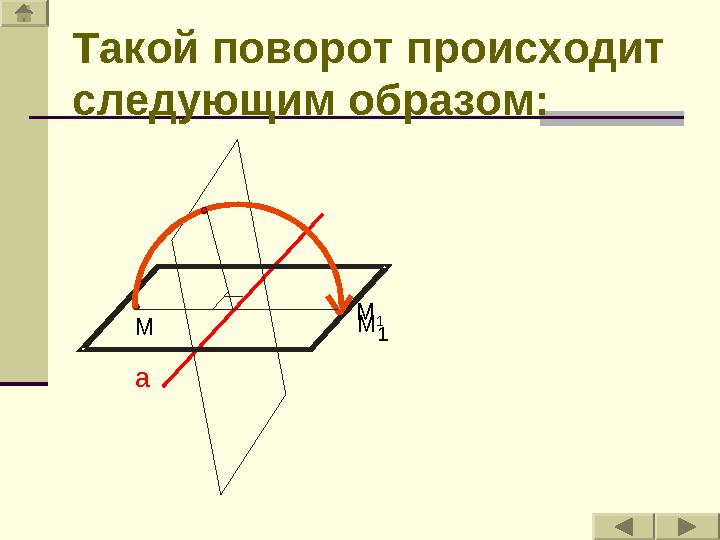
а М 1 М М 1Такой поворот происходит следующим образом :

8 слайд

а М 1 М М 1Такой поворот происходит следующим образом :

9 слайд
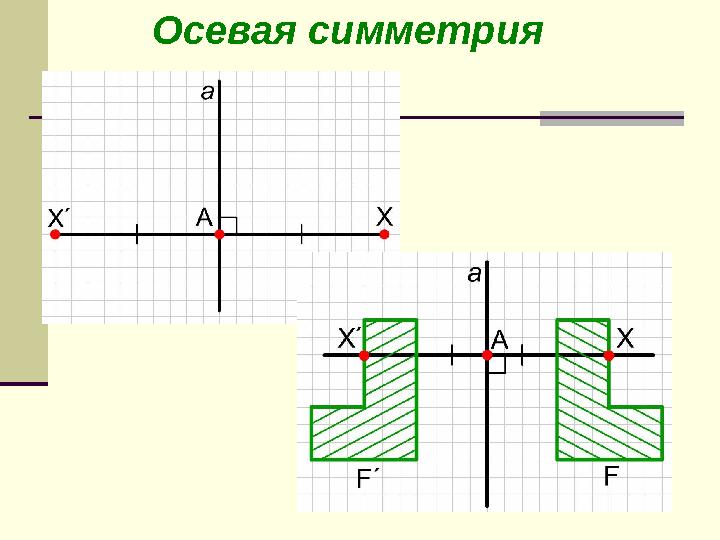
Осевая симметрияОсевая симметрия

9 слайд

Осевая симметрияОсевая симметрия

Основное свойство осевой симметрииОсновное свойство осевой симметрии Теорема Осевая симметрия является движением Доказательство

10 слайд
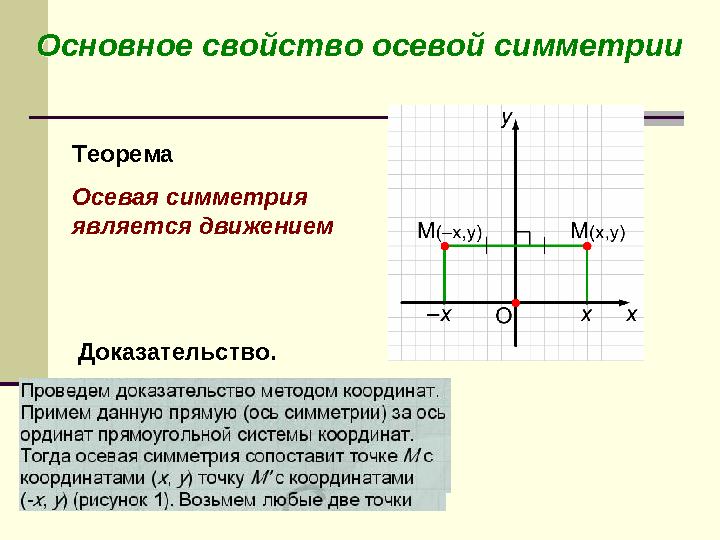
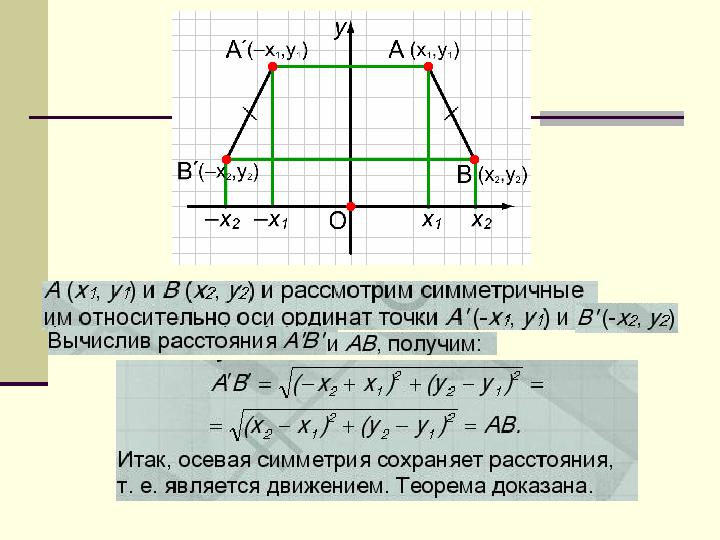
Основное свойство осевой симметрииОсновное свойство осевой симметрии Теорема Осевая симметрия является движением Доказательство.

10 слайд

Основное свойство осевой симметрииОсновное свойство осевой симметрии Теорема Осевая симметрия является движением Доказательство.

11 слайд

12 слайд
-X 0 X 0 f (-x)=f(x)Y XОсевая симметрия в системе координат.

12 слайд

-X 0 X 0 f (-x)=f(x)Y XОсевая симметрия в системе координат.

13 слайд
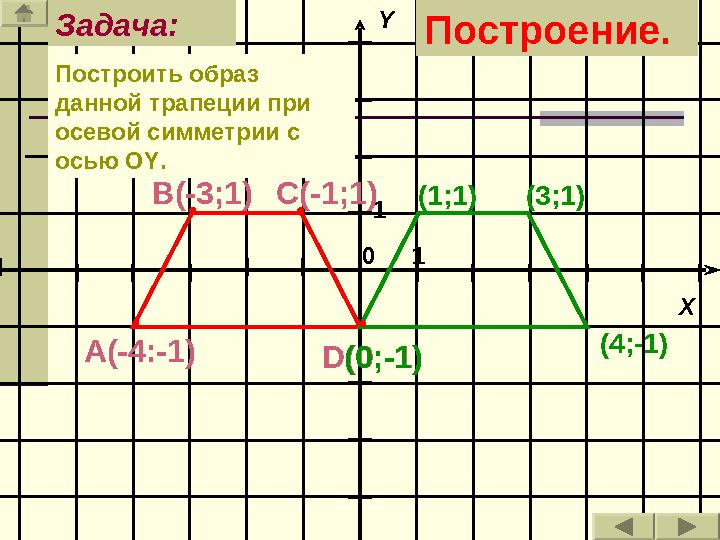
11 XY 0Построить образ данной трапеции при осевой симметрии с осью О Y .Задача: А(-4:-1) В(-3;1) С(-1;1) D (0;-1) (3;1)(1;1) (0;-1) (4;-1)Построение.

13 слайд

11 XY 0Построить образ данной трапеции при осевой симметрии с осью О Y .Задача: А(-4:-1) В(-3;1) С(-1;1) D (0;-1) (3;1)(1;1) (0;-1) (4;-1)Построение.

14 слайд
Симметрия фигуры. • Фигура называется симметричной относительно прямой a , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Фигура F симметрична относительно прямой а . Прямая а является ее осью симметрии . А ВС F a

14 слайд

Симметрия фигуры. • Фигура называется симметричной относительно прямой a , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Фигура F симметрична относительно прямой а . Прямая а является ее осью симметрии . А ВС F a

15 слайд
 Точки X и Х ' называются симметричными относительно заданной точки O , если ОХ=О Х ' , а лучи OX и О Х ' являются дополнительными . Точка O считается симметричной самой себе. Центральная симметрия. X X' O

15 слайд

 Точки X и Х ' называются симметричными относительно заданной точки O , если ОХ=О Х ' , а лучи OX и О Х ' являются дополнительными . Точка O считается симметричной самой себе. Центральная симметрия. X X' O

16 слайд
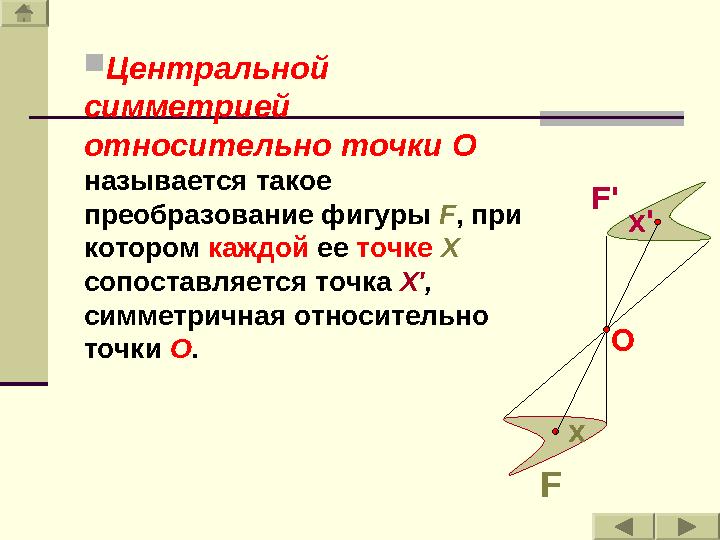
 Центральной симметрией относительно точки O называется такое преобразование фигуры F , при котором каждой ее точке X сопоставляется точка Х ' , симметричная относительно точки O . F x x'F' O

16 слайд

 Центральной симметрией относительно точки O называется такое преобразование фигуры F , при котором каждой ее точке X сопоставляется точка Х ' , симметричная относительно точки O . F x x'F' O

17 слайд
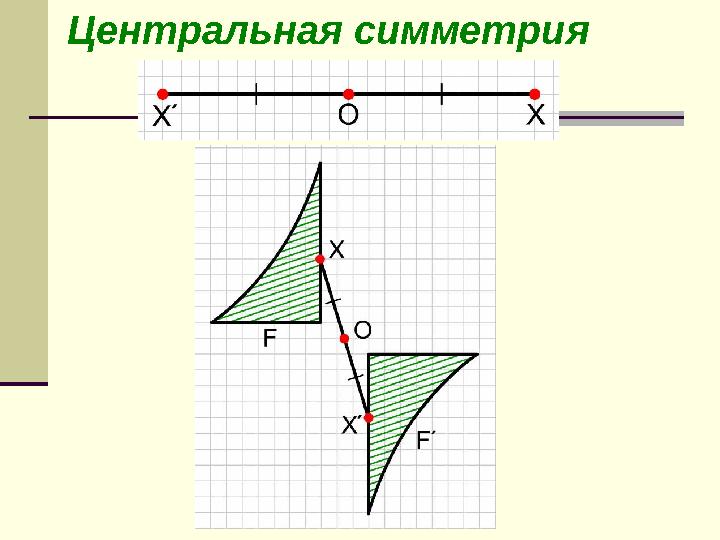
Центральная симметрияЦентральная симметрия

17 слайд

Центральная симметрияЦентральная симметрия

18 слайд
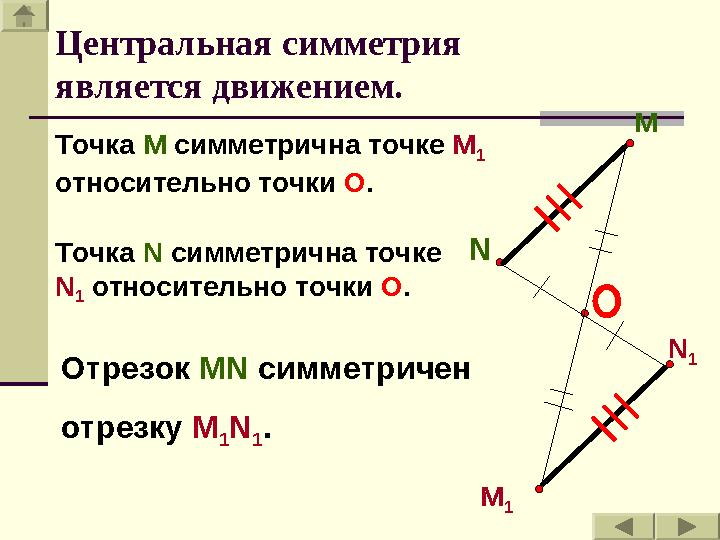
M N N 1 M 1Точка М симметрична точке М 1 относительно точки О . Точка N симметрична точке N 1 относительно точки О . Отрезок MN симметричен отрезку M 1 N 1 .Центральная симметрия является движением.

18 слайд

M N N 1 M 1Точка М симметрична точке М 1 относительно точки О . Точка N симметрична точке N 1 относительно точки О . Отрезок MN симметричен отрезку M 1 N 1 .Центральная симметрия является движением.

Основное свойство центральной симметрииОсновное свойство центральной симметрии Теорема Центральная симметрия является движени

19 слайд
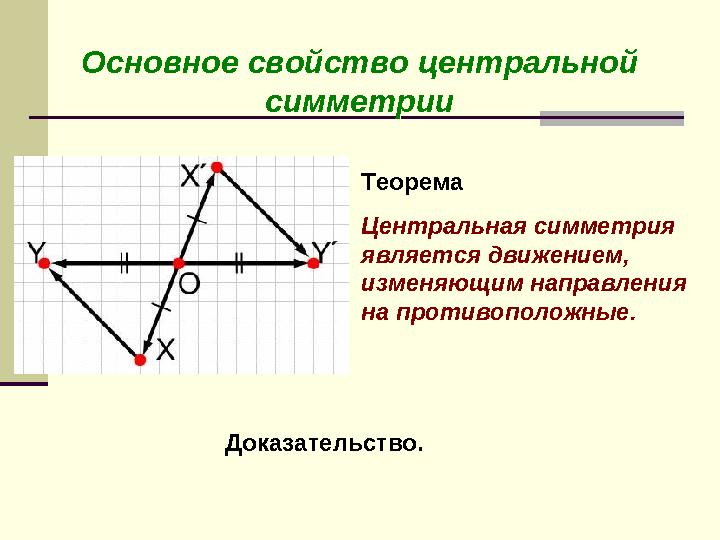
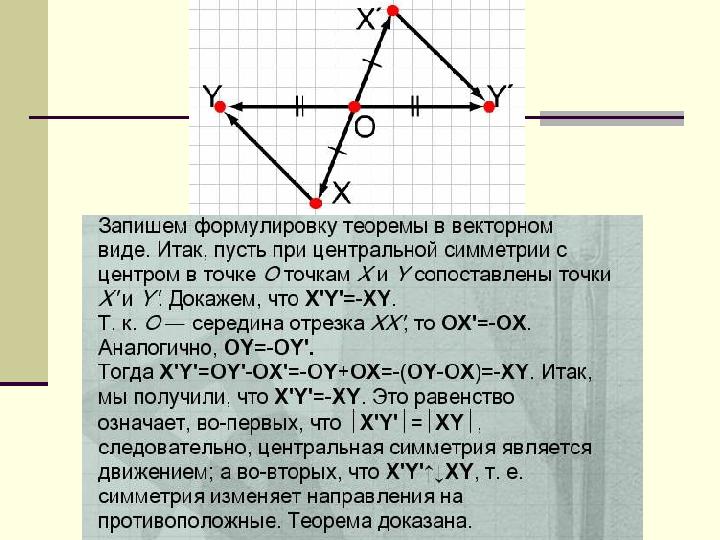
Основное свойство центральной симметрииОсновное свойство центральной симметрии Теорема Центральная симметрия является движением, изменяющим направления на противоположные. Доказательство.

19 слайд

Основное свойство центральной симметрииОсновное свойство центральной симметрии Теорема Центральная симметрия является движением, изменяющим направления на противоположные. Доказательство.

20 слайд

21 слайд
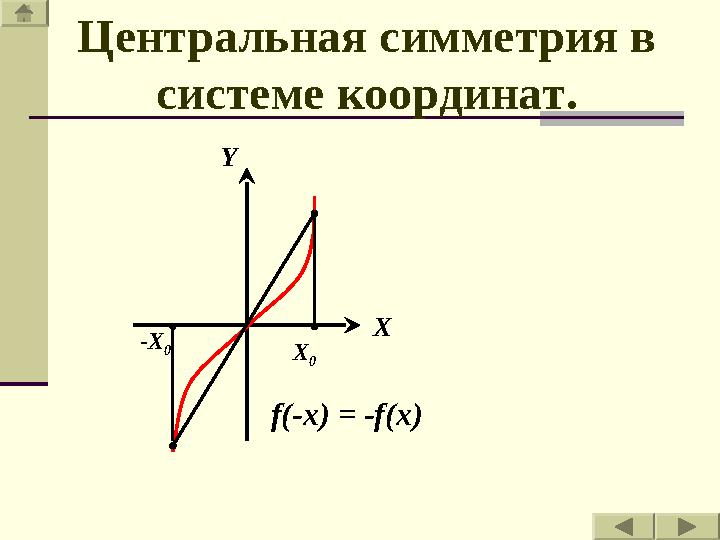
X 0-X 0 XY f(-x) = -f(x)Центральная симметрия в системе координат.

21 слайд

X 0-X 0 XY f(-x) = -f(x)Центральная симметрия в системе координат.

22 слайд
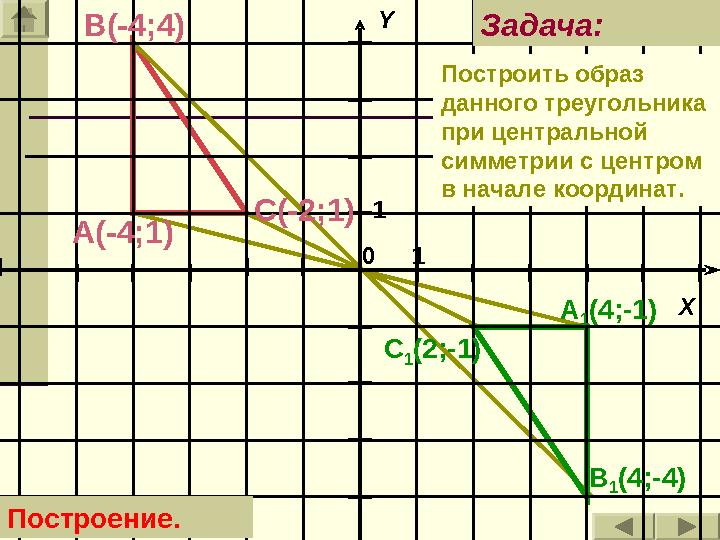
11 XY 0 B 1 (4;- 4 )С(- 2 ;1) A 1 (4;-1) C 1 ( 2 ; - 1)А(-4;1) В(- 4 ; 4 ) Задача: Построение. Построить образ данного треугольника при центральной симметрии с центром в начале координат.

22 слайд

11 XY 0 B 1 (4;- 4 )С(- 2 ;1) A 1 (4;-1) C 1 ( 2 ; - 1)А(-4;1) В(- 4 ; 4 ) Задача: Построение. Построить образ данного треугольника при центральной симметрии с центром в начале координат.

23 слайд
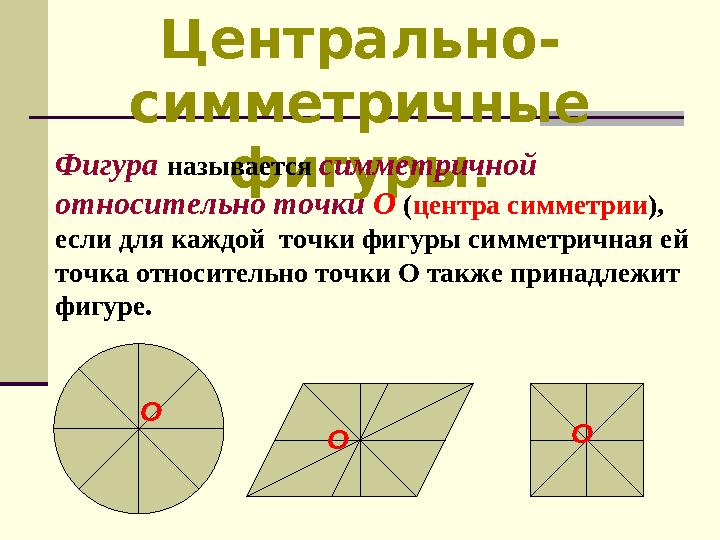
Центрально- симметричные фигуры.Фигура называется симметричной относительно точки О ( центра симметрии ), если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит фигуре. О О О

23 слайд

Центрально- симметричные фигуры.Фигура называется симметричной относительно точки О ( центра симметрии ), если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит фигуре. О О О

24 слайд
ПОВОРОТ

24 слайд

ПОВОРОТ

25 слайд
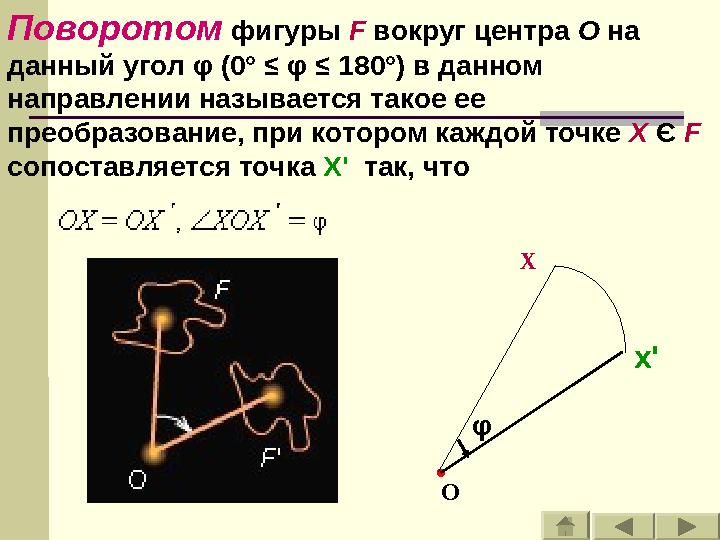
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X Є F сопоставляется точка X' так, что О X φ x'

25 слайд

Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X Є F сопоставляется точка X' так, что О X φ x'

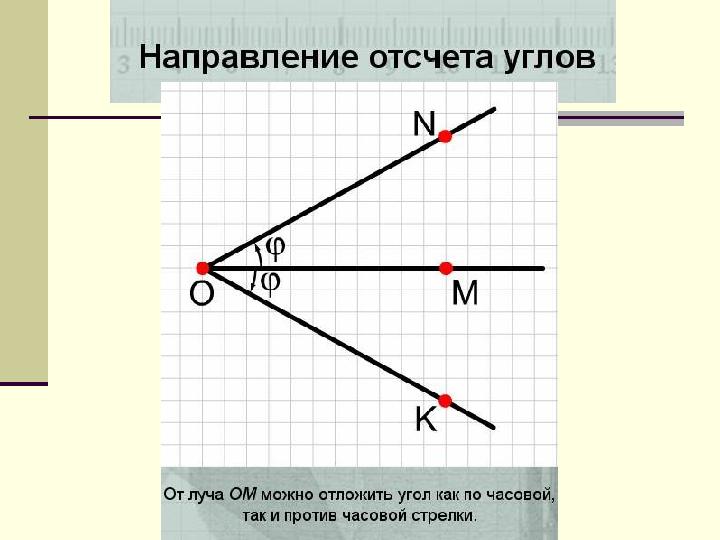
26 слайд

27 слайд

28 слайд
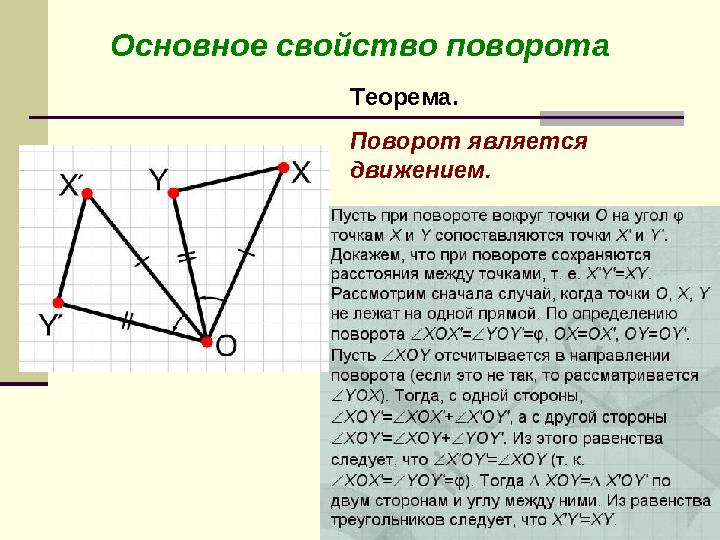
Основное свойство поворотаОсновное свойство поворота Теорема. Поворот является движением.

28 слайд

Основное свойство поворотаОсновное свойство поворота Теорема. Поворот является движением.

29 слайд

30 слайд
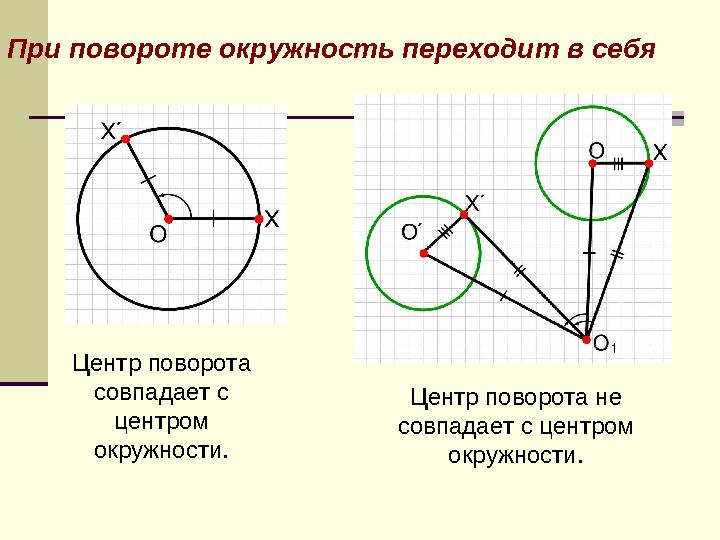
При повороте окружность переходит в себя Центр поворота совпадает с центром окружности. Центр поворота не совпадает с центром окружности.

30 слайд

При повороте окружность переходит в себя Центр поворота совпадает с центром окружности. Центр поворота не совпадает с центром окружности.

31 слайд
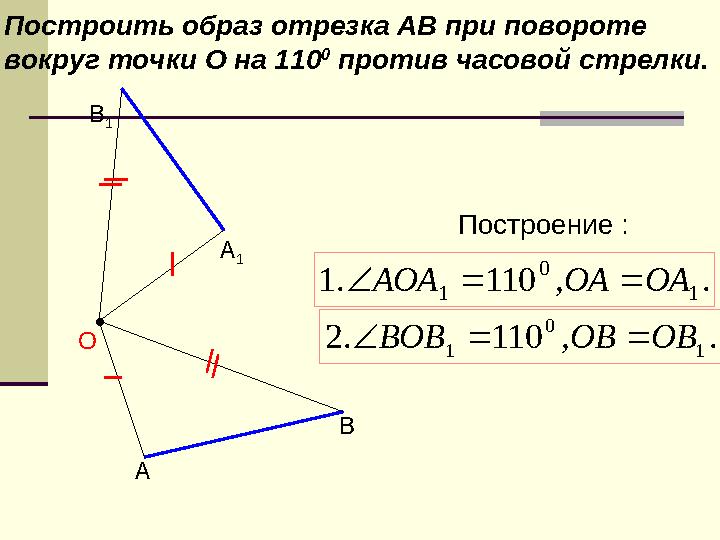
Построить образ отрезка АВ при повороте вокруг точки О на 110 0 против часовой стрелки. А ВО Построение : . , 110 . 1 1 0 1 ОА ОА АОА    . , 110 . 2 1 0 1 ОВ ОВ ВОВ    А 1В 1

31 слайд

Построить образ отрезка АВ при повороте вокруг точки О на 110 0 против часовой стрелки. А ВО Построение : . , 110 . 1 1 0 1 ОА ОА АОА    . , 110 . 2 1 0 1 ОВ ОВ ВОВ    А 1В 1

32 слайд
1. Построить образ треугольника АВС при повороте вокруг точки А на 45 0 по часовой стрелке. 2. Докажите, что при повороте правильного шестиугольника на 120 0 вокруг своего центра он отображается сам на себя.

32 слайд

1. Построить образ треугольника АВС при повороте вокруг точки А на 45 0 по часовой стрелке. 2. Докажите, что при повороте правильного шестиугольника на 120 0 вокруг своего центра он отображается сам на себя.

33 слайд
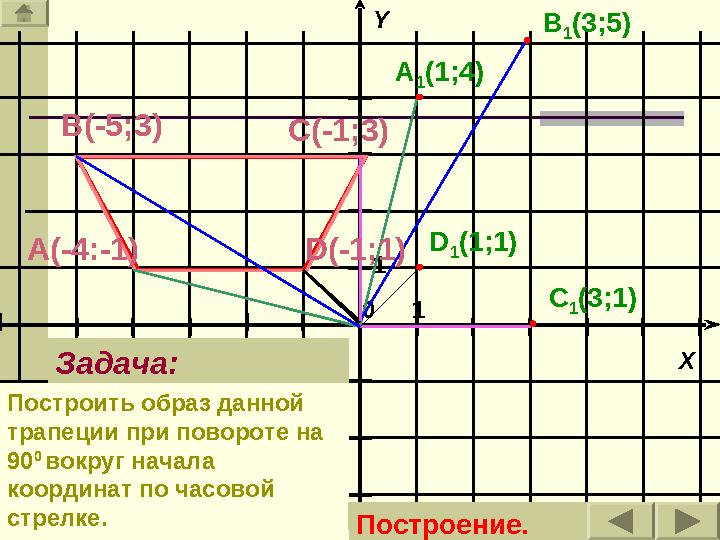
11 XY 0А(-4:-1) В(-5;3) D (-1;1)С(-1;3) A 1 (1; 4 ) B 1 (3; 5 ) C 1 (3;1)D 1 (1;1) Задача: Построить образ данной трапеции при повороте на 90 0 вокруг начала координат по часовой стрелке. Построение.

33 слайд

11 XY 0А(-4:-1) В(-5;3) D (-1;1)С(-1;3) A 1 (1; 4 ) B 1 (3; 5 ) C 1 (3;1)D 1 (1;1) Задача: Построить образ данной трапеции при повороте на 90 0 вокруг начала координат по часовой стрелке. Построение.

34 слайд
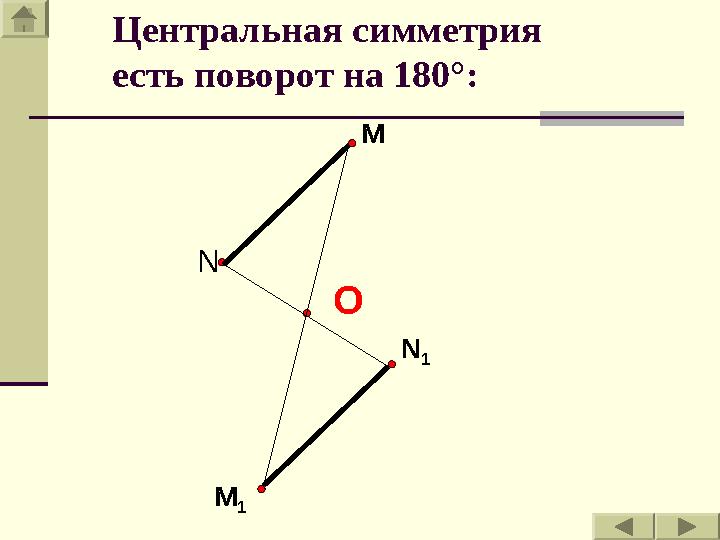
M N N 1 M 1Центральная симметрия есть поворот на 180°: О

34 слайд

M N N 1 M 1Центральная симметрия есть поворот на 180°: О

35 слайд
Параллельный перенос

35 слайд

Параллельный перенос

36 слайд
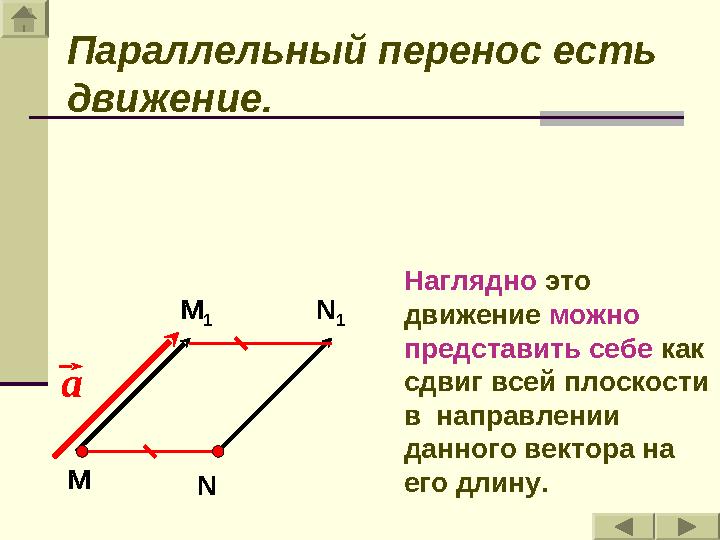
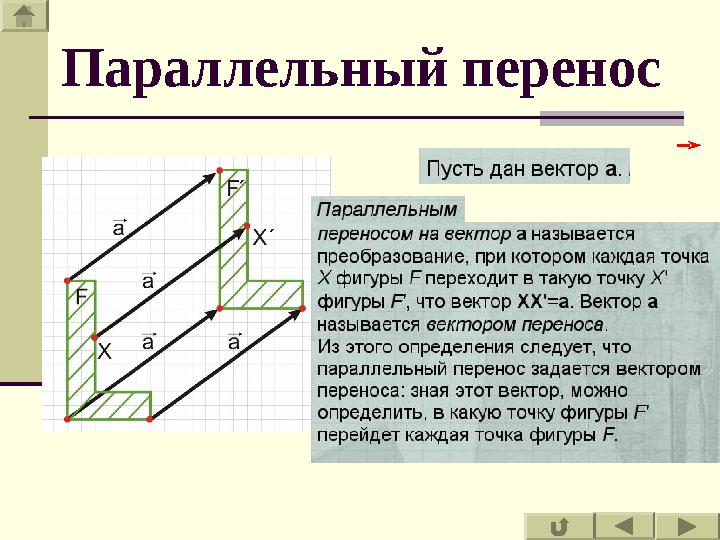
Параллельный перенос есть движение. a М NM 1 N 1 Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

36 слайд

Параллельный перенос есть движение. a М NM 1 N 1 Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

37 слайд
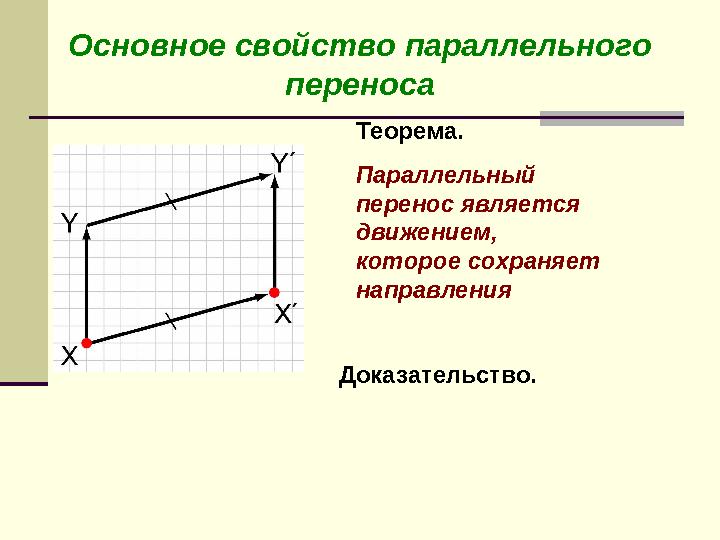
Основное свойство параллельного переносаОсновное свойство параллельного переноса Теорема. Параллельный перенос является движением, которое сохраняет направления Доказательство.

37 слайд

Основное свойство параллельного переносаОсновное свойство параллельного переноса Теорема. Параллельный перенос является движением, которое сохраняет направления Доказательство.

38 слайд

39 слайд
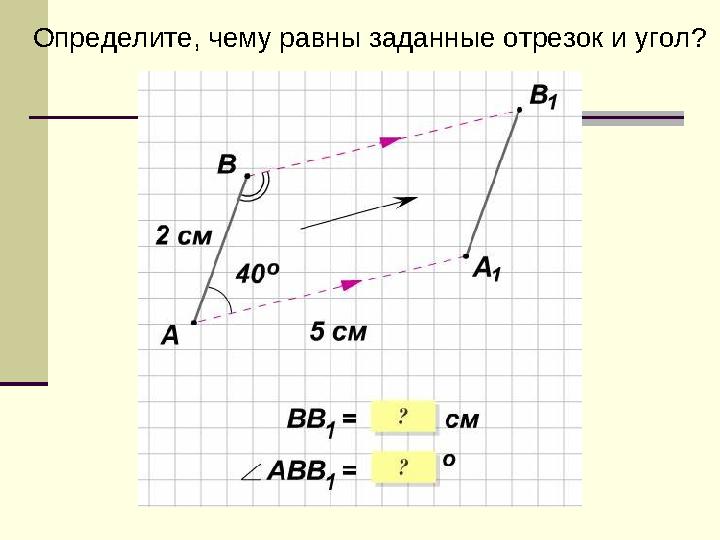
Определите, чему равны заданные отрезок и угол?

39 слайд

Определите, чему равны заданные отрезок и угол?

40 слайд
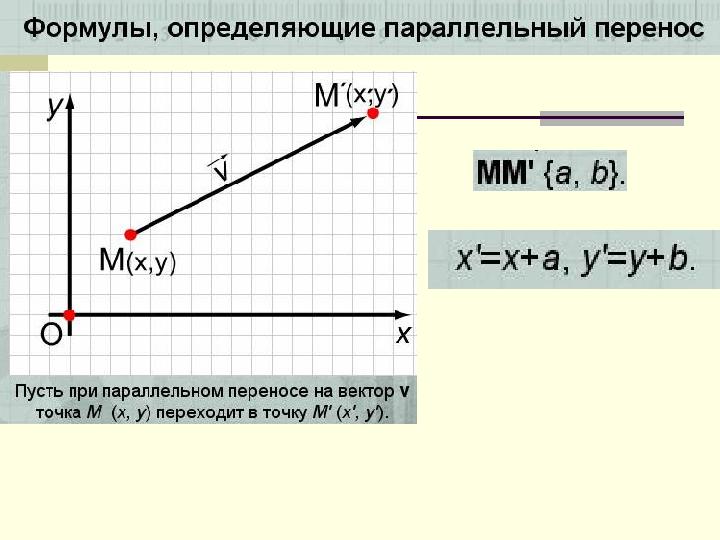
Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O , X , Y . Преобразование фигуры F , при котором произвольная ее точка M ( x ; y ) переходит в точку M ' (x+a ; y+b) , где a и b – одни и те же для всех точек ( x ; y ), называется параллельным переносом.

40 слайд

Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O , X , Y . Преобразование фигуры F , при котором произвольная ее точка M ( x ; y ) переходит в точку M ' (x+a ; y+b) , где a и b – одни и те же для всех точек ( x ; y ), называется параллельным переносом.

41 слайд

42 слайд
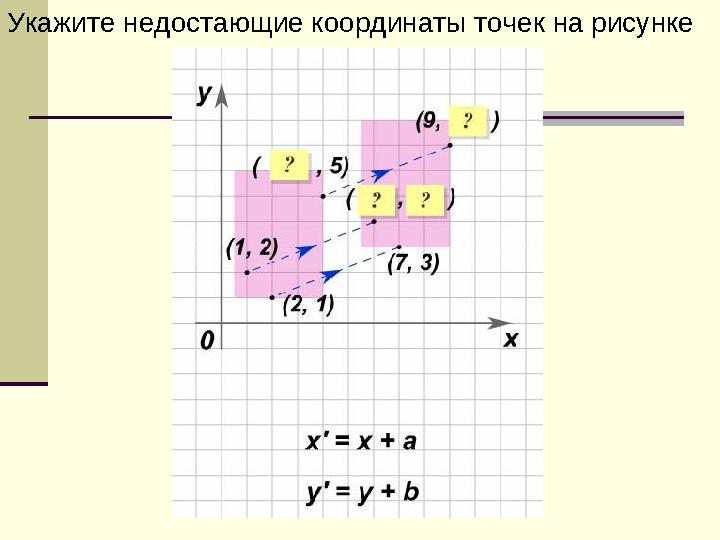
Укажите недостающие координаты точек на рисунке

42 слайд

Укажите недостающие координаты точек на рисунке

43 слайд
Задача 1. В результате параллельного переноса вершины квадрата ABCD переходят соответственно в вершины квадрата А 1 В 1 С 1 D 1 . Найдите координаты точек В 1 , С 1 , D 1 , если А(1;-2), А 1 (5;6), В(4;2), С(0;5), D (-3;1). Ответ. В 1 (8;10), С 1 (4;13), D 1 (1 ; 9)

43 слайд

Задача 1. В результате параллельного переноса вершины квадрата ABCD переходят соответственно в вершины квадрата А 1 В 1 С 1 D 1 . Найдите координаты точек В 1 , С 1 , D 1 , если А(1;-2), А 1 (5;6), В(4;2), С(0;5), D (-3;1). Ответ. В 1 (8;10), С 1 (4;13), D 1 (1 ; 9)

44 слайд
Задача 2. Составьте уравнение образа окружности х 2 +у 2 -2х-4у-10=0 при параллельном переносе на вектор   . 4 ; 2 а  Ответ. (х-3) 2 +(у-6) 2 =15.

44 слайд

Задача 2. Составьте уравнение образа окружности х 2 +у 2 -2х-4у-10=0 при параллельном переносе на вектор   . 4 ; 2 а  Ответ. (х-3) 2 +(у-6) 2 =15.

45 слайд
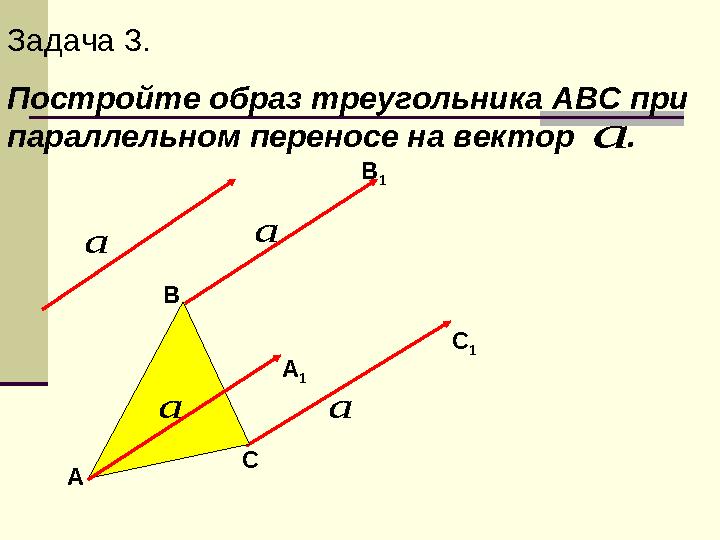
Задача 3. Постройте образ треугольника АВС при параллельном переносе на вектор . а  А В С А 1 В 1 С 1 а  а  а  а 

45 слайд

Задача 3. Постройте образ треугольника АВС при параллельном переносе на вектор . а  А В С А 1 В 1 С 1 а  а  а  а 

46 слайд
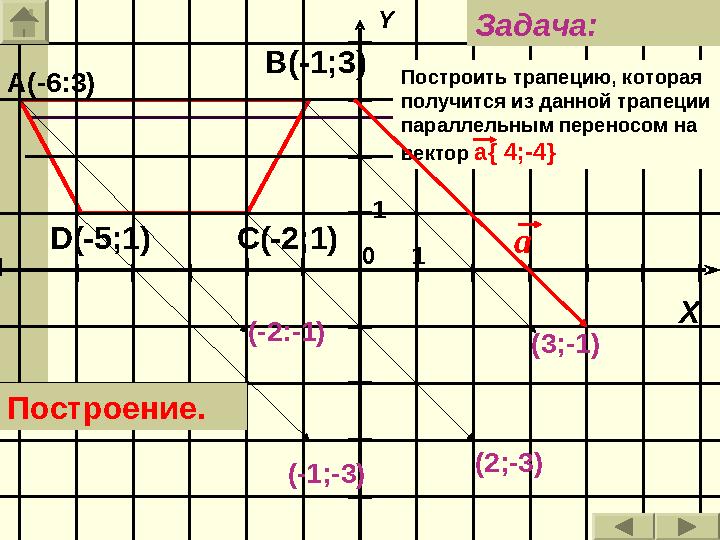
11 XY 0А(-6:3) В(-1;3) С(-2;1)D (-5;1) Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор а { 4;-4 }Задача: а Построение. (-2:-1) (3;-1) (2;-3) (-1;-3)

46 слайд

11 XY 0А(-6:3) В(-1;3) С(-2;1)D (-5;1) Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор а { 4;-4 }Задача: а Построение. (-2:-1) (3;-1) (2;-3) (-1;-3)

47 слайд
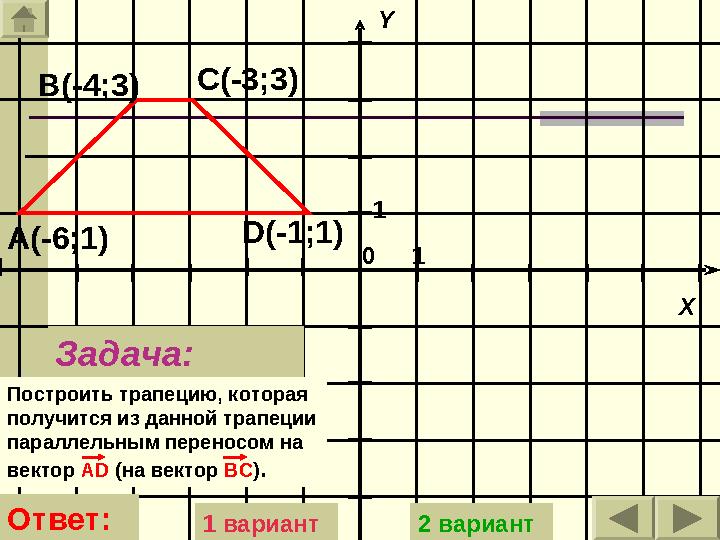
11 XY 0 Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор А D (на вектор BC ) .А(-6;1) В(-4;3) С(-3;3) D (-1;1) Ответ: 1 вариант 2 вариант

47 слайд

11 XY 0 Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор А D (на вектор BC ) .А(-6;1) В(-4;3) С(-3;3) D (-1;1) Ответ: 1 вариант 2 вариант

48 слайд
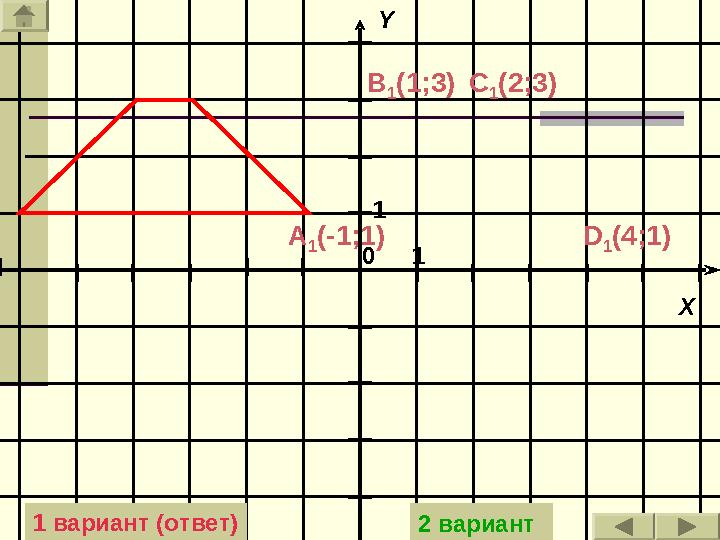
11 XY 0 C 1 (2;3) D 1 (4;1)B 1 (1;3) A 1 (-1;1) 1 вариант (ответ) 2 вариант

48 слайд

11 XY 0 C 1 (2;3) D 1 (4;1)B 1 (1;3) A 1 (-1;1) 1 вариант (ответ) 2 вариант

49 слайд
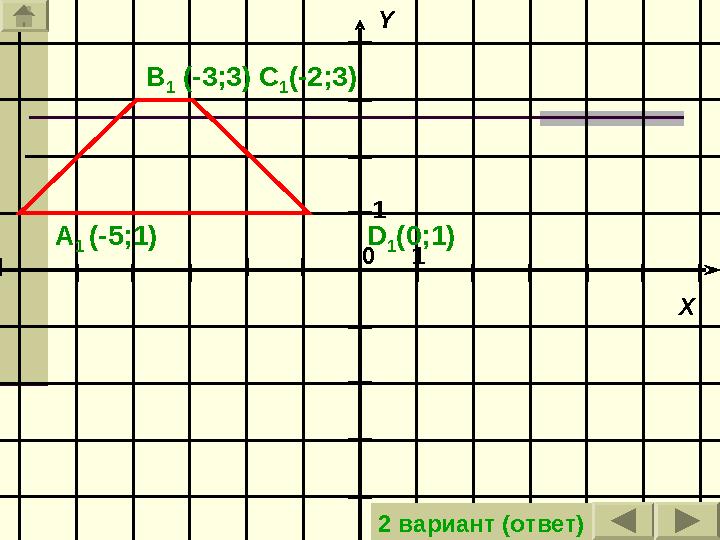
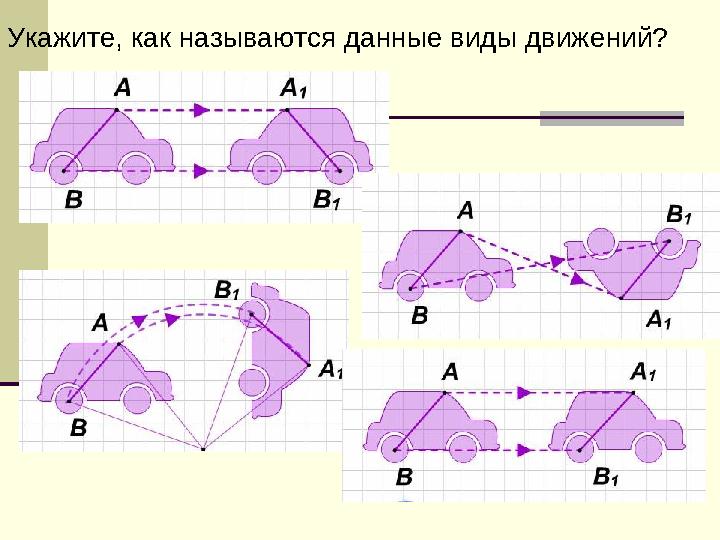
11 XY 0A 1 (-5;1) B 1 (-3;3) C 1 (-2;3) D 1 (0;1) 2 вариант (ответ)

49 слайд

11 XY 0A 1 (-5;1) B 1 (-3;3) C 1 (-2;3) D 1 (0;1) 2 вариант (ответ)

50 слайд
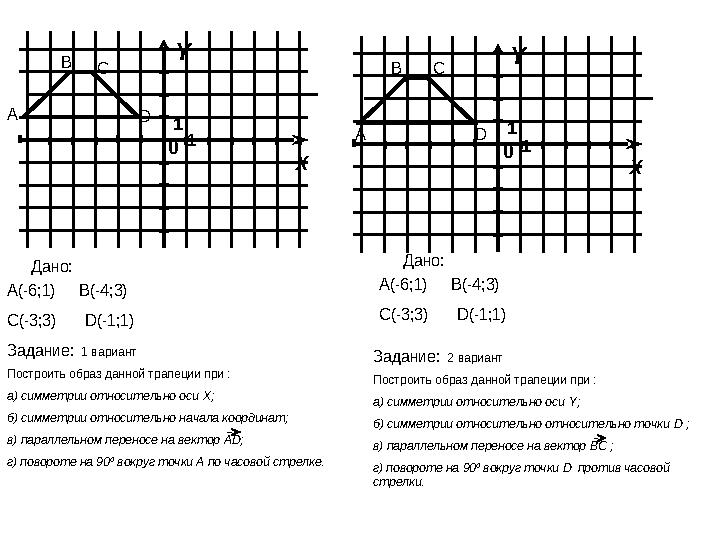
Укажите, как называются данные виды движений?

50 слайд

Укажите, как называются данные виды движений?

51 слайд
1. Построить образ треугольника АВС при повороте вокруг точки А на 45 0 по часовой стрелке. 2. Докажите, что при повороте правильного шестиугольника на 120 0 вокруг своего центра он отображается сам на себя.

51 слайд

52 слайд
Индивидуальная работа

52 слайд

Индивидуальная работа

53 слайд
А Задание: 1 вариант Построить образ данной трапеции при : а) симметрии относительно оси X ; б) симметрии относительно начала координат; в) параллельном переносе на вектор AD ; г) повороте на 90 0 вокруг точки А по часовой стрелке.D (-1;1)А(-6;1) С(-3;3) В(-4;3) 11 XY 0В С D Дано: 11 XY 0В С D D (-1;1)А(-6;1) С(-3;3) В(-4;3)Дано: Задание: 2 вариант Построить образ данной трапеции при : а) симметрии относительно оси Y ; б) симметрии относительно относительно точки D ; в) параллельном переносе на вектор BC ; г) повороте на 90 0 вокруг точки D против часовой стрелки.А

53 слайд

А Задание: 1 вариант Построить образ данной трапеции при : а) симметрии относительно оси X ; б) симметрии относительно начала координат; в) параллельном переносе на вектор AD ; г) повороте на 90 0 вокруг точки А по часовой стрелке.D (-1;1)А(-6;1) С(-3;3) В(-4;3) 11 XY 0В С D Дано: 11 XY 0В С D D (-1;1)А(-6;1) С(-3;3) В(-4;3)Дано: Задание: 2 вариант Построить образ данной трапеции при : а) симметрии относительно оси Y ; б) симметрии относительно относительно точки D ; в) параллельном переносе на вектор BC ; г) повороте на 90 0 вокруг точки D против часовой стрелки.А

54 слайд
Домашнее задание: Учебник Математика 9 класс часть 2, стр.127-137, №№ 9.21, 9.30, 9.40, 9.52

54 слайд

Домашнее задание: Учебник Математика 9 класс часть 2, стр.127-137, №№ 9.21, 9.30, 9.40, 9.52

55 слайд
9.3.4.18 знать виды движений и их свойства ; 9.3.4.19 уметь строить образы и прообразы фигур при симметриях, параллельном переносе, повороте, в том числе с использованием программного обеспечения; Рефлексия

55 слайд

9.3.4.18 знать виды движений и их свойства ; 9.3.4.19 уметь строить образы и прообразы фигур при симметриях, параллельном переносе, повороте, в том числе с использованием программного обеспечения; Рефлексия