
БҚО Ақжайық ауданының білім бөлімінің әдістемелік кабинеті
Анықталған және анықталмаған интеграл
(Әдістемелік құрал)
(№1 орта жалпы білім беретін мектебінің екінші
санатты математика пәні мұғалімдері
Т.Б.Нургалиеваның іс-тәжірибесінен )
Чапаев, 2017 жыл
№1 орта жалпы білім беретін мектебінің әдістемелік бірлестігінің сараптама кеңесінде қаралып, аудан көлемінде таратуға мақұлданды.
Хаттама №1
Т.Б.Нургалиева математика пәні мұғалімдері
Пікір жазған:
№1 орта жалпы білім беретін мектебінің жоғары санатты математика
пәні мұғалімі Смаилова Гулжанат Иратовна
Ұстаз-ұрпақ тәрбиелеп өсіруші қоғам тапсырып сенген өкіл. Ұстаздық қызметтің қыры мен сыры мол, сан қилы және әр тарапты.
Нургалиева Турсынай Болатовна -2009 жылдан бері өзінің еңбек жолын бастады. Проблемалық тақырыбы «Математика сабағында логикалық есептерді қолдану арқылы оқушылардың ойлау қабілеттерін дамыту», Жантемирова Назгуль Орынбасаровна проблемалық тақырыбы «»Турсынай Болатқызы және Назгуль Орынбасаровна –жаңа технологияға негізделген жаңашыл ұстаз. Сабақтың сапалы болуын және тиімді жағын арттырып отырады. Сабақ өткізу барысында пәнге деген қызығушылығын арттыру мақсатында оқушылардың бір-біріне деген жолдастық қарым-қатынасы арта түсіп, бір-біріне бар ынта жігерімен көмектесіп, үйретуге, есептердің шығару жолдарын қолдануда оқушылардың ойлау қабілеттерін арта түсетіндігі байқалады. Бүгінгі жас маман ертеңгі ұлағатты ұстаздардың орнын басатын, олардан үлгі алатын, шәкірттердің сүйікті ұстазына айналатын тұлға болатынына сенімдімін.
Түсінік хат
Ұсынылып отырған әдістемелік құрал орта мектептің жаратылыстану-математика бейіндік бағытында математика пәнін тереңдетіп оқытуда қолдануға арналған. Әдістемелік құралда қысқаша теориялық түсінік пен интегралдық есептеуге арналған әр түрлі есептер жинақталып, оларды шешу әдістемесі көрсетілген, есептердің күрделілігіне қарай деңгейлік жаттығу жұмыстары мен бақылау жұмысы тапсырмалары, тестік тапсырмалар берілген.
Әдістемелік құралдың негізгі мақсаты- жан-жақты ойластырылып құрастырылған есептерді оқушыларға шешу арқылы олардың ойлау қабілеті мен шығармашылық белсенділігінің дамуына ықпал ету, есептерді шығару дағдысын жетілдіре түсуге көмектесу болып табылады. Сонымен қатар, математика пәнінің қолданбалы салаларын оқушыларға таныстыру, соның негізінде математиканы қолдану салаларын оқушыларға айқындау болып табылады.
МАЗМҰНЫ
Кіріспе
Функцияны интегралдау
-
Анықталмаған интеграл
-
Функцияның алғашқы бейнесі және анықталмаған интеграл
-
Интегралдар кестесі
-
Анықталмаған интегралдарды есептеу әдістері
-
Тікелей интегралдау әдісі
-
Айнымалыларды ауыстыру арқылы интегралдау әдісі
-
Бөліктеп интегралдау әдісі
-
-
Жаттығулар
Деңгейлік тестік тапсырмалар
-
Анықталған интеграл
-
Анықталған интеграл әдісі
-
Анықталған интегралды есептеу
-
Ньютон-Лейбниц формуласы
-
Айнымалыны алмастыру әдісі
-
Бөліктеп интегралдау әдісі
-
-
Жаттығулар
Деңгейлік тестік тапсырмалар
-
Анықталған интегралдың геометрияда қолданылуы
-
Тік бұрышты координаталардағы аудан
-
Қисық доғасының ұзындығы
-
Айналу денесінің көлемі
-
Айналу бетінің ауаны
-
Жаттығулар
Деңгейлік тестік тапсырмалар
Білімін тексеруге арналған қосымша тестік тапсырмалар
Функцияны интегралдау
-
Анықталмаған интеграл
-
Функцияның алғашқы бейнесі және анықталмаған интеграл
-
Есеп қарастырайық. f(x) функциясы берілсін: туындысы f(x) функциясына тең болатын F(x) функциясын табу керек, яғни F/(x)=f(x).
1-анықтама. Егер х[а,в] аралығында F/(x)=f(x) теңдігі орындалса, онда осы аралықта F(x) функциясы f(x) функциясы үшін алғашқы бей+несі деп аталады.
Мысал
f(x)=х2
функциясының алғашқы бейнесін
табу керек. Алғашқы бейненің анықтамасы бойынша
F(x)= функциясы алғашқы бейне
болады, себебі
функциясы алғашқы бейне
болады, себебі  =х2.
=х2.
Бұл функцияның алғашқы бейнесі
бір мәнді болмайды, себебі F(x)= +1,
F(x)=
+1,
F(x)= -7 немесе жалпы
F(x)=
-7 немесе жалпы
F(x)= +C (мұндағы С-ерікті
тұрақты) функциясы да С-ның кез келген мәнінде
f(x)=х2
функциясының алғашқы бейнесі
болады, яғни (
+C (мұндағы С-ерікті
тұрақты) функциясы да С-ның кез келген мәнінде
f(x)=х2
функциясының алғашқы бейнесі
болады, яғни ( )/=x2.
)/=x2.
Қорыта айтқанда, егер берілген f(x) функциясының алғашқы бейнесі F(x) болса, онда бұдан басқа алғашқы бейненің түрі F(x)+С болады. Бұл келесі теоремадан шығды.
Теорема. Егер f(x)функциясының алғашқы бейнелері бар болса, онда олардың айырымы тұрақты шамаға тең.
2-анықтама. Егер F(x) функциясы берілген f(x) функциясының алғашқы бейнесі болса, онда F(x)+С өрнегі f(x) фунциясының анықталмаған интегралы деп аталады және ∫f(x)dxсимволымен белгіленеді, яғни анықтама бойынша ∫f(x)dx =F(x)+С, мұндағы f(x)- интеграл астындағы функция, f(x)dx – интеграл астындағы өрнек, ∫- интеграл әдісі.
Берілген функцияның алғашқы бе+йнесін табу интегралдау амалы деп аталады.
Геометриялық тұрғыдан анықталмаған интеграл жазықтықта бір-бірінен айырымы тұрақты шама болатындай қисықтар жиынын көрсетеді. Бқл қисықтарды интегралдық қисықтар деп атайды.
Мысалы, f/(x)=2x және f(2)=5болса, онда , f/(x) функциясын табыңыз.
Шешуі:
f/(x)= =2x . Бұдан
dy=2x*dx
=2x . Бұдан
dy=2x*dx
∫dy=∫2x*dx , онда y=x2+C болады. y=f(x)=x2+C онда C=1 шығады. Ендеше f(x)=x2+1 болады.
Анықталмаған интегралдың негізгі қасиеттері:
10. (∫f(x)dx)/=(F(x)+C)/=f(x)
20. ∫kf (x)dx=k ∫f(x)dx
30. ∫ (f(x)+g(x))dx= ∫f(x)dx+∫g(x)dx
40.
 ∫
f(x)dx=f(x)
∫
f(x)dx=f(x)
50. ∫df (x)=f(x)+C
60. ∫
f(ax+b)dx= F
(ax+b)+C
F
(ax+b)+C
Мысалдар
-
а)
 [∫ (x2+5)dx]=x2+5
[∫ (x2+5)dx]=x2+5
b)
 (∫
(∫ )=
)=
g) ∫d(sinx)=
∫ (sinx)dx=sinx+C
(sinx)dx=sinx+C
d)
 ∫ d
(x3+x2+x+5)=
∫ d
(x3+x2+x+5)= (x3+x2+x+5)=
3x2+2x+1.
(x3+x2+x+5)=
3x2+2x+1.
-
Егер f(x)=∫d(x2-4) болса, онда f/(5) неге тең?
Шешуі: Теңдіктен f(x)= x2-4 шығады. Бұдан f/(х)=2x. f/(5)=2*5=10 болады.
-
Егер f(x)= ∫(x3-4x+5)dx болса, онда x=2 нүктесінде жанаманың бұрыштық коэффициенті неге тең?
Шешуі: f(x)=∫ f/(x)dx қасиетін пайдалансақ, онда f(x)=(x3-4x+5) болады. Ендеше f/(2) =23-4*2+5=5
-
Егер ∫x*f(x)dx=2x2+5x-3 болса, онда f(x) неге тең?
Шешуі: Анықталмаған
интегралдың қасиетін пайдалансақ:
x*f(x)=(2x2+5x-3)/. Ендеше x*f(x)=(4х+5), бұдан
f(x)= =4+
=4+ болады.
болады.
-
Егер F(x)=∫

-
f(x)=∫(х2-2х+3)dx фунциясының иілу нүтесін табыңыз.
-
Интегралдар кестесі
Интегралдау амалы дифференциалдау амалына кері амал.
-
∫xndx=
 +C
+C -
∫
 =ln|x|+C
=ln|x|+C -
∫ax*dx=
 +C
(a≠1)
+C
(a≠1) -
∫eˣ*dx=eˣ+C
-
∫sinx*dx=-cosx+C
-
∫cosx*dx=sinx+C
-
∫

-
∫
 =-ctgx+C
=-ctgx+C -
∫tgx*dx=-ln|cosx|+C
-
∫ctgx*dx=ln|sinx|+C
-
∫
 rctgx+C
(-arcctgx+C)
rctgx+C
(-arcctgx+C)
11/.
∫ =
= arctg
arctg +C
(-
+C
(- arcctg
arcctg )
)
-
∫
 =
= ln
ln |+C
(a≠0)
|+C
(a≠0) -
∫
 =arcsinx+C
(-arccosx+C)
=arcsinx+C
(-arccosx+C)
13/.

-
∫

Мысалдар:
-
A) ∫x3dx=

b) ∫5dx=5x+C
c)
∫5xdx=5∫xdx=5*
d) ∫
(5x²+2)dx=5∫x²dx+2∫dx=5*
2. a)
∫
b) ∫
 dx.
dx.
3. a) ∫ 5³ˣdx b) ∫ 5³ˣ+4dx g) ∫e2xdx
4. a)
∫sin5xdx=-
b) ∫cos
(5x+3)dx=
d)
∫
g)
∫
1.3 Анықталмаған интегралдарды есептеу әдістері
Интегралды интегралдау әдістері интеграл астындағы функцияның берілуіне және интегралдау кестесінің қорына байланысты:
-
Тікелей интегралдау;
-
Айнымалыларды ауыстыру арқылы интегралдау;
-
Бөліктеп интегралдау.
Осы тәсілдерді жеке қарастырайық:
-
Тікелей интегралдау әдісі
Функцияларды анықталмаған интегралдың қасиеттері мен интегралдар кестесіне сүйеніп тікелей интегралдауға болады. Ал, тригонометриялық фнкцияларды интегралдағанда қосымша келесі келтіру формулаларын пайдалануға болады:
-
sin²x+cos²x=1, sinx=

-
ctgx=
 ,
tgx*ctgx=1
,
tgx*ctgx=1 -
cosec
 ,
secx=
,
secx=
-
sin2x=2sinx*cosx, cos2x=cos²x-sin²x=2cos²x-1=1-2sin²x
-
sinx*cosy=

cosx*siny=  (sin(x+y)-sin(x-y))
(sin(x+y)-sin(x-y))
cos*cosy= (cos(x+y)+cos(x-y))
(cos(x+y)+cos(x-y))
sinx*siny= (cos(x+y)-cos(x-y)).
(cos(x+y)-cos(x-y)).
Мысал,
∫ интегралын есептеп, нәтижесін
дифференциалдау арқылы тексеріңдер. Алымын бөліміне бөліп,
интегралдың қасиетін және кестені пайдаланып, шығарамыз:1.
∫
интегралын есептеп, нәтижесін
дифференциалдау арқылы тексеріңдер. Алымын бөліміне бөліп,
интегралдың қасиетін және кестені пайдаланып, шығарамыз:1.
∫ -1/4dx-2∫
x15/4dx+∫
x5/12dx=4x3/4-
-1/4dx-2∫
x15/4dx+∫
x5/12dx=4x3/4- x19/4+
x19/4+ x17/12+C=4
x17/12+C=4 -
- 19+
19+ 12√x17+C.
12√x17+C.
-
∫

-
∫ cos7xdx
-
∫sin(2x-6)dx
-
∫ sin²xdx
Интеграл астындағы функцияның
бөліміндегі өрнектен толық квадратты бөліп аламыз. Сонда 1.
∫  =
= ∫
∫
 =
=  =4√3/6√13arctg
=4√3/6√13arctg
-
∫

-
∫
 dx
dx
Алымында бөлімінің туындысына
тең болатын қосылғышты айырып алып, алатынымыз: 4.
∫ =∫(4-8x)-2/5dx=-
=∫(4-8x)-2/5dx=- (4-8x)3/5+C=-
(4-8x)3/5+C=- ⁵√(4-8x)³+C
⁵√(4-8x)³+C
5.∫
6.
∫ dx
dx
7.
∫ dx=
∫
dx=
∫ dx=
∫
dx=
∫ =dx=
∫(1-cosx)dx=x-sinx+C
=dx=
∫(1-cosx)dx=x-sinx+C
1.3.2 Айнымалыларды ауыстыру арқылы интегралдау әдісі
Кейде интегралдағы х айнымалысының орнына жаңа t айнымалысын енгізіп, берілген ∫f(x)dx интегралын тікелей интегралданатын кестелік интегралдың біріне келтіруге болады. Бұл интегралдау әдісін айнымалыларды ауыстыру әдісі деп атайды Бұл әдістің негізі күрделі функциялардың дифференциалдау формуласы болып табылады.
Теорема. Анықталмаған ∫f(x)dx интегралындағы х айнымалысының орнына x=φ(t) формуласы бойынша жаңа t айнымалысын енгізсек, берілген анықталмаған интеграл үшін
∫ f(x)dx=∫f[φ(t)]φ/(t)dt (1)
теңдігі орындалады.
Бұл әдісті қолдану берілген айнымалыны қандай формула бойынша ауыстыруға байланысты.
Мысалдар:
-
∫ х√х-3dx
Квадрат түбірден құтылу үшін √х-3=t деп жаңа t айнымалысын енгіземіз. Сонда x=t²+3және dx=2t dt. Ауыстыруды енгізген соң, аламыз:
∫ x√x-3xdx= ∫ (t²+3)t2tdt= ∫
(2t⁴+6t²)dt=
 5/2+2
(x-3)3/2+C
5/2+2
(x-3)3/2+C
-
∫

-
∫ √sinxcosxdx= |t=sinx, dt=cosxdx|=∫√tdt=∫ t1/2dt=
 t2/3+C=
t2/3+C= sin3/2x+C
sin3/2x+C -
∫ x(x²+1)3/2dx
-
∫ esinxcosxdx
Интеграл астындағы өрнек екі көбейткіштен тұрады, түбірден құтылатындай жаңа айнымалы енгіземіз:
t=sinx , x=arcsint
dx= , cosx=
√1-sin²x=√1-t²
, cosx=
√1-sin²x=√1-t²
∫esinxcosxdx=
∫et√1-t² =
∫etdt=
et+C=esinx+C
=
∫etdt=
et+C=esinx+C
-
∫ √a²-x²dx
1.3.3 Бөліктепинтегралдауәдісі
Бұл әдіс көбейтіндінің туындысы формуласына негізделген:
(uv)/=u/*v+v/*u
мұндағы u=u(x) және v=v(x)-дифференциалдары үзіліссіз х-ке байланысты функциялар. Дифференциалдық түрде былай жазуға болады:
d(uv)= udv+vdu
Бұл теңдіктің екі жағын да интегралдасақ: ∫ d(uv)= ∫ udv+ ∫ vdu Анықталмаған интегралдың келтірілген қасиеттеріне байланысты шығатыны:
uv=∫udv+∫ vdu немесе ∫ udv= uv-∫ vdu (2)
(2) формула бөліктеп интегралдау формуласы деп аталады. Бұл әдісті қолданғанда интеграл астындағы өрнекті екі көбейткіштің (u және dv) кһбейтіндісі түрінде қарастырады. Сол себепті бөліктеп интегралдау әдісінің тиімділігі u және dv көбейткіштерін дұрыс таңдап алуға байланысты болады.
Мысалдар:
-
∫ x²sinxdx
-
∫e2xcosxdx
-
∫ (x-7)sin5xdx= |
 |=
-
|=
-  (x-7)cos5x+
(x-7)cos5x+ ∫
cos5xdx=-
∫
cos5xdx=-  (x-7)cos5x+
(x-7)cos5x+ sin5x+C
sin5x+C -
∫
 dx
dx
Өзін-өзі тексеруге арналған сұрақтар
-
«Функцияның алғашқы бейнесі» ұғымының анықтамасы
-
Анықталмаған интегралдың негізгі қасиеттері
-
Интегралдар кестесі
-
Интегралдау әдісі
-
Айнымалыны алмастыру әдісі
-
Бөліктеп интегралдау әдісі.
Жаттығулар
-
Тікелей интегралдау әдісін пайдаланып, төмендегі интегралды есептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫ √3+xdx |
∫ ³√(1+x)²dx |
|
2 |
∫ |
∫ |
|
3 |
∫ |
∫ |
|
4 |
∫sin(2-3x)dx |
∫sin(3+4x)dx |
|
5 |
∫ |
∫ |
|
6 |
∫ |
∫ |
|
7 |
∫ |
∫ |
|
8 |
∫ |
∫ |
|
9 |
∫ |
∫ |
|
10 |
∫ |
∫ |
ІІ. Айнымалылардыалмастыру әдісін пайдаланып, төмендегі интегралды есептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫ |
∫ |
|
2 |
∫2xexdx |
∫34xdx |
|
3 |
∫tg²7xdx |
∫sin²xdx |
|
4 |
∫ |
∫ |
|
5 |
∫ |
∫ |
III. Бөліктепинтегралдауәдісінпайдаланып, төмендегіинтегралдардыесептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫xlnxdx |
∫ |
|
2 |
∫ (1-x) cos5xdx |
∫ (x-7) cos2xdx |
|
3 |
∫(x-4)sin2xdx |
∫(x+4)sin2xdx |
|
4 |
∫ x²(sinx+1)dx |
∫ x²(sin2x-3)dx |
|
5 |
∫x²cos2xdx |
∫(x-3)²cosxdx |
|
6 |
∫ (x²+x)e-xdx |
∫(x+1)e2xdx |
|
7 |
∫ |
∫ |
|
8 |
∫xsin²xdx |
∫xsin²(x+3)dx |
Тестік тапсырмалар
ТЕСТ 1
-
∫
 dx
dx
-
ln(x-1)+x+C
-
x-lnx+C
-
2lnx+C
-
x+lnx+C
-
3x-2lnx+C
-
∫ (
 )dx
)dx
-
-
 +
+ +C
+C -
X-lnx+C
-
lnx+
 +C
+C -
x+lnx+C
-
2lnx-
 +C
+C
-
∫
 dx
dx
-
1/2x²-3x+4ln|x+2|+C
-
1/3x³-2x+ln|x+2|+C
-
x²-3x+ln|x+2|+C
-
1/2x²+3x+C
-
1/4x²-4x+4ln|x+2|+C
-
∫
 dx
dx
-
ln(x²+1+x+C)
-
x-
 +C
+C -
x+2arctg(x²+1)+C
-
arctgx+C
-
x+2arcrgx+C
-
∫

-
³√x²+7+x+C
-
x√x²+7+C
-
1/2√x²+7+C
-
√x²+7+C
-
½(x²+7)+C
-
∫
 dx
dx
-
 arctg3ˣ+C
arctg3ˣ+C -

-
arcsin3ˣ+C
-

-

-
∫
 dx
dx
-
tg(lnx)-lnx+C
-
tg(lnx)+C
-
tg²(lnx)+C
-
tg(lnx)-
 +C
+C -

-
∫
 dx
dx
-
-
 x²-3x+4ln|x+2|+C
x²-3x+4ln|x+2|+C -
1/3x³-2x+ln|x+2|+C
-
x²-3x+ln|x+2|+C
-
 x²+3x+C
x²+3x+C -
 x²-4x+4ln|x+2|+C
x²-4x+4ln|x+2|+C
-
∫(√x+1)²dx
-
 (√x+1)²+C
(√x+1)²+C -
 √x+1+C
√x+1+C -
 x²-
x²- x√x+x+C
x√x+x+C -

-

-
∫
 dx
dx
-
 arctg³x+C
arctg³x+C -

-
X+2arctgx+C
-
Arctgx+C
-
 arctg²x+C
arctg²x+C
ТЕСТ 2
-
∫ (
 )dxболса, ондаf/(0)=?
)dxболса, ондаf/(0)=?
-

-

-
3
-
0
-

-
f(x)=∫ (eˣlnx+x+3)dxболса, ондаfn(1)=?
-
4
-
2
-
2e
-
e+1
-
2e+1
-
∫ (x-2)f(x)dx=2x²-3x+1 болса, онда f(x) функциясықандай?
-
4x-3
-

-
X+3
-

-

-
∫ (3x²-3)dx
-
 x³-3x+C
x³-3x+C -

-

-

-
x³-3x+C
-
∫ (eˣ-
 )dx
)dx
-
eˣ+
 +C
+C -
xeˣ-
 +C
+C -
eˣ-lnx+C
-
eˣ+lnx+C
-
2eˣ-lnx+C
-
∫
 dx
dx
-
1/2ln(x²+2)+C
-
½(√x+1)²+C
-
1/2ln²(x²+2)+C
-
½(x²+2)+C
-
1/2x+x+C
-
∫ eˣ³x²dx
-
1/3eˣ³+x²+C
-
½(eˣ+1)²+C
-
1/3eˣ³+C
-
½(x²+eˣ)+C
-
1/2(eˣ+x)²+C
-
∫

-
Sinx+2cosx+C
-
–sinx-2cosx+C
-
2sinx+cosx+C
-
sin²x+2cos²x+C
-
sinx-2cosx+C
-
∫ sin6xcosxdx
-
 sin7x+C
sin7x+C -
 sin5x-cosx+C
sin5x-cosx+C -

-
 sin7x+C
sin7x+C -
 sin5x+C
sin5x+C
-
∫

-
1/3arctg³x+C
-
x-

-
x+2arctgx+C
-
2/3√arctg³x+C
-
1/3arctg²x+C
-
Анықталған интеграл
Оқушы білуі керек: анықталған интегралдың жазылуы мен анықтамасын; анықталған интеградың геометриялық мағынасын; анықталған интегралдың қасиеттерін; анықталған интегралдың шешу әдістерін.
Оқушы білуі қажет: анықталған интегралды есептеуді.
-
Анықталған интеграл ұғымы.
Анықтама. [а,в] аралығында
үзіліссіз y=f(x) функциясы берілсін. [а,в] аралығын
a=x0<x1<x2<…<xn=b нүктелерімен n бөлікке
бөлейік. Δxi=xi-xi-1
(i=1,2,…n) элементар
аралықтарынан сәйкес ζi
(i=1,2,…n) нүктесін алып, осы
нүктелердегі функцияның f(ζ1),
f(ζ2),…f(ζn) мәндерін есептеп,
f(ζi)Δi
(i=1,2,…n) көбейтінділерінен
қосынды құрып,  n=f(xi)Δxi+f(x2)Δx2+…+f(xn)Δxn=Σni=1f(xi)Δxiқосынды f(x) функциясының
[а,в] аралығындағы интегралдық қосынды деп
аталады.
n=f(xi)Δxi+f(x2)Δx2+…+f(xn)Δxn=Σni=1f(xi)Δxiқосынды f(x) функциясының
[а,в] аралығындағы интегралдық қосынды деп
аталады.
Анықтама. Егер maxΔxi→0 (n→∞) болғанда интегралдық өосындының ақырлы шегі бар болса, онда ол f(x) функциясының [а,в] аралығындағы анықталған интегралы деп аталады. Белгіленуі: ba∫ f(x)dx.
Сонымен ,
lim Σn
f(xi)Δxi= f(x)dx.
(1)
f(x)dx.
(1)
max→0 i=1
мұндағы f(x)- интеграл астындағы функция. f(x)dx –интеграл астындағы өрнек, а саны- интегралдың төменгі шегі, в саны- интегралдың жоғарғы шегі, х айнымалысы- интегралдау айнымалысы деп аталады.
Анықталған интегралдың негізгі қасиеттері:
-

-

-

-

-

-
Егер [а,в] (а<в) аралығындағы х айнымалысының барлық мәндері үшін f(x)≥0 болса, онда
 ≥0
≥0 -
Егер [а,в] (а<в) аралығындағы f(x)≤φ(x) болса, онда

-
Анықталған интегралды есептеу
-
Ньютон-Лейбниц формуласы
-
Теорема. Егер F(x) функциясы
[а,в] аралағындағы  функциясының алғашқы
бейнесі болса, онда
функциясының алғашқы
бейнесі болса, онда
 (2)
(2)
Бұл теңдік Ньютон-Лейбниц формуласы деп аталады.
Кейде мына белгілеу
қолданылады:  ba.
ba.
Ньютон-Лейбниц формуласы анықталған интегралды есептеуге арналған жалпы формула. Ал анықталған интегралды есептеу әдістері анықталмаған интегралды есептеу әдістерімен бірдей. Мысалдар:
-
 |31=
|31=

-

-

-

-

-
Айнымалыны алмастыру әдісі
Теорема. [а,в] аралығында
үзіліссіз y=f(x) функциясы үшін  анықталған интеграл
берілсін. X=φ(t) формуласы бойынша жаңа t
айнымалысын енгізейік:
анықталған интеграл
берілсін. X=φ(t) формуласы бойынша жаңа t
айнымалысын енгізейік:
 [φ(t)φ/(t)dt]
(3)
[φ(t)φ/(t)dt]
(3)
Мысалдар:
-
 =
= 32=
32= (3³-2³)=
(3³-2³)=
-

-

-

-

-
Бөліктеп интегралдау әдісі
u(x), v(x) функциялары х аргументі бойынша [а,в] аралығында дифференциалданатын функциялар болсын. Сонда d(uv)=udv+vdu болатыны белгілі. Осыдан теңдікті [а,в] аралығында интегралдасақ, онда
 ba-
ba-
 (4)
(4)
(4) формуласы анықталған интегралды бөліктеп интегралдау формуласы деп аталады.
Мысалдар:
-
 =
-xctgx|π/3π/4+
=
-xctgx|π/3π/4+ |π/3π/4+ln|sinx||π/3π/4=-
|π/3π/4+ln|sinx||π/3π/4=-

-
 x+lnxdxdx
x+lnxdxdx -

-

-

Өзін-өзі тексеруге арналған сұрақтар
-
Анықталған интегралдың анықтамасы
-
Ньютон-Лейбниц формуласы
-
Анықталған интегралда айнымалыны алмастыру формуласы
-
Анықталған интегралда бөліктеп интегралдау әдісі.
Жаттығулар
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Деңгейлік тест тапсырмалары
Тест1
-
 dx
dx
А)ln(е+1)
В) ln(3+е)
С)1+ ln3
D)3+ln3
E)е+ ln3
2. dx
dx
A)2 -2е
-2е
В) -е
-е
С)2 -е
-е
D)е-
2
Е) -2е
-2е
3. -6х+9)dx
-6х+9)dx
A)2 В)3 С)6 D)5 Е)1,5
4. dx
dx
A)cos1
В)-cos1
С)1-sin1
D)sin1-1
Е)
5. dx
dx
A)
В)
С)
D)
Е)
6. dx
dx
A)
В)32
С)
D)64
Е)
7.
A)3
В)2
С)1
D)4
Е)
8. dx
dx
A)-24
В)
С)
D)
Е)
9. dx
dx
A)
В)
С) D)
D) Е)
Е)
10. dx
dx
A)
 B) 2
C)
B) 2
C)  D) 3
E)
D) 3
E)
ТЕСТ
2
1. dx
dx
A) 9 B)-12
C) D) 12
E)-9
D) 12
E)-9
2. dx
dx
A)
 B) 24
C)
B) 24
C) D)
D)
 E)-4
E)-4
3. dx
dx
A)
 B) 2 C)1
D)
B) 2 C)1
D)  E)
E)
4. dx
dx
A)
 B)
2
B)
2 C)
C) D)
D)
 E)
E)
5. )dx
)dx
A)-1 B) 1
C) D)
D)
 E)2
E)2
6.
A)1+
 B) 1
C)
B) 1
C) D)
D)
 E)
E)
7. dx
dx
A)
 B)
2
B)
2 C)
C) D)
D)
 E)
0
E)
0
8. dx
dx
A)e B)
2 C)
C) -1
D)
-1
D)  E)
e-
E)
e-
9. 4 *(3
4 *(3 )dx
)dx
A)-
 B) 1
C)
B) 1
C) D)
D)
 E)
E)
10.
A)0 B) -2
C) D)
D)
 E)2
E)2
2.3 Анықталған интегралдың геометрияда қолданылуы
2.3.1. Тікбұрышты координаталардағы аудан
а)Егер
[a,b]кесіндісінде  болса,онда осы
кесіндіде
болса,онда осы
кесіндіде
S(x)= dx
dx
Интегралы қисық сызықты трапецияның ауданын өрнектейді.
Егер
[a,b]кесіндісінде  болса,онда қисық сызықты
трапеция Ох осінің төменгі жағында орналасқан
және
болса,онда қисық сызықты
трапеция Ох осінің төменгі жағында орналасқан
және  dx
dx 0. Бұл интеграл
трапецияның ауданын «минус» таңбасымен
анықтайды.
0. Бұл интеграл
трапецияның ауданын «минус» таңбасымен
анықтайды.
Мысалы y=sinx синусойдасымен және Ох осімен шектелген аймақтық ауданды табу керек. (0≤x≤2π)
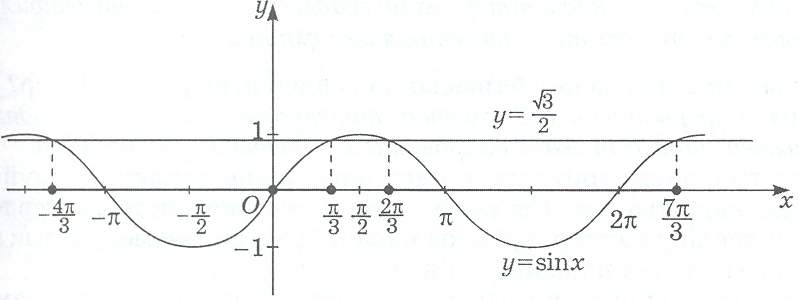
2 cурет Функцияның графигі
[0 ] аралығында
sinx
] аралығында
sinx 0, ал
[
0, ал
[ ] аралығында
sinx
] аралығында
sinx 0 болғандықтан, берілген
аймақтың ауданын табамыз.
0 болғандықтан, берілген
аймақтың ауданын табамыз.
S(G)= -
- =-cosx
=-cosx +cosx
+cosx =-cos
=-cos -cos
-cos =4
=4
б)x=a,x=b
түзулерімен
және [a,b]
аралығында үзіліссіз
у=f1(x),
у=f2(x)
(мұндағы
f1(x) f2(x))
функциялардың графиктерімен
шектелген аймақтың ауданы мына формуламен
табылады:
f2(x))
функциялардың графиктерімен
шектелген аймақтың ауданы мына формуламен
табылады:
S(x)= dx
dx
Мысалдар:1.
y= ,
y=x2
параболамен шектелген G
аймағының ауданын табу керек.
,
y=x2
параболамен шектелген G
аймағының ауданын табу керек.
Шешуі
 теңдеулер жүйесін ,
осы қисықтардың (0;0) және (1;1) қиылысу нүктелерін табамыз. [0;1]
кесіндісінде
теңдеулер жүйесін ,
осы қисықтардың (0;0) және (1;1) қиылысу нүктелерін табамыз. [0;1]
кесіндісінде  ≥х2
орындалатын
болғандықтан
≥х2
орындалатын
болғандықтан
S(G)= dx=
dx= -
- =
= -
- =
=

4сурет. Фигураның ауданы.
-
y=lnx және y=
 x қисықтарымен шектелген
фигураның ауданын табыңдар.
x қисықтарымен шектелген
фигураның ауданын табыңдар.
Шешуі. Қисықтардың қиылысу нүктелерін табамыз: М1(1,0),М2(е,1)
S(x)= dxформуласын
қолданамыз. S=
dxформуласын
қолданамыз. S= dx
dx
 xdx=
xdx= =x
=x

![]()
![]() xdx=
xdx= =x
=x =xlnx-x+С
Сонда
=xlnx-x+С
Сонда
 =
= =(xlnx-x)
=(xlnx-x) -
(x
-
(x +2x)
+2x) =elne-e+1-(e
=elne-e+1-(e )+2=3-e
)+2=3-e
3.y=2x-x2параболасы және у=-xтүзумен шектелген фигураның ауданын табыңдар.
Шешуі : Параболаның теудеуін қарастырайық:
y= -x2+2x y=-(x2-2x+1)+1 y-1=(x-1)2
Бұл параболаның төбесі (1,1) нүктесінде және ол х=1 түзуі бойынша симметриялы орналасқан.Берілген параболаның және түзудің графигін салайық. Парабола мен түзудің теңдеулерін біріктіріп шешіп , А мен В нүктелерінің абсциссаларын табайық:
 3x-x2=0 x(3-x)=0.
x1
=0.
x2=3
3x-x2=0 x(3-x)=0.
x1
=0.
x2=3

S= =
= dx=
dx= -
- )
)  =
= -
-  =
= (кв.бірлік)
(кв.бірлік)
4.y=x2 параболасы және y=3-x түзуімен шектелген фигураның ауданын табыңдар.
Шешуі . Парабола мен түзудің теңдеулерін біріктіріп шешіп,қиылысу нүктелерінің абсциссаларын табайық:
 =3-x,
x2+x-3=0,
x1
=3-x,
x2+x-3=0,
x1 1.3,x2
1.3,x2
S= dx=(3x-
dx=(3x- )
)  =3*1,3-
=3*1,3- -
-  -(3*(-2.3)-
-(3*(-2.3)- )=7,84
)=7,84
5. у=х2-3х+5 және у=3 сызықтарымен шектелген дененің ауданын табыңдар.
Шешуі : Парабола мен түзудің теңдеулерін біріктіріп шешіп,қиылысу нүктелерінің абсцисаларын табайық:
 =
= , (x-1)(x-2)=0,
x1=1,x2=2
, (x-1)(x-2)=0,
x1=1,x2=2
Cонда
S= =
= dx=(
dx=( -
- )
)
 =
= -
- =
=
-
Қисық доғаның ұзындығы
Жазықтықта y=f(x) , x€[a,b] үзіліссіз дифференциалданатын функцияның графигімен берілген ұштары А және В нүктелерінде болатын Lқисығын қарастырайық. Осы қисықты n бөлікке бөлеміз. М1, М2,,,,,,,, Мn-1, Мn нүктелерінің координаталары (х1,у1)
Төбелері таңдап алынған нүктелерде жататын L қисығына іштей сызылған сынықтың ұзындығын Ln деп белгілейміз.
Ln= +
+
 қосындысының шегі L
қисығының ұзындығы деп аталады.
қосындысының шегі L
қисығының ұзындығы деп аталады.
Теорема. Түзуленетін y=f(x) функциясының [a,b] – да үзіліссіз дифференционалданатын графигі және оның ұзындығы мына формула арқылы анықталады:
l(L)= 2dx
2dx
мысалдар:
1.x=( cost+2tsint
(0
cost+2tsint
(0 t≤
t≤ )
)
Осы сызық доғасының ұзындығын табыңдар.
Шешуі:
l= dt немесе
l=
dt немесе
l= dt
dt
Формулаларын қолданамыз.
 =
2tsint+(
=
2tsint+( cost+2cost-2tsint)
=
cost+2cost-2tsint)
= cost
cost
 =-2tcost-(2-
=-2tcost-(2- )sint+2sint+2tcost=
)sint+2sint+2tcost= sint
sint
 +(
+( )=
)= =
=
Сонымен,
l= =
=  =
=
2.y= қисығының координат бас
нүктесінен В(4,8) нүктесінің арасындағы доғаның
ұзындығын табыңдар.
қисығының координат бас
нүктесінен В(4,8) нүктесінің арасындағы доғаның
ұзындығын табыңдар.
Шешуі: Қисықтың теңдеуінен
у1= табамыз.
Сонда
табамыз.
Сонда
l![]() =
= xdx=
xdx= d(
d( )=
)= (1+
(1+ =
= (10
(10 -1)
-1)
-
l=ln
 (0≤x≤
(0≤x≤ ) теңдеуімен берілген қисықтың
ұзындығые табыңдар.
) теңдеуімен берілген қисықтың
ұзындығые табыңдар.
Шешуі : Қисықтың теңдеуінен
у1= табамыз.
Сонда
табамыз.
Сонда
l![]() =
=  dx=
dx= dx=
dx= )dx=(-x+ln
)dx=(-x+ln )
)  = -
= - +ln3
+ln3
-
y=1-lncosx (0≤x≤
 ) теңдеуімен берілген қисықтың
ұзындығын табыңдар.
) теңдеуімен берілген қисықтың
ұзындығын табыңдар.
Шешуі:
l= dx=
dx= 2dx=
2dx= 2dx=
2dx= dx=
dx= dx=
dx=
t![]() gx
gx  =tg
=tg -tg0=
-tg0=
2.3.3.Айналу денесінің көлемі
Кеңістікте Т денесі және Ох өсі берілген. Осы Т денесіне х нүктесінен өтетін Ох өсіне перпендикуляр қима жүргіземіз. Оның ауданын Ǫ(x)деп белгілейік.
Т денесінің Ох өсіндегі проекциясы [a.b] кесіндісі болсын,яғни у=Ǫ(x)функциясы осы кесіндіде анықталған. Осы Ǫ(x) функциясын [a.b] кесіндісінде үзіліссіз функция деп есептейміз.
Т денесі [a.b] кесіндісінде анықталған y=f(x) үзіліссіз функциясымен берілген қисық сызықты трапецияның Ох өсінен айналуынан шыққан дене болсын. Дөңгелектің ауданы
Ǫ(x)=πf(x)2 формуласымен табылады, мұндағы f(x) дөңгелектің радиусы. Пайда болған айналу денесінің көлемі мына қатыспен анықталады:
V(T)=π (x)dx
(x)dx
2.3.4. Айналу бетінің ауданы
Үзіліссіз дифференциалданатын y=f(x),(x€[a,b] және f(x)≥0) функциясының графигі Ох өсінен айналсын. Пайда болған Н- айналу бетінің ауданы
S(H)=2π )2
dx
)2
dx
формуласымен табылады.
Өзін-өзі тексеруге арналған сұрақтар
-
Анықталған интегралды қолданып аудандарды есептеу
-
Қисық доғасының ұзындығын есептеу
-
Айналу денесінің көлемін есептеу
-
Айналу бетінің ауданын есептеу
Жаттығулар
-
Берілген қисықтармен шектелген фигураның ауданын есептеңдар
1.
y=
 ,y=x3
,y=x32.
y=x2,y=3-2x
3.
y=x3,x=1,x=3
4.
y=x2-3,y+3x-4=0
Берілген қисықтың доғасының ұзындығын есептеңдер
1.
y2=(x+3)3,x=4
2.
 +
+ =
=
3.
y=ln(1-x2),x=
 ,x=
,x=
4.
x=
 ,
y=0,y=3
,
y=0,y=3Көрсетілген координата өсін айналдыру арқылы берілген қисықтармен шектелген фигураның айналуынан пайда болған дененің көлемін есептеңдер
1.
y=sinx,y=0 (0
 )
Ox
)
Ox2.
y3=x2, y=1 Ox
3.
y2=(x-1)3,x=2,Ox
4.
y2=x, x2=y,Ox
Көрсетілген аралықта берілген қисықтың айналуынан пайда болған бетінің ауданын есептеңдер
1.
y=1-x2, y
 ,
Ox
,
Ox2.
y=x3,(0
 ),Ox
),Ox3.
y=
 ,
(-2
,
(-2 ),Ox
),Ox4.
y=sinx, (0
 ),
Ox
),
Ox
Деңгейлік тестік тапсырмалар
ТЕСТ 1
-
x=2-y+y2 және x=0 сызықтарымен шектелген фигураның ауданы
А) 3 B)4
C) D)
D)
 E)
E)
2.y=3x,y= , x=1, x=2 сызықтарымен
шектелген фигураның ауданы
, x=1, x=2 сызықтарымен
шектелген фигураның ауданы
А) В)
В)
 С)
С)  D)
D) E)
E)
3. y= x2 жәнеy=6x-x2 сызықтарымен шектелген
фигураның ауданы
x2 жәнеy=6x-x2 сызықтарымен шектелген
фигураның ауданы
А) 16 B)14 C)12 D)10 E)8
4. y=x2,y=0,x=1,x=2 сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
5.y=sinx,y=0,x= ,x=
,x= сызықтарымен шектелген
фигураның ауданы
сызықтарымен шектелген
фигураның ауданы
А)
 B)1
C)
B)1
C) D)
D)
 E)
E)
6.y= ,y=2 және у осі
сызықтарымен шектелген фигураның ОУ осінен айналуынан пайда болған
дененің көлемі неге тең?
,y=2 және у осі
сызықтарымен шектелген фигураның ОУ осінен айналуынан пайда болған
дененің көлемі неге тең?
А)  B)
B) C)
C) D)
D)  E)
E)
7. y=lnx,x=e және х осі сызықтарымен шектелген фигураның ОХ осінен айналуынан пайда болған дененің көлемі
А)  (e-1) B)
(e-1) B) (e+1) C)
(e+1) C) D)3
D)3 E)
E)
8. y=cosx,x= , х осі және у осімен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
, х осі және у осімен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
А)  B)
B)  C)
C) D)
D)  E)
E)
9. y=-x2 және y=x2-2 функцияларымен шектелген ауданның х осінен айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
10.
y= параболасының мына екі
нүктенің арасындағы доғаның ұзындығы:О(0,0)
және
параболасының мына екі
нүктенің арасындағы доғаның ұзындығы:О(0,0)
және
А( ;
; )
)
А) +
+ ln(
ln( ) B)
) B)  ln(
ln( ) C)
) C)  +ln(
+ln( ) D)
) D)  E)
E) -
- ln(
ln( )
)
Тест 2
1.y= ,y=0,x=1,x=0
сызықтарымен шектелген фигураның ауданы
,y=0,x=1,x=0
сызықтарымен шектелген фигураның ауданы
А)1 B)е C)2е+1 D)е-1
E)
2. y=x2-4x+4 және y=x сызықтарымен шектелген фигураның ауданы
А)2 B)5 C)12
D)  E)
E)
3.y=x2-2x y=6x-x2 сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
4. y=x2 және y=x сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
5.y=x2-2x және y=-x2+2x сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
6.y=cosx және
x= ,x=
,x= сызықтарымен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
сызықтарымен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
А) B)
B) C)
C) D)
D)  E)
E)
7.y=x2-2 және y=1 функцияларымен шектелген ауданның у осінен айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
8.y2=4-x және x=0 сызықтарымен шектелген, у осін айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
9.у2=4x параболасының мына екі нүкте арасындағы доғаның ұзындығы:
О(0,0) және
А( )
)
А)  +ln(
+ln( +2) B)
+2) B) ln(
ln( ) C)
) C) D)
D) E)
E) + ln(
+ ln( )
)
10.y=x2параболасының мына екі нүкте
арасындағы доғаның ұзындығы О(0,0) және
А( )
)
А)
 +ln(
+ln( +2)
B)
+2)
B) +
+ ln(
ln( )
C)
)
C) -
ln(
-
ln( +3)
D)
+3)
D) E)
E) -
- ln(
ln( )
)
Білімін тексеруге арналған қосымша тестік тапсырмалар:
1. dx
dx
А) +2x+CB)
+2x+CB) C)
C) D)
D)  +5x+CE)
+5x+CE) +5x+C
+5x+C
2. (x-
(x- )dx
)dx
A)
 x2
x2 B)
B)
 x2
x2 C)
C)
 x
x D)
D)
 x
x E)
E) x
x
3. dx
dx
A)
 +C
B)
+C
B) +C
C)
+C
C) +C
D)
+C
D) +C
E)
+C
E) +C
+C
4. dx
dx
A)2ln +C
B)ln
+C
B)ln +C C)
2x2+C
D)2x-2+C
E)2x-1+C
+C C)
2x2+C
D)2x-2+C
E)2x-1+C
5.
 dx
dx
A)
 x4+C
B)5x4+C
C)5x6
+C D)
x4+C
B)5x4+C
C)5x6
+C D)
 +C
E)
+C
E)  +C
+C
6.
A) +C
B)
+C
B) +C
C)
+C
C)  +C
D)
+C
D) +C
E)6x5+C
+C
E)6x5+C
7.

A)
 arctgx+C
B)
arctgx+C
B) arcctg
arcctg +C
C)
+C
C) arctg
arctg +C
D)
+C
D)  C
E)
C
E) +C
+C
8. dx
dx
A)
C+x-e-x(x+1)
B) +
+ +arcsinx+C
C)
+arcsinx+C
C) -x+arctgx+C
D)C-
-x+arctgx+C
D)C- (x+1) E)
C-
(x+1) E)
C- (x-1)
(x-1)
9. dx
dx
A)
0.2(x3-8)5+C
B)x4+x2+8x+C
C) (
( -8)6\5+C D)
5(x3-8)7\5+C E)
0.2(e+1)5
-8)6\5+C D)
5(x3-8)7\5+C E)
0.2(e+1)5
10.
 dx
dx
A)
arcsinx-2 +C B)
arcsinx-
+C B)
arcsinx- +C C)
arcsinx+
+C C)
arcsinx+ +C D)
arcsinx+2
+C D)
arcsinx+2 +C
+C
E)
 -
arcsinx+C
-
arcsinx+C
11.
 dx
dx
A)ex+e-x+C B)
ex-e-x+C C)
e-x-ex+C
D)2(ex+e-x)+C E)
 (ex+e-x)+C
(ex+e-x)+C
12. (tgx)
(tgx)
A)
 x+C
B)
x+C
B) x+C
C)
x+C
C) x+C
D)
x+C
D) x+C
E)
x+C
E)  x+C
x+C
13.
A)
 x+C
B)
x+C
B)  x+C
C)
x+C
C) x+C
D)
x+C
D) x+C
E)
x+C
E) x+C
x+C
14.
 dx
dx
A)
3* ln2+C
B)
ln2+C
B)  *
* ln2+C
C)
ln2+C
C)  +C
D)
+C
D)  ln2+C
E)
ln2+C
E)  *
* +C
+C
15. dx
dx
A)
 +C
B)
+C
B) +C
C)
+C
C) +C
D)
+C
D)  E)
E) +C
+C
16.
A)C- B)
C-
B)
C- C)
C-
C)
C- D)
C-
D)
C- E)
C-
E)
C-
17.
A)
 +C
B)
+C
B)  3 +C C)
2
3 +C C)
2 3 D)
3 D)
 +C
E)
+C
E) +C
+C
18. dx
dx
A)3cosx+12x2+C B)-3cosx+x4+C C)3sinx+x4+C D)3cosx+x4+C E)-3cosx+12x2+C
19. dx
dx
A)
e3x-5+C B)
5e3x-5+C C)
3e3x-5+C
D) e3x-5+C E)
e3x-5+C E)
 e3x-5+C
e3x-5+C
20.

A) +C
B)
+C
B)  +C
C)
+C
C)  +C
D)
+C
D)  +C
E)
+C
E)  +C
+C
Қолданған әдебиеттер тізімі
-
Әбілқасымова А.Е және т.б. Алгебра және анализ бастамалары 11 сынып- Алматы
-
Гусев В.А, Мордкович А.Г Математика: Анықтама материалдар. Оқушыларға арналған кітап.
-
Анарбекова Ә, Бейсеков Ж, Назанов Ж. «Алгебрадан ҰБТ-ға дайындауға арналған әртүрлі деңгейдегі тест тапсырмаларының жинағы»
-
П.А.Ларичев, «Алгебра есептерінің жинағы»
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Анықталған және анықталмаған интеграл әдістемелік құрал
Анықталған және анықталмаған интеграл әдістемелік құрал
БҚО Ақжайық ауданының білім бөлімінің әдістемелік кабинеті
Анықталған және анықталмаған интеграл
(Әдістемелік құрал)
(№1 орта жалпы білім беретін мектебінің екінші
санатты математика пәні мұғалімдері
Т.Б.Нургалиеваның іс-тәжірибесінен )
Чапаев, 2017 жыл
№1 орта жалпы білім беретін мектебінің әдістемелік бірлестігінің сараптама кеңесінде қаралып, аудан көлемінде таратуға мақұлданды.
Хаттама №1
Т.Б.Нургалиева математика пәні мұғалімдері
Пікір жазған:
№1 орта жалпы білім беретін мектебінің жоғары санатты математика
пәні мұғалімі Смаилова Гулжанат Иратовна
Ұстаз-ұрпақ тәрбиелеп өсіруші қоғам тапсырып сенген өкіл. Ұстаздық қызметтің қыры мен сыры мол, сан қилы және әр тарапты.
Нургалиева Турсынай Болатовна -2009 жылдан бері өзінің еңбек жолын бастады. Проблемалық тақырыбы «Математика сабағында логикалық есептерді қолдану арқылы оқушылардың ойлау қабілеттерін дамыту», Жантемирова Назгуль Орынбасаровна проблемалық тақырыбы «»Турсынай Болатқызы және Назгуль Орынбасаровна –жаңа технологияға негізделген жаңашыл ұстаз. Сабақтың сапалы болуын және тиімді жағын арттырып отырады. Сабақ өткізу барысында пәнге деген қызығушылығын арттыру мақсатында оқушылардың бір-біріне деген жолдастық қарым-қатынасы арта түсіп, бір-біріне бар ынта жігерімен көмектесіп, үйретуге, есептердің шығару жолдарын қолдануда оқушылардың ойлау қабілеттерін арта түсетіндігі байқалады. Бүгінгі жас маман ертеңгі ұлағатты ұстаздардың орнын басатын, олардан үлгі алатын, шәкірттердің сүйікті ұстазына айналатын тұлға болатынына сенімдімін.
Түсінік хат
Ұсынылып отырған әдістемелік құрал орта мектептің жаратылыстану-математика бейіндік бағытында математика пәнін тереңдетіп оқытуда қолдануға арналған. Әдістемелік құралда қысқаша теориялық түсінік пен интегралдық есептеуге арналған әр түрлі есептер жинақталып, оларды шешу әдістемесі көрсетілген, есептердің күрделілігіне қарай деңгейлік жаттығу жұмыстары мен бақылау жұмысы тапсырмалары, тестік тапсырмалар берілген.
Әдістемелік құралдың негізгі мақсаты- жан-жақты ойластырылып құрастырылған есептерді оқушыларға шешу арқылы олардың ойлау қабілеті мен шығармашылық белсенділігінің дамуына ықпал ету, есептерді шығару дағдысын жетілдіре түсуге көмектесу болып табылады. Сонымен қатар, математика пәнінің қолданбалы салаларын оқушыларға таныстыру, соның негізінде математиканы қолдану салаларын оқушыларға айқындау болып табылады.
МАЗМҰНЫ
Кіріспе
Функцияны интегралдау
-
Анықталмаған интеграл
-
Функцияның алғашқы бейнесі және анықталмаған интеграл
-
Интегралдар кестесі
-
Анықталмаған интегралдарды есептеу әдістері
-
Тікелей интегралдау әдісі
-
Айнымалыларды ауыстыру арқылы интегралдау әдісі
-
Бөліктеп интегралдау әдісі
-
-
Жаттығулар
Деңгейлік тестік тапсырмалар
-
Анықталған интеграл
-
Анықталған интеграл әдісі
-
Анықталған интегралды есептеу
-
Ньютон-Лейбниц формуласы
-
Айнымалыны алмастыру әдісі
-
Бөліктеп интегралдау әдісі
-
-
Жаттығулар
Деңгейлік тестік тапсырмалар
-
Анықталған интегралдың геометрияда қолданылуы
-
Тік бұрышты координаталардағы аудан
-
Қисық доғасының ұзындығы
-
Айналу денесінің көлемі
-
Айналу бетінің ауаны
-
Жаттығулар
Деңгейлік тестік тапсырмалар
Білімін тексеруге арналған қосымша тестік тапсырмалар
Функцияны интегралдау
-
Анықталмаған интеграл
-
Функцияның алғашқы бейнесі және анықталмаған интеграл
-
Есеп қарастырайық. f(x) функциясы берілсін: туындысы f(x) функциясына тең болатын F(x) функциясын табу керек, яғни F/(x)=f(x).
1-анықтама. Егер х[а,в] аралығында F/(x)=f(x) теңдігі орындалса, онда осы аралықта F(x) функциясы f(x) функциясы үшін алғашқы бей+несі деп аталады.
Мысал
f(x)=х2
функциясының алғашқы бейнесін
табу керек. Алғашқы бейненің анықтамасы бойынша
F(x)= функциясы алғашқы бейне
болады, себебі
функциясы алғашқы бейне
болады, себебі  =х2.
=х2.
Бұл функцияның алғашқы бейнесі
бір мәнді болмайды, себебі F(x)= +1,
F(x)=
+1,
F(x)= -7 немесе жалпы
F(x)=
-7 немесе жалпы
F(x)= +C (мұндағы С-ерікті
тұрақты) функциясы да С-ның кез келген мәнінде
f(x)=х2
функциясының алғашқы бейнесі
болады, яғни (
+C (мұндағы С-ерікті
тұрақты) функциясы да С-ның кез келген мәнінде
f(x)=х2
функциясының алғашқы бейнесі
болады, яғни ( )/=x2.
)/=x2.
Қорыта айтқанда, егер берілген f(x) функциясының алғашқы бейнесі F(x) болса, онда бұдан басқа алғашқы бейненің түрі F(x)+С болады. Бұл келесі теоремадан шығды.
Теорема. Егер f(x)функциясының алғашқы бейнелері бар болса, онда олардың айырымы тұрақты шамаға тең.
2-анықтама. Егер F(x) функциясы берілген f(x) функциясының алғашқы бейнесі болса, онда F(x)+С өрнегі f(x) фунциясының анықталмаған интегралы деп аталады және ∫f(x)dxсимволымен белгіленеді, яғни анықтама бойынша ∫f(x)dx =F(x)+С, мұндағы f(x)- интеграл астындағы функция, f(x)dx – интеграл астындағы өрнек, ∫- интеграл әдісі.
Берілген функцияның алғашқы бе+йнесін табу интегралдау амалы деп аталады.
Геометриялық тұрғыдан анықталмаған интеграл жазықтықта бір-бірінен айырымы тұрақты шама болатындай қисықтар жиынын көрсетеді. Бқл қисықтарды интегралдық қисықтар деп атайды.
Мысалы, f/(x)=2x және f(2)=5болса, онда , f/(x) функциясын табыңыз.
Шешуі:
f/(x)= =2x . Бұдан
dy=2x*dx
=2x . Бұдан
dy=2x*dx
∫dy=∫2x*dx , онда y=x2+C болады. y=f(x)=x2+C онда C=1 шығады. Ендеше f(x)=x2+1 болады.
Анықталмаған интегралдың негізгі қасиеттері:
10. (∫f(x)dx)/=(F(x)+C)/=f(x)
20. ∫kf (x)dx=k ∫f(x)dx
30. ∫ (f(x)+g(x))dx= ∫f(x)dx+∫g(x)dx
40.
 ∫
f(x)dx=f(x)
∫
f(x)dx=f(x)
50. ∫df (x)=f(x)+C
60. ∫
f(ax+b)dx= F
(ax+b)+C
F
(ax+b)+C
Мысалдар
-
а)
 [∫ (x2+5)dx]=x2+5
[∫ (x2+5)dx]=x2+5
b)
 (∫
(∫ )=
)=
g) ∫d(sinx)=
∫ (sinx)dx=sinx+C
(sinx)dx=sinx+C
d)
 ∫ d
(x3+x2+x+5)=
∫ d
(x3+x2+x+5)= (x3+x2+x+5)=
3x2+2x+1.
(x3+x2+x+5)=
3x2+2x+1.
-
Егер f(x)=∫d(x2-4) болса, онда f/(5) неге тең?
Шешуі: Теңдіктен f(x)= x2-4 шығады. Бұдан f/(х)=2x. f/(5)=2*5=10 болады.
-
Егер f(x)= ∫(x3-4x+5)dx болса, онда x=2 нүктесінде жанаманың бұрыштық коэффициенті неге тең?
Шешуі: f(x)=∫ f/(x)dx қасиетін пайдалансақ, онда f(x)=(x3-4x+5) болады. Ендеше f/(2) =23-4*2+5=5
-
Егер ∫x*f(x)dx=2x2+5x-3 болса, онда f(x) неге тең?
Шешуі: Анықталмаған
интегралдың қасиетін пайдалансақ:
x*f(x)=(2x2+5x-3)/. Ендеше x*f(x)=(4х+5), бұдан
f(x)= =4+
=4+ болады.
болады.
-
Егер F(x)=∫

-
f(x)=∫(х2-2х+3)dx фунциясының иілу нүтесін табыңыз.
-
Интегралдар кестесі
Интегралдау амалы дифференциалдау амалына кері амал.
-
∫xndx=
 +C
+C -
∫
 =ln|x|+C
=ln|x|+C -
∫ax*dx=
 +C
(a≠1)
+C
(a≠1) -
∫eˣ*dx=eˣ+C
-
∫sinx*dx=-cosx+C
-
∫cosx*dx=sinx+C
-
∫

-
∫
 =-ctgx+C
=-ctgx+C -
∫tgx*dx=-ln|cosx|+C
-
∫ctgx*dx=ln|sinx|+C
-
∫
 rctgx+C
(-arcctgx+C)
rctgx+C
(-arcctgx+C)
11/.
∫ =
= arctg
arctg +C
(-
+C
(- arcctg
arcctg )
)
-
∫
 =
= ln
ln |+C
(a≠0)
|+C
(a≠0) -
∫
 =arcsinx+C
(-arccosx+C)
=arcsinx+C
(-arccosx+C)
13/.

-
∫

Мысалдар:
-
A) ∫x3dx=

b) ∫5dx=5x+C
c)
∫5xdx=5∫xdx=5*
d) ∫
(5x²+2)dx=5∫x²dx+2∫dx=5*
2. a)
∫
b) ∫
 dx.
dx.
3. a) ∫ 5³ˣdx b) ∫ 5³ˣ+4dx g) ∫e2xdx
4. a)
∫sin5xdx=-
b) ∫cos
(5x+3)dx=
d)
∫
g)
∫
1.3 Анықталмаған интегралдарды есептеу әдістері
Интегралды интегралдау әдістері интеграл астындағы функцияның берілуіне және интегралдау кестесінің қорына байланысты:
-
Тікелей интегралдау;
-
Айнымалыларды ауыстыру арқылы интегралдау;
-
Бөліктеп интегралдау.
Осы тәсілдерді жеке қарастырайық:
-
Тікелей интегралдау әдісі
Функцияларды анықталмаған интегралдың қасиеттері мен интегралдар кестесіне сүйеніп тікелей интегралдауға болады. Ал, тригонометриялық фнкцияларды интегралдағанда қосымша келесі келтіру формулаларын пайдалануға болады:
-
sin²x+cos²x=1, sinx=

-
ctgx=
 ,
tgx*ctgx=1
,
tgx*ctgx=1 -
cosec
 ,
secx=
,
secx=
-
sin2x=2sinx*cosx, cos2x=cos²x-sin²x=2cos²x-1=1-2sin²x
-
sinx*cosy=

cosx*siny=  (sin(x+y)-sin(x-y))
(sin(x+y)-sin(x-y))
cos*cosy= (cos(x+y)+cos(x-y))
(cos(x+y)+cos(x-y))
sinx*siny= (cos(x+y)-cos(x-y)).
(cos(x+y)-cos(x-y)).
Мысал,
∫ интегралын есептеп, нәтижесін
дифференциалдау арқылы тексеріңдер. Алымын бөліміне бөліп,
интегралдың қасиетін және кестені пайдаланып, шығарамыз:1.
∫
интегралын есептеп, нәтижесін
дифференциалдау арқылы тексеріңдер. Алымын бөліміне бөліп,
интегралдың қасиетін және кестені пайдаланып, шығарамыз:1.
∫ -1/4dx-2∫
x15/4dx+∫
x5/12dx=4x3/4-
-1/4dx-2∫
x15/4dx+∫
x5/12dx=4x3/4- x19/4+
x19/4+ x17/12+C=4
x17/12+C=4 -
- 19+
19+ 12√x17+C.
12√x17+C.
-
∫

-
∫ cos7xdx
-
∫sin(2x-6)dx
-
∫ sin²xdx
Интеграл астындағы функцияның
бөліміндегі өрнектен толық квадратты бөліп аламыз. Сонда 1.
∫  =
= ∫
∫
 =
=  =4√3/6√13arctg
=4√3/6√13arctg
-
∫

-
∫
 dx
dx
Алымында бөлімінің туындысына
тең болатын қосылғышты айырып алып, алатынымыз: 4.
∫ =∫(4-8x)-2/5dx=-
=∫(4-8x)-2/5dx=- (4-8x)3/5+C=-
(4-8x)3/5+C=- ⁵√(4-8x)³+C
⁵√(4-8x)³+C
5.∫
6.
∫ dx
dx
7.
∫ dx=
∫
dx=
∫ dx=
∫
dx=
∫ =dx=
∫(1-cosx)dx=x-sinx+C
=dx=
∫(1-cosx)dx=x-sinx+C
1.3.2 Айнымалыларды ауыстыру арқылы интегралдау әдісі
Кейде интегралдағы х айнымалысының орнына жаңа t айнымалысын енгізіп, берілген ∫f(x)dx интегралын тікелей интегралданатын кестелік интегралдың біріне келтіруге болады. Бұл интегралдау әдісін айнымалыларды ауыстыру әдісі деп атайды Бұл әдістің негізі күрделі функциялардың дифференциалдау формуласы болып табылады.
Теорема. Анықталмаған ∫f(x)dx интегралындағы х айнымалысының орнына x=φ(t) формуласы бойынша жаңа t айнымалысын енгізсек, берілген анықталмаған интеграл үшін
∫ f(x)dx=∫f[φ(t)]φ/(t)dt (1)
теңдігі орындалады.
Бұл әдісті қолдану берілген айнымалыны қандай формула бойынша ауыстыруға байланысты.
Мысалдар:
-
∫ х√х-3dx
Квадрат түбірден құтылу үшін √х-3=t деп жаңа t айнымалысын енгіземіз. Сонда x=t²+3және dx=2t dt. Ауыстыруды енгізген соң, аламыз:
∫ x√x-3xdx= ∫ (t²+3)t2tdt= ∫
(2t⁴+6t²)dt=
 5/2+2
(x-3)3/2+C
5/2+2
(x-3)3/2+C
-
∫

-
∫ √sinxcosxdx= |t=sinx, dt=cosxdx|=∫√tdt=∫ t1/2dt=
 t2/3+C=
t2/3+C= sin3/2x+C
sin3/2x+C -
∫ x(x²+1)3/2dx
-
∫ esinxcosxdx
Интеграл астындағы өрнек екі көбейткіштен тұрады, түбірден құтылатындай жаңа айнымалы енгіземіз:
t=sinx , x=arcsint
dx= , cosx=
√1-sin²x=√1-t²
, cosx=
√1-sin²x=√1-t²
∫esinxcosxdx=
∫et√1-t² =
∫etdt=
et+C=esinx+C
=
∫etdt=
et+C=esinx+C
-
∫ √a²-x²dx
1.3.3 Бөліктепинтегралдауәдісі
Бұл әдіс көбейтіндінің туындысы формуласына негізделген:
(uv)/=u/*v+v/*u
мұндағы u=u(x) және v=v(x)-дифференциалдары үзіліссіз х-ке байланысты функциялар. Дифференциалдық түрде былай жазуға болады:
d(uv)= udv+vdu
Бұл теңдіктің екі жағын да интегралдасақ: ∫ d(uv)= ∫ udv+ ∫ vdu Анықталмаған интегралдың келтірілген қасиеттеріне байланысты шығатыны:
uv=∫udv+∫ vdu немесе ∫ udv= uv-∫ vdu (2)
(2) формула бөліктеп интегралдау формуласы деп аталады. Бұл әдісті қолданғанда интеграл астындағы өрнекті екі көбейткіштің (u және dv) кһбейтіндісі түрінде қарастырады. Сол себепті бөліктеп интегралдау әдісінің тиімділігі u және dv көбейткіштерін дұрыс таңдап алуға байланысты болады.
Мысалдар:
-
∫ x²sinxdx
-
∫e2xcosxdx
-
∫ (x-7)sin5xdx= |
 |=
-
|=
-  (x-7)cos5x+
(x-7)cos5x+ ∫
cos5xdx=-
∫
cos5xdx=-  (x-7)cos5x+
(x-7)cos5x+ sin5x+C
sin5x+C -
∫
 dx
dx
Өзін-өзі тексеруге арналған сұрақтар
-
«Функцияның алғашқы бейнесі» ұғымының анықтамасы
-
Анықталмаған интегралдың негізгі қасиеттері
-
Интегралдар кестесі
-
Интегралдау әдісі
-
Айнымалыны алмастыру әдісі
-
Бөліктеп интегралдау әдісі.
Жаттығулар
-
Тікелей интегралдау әдісін пайдаланып, төмендегі интегралды есептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫ √3+xdx |
∫ ³√(1+x)²dx |
|
2 |
∫ |
∫ |
|
3 |
∫ |
∫ |
|
4 |
∫sin(2-3x)dx |
∫sin(3+4x)dx |
|
5 |
∫ |
∫ |
|
6 |
∫ |
∫ |
|
7 |
∫ |
∫ |
|
8 |
∫ |
∫ |
|
9 |
∫ |
∫ |
|
10 |
∫ |
∫ |
ІІ. Айнымалылардыалмастыру әдісін пайдаланып, төмендегі интегралды есептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫ |
∫ |
|
2 |
∫2xexdx |
∫34xdx |
|
3 |
∫tg²7xdx |
∫sin²xdx |
|
4 |
∫ |
∫ |
|
5 |
∫ |
∫ |
III. Бөліктепинтегралдауәдісінпайдаланып, төмендегіинтегралдардыесептеңдер:
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
∫xlnxdx |
∫ |
|
2 |
∫ (1-x) cos5xdx |
∫ (x-7) cos2xdx |
|
3 |
∫(x-4)sin2xdx |
∫(x+4)sin2xdx |
|
4 |
∫ x²(sinx+1)dx |
∫ x²(sin2x-3)dx |
|
5 |
∫x²cos2xdx |
∫(x-3)²cosxdx |
|
6 |
∫ (x²+x)e-xdx |
∫(x+1)e2xdx |
|
7 |
∫ |
∫ |
|
8 |
∫xsin²xdx |
∫xsin²(x+3)dx |
Тестік тапсырмалар
ТЕСТ 1
-
∫
 dx
dx
-
ln(x-1)+x+C
-
x-lnx+C
-
2lnx+C
-
x+lnx+C
-
3x-2lnx+C
-
∫ (
 )dx
)dx
-
-
 +
+ +C
+C -
X-lnx+C
-
lnx+
 +C
+C -
x+lnx+C
-
2lnx-
 +C
+C
-
∫
 dx
dx
-
1/2x²-3x+4ln|x+2|+C
-
1/3x³-2x+ln|x+2|+C
-
x²-3x+ln|x+2|+C
-
1/2x²+3x+C
-
1/4x²-4x+4ln|x+2|+C
-
∫
 dx
dx
-
ln(x²+1+x+C)
-
x-
 +C
+C -
x+2arctg(x²+1)+C
-
arctgx+C
-
x+2arcrgx+C
-
∫

-
³√x²+7+x+C
-
x√x²+7+C
-
1/2√x²+7+C
-
√x²+7+C
-
½(x²+7)+C
-
∫
 dx
dx
-
 arctg3ˣ+C
arctg3ˣ+C -

-
arcsin3ˣ+C
-

-

-
∫
 dx
dx
-
tg(lnx)-lnx+C
-
tg(lnx)+C
-
tg²(lnx)+C
-
tg(lnx)-
 +C
+C -

-
∫
 dx
dx
-
-
 x²-3x+4ln|x+2|+C
x²-3x+4ln|x+2|+C -
1/3x³-2x+ln|x+2|+C
-
x²-3x+ln|x+2|+C
-
 x²+3x+C
x²+3x+C -
 x²-4x+4ln|x+2|+C
x²-4x+4ln|x+2|+C
-
∫(√x+1)²dx
-
 (√x+1)²+C
(√x+1)²+C -
 √x+1+C
√x+1+C -
 x²-
x²- x√x+x+C
x√x+x+C -

-

-
∫
 dx
dx
-
 arctg³x+C
arctg³x+C -

-
X+2arctgx+C
-
Arctgx+C
-
 arctg²x+C
arctg²x+C
ТЕСТ 2
-
∫ (
 )dxболса, ондаf/(0)=?
)dxболса, ондаf/(0)=?
-

-

-
3
-
0
-

-
f(x)=∫ (eˣlnx+x+3)dxболса, ондаfn(1)=?
-
4
-
2
-
2e
-
e+1
-
2e+1
-
∫ (x-2)f(x)dx=2x²-3x+1 болса, онда f(x) функциясықандай?
-
4x-3
-

-
X+3
-

-

-
∫ (3x²-3)dx
-
 x³-3x+C
x³-3x+C -

-

-

-
x³-3x+C
-
∫ (eˣ-
 )dx
)dx
-
eˣ+
 +C
+C -
xeˣ-
 +C
+C -
eˣ-lnx+C
-
eˣ+lnx+C
-
2eˣ-lnx+C
-
∫
 dx
dx
-
1/2ln(x²+2)+C
-
½(√x+1)²+C
-
1/2ln²(x²+2)+C
-
½(x²+2)+C
-
1/2x+x+C
-
∫ eˣ³x²dx
-
1/3eˣ³+x²+C
-
½(eˣ+1)²+C
-
1/3eˣ³+C
-
½(x²+eˣ)+C
-
1/2(eˣ+x)²+C
-
∫

-
Sinx+2cosx+C
-
–sinx-2cosx+C
-
2sinx+cosx+C
-
sin²x+2cos²x+C
-
sinx-2cosx+C
-
∫ sin6xcosxdx
-
 sin7x+C
sin7x+C -
 sin5x-cosx+C
sin5x-cosx+C -

-
 sin7x+C
sin7x+C -
 sin5x+C
sin5x+C
-
∫

-
1/3arctg³x+C
-
x-

-
x+2arctgx+C
-
2/3√arctg³x+C
-
1/3arctg²x+C
-
Анықталған интеграл
Оқушы білуі керек: анықталған интегралдың жазылуы мен анықтамасын; анықталған интеградың геометриялық мағынасын; анықталған интегралдың қасиеттерін; анықталған интегралдың шешу әдістерін.
Оқушы білуі қажет: анықталған интегралды есептеуді.
-
Анықталған интеграл ұғымы.
Анықтама. [а,в] аралығында
үзіліссіз y=f(x) функциясы берілсін. [а,в] аралығын
a=x0<x1<x2<…<xn=b нүктелерімен n бөлікке
бөлейік. Δxi=xi-xi-1
(i=1,2,…n) элементар
аралықтарынан сәйкес ζi
(i=1,2,…n) нүктесін алып, осы
нүктелердегі функцияның f(ζ1),
f(ζ2),…f(ζn) мәндерін есептеп,
f(ζi)Δi
(i=1,2,…n) көбейтінділерінен
қосынды құрып,  n=f(xi)Δxi+f(x2)Δx2+…+f(xn)Δxn=Σni=1f(xi)Δxiқосынды f(x) функциясының
[а,в] аралығындағы интегралдық қосынды деп
аталады.
n=f(xi)Δxi+f(x2)Δx2+…+f(xn)Δxn=Σni=1f(xi)Δxiқосынды f(x) функциясының
[а,в] аралығындағы интегралдық қосынды деп
аталады.
Анықтама. Егер maxΔxi→0 (n→∞) болғанда интегралдық өосындының ақырлы шегі бар болса, онда ол f(x) функциясының [а,в] аралығындағы анықталған интегралы деп аталады. Белгіленуі: ba∫ f(x)dx.
Сонымен ,
lim Σn
f(xi)Δxi= f(x)dx.
(1)
f(x)dx.
(1)
max→0 i=1
мұндағы f(x)- интеграл астындағы функция. f(x)dx –интеграл астындағы өрнек, а саны- интегралдың төменгі шегі, в саны- интегралдың жоғарғы шегі, х айнымалысы- интегралдау айнымалысы деп аталады.
Анықталған интегралдың негізгі қасиеттері:
-

-

-

-

-

-
Егер [а,в] (а<в) аралығындағы х айнымалысының барлық мәндері үшін f(x)≥0 болса, онда
 ≥0
≥0 -
Егер [а,в] (а<в) аралығындағы f(x)≤φ(x) болса, онда

-
Анықталған интегралды есептеу
-
Ньютон-Лейбниц формуласы
-
Теорема. Егер F(x) функциясы
[а,в] аралағындағы  функциясының алғашқы
бейнесі болса, онда
функциясының алғашқы
бейнесі болса, онда
 (2)
(2)
Бұл теңдік Ньютон-Лейбниц формуласы деп аталады.
Кейде мына белгілеу
қолданылады:  ba.
ba.
Ньютон-Лейбниц формуласы анықталған интегралды есептеуге арналған жалпы формула. Ал анықталған интегралды есептеу әдістері анықталмаған интегралды есептеу әдістерімен бірдей. Мысалдар:
-
 |31=
|31=

-

-

-

-

-
Айнымалыны алмастыру әдісі
Теорема. [а,в] аралығында
үзіліссіз y=f(x) функциясы үшін  анықталған интеграл
берілсін. X=φ(t) формуласы бойынша жаңа t
айнымалысын енгізейік:
анықталған интеграл
берілсін. X=φ(t) формуласы бойынша жаңа t
айнымалысын енгізейік:
 [φ(t)φ/(t)dt]
(3)
[φ(t)φ/(t)dt]
(3)
Мысалдар:
-
 =
= 32=
32= (3³-2³)=
(3³-2³)=
-

-

-

-

-
Бөліктеп интегралдау әдісі
u(x), v(x) функциялары х аргументі бойынша [а,в] аралығында дифференциалданатын функциялар болсын. Сонда d(uv)=udv+vdu болатыны белгілі. Осыдан теңдікті [а,в] аралығында интегралдасақ, онда
 ba-
ba-
 (4)
(4)
(4) формуласы анықталған интегралды бөліктеп интегралдау формуласы деп аталады.
Мысалдар:
-
 =
-xctgx|π/3π/4+
=
-xctgx|π/3π/4+ |π/3π/4+ln|sinx||π/3π/4=-
|π/3π/4+ln|sinx||π/3π/4=-

-
 x+lnxdxdx
x+lnxdxdx -

-

-

Өзін-өзі тексеруге арналған сұрақтар
-
Анықталған интегралдың анықтамасы
-
Ньютон-Лейбниц формуласы
-
Анықталған интегралда айнымалыны алмастыру формуласы
-
Анықталған интегралда бөліктеп интегралдау әдісі.
Жаттығулар
|
№ |
І нұсқа |
ІІ нұсқа |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Деңгейлік тест тапсырмалары
Тест1
-
 dx
dx
А)ln(е+1)
В) ln(3+е)
С)1+ ln3
D)3+ln3
E)е+ ln3
2. dx
dx
A)2 -2е
-2е
В) -е
-е
С)2 -е
-е
D)е-
2
Е) -2е
-2е
3. -6х+9)dx
-6х+9)dx
A)2 В)3 С)6 D)5 Е)1,5
4. dx
dx
A)cos1
В)-cos1
С)1-sin1
D)sin1-1
Е)
5. dx
dx
A)
В)
С)
D)
Е)
6. dx
dx
A)
В)32
С)
D)64
Е)
7.
A)3
В)2
С)1
D)4
Е)
8. dx
dx
A)-24
В)
С)
D)
Е)
9. dx
dx
A)
В)
С) D)
D) Е)
Е)
10. dx
dx
A)
 B) 2
C)
B) 2
C)  D) 3
E)
D) 3
E)
ТЕСТ
2
1. dx
dx
A) 9 B)-12
C) D) 12
E)-9
D) 12
E)-9
2. dx
dx
A)
 B) 24
C)
B) 24
C) D)
D)
 E)-4
E)-4
3. dx
dx
A)
 B) 2 C)1
D)
B) 2 C)1
D)  E)
E)
4. dx
dx
A)
 B)
2
B)
2 C)
C) D)
D)
 E)
E)
5. )dx
)dx
A)-1 B) 1
C) D)
D)
 E)2
E)2
6.
A)1+
 B) 1
C)
B) 1
C) D)
D)
 E)
E)
7. dx
dx
A)
 B)
2
B)
2 C)
C) D)
D)
 E)
0
E)
0
8. dx
dx
A)e B)
2 C)
C) -1
D)
-1
D)  E)
e-
E)
e-
9. 4 *(3
4 *(3 )dx
)dx
A)-
 B) 1
C)
B) 1
C) D)
D)
 E)
E)
10.
A)0 B) -2
C) D)
D)
 E)2
E)2
2.3 Анықталған интегралдың геометрияда қолданылуы
2.3.1. Тікбұрышты координаталардағы аудан
а)Егер
[a,b]кесіндісінде  болса,онда осы
кесіндіде
болса,онда осы
кесіндіде
S(x)= dx
dx
Интегралы қисық сызықты трапецияның ауданын өрнектейді.
Егер
[a,b]кесіндісінде  болса,онда қисық сызықты
трапеция Ох осінің төменгі жағында орналасқан
және
болса,онда қисық сызықты
трапеция Ох осінің төменгі жағында орналасқан
және  dx
dx 0. Бұл интеграл
трапецияның ауданын «минус» таңбасымен
анықтайды.
0. Бұл интеграл
трапецияның ауданын «минус» таңбасымен
анықтайды.
Мысалы y=sinx синусойдасымен және Ох осімен шектелген аймақтық ауданды табу керек. (0≤x≤2π)

2 cурет Функцияның графигі
[0 ] аралығында
sinx
] аралығында
sinx 0, ал
[
0, ал
[ ] аралығында
sinx
] аралығында
sinx 0 болғандықтан, берілген
аймақтың ауданын табамыз.
0 болғандықтан, берілген
аймақтың ауданын табамыз.
S(G)= -
- =-cosx
=-cosx +cosx
+cosx =-cos
=-cos -cos
-cos =4
=4
б)x=a,x=b
түзулерімен
және [a,b]
аралығында үзіліссіз
у=f1(x),
у=f2(x)
(мұндағы
f1(x) f2(x))
функциялардың графиктерімен
шектелген аймақтың ауданы мына формуламен
табылады:
f2(x))
функциялардың графиктерімен
шектелген аймақтың ауданы мына формуламен
табылады:
S(x)= dx
dx
Мысалдар:1.
y= ,
y=x2
параболамен шектелген G
аймағының ауданын табу керек.
,
y=x2
параболамен шектелген G
аймағының ауданын табу керек.
Шешуі
 теңдеулер жүйесін ,
осы қисықтардың (0;0) және (1;1) қиылысу нүктелерін табамыз. [0;1]
кесіндісінде
теңдеулер жүйесін ,
осы қисықтардың (0;0) және (1;1) қиылысу нүктелерін табамыз. [0;1]
кесіндісінде  ≥х2
орындалатын
болғандықтан
≥х2
орындалатын
болғандықтан
S(G)= dx=
dx= -
- =
= -
- =
=

4сурет. Фигураның ауданы.
-
y=lnx және y=
 x қисықтарымен шектелген
фигураның ауданын табыңдар.
x қисықтарымен шектелген
фигураның ауданын табыңдар.
Шешуі. Қисықтардың қиылысу нүктелерін табамыз: М1(1,0),М2(е,1)
S(x)= dxформуласын
қолданамыз. S=
dxформуласын
қолданамыз. S= dx
dx
 xdx=
xdx= =x
=x

![]()
![]() xdx=
xdx= =x
=x =xlnx-x+С
Сонда
=xlnx-x+С
Сонда
 =
= =(xlnx-x)
=(xlnx-x) -
(x
-
(x +2x)
+2x) =elne-e+1-(e
=elne-e+1-(e )+2=3-e
)+2=3-e
3.y=2x-x2параболасы және у=-xтүзумен шектелген фигураның ауданын табыңдар.
Шешуі : Параболаның теудеуін қарастырайық:
y= -x2+2x y=-(x2-2x+1)+1 y-1=(x-1)2
Бұл параболаның төбесі (1,1) нүктесінде және ол х=1 түзуі бойынша симметриялы орналасқан.Берілген параболаның және түзудің графигін салайық. Парабола мен түзудің теңдеулерін біріктіріп шешіп , А мен В нүктелерінің абсциссаларын табайық:
 3x-x2=0 x(3-x)=0.
x1
=0.
x2=3
3x-x2=0 x(3-x)=0.
x1
=0.
x2=3

S= =
= dx=
dx= -
- )
)  =
= -
-  =
= (кв.бірлік)
(кв.бірлік)
4.y=x2 параболасы және y=3-x түзуімен шектелген фигураның ауданын табыңдар.
Шешуі . Парабола мен түзудің теңдеулерін біріктіріп шешіп,қиылысу нүктелерінің абсциссаларын табайық:
 =3-x,
x2+x-3=0,
x1
=3-x,
x2+x-3=0,
x1 1.3,x2
1.3,x2
S= dx=(3x-
dx=(3x- )
)  =3*1,3-
=3*1,3- -
-  -(3*(-2.3)-
-(3*(-2.3)- )=7,84
)=7,84
5. у=х2-3х+5 және у=3 сызықтарымен шектелген дененің ауданын табыңдар.
Шешуі : Парабола мен түзудің теңдеулерін біріктіріп шешіп,қиылысу нүктелерінің абсцисаларын табайық:
 =
= , (x-1)(x-2)=0,
x1=1,x2=2
, (x-1)(x-2)=0,
x1=1,x2=2
Cонда
S= =
= dx=(
dx=( -
- )
)
 =
= -
- =
=
-
Қисық доғаның ұзындығы
Жазықтықта y=f(x) , x€[a,b] үзіліссіз дифференциалданатын функцияның графигімен берілген ұштары А және В нүктелерінде болатын Lқисығын қарастырайық. Осы қисықты n бөлікке бөлеміз. М1, М2,,,,,,,, Мn-1, Мn нүктелерінің координаталары (х1,у1)
Төбелері таңдап алынған нүктелерде жататын L қисығына іштей сызылған сынықтың ұзындығын Ln деп белгілейміз.
Ln= +
+
 қосындысының шегі L
қисығының ұзындығы деп аталады.
қосындысының шегі L
қисығының ұзындығы деп аталады.
Теорема. Түзуленетін y=f(x) функциясының [a,b] – да үзіліссіз дифференционалданатын графигі және оның ұзындығы мына формула арқылы анықталады:
l(L)= 2dx
2dx
мысалдар:
1.x=( cost+2tsint
(0
cost+2tsint
(0 t≤
t≤ )
)
Осы сызық доғасының ұзындығын табыңдар.
Шешуі:
l= dt немесе
l=
dt немесе
l= dt
dt
Формулаларын қолданамыз.
 =
2tsint+(
=
2tsint+( cost+2cost-2tsint)
=
cost+2cost-2tsint)
= cost
cost
 =-2tcost-(2-
=-2tcost-(2- )sint+2sint+2tcost=
)sint+2sint+2tcost= sint
sint
 +(
+( )=
)= =
=
Сонымен,
l= =
=  =
=
2.y= қисығының координат бас
нүктесінен В(4,8) нүктесінің арасындағы доғаның
ұзындығын табыңдар.
қисығының координат бас
нүктесінен В(4,8) нүктесінің арасындағы доғаның
ұзындығын табыңдар.
Шешуі: Қисықтың теңдеуінен
у1= табамыз.
Сонда
табамыз.
Сонда
l![]() =
= xdx=
xdx= d(
d( )=
)= (1+
(1+ =
= (10
(10 -1)
-1)
-
l=ln
 (0≤x≤
(0≤x≤ ) теңдеуімен берілген қисықтың
ұзындығые табыңдар.
) теңдеуімен берілген қисықтың
ұзындығые табыңдар.
Шешуі : Қисықтың теңдеуінен
у1= табамыз.
Сонда
табамыз.
Сонда
l![]() =
=  dx=
dx= dx=
dx= )dx=(-x+ln
)dx=(-x+ln )
)  = -
= - +ln3
+ln3
-
y=1-lncosx (0≤x≤
 ) теңдеуімен берілген қисықтың
ұзындығын табыңдар.
) теңдеуімен берілген қисықтың
ұзындығын табыңдар.
Шешуі:
l= dx=
dx= 2dx=
2dx= 2dx=
2dx= dx=
dx= dx=
dx=
t![]() gx
gx  =tg
=tg -tg0=
-tg0=
2.3.3.Айналу денесінің көлемі
Кеңістікте Т денесі және Ох өсі берілген. Осы Т денесіне х нүктесінен өтетін Ох өсіне перпендикуляр қима жүргіземіз. Оның ауданын Ǫ(x)деп белгілейік.
Т денесінің Ох өсіндегі проекциясы [a.b] кесіндісі болсын,яғни у=Ǫ(x)функциясы осы кесіндіде анықталған. Осы Ǫ(x) функциясын [a.b] кесіндісінде үзіліссіз функция деп есептейміз.
Т денесі [a.b] кесіндісінде анықталған y=f(x) үзіліссіз функциясымен берілген қисық сызықты трапецияның Ох өсінен айналуынан шыққан дене болсын. Дөңгелектің ауданы
Ǫ(x)=πf(x)2 формуласымен табылады, мұндағы f(x) дөңгелектің радиусы. Пайда болған айналу денесінің көлемі мына қатыспен анықталады:
V(T)=π (x)dx
(x)dx
2.3.4. Айналу бетінің ауданы
Үзіліссіз дифференциалданатын y=f(x),(x€[a,b] және f(x)≥0) функциясының графигі Ох өсінен айналсын. Пайда болған Н- айналу бетінің ауданы
S(H)=2π )2
dx
)2
dx
формуласымен табылады.
Өзін-өзі тексеруге арналған сұрақтар
-
Анықталған интегралды қолданып аудандарды есептеу
-
Қисық доғасының ұзындығын есептеу
-
Айналу денесінің көлемін есептеу
-
Айналу бетінің ауданын есептеу
Жаттығулар
-
Берілген қисықтармен шектелген фигураның ауданын есептеңдар
1.
y=
 ,y=x3
,y=x32.
y=x2,y=3-2x
3.
y=x3,x=1,x=3
4.
y=x2-3,y+3x-4=0
Берілген қисықтың доғасының ұзындығын есептеңдер
1.
y2=(x+3)3,x=4
2.
 +
+ =
=
3.
y=ln(1-x2),x=
 ,x=
,x=
4.
x=
 ,
y=0,y=3
,
y=0,y=3Көрсетілген координата өсін айналдыру арқылы берілген қисықтармен шектелген фигураның айналуынан пайда болған дененің көлемін есептеңдер
1.
y=sinx,y=0 (0
 )
Ox
)
Ox2.
y3=x2, y=1 Ox
3.
y2=(x-1)3,x=2,Ox
4.
y2=x, x2=y,Ox
Көрсетілген аралықта берілген қисықтың айналуынан пайда болған бетінің ауданын есептеңдер
1.
y=1-x2, y
 ,
Ox
,
Ox2.
y=x3,(0
 ),Ox
),Ox3.
y=
 ,
(-2
,
(-2 ),Ox
),Ox4.
y=sinx, (0
 ),
Ox
),
Ox
Деңгейлік тестік тапсырмалар
ТЕСТ 1
-
x=2-y+y2 және x=0 сызықтарымен шектелген фигураның ауданы
А) 3 B)4
C) D)
D)
 E)
E)
2.y=3x,y= , x=1, x=2 сызықтарымен
шектелген фигураның ауданы
, x=1, x=2 сызықтарымен
шектелген фигураның ауданы
А) В)
В)
 С)
С)  D)
D) E)
E)
3. y= x2 жәнеy=6x-x2 сызықтарымен шектелген
фигураның ауданы
x2 жәнеy=6x-x2 сызықтарымен шектелген
фигураның ауданы
А) 16 B)14 C)12 D)10 E)8
4. y=x2,y=0,x=1,x=2 сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
5.y=sinx,y=0,x= ,x=
,x= сызықтарымен шектелген
фигураның ауданы
сызықтарымен шектелген
фигураның ауданы
А)
 B)1
C)
B)1
C) D)
D)
 E)
E)
6.y= ,y=2 және у осі
сызықтарымен шектелген фигураның ОУ осінен айналуынан пайда болған
дененің көлемі неге тең?
,y=2 және у осі
сызықтарымен шектелген фигураның ОУ осінен айналуынан пайда болған
дененің көлемі неге тең?
А)  B)
B) C)
C) D)
D)  E)
E)
7. y=lnx,x=e және х осі сызықтарымен шектелген фигураның ОХ осінен айналуынан пайда болған дененің көлемі
А)  (e-1) B)
(e-1) B) (e+1) C)
(e+1) C) D)3
D)3 E)
E)
8. y=cosx,x= , х осі және у осімен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
, х осі және у осімен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
А)  B)
B)  C)
C) D)
D)  E)
E)
9. y=-x2 және y=x2-2 функцияларымен шектелген ауданның х осінен айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
10.
y= параболасының мына екі
нүктенің арасындағы доғаның ұзындығы:О(0,0)
және
параболасының мына екі
нүктенің арасындағы доғаның ұзындығы:О(0,0)
және
А( ;
; )
)
А) +
+ ln(
ln( ) B)
) B)  ln(
ln( ) C)
) C)  +ln(
+ln( ) D)
) D)  E)
E) -
- ln(
ln( )
)
Тест 2
1.y= ,y=0,x=1,x=0
сызықтарымен шектелген фигураның ауданы
,y=0,x=1,x=0
сызықтарымен шектелген фигураның ауданы
А)1 B)е C)2е+1 D)е-1
E)
2. y=x2-4x+4 және y=x сызықтарымен шектелген фигураның ауданы
А)2 B)5 C)12
D)  E)
E)
3.y=x2-2x y=6x-x2 сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
4. y=x2 және y=x сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
5.y=x2-2x және y=-x2+2x сызықтарымен шектелген фигураның ауданы
А)
 B)
B) C)
C) D)
D)
 E)
E)
6.y=cosx және
x= ,x=
,x= сызықтарымен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
сызықтарымен шектелген
ауданның х осінен айналуынан пайда болған дененің
көлемі
А) B)
B) C)
C) D)
D)  E)
E)
7.y=x2-2 және y=1 функцияларымен шектелген ауданның у осінен айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
8.y2=4-x және x=0 сызықтарымен шектелген, у осін айналуынан пайда болған дененің көлемі
А)  B)
B) C)
C) D)
D)  E)
E)
9.у2=4x параболасының мына екі нүкте арасындағы доғаның ұзындығы:
О(0,0) және
А( )
)
А)  +ln(
+ln( +2) B)
+2) B) ln(
ln( ) C)
) C) D)
D) E)
E) + ln(
+ ln( )
)
10.y=x2параболасының мына екі нүкте
арасындағы доғаның ұзындығы О(0,0) және
А( )
)
А)
 +ln(
+ln( +2)
B)
+2)
B) +
+ ln(
ln( )
C)
)
C) -
ln(
-
ln( +3)
D)
+3)
D) E)
E) -
- ln(
ln( )
)
Білімін тексеруге арналған қосымша тестік тапсырмалар:
1. dx
dx
А) +2x+CB)
+2x+CB) C)
C) D)
D)  +5x+CE)
+5x+CE) +5x+C
+5x+C
2. (x-
(x- )dx
)dx
A)
 x2
x2 B)
B)
 x2
x2 C)
C)
 x
x D)
D)
 x
x E)
E) x
x
3. dx
dx
A)
 +C
B)
+C
B) +C
C)
+C
C) +C
D)
+C
D) +C
E)
+C
E) +C
+C
4. dx
dx
A)2ln +C
B)ln
+C
B)ln +C C)
2x2+C
D)2x-2+C
E)2x-1+C
+C C)
2x2+C
D)2x-2+C
E)2x-1+C
5.
 dx
dx
A)
 x4+C
B)5x4+C
C)5x6
+C D)
x4+C
B)5x4+C
C)5x6
+C D)
 +C
E)
+C
E)  +C
+C
6.
A) +C
B)
+C
B) +C
C)
+C
C)  +C
D)
+C
D) +C
E)6x5+C
+C
E)6x5+C
7.

A)
 arctgx+C
B)
arctgx+C
B) arcctg
arcctg +C
C)
+C
C) arctg
arctg +C
D)
+C
D)  C
E)
C
E) +C
+C
8. dx
dx
A)
C+x-e-x(x+1)
B) +
+ +arcsinx+C
C)
+arcsinx+C
C) -x+arctgx+C
D)C-
-x+arctgx+C
D)C- (x+1) E)
C-
(x+1) E)
C- (x-1)
(x-1)
9. dx
dx
A)
0.2(x3-8)5+C
B)x4+x2+8x+C
C) (
( -8)6\5+C D)
5(x3-8)7\5+C E)
0.2(e+1)5
-8)6\5+C D)
5(x3-8)7\5+C E)
0.2(e+1)5
10.
 dx
dx
A)
arcsinx-2 +C B)
arcsinx-
+C B)
arcsinx- +C C)
arcsinx+
+C C)
arcsinx+ +C D)
arcsinx+2
+C D)
arcsinx+2 +C
+C
E)
 -
arcsinx+C
-
arcsinx+C
11.
 dx
dx
A)ex+e-x+C B)
ex-e-x+C C)
e-x-ex+C
D)2(ex+e-x)+C E)
 (ex+e-x)+C
(ex+e-x)+C
12. (tgx)
(tgx)
A)
 x+C
B)
x+C
B) x+C
C)
x+C
C) x+C
D)
x+C
D) x+C
E)
x+C
E)  x+C
x+C
13.
A)
 x+C
B)
x+C
B)  x+C
C)
x+C
C) x+C
D)
x+C
D) x+C
E)
x+C
E) x+C
x+C
14.
 dx
dx
A)
3* ln2+C
B)
ln2+C
B)  *
* ln2+C
C)
ln2+C
C)  +C
D)
+C
D)  ln2+C
E)
ln2+C
E)  *
* +C
+C
15. dx
dx
A)
 +C
B)
+C
B) +C
C)
+C
C) +C
D)
+C
D)  E)
E) +C
+C
16.
A)C- B)
C-
B)
C- C)
C-
C)
C- D)
C-
D)
C- E)
C-
E)
C-
17.
A)
 +C
B)
+C
B)  3 +C C)
2
3 +C C)
2 3 D)
3 D)
 +C
E)
+C
E) +C
+C
18. dx
dx
A)3cosx+12x2+C B)-3cosx+x4+C C)3sinx+x4+C D)3cosx+x4+C E)-3cosx+12x2+C
19. dx
dx
A)
e3x-5+C B)
5e3x-5+C C)
3e3x-5+C
D) e3x-5+C E)
e3x-5+C E)
 e3x-5+C
e3x-5+C
20.

A) +C
B)
+C
B)  +C
C)
+C
C)  +C
D)
+C
D)  +C
E)
+C
E)  +C
+C
Қолданған әдебиеттер тізімі
-
Әбілқасымова А.Е және т.б. Алгебра және анализ бастамалары 11 сынып- Алматы
-
Гусев В.А, Мордкович А.Г Математика: Анықтама материалдар. Оқушыларға арналған кітап.
-
Анарбекова Ә, Бейсеков Ж, Назанов Ж. «Алгебрадан ҰБТ-ға дайындауға арналған әртүрлі деңгейдегі тест тапсырмаларының жинағы»
-
П.А.Ларичев, «Алгебра есептерінің жинағы»

шағым қалдыра аласыз

















































