0 / 1
Барлық 400 000 материалдарды тегін жүктеу үшін
Ұнаған тарифті таңдаңыз
Айлық
Жылдық
1 - күндік
Танысу 690 ₸ / 1 күнге
Таңдау
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. 10 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 30 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу5 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
1 - айлық
Стандарт
2990 ₸ / айына
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. жасау 30 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 900 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу 150 файлды тегін жүктеу
Жинақталған ҚМЖ бөлімінде 10 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
Іс-шаралар (мини-курстар, семинарлар, конференциялар) тегін қатысу
1 - айлық
Шебер 7990 ₸ / айына
Таңдау
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. жасау 150 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 900 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу 300 файлды тегін жүктеу
Жинақталған ҚМЖ бөлімінде 50 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
Іс-шаралар (мини-курстар, семинарлар, конференциялар) тегін қатысу

Назар аударыңыз!
Сіз барлық мүмкіндікті қолдандыңыз.
Қалған материалдарды ертең жүктей аласыз.
Ок
Материалдың қысқаша нұсқасы
ЖИ арқылы жасау
ЖИ арқылы жасау
Бөлісу
1 - айлық
Материал тарифі-96% жеңілдік
00
05
00
ҚМЖ
Ашық сабақ
Тәрбие сағаты
Презентация
БЖБ, ТЖБ тесттер
Көрнекіліктер
Балабақшаға арнарлған құжаттар
Мақала, Эссе
Дидактикалық ойындар
және тағы басқа 400 000 материал
Барлық 400 000 материалдарды шексіз
жүктеу мүмкіндігіне ие боласыз
жүктеу мүмкіндігіне ие боласыз
1 990 ₸ 49 000₸
1 айға қосылу
Материалға шағымдану
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жариялаған:
Елемесова Злиха ЗейнелхановнаШағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз
Ашық сабақ: "Тік бұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі"
Тақырып бойынша 11 материал табылды
Ашық сабақ: "Тік бұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі"
Материал туралы қысқаша түсінік
Тік бұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі
Оқушылар тақырып мазмұнын өмірмен байланыстыра отырып түсінуге мүмкіндік беру тақырып идеясындағы мәселелерді жан –жақты іздестіру арқылы баланың шындыққа көзқарасын айқындауға жағдай туғызу.
Жұмыс жайлы білімін тиімді қолдануға үйренеді. Шығармашылық қабілеттері іс-әрекетте көрінеді.
Материалдың қысқаша нұсқасы
Бөлісу
ЖИ арқылы жасау
Файл форматы:

docx
29.12.2017
2089
ЖИ арқылы жасау
Жариялаған:
Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз,
шағым қалдыра аласыз
шағым қалдыра аласыз


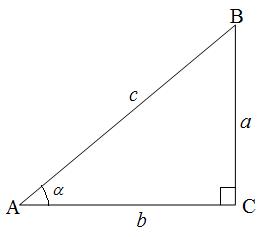
 А=α деп белгілейік.
А=α деп белгілейік.  (1) түрінде жазады. (1) қатынас α бұрышының
шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді
емес.
(1) түрінде жазады. (1) қатынас α бұрышының
шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді
емес.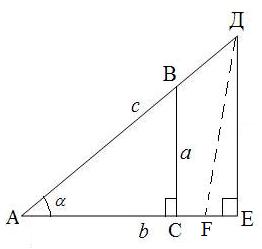
 екенін
дәлелдейміз. Шынында
екенін
дәлелдейміз. Шынында  болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне
перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF
перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты
үшбұрышы үшін cos
болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне
перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF
перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты
үшбұрышы үшін cos
 аламыз, бірақ
аламыз, бірақ  немесе
немесе  болып қалады. Онда AE=AF және
cos
болып қалады. Онда AE=AF және
cos (2)
(2) (3)
(3) (4)
(4)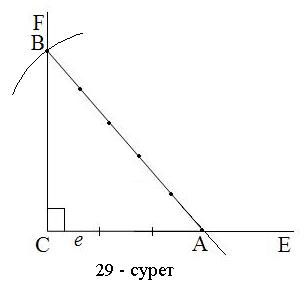 cos
cos теңдігі орындалу керек. Бірлік кесінді е таңдап
аламыз.
теңдігі орындалу керек. Бірлік кесінді е таңдап
аламыз.  сәулелерін жүргіземіз. 29
–сурет.
сәулелерін жүргіземіз. 29
–сурет. болады. Демек, салынған үшбұрыш есептің шартын
қанағаттандырады.
болады. Демек, салынған үшбұрыш есептің шартын
қанағаттандырады. ; 3) 0,6-ға тең тікбұрышты үшбұрыш
салыңдар.
; 3) 0,6-ға тең тікбұрышты үшбұрыш
салыңдар.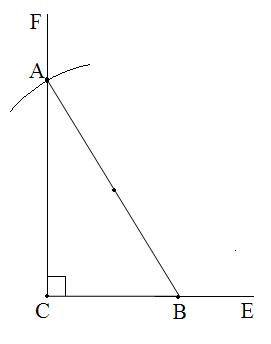
 СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1
саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А
нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын
қанағаттандырады.
СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1
саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А
нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын
қанағаттандырады.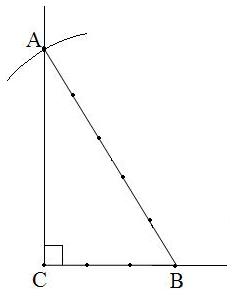

 ; 3) 1-ге тең тікбұрышты үшбұрыш
салыңдар.
; 3) 1-ге тең тікбұрышты үшбұрыш
салыңдар.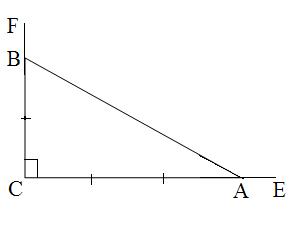 )
)  ,
, 
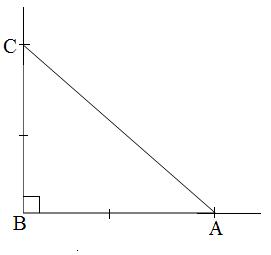 ешуі:
ешуі:  да а=b екені белгілі болып
отыр.
да а=b екені белгілі болып
отыр.












