Пояснительная записка
Актуальность программы обусловлена возрастающей ролью вероятностно-статистического мышления в современном мире. В условиях постоянно увеличивающегося потока информации и необходимости принимать решения в условиях неопределенности, теория вероятностей становится незаменимым инструментом для анализа и прогнозирования различных процессов.
Потребность в программе связана с необходимостью формирования у учащихся вероятностного мышления, навыков статистического анализа и умения работать с большими массивами данных, что является важным требованием современного образования и будущей профессиональной деятельности.
Научно-методический уровень программы характеризуется системным подходом к изучению теории вероятностей, включающим как теоретические основы, так и практическое применение. Программа предусматривает использование современных цифровых инструментов для статистической обработки данных и визуализации вероятностных моделей.
Направленность программы:
-
Развитие вероятностного мышления
-
Формирование навыков статистического анализа
-
Развитие умения моделировать реальные процессы
-
Применение теории вероятностей в практических задачах
Основная цель программы: формирование у учащихся вероятностно-статистической грамотности и развитие навыков применения теории вероятностей для решения практических задач.
Задачи программы:
-
Сформировать понимание основных концепций теории вероятностей
-
Развить навыки вероятностного моделирования
-
Научить применять статистические методы анализа
-
Развить умение интерпретировать вероятностные результаты
-
Сформировать навыки работы с компьютерными программами для статистической обработки данных
-
Развить аналитическое мышление
-
Научить применять вероятностные методы в различных областях
-
Подготовить к решению практических задач с вероятностным содержанием
Ожидаемые результаты:
-
Учащиеся освоят основные понятия и методы теории вероятностей
-
Научатся решать вероятностные задачи различного уровня сложности
-
Приобретут навыки работы со статистическими программами
-
Освоят методы вероятностного моделирования
-
Сформируют навыки анализа статистических данных
-
Приобретут опыт исследовательской деятельности в области теории вероятностей
-
Научатся применять вероятностные методы в реальных ситуациях
-
Продемонстрируют готовность к решению прикладных задач
Отличительной особенностью программы является её практическая направленность и использование современных цифровых инструментов для анализа данных. Программа построена по принципу возрастающей сложности, что обеспечивает последовательное развитие вероятностного мышления учащихся.
Принципы отбора материала основаны на логической последовательности изучения тем, их взаимосвязи и практической значимости. Особое внимание уделяется связи теории вероятностей с реальными жизненными ситуациями и другими областями знаний.
Обоснованность и достоверность ожидаемых результатов подтверждается соответствием программы современным образовательным стандартам и успешным опытом применения вероятностно-статистических методов в различных областях. Программа предусматривает регулярный мониторинг успеваемости учащихся и корректировку методов обучения при необходимости.
Содержание:
Раздел 1. Основы теории вероятностей и комбинаторика
-
Введение в теорию вероятностей
-
Основные понятия теории вероятностей
-
Элементы комбинаторики: перестановки
-
Элементы комбинаторики: размещения и сочетания
-
Применение комбинаторики в вероятности
Раздел 2. События и классическая вероятность
-
События и их виды
-
Классическое определение вероятности
-
Геометрическая вероятность
-
Свойства вероятности. Часть 1
-
Свойства вероятности. Часть 2
Раздел 3. Условная вероятность и основные теоремы
-
Условная вероятность: основные понятия
-
Условная вероятность: решение задач
-
Правило сложения вероятностей
-
Правило умножения вероятностей
-
Формула полной вероятности: теория
-
Формула полной вероятности: практика
-
Формула Байеса: основные понятия
-
Формула Байеса: решение задач
Раздел 4. Схема Бернулли
-
Схема Бернулли
-
Формула Бернулли и её применение
-
Наивероятнейшее число успехов в схеме Бернулли
Раздел 5. Случайные величины и их характеристики
-
Случайные величины: основные понятия
-
Дискретные случайные величины
-
Непрерывные случайные величины
-
Числовые характеристики случайных величин
-
Математическое ожидание и его свойства
-
Дисперсия и среднее квадратическое отклонение
Раздел 6. Законы распределения случайных величин
-
Биномиальное распределение
-
Распределение Пуассона
-
Нормальное распределение
-
Закон больших чисел
Раздел 7. Элементы математической статистики
-
Генеральная совокупность и выборка: основные понятия
-
Вариационные ряды и их характеристики
-
Статистические оценки параметров распределения
Нормативная часть
Всего 34 час, в неделю 1 час.
Предназначено для 9-11 классов.
|
№ |
Тема |
Цели обучения |
Количество часов |
Образовательный продукт |
||
|
Всего |
Теория |
Практика |
||||
|
1 |
Введение в теорию вероятностей |
Анализировать роль теории вероятностей |
1 |
1 |
|
Анализируют примеры применения в жизни |
|
2 |
Основные понятия теории вероятностей |
Систематизировать основные определения |
1 |
|
1 |
Систематизируют термины в виде схемы |
|
3 |
Элементы комбинаторики: перестановки |
Исследовать правила составления перестановок |
1 |
|
1 |
Исследуют и составляют алгоритм решения |
|
4 |
Элементы комбинаторики: размещения и сочетания |
Сравнивать формулы размещений и сочетаний |
1 |
|
1 |
Сравнивают и составляют таблицу различий |
|
5 |
Применение комбинаторики в вероятности |
Интегрировать знания комбинаторики и вероятности |
1 |
|
1 |
Интегрируют методы решения в задачах |
|
6 |
События и их виды |
Классифицировать виды событий |
1 |
1 |
|
Классифицируют события по признакам |
|
7 |
Классическое определение вероятности |
Анализировать классическое определение |
1 |
|
1 |
Анализируют и решают типовые задачи |
|
8 |
Геометрическая вероятность |
Применять геометрический подход |
1 |
|
1 |
Применяют формулы в геометрических задачах |
|
9 |
Свойства вероятности. Часть 1 |
Исследовать основные свойства вероятности |
1 |
1 |
|
Исследуют свойства на конкретных примерах |
|
10 |
Свойства вероятности. Часть 2 |
Доказывать свойства вероятности |
1 |
|
1 |
Доказывают и применяют свойства |
|
11 |
Условная вероятность: основные понятия |
Интерпретировать понятие условной вероятности |
1 |
1 |
|
Интерпретируют условия в задачах |
|
12 |
Условная вероятность: решение задач |
Синтезировать способы решения |
1 |
|
1 |
Синтезируют алгоритм решения задач |
|
13 |
Правило сложения вероятностей |
Анализировать случаи применения правила |
1 |
1 |
|
Анализируют и решают комбинированные задачи |
|
14 |
Правило умножения вероятностей |
Оценивать применимость правила |
1 |
|
1 |
Оценивают и выбирают способ решения |
|
15 |
Формула полной вероятности: теория |
Исследовать структуру формулы |
1 |
1 |
|
Исследуют компоненты формулы |
|
16 |
Формула полной вероятности: практика |
Применять формулу в различных ситуациях |
1 |
|
1 |
Применяют формулу к практическим задачам |
|
17 |
Формула Байеса: основные понятия |
Интерпретировать смысл формулы |
1 |
1 |
|
Интерпретируют условия применения |
|
18 |
Формула Байеса: решение задач |
Синтезировать методы решения |
1 |
|
1 |
Синтезируют способы применения формулы |
|
19 |
Схема Бернулли |
Анализировать условия применения схемы |
1 |
|
1 |
Анализируют и составляют схему решения |
|
20 |
Формула Бернулли и её применение |
Применять формулу в различных задачах |
1 |
|
1 |
Применяют формулу в практических задачах |
|
21 |
Наивероятнейшее число успехов |
Вычислять вероятность успехов |
1 |
|
1 |
Вычисляют и интерпретируют результаты |
|
22 |
Случайные величины: основные понятия |
Классифицировать случайные величины |
1 |
|
1 |
Классифицируют виды величин |
|
23 |
Дискретные случайные величины |
Исследовать характеристики величин |
1 |
|
1 |
Исследуют и описывают свойства |
|
24 |
Непрерывные случайные величины |
Сравнивать виды случайных величин |
1 |
|
1 |
Сравнивают характеристики величин |
|
25 |
Числовые характеристики случайных величин |
Вычислять основные характеристики |
1 |
|
1 |
Вычисляют параметры распределений |
|
26 |
Математическое ожидание и свойства |
Доказывать свойства мат.ожидания |
1 |
|
1 |
Доказывают и применяют свойства |
|
27 |
Дисперсия и среднее квадратическое отклонение |
Анализировать меры разброса |
1 |
|
1 |
Анализируют и вычисляют параметры |
|
28 |
Биномиальное распределение |
Исследовать свойства распределения |
1 |
|
1 |
Исследуют характеристики распределения |
|
29 |
Распределение Пуассона |
Применять распределение в задачах |
1 |
|
1 |
Применяют формулы распределения |
|
30 |
Нормальное распределение |
Интерпретировать график распределения |
1 |
|
1 |
Интерпретируют параметры распределения |
|
31 |
Закон больших чисел |
Анализировать следствия закона |
1 |
|
1 |
Анализируют примеры применения |
|
32 |
Генеральная совокупность и выборка |
Сравнивать характеристики совокупностей |
1 |
|
1 |
Сравнивают параметры выборок |
|
33 |
Вариационные ряды |
Систематизировать данные в ряды |
1 |
|
1 |
Систематизируют и строят ряды |
|
34 |
Статистические оценки параметров |
Оценивать параметры распределения |
1 |
|
1 |
Оценивают точность параметров |
|
Всего |
34 |
6 |
28 |
|
||
Информационно-методический отдел
Авторская программа "Теория вероятностей" для 9-11 классов направлена на формирование вероятностного мышления и развитие навыков статистического анализа. Темы, представленные в семи разделах программы, включают материалы, соответствующие образовательным стандартам. Практико-ориентированный подход к изучению способствует глубокому пониманию теории вероятностей и её применению в реальных ситуациях.
Критериальная система оценивания по 10-балльной шкале
|
Баллы |
Процент |
Уровень учебных достижений |
Критерии оценивания |
|
10 |
95-100% |
Высокий |
Глубокое понимание теории вероятностей, свободное решение сложных задач, способность анализировать и интерпретировать результаты |
|
9 |
90-94% |
Высокий |
Отличное знание материала, умение решать задачи повышенной сложности, незначительные недочеты |
|
8 |
85-89% |
Достаточный |
Хорошее владение материалом, способность решать стандартные и усложненные задачи |
|
7 |
80-84% |
Достаточный |
Хорошее понимание основных концепций, умение решать типовые задачи |
|
6 |
70-79% |
Средний |
Понимание основного материала, решение задач среднего уровня сложности |
|
5 |
60-69% |
Средний |
Базовое понимание материала, решение простых задач с некоторыми ошибками |
|
4 |
50-59% |
Удовлетворительный |
Частичное понимание материала, решение простых задач |
|
3 |
30-49% |
Низкий |
Слабое владение материалом, существенные ошибки в решениях |
|
2 |
15-29% |
Низкий |
Серьезные пробелы в знаниях, неспособность решать базовые задачи |
|
1 |
0-14% |
Низкий |
Отсутствие базовых знаний и умений |
Содержание программы:
-
Основы теории вероятностей и комбинаторика
-
События и классическая вероятность
-
Условная вероятность и основные теоремы
-
Схема Бернулли
-
Случайные величины и их характеристики
-
Законы распределения случайных величин
-
Элементы математической статистики
Приложения:
-
Практические задания по каждому разделу
-
Контрольные работы и тесты
-
Методические рекомендации для учителей
-
Учебные материалы в цифровом формате
-
Оценочные материалы
-
Дополнительные материалы для подготовки к олимпиадам
Рекомендуемые цифровые инструменты:
-
Microsoft Excel — статистическая обработка данных, построение графиков
-
GeoGebra Probability Calculator — визуализация вероятностных моделей
-
R Studio — статистический анализ данных
-
Python с библиотекой Pandas — обработка больших наборов данных
Формативное оценивание включает:
-
Устные ответы
-
Решение задач у доски
-
Самостоятельные работы
-
Домашние задания
-
Практические работы
-
Проектная деятельность
Суммативное оценивание включает:
-
Контрольные работы по разделам
-
Четвертные контрольные работы
-
Итоговая контрольная работа
-
Защита проектов
Список литературы:
Для учителей:
-
Алдамуратов Е.С., Байсалов Ж.К. "Методика преподавания теории вероятностей в школе" (Алматы, 2021)
-
Нурпеисова Г.М. "Современные подходы к обучению теории вероятностей" (Нур-Султан, 2020)
-
Жумагулова К.А. "Организация проектной деятельности на уроках теории вероятностей" (Алматы, 2019)
-
Сатыбалдиев О.С. "Практикум по решению вероятностных задач" (Караганда, 2022)
-
Мусабеков А.К. "Дифференцированный подход в обучении теории вероятностей" (Шымкент, 2021)
Для учащихся:
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 9 класса" (Алматы, 2019)
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 10 класса" (Алматы, 2019)
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 11 класса" (Алматы, 2019)
-
Искаков Б.А. "Теория вероятностей в таблицах и схемах" (Павлодар, 2021)
-
Муканова Р.А. "Готовимся к олимпиадам по теории вероятностей" (Алматы, 2022)
Для родителей:
-
Ахметов М.А. "Как помочь ребенку в изучении теории вероятностей" (Астана, 2022)
-
Тулегенова Г.С. "Теория вероятностей: помощь родителям" (Алматы, 2021)
-
Байжуманов А.А. "Родительское руководство по поддержке изучения математики" (Караганда, 2020)
-
Сагиндыков Е.Н. "Математика в семье: советы родителям" (Костанай, 2021)
-
Нурмухамедова Ж.М. "Как развивать вероятностное мышление у детей" (Алматы, 2022)
Приложение.
Задача №1.
Посмотреть видеоматериал.

Задача №2.
Текстовые задачи.
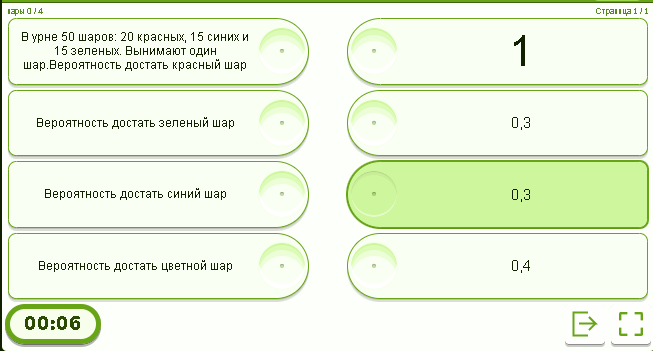
В классе из 30 учеников 18 занимаются спортом, 15 изучают английский язык, а 10 учеников совмещают спорт и английский. Какова вероятность того, что случайно выбранный ученик не занимается ни спортом, ни английским?
В магазине продаются 200 телефонов, из них 120 - черного цвета, 50 - белого, остальные - синего. Какова вероятность купить телефон не черного цвета?
На полке стоят 15 книг, из них 6 - на казахском языке, 5 - на русском, 4 - на английском. Какова вероятность взять книгу на казахском языке?
В коробке 10 красных, 8 синих и 7 зеленых шаров. Какова вероятность достать шар синего цвета?
Задача №3.
«Froggy jumps»


Задача №4.
Групповая работа.
Игра «ОХО»
Задача 1: "Мишень"
На квадратном листе картона со стороной 50 см нарисована круглая мишень радиусом 20 см. Случайным образом в лист картона попадает дротик. Найти вероятность того, что дротик попадет в мишень.
Задача 2: "Парковка"
Длина парковочного места 5 метров. Водитель паркует автомобиль длиной 4 метра. Чтобы припарковаться правильно, центр автомобиля должен находиться в средней части парковочного места на расстоянии не более 0,3 метра от его центра. Найти вероятность правильной парковки.
Задача 3: "Художник"
На прямоугольном холсте размером 80×60 см художник нарисовал квадрат со стороной 40 см. Если случайным образом поставить точку на холсте, какова вероятность, что она попадет в квадрат?
Задача 4: "Часовая стрелка"
Часовая стрелка движется по циферблату. Найти вероятность того, что в случайный момент времени она находится между 3 и 5 часами.
Задача 5: "Городской пруд"
В городском парке есть прямоугольный пруд размером 30×20 метров. Внутри пруда есть круглый остров радиусом 5 метров. Какова вероятность того, что брошенный случайным образом в пруд камень попадет в воду, а не на остров?
Задача 6: "Детская площадка"
На квадратной детской площадке со стороной 10 метров расположена круглая песочница радиусом 2 метра и прямоугольная беседка размером 3×2 метра. Найти вероятность того, что случайно брошенный мяч попадет на свободную территорию площадки.
Задача 7: "Велосипедист"
Велосипедист должен приехать в пункт назначения между 12:00 и 13:00. Он приезжает в случайный момент в этом промежутке. Найти вероятность того, что он приедет между 12:20 и 12:40.
Задача 8: "Линейка"
На отрезке длиной 20 см случайным образом ставятся две точки. Найти вероятность того, что расстояние между ними будет меньше 5 см.
Задача 9: "Спортивная площадка"
На прямоугольной спортивной площадке размером 40×30 метров начерчены две круглые зоны для игр радиусом 5 метров каждая. Найти вероятность того, что случайно брошенный мяч попадет в одну из игровых зон.
Задача №5.
Задачи с рисунками.
Задача 1: "Мишень"
В квадратную мишень со стороной 100 см вписан красный круг радиусом 40 см. Стрелок стреляет случайным образом по мишени. Найти вероятность того, что стрела попадет в красную область мишени.
Задача 2: "Цветник"
На квадратном участке земли со стороной 10 метров расположены два круглых цветника радиусом 2 метра каждый и прямоугольная клумба размером 4×3 метра. Найти вероятность того, что случайно упавшее семя попадет на свободную землю (не в цветник и не в клумбу).
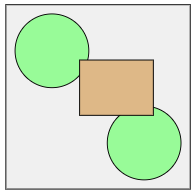
Задача 3: "Картина"
На прямоугольном холсте размером 100×100 см художник нарисовал прямоугольное озеро размером 80×40 см и круглое солнце радиусом 20 см. Если случайным образом поставить точку на холсте, какова вероятность того, что она попадет либо в озеро, либо в солнце?
Задача №6.
Математический диктант.
-
Дайте определение условной вероятности
-
Запишите формулу умножения вероятностей для зависимых событий
-
Как обозначается условная вероятность события А при условии В?
-
Запишите формулу Байеса
-
Что такое гипотеза в теории вероятностей?
Задача №7.
Сопоставление.
|
Описание события |
Формула |
|
Условная вероятность |
|
|
Произведение независимых событий |
|
|
Произведение зависимых событий |
|
|
Противоположное событие |
|
|
Полная вероятность |
|
Задача №8.
Парная работа.

Задача №9.
Тестовая задача.
1. Схема Бернулли - это:
A) Последовательность взаимозависимых испытаний B) Последовательность независимых испытаний с двумя исходами
C) Последовательность зависимых испытаний с тремя исходами
D) Одно испытание с двумя исходами
E) Испытание с множеством исходов
2. В формуле P(X=k) = C(n,k)·pᵏ·qⁿ⁻ᵏ для схемы Бернулли, q равно:
A) Вероятности успеха
B) 1 + p
C) 1 - p
D) p²
E) p/n
3. Локальная формула Муавра-Лапласа применяется, когда:
A) n < 10
B) n > 100
C) np < 10
D) n = 100
E) p = q
4. В схеме Бернулли вероятность успеха p:
A) Меняется от испытания к испытанию
B) Зависит от числа испытаний
C) Остается постоянной во всех испытаниях
D) Равна 1
E) Равна 0
5. Наивероятнейшее число успехов k₀ в схеме Бернулли определяется неравенством:
A) np - q ≤ k₀ ≤ np + p
B) np - p ≤ k₀ ≤ np + q
C) np - 1 ≤ k₀ ≤ np + 1
D) np ≤ k₀ ≤ np + 1
E) np – 2 ≤ k₀ ≤ np + 2
Задача №10.
Работа с таблицой.
|
Термин |
Определение |
Пример |
|
Схема Бернулли |
|
|
|
Успех |
|
|
|
Число испытаний |
|
|
|
Вероятность успеха |
|
|
|
Наивероятнейшее число |
|
|
Модель краткосрочного планирования
Урок №1
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Введение в теорию вероятностей |
|||||
|
Цели обучения согласно программе |
Анализировать роль теории вероятностей |
|||||
|
Цель урока |
Анализируют примеры применения в жизни |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
-Приветствие и краткое введение в тему урока. - Объяснить цели и задачи урока. |
-Слушают объяснение. - Задают вопросы для уточнения. -Записывают основные моменты в тетрадь. |
Метод оценки «Юрта» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Текстовые задачи. В классе из 30 учеников 18 занимаются спортом, 15 изучают английский язык, а 10 учеников совмещают спорт и английский. Какова вероятность того, что случайно выбранный ученик не занимается ни спортом, ни английским? В магазине продаются 200 телефонов, из них 120 - черного цвета, 50 - белого, остальные - синего. Какова вероятность купить телефон не черного цвета? На полке стоят 15 книг, из них 6 - на казахском языке, 5 - на русском, 4 - на английском. Какова вероятность взять книгу на казахском языке? В коробке 10 красных, 8 синих и 7 зеленых шаров. Какова вероятность достать шар синего цвета? Задача №3. Игра «Froggy jumps»
|
Ученики смотрят видеоматериал и понимают тему. Ученики решают текстовые задачи.
Ученики играют игру. |
Метод оценки «Юрта» |
https://youtu.be/_ZNvsnxaQr0?si=HK8vvdv_8i8JJhRz
https://www.educaplay.com/learning-resources/21203293-learning_resource.html |
||
|
Конец урока 5 минут |
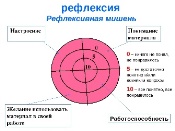
Рефлексия
|
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||
Урок №2
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Основные понятия теории вероятностей |
|||||
|
Цели обучения согласно программе |
Систематизировать основные определения |
|||||
|
Цель урока |
Систематизируют термины в виде схемы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5–10 минут |
Приветствие и проверка присутствующих. Введение в тему урока, объяснение целей урока. |
Слушают и записывают цели урока. Участвуют в обсуждении предыдущего материала. |
Дескриптор
Метод оценки «Бургер»
|
|
||
|
Середина урока 35 минут |
Задача №1. Текстовые задачи. В урне 20 шаров: 8 белых и 12 черных. Наудачу вынимают один шар. Описать элементарные исходы, благоприятные исходы и пространство элементарных исходов. Бросают игральный кубик. Описать события: А – выпало четное число, В – выпало число больше 4. При стрельбе по мишени рассматриваются события: А – попадание в цель, В – промах. Являются ли эти события совместными? В семье двое детей. Описать пространство элементарных исходов для пола детей (М - мальчик, Д - девочка). Задача №2. Метод «Верно, неверно»
Задача №3. Игра «Скачки»
|
Ученик анализирует условия задачи и определяет элементарные исходы, благоприятные события и пространство элементарных исходов в различных вероятностных ситуациях. Ученик анализирует каждое утверждение и определяет его истинность или ложность на основе теории вероятностей. Ученик применяет знания о вероятности в игровой ситуации, рассчитывая шансы на выигрыш. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность каждого ученика по заработанным наградам. |
|
|
||
Урок №3
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Элементы комбинаторики: перестановки |
|||||
|
Цели обучения согласно программе |
Исследовать правила составления перестановок |
|||||
|
Цель урока |
Исследуют и составляют алгоритм решения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Приветствие учеников и краткое введение в тему урока. Объяснение целей урока. Проведение короткого опроса для проверки начальных знаний. |
Приветствие учителя. Слушают объяснение целей урока. Участвуют в опросе. |
Дескриптор
Метод оценки «Цветок»
|
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Задание "Найди ошибку и исправь" В городском конкурсе участвуют 6 школ. Организаторы составляют порядок выступления школ. Ученик решил найти количество возможных вариантов порядка выступления школ. Решение ученика:
Задания:
Задача №3.
|
Ученик просматривает видеоматериал, анализирует и фиксирует ключевые моменты по теме. Ученик анализирует предложенное решение, находит ошибки и представляет правильное решение задачи. Ученик решает комбинаторные задачи, применяя формулы перестановок и размещений. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по количеству цветочков и оценкам учеников парной работы |
|
|
||
Урок №4
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Элементы комбинаторики: размещения и сочетания |
|||||
|
Цели обучения согласно программе |
Сравнивать формулы размещений и сочетаний |
|||||
|
Цель урока |
Сравнивают и составляют таблицу различий |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Приветствие и проверка присутствующих. Постановка целей урока перед учениками. |
Слушают учителя, отмечают присутствующих. Внимательно слушают введение и записывают цели урока. |
Дескриптор
Метод оценки «Разбаловка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Текстовые задачи.
Задача №3. Незаконченное предложение. Размещением из n элементов по k называется... а) любая упорядоченная подгруппа из k элементов данного множества б) любая неупорядоченная подгруппа из k элементов данного множества в) любой набор из n элементов Число размещений из n элементов по k обозначается... а) Сₖⁿ б) Aₖⁿ в) Pₙ Сочетанием из n элементов по k называется... а) размещение, где порядок элементов важен б) неупорядоченный набор из k элементов в) перестановка из n элементов В формуле числа размещений Aₖⁿ = n!/(n-k)! важен порядок элементов, потому что... а) в числителе стоит факториал б) учитывается последовательность расположения элементов в) в знаменателе стоит разность Формула числа сочетаний имеет вид... а) Сₖⁿ = n! б) Сₖⁿ = n!/(k!(n-k)!) в) Сₖⁿ = n!/(n-k)! |
Ученик просматривает видеоматериал, анализирует и фиксирует ключевые моменты по теме. Ученики решают текстовых задач. Ученик анализирует каждое незаконченное предложение и выбирает правильное продолжение, демонстрируя понимание основных понятий комбинаторики. |
Дескрипторы:
Правильно решают текстовых задач. Дескрипторы:
|
|
||
|
Конец урока 5 минут |
Рефлексия Ученики в конце урока оценивают урок через онлайн рефлекс. |
В конце урока учитель оценивает активность учеников по набранным баллам. |
|
|
||
Урок №5
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Применение комбинаторики в вероятности |
|||||
|
Цели обучения согласно программе |
Интегрировать знания комбинаторики и вероятности |
|||||
|
Цель урока |
Интегрируют методы решения в задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1. Приветствует учеников и объявляет тему урока. 2. Представляет цели урока. 3. Проводит короткий вводный опрос для проверки предыдущих знаний |
1. Слушают учителя и записывают тему урока. 2. Знакомятся с целями урока. 3. Участвуют в вводном опросе. |
Дескриптор
Метод оценки Копилка» |
|
||
|
Середина урока 35 минут |
Задача №1. Текстовые задачи.
Задача №2.
Задача №3. Контекстная задача "Школьный фестиваль талантов" В школе проводится ежегодный фестиваль талантов. В этом году подали заявки:
Организаторы планируют:
Задания:
|
Ученики решают текстовых задач. Ученик решает тестовые задания, применяя формулы комбинаторики для нахождения вероятности событий. Ученик анализирует реальную ситуацию, применяет комбинаторные формулы для решения практических задач и находит вероятности событий. |
Метод оценки Копилка» Дескрипторы: Правильно решают текстовых задач. Дескрипторы:
Дескрипторы:
|
https://wordwall.net/ru/resource/81440785
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает работу учеников по копилкам. |
|
|
||
Урок №6
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
События и их виды |
|||||
|
Цели обучения согласно программе |
Классифицировать виды событий |
|||||
|
Цель урока |
Классифицируют события по признакам |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Демонстрирует видео, показывающее основные законы химии. 2.Эмоцианальная подготовка учеников. Ученики делятся с хорошими пожеланиями на день. 3.Ученики делятся на 3 группы по методу Жребий
|
Ученики делятся хорошими эмоциями с друзьями. После выбирают листы с номерами и делятся на группы. |
Оценивание по методу «Яблоко» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Логические задачи. Задача 1. "Школьная олимпиада" На школьной олимпиаде по математике рассматриваются события: A – участник решит все задачи B – участник решит хотя бы одну задачу C – участник не решит ни одной задачи Определите:
Задача 2. "Игральные кубики" При одновременном бросании двух игральных кубиков рассмотрите события: A – сумма выпавших очков равна 7 B – произведение выпавших чисел четное C – хотя бы на одном кубике выпало число 6 Определите:
Задача 3. "Погодные явления" В течение дня могут произойти события: A – пойдет дождь B – будет пасмурно C – будет солнечно D – будет ветрено Определите:
Задача 4. "Спортивные соревнования" На соревнованиях по бегу рассматриваются события: A – спортсмен займет первое место B – спортсмен попадет в тройку призеров C – спортсмен не финиширует Определите:
Задача 5. "Библиотека" Читатель берет книгу в библиотеке. Рассмотрите события: A – книга окажется детективом B – книга окажется в твердом переплете C – книга будет новой Определите:
Задача 6. "Транспорт" При поездке в школу рассматриваются события: A – опоздать на урок B – сесть в переполненный автобус C – встретить одноклассника Определите:
Задача 7. "Экзамен" На экзамене рассматриваются события: A – вытянуть легкий билет B – получить оценку "5" C – не сдать экзамен D – ответить на все дополнительные вопросы Определите:
Задача №3. Игра Квест
|
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует различные события, определяет их виды и устанавливает связи между ними. Ученик участвует в математическом квесте, решая последовательные задачи по теории вероятностей и комбинаторике, применяя знания в игровой форме и продвигаясь по маршруту в зависимости от правильности решений. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Блиц-опрос (Учитель задает вопросы, на которые студенты отвечают по очереди). |
В конце урока учитель оценивает каждого по набранным наградам. |
|
|
||
Урок №7
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Классическое определение вероятности |
|||||
|
Цели обучения согласно программе |
Анализировать классическое определение |
|||||
|
Цель урока |
Анализируют и решают типовые задачи |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. 2.Ученики делятся на 2 группы по методу “Сегментация круга” |
Группу можно разделить пополам, проведя воображаемый диаметр круга от себя (ведущего) к участнику, сидящему напротив. В случае, если требуется более двух команд, то круг просто разбивается на нужное число сегментов. |
Метод оценки «Галочка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Контекстные задачи. Задача 1: "Книжный клуб" В книжном клубе школы есть 40 книг, из которых 15 - фэнтези, 10 - детективы, а остальные - научная фантастика. Библиотекарь наугад выбирает одну книгу для чтения на следующем собрании клуба. Найти вероятности следующих событий: а) будет выбрана книга жанра фэнтези б) будет выбран детектив в) будет выбрана научная фантастика Задача 2: "Школьная олимпиада" В школьной олимпиаде по математике участвуют 30 учеников: 12 из 9-го класса, 10 из 10-го класса и 8 из 11-го класса. Случайным образом выбирается один участник для награждения специальным призом. Найти вероятность того, что будет выбран: а) ученик 9-го класса б) ученик 10-го класса в) ученик 11-го класса Задача 3: "Цветочная клумба" На клумбе растут 60 цветов: 20 красных роз, 15 белых роз, 15 розовых тюльпанов и 10 желтых тюльпанов. Садовник случайным образом срывает один цветок для букета. Найти вероятности следующих событий: а) будет сорвана роза (любого цвета) б) будет сорван тюльпан (любого цвета) в) будет сорван красный цветок г) будет сорвана белая роза Задача №3. Игра «Найди пару»
|
Ученики смотрят видеоматериал и понимают тему.
Ученик решает три контекстные задачи на вычисление классической вероятности, применяя соответствующие формулы. Ученик находит соответствующие пары между событиями и их вероятностями, основываясь на правилах классической вероятности. |
Дескрипторы:
Дескрипторы:
|
https://youtu.be/_n-4BHsRnPc?si=__fl3kJbepJ4Z1vH https://www.educaplay.com/learning-resources/21243615-learning_resource.html |
||
|
Конец урока 5 минут |
Рефлексия Ученики оценивают урок по 10 баллной шкале. |
В конце урока учитель оценивает каждую группу и ученика по набранным наградам. |
|
|
||
Урок №8
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Геометрическая вероятность |
|||||
|
Цели обучения согласно программе |
Применять геометрический подход |
|||||
|
Цель урока |
Применяют формулы в геометрических задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
|
Ученики настраиваются на урок, разминаются. |
Дескриптор
Метод оценки «Апельсин» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Групповая работа. Игра «ОХО»
Задача 1: "Мишень" На квадратном листе картона со стороной 50 см нарисована круглая мишень радиусом 20 см. Случайным образом в лист картона попадает дротик. Найти вероятность того, что дротик попадет в мишень. Задача 2: "Парковка" Длина парковочного места 5 метров. Водитель паркует автомобиль длиной 4 метра. Чтобы припарковаться правильно, центр автомобиля должен находиться в средней части парковочного места на расстоянии не более 0,3 метра от его центра. Найти вероятность правильной парковки. Задача 3: "Художник" На прямоугольном холсте размером 80×60 см художник нарисовал квадрат со стороной 40 см. Если случайным образом поставить точку на холсте, какова вероятность, что она попадет в квадрат? Задача 4: "Часовая стрелка" Часовая стрелка движется по циферблату. Найти вероятность того, что в случайный момент времени она находится между 3 и 5 часами. Задача 5: "Городской пруд" В городском парке есть прямоугольный пруд размером 30×20 метров. Внутри пруда есть круглый остров радиусом 5 метров. Какова вероятность того, что брошенный случайным образом в пруд камень попадет в воду, а не на остров? Задача 6: "Детская площадка" На квадратной детской площадке со стороной 10 метров расположена круглая песочница радиусом 2 метра и прямоугольная беседка размером 3×2 метра. Найти вероятность того, что случайно брошенный мяч попадет на свободную территорию площадки. Задача 7: "Велосипедист" Велосипедист должен приехать в пункт назначения между 12:00 и 13:00. Он приезжает в случайный момент в этом промежутке. Найти вероятность того, что он приедет между 12:20 и 12:40. Задача 8: "Линейка" На отрезке длиной 20 см случайным образом ставятся две точки. Найти вероятность того, что расстояние между ними будет меньше 5 см. Задача 9: "Спортивная площадка" На прямоугольной спортивной площадке размером 40×30 метров начерчены две круглые зоны для игр радиусом 5 метров каждая. Найти вероятность того, что случайно брошенный мяч попадет в одну из игровых зон. Задача №3. Задачи с рисунками. Задача 1: "Мишень" В квадратную мишень со стороной 100 см вписан красный круг радиусом 40 см. Стрелок стреляет случайным образом по мишени. Найти вероятность того, что стрела попадет в красную область мишени.
Задача 2: "Цветник" На квадратном участке земли со стороной 10 метров расположены два круглых цветника радиусом 2 метра каждый и прямоугольная клумба размером 4×3 метра. Найти вероятность того, что случайно упавшее семя попадет на свободную землю (не в цветник и не в клумбу).
Задача 3: "Картина" На прямоугольном холсте размером 100×100 см художник нарисовал прямоугольное озеро размером 80×40 см и круглое солнце радиусом 20 см. Если случайным образом поставить точку на холсте, какова вероятность того, что она попадет либо в озеро, либо в солнце?
|
Ученики смотрят видеоматериал и понимают тему. Ученик в группе решает предложенные задачи на геометрическую вероятность, обсуждая решение с одноклассниками. Ученик анализирует геометрические фигуры на рисунках и решает задачи с использованием формул площадей фигур. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Учитель раздает стикеры-листочки. Ученики пишут мнения об уроке анонимно и клеят на лучики солнца. |
Учитель в конце урока оценивает активность и количество листочков. |
|
|
||
Урок №9
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Свойства вероятности. Часть 1 |
|||||
|
Цели обучения согласно программе |
Исследовать основные свойства вероятности |
|||||
|
Цель урока |
Исследуют свойства на конкретных примерах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. 2. Ученики делятся на пары по желанию (мини группа). |
Ученики знакомятся и делятся на мини группы из 2 человек. |
Дескриптор Метод оценивания «Попкорн» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. 1.Какое из следующих утверждений о вероятности события верно? A) Вероятность может быть отрицательным числом B) Вероятность может быть больше 1 C) Вероятность может быть равна 1,5 D) Вероятность всегда находится в пределах от 0 до 1 E) Вероятность всегда больше 0,5 2.Вероятность достоверного события равна... A) -1 B) 0 C) 0,5 D) 1 E) 2 3.Если вероятность события A равна 0,7, то вероятность противоположного события Ā равна... A) 0,7 B) 0,3 C) 1,7 D) -0,7 E) 1,4 4.Если события A и B несовместны, то вероятность их суммы P(A + B) равна... A) P(A) × P(B) B) P(A) - P(B) C) P(A) + P(B) D) P(A)/P(B) E) max(P(A), P(B)) 5.Сумма вероятностей противоположных событий всегда равна... A) 0 B) 0,5 C) 1 D) 2 E) 100 6.Если вероятность события A равна 0,4, а события B равна 0,3, то вероятность их суммы P(A + B) для несовместных событий равна... A) 0,12 B) 0,1 C) 0,7 D) 1,0 E) 0,35 Задача №3. Метод «Фри»
1.В коробке лежат 20 цветных карандашей: 8 красных, 7 синих и 5 зеленых. Наугад вытаскивают один карандаш. Найдите вероятность того, что вытащенный карандаш будет красный, не красный, синий или зеленый. 2.В урне находятся 15 шаров: белые и черные. Вероятность вытащить белый шар равна 0,4. Сколько белых шаров в урне? 3.В группе 25 студентов, из них 15 девушек. Случайным образом выбирают одного студента. Найдите вероятность того, что выбранный студент девушка или юноша. Проверьте, чему равна сумма этих вероятностей. 4.На полке стоят 30 книг, из них 12 – учебники. Случайным образом берут одну книгу. Найдите вероятность того, что взятая книга учебник или не учебник. Докажите, что эти события противоположные. 5.В коробке 10 конфет: 6 шоколадных и 4 карамельки. Наугад берут две конфеты. Найдите вероятность того, что обе конфеты будут шоколадные или разные. 6.В классе 20 учеников. Из них 8 занимаются спортом, 12 занимаются музыкой, а 4 ученика занимаются и спортом, и музыкой. Какова вероятность того, что случайно выбранный ученик занимается спортом или музыкой, либо не занимается ничем. |
Ученики смотрят видеоматериал и понимают тему. Ученик решает тестовые задания, применяя знания о свойствах вероятности. Ученик самостоятельно решает задачи на применение свойств вероятности, выбирая наиболее подходящий метод решения. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Студенты заполняют карточки с вопросами о том, что нового они узнали и что осталось непонятным. |
В конце урока учитель оценивает обучающихся по набранным наградам и активности. |
|
|
||
Урок №10
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Свойства вероятности. Часть 2 |
|||||
|
Цели обучения согласно программе |
Доказывать свойства вероятности |
|||||
|
Цель урока |
Доказывают и применяют свойства |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой |
Ученики приветствуют. |
Метод оценивания «Букет цветок». |
|
||
|
Середина урока 35 минут |
Задача №1. Уровень А (базовый уровень) Метод «Кто быстрый?» Задача А1 В коробке 20 шаров: 12 красных и 8 синих. Вынимают два шара подряд. Найдите вероятность того, что оба шара будут красными. Задача А2 На полке 15 книг, из которых 6 – учебники математики. Случайным образом берут две книги. Найдите вероятность того, что обе книги окажутся учебниками математики. Задача А3 В урне 10 шаров: 4 белых и 6 черных. Вынимают три шара подряд. Найдите вероятность того, что первый шар белый, второй черный, третий белый. Задача А4 В классе 30 учеников, из них 18 девочек. Случайным образом выбирают двух учеников. Найдите вероятность того, что выбраны две девочки. Задача А5 В мешке 25 конфет: 15 шоколадных и 10 карамелек. Вынимают две конфеты подряд. Найдите вероятность того, что обе конфеты окажутся шоколадными. Задача №2. Групповая работа. Метод «Банкомат»
Уровень В (средний уровень) Задача В1 В коробке 40 деталей, из них 5 бракованных. Наудачу извлекают три детали. Найдите вероятность того, что все извлеченные детали окажутся качественными. Задача В2 На стоянке 12 автомобилей, из них 7 белых, 3 черных и 2 красных. Случайным образом выбирают два автомобиля. Найдите вероятность того, что они будут разного цвета. Задача В3 В группе 20 студентов. 8 из них занимаются спортом, 12 изучают английский язык, а 4 студента и занимаются спортом, и изучают английский. Найдите вероятность того, что случайно выбранный студент либо занимается спортом, либо изучает английский. Задача В4 В вазе лежат 30 конфет трех сортов: 10 молочных, 12 фруктовых и 8 ореховых. Наугад берут три конфеты. Найдите вероятность того, что будут взяты конфеты всех трех сортов. Задача №3. Уровень С (высокий уровень) Задача С1 В классе 25 учеников. Из них 15 занимаются музыкой, 12 – спортом, 8 – рисованием. 7 человек занимаются музыкой и спортом, 5 – музыкой и рисованием, 4 – спортом и рисованием, а 3 ученика занимаются всем. Найдите вероятность того, что случайно выбранный ученик занимается хотя бы одним видом деятельности. Задача С2 В урне 20 шаров: красные, синие и зеленые. Вероятность вытащить красный шар равна 0,4, синий – 0,35. Найдите вероятность того, что случайно вытащенный шар окажется зеленым. Сколько зеленых шаров в урне? Задача С3 В соревнованиях участвуют 8 спортсменов. Вероятность победы первого спортсмена 0,3, второго – 0,25, третьего – 0,2. Найдите вероятность того, что победит кто-то из остальных спортсменов. |
Ученик решает базовые задачи на вычисление вероятности простых событий, применяя основные формулы теории вероятностей. Ученик решает задачи среднего уровня сложности, требующие применения нескольких формул теории вероятностей и понимания связей между событиями. Ученик решает сложные задачи, требующие глубокого понимания свойств вероятности и умения комбинировать различные методы решения. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным розам. |
|
|
||
Урок №11
|
Фамилия имя педагога |
|
||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||||
|
Тема урока: |
Условная вероятность: основные понятия |
||||||||||||||||||||||
|
Цели обучения согласно программе |
Интерпретировать понятие условной вероятности |
||||||||||||||||||||||
|
Цель урока |
Интерпретируют условия в задачах |
||||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “случайных цифр” |
Ученики приветствуют и делятся на 3 группы по методу “случайные цифры”. |
Метод оценки «Мороженное» |
|
|||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Работа с таблицой.
Задача №3. Метод «Двери»
Уровень А Задача 1. "Школьный тест" В школе проводится тестирование по математике. Известно, что 80% учеников регулярно готовятся к урокам. Среди подготовленных учеников 90% успешно справляются с тестом, а среди неподготовленных только 30% получают положительную оценку. Ученик успешно написал тест. Какова вероятность того, что он регулярно готовился к урокам? Задача 2. "Медицинский тест" В поликлинике проводится диагностический тест на определенное заболевание. Известно, что 5% пациентов имеют это заболевание. Тест показывает правильный результат у 95% больных людей и у 90% здоровых. Пациент сдал тест, и он оказался положительным. Какова вероятность того, что пациент действительно болен? Задача 3. "Интернет-магазин" В интернет-магазине 70% покупателей оставляют отзывы о товарах. Из тех, кто оставляет отзывы, 85% делают повторные покупки. Среди не оставивших отзывы повторные покупки делают только 40% клиентов. Случайный клиент сделал повторную покупку. Какова вероятность того, что он оставлял отзыв о предыдущей покупке? Задача 4. "Спортивная секция" В спортивной секции 60% учеников регулярно посещают дополнительные тренировки. Среди регулярно тренирующихся 80% успешно сдают нормативы, а среди остальных - только 35%. Случайно выбранный ученик успешно сдал нормативы. Какова вероятность того, что он посещал дополнительные тренировки? Задача 5. "Подготовительные курсы" На подготовительных курсах к экзамену 75% слушателей выполняют все домашние задания. Среди выполняющих домашние задания 95% успешно сдают экзамен, а среди остальных - только 45%. Случайно выбранный слушатель успешно сдал экзамен. Найдите вероятность того, что он выполнял все домашние задания. |
Ученики смотрят видеоматериал и понимают тему. Ученик заполняет таблицу терминов и определений, используя учебный материал и конспект. Ученик решает практические задачи на условную вероятность, применяя формулу Байеса и используя реальные жизненные ситуации. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
https://youtu.be/lejq7LEMCeQ?si=2opSNHO29SBX0GCY
|
|||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным наградам |
|
|
|||||||||||||||||||
Урок №12
|
Фамилия имя педагога |
|
||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||
|
Тема урока: |
Условная вероятность: решение задач |
||||||||||||||||
|
Цели обучения согласно программе |
Синтезировать способы решения |
||||||||||||||||
|
Цель урока |
Синтезируют алгоритм решения задач |
||||||||||||||||
|
Процесс урока: |
|||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой |
Ученики приветствуют и делятся на пары. |
Метод оценки «Звезда» |
|
|||||||||||||
|
Середина урока 35 минут |
Задача №1. Математический диктант.
Задача №2. Сопоставление.
Задача №3. Парная работа.
|
Ученик письменно отвечает на вопросы математического диктанта, демонстрируя знание определений и формул по теме "Условная вероятность". Ученик заполняет таблицу соответствия, устанавливая правильные связи между описанием события и соответствующими формулами. Ученики в парах решают задачи на условную вероятность, обсуждая и проверяя решения друг друга. |
Дескрипторы:
Дескрипторы:
Дескриптор: Правильно применяет формулы Выполняет вычисления без ошибок Проверяет логичность результата |
|
|||||||||||||
|
Конец урока 5 минут |
Рефлексия Вопрос-ответ от учителя -Вам понравился урок? -Чтобы вы хотели еще добавить? -Оцените урок от 1 до 10 |
В конце урока учитель оценивает знания учеников и активность по набранным наградам. |
|
|
|||||||||||||
Урок №13
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Правило сложения вероятностей |
|||||
|
Цели обучения согласно программе |
Анализировать случаи применения правила |
|||||
|
Цель урока |
Анализируют и решают комбинированные задачи |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Выбери цвет”.
|
Каждый ученик выбирает 1 лист с закрытыми глазами из 3 разноцветных бумаг. По цветам ученики делятся на 3 группы. |
Метод оценки «Money» |
|
||
|
Середина 35 урока |
Задача №1. Посмотреть видеоматериал.
Задача №2. "Верно/Неверно" Определите, являются ли утверждения верными или неверными:
Задача №3. Метод «Бургер»
Задача 1. "Кинотеатр" В кинотеатре было проведено исследование среди 400 зрителей. 180 человек предпочитают смотреть фильмы в формате 3D, 220 любят смотреть фильмы в IMAX, а 120 зрителей любят оба формата. Найдите вероятность того, что случайно выбранный зритель: а) предпочитает хотя бы один из форматов б) любит только IMAX в) не интересуется ни одним из этих форматов Задача 2. "Автосалон" В автосалоне из 160 проданных за месяц автомобилей 90 были черного цвета, 70 - с автоматической коробкой передач, а 45 автомобилей были черными и с автоматической коробкой. Найдите вероятность того, что случайно выбранный проданный автомобиль: а) либо черный, либо с автоматической коробкой б) черный, но с механической коробкой в) не черный и не с автоматической коробкой Задача 3. "Кафе" В кафе за день побывало 250 посетителей. 140 человек заказали кофе, 120 заказали десерт, а 80 человек заказали и кофе, и десерт. Найдите вероятность того, что случайно выбранный посетитель: а) заказал что-то одно (либо кофе, либо десерт) б) заказал и кофе, и десерт в) не заказал ни кофе, ни десерт Задача 4. "Туристическая фирма" В туристической фирме из 350 клиентов 180 выбрали отдых на море, 160 выбрали экскурсионные туры, а 70 клиентов выбрали путевки, включающие и море, и экскурсии. Найдите вероятность того, что случайно выбранный клиент: а) выбрал хотя бы один вид отдыха б) выбрал только экскурсионный тур в) выбрал оба вида отдыха |
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует каждое утверждение и определяет его истинность, основываясь на знании правил сложения вероятностей. Ученик решает практические задачи на применение правила сложения вероятностей для совместных событий. |
Дескрипторы:
Дескрипторы:
Выбирает правильную формулу для решения Учитывает вероятность пересечения событий Правильно записывает все необходимые вычисления |
|||
|
Конец урока 5 минут |
Рефлексия «Шарики» |
В конце урока учитель оценивает активность учеников по собранным наградам. |
|
|
||
Урок №14
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Правило умножения вероятностей |
|||||
|
Цели обучения согласно программе |
Оценивать применимость правила |
|||||
|
Цель урока |
Оценивают и выбирают способ решения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
2. Ученики делятся на 2 группы по методу “3 цвета”
|
Ученики настраиваются на урок, разминаются.
Ученики выбирают карты и делятся на группы по цветам. |
Дескриптор
Метод оценки «Клубника» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. Игра «Скачки»
Задача №3. Метод «Баскетбол»
"Асык ойыны" В ауле четыре места, где обычно играют в асық. Айдар ищет Ерлана. Вероятность того, что Ерлан находится в любом из этих мест одинакова. Айдар проверяет места по порядку. После каждой проверки, если он не находит Ерлана, тот может незаметно перебежать в уже проверенное место (вероятность такого события 0,3). Какова вероятность того, что Айдар найдет Ерлана: а) в первом месте б) во втором месте в) в последнем месте? "Айтыс" На айтысе выступают три акына: Әсет, Бақыт и Сәуле. Вероятность победы Әсета в первом туре 0,7, Бақыта - 0,8, Сәуле - 0,9. При этом каждый следующий акын, прежде чем начать свое выступление, слышит предыдущего и может изменить тему своего выступления с вероятностью 0,4, чтобы она перекликалась с предыдущим выступлением. Какова вероятность того, что все три акына выступят на схожие темы? "Кокпар" В соревнованиях по көкпару всадник Нұрлан должен пройти три этапа. Вероятность успешного прохождения первого этапа 0,8. Если всадник успешно проходит этап, его конь получает дополнительную энергию, и вероятность успеха на следующем этапе увеличивается на 10% от предыдущей вероятности. Если всадник не справляется с этапом, то конь устает, и вероятность успеха на следующем этапе уменьшается на 20% от предыдущей. Найти вероятность того, что Нұрлан: а) успешно пройдет все три этапа подряд б) не справится со всеми тремя этапами в) успешно пройдет ровно два этапа |
Ученики смотрят видеоматериал и понимают тему. Ученик выполняет тестовые задания, применяя знания о правиле умножения вероятностей. Ученик решает практические задачи на применение правила умножения вероятностей в различных ситуациях. |
Дескрипторы:
Дескрипторы:
Использует правильные формулы Учитывает изменение вероятностей Составляет план решения |
https://youtu.be/XJoBnZFfois?si=BXxGa-ra8k13yBw_ |
||
|
Конец урока 5минут |
Устная рефлексия |
Учитель в конце урока оценивает активность по количеству награды. |
|
|
||
Урок №15
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула полной вероятности: теория |
|||||
|
Цели обучения согласно программе |
Исследовать структуру формулы |
|||||
|
Цель урока |
Исследуют компоненты формулы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветствие и ознакомление с новой темой. 2. Ученики делятся на 3 группы по методу “колесо” |
Ученики концентрируются на уроки делятся на группы. |
Дескриптор
Метод оценки «Like» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод Джигсо Объясните, что такое формула полной вероятности и в каких ситуациях она используется. Приведите примеры из жизни, где данная формула может применяться. Задача №3. Тестовая задача. Задание 1 Формула полной вероятности используется, когда: A) События зависимы B) События независимы C) Событие может произойти совместно с одним из полной группы событий D) События несовместны E) События противоположны Задание 2 В формуле полной вероятности P(A) = ∑P(Hi)P(A|Hi) числа P(Hi) называются: A) Условными вероятностями B) Вероятностями гипотез C) Полными вероятностями D) Случайными величинами E) Классическими вероятностями Задание 3 Сумма вероятностей гипотез в формуле полной вероятности должна быть равна: A) 0 B) 0,5 C) 1 D) 2 E) Любому числу от 0 до 1 Задание 4 Если событие A может произойти только при осуществлении одной из трёх гипотез H₁, H₂, H₃, то формула полной вероятности имеет вид: A) P(A) = P(H₁) + P(H₂) + P(H₃) B) P(A) = P(H₁)P(A|H₁) + P(H₂)P(A|H₂) + P(H₃)P(A|H₃) C) P(A) = P(H₁) × P(H₂) × P(H₃) D) P(A) = P(A|H₁) + P(A|H₂) + P(A|H₃) E) P(A) = P(H₁) × P(A|H₁) Задание 5 Условные вероятности P(A|Hi) в формуле полной вероятности - это: A) Вероятность гипотезы Hi B) Вероятность события A при условии появления гипотезы Hi C) Сумма вероятностей всех гипотез D) Произведение вероятностей события и гипотезы E) Отношение числа благоприятных исходов к общему числу исходов |
Ученики смотрят видеоматериал и понимают тему. Ученик объясняет, что такое формула полной вероятности, и может описать ее словами. Ученик выполняет тестовых задач. |
Дескрипторы:
Ученик приводит хотя бы один пример из жизни, где можно использовать формулу полной вероятности. Выбирает правильный вариант. |
|||
|
Конец урока 5 минут |
Рефлексия «Мишень» |
В конце урока учитель оценивает каждую группу по набранным наградам. |
|
|
||
Урок №16
|
Фамилия имя педагога |
|
|||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||
|
Тема урока: |
Формула полной вероятности: практика |
|||||||||||||||||
|
Цели обучения согласно программе |
Применять формулу в различных ситуациях |
|||||||||||||||||
|
Цель урока |
Применяют формулу к практическим задачам |
|||||||||||||||||
|
Процесс урока: |
||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие через метод “Время добрых пожелании”. Ученики желают приятные пожелания на день. 2. Ученики делятся на 2 группы по методу “Колесо фортуны” https://clck.ru/3A5caP |
Ученики настраиваются к уроку с хорошим настроением и делятся на 2 группы. |
Метод оценки «Леденец» |
|
||||||||||||||
|
Середина урока 35 минут |
Задача №1. Игра "Установите соответствие"
Задача 2. "Заполните пропуски" В магазин поступают товары от трех поставщиков. От первого поставщика приходит ___ % всех товаров, от второго - 35%, от третьего - остальные. Вероятность брака в товарах первого поставщика составляет 0,02, второго - ___, третьего - 0,03. Используя формулу полной вероятности, найдите вероятность того, что случайно выбранный товар окажется бракованным, если известно, что эта вероятность равна 0,025. Заполните пропущенные числа и решите задачу. Задача 3. "Практическая задача с выбором" Ақжол готовится к соревнованиям по национальной борьбе құрес. У него есть три тренера:
При подготовке с каждым тренером вероятность победы Ақжола в соревновании различна:
Найдите: а) Вероятность победы Ақжола в соревновании б) Если Ақжол победил, то какова вероятность, что его тренировал Асқар-ага? в) Какой тренер наиболее вероятно подготовил Ақжола, если он проиграл? |
Ученик анализирует предложенные формулы и их описания, устанавливает логические связи между ними. Ученик находит неизвестные значения и решает задачу, используя формулу полной вероятности. Ученик решает многоэтапную задачу, выбирая нужные формулы для каждой части. |
Метод оценки «Леденец» Дескрипторы:
Дескрипторы:
Правильно выбирает формулы для каждого пункта Обосновывает свой выбор Составляет план решения |
|
||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||||||||||||||
Урок №17
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Байеса: основные понятия |
|||||
|
Цели обучения согласно программе |
Интерпретировать смысл формулы |
|||||
|
Цель урока |
Интерпретируют условия применения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Знакомтсво с новой темой 2.Ученики делятся на группы 2 группы методом “Стрельба глазами”. |
Участники встают в круг, опустив глаза. По сигналу учителя все поднимают глаза, стремясь встретиться с кем-то взглядом. Если это удалось, то образовавшиеся пары покидают круг. Игра продолжается до тех пор, пока все участники не окажутся разбиты по парам. |
Дескриптор
Оценка методом «Букет бабочек» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Исправь ошибку" Даны следующие утверждения о формуле Байеса. Найдите ошибки и исправьте их:
Задача 3. "Медицинская диагностика" В поликлинике используется новый тест для диагностики заболевания. Составьте задачу для своих одноклассников, используя следующие данные:
Задача должна включать:
|
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует каждое утверждение, находит ошибки и исправляет их, опираясь на теорию. Ученик составляет задачу на применение формулы Байеса, используя предложенные данные. |
Дескрипторы:
Знание формулы Байеса Понимание её применения Различение видов вероятностей |
https://youtu.be/LYTGddixYfw?si=jRhzcZl396B7WJxq
|
||
|
Конец урока 5 минут |
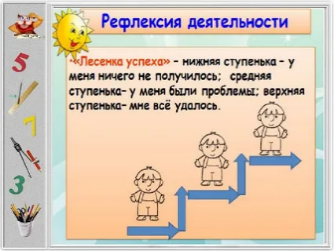
Рефлексия «Лестница успеха» |
В конце урока учитель оценивает активность по набранным наградам. |
|
|
||
Урок №18
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Байеса: решение задач |
|||||
|
Цели обучения согласно программе |
Синтезировать методы решения |
|||||
|
Цель урока |
Синтезируют способы применения формулы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Эмоциональная подготовка учеников. Время разминки!
|
Ученики повторяют и разминаются, и заряжаются энергией перед занятием. |
Метод оценки «Шарики» |
|
||
|
Середина урока 35 минут |
Задач №1. "Логическая цепочка" Расположите этапы решения задачи в правильном порядке:
Задача №2. В соревнованиях по тоғыз құмалақ участвуют три спортсмена: Арман, Бауыржан и Сәкен. Вероятность участия в финале для Армана - 0,5, для Бауыржана - 0,3, для Сәкена - 0,2. Вероятность победы в финале составляет 0,8 для Армана, 0,7 для Бауыржана и 0,9 для Сәкена. Если известно, что соревнование выиграно, определите: а) Вероятность того, что победил Арман б) Кто наиболее вероятно стал победителем? Задача №3. Создайте задачу на применение формулы Байеса, используя следующий шаблон: В ауле есть три табуна лошадей. В первом табуне ___ лошадей (впишите число), во втором ___, в третьем ___. Вероятность того, что скакун для байги будет выбран из каждого табуна, пропорциональна количеству лошадей в нем. Вероятность победы в байге для лошади из первого табуна ___, из второго ___, из третьего ___. Скакун победил в байге. Какова вероятность, что он был из ... табуна? |
Ученик анализирует этапы решения и выстраивает их в логическую последовательность. Ученик решает задачу с применением формулы Байеса, используя данные о национальной игре. Ученик составляет собственную задачу по шаблону, подбирая реалистичные числовые данные. |
Метод оценки «Шарики» Дескрипторы:
Дескриптор:
Дескриптор:
|
|
||
|
Конец урока 5 минут |
Рефлексия «Дерево успеха» |
В конце урока учитель оценивает активность ученика по количеству собранной награды. |
|
|
||
Урок №19
|
Фамилия имя педагога |
|
|||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||
|
Тема урока: |
Схема Бернулли |
|||||||||||||||||||||||
|
Цели обучения согласно программе |
Анализировать условия применения схемы |
|||||||||||||||||||||||
|
Цель урока |
Анализируют и составляют схему решения |
|||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Расчет”. |
Это самый элементарный способ. Произвести расчет на «первый-второй», «первый-второй-третий» и т. д. в зависимости от того, сколько требуется групп. |
Дескриптор
Метод оценки «Стикеры» |
|
||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. 1. Схема Бернулли - это: A) Последовательность взаимозависимых испытаний B) Последовательность независимых испытаний с двумя исходами C) Последовательность зависимых испытаний с тремя исходами D) Одно испытание с двумя исходами E) Испытание с множеством исходов 2. В формуле P(X=k) = C(n,k)·pᵏ·qⁿ⁻ᵏ для схемы Бернулли, q равно: A) Вероятности успеха B) 1 + p C) 1 - p D) p² E) p/n 3. Локальная формула Муавра-Лапласа применяется, когда: A) n < 10 B) n > 100 C) np < 10 D) n = 100 E) p = q 4. В схеме Бернулли вероятность успеха p: A) Меняется от испытания к испытанию B) Зависит от числа испытаний C) Остается постоянной во всех испытаниях D) Равна 1 E) Равна 0 5. Наивероятнейшее число успехов k₀ в схеме Бернулли определяется неравенством: A) np - q ≤ k₀ ≤ np + p B) np - p ≤ k₀ ≤ np + q C) np - 1 ≤ k₀ ≤ np + 1 D) np ≤ k₀ ≤ np + 1 E) np – 2 ≤ k₀ ≤ np + 2 Задача №3. Работа с таблицой.
|
Ученики смотрят видеоматериал и понимают тему. Ученик решает тестовые задания, выбирая правильные ответы на основе знания теории схемы Бернулли. Ученик заполняет таблицу соответствия, устанавливая связи между терминами, их определениями и примерами. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает по набранным наградам |
|
|
||||||||||||||||||||
Урок №20
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Бернулли и её применение |
|||||
|
Цели обучения согласно программе |
Применять формулу в различных задачах |
|||||
|
Цель урока |
Применяют формулу в практических задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 2 группы по методу “Собери открытку”. |
Перед игрой готовятся открытки по количеству будущих команд. Одну открытку учитель разрезает на столько частей, сколько человек должно быть в одной команде. Предварительно перемешав разрезанные открытки, ведущий раздает их участникам. По сигналу команды организуются, составляя картинки. |
Метод оценивания «Мяч» |
|
||
|
Середина урока 35 минут |
Уровень А (базовый уровень) Задача А1. "Национальные игры" В соревнованиях по асық ату игрок делает 5 бросков. Вероятность успешного броска 0,6. Найти вероятность: а) двух успешных бросков б) не менее трех успешных бросков в) хотя бы одного успешного броска Задача А2. "Контроль качества" На фабрике по производству қамшы (плетей) вероятность изготовления изделия высшего качества равна 0,8. В партии 4 изделия. Найти вероятность того, что высшего качества будут: а) все изделия б) ровно три изделия в) не более двух изделий Задача А3. "Стрельба из лука" Вероятность попадания в цель при стрельбе из традиционного лука равна 0,7. Производится 6 выстрелов. Найти вероятность: а) четырех попаданий б) не менее пяти попаданий в) от трех до пяти попаданий Уровень В (повышенный уровень) Задача В1. "Спортивные соревнования" В турнире по тоғыз құмалақ спортсмен проводит 8 игр. Вероятность победы в каждой игре 0,75. Найти вероятность того, что он: а) победит ровно в 6 играх б) победит не менее чем в 7 играх в) одержит четное число побед Задача В2. "Производство сувениров" На предприятии изготавливают национальные сувениры. Вероятность брака 0,1. В партии 10 изделий. Найти: а) вероятность наличия двух бракованных изделий б) наивероятнейшее число бракованных изделий в) вероятность наличия наивероятнейшего числа бракованных изделий Задача В3. "Ювелирные изделия" Мастер изготавливает 12 серебряных колец. Вероятность изготовления кольца высшего качества 0,85. Найти: а) вероятность того, что высшего качества будут ровно 10 колец б) математическое ожидание числа колец высшего качества в) наивероятнейшее число колец высшего качества |
Ученик решает задачи, применяя формулу Бернулли для простых случаев. Ученик решает более сложные задачи с применением дополнительных формул и свойств. |
Метод оценивания «Мяч» Дескриптор: Использует формулу Бернулли Вычисляет число сочетаний Выполняет расчеты без ошибок Дескриптор: Проводит сложные вычисления Проверяет промежуточные результаты Анализирует полученные ответы |
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока индивидуально оценивает активность по набранным наградам. |
|
|
||
Урок №21
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Наивероятнейшее число успехов |
|||||
|
Цели обучения согласно программе |
Вычислять вероятность успехов |
|||||
|
Цель урока |
Вычисляют и интерпретируют результаты |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветствие и ознакомление с новой темой. 2. Ученики делятся на 3 группы по методу “колесо” |
Ученики концентрируются на уроки делятся на группы. |
Дескриптор
Метод оценки «Звезда» |
|
||
|
Середина урока 35 минут |
I. Тестовые задания
II. Незавершенные утверждения
III. Контекстные задачи
ІV. Логические задачи
|
Ученик решает тестовые задания, применяя формулу Бернулли для вычисления вероятностей. Ученик формулирует основные теоретические положения схемы Бернулли. Ученик решает практические задачи, используя формулу Бернулли в конкретных ситуациях. Ученик анализирует теоретические аспекты схемы Бернулли, применяя логическое мышление. |
Дескрипторы:
Дескрипторы:
Выбирает нужную формулу для каждого пункта Правильно подставляет значения Учитывает все условия задачи Составляет план решения Проводит необходимые вычисления Формулирует логические выводы |
|
||
|
Конец урока 5 минут |
Рефлексия «Мозг» |
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||
Урок №22
|
Фамилия имя педагога |
|
|||||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||||||
|
Тема урока: |
Случайные величины: основные понятия |
|||||||||||||||||||||||||||
|
Цели обучения согласно программе |
Классифицировать случайные величины |
|||||||||||||||||||||||||||
|
Цель урока |
Классифицируют виды величин |
|||||||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||||||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. Эмоциональный разряд. Время добрых пожелании.
Каждый ученик желает своему соседу по парте добрые слова. |
Ученик обращается к своим друзьям с хорошим пожеланием. |
Оценивание по методу «Сердце»
|
|
||||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Теоретический диктант Дайте определения следующих понятий:
Задача №3. Задание на соответствие "Найди пару" Соедините термин и его пример:
Задача №4. Практическая задача "Асык ату" В национальной игре асык ату игрок может выиграть 1, 2 или 3 асыка за один бросок с вероятностями 0,5, 0,3 и 0,2 соответственно. Задания:
Задача №5. "Исправь ошибку" В таблице распределения случайной величины допущены ошибки. Найдите и исправьте их:
Задача №6. Визуальное задание "Построй график" Постройте графики:
Задача №7. Контекстная задача "Национальные блюда" В ресторане казахской кухни заказы на бешбармак поступают случайным образом. За час может быть 0, 1, 2 или 3 заказа с вероятностями 0,1, 0,3, 0,4 и 0,2 соответственно. Требуется:
|
Ученики смотрят видеоматериал и понимают тему. Ученик письменно формулирует определения основных понятий теории случайных величин. Ученик устанавливает соответствие между терминами и их примерами. Ученик решает практические задачи на составление закона распределения и исправление ошибок. Ученик строит графики распределения вероятностей. Ученик решает комплексную задачу с практическим контекстом. |
Дескрипторы:
Дескрипторы:
Дескрипторы: Различает типы случайных величин Понимает сущность каждого термина Правильно соотносит теорию с практическими примерами Дескрипторы:
Дескрипторы:
Записывает закон распределения Вычисляет характеристики Строит требуемые графики |
|||||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Метод “Светофор”: студенты показывают зеленую карточку, если урок был понятен, желтую - если остались вопросы, красную - если тема требует повторного объяснения. |
В конце урока учитель оценивает активность каждого ученика по заработанным сердцам. |
|
|
||||||||||||||||||||||||
Урок №23
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Дискретные случайные величины |
|||||
|
Цели обучения согласно программе |
Исследовать характеристики величин |
|||||
|
Цель урока |
Исследуют и описывают свойства |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Психическая и эмоциональная подготовка к уроку. |
Разминка для улучшения настроения и самочувствия ученика |
Оценивание по методу «Медаль» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Игра «Случайное колесо»
Задача №3. Метод «Банкомат»
Задача 1. "Конный спорт" В соревнованиях по кокпар участвуют 3 команды. Вероятность победы первой команды 0,5, второй - 0,3, третьей - 0,2. Составить закон распределения числа очков, если за победу дается 2 очка. Задача 2. "Стрелковый тир" Стрелок делает два выстрела по мишени. Вероятность попадания при каждом выстреле 0,7. Составить закон распределения числа попаданий и найти математическое ожидание. Задача 3. "Домбра" В музыкальной школе ученик разучивает новый кюй. Вероятность безошибочного исполнения первой части 0,8, второй части 0,7. Найти закон распределения числа безошибочно исполненных частей произведения. Задача 4. "Национальные украшения" Мастер изготавливает сырға (серьги). Вероятность изготовления изделия высшего качества 0,9. В партии 3 изделия. Составить закон распределения числа изделий высшего качества в партии. Задача 5. "Спортивная школа" В спортивной секции по қазақша күрес тренируются 4 борца. Вероятность победы в схватке для каждого 0,6. Найти математическое ожидание числа побед в день, если каждый проводит одну схватку. Задача 6. "Чайхана" В чайхане посетитель может заказать один из трех видов плова. Вероятность заказа первого вида 0,5, второго - 0,3, третьего - 0,2. Стоимость первого вида 2000 тенге, второго - 2500 тенге, третьего - 3000 тенге. Найти математическое ожидание выручки с одного заказа. |
Ученики смотрят видеоматериал и понимают тему. Играют игру. Решают текстовых задач. |
Дескриптор: Выписывает определения основных понятий. Дескриптор: Правильно отвечает на вопросы. Дескриптор: Правильно решает текстовых задач. |
https://youtu.be/EMGLxRoZTfw?si=9V5ecNfIYU4Tj3kq |
||
|
Конец урока 5 минут |
Рефлексия Метод “Светофор”: студенты показывают зеленую карточку, если урок был понятен, желтую - если остались вопросы, красную - если тема требует повторного объяснения. |
В конце урока учитель оценивает активность каждого ученика по медалям |
|
|
||
Урок №24
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Непрерывные случайные величины |
|||||
|
Цели обучения согласно программе |
Сравнивать виды случайных величин |
|||||
|
Цель урока |
Сравнивают характеристики величин |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. Ученики делятся на 2 они выбирают названия геометрических форм по методу “жребии” |
Ученики онлайн выбирают жребий номеров и делятся на группы. |
Дескриптор
Метод оценки «Букет цветок» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Заполни пропуски" Заполните пропуски в утверждениях о непрерывных случайных величинах:
Задание 3. "Практическая задача" Время ожидания автобуса на остановке является непрерывной случайной величиной, равномерно распределенной на отрезке [0; 15] минут. Найти: а) функцию плотности вероятности б) вероятность того, что ждать придется не более 5 минут в) математическое ожидание времени ожидания Задание 4. "Историческая задача" Метод «Google»
Изучите историю появления нормального распределения и ответьте на вопросы:
Задание 5. "Исследовательская работа" Измерьте рост 30 учеников вашего класса. Постройте гистограмму распределения роста и проверьте, можно ли считать рост нормально распределенной величиной. |
Ученики смотрят видеоматериал и понимают тему. Ученик заполняет пропуски, используя знания о свойствах непрерывных случайных величин. Ученик решает задачу, применяя формулы для равномерного распределения. Ученик изучает историческую информацию и отвечает на вопросы. Ученик проводит исследование, собирает и анализирует данные. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
Строит гистограмму Проверяет свойства нормального распределения Делает выводы |
https://youtu.be/SgfGqNB6qoA?si=vTRZeQl6GNeQBGJo
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по количеству цветочков и оценкам учеников парной работы |
|
|
||
Урок №25
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Числовые характеристики случайных величин |
|||||
|
Цели обучения согласно программе |
Вычислять основные характеристики |
|||||
|
Цель урока |
Вычисляют параметры распределений |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы через метод “Колесо фортуны”. https://clck.ru/3AGMsQ?clckid=2ff9c35f
|
Ученики делятся на 3 группы методу учителя. |
Оценка по методу «Разбалловка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Бинго»
"Турнир по тогыз кумалак" В турнире участвуют три игрока. Вероятность победы первого игрока 0,5, второго - 0,3, третьего - 0,2. За победу дается 10 баллов. Найти математическое ожидание числа баллов победителя. "Национальные сувениры" Мастер изготавливает сувениры трех видов. Вероятность изготовления первого вида 0,4, второго - 0,35, третьего - 0,25. Стоимость первого вида 2000 тенге, второго - 3000 тенге, третьего - 4000 тенге. Найти математическое ожидание и дисперсию стоимости случайно выбранного сувенира. "Спортивные соревнования" В соревнованиях по қазақша күрес спортсмен проводит три схватки. Вероятность победы в каждой схватке 0,7. За победу дается 5 очков, за поражение 0 очков. Найти математическое ожидание и среднее квадратическое отклонение набранных очков. "Стрельба из лука" Лучник делает два выстрела. Вероятность попадания в цель при первом выстреле 0,8, при втором - 0,75. За каждое попадание начисляется 10 баллов. Найти дисперсию числа набранных баллов. "Чайхана" В чайхане клиент заказывает 1, 2 или 3 блюда с вероятностями 0,3, 0,5 и 0,2 соответственно. Среднее время приготовления одного блюда 15 минут. Найти математическое ожидание времени выполнения заказа. "Ювелирная мастерская" Ювелир изготавливает украшения. Вероятность изготовления изделия высшего качества 0,85, первого сорта - 0,12, второго сорта - 0,03. Стоимость изделий соответственно 50000, 35000 и 20000 тенге. Найти математическое ожидание и дисперсию стоимости изделия. Задача №3. Тестовые задания
|
Ученики смотрят видеоматериал и понимают тему. Ученик решает практические задачи на вычисление числовых характеристик случайных величин. Ученик выбирает правильные ответы на тестовые вопросы, демонстрируя знание основных формул и свойств числовых характеристик случайных величин. |
Дескриптор: Находит математическое ожидание Вычисляет дисперсию (если требуется) Находит среднее квадратическое отклонение Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Ученики в конце урока оценивают урок через онлайн рефлекс. |
В конце урока учитель оценивает активность учеников по набранным баллам. |
|
|
||
Урок №26
|
Фамилия имя педагога |
|
|||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||||
|
Тема урока: |
Математическое ожидание и свойства |
|||||||||||||||||||||||||
|
Цели обучения согласно программе |
Доказывать свойства мат.ожидания |
|||||||||||||||||||||||||
|
Цель урока |
Доказывают и применяют свойства |
|||||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу ‘Собери открытку”. |
Перед игрой готовятся открытки по количеству будущих команд. Одну открытку ведущий разрезает на столько частей, сколько человек должно быть в одной команде. Предварительно перемешав разрезанные открытки, ведущий раздает их участникам. По сигналу команды организуются, составляя картинки.
|
Дескриптор
Метод оценки «Фрукты» |
|
||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. «Найди ошибку» Проанализируйте решение задачи и найдите ошибки: Дано: X и Y – независимые случайные величины M(X) = 2, M(Y) = 3 Найти: M(2X + 3Y – 1) Решение ученика: M(2X + 3Y – 1) = 2M(X) + 3M(Y) – 1 = 2·2 + 3·3 – 1 = 4 + 9 – 1 = 12 Задача №3. Заполните таблицу для случайной величины X:
Задача №4. Метод «Кто быстрый?» Задача 1. "Байтерек кафе" В национальном кафе "Байтерек" посетитель может заказать:
Найти:
Задача 2. "Ярмарка ремесленников" На ярмарке мастер продает традиционные казахские украшения:
Вероятность продажи сырга - 0,5, билезик - 0,3, алка - 0,2. Найти математическое ожидание дневной выручки, если в среднем совершается 5 покупок. Задача 3. "Скачки" В соревнованиях по байге участвуют три скакуна:
Призовой фонд:
Найти математическое ожидание выигрыша для каждого скакуна. Задача 4. "Асык ату" В соревнованиях по асык ату игрок может выиграть:
Найти:
|
Ученики смотрят видеоматериал и понимают тему. Ученик найдет ошибку. Заполняют таблицу. Ученики решают текстовых задач. |
Метод оценки «Фрукты» Дескрипторы: Выписывают основных определения основных понятий. Праавильно найдет ошибку. Правильно заполняют таблицу. Правильно выполняют вычислению. |
|||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает работу групп и учеников по копилкам. |
|
|
||||||||||||||||||||||
Урок №27
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Дисперсия и среднее квадратическое отклонение |
|||||
|
Цели обучения согласно программе |
Анализировать меры разброса |
|||||
|
Цель урока |
Анализируют и вычисляют параметры |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с практической работой. 2.Эмоцианальная подготовка учеников. Ученики делятся с хорошими пожеланиями на день. 3.Ученики делятся на 3 группы по методу Жребий
|
Ученики делятся хорошими эмоциями с друзьями. После выбирают листы с номерами и делятся на группы. |
Дескриптор
Индивидуальная оценка ученика по методу «Подарка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Уровень А. Задача 1. "Бауырсаки" В пекарне изготавливают бауырсаки. Их количество в одной порции может быть:
Найти:
Задача 2. "Урок домбры" Время выполнения домашнего задания по игре на домбре составляет:
Определить:
Задача 3. "Магазин сувениров" Ежедневная выручка магазина национальных сувениров может составлять:
Найти:
Задача 4. "Конные скачки" Время прохождения дистанции скакуном составляет:
Вычислить:
Задача 5. "Мастерская по пошиву" Время пошива одного камзола может быть:
Определить:
Задача №3. Ввод ответа.
|
Ученики смотрят видеоматериал и понимают тему. Решают задачи. Решают задачи, играя игру. |
Индивидуальная оценка ученика по методу «Подарка» Дескрипторы: Выписывают основных определения основных понятий. Правильно выполняют вычислений. Играют интеллектуальную игру. |
|||
|
Конец урока 5 минут |
Учитель проводит рефлексию, спрашивая учеников, что нового они узнали и что показалось наиболее интересным. Ученики устно делятся своими впечатлениями. |
В конце урока учитель оценивает каждую группу по набранным наградам. |
|
|
||
Урок №28
|
Фамилия имя педагога |
|
||||||||||||||||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||||||||||||||||||||
|
Тема урока: |
Биномиальное распределение |
||||||||||||||||||||||||||||||||||||||
|
Цели обучения согласно программе |
Исследовать свойства распределения |
||||||||||||||||||||||||||||||||||||||
|
Цель урока |
Исследуют характеристики распределения |
||||||||||||||||||||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||||||||||||||||||||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. 2.Ученики делятся на 2 группы по методу “Сегментация круга” |
Группу можно разделить пополам, проведя воображаемый диаметр круга от себя (ведущего) к участнику, сидящему напротив. В случае, если требуется более двух команд, то круг просто разбивается на нужное число сегментов. |
Метод оценки +1 награда за каждый правильный ответ.
|
|
|||||||||||||||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Работа с терминами.
Задача №3. Метод «» Задача 1. "Производство кумыса" На предприятии по производству кумыса вероятность того, что бутылка будет заполнена точно до метки, равна 0,9. Найти вероятность того, что из 6 случайно выбранных бутылок: а) ровно 5 заполнены правильно б) хотя бы 5 заполнены правильно в) все заполнены правильно Задача 2. "Ювелирная мастерская" Мастер изготавливает национальные серебряные украшения. Вероятность изготовления изделия высшего качества 0,85. В партии 8 изделий. Найти: а) наивероятнейшее число изделий высшего качества б) вероятность получения наивероятнейшего числа изделий высшего качества в) математическое ожидание числа качественных изделий Задача 3. "Стрельба из лука" На соревнованиях по стрельбе из традиционного лука вероятность попадания в цель для опытного лучника составляет 0,7. Лучник делает 10 выстрелов. Найти: а) вероятность 7 попаданий б) математическое ожидание числа попаданий в) дисперсию числа попаданий Задача 4. "Национальные орнаменты" При вышивании национального орнамента вероятность правильного выполнения одного элемента равна 0,95. Мастерица выполняет 12 элементов. Найти: а) вероятность того, что все элементы выполнены правильно б) вероятность того, что правильно выполнено не менее 10 элементов в) наивероятнейшее число правильно выполненных элементов Задача 5. "Сборка юрты" При установке юрты вероятность правильной установки одного кереге (решетчатой секции) равна 0,8. Всего устанавливается 6 кереге. Определить: а) вероятность того, что все кереге установлены правильно б) математическое ожидание числа правильно установленных кереге в) среднее квадратическое отклонение |
Ученики смотрят видеоматериал и понимают тему. Дает определения терминам. Решают задачи. |
Метод оценки +1 награда за каждый правильный ответ. Дескрипторы: Выписывают основных определения основных понятий. Дескриптор: Правильно заполняют таблицу. Правильно решают задачи. |
||||||||||||||||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Ученики оценивают урок по 10 бальной шкале. |
В конце урока учитель оценивает каждую группу и ученика по набранным наградам. |
|
|
|||||||||||||||||||||||||||||||||||
Урок №29
|
Фамилия имя педагога |
|
||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||
|
Тема урока: |
Распределение Пуассона |
||||||||||||||||||||
|
Цели обучения согласно программе |
Применять распределение в задачах |
||||||||||||||||||||
|
Цель урока |
Применяют формулы распределения |
||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||
|
Начало урока 5 минут |
Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
|
Ученики настраиваются на урок, разминаются. |
Дескриптор
Метод оценки «Апельсин» |
|
|||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Историческое исследование" Подготовьте краткое сообщение:
Задание 3. «Формула и её компоненты» Заполните таблицу для формулы Пуассона P(X=k) = (λᵏe⁻λ)/k!
Задание 4. "Практическая задача" В национальной кондитерской в среднем продается 4 торта "Шакарпаре" в час. Найти вероятность того, что за час будет продано: а) ровно 3 торта б) не более 2 тортов в) более 5 тортов |
Ученики смотрят видеоматериал и понимают тему. Ученик изучает историю открытия распределения Пуассона и готовит сообщение. Ученик анализирует формулу Пуассона и описывает все её компоненты. Ученик решает задачу, применяя формулу Пуассона. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Учитель раздает стикеры-листочки. Ученики пишут мнения об уроке анонимно и клеят на лучики солнца. |
Учитель в конце урока оценивает активность и количество листочков. |
|
|
|||||||||||||||||
Урок №30
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Нормальное распределение |
|||||
|
Цели обучения согласно программе |
Интерпретировать график распределения |
|||||
|
Цель урока |
Интерпретируют параметры распределения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. 2. Ученики делятся на пары по желанию (мини группа). |
Ученики знакомятся и делятся на мини группы из 2 человек. |
Дескриптор
Метод оценивания «Мяч»
|
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Острый ум» Задача 1. "Ежедневная выручка" Ежедневная выручка в магазине национальных сувениров распределена нормально со средним значением 80000 тенге и средним квадратическим отклонением 5000 тенге. Найти:
Задача 2. "Производство курта" На предприятии по производству курта масса одной упаковки распределена нормально со средним значением 200 г и средним квадратическим отклонением 3 г. Определить:
Задача 3. "Национальная одежда" Длина национального камзола, производимого на фабрике, распределена нормально со средним значением 100 см и средним квадратическим отклонением 2 см. Вычислить:
Задача 4. "Спортивные соревнования" Результаты спортсменов в беге на 100 метров распределены нормально со средним значением 12 секунд и средним квадратическим отклонением 0,5 секунды. Найти:
Задача 5. "Выставочный центр" Время осмотра экспозиции в музее национального искусства распределено нормально со средним значением 45 минут и средним квадратическим отклонением 10 минут. Определить:
Задача №3. Тестовая задача.
A) Только математическим ожиданием B) Только дисперсией C) Математическим ожиданием и дисперсией D) Только средним квадратическим отклонением E) Медианой и модой
|
Ученики смотрят видеоматериал и понимают тему. Ученики решают контекстных задач. Выполняют тестовых задач. |
Метод оценивания «Мяч» Дескрипторы: Выписывают основных определения основных понятий. Правильно решают задачи. Выбирают правильный ответ. |
https://youtu.be/5rRQnN8Q_sc?si=jqXJJx4-uX8pMTK4
|
||
|
Конец урока 5 минут |
Рефлексия «Незаконченное предложение» |
В конце урока учитель оценивает обучающихся по набранным наградам и активности. |
|
|
||
Урок №31
|
Фамилия имя педагога |
|
|||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||
|
Тема урока: |
Закон больших чисел |
|||||||||||||||||
|
Цели обучения согласно программе |
Анализировать следствия закона |
|||||||||||||||||
|
Цель урока |
Анализируют примеры применения |
|||||||||||||||||
|
Процесс урока: |
||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “барабан” |
Ученики приветствуют и делятся на 3 группы. |
Дескриптор
Метод оценивания «Букет цветок» |
|
||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Таблица терминов и определений
Задача №3. Решение задач. Задача 1. "Контроль качества" На фабрике по производству национальных украшений проверяется качество изделий. По теоретическим расчетам, вероятность брака составляет 0,1. Какова вероятность того, что в партии из 1000 изделий относительная частота бракованных изделий отклонится от теоретической вероятности не более чем на 0,02? Задача 2. "Социологический опрос" При опросе жителей города об их отношении к строительству нового культурного центра опрашивается 900 человек. Какое минимальное количество человек нужно опросить, чтобы с вероятностью 0,95 относительная частота положительных ответов отклонялась от истинной вероятности не более чем на 0,05? Задача 3. "Спортивные достижения" В спортивной секции по национальной борьбе қазақша күрес тренируются 500 спортсменов. Вероятность победы в схватке для каждого спортсмена 0,6. Найти вероятность того, что среднее число побед в серии схваток отклонится от математического ожидания не более чем на 0,05. Задача 4. "Метеорологические наблюдения" Метеостанция проводит измерения температуры воздуха. Известно, что среднее квадратическое отклонение измерений составляет 2°C. Сколько измерений нужно провести, чтобы с вероятностью 0,99 среднее арифметическое температуры отклонялось от истинного значения не более чем на 0,5°C? |
Ученики смотрят видеоматериал и понимают тему. Ученик изучает и заполняет таблицу терминов и определений. Ученик решает задачу о контроле качества с применением закона больших чисел. |
Дескрипторы: Выписывают основных определения основных понятий. Дескрипторы:
Дескриптор: Правильно выбирает нужную формулу Подставляет значения Выполняет вычисления |
|||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным розам. |
|
|
||||||||||||||
Урок №32
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Генеральная совокупность и выборка |
|||||
|
Цели обучения согласно программе |
Сравнивать характеристики совокупностей |
|||||
|
Цель урока |
Сравнивают параметры выборок |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “случайных цифр” |
Ученики приветствуют и делятся на 3 группы по методу “случайные цифры”. |
Метод оценки «Мороженное» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Групповая работа. Задача 1. "Школьный опрос" В школе 500 учеников (генеральная совокупность). Для изучения отношения к национальным видам спорта было опрошено 50 случайно выбранных учеников (выборка). Среди опрошенных 35 учеников проявили интерес к национальным видам спорта.
Задача 2. "Статистика предприятия" На фабрике по производству национальных сувениров работает 300 человек (генеральная совокупность). Для исследования стажа работы случайным образом отобрали 30 сотрудников (выборка). Получены следующие данные о стаже:
Задача 3. "Контроль качества" На складе хранится 1000 изделий (генеральная совокупность). Для проверки качества отобрано 100 изделий (выборка). Среди них обнаружено 5 бракованных.
Задача 4. "Социологическое исследование" В городе проживает 50000 человек (генеральная совокупность). Для изучения общественного мнения о проведении национального праздника Наурыз было опрошено 500 человек (выборка). 400 опрошенных поддержали традиционный формат праздника, 80 предложили современный формат, остальные воздержались. Построить интервальную оценку для доли поддерживающих традиционный формат во всем городе. Задача 5. "Спортивная статистика" В спортивной школе занимается 400 учеников (генеральная совокупность). Для анализа физической подготовки случайным образом отобрали 40 учеников (выборка) и измерили время бега на 100 метров. Средний результат в выборке составил 14,5 секунд, среднее квадратическое отклонение 1,2 секунды. Построить доверительный интервал для среднего времени бега всех учеников школы с надежностью 0,95. Задача 6. "Анализ цен" В городе 200 магазинов национальной одежды (генеральная совокупность). Для анализа цен случайным образом выбрали 20 магазинов (выборка) и зафиксировали цену на традиционный камзол. Получены следующие данные:
Задача №3. Метод «Арбуз»
|
Ученики смотрят видеоматериал и понимают тему. Решают текстовых задач. Отвечают на вопросы. |
Метод оценки «Мороженное» Дескрипторы: Выписывают основных определения основных понятий. Правильно решают текстовых задач. Правильно отвечают на вопросы. |
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным наградам |
|
|
||
Урок №33
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Вариационные ряды |
|||||
|
Цели обучения согласно программе |
Систематизировать данные в ряды |
|||||
|
Цель урока |
Систематизируют и строят ряды |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики работают в паре по выбору. |
Ученики приветствуют и делятся на пары. |
Дескриптор
Метод оценки «Звездочка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Уровень А (базовый уровень) Задача А1. "Рост спортсменов" В секции национальной борьбы измерили рост 20 спортсменов (в см): 165, 170, 168, 172, 170, 175, 168, 170, 172, 175, 168, 170, 172, 168, 175, 170, 172, 175, 170, 168 Требуется:
Задача А2. "Стаж работы" Дан стаж работы 15 мастеров по изготовлению национальных музыкальных инструментов (в годах): 5, 3, 7, 5, 8, 3, 5, 7, 4, 5, 3, 7, 5, 4, 5 Найти:
Задача А3. "Цена товара" В 25 магазинах национальной одежды зафиксирована цена на традиционный жилет (в тысячах тенге): 15, 18, 20, 15, 17, 20, 15, 18, 20, 17, 15, 17, 18, 20, 15, 17, 18, 20, 15, 17, 18, 20, 15, 17, 18 Требуется:
Задача №3. Уровень В (повышенный уровень) Задача В1. "Спортивные результаты" Результаты забега на 100 метров 30 спортсменов распределились следующим образом:
Требуется:
Задача В2. "Анализ продаж" Дневная выручка магазина сувениров за месяц (30 дней) распределилась по интервалам:
Найти:
Задача В3. "Производство изделий" На фабрике проведен анализ веса готовых изделий (в граммах). Получены данные:
Требуется:
|
Ученики смотрят видеоматериал и понимают тему. Ученик работает с простыми вариационными рядами, выполняет базовые вычисления и построения. Ученик работает с интервальными вариационными рядами, выполняет более сложные вычисления и анализ. |
Дескрипторы: Выписывают основных определения основных понятий. Дескриптор: Находит среднее значение Определяет моду и медиану Вычисляет относительные частоты Дескриптор: Вычисляет среднее значение интервального ряда Определяет модальный и медианный интервалы Находит основные числовые характеристики |
|||
|
Конец урока 5 минут |
Рефлексия Вопрос-ответ от учителя -Вам понравился урок? -Чтобы вы хотели еще добавить? -Оцените урок от 1 до 10 |
В конце урока учитель оценивает знания учеников и активность по набранным наградам. |
|
|
||
Урок №34
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Статистические оценки параметров |
|||||
|
Цели обучения согласно программе |
Оценивать параметры распределения |
|||||
|
Цель урока |
Оценивают точность параметров |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Выбери цвет”.
|
Каждый ученик выбирает 1 лист с закрытыми глазами из 3 разноцветных бумаг. По цветам ученики делятся на 3 группы. |
Метод оценки «Мои достижения» |
|
||
|
Середина 35 урока |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Пчела»
Что такое точечная оценка параметра? Какими свойствами должна обладать несмещенная оценка? Что такое эффективная оценка? Когда оценка называется состоятельной? Как связаны доверительный интервал и надежность оценки? Задание 3. "Комплексная задача" В магазине национальных сувениров проводится анализ цен. Из 200 товаров случайным образом отобрано 20. Найдены выборочное среднее (5000 тенге) и выборочное среднее квадратическое отклонение (500 тенге). Требуется:
Задание 4. "Построение доверительных интервалов" На основе выборки из 50 измерений получено выборочное среднее x̄ = 25 и среднее квадратическое отклонение s = 2. Построить доверительный интервал для математического ожидания с надежностью 0,95. |
Ученики смотрят видеоматериал и понимают тему. Ученик демонстрирует теоретические знания о статистических оценках. Ученик решает комплексную задачу с практическим применением. Ученик строит доверительный интервал, используя необходимые формулы. |
Метод оценки «Мои достижения» Дескрипторы: Выписывают основных определения основных понятий. Дескрипторы:
Применяет нужные формулы Проводит вычисления Проверяет результаты Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия «Радуга» |
В конце урока учитель оценивает активность учеников по собранным наградам. |
|
|
||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Авторская программа "Теория вероятностей"
Авторская программа "Теория вероятностей"
Пояснительная записка
Актуальность программы обусловлена возрастающей ролью вероятностно-статистического мышления в современном мире. В условиях постоянно увеличивающегося потока информации и необходимости принимать решения в условиях неопределенности, теория вероятностей становится незаменимым инструментом для анализа и прогнозирования различных процессов.
Потребность в программе связана с необходимостью формирования у учащихся вероятностного мышления, навыков статистического анализа и умения работать с большими массивами данных, что является важным требованием современного образования и будущей профессиональной деятельности.
Научно-методический уровень программы характеризуется системным подходом к изучению теории вероятностей, включающим как теоретические основы, так и практическое применение. Программа предусматривает использование современных цифровых инструментов для статистической обработки данных и визуализации вероятностных моделей.
Направленность программы:
-
Развитие вероятностного мышления
-
Формирование навыков статистического анализа
-
Развитие умения моделировать реальные процессы
-
Применение теории вероятностей в практических задачах
Основная цель программы: формирование у учащихся вероятностно-статистической грамотности и развитие навыков применения теории вероятностей для решения практических задач.
Задачи программы:
-
Сформировать понимание основных концепций теории вероятностей
-
Развить навыки вероятностного моделирования
-
Научить применять статистические методы анализа
-
Развить умение интерпретировать вероятностные результаты
-
Сформировать навыки работы с компьютерными программами для статистической обработки данных
-
Развить аналитическое мышление
-
Научить применять вероятностные методы в различных областях
-
Подготовить к решению практических задач с вероятностным содержанием
Ожидаемые результаты:
-
Учащиеся освоят основные понятия и методы теории вероятностей
-
Научатся решать вероятностные задачи различного уровня сложности
-
Приобретут навыки работы со статистическими программами
-
Освоят методы вероятностного моделирования
-
Сформируют навыки анализа статистических данных
-
Приобретут опыт исследовательской деятельности в области теории вероятностей
-
Научатся применять вероятностные методы в реальных ситуациях
-
Продемонстрируют готовность к решению прикладных задач
Отличительной особенностью программы является её практическая направленность и использование современных цифровых инструментов для анализа данных. Программа построена по принципу возрастающей сложности, что обеспечивает последовательное развитие вероятностного мышления учащихся.
Принципы отбора материала основаны на логической последовательности изучения тем, их взаимосвязи и практической значимости. Особое внимание уделяется связи теории вероятностей с реальными жизненными ситуациями и другими областями знаний.
Обоснованность и достоверность ожидаемых результатов подтверждается соответствием программы современным образовательным стандартам и успешным опытом применения вероятностно-статистических методов в различных областях. Программа предусматривает регулярный мониторинг успеваемости учащихся и корректировку методов обучения при необходимости.
Содержание:
Раздел 1. Основы теории вероятностей и комбинаторика
-
Введение в теорию вероятностей
-
Основные понятия теории вероятностей
-
Элементы комбинаторики: перестановки
-
Элементы комбинаторики: размещения и сочетания
-
Применение комбинаторики в вероятности
Раздел 2. События и классическая вероятность
-
События и их виды
-
Классическое определение вероятности
-
Геометрическая вероятность
-
Свойства вероятности. Часть 1
-
Свойства вероятности. Часть 2
Раздел 3. Условная вероятность и основные теоремы
-
Условная вероятность: основные понятия
-
Условная вероятность: решение задач
-
Правило сложения вероятностей
-
Правило умножения вероятностей
-
Формула полной вероятности: теория
-
Формула полной вероятности: практика
-
Формула Байеса: основные понятия
-
Формула Байеса: решение задач
Раздел 4. Схема Бернулли
-
Схема Бернулли
-
Формула Бернулли и её применение
-
Наивероятнейшее число успехов в схеме Бернулли
Раздел 5. Случайные величины и их характеристики
-
Случайные величины: основные понятия
-
Дискретные случайные величины
-
Непрерывные случайные величины
-
Числовые характеристики случайных величин
-
Математическое ожидание и его свойства
-
Дисперсия и среднее квадратическое отклонение
Раздел 6. Законы распределения случайных величин
-
Биномиальное распределение
-
Распределение Пуассона
-
Нормальное распределение
-
Закон больших чисел
Раздел 7. Элементы математической статистики
-
Генеральная совокупность и выборка: основные понятия
-
Вариационные ряды и их характеристики
-
Статистические оценки параметров распределения
Нормативная часть
Всего 34 час, в неделю 1 час.
Предназначено для 9-11 классов.
|
№ |
Тема |
Цели обучения |
Количество часов |
Образовательный продукт |
||
|
Всего |
Теория |
Практика |
||||
|
1 |
Введение в теорию вероятностей |
Анализировать роль теории вероятностей |
1 |
1 |
|
Анализируют примеры применения в жизни |
|
2 |
Основные понятия теории вероятностей |
Систематизировать основные определения |
1 |
|
1 |
Систематизируют термины в виде схемы |
|
3 |
Элементы комбинаторики: перестановки |
Исследовать правила составления перестановок |
1 |
|
1 |
Исследуют и составляют алгоритм решения |
|
4 |
Элементы комбинаторики: размещения и сочетания |
Сравнивать формулы размещений и сочетаний |
1 |
|
1 |
Сравнивают и составляют таблицу различий |
|
5 |
Применение комбинаторики в вероятности |
Интегрировать знания комбинаторики и вероятности |
1 |
|
1 |
Интегрируют методы решения в задачах |
|
6 |
События и их виды |
Классифицировать виды событий |
1 |
1 |
|
Классифицируют события по признакам |
|
7 |
Классическое определение вероятности |
Анализировать классическое определение |
1 |
|
1 |
Анализируют и решают типовые задачи |
|
8 |
Геометрическая вероятность |
Применять геометрический подход |
1 |
|
1 |
Применяют формулы в геометрических задачах |
|
9 |
Свойства вероятности. Часть 1 |
Исследовать основные свойства вероятности |
1 |
1 |
|
Исследуют свойства на конкретных примерах |
|
10 |
Свойства вероятности. Часть 2 |
Доказывать свойства вероятности |
1 |
|
1 |
Доказывают и применяют свойства |
|
11 |
Условная вероятность: основные понятия |
Интерпретировать понятие условной вероятности |
1 |
1 |
|
Интерпретируют условия в задачах |
|
12 |
Условная вероятность: решение задач |
Синтезировать способы решения |
1 |
|
1 |
Синтезируют алгоритм решения задач |
|
13 |
Правило сложения вероятностей |
Анализировать случаи применения правила |
1 |
1 |
|
Анализируют и решают комбинированные задачи |
|
14 |
Правило умножения вероятностей |
Оценивать применимость правила |
1 |
|
1 |
Оценивают и выбирают способ решения |
|
15 |
Формула полной вероятности: теория |
Исследовать структуру формулы |
1 |
1 |
|
Исследуют компоненты формулы |
|
16 |
Формула полной вероятности: практика |
Применять формулу в различных ситуациях |
1 |
|
1 |
Применяют формулу к практическим задачам |
|
17 |
Формула Байеса: основные понятия |
Интерпретировать смысл формулы |
1 |
1 |
|
Интерпретируют условия применения |
|
18 |
Формула Байеса: решение задач |
Синтезировать методы решения |
1 |
|
1 |
Синтезируют способы применения формулы |
|
19 |
Схема Бернулли |
Анализировать условия применения схемы |
1 |
|
1 |
Анализируют и составляют схему решения |
|
20 |
Формула Бернулли и её применение |
Применять формулу в различных задачах |
1 |
|
1 |
Применяют формулу в практических задачах |
|
21 |
Наивероятнейшее число успехов |
Вычислять вероятность успехов |
1 |
|
1 |
Вычисляют и интерпретируют результаты |
|
22 |
Случайные величины: основные понятия |
Классифицировать случайные величины |
1 |
|
1 |
Классифицируют виды величин |
|
23 |
Дискретные случайные величины |
Исследовать характеристики величин |
1 |
|
1 |
Исследуют и описывают свойства |
|
24 |
Непрерывные случайные величины |
Сравнивать виды случайных величин |
1 |
|
1 |
Сравнивают характеристики величин |
|
25 |
Числовые характеристики случайных величин |
Вычислять основные характеристики |
1 |
|
1 |
Вычисляют параметры распределений |
|
26 |
Математическое ожидание и свойства |
Доказывать свойства мат.ожидания |
1 |
|
1 |
Доказывают и применяют свойства |
|
27 |
Дисперсия и среднее квадратическое отклонение |
Анализировать меры разброса |
1 |
|
1 |
Анализируют и вычисляют параметры |
|
28 |
Биномиальное распределение |
Исследовать свойства распределения |
1 |
|
1 |
Исследуют характеристики распределения |
|
29 |
Распределение Пуассона |
Применять распределение в задачах |
1 |
|
1 |
Применяют формулы распределения |
|
30 |
Нормальное распределение |
Интерпретировать график распределения |
1 |
|
1 |
Интерпретируют параметры распределения |
|
31 |
Закон больших чисел |
Анализировать следствия закона |
1 |
|
1 |
Анализируют примеры применения |
|
32 |
Генеральная совокупность и выборка |
Сравнивать характеристики совокупностей |
1 |
|
1 |
Сравнивают параметры выборок |
|
33 |
Вариационные ряды |
Систематизировать данные в ряды |
1 |
|
1 |
Систематизируют и строят ряды |
|
34 |
Статистические оценки параметров |
Оценивать параметры распределения |
1 |
|
1 |
Оценивают точность параметров |
|
Всего |
34 |
6 |
28 |
|
||
Информационно-методический отдел
Авторская программа "Теория вероятностей" для 9-11 классов направлена на формирование вероятностного мышления и развитие навыков статистического анализа. Темы, представленные в семи разделах программы, включают материалы, соответствующие образовательным стандартам. Практико-ориентированный подход к изучению способствует глубокому пониманию теории вероятностей и её применению в реальных ситуациях.
Критериальная система оценивания по 10-балльной шкале
|
Баллы |
Процент |
Уровень учебных достижений |
Критерии оценивания |
|
10 |
95-100% |
Высокий |
Глубокое понимание теории вероятностей, свободное решение сложных задач, способность анализировать и интерпретировать результаты |
|
9 |
90-94% |
Высокий |
Отличное знание материала, умение решать задачи повышенной сложности, незначительные недочеты |
|
8 |
85-89% |
Достаточный |
Хорошее владение материалом, способность решать стандартные и усложненные задачи |
|
7 |
80-84% |
Достаточный |
Хорошее понимание основных концепций, умение решать типовые задачи |
|
6 |
70-79% |
Средний |
Понимание основного материала, решение задач среднего уровня сложности |
|
5 |
60-69% |
Средний |
Базовое понимание материала, решение простых задач с некоторыми ошибками |
|
4 |
50-59% |
Удовлетворительный |
Частичное понимание материала, решение простых задач |
|
3 |
30-49% |
Низкий |
Слабое владение материалом, существенные ошибки в решениях |
|
2 |
15-29% |
Низкий |
Серьезные пробелы в знаниях, неспособность решать базовые задачи |
|
1 |
0-14% |
Низкий |
Отсутствие базовых знаний и умений |
Содержание программы:
-
Основы теории вероятностей и комбинаторика
-
События и классическая вероятность
-
Условная вероятность и основные теоремы
-
Схема Бернулли
-
Случайные величины и их характеристики
-
Законы распределения случайных величин
-
Элементы математической статистики
Приложения:
-
Практические задания по каждому разделу
-
Контрольные работы и тесты
-
Методические рекомендации для учителей
-
Учебные материалы в цифровом формате
-
Оценочные материалы
-
Дополнительные материалы для подготовки к олимпиадам
Рекомендуемые цифровые инструменты:
-
Microsoft Excel — статистическая обработка данных, построение графиков
-
GeoGebra Probability Calculator — визуализация вероятностных моделей
-
R Studio — статистический анализ данных
-
Python с библиотекой Pandas — обработка больших наборов данных
Формативное оценивание включает:
-
Устные ответы
-
Решение задач у доски
-
Самостоятельные работы
-
Домашние задания
-
Практические работы
-
Проектная деятельность
Суммативное оценивание включает:
-
Контрольные работы по разделам
-
Четвертные контрольные работы
-
Итоговая контрольная работа
-
Защита проектов
Список литературы:
Для учителей:
-
Алдамуратов Е.С., Байсалов Ж.К. "Методика преподавания теории вероятностей в школе" (Алматы, 2021)
-
Нурпеисова Г.М. "Современные подходы к обучению теории вероятностей" (Нур-Султан, 2020)
-
Жумагулова К.А. "Организация проектной деятельности на уроках теории вероятностей" (Алматы, 2019)
-
Сатыбалдиев О.С. "Практикум по решению вероятностных задач" (Караганда, 2022)
-
Мусабеков А.К. "Дифференцированный подход в обучении теории вероятностей" (Шымкент, 2021)
Для учащихся:
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 9 класса" (Алматы, 2019)
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 10 класса" (Алматы, 2019)
-
Абылкасымова А.Е. "Алгебра и начала анализа: учебник для 11 класса" (Алматы, 2019)
-
Искаков Б.А. "Теория вероятностей в таблицах и схемах" (Павлодар, 2021)
-
Муканова Р.А. "Готовимся к олимпиадам по теории вероятностей" (Алматы, 2022)
Для родителей:
-
Ахметов М.А. "Как помочь ребенку в изучении теории вероятностей" (Астана, 2022)
-
Тулегенова Г.С. "Теория вероятностей: помощь родителям" (Алматы, 2021)
-
Байжуманов А.А. "Родительское руководство по поддержке изучения математики" (Караганда, 2020)
-
Сагиндыков Е.Н. "Математика в семье: советы родителям" (Костанай, 2021)
-
Нурмухамедова Ж.М. "Как развивать вероятностное мышление у детей" (Алматы, 2022)
Приложение.
Задача №1.
Посмотреть видеоматериал.

Задача №2.
Текстовые задачи.
В классе из 30 учеников 18 занимаются спортом, 15 изучают английский язык, а 10 учеников совмещают спорт и английский. Какова вероятность того, что случайно выбранный ученик не занимается ни спортом, ни английским?
В магазине продаются 200 телефонов, из них 120 - черного цвета, 50 - белого, остальные - синего. Какова вероятность купить телефон не черного цвета?
На полке стоят 15 книг, из них 6 - на казахском языке, 5 - на русском, 4 - на английском. Какова вероятность взять книгу на казахском языке?
В коробке 10 красных, 8 синих и 7 зеленых шаров. Какова вероятность достать шар синего цвета?
Задача №3.
«Froggy jumps»


Задача №4.
Групповая работа.
Игра «ОХО»

Задача 1: "Мишень"
На квадратном листе картона со стороной 50 см нарисована круглая мишень радиусом 20 см. Случайным образом в лист картона попадает дротик. Найти вероятность того, что дротик попадет в мишень.
Задача 2: "Парковка"
Длина парковочного места 5 метров. Водитель паркует автомобиль длиной 4 метра. Чтобы припарковаться правильно, центр автомобиля должен находиться в средней части парковочного места на расстоянии не более 0,3 метра от его центра. Найти вероятность правильной парковки.
Задача 3: "Художник"
На прямоугольном холсте размером 80×60 см художник нарисовал квадрат со стороной 40 см. Если случайным образом поставить точку на холсте, какова вероятность, что она попадет в квадрат?
Задача 4: "Часовая стрелка"
Часовая стрелка движется по циферблату. Найти вероятность того, что в случайный момент времени она находится между 3 и 5 часами.
Задача 5: "Городской пруд"
В городском парке есть прямоугольный пруд размером 30×20 метров. Внутри пруда есть круглый остров радиусом 5 метров. Какова вероятность того, что брошенный случайным образом в пруд камень попадет в воду, а не на остров?
Задача 6: "Детская площадка"
На квадратной детской площадке со стороной 10 метров расположена круглая песочница радиусом 2 метра и прямоугольная беседка размером 3×2 метра. Найти вероятность того, что случайно брошенный мяч попадет на свободную территорию площадки.
Задача 7: "Велосипедист"
Велосипедист должен приехать в пункт назначения между 12:00 и 13:00. Он приезжает в случайный момент в этом промежутке. Найти вероятность того, что он приедет между 12:20 и 12:40.
Задача 8: "Линейка"
На отрезке длиной 20 см случайным образом ставятся две точки. Найти вероятность того, что расстояние между ними будет меньше 5 см.
Задача 9: "Спортивная площадка"
На прямоугольной спортивной площадке размером 40×30 метров начерчены две круглые зоны для игр радиусом 5 метров каждая. Найти вероятность того, что случайно брошенный мяч попадет в одну из игровых зон.
Задача №5.
Задачи с рисунками.
Задача 1: "Мишень"
В квадратную мишень со стороной 100 см вписан красный круг радиусом 40 см. Стрелок стреляет случайным образом по мишени. Найти вероятность того, что стрела попадет в красную область мишени.
Задача 2: "Цветник"
На квадратном участке земли со стороной 10 метров расположены два круглых цветника радиусом 2 метра каждый и прямоугольная клумба размером 4×3 метра. Найти вероятность того, что случайно упавшее семя попадет на свободную землю (не в цветник и не в клумбу).

Задача 3: "Картина"
На прямоугольном холсте размером 100×100 см художник нарисовал прямоугольное озеро размером 80×40 см и круглое солнце радиусом 20 см. Если случайным образом поставить точку на холсте, какова вероятность того, что она попадет либо в озеро, либо в солнце?

Задача №6.
Математический диктант.
-
Дайте определение условной вероятности
-
Запишите формулу умножения вероятностей для зависимых событий
-
Как обозначается условная вероятность события А при условии В?
-
Запишите формулу Байеса
-
Что такое гипотеза в теории вероятностей?
Задача №7.
Сопоставление.
|
Описание события |
Формула |
|
Условная вероятность |
|
|
Произведение независимых событий |
|
|
Произведение зависимых событий |
|
|
Противоположное событие |
|
|
Полная вероятность |
|
Задача №8.
Парная работа.

Задача №9.
Тестовая задача.
1. Схема Бернулли - это:
A) Последовательность взаимозависимых испытаний B) Последовательность независимых испытаний с двумя исходами
C) Последовательность зависимых испытаний с тремя исходами
D) Одно испытание с двумя исходами
E) Испытание с множеством исходов
2. В формуле P(X=k) = C(n,k)·pᵏ·qⁿ⁻ᵏ для схемы Бернулли, q равно:
A) Вероятности успеха
B) 1 + p
C) 1 - p
D) p²
E) p/n
3. Локальная формула Муавра-Лапласа применяется, когда:
A) n < 10
B) n > 100
C) np < 10
D) n = 100
E) p = q
4. В схеме Бернулли вероятность успеха p:
A) Меняется от испытания к испытанию
B) Зависит от числа испытаний
C) Остается постоянной во всех испытаниях
D) Равна 1
E) Равна 0
5. Наивероятнейшее число успехов k₀ в схеме Бернулли определяется неравенством:
A) np - q ≤ k₀ ≤ np + p
B) np - p ≤ k₀ ≤ np + q
C) np - 1 ≤ k₀ ≤ np + 1
D) np ≤ k₀ ≤ np + 1
E) np – 2 ≤ k₀ ≤ np + 2
Задача №10.
Работа с таблицой.
|
Термин |
Определение |
Пример |
|
Схема Бернулли |
|
|
|
Успех |
|
|
|
Число испытаний |
|
|
|
Вероятность успеха |
|
|
|
Наивероятнейшее число |
|
|
Модель краткосрочного планирования
Урок №1
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Введение в теорию вероятностей |
|||||
|
Цели обучения согласно программе |
Анализировать роль теории вероятностей |
|||||
|
Цель урока |
Анализируют примеры применения в жизни |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
-Приветствие и краткое введение в тему урока. - Объяснить цели и задачи урока. |
-Слушают объяснение. - Задают вопросы для уточнения. -Записывают основные моменты в тетрадь. |
Метод оценки «Юрта» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Текстовые задачи. В классе из 30 учеников 18 занимаются спортом, 15 изучают английский язык, а 10 учеников совмещают спорт и английский. Какова вероятность того, что случайно выбранный ученик не занимается ни спортом, ни английским? В магазине продаются 200 телефонов, из них 120 - черного цвета, 50 - белого, остальные - синего. Какова вероятность купить телефон не черного цвета? На полке стоят 15 книг, из них 6 - на казахском языке, 5 - на русском, 4 - на английском. Какова вероятность взять книгу на казахском языке? В коробке 10 красных, 8 синих и 7 зеленых шаров. Какова вероятность достать шар синего цвета? Задача №3. Игра «Froggy jumps»
|
Ученики смотрят видеоматериал и понимают тему. Ученики решают текстовые задачи.
Ученики играют игру. |
Метод оценки «Юрта» |
https://youtu.be/_ZNvsnxaQr0?si=HK8vvdv_8i8JJhRz
https://www.educaplay.com/learning-resources/21203293-learning_resource.html |
||
|
Конец урока 5 минут |
Рефлексия
|
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||
Урок №2
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Основные понятия теории вероятностей |
|||||
|
Цели обучения согласно программе |
Систематизировать основные определения |
|||||
|
Цель урока |
Систематизируют термины в виде схемы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5–10 минут |
Приветствие и проверка присутствующих. Введение в тему урока, объяснение целей урока. |
Слушают и записывают цели урока. Участвуют в обсуждении предыдущего материала. |
Дескриптор
Метод оценки «Бургер»
|
|
||
|
Середина урока 35 минут |
Задача №1. Текстовые задачи. В урне 20 шаров: 8 белых и 12 черных. Наудачу вынимают один шар. Описать элементарные исходы, благоприятные исходы и пространство элементарных исходов. Бросают игральный кубик. Описать события: А – выпало четное число, В – выпало число больше 4. При стрельбе по мишени рассматриваются события: А – попадание в цель, В – промах. Являются ли эти события совместными? В семье двое детей. Описать пространство элементарных исходов для пола детей (М - мальчик, Д - девочка). Задача №2. Метод «Верно, неверно»
Задача №3. Игра «Скачки»
|
Ученик анализирует условия задачи и определяет элементарные исходы, благоприятные события и пространство элементарных исходов в различных вероятностных ситуациях. Ученик анализирует каждое утверждение и определяет его истинность или ложность на основе теории вероятностей. Ученик применяет знания о вероятности в игровой ситуации, рассчитывая шансы на выигрыш. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность каждого ученика по заработанным наградам. |
|
|
||
Урок №3
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Элементы комбинаторики: перестановки |
|||||
|
Цели обучения согласно программе |
Исследовать правила составления перестановок |
|||||
|
Цель урока |
Исследуют и составляют алгоритм решения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Приветствие учеников и краткое введение в тему урока. Объяснение целей урока. Проведение короткого опроса для проверки начальных знаний. |
Приветствие учителя. Слушают объяснение целей урока. Участвуют в опросе. |
Дескриптор
Метод оценки «Цветок»
|
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Задание "Найди ошибку и исправь" В городском конкурсе участвуют 6 школ. Организаторы составляют порядок выступления школ. Ученик решил найти количество возможных вариантов порядка выступления школ. Решение ученика:
Задания:
Задача №3.
|
Ученик просматривает видеоматериал, анализирует и фиксирует ключевые моменты по теме. Ученик анализирует предложенное решение, находит ошибки и представляет правильное решение задачи. Ученик решает комбинаторные задачи, применяя формулы перестановок и размещений. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по количеству цветочков и оценкам учеников парной работы |
|
|
||
Урок №4
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Элементы комбинаторики: размещения и сочетания |
|||||
|
Цели обучения согласно программе |
Сравнивать формулы размещений и сочетаний |
|||||
|
Цель урока |
Сравнивают и составляют таблицу различий |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Приветствие и проверка присутствующих. Постановка целей урока перед учениками. |
Слушают учителя, отмечают присутствующих. Внимательно слушают введение и записывают цели урока. |
Дескриптор
Метод оценки «Разбаловка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Текстовые задачи.
Задача №3. Незаконченное предложение. Размещением из n элементов по k называется... а) любая упорядоченная подгруппа из k элементов данного множества б) любая неупорядоченная подгруппа из k элементов данного множества в) любой набор из n элементов Число размещений из n элементов по k обозначается... а) Сₖⁿ б) Aₖⁿ в) Pₙ Сочетанием из n элементов по k называется... а) размещение, где порядок элементов важен б) неупорядоченный набор из k элементов в) перестановка из n элементов В формуле числа размещений Aₖⁿ = n!/(n-k)! важен порядок элементов, потому что... а) в числителе стоит факториал б) учитывается последовательность расположения элементов в) в знаменателе стоит разность Формула числа сочетаний имеет вид... а) Сₖⁿ = n! б) Сₖⁿ = n!/(k!(n-k)!) в) Сₖⁿ = n!/(n-k)! |
Ученик просматривает видеоматериал, анализирует и фиксирует ключевые моменты по теме. Ученики решают текстовых задач. Ученик анализирует каждое незаконченное предложение и выбирает правильное продолжение, демонстрируя понимание основных понятий комбинаторики. |
Дескрипторы:
Правильно решают текстовых задач. Дескрипторы:
|
|
||
|
Конец урока 5 минут |
Рефлексия Ученики в конце урока оценивают урок через онлайн рефлекс. |
В конце урока учитель оценивает активность учеников по набранным баллам. |
|
|
||
Урок №5
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Применение комбинаторики в вероятности |
|||||
|
Цели обучения согласно программе |
Интегрировать знания комбинаторики и вероятности |
|||||
|
Цель урока |
Интегрируют методы решения в задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1. Приветствует учеников и объявляет тему урока. 2. Представляет цели урока. 3. Проводит короткий вводный опрос для проверки предыдущих знаний |
1. Слушают учителя и записывают тему урока. 2. Знакомятся с целями урока. 3. Участвуют в вводном опросе. |
Дескриптор
Метод оценки Копилка» |
|
||
|
Середина урока 35 минут |
Задача №1. Текстовые задачи.
Задача №2.
Задача №3. Контекстная задача "Школьный фестиваль талантов" В школе проводится ежегодный фестиваль талантов. В этом году подали заявки:
Организаторы планируют:
Задания:
|
Ученики решают текстовых задач. Ученик решает тестовые задания, применяя формулы комбинаторики для нахождения вероятности событий. Ученик анализирует реальную ситуацию, применяет комбинаторные формулы для решения практических задач и находит вероятности событий. |
Метод оценки Копилка» Дескрипторы: Правильно решают текстовых задач. Дескрипторы:
Дескрипторы:
|
https://wordwall.net/ru/resource/81440785
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает работу учеников по копилкам. |
|
|
||
Урок №6
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
События и их виды |
|||||
|
Цели обучения согласно программе |
Классифицировать виды событий |
|||||
|
Цель урока |
Классифицируют события по признакам |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Демонстрирует видео, показывающее основные законы химии. 2.Эмоцианальная подготовка учеников. Ученики делятся с хорошими пожеланиями на день. 3.Ученики делятся на 3 группы по методу Жребий
|
Ученики делятся хорошими эмоциями с друзьями. После выбирают листы с номерами и делятся на группы. |
Оценивание по методу «Яблоко» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Логические задачи. Задача 1. "Школьная олимпиада" На школьной олимпиаде по математике рассматриваются события: A – участник решит все задачи B – участник решит хотя бы одну задачу C – участник не решит ни одной задачи Определите:
Задача 2. "Игральные кубики" При одновременном бросании двух игральных кубиков рассмотрите события: A – сумма выпавших очков равна 7 B – произведение выпавших чисел четное C – хотя бы на одном кубике выпало число 6 Определите:
Задача 3. "Погодные явления" В течение дня могут произойти события: A – пойдет дождь B – будет пасмурно C – будет солнечно D – будет ветрено Определите:
Задача 4. "Спортивные соревнования" На соревнованиях по бегу рассматриваются события: A – спортсмен займет первое место B – спортсмен попадет в тройку призеров C – спортсмен не финиширует Определите:
Задача 5. "Библиотека" Читатель берет книгу в библиотеке. Рассмотрите события: A – книга окажется детективом B – книга окажется в твердом переплете C – книга будет новой Определите:
Задача 6. "Транспорт" При поездке в школу рассматриваются события: A – опоздать на урок B – сесть в переполненный автобус C – встретить одноклассника Определите:
Задача 7. "Экзамен" На экзамене рассматриваются события: A – вытянуть легкий билет B – получить оценку "5" C – не сдать экзамен D – ответить на все дополнительные вопросы Определите:
Задача №3. Игра Квест
|
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует различные события, определяет их виды и устанавливает связи между ними. Ученик участвует в математическом квесте, решая последовательные задачи по теории вероятностей и комбинаторике, применяя знания в игровой форме и продвигаясь по маршруту в зависимости от правильности решений. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Блиц-опрос (Учитель задает вопросы, на которые студенты отвечают по очереди). |
В конце урока учитель оценивает каждого по набранным наградам. |
|
|
||
Урок №7
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Классическое определение вероятности |
|||||
|
Цели обучения согласно программе |
Анализировать классическое определение |
|||||
|
Цель урока |
Анализируют и решают типовые задачи |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. 2.Ученики делятся на 2 группы по методу “Сегментация круга” |
Группу можно разделить пополам, проведя воображаемый диаметр круга от себя (ведущего) к участнику, сидящему напротив. В случае, если требуется более двух команд, то круг просто разбивается на нужное число сегментов. |
Метод оценки «Галочка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Контекстные задачи. Задача 1: "Книжный клуб" В книжном клубе школы есть 40 книг, из которых 15 - фэнтези, 10 - детективы, а остальные - научная фантастика. Библиотекарь наугад выбирает одну книгу для чтения на следующем собрании клуба. Найти вероятности следующих событий: а) будет выбрана книга жанра фэнтези б) будет выбран детектив в) будет выбрана научная фантастика Задача 2: "Школьная олимпиада" В школьной олимпиаде по математике участвуют 30 учеников: 12 из 9-го класса, 10 из 10-го класса и 8 из 11-го класса. Случайным образом выбирается один участник для награждения специальным призом. Найти вероятность того, что будет выбран: а) ученик 9-го класса б) ученик 10-го класса в) ученик 11-го класса Задача 3: "Цветочная клумба" На клумбе растут 60 цветов: 20 красных роз, 15 белых роз, 15 розовых тюльпанов и 10 желтых тюльпанов. Садовник случайным образом срывает один цветок для букета. Найти вероятности следующих событий: а) будет сорвана роза (любого цвета) б) будет сорван тюльпан (любого цвета) в) будет сорван красный цветок г) будет сорвана белая роза Задача №3. Игра «Найди пару»
|
Ученики смотрят видеоматериал и понимают тему.
Ученик решает три контекстные задачи на вычисление классической вероятности, применяя соответствующие формулы. Ученик находит соответствующие пары между событиями и их вероятностями, основываясь на правилах классической вероятности. |
Дескрипторы:
Дескрипторы:
|
https://youtu.be/_n-4BHsRnPc?si=__fl3kJbepJ4Z1vH https://www.educaplay.com/learning-resources/21243615-learning_resource.html |
||
|
Конец урока 5 минут |
Рефлексия Ученики оценивают урок по 10 баллной шкале. |
В конце урока учитель оценивает каждую группу и ученика по набранным наградам. |
|
|
||
Урок №8
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Геометрическая вероятность |
|||||
|
Цели обучения согласно программе |
Применять геометрический подход |
|||||
|
Цель урока |
Применяют формулы в геометрических задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
|
Ученики настраиваются на урок, разминаются. |
Дескриптор
Метод оценки «Апельсин» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Групповая работа. Игра «ОХО»
Задача 1: "Мишень" На квадратном листе картона со стороной 50 см нарисована круглая мишень радиусом 20 см. Случайным образом в лист картона попадает дротик. Найти вероятность того, что дротик попадет в мишень. Задача 2: "Парковка" Длина парковочного места 5 метров. Водитель паркует автомобиль длиной 4 метра. Чтобы припарковаться правильно, центр автомобиля должен находиться в средней части парковочного места на расстоянии не более 0,3 метра от его центра. Найти вероятность правильной парковки. Задача 3: "Художник" На прямоугольном холсте размером 80×60 см художник нарисовал квадрат со стороной 40 см. Если случайным образом поставить точку на холсте, какова вероятность, что она попадет в квадрат? Задача 4: "Часовая стрелка" Часовая стрелка движется по циферблату. Найти вероятность того, что в случайный момент времени она находится между 3 и 5 часами. Задача 5: "Городской пруд" В городском парке есть прямоугольный пруд размером 30×20 метров. Внутри пруда есть круглый остров радиусом 5 метров. Какова вероятность того, что брошенный случайным образом в пруд камень попадет в воду, а не на остров? Задача 6: "Детская площадка" На квадратной детской площадке со стороной 10 метров расположена круглая песочница радиусом 2 метра и прямоугольная беседка размером 3×2 метра. Найти вероятность того, что случайно брошенный мяч попадет на свободную территорию площадки. Задача 7: "Велосипедист" Велосипедист должен приехать в пункт назначения между 12:00 и 13:00. Он приезжает в случайный момент в этом промежутке. Найти вероятность того, что он приедет между 12:20 и 12:40. Задача 8: "Линейка" На отрезке длиной 20 см случайным образом ставятся две точки. Найти вероятность того, что расстояние между ними будет меньше 5 см. Задача 9: "Спортивная площадка" На прямоугольной спортивной площадке размером 40×30 метров начерчены две круглые зоны для игр радиусом 5 метров каждая. Найти вероятность того, что случайно брошенный мяч попадет в одну из игровых зон. Задача №3. Задачи с рисунками. Задача 1: "Мишень" В квадратную мишень со стороной 100 см вписан красный круг радиусом 40 см. Стрелок стреляет случайным образом по мишени. Найти вероятность того, что стрела попадет в красную область мишени.
Задача 2: "Цветник" На квадратном участке земли со стороной 10 метров расположены два круглых цветника радиусом 2 метра каждый и прямоугольная клумба размером 4×3 метра. Найти вероятность того, что случайно упавшее семя попадет на свободную землю (не в цветник и не в клумбу).
Задача 3: "Картина" На прямоугольном холсте размером 100×100 см художник нарисовал прямоугольное озеро размером 80×40 см и круглое солнце радиусом 20 см. Если случайным образом поставить точку на холсте, какова вероятность того, что она попадет либо в озеро, либо в солнце?
|
Ученики смотрят видеоматериал и понимают тему. Ученик в группе решает предложенные задачи на геометрическую вероятность, обсуждая решение с одноклассниками. Ученик анализирует геометрические фигуры на рисунках и решает задачи с использованием формул площадей фигур. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Учитель раздает стикеры-листочки. Ученики пишут мнения об уроке анонимно и клеят на лучики солнца. |
Учитель в конце урока оценивает активность и количество листочков. |
|
|
||
Урок №9
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Свойства вероятности. Часть 1 |
|||||
|
Цели обучения согласно программе |
Исследовать основные свойства вероятности |
|||||
|
Цель урока |
Исследуют свойства на конкретных примерах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. 2. Ученики делятся на пары по желанию (мини группа). |
Ученики знакомятся и делятся на мини группы из 2 человек. |
Дескриптор Метод оценивания «Попкорн» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. 1.Какое из следующих утверждений о вероятности события верно? A) Вероятность может быть отрицательным числом B) Вероятность может быть больше 1 C) Вероятность может быть равна 1,5 D) Вероятность всегда находится в пределах от 0 до 1 E) Вероятность всегда больше 0,5 2.Вероятность достоверного события равна... A) -1 B) 0 C) 0,5 D) 1 E) 2 3.Если вероятность события A равна 0,7, то вероятность противоположного события Ā равна... A) 0,7 B) 0,3 C) 1,7 D) -0,7 E) 1,4 4.Если события A и B несовместны, то вероятность их суммы P(A + B) равна... A) P(A) × P(B) B) P(A) - P(B) C) P(A) + P(B) D) P(A)/P(B) E) max(P(A), P(B)) 5.Сумма вероятностей противоположных событий всегда равна... A) 0 B) 0,5 C) 1 D) 2 E) 100 6.Если вероятность события A равна 0,4, а события B равна 0,3, то вероятность их суммы P(A + B) для несовместных событий равна... A) 0,12 B) 0,1 C) 0,7 D) 1,0 E) 0,35 Задача №3. Метод «Фри»
1.В коробке лежат 20 цветных карандашей: 8 красных, 7 синих и 5 зеленых. Наугад вытаскивают один карандаш. Найдите вероятность того, что вытащенный карандаш будет красный, не красный, синий или зеленый. 2.В урне находятся 15 шаров: белые и черные. Вероятность вытащить белый шар равна 0,4. Сколько белых шаров в урне? 3.В группе 25 студентов, из них 15 девушек. Случайным образом выбирают одного студента. Найдите вероятность того, что выбранный студент девушка или юноша. Проверьте, чему равна сумма этих вероятностей. 4.На полке стоят 30 книг, из них 12 – учебники. Случайным образом берут одну книгу. Найдите вероятность того, что взятая книга учебник или не учебник. Докажите, что эти события противоположные. 5.В коробке 10 конфет: 6 шоколадных и 4 карамельки. Наугад берут две конфеты. Найдите вероятность того, что обе конфеты будут шоколадные или разные. 6.В классе 20 учеников. Из них 8 занимаются спортом, 12 занимаются музыкой, а 4 ученика занимаются и спортом, и музыкой. Какова вероятность того, что случайно выбранный ученик занимается спортом или музыкой, либо не занимается ничем. |
Ученики смотрят видеоматериал и понимают тему. Ученик решает тестовые задания, применяя знания о свойствах вероятности. Ученик самостоятельно решает задачи на применение свойств вероятности, выбирая наиболее подходящий метод решения. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Студенты заполняют карточки с вопросами о том, что нового они узнали и что осталось непонятным. |
В конце урока учитель оценивает обучающихся по набранным наградам и активности. |
|
|
||
Урок №10
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Свойства вероятности. Часть 2 |
|||||
|
Цели обучения согласно программе |
Доказывать свойства вероятности |
|||||
|
Цель урока |
Доказывают и применяют свойства |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой |
Ученики приветствуют. |
Метод оценивания «Букет цветок». |
|
||
|
Середина урока 35 минут |
Задача №1. Уровень А (базовый уровень) Метод «Кто быстрый?» Задача А1 В коробке 20 шаров: 12 красных и 8 синих. Вынимают два шара подряд. Найдите вероятность того, что оба шара будут красными. Задача А2 На полке 15 книг, из которых 6 – учебники математики. Случайным образом берут две книги. Найдите вероятность того, что обе книги окажутся учебниками математики. Задача А3 В урне 10 шаров: 4 белых и 6 черных. Вынимают три шара подряд. Найдите вероятность того, что первый шар белый, второй черный, третий белый. Задача А4 В классе 30 учеников, из них 18 девочек. Случайным образом выбирают двух учеников. Найдите вероятность того, что выбраны две девочки. Задача А5 В мешке 25 конфет: 15 шоколадных и 10 карамелек. Вынимают две конфеты подряд. Найдите вероятность того, что обе конфеты окажутся шоколадными. Задача №2. Групповая работа. Метод «Банкомат»
Уровень В (средний уровень) Задача В1 В коробке 40 деталей, из них 5 бракованных. Наудачу извлекают три детали. Найдите вероятность того, что все извлеченные детали окажутся качественными. Задача В2 На стоянке 12 автомобилей, из них 7 белых, 3 черных и 2 красных. Случайным образом выбирают два автомобиля. Найдите вероятность того, что они будут разного цвета. Задача В3 В группе 20 студентов. 8 из них занимаются спортом, 12 изучают английский язык, а 4 студента и занимаются спортом, и изучают английский. Найдите вероятность того, что случайно выбранный студент либо занимается спортом, либо изучает английский. Задача В4 В вазе лежат 30 конфет трех сортов: 10 молочных, 12 фруктовых и 8 ореховых. Наугад берут три конфеты. Найдите вероятность того, что будут взяты конфеты всех трех сортов. Задача №3. Уровень С (высокий уровень) Задача С1 В классе 25 учеников. Из них 15 занимаются музыкой, 12 – спортом, 8 – рисованием. 7 человек занимаются музыкой и спортом, 5 – музыкой и рисованием, 4 – спортом и рисованием, а 3 ученика занимаются всем. Найдите вероятность того, что случайно выбранный ученик занимается хотя бы одним видом деятельности. Задача С2 В урне 20 шаров: красные, синие и зеленые. Вероятность вытащить красный шар равна 0,4, синий – 0,35. Найдите вероятность того, что случайно вытащенный шар окажется зеленым. Сколько зеленых шаров в урне? Задача С3 В соревнованиях участвуют 8 спортсменов. Вероятность победы первого спортсмена 0,3, второго – 0,25, третьего – 0,2. Найдите вероятность того, что победит кто-то из остальных спортсменов. |
Ученик решает базовые задачи на вычисление вероятности простых событий, применяя основные формулы теории вероятностей. Ученик решает задачи среднего уровня сложности, требующие применения нескольких формул теории вероятностей и понимания связей между событиями. Ученик решает сложные задачи, требующие глубокого понимания свойств вероятности и умения комбинировать различные методы решения. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным розам. |
|
|
||
Урок №11
|
Фамилия имя педагога |
|
||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||||
|
Тема урока: |
Условная вероятность: основные понятия |
||||||||||||||||||||||
|
Цели обучения согласно программе |
Интерпретировать понятие условной вероятности |
||||||||||||||||||||||
|
Цель урока |
Интерпретируют условия в задачах |
||||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “случайных цифр” |
Ученики приветствуют и делятся на 3 группы по методу “случайные цифры”. |
Метод оценки «Мороженное» |
|
|||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Работа с таблицой.
Задача №3. Метод «Двери»
Уровень А Задача 1. "Школьный тест" В школе проводится тестирование по математике. Известно, что 80% учеников регулярно готовятся к урокам. Среди подготовленных учеников 90% успешно справляются с тестом, а среди неподготовленных только 30% получают положительную оценку. Ученик успешно написал тест. Какова вероятность того, что он регулярно готовился к урокам? Задача 2. "Медицинский тест" В поликлинике проводится диагностический тест на определенное заболевание. Известно, что 5% пациентов имеют это заболевание. Тест показывает правильный результат у 95% больных людей и у 90% здоровых. Пациент сдал тест, и он оказался положительным. Какова вероятность того, что пациент действительно болен? Задача 3. "Интернет-магазин" В интернет-магазине 70% покупателей оставляют отзывы о товарах. Из тех, кто оставляет отзывы, 85% делают повторные покупки. Среди не оставивших отзывы повторные покупки делают только 40% клиентов. Случайный клиент сделал повторную покупку. Какова вероятность того, что он оставлял отзыв о предыдущей покупке? Задача 4. "Спортивная секция" В спортивной секции 60% учеников регулярно посещают дополнительные тренировки. Среди регулярно тренирующихся 80% успешно сдают нормативы, а среди остальных - только 35%. Случайно выбранный ученик успешно сдал нормативы. Какова вероятность того, что он посещал дополнительные тренировки? Задача 5. "Подготовительные курсы" На подготовительных курсах к экзамену 75% слушателей выполняют все домашние задания. Среди выполняющих домашние задания 95% успешно сдают экзамен, а среди остальных - только 45%. Случайно выбранный слушатель успешно сдал экзамен. Найдите вероятность того, что он выполнял все домашние задания. |
Ученики смотрят видеоматериал и понимают тему. Ученик заполняет таблицу терминов и определений, используя учебный материал и конспект. Ученик решает практические задачи на условную вероятность, применяя формулу Байеса и используя реальные жизненные ситуации. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
https://youtu.be/lejq7LEMCeQ?si=2opSNHO29SBX0GCY
|
|||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным наградам |
|
|
|||||||||||||||||||
Урок №12
|
Фамилия имя педагога |
|
||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||
|
Тема урока: |
Условная вероятность: решение задач |
||||||||||||||||
|
Цели обучения согласно программе |
Синтезировать способы решения |
||||||||||||||||
|
Цель урока |
Синтезируют алгоритм решения задач |
||||||||||||||||
|
Процесс урока: |
|||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой |
Ученики приветствуют и делятся на пары. |
Метод оценки «Звезда» |
|
|||||||||||||
|
Середина урока 35 минут |
Задача №1. Математический диктант.
Задача №2. Сопоставление.
Задача №3. Парная работа.
|
Ученик письменно отвечает на вопросы математического диктанта, демонстрируя знание определений и формул по теме "Условная вероятность". Ученик заполняет таблицу соответствия, устанавливая правильные связи между описанием события и соответствующими формулами. Ученики в парах решают задачи на условную вероятность, обсуждая и проверяя решения друг друга. |
Дескрипторы:
Дескрипторы:
Дескриптор: Правильно применяет формулы Выполняет вычисления без ошибок Проверяет логичность результата |
|
|||||||||||||
|
Конец урока 5 минут |
Рефлексия Вопрос-ответ от учителя -Вам понравился урок? -Чтобы вы хотели еще добавить? -Оцените урок от 1 до 10 |
В конце урока учитель оценивает знания учеников и активность по набранным наградам. |
|
|
|||||||||||||
Урок №13
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Правило сложения вероятностей |
|||||
|
Цели обучения согласно программе |
Анализировать случаи применения правила |
|||||
|
Цель урока |
Анализируют и решают комбинированные задачи |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Выбери цвет”.
|
Каждый ученик выбирает 1 лист с закрытыми глазами из 3 разноцветных бумаг. По цветам ученики делятся на 3 группы. |
Метод оценки «Money» |
|
||
|
Середина 35 урока |
Задача №1. Посмотреть видеоматериал.
Задача №2. "Верно/Неверно" Определите, являются ли утверждения верными или неверными:
Задача №3. Метод «Бургер»
Задача 1. "Кинотеатр" В кинотеатре было проведено исследование среди 400 зрителей. 180 человек предпочитают смотреть фильмы в формате 3D, 220 любят смотреть фильмы в IMAX, а 120 зрителей любят оба формата. Найдите вероятность того, что случайно выбранный зритель: а) предпочитает хотя бы один из форматов б) любит только IMAX в) не интересуется ни одним из этих форматов Задача 2. "Автосалон" В автосалоне из 160 проданных за месяц автомобилей 90 были черного цвета, 70 - с автоматической коробкой передач, а 45 автомобилей были черными и с автоматической коробкой. Найдите вероятность того, что случайно выбранный проданный автомобиль: а) либо черный, либо с автоматической коробкой б) черный, но с механической коробкой в) не черный и не с автоматической коробкой Задача 3. "Кафе" В кафе за день побывало 250 посетителей. 140 человек заказали кофе, 120 заказали десерт, а 80 человек заказали и кофе, и десерт. Найдите вероятность того, что случайно выбранный посетитель: а) заказал что-то одно (либо кофе, либо десерт) б) заказал и кофе, и десерт в) не заказал ни кофе, ни десерт Задача 4. "Туристическая фирма" В туристической фирме из 350 клиентов 180 выбрали отдых на море, 160 выбрали экскурсионные туры, а 70 клиентов выбрали путевки, включающие и море, и экскурсии. Найдите вероятность того, что случайно выбранный клиент: а) выбрал хотя бы один вид отдыха б) выбрал только экскурсионный тур в) выбрал оба вида отдыха |
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует каждое утверждение и определяет его истинность, основываясь на знании правил сложения вероятностей. Ученик решает практические задачи на применение правила сложения вероятностей для совместных событий. |
Дескрипторы:
Дескрипторы:
Выбирает правильную формулу для решения Учитывает вероятность пересечения событий Правильно записывает все необходимые вычисления |
|||
|
Конец урока 5 минут |
Рефлексия «Шарики» |
В конце урока учитель оценивает активность учеников по собранным наградам. |
|
|
||
Урок №14
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Правило умножения вероятностей |
|||||
|
Цели обучения согласно программе |
Оценивать применимость правила |
|||||
|
Цель урока |
Оценивают и выбирают способ решения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
2. Ученики делятся на 2 группы по методу “3 цвета”
|
Ученики настраиваются на урок, разминаются.
Ученики выбирают карты и делятся на группы по цветам. |
Дескриптор
Метод оценки «Клубника» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. Игра «Скачки»
Задача №3. Метод «Баскетбол»
"Асык ойыны" В ауле четыре места, где обычно играют в асық. Айдар ищет Ерлана. Вероятность того, что Ерлан находится в любом из этих мест одинакова. Айдар проверяет места по порядку. После каждой проверки, если он не находит Ерлана, тот может незаметно перебежать в уже проверенное место (вероятность такого события 0,3). Какова вероятность того, что Айдар найдет Ерлана: а) в первом месте б) во втором месте в) в последнем месте? "Айтыс" На айтысе выступают три акына: Әсет, Бақыт и Сәуле. Вероятность победы Әсета в первом туре 0,7, Бақыта - 0,8, Сәуле - 0,9. При этом каждый следующий акын, прежде чем начать свое выступление, слышит предыдущего и может изменить тему своего выступления с вероятностью 0,4, чтобы она перекликалась с предыдущим выступлением. Какова вероятность того, что все три акына выступят на схожие темы? "Кокпар" В соревнованиях по көкпару всадник Нұрлан должен пройти три этапа. Вероятность успешного прохождения первого этапа 0,8. Если всадник успешно проходит этап, его конь получает дополнительную энергию, и вероятность успеха на следующем этапе увеличивается на 10% от предыдущей вероятности. Если всадник не справляется с этапом, то конь устает, и вероятность успеха на следующем этапе уменьшается на 20% от предыдущей. Найти вероятность того, что Нұрлан: а) успешно пройдет все три этапа подряд б) не справится со всеми тремя этапами в) успешно пройдет ровно два этапа |
Ученики смотрят видеоматериал и понимают тему. Ученик выполняет тестовые задания, применяя знания о правиле умножения вероятностей. Ученик решает практические задачи на применение правила умножения вероятностей в различных ситуациях. |
Дескрипторы:
Дескрипторы:
Использует правильные формулы Учитывает изменение вероятностей Составляет план решения |
https://youtu.be/XJoBnZFfois?si=BXxGa-ra8k13yBw_ |
||
|
Конец урока 5минут |
Устная рефлексия |
Учитель в конце урока оценивает активность по количеству награды. |
|
|
||
Урок №15
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула полной вероятности: теория |
|||||
|
Цели обучения согласно программе |
Исследовать структуру формулы |
|||||
|
Цель урока |
Исследуют компоненты формулы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветствие и ознакомление с новой темой. 2. Ученики делятся на 3 группы по методу “колесо” |
Ученики концентрируются на уроки делятся на группы. |
Дескриптор
Метод оценки «Like» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод Джигсо Объясните, что такое формула полной вероятности и в каких ситуациях она используется. Приведите примеры из жизни, где данная формула может применяться. Задача №3. Тестовая задача. Задание 1 Формула полной вероятности используется, когда: A) События зависимы B) События независимы C) Событие может произойти совместно с одним из полной группы событий D) События несовместны E) События противоположны Задание 2 В формуле полной вероятности P(A) = ∑P(Hi)P(A|Hi) числа P(Hi) называются: A) Условными вероятностями B) Вероятностями гипотез C) Полными вероятностями D) Случайными величинами E) Классическими вероятностями Задание 3 Сумма вероятностей гипотез в формуле полной вероятности должна быть равна: A) 0 B) 0,5 C) 1 D) 2 E) Любому числу от 0 до 1 Задание 4 Если событие A может произойти только при осуществлении одной из трёх гипотез H₁, H₂, H₃, то формула полной вероятности имеет вид: A) P(A) = P(H₁) + P(H₂) + P(H₃) B) P(A) = P(H₁)P(A|H₁) + P(H₂)P(A|H₂) + P(H₃)P(A|H₃) C) P(A) = P(H₁) × P(H₂) × P(H₃) D) P(A) = P(A|H₁) + P(A|H₂) + P(A|H₃) E) P(A) = P(H₁) × P(A|H₁) Задание 5 Условные вероятности P(A|Hi) в формуле полной вероятности - это: A) Вероятность гипотезы Hi B) Вероятность события A при условии появления гипотезы Hi C) Сумма вероятностей всех гипотез D) Произведение вероятностей события и гипотезы E) Отношение числа благоприятных исходов к общему числу исходов |
Ученики смотрят видеоматериал и понимают тему. Ученик объясняет, что такое формула полной вероятности, и может описать ее словами. Ученик выполняет тестовых задач. |
Дескрипторы:
Ученик приводит хотя бы один пример из жизни, где можно использовать формулу полной вероятности. Выбирает правильный вариант. |
|||
|
Конец урока 5 минут |
Рефлексия «Мишень» |
В конце урока учитель оценивает каждую группу по набранным наградам. |
|
|
||
Урок №16
|
Фамилия имя педагога |
|
|||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||
|
Тема урока: |
Формула полной вероятности: практика |
|||||||||||||||||
|
Цели обучения согласно программе |
Применять формулу в различных ситуациях |
|||||||||||||||||
|
Цель урока |
Применяют формулу к практическим задачам |
|||||||||||||||||
|
Процесс урока: |
||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие через метод “Время добрых пожелании”. Ученики желают приятные пожелания на день. 2. Ученики делятся на 2 группы по методу “Колесо фортуны” https://clck.ru/3A5caP |
Ученики настраиваются к уроку с хорошим настроением и делятся на 2 группы. |
Метод оценки «Леденец» |
|
||||||||||||||
|
Середина урока 35 минут |
Задача №1. Игра "Установите соответствие"
Задача 2. "Заполните пропуски" В магазин поступают товары от трех поставщиков. От первого поставщика приходит ___ % всех товаров, от второго - 35%, от третьего - остальные. Вероятность брака в товарах первого поставщика составляет 0,02, второго - ___, третьего - 0,03. Используя формулу полной вероятности, найдите вероятность того, что случайно выбранный товар окажется бракованным, если известно, что эта вероятность равна 0,025. Заполните пропущенные числа и решите задачу. Задача 3. "Практическая задача с выбором" Ақжол готовится к соревнованиям по национальной борьбе құрес. У него есть три тренера:
При подготовке с каждым тренером вероятность победы Ақжола в соревновании различна:
Найдите: а) Вероятность победы Ақжола в соревновании б) Если Ақжол победил, то какова вероятность, что его тренировал Асқар-ага? в) Какой тренер наиболее вероятно подготовил Ақжола, если он проиграл? |
Ученик анализирует предложенные формулы и их описания, устанавливает логические связи между ними. Ученик находит неизвестные значения и решает задачу, используя формулу полной вероятности. Ученик решает многоэтапную задачу, выбирая нужные формулы для каждой части. |
Метод оценки «Леденец» Дескрипторы:
Дескрипторы:
Правильно выбирает формулы для каждого пункта Обосновывает свой выбор Составляет план решения |
|
||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||||||||||||||
Урок №17
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Байеса: основные понятия |
|||||
|
Цели обучения согласно программе |
Интерпретировать смысл формулы |
|||||
|
Цель урока |
Интерпретируют условия применения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Знакомтсво с новой темой 2.Ученики делятся на группы 2 группы методом “Стрельба глазами”. |
Участники встают в круг, опустив глаза. По сигналу учителя все поднимают глаза, стремясь встретиться с кем-то взглядом. Если это удалось, то образовавшиеся пары покидают круг. Игра продолжается до тех пор, пока все участники не окажутся разбиты по парам. |
Дескриптор
Оценка методом «Букет бабочек» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Исправь ошибку" Даны следующие утверждения о формуле Байеса. Найдите ошибки и исправьте их:
Задача 3. "Медицинская диагностика" В поликлинике используется новый тест для диагностики заболевания. Составьте задачу для своих одноклассников, используя следующие данные:
Задача должна включать:
|
Ученики смотрят видеоматериал и понимают тему. Ученик анализирует каждое утверждение, находит ошибки и исправляет их, опираясь на теорию. Ученик составляет задачу на применение формулы Байеса, используя предложенные данные. |
Дескрипторы:
Знание формулы Байеса Понимание её применения Различение видов вероятностей |
https://youtu.be/LYTGddixYfw?si=jRhzcZl396B7WJxq
|
||
|
Конец урока 5 минут |
Рефлексия «Лестница успеха» |
В конце урока учитель оценивает активность по набранным наградам. |
|
|
||
Урок №18
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Байеса: решение задач |
|||||
|
Цели обучения согласно программе |
Синтезировать методы решения |
|||||
|
Цель урока |
Синтезируют способы применения формулы |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Эмоциональная подготовка учеников. Время разминки!
|
Ученики повторяют и разминаются, и заряжаются энергией перед занятием. |
Метод оценки «Шарики» |
|
||
|
Середина урока 35 минут |
Задач №1. "Логическая цепочка" Расположите этапы решения задачи в правильном порядке:
Задача №2. В соревнованиях по тоғыз құмалақ участвуют три спортсмена: Арман, Бауыржан и Сәкен. Вероятность участия в финале для Армана - 0,5, для Бауыржана - 0,3, для Сәкена - 0,2. Вероятность победы в финале составляет 0,8 для Армана, 0,7 для Бауыржана и 0,9 для Сәкена. Если известно, что соревнование выиграно, определите: а) Вероятность того, что победил Арман б) Кто наиболее вероятно стал победителем? Задача №3. Создайте задачу на применение формулы Байеса, используя следующий шаблон: В ауле есть три табуна лошадей. В первом табуне ___ лошадей (впишите число), во втором ___, в третьем ___. Вероятность того, что скакун для байги будет выбран из каждого табуна, пропорциональна количеству лошадей в нем. Вероятность победы в байге для лошади из первого табуна ___, из второго ___, из третьего ___. Скакун победил в байге. Какова вероятность, что он был из ... табуна? |
Ученик анализирует этапы решения и выстраивает их в логическую последовательность. Ученик решает задачу с применением формулы Байеса, используя данные о национальной игре. Ученик составляет собственную задачу по шаблону, подбирая реалистичные числовые данные. |
Метод оценки «Шарики» Дескрипторы:
Дескриптор:
Дескриптор:
|
|
||
|
Конец урока 5 минут |
Рефлексия «Дерево успеха» |
В конце урока учитель оценивает активность ученика по количеству собранной награды. |
|
|
||
Урок №19
|
Фамилия имя педагога |
|
|||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||
|
Тема урока: |
Схема Бернулли |
|||||||||||||||||||||||
|
Цели обучения согласно программе |
Анализировать условия применения схемы |
|||||||||||||||||||||||
|
Цель урока |
Анализируют и составляют схему решения |
|||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Расчет”. |
Это самый элементарный способ. Произвести расчет на «первый-второй», «первый-второй-третий» и т. д. в зависимости от того, сколько требуется групп. |
Дескриптор
Метод оценки «Стикеры» |
|
||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Тестовая задача. 1. Схема Бернулли - это: A) Последовательность взаимозависимых испытаний B) Последовательность независимых испытаний с двумя исходами C) Последовательность зависимых испытаний с тремя исходами D) Одно испытание с двумя исходами E) Испытание с множеством исходов 2. В формуле P(X=k) = C(n,k)·pᵏ·qⁿ⁻ᵏ для схемы Бернулли, q равно: A) Вероятности успеха B) 1 + p C) 1 - p D) p² E) p/n 3. Локальная формула Муавра-Лапласа применяется, когда: A) n < 10 B) n > 100 C) np < 10 D) n = 100 E) p = q 4. В схеме Бернулли вероятность успеха p: A) Меняется от испытания к испытанию B) Зависит от числа испытаний C) Остается постоянной во всех испытаниях D) Равна 1 E) Равна 0 5. Наивероятнейшее число успехов k₀ в схеме Бернулли определяется неравенством: A) np - q ≤ k₀ ≤ np + p B) np - p ≤ k₀ ≤ np + q C) np - 1 ≤ k₀ ≤ np + 1 D) np ≤ k₀ ≤ np + 1 E) np – 2 ≤ k₀ ≤ np + 2 Задача №3. Работа с таблицой.
|
Ученики смотрят видеоматериал и понимают тему. Ученик решает тестовые задания, выбирая правильные ответы на основе знания теории схемы Бернулли. Ученик заполняет таблицу соответствия, устанавливая связи между терминами, их определениями и примерами. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
|||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает по набранным наградам |
|
|
||||||||||||||||||||
Урок №20
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Формула Бернулли и её применение |
|||||
|
Цели обучения согласно программе |
Применять формулу в различных задачах |
|||||
|
Цель урока |
Применяют формулу в практических задачах |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 2 группы по методу “Собери открытку”. |
Перед игрой готовятся открытки по количеству будущих команд. Одну открытку учитель разрезает на столько частей, сколько человек должно быть в одной команде. Предварительно перемешав разрезанные открытки, ведущий раздает их участникам. По сигналу команды организуются, составляя картинки. |
Метод оценивания «Мяч» |
|
||
|
Середина урока 35 минут |
Уровень А (базовый уровень) Задача А1. "Национальные игры" В соревнованиях по асық ату игрок делает 5 бросков. Вероятность успешного броска 0,6. Найти вероятность: а) двух успешных бросков б) не менее трех успешных бросков в) хотя бы одного успешного броска Задача А2. "Контроль качества" На фабрике по производству қамшы (плетей) вероятность изготовления изделия высшего качества равна 0,8. В партии 4 изделия. Найти вероятность того, что высшего качества будут: а) все изделия б) ровно три изделия в) не более двух изделий Задача А3. "Стрельба из лука" Вероятность попадания в цель при стрельбе из традиционного лука равна 0,7. Производится 6 выстрелов. Найти вероятность: а) четырех попаданий б) не менее пяти попаданий в) от трех до пяти попаданий Уровень В (повышенный уровень) Задача В1. "Спортивные соревнования" В турнире по тоғыз құмалақ спортсмен проводит 8 игр. Вероятность победы в каждой игре 0,75. Найти вероятность того, что он: а) победит ровно в 6 играх б) победит не менее чем в 7 играх в) одержит четное число побед Задача В2. "Производство сувениров" На предприятии изготавливают национальные сувениры. Вероятность брака 0,1. В партии 10 изделий. Найти: а) вероятность наличия двух бракованных изделий б) наивероятнейшее число бракованных изделий в) вероятность наличия наивероятнейшего числа бракованных изделий Задача В3. "Ювелирные изделия" Мастер изготавливает 12 серебряных колец. Вероятность изготовления кольца высшего качества 0,85. Найти: а) вероятность того, что высшего качества будут ровно 10 колец б) математическое ожидание числа колец высшего качества в) наивероятнейшее число колец высшего качества |
Ученик решает задачи, применяя формулу Бернулли для простых случаев. Ученик решает более сложные задачи с применением дополнительных формул и свойств. |
Метод оценивания «Мяч» Дескриптор: Использует формулу Бернулли Вычисляет число сочетаний Выполняет расчеты без ошибок Дескриптор: Проводит сложные вычисления Проверяет промежуточные результаты Анализирует полученные ответы |
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока индивидуально оценивает активность по набранным наградам. |
|
|
||
Урок №21
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Наивероятнейшее число успехов |
|||||
|
Цели обучения согласно программе |
Вычислять вероятность успехов |
|||||
|
Цель урока |
Вычисляют и интерпретируют результаты |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветствие и ознакомление с новой темой. 2. Ученики делятся на 3 группы по методу “колесо” |
Ученики концентрируются на уроки делятся на группы. |
Дескриптор
Метод оценки «Звезда» |
|
||
|
Середина урока 35 минут |
I. Тестовые задания
II. Незавершенные утверждения
III. Контекстные задачи
ІV. Логические задачи
|
Ученик решает тестовые задания, применяя формулу Бернулли для вычисления вероятностей. Ученик формулирует основные теоретические положения схемы Бернулли. Ученик решает практические задачи, используя формулу Бернулли в конкретных ситуациях. Ученик анализирует теоретические аспекты схемы Бернулли, применяя логическое мышление. |
Дескрипторы:
Дескрипторы:
Выбирает нужную формулу для каждого пункта Правильно подставляет значения Учитывает все условия задачи Составляет план решения Проводит необходимые вычисления Формулирует логические выводы |
|
||
|
Конец урока 5 минут |
Рефлексия «Мозг» |
В конце урока учитель оценивает активность учеников по набранным наградам. |
|
|
||
Урок №22
|
Фамилия имя педагога |
|
|||||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||||||
|
Тема урока: |
Случайные величины: основные понятия |
|||||||||||||||||||||||||||
|
Цели обучения согласно программе |
Классифицировать случайные величины |
|||||||||||||||||||||||||||
|
Цель урока |
Классифицируют виды величин |
|||||||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||||||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. Эмоциональный разряд. Время добрых пожелании.
Каждый ученик желает своему соседу по парте добрые слова. |
Ученик обращается к своим друзьям с хорошим пожеланием. |
Оценивание по методу «Сердце»
|
|
||||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Теоретический диктант Дайте определения следующих понятий:
Задача №3. Задание на соответствие "Найди пару" Соедините термин и его пример:
Задача №4. Практическая задача "Асык ату" В национальной игре асык ату игрок может выиграть 1, 2 или 3 асыка за один бросок с вероятностями 0,5, 0,3 и 0,2 соответственно. Задания:
Задача №5. "Исправь ошибку" В таблице распределения случайной величины допущены ошибки. Найдите и исправьте их:
Задача №6. Визуальное задание "Построй график" Постройте графики:
Задача №7. Контекстная задача "Национальные блюда" В ресторане казахской кухни заказы на бешбармак поступают случайным образом. За час может быть 0, 1, 2 или 3 заказа с вероятностями 0,1, 0,3, 0,4 и 0,2 соответственно. Требуется:
|
Ученики смотрят видеоматериал и понимают тему. Ученик письменно формулирует определения основных понятий теории случайных величин. Ученик устанавливает соответствие между терминами и их примерами. Ученик решает практические задачи на составление закона распределения и исправление ошибок. Ученик строит графики распределения вероятностей. Ученик решает комплексную задачу с практическим контекстом. |
Дескрипторы:
Дескрипторы:
Дескрипторы: Различает типы случайных величин Понимает сущность каждого термина Правильно соотносит теорию с практическими примерами Дескрипторы:
Дескрипторы:
Записывает закон распределения Вычисляет характеристики Строит требуемые графики |
|||||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Метод “Светофор”: студенты показывают зеленую карточку, если урок был понятен, желтую - если остались вопросы, красную - если тема требует повторного объяснения. |
В конце урока учитель оценивает активность каждого ученика по заработанным сердцам. |
|
|
||||||||||||||||||||||||
Урок №23
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Дискретные случайные величины |
|||||
|
Цели обучения согласно программе |
Исследовать характеристики величин |
|||||
|
Цель урока |
Исследуют и описывают свойства |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Психическая и эмоциональная подготовка к уроку. |
Разминка для улучшения настроения и самочувствия ученика |
Оценивание по методу «Медаль» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Игра «Случайное колесо»
Задача №3. Метод «Банкомат»
Задача 1. "Конный спорт" В соревнованиях по кокпар участвуют 3 команды. Вероятность победы первой команды 0,5, второй - 0,3, третьей - 0,2. Составить закон распределения числа очков, если за победу дается 2 очка. Задача 2. "Стрелковый тир" Стрелок делает два выстрела по мишени. Вероятность попадания при каждом выстреле 0,7. Составить закон распределения числа попаданий и найти математическое ожидание. Задача 3. "Домбра" В музыкальной школе ученик разучивает новый кюй. Вероятность безошибочного исполнения первой части 0,8, второй части 0,7. Найти закон распределения числа безошибочно исполненных частей произведения. Задача 4. "Национальные украшения" Мастер изготавливает сырға (серьги). Вероятность изготовления изделия высшего качества 0,9. В партии 3 изделия. Составить закон распределения числа изделий высшего качества в партии. Задача 5. "Спортивная школа" В спортивной секции по қазақша күрес тренируются 4 борца. Вероятность победы в схватке для каждого 0,6. Найти математическое ожидание числа побед в день, если каждый проводит одну схватку. Задача 6. "Чайхана" В чайхане посетитель может заказать один из трех видов плова. Вероятность заказа первого вида 0,5, второго - 0,3, третьего - 0,2. Стоимость первого вида 2000 тенге, второго - 2500 тенге, третьего - 3000 тенге. Найти математическое ожидание выручки с одного заказа. |
Ученики смотрят видеоматериал и понимают тему. Играют игру. Решают текстовых задач. |
Дескриптор: Выписывает определения основных понятий. Дескриптор: Правильно отвечает на вопросы. Дескриптор: Правильно решает текстовых задач. |
https://youtu.be/EMGLxRoZTfw?si=9V5ecNfIYU4Tj3kq |
||
|
Конец урока 5 минут |
Рефлексия Метод “Светофор”: студенты показывают зеленую карточку, если урок был понятен, желтую - если остались вопросы, красную - если тема требует повторного объяснения. |
В конце урока учитель оценивает активность каждого ученика по медалям |
|
|
||
Урок №24
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Непрерывные случайные величины |
|||||
|
Цели обучения согласно программе |
Сравнивать виды случайных величин |
|||||
|
Цель урока |
Сравнивают характеристики величин |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. Ученики делятся на 2 они выбирают названия геометрических форм по методу “жребии” |
Ученики онлайн выбирают жребий номеров и делятся на группы. |
Дескриптор
Метод оценки «Букет цветок» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Заполни пропуски" Заполните пропуски в утверждениях о непрерывных случайных величинах:
Задание 3. "Практическая задача" Время ожидания автобуса на остановке является непрерывной случайной величиной, равномерно распределенной на отрезке [0; 15] минут. Найти: а) функцию плотности вероятности б) вероятность того, что ждать придется не более 5 минут в) математическое ожидание времени ожидания Задание 4. "Историческая задача" Метод «Google»
Изучите историю появления нормального распределения и ответьте на вопросы:
Задание 5. "Исследовательская работа" Измерьте рост 30 учеников вашего класса. Постройте гистограмму распределения роста и проверьте, можно ли считать рост нормально распределенной величиной. |
Ученики смотрят видеоматериал и понимают тему. Ученик заполняет пропуски, используя знания о свойствах непрерывных случайных величин. Ученик решает задачу, применяя формулы для равномерного распределения. Ученик изучает историческую информацию и отвечает на вопросы. Ученик проводит исследование, собирает и анализирует данные. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
Строит гистограмму Проверяет свойства нормального распределения Делает выводы |
https://youtu.be/SgfGqNB6qoA?si=vTRZeQl6GNeQBGJo
|
||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает активность учеников по количеству цветочков и оценкам учеников парной работы |
|
|
||
Урок №25
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Числовые характеристики случайных величин |
|||||
|
Цели обучения согласно программе |
Вычислять основные характеристики |
|||||
|
Цель урока |
Вычисляют параметры распределений |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы через метод “Колесо фортуны”. https://clck.ru/3AGMsQ?clckid=2ff9c35f
|
Ученики делятся на 3 группы методу учителя. |
Оценка по методу «Разбалловка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Бинго»
"Турнир по тогыз кумалак" В турнире участвуют три игрока. Вероятность победы первого игрока 0,5, второго - 0,3, третьего - 0,2. За победу дается 10 баллов. Найти математическое ожидание числа баллов победителя. "Национальные сувениры" Мастер изготавливает сувениры трех видов. Вероятность изготовления первого вида 0,4, второго - 0,35, третьего - 0,25. Стоимость первого вида 2000 тенге, второго - 3000 тенге, третьего - 4000 тенге. Найти математическое ожидание и дисперсию стоимости случайно выбранного сувенира. "Спортивные соревнования" В соревнованиях по қазақша күрес спортсмен проводит три схватки. Вероятность победы в каждой схватке 0,7. За победу дается 5 очков, за поражение 0 очков. Найти математическое ожидание и среднее квадратическое отклонение набранных очков. "Стрельба из лука" Лучник делает два выстрела. Вероятность попадания в цель при первом выстреле 0,8, при втором - 0,75. За каждое попадание начисляется 10 баллов. Найти дисперсию числа набранных баллов. "Чайхана" В чайхане клиент заказывает 1, 2 или 3 блюда с вероятностями 0,3, 0,5 и 0,2 соответственно. Среднее время приготовления одного блюда 15 минут. Найти математическое ожидание времени выполнения заказа. "Ювелирная мастерская" Ювелир изготавливает украшения. Вероятность изготовления изделия высшего качества 0,85, первого сорта - 0,12, второго сорта - 0,03. Стоимость изделий соответственно 50000, 35000 и 20000 тенге. Найти математическое ожидание и дисперсию стоимости изделия. Задача №3. Тестовые задания
|
Ученики смотрят видеоматериал и понимают тему. Ученик решает практические задачи на вычисление числовых характеристик случайных величин. Ученик выбирает правильные ответы на тестовые вопросы, демонстрируя знание основных формул и свойств числовых характеристик случайных величин. |
Дескриптор: Находит математическое ожидание Вычисляет дисперсию (если требуется) Находит среднее квадратическое отклонение Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия Ученики в конце урока оценивают урок через онлайн рефлекс. |
В конце урока учитель оценивает активность учеников по набранным баллам. |
|
|
||
Урок №26
|
Фамилия имя педагога |
|
|||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||||||||||
|
Тема урока: |
Математическое ожидание и свойства |
|||||||||||||||||||||||||
|
Цели обучения согласно программе |
Доказывать свойства мат.ожидания |
|||||||||||||||||||||||||
|
Цель урока |
Доказывают и применяют свойства |
|||||||||||||||||||||||||
|
Процесс урока: |
||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||||||||||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу ‘Собери открытку”. |
Перед игрой готовятся открытки по количеству будущих команд. Одну открытку ведущий разрезает на столько частей, сколько человек должно быть в одной команде. Предварительно перемешав разрезанные открытки, ведущий раздает их участникам. По сигналу команды организуются, составляя картинки.
|
Дескриптор
Метод оценки «Фрукты» |
|
||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. «Найди ошибку» Проанализируйте решение задачи и найдите ошибки: Дано: X и Y – независимые случайные величины M(X) = 2, M(Y) = 3 Найти: M(2X + 3Y – 1) Решение ученика: M(2X + 3Y – 1) = 2M(X) + 3M(Y) – 1 = 2·2 + 3·3 – 1 = 4 + 9 – 1 = 12 Задача №3. Заполните таблицу для случайной величины X:
Задача №4. Метод «Кто быстрый?» Задача 1. "Байтерек кафе" В национальном кафе "Байтерек" посетитель может заказать:
Найти:
Задача 2. "Ярмарка ремесленников" На ярмарке мастер продает традиционные казахские украшения:
Вероятность продажи сырга - 0,5, билезик - 0,3, алка - 0,2. Найти математическое ожидание дневной выручки, если в среднем совершается 5 покупок. Задача 3. "Скачки" В соревнованиях по байге участвуют три скакуна:
Призовой фонд:
Найти математическое ожидание выигрыша для каждого скакуна. Задача 4. "Асык ату" В соревнованиях по асык ату игрок может выиграть:
Найти:
|
Ученики смотрят видеоматериал и понимают тему. Ученик найдет ошибку. Заполняют таблицу. Ученики решают текстовых задач. |
Метод оценки «Фрукты» Дескрипторы: Выписывают основных определения основных понятий. Праавильно найдет ошибку. Правильно заполняют таблицу. Правильно выполняют вычислению. |
|||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает работу групп и учеников по копилкам. |
|
|
||||||||||||||||||||||
Урок №27
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Дисперсия и среднее квадратическое отклонение |
|||||
|
Цели обучения согласно программе |
Анализировать меры разброса |
|||||
|
Цель урока |
Анализируют и вычисляют параметры |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с практической работой. 2.Эмоцианальная подготовка учеников. Ученики делятся с хорошими пожеланиями на день. 3.Ученики делятся на 3 группы по методу Жребий
|
Ученики делятся хорошими эмоциями с друзьями. После выбирают листы с номерами и делятся на группы. |
Дескриптор
Индивидуальная оценка ученика по методу «Подарка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Уровень А. Задача 1. "Бауырсаки" В пекарне изготавливают бауырсаки. Их количество в одной порции может быть:
Найти:
Задача 2. "Урок домбры" Время выполнения домашнего задания по игре на домбре составляет:
Определить:
Задача 3. "Магазин сувениров" Ежедневная выручка магазина национальных сувениров может составлять:
Найти:
Задача 4. "Конные скачки" Время прохождения дистанции скакуном составляет:
Вычислить:
Задача 5. "Мастерская по пошиву" Время пошива одного камзола может быть:
Определить:
Задача №3. Ввод ответа.
|
Ученики смотрят видеоматериал и понимают тему. Решают задачи. Решают задачи, играя игру. |
Индивидуальная оценка ученика по методу «Подарка» Дескрипторы: Выписывают основных определения основных понятий. Правильно выполняют вычислений. Играют интеллектуальную игру. |
|||
|
Конец урока 5 минут |
Учитель проводит рефлексию, спрашивая учеников, что нового они узнали и что показалось наиболее интересным. Ученики устно делятся своими впечатлениями. |
В конце урока учитель оценивает каждую группу по набранным наградам. |
|
|
||
Урок №28
|
Фамилия имя педагога |
|
||||||||||||||||||||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||||||||||||||||||||
|
Тема урока: |
Биномиальное распределение |
||||||||||||||||||||||||||||||||||||||
|
Цели обучения согласно программе |
Исследовать свойства распределения |
||||||||||||||||||||||||||||||||||||||
|
Цель урока |
Исследуют характеристики распределения |
||||||||||||||||||||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||||||||||||||||||||
|
Начало урока 5 минут |
1.Ознакомление с новой темой. 2.Ученики делятся на 2 группы по методу “Сегментация круга” |
Группу можно разделить пополам, проведя воображаемый диаметр круга от себя (ведущего) к участнику, сидящему напротив. В случае, если требуется более двух команд, то круг просто разбивается на нужное число сегментов. |
Метод оценки +1 награда за каждый правильный ответ.
|
|
|||||||||||||||||||||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Работа с терминами.
Задача №3. Метод «» Задача 1. "Производство кумыса" На предприятии по производству кумыса вероятность того, что бутылка будет заполнена точно до метки, равна 0,9. Найти вероятность того, что из 6 случайно выбранных бутылок: а) ровно 5 заполнены правильно б) хотя бы 5 заполнены правильно в) все заполнены правильно Задача 2. "Ювелирная мастерская" Мастер изготавливает национальные серебряные украшения. Вероятность изготовления изделия высшего качества 0,85. В партии 8 изделий. Найти: а) наивероятнейшее число изделий высшего качества б) вероятность получения наивероятнейшего числа изделий высшего качества в) математическое ожидание числа качественных изделий Задача 3. "Стрельба из лука" На соревнованиях по стрельбе из традиционного лука вероятность попадания в цель для опытного лучника составляет 0,7. Лучник делает 10 выстрелов. Найти: а) вероятность 7 попаданий б) математическое ожидание числа попаданий в) дисперсию числа попаданий Задача 4. "Национальные орнаменты" При вышивании национального орнамента вероятность правильного выполнения одного элемента равна 0,95. Мастерица выполняет 12 элементов. Найти: а) вероятность того, что все элементы выполнены правильно б) вероятность того, что правильно выполнено не менее 10 элементов в) наивероятнейшее число правильно выполненных элементов Задача 5. "Сборка юрты" При установке юрты вероятность правильной установки одного кереге (решетчатой секции) равна 0,8. Всего устанавливается 6 кереге. Определить: а) вероятность того, что все кереге установлены правильно б) математическое ожидание числа правильно установленных кереге в) среднее квадратическое отклонение |
Ученики смотрят видеоматериал и понимают тему. Дает определения терминам. Решают задачи. |
Метод оценки +1 награда за каждый правильный ответ. Дескрипторы: Выписывают основных определения основных понятий. Дескриптор: Правильно заполняют таблицу. Правильно решают задачи. |
||||||||||||||||||||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Ученики оценивают урок по 10 бальной шкале. |
В конце урока учитель оценивает каждую группу и ученика по набранным наградам. |
|
|
|||||||||||||||||||||||||||||||||||
Урок №29
|
Фамилия имя педагога |
|
||||||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
|||||||||||||||||||
|
Тема урока: |
Распределение Пуассона |
||||||||||||||||||||
|
Цели обучения согласно программе |
Применять распределение в задачах |
||||||||||||||||||||
|
Цель урока |
Применяют формулы распределения |
||||||||||||||||||||
|
Процесс урока: |
|||||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
|||||||||||||||||
|
Начало урока 5 минут |
Знакомство с новой темой. Эмоциональная подготовка учеников через разминки.
|
Ученики настраиваются на урок, разминаются. |
Дескриптор
Метод оценки «Апельсин» |
|
|||||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задание 2. "Историческое исследование" Подготовьте краткое сообщение:
Задание 3. «Формула и её компоненты» Заполните таблицу для формулы Пуассона P(X=k) = (λᵏe⁻λ)/k!
Задание 4. "Практическая задача" В национальной кондитерской в среднем продается 4 торта "Шакарпаре" в час. Найти вероятность того, что за час будет продано: а) ровно 3 торта б) не более 2 тортов в) более 5 тортов |
Ученики смотрят видеоматериал и понимают тему. Ученик изучает историю открытия распределения Пуассона и готовит сообщение. Ученик анализирует формулу Пуассона и описывает все её компоненты. Ученик решает задачу, применяя формулу Пуассона. |
Дескрипторы:
Дескрипторы:
Дескрипторы:
|
||||||||||||||||||
|
Конец урока 5 минут |
Рефлексия Учитель раздает стикеры-листочки. Ученики пишут мнения об уроке анонимно и клеят на лучики солнца. |
Учитель в конце урока оценивает активность и количество листочков. |
|
|
|||||||||||||||||
Урок №30
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Нормальное распределение |
|||||
|
Цели обучения согласно программе |
Интерпретировать график распределения |
|||||
|
Цель урока |
Интерпретируют параметры распределения |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Ознакомление с темой. 2. Ученики делятся на пары по желанию (мини группа). |
Ученики знакомятся и делятся на мини группы из 2 человек. |
Дескриптор
Метод оценивания «Мяч»
|
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Острый ум» Задача 1. "Ежедневная выручка" Ежедневная выручка в магазине национальных сувениров распределена нормально со средним значением 80000 тенге и средним квадратическим отклонением 5000 тенге. Найти:
Задача 2. "Производство курта" На предприятии по производству курта масса одной упаковки распределена нормально со средним значением 200 г и средним квадратическим отклонением 3 г. Определить:
Задача 3. "Национальная одежда" Длина национального камзола, производимого на фабрике, распределена нормально со средним значением 100 см и средним квадратическим отклонением 2 см. Вычислить:
Задача 4. "Спортивные соревнования" Результаты спортсменов в беге на 100 метров распределены нормально со средним значением 12 секунд и средним квадратическим отклонением 0,5 секунды. Найти:
Задача 5. "Выставочный центр" Время осмотра экспозиции в музее национального искусства распределено нормально со средним значением 45 минут и средним квадратическим отклонением 10 минут. Определить:
Задача №3. Тестовая задача.
A) Только математическим ожиданием B) Только дисперсией C) Математическим ожиданием и дисперсией D) Только средним квадратическим отклонением E) Медианой и модой
|
Ученики смотрят видеоматериал и понимают тему. Ученики решают контекстных задач. Выполняют тестовых задач. |
Метод оценивания «Мяч» Дескрипторы: Выписывают основных определения основных понятий. Правильно решают задачи. Выбирают правильный ответ. |
https://youtu.be/5rRQnN8Q_sc?si=jqXJJx4-uX8pMTK4
|
||
|
Конец урока 5 минут |
Рефлексия «Незаконченное предложение» |
В конце урока учитель оценивает обучающихся по набранным наградам и активности. |
|
|
||
Урок №31
|
Фамилия имя педагога |
|
|||||||||||||||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||||||||||||||
|
Тема урока: |
Закон больших чисел |
|||||||||||||||||
|
Цели обучения согласно программе |
Анализировать следствия закона |
|||||||||||||||||
|
Цель урока |
Анализируют примеры применения |
|||||||||||||||||
|
Процесс урока: |
||||||||||||||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||||||||||||||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “барабан” |
Ученики приветствуют и делятся на 3 группы. |
Дескриптор
Метод оценивания «Букет цветок» |
|
||||||||||||||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Таблица терминов и определений
Задача №3. Решение задач. Задача 1. "Контроль качества" На фабрике по производству национальных украшений проверяется качество изделий. По теоретическим расчетам, вероятность брака составляет 0,1. Какова вероятность того, что в партии из 1000 изделий относительная частота бракованных изделий отклонится от теоретической вероятности не более чем на 0,02? Задача 2. "Социологический опрос" При опросе жителей города об их отношении к строительству нового культурного центра опрашивается 900 человек. Какое минимальное количество человек нужно опросить, чтобы с вероятностью 0,95 относительная частота положительных ответов отклонялась от истинной вероятности не более чем на 0,05? Задача 3. "Спортивные достижения" В спортивной секции по национальной борьбе қазақша күрес тренируются 500 спортсменов. Вероятность победы в схватке для каждого спортсмена 0,6. Найти вероятность того, что среднее число побед в серии схваток отклонится от математического ожидания не более чем на 0,05. Задача 4. "Метеорологические наблюдения" Метеостанция проводит измерения температуры воздуха. Известно, что среднее квадратическое отклонение измерений составляет 2°C. Сколько измерений нужно провести, чтобы с вероятностью 0,99 среднее арифметическое температуры отклонялось от истинного значения не более чем на 0,5°C? |
Ученики смотрят видеоматериал и понимают тему. Ученик изучает и заполняет таблицу терминов и определений. Ученик решает задачу о контроле качества с применением закона больших чисел. |
Дескрипторы: Выписывают основных определения основных понятий. Дескрипторы:
Дескриптор: Правильно выбирает нужную формулу Подставляет значения Выполняет вычисления |
|||||||||||||||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным розам. |
|
|
||||||||||||||
Урок №32
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Генеральная совокупность и выборка |
|||||
|
Цели обучения согласно программе |
Сравнивать характеристики совокупностей |
|||||
|
Цель урока |
Сравнивают параметры выборок |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики делятся на 3 группы по методу “случайных цифр” |
Ученики приветствуют и делятся на 3 группы по методу “случайные цифры”. |
Метод оценки «Мороженное» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Групповая работа. Задача 1. "Школьный опрос" В школе 500 учеников (генеральная совокупность). Для изучения отношения к национальным видам спорта было опрошено 50 случайно выбранных учеников (выборка). Среди опрошенных 35 учеников проявили интерес к национальным видам спорта.
Задача 2. "Статистика предприятия" На фабрике по производству национальных сувениров работает 300 человек (генеральная совокупность). Для исследования стажа работы случайным образом отобрали 30 сотрудников (выборка). Получены следующие данные о стаже:
Задача 3. "Контроль качества" На складе хранится 1000 изделий (генеральная совокупность). Для проверки качества отобрано 100 изделий (выборка). Среди них обнаружено 5 бракованных.
Задача 4. "Социологическое исследование" В городе проживает 50000 человек (генеральная совокупность). Для изучения общественного мнения о проведении национального праздника Наурыз было опрошено 500 человек (выборка). 400 опрошенных поддержали традиционный формат праздника, 80 предложили современный формат, остальные воздержались. Построить интервальную оценку для доли поддерживающих традиционный формат во всем городе. Задача 5. "Спортивная статистика" В спортивной школе занимается 400 учеников (генеральная совокупность). Для анализа физической подготовки случайным образом отобрали 40 учеников (выборка) и измерили время бега на 100 метров. Средний результат в выборке составил 14,5 секунд, среднее квадратическое отклонение 1,2 секунды. Построить доверительный интервал для среднего времени бега всех учеников школы с надежностью 0,95. Задача 6. "Анализ цен" В городе 200 магазинов национальной одежды (генеральная совокупность). Для анализа цен случайным образом выбрали 20 магазинов (выборка) и зафиксировали цену на традиционный камзол. Получены следующие данные:
Задача №3. Метод «Арбуз»
|
Ученики смотрят видеоматериал и понимают тему. Решают текстовых задач. Отвечают на вопросы. |
Метод оценки «Мороженное» Дескрипторы: Выписывают основных определения основных понятий. Правильно решают текстовых задач. Правильно отвечают на вопросы. |
|||
|
Конец урока 5 минут |
Рефлексия |
В конце урока учитель оценивает знания учеников и активность по набранным наградам |
|
|
||
Урок №33
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Вариационные ряды |
|||||
|
Цели обучения согласно программе |
Систематизировать данные в ряды |
|||||
|
Цель урока |
Систематизируют и строят ряды |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
1.Приветсвие 2.Ознакомление с темой 3. Ученики работают в паре по выбору. |
Ученики приветствуют и делятся на пары. |
Дескриптор
Метод оценки «Звездочка» |
|
||
|
Середина урока 35 минут |
Задача №1. Посмотреть видеоматериал.
Задача №2. Уровень А (базовый уровень) Задача А1. "Рост спортсменов" В секции национальной борьбы измерили рост 20 спортсменов (в см): 165, 170, 168, 172, 170, 175, 168, 170, 172, 175, 168, 170, 172, 168, 175, 170, 172, 175, 170, 168 Требуется:
Задача А2. "Стаж работы" Дан стаж работы 15 мастеров по изготовлению национальных музыкальных инструментов (в годах): 5, 3, 7, 5, 8, 3, 5, 7, 4, 5, 3, 7, 5, 4, 5 Найти:
Задача А3. "Цена товара" В 25 магазинах национальной одежды зафиксирована цена на традиционный жилет (в тысячах тенге): 15, 18, 20, 15, 17, 20, 15, 18, 20, 17, 15, 17, 18, 20, 15, 17, 18, 20, 15, 17, 18, 20, 15, 17, 18 Требуется:
Задача №3. Уровень В (повышенный уровень) Задача В1. "Спортивные результаты" Результаты забега на 100 метров 30 спортсменов распределились следующим образом:
Требуется:
Задача В2. "Анализ продаж" Дневная выручка магазина сувениров за месяц (30 дней) распределилась по интервалам:
Найти:
Задача В3. "Производство изделий" На фабрике проведен анализ веса готовых изделий (в граммах). Получены данные:
Требуется:
|
Ученики смотрят видеоматериал и понимают тему. Ученик работает с простыми вариационными рядами, выполняет базовые вычисления и построения. Ученик работает с интервальными вариационными рядами, выполняет более сложные вычисления и анализ. |
Дескрипторы: Выписывают основных определения основных понятий. Дескриптор: Находит среднее значение Определяет моду и медиану Вычисляет относительные частоты Дескриптор: Вычисляет среднее значение интервального ряда Определяет модальный и медианный интервалы Находит основные числовые характеристики |
|||
|
Конец урока 5 минут |
Рефлексия Вопрос-ответ от учителя -Вам понравился урок? -Чтобы вы хотели еще добавить? -Оцените урок от 1 до 10 |
В конце урока учитель оценивает знания учеников и активность по набранным наградам. |
|
|
||
Урок №34
|
Фамилия имя педагога |
|
|||||
|
Класс: |
Количество участников: |
Количество отсутствующих: |
||||
|
Тема урока: |
Статистические оценки параметров |
|||||
|
Цели обучения согласно программе |
Оценивать параметры распределения |
|||||
|
Цель урока |
Оценивают точность параметров |
|||||
|
Процесс урока: |
||||||
|
Часть/время урока |
Действия преподавателя |
Действия ученика |
Оценка |
Ресурсы |
||
|
Начало урока 5 минут |
Ученики делятся на 3 группы по методу “Выбери цвет”.
|
Каждый ученик выбирает 1 лист с закрытыми глазами из 3 разноцветных бумаг. По цветам ученики делятся на 3 группы. |
Метод оценки «Мои достижения» |
|
||
|
Середина 35 урока |
Задача №1. Посмотреть видеоматериал.
Задача №2. Метод «Пчела»
Что такое точечная оценка параметра? Какими свойствами должна обладать несмещенная оценка? Что такое эффективная оценка? Когда оценка называется состоятельной? Как связаны доверительный интервал и надежность оценки? Задание 3. "Комплексная задача" В магазине национальных сувениров проводится анализ цен. Из 200 товаров случайным образом отобрано 20. Найдены выборочное среднее (5000 тенге) и выборочное среднее квадратическое отклонение (500 тенге). Требуется:
Задание 4. "Построение доверительных интервалов" На основе выборки из 50 измерений получено выборочное среднее x̄ = 25 и среднее квадратическое отклонение s = 2. Построить доверительный интервал для математического ожидания с надежностью 0,95. |
Ученики смотрят видеоматериал и понимают тему. Ученик демонстрирует теоретические знания о статистических оценках. Ученик решает комплексную задачу с практическим применением. Ученик строит доверительный интервал, используя необходимые формулы. |
Метод оценки «Мои достижения» Дескрипторы: Выписывают основных определения основных понятий. Дескрипторы:
Применяет нужные формулы Проводит вычисления Проверяет результаты Дескрипторы:
|
|||
|
Конец урока 5 минут |
Рефлексия «Радуга» |
В конце урока учитель оценивает активность учеников по собранным наградам. |
|
|
||

шағым қалдыра аласыз