
250+150+170=400+170=570
360+340+270=700+270=970
580+120+240=700+240=940
390+110+250=500+250=750
230+170+560=400+560=960
270+180+50=450+50=500
Мына есепті тиімді тәсілмен шығару керек?
1) 45*52-52*42+42*51-51*39+39*50-50*36+36*49-49*33 Жауабы: 606 шығу керек
2) 9,3*2,5-2,5*8,9+8,9*2,4-2,4*8,5+8,5*2,3-2,3*8,1+8,1*2,2-2,2*7,7 Жауабы: 3,76 шығу керек
52(45-42)+51(49-39)+50(39-36)+49(36-33) сосын 52*3+51*3+50*3+49*3 шығады бул жерден 3ті жақшанынң сыртына шығарамыз сонда 3(52+51+50+49) әрі қарай 3*202=606 Екінші есептіде осы тәсілмен шығар оны өзің!
Пайызға берілген есептерді 100 –ге балап сызба арқылы тиімді шешу
Негізгі шығарылу жолы:
№2. Квадраттың қабырғалары 25%-ке ұзартылған. Квадраттың ауданы қанша %-ке көбейеді?
Шешуі: Квадраттың бастапқы қабырғасы а 25%-ке ұзартылғаннан кейінгі қабырғасының ұзындығы. Бастапқы ауданы – а2 Ұзартылғаннан кейінгі аудан –
Пропорция: а2 – 100% – х% : х=156,25% 100=56,25 56,25%
Тиімді тәсілмен шығарылу жолы:
100 100 25


 (100)2=10 000
(100)2=10 000
100% 100 125 (125)2=15 625
25 15 625 – 10 000=5625
5625 : 100%=56,25%
Негізгі шығарылу жолы:
8-сынып алгебра, Шыныбеков.
№359. (С тобының есебі)
Әуежайдан бір уақытта ұшып шыққан ұшақтардың біреуі батысқа, ал екіншісі оңтүстікке бет алды. Олар 2 сағ ұшқаннан кейін бір-бірінен 2000 км қашықтықта болды. Егер бір ұшақтың жылдамдығы екіншісінің жылдамдығының 75%-індей болса, онда әрбір ұшақтың жылдамдықтары қандай?
Шешуі:
1-ұшақ – 0,75х км/сағ
2-ұшақ – х км/сағ
2 сағ кейін: 2х 2000км
1-ұшақ – 1,5х км/сағ
2-ұшақ – 2х км/сағ
1,5х
П.т.б.: 2,25х2+4х2=4000000
6,25х2=4000000
х2=640000
х=800 (км/сағ)
Жауабы: 600км/сағ, 800км/сағ.
Тиімді тәсілмен шығарылу жолы:
t=2 сағ
 1002+752=15625=1252
1002+752=15625=1252
2000 км
75 2000 : 125=16
16*75=1200 км 16*100=1600
100 1200 км : 2 сағ=600 км/сағ 1600 км : 2 сағ=800 км/сағ
Көрсеткіштік теңсіздіктерді тиімді тәсілмен шешу.
Негізгі шығарылу жолы:






Жауабы: 
Тиімді тәсілмен шығарылу жолы:




Жауабы:  себебі -2 ден кіші -3 теңсіздікті
қанағаттандырмайды.
себебі -2 ден кіші -3 теңсіздікті
қанағаттандырмайды.
Көрсеткіштік теңдеулер жүйесін тиімді тәсілмен шешу.
Негізгі шығарылу жолы:



Тиімді тәсілмен шығарылу жолы:
Бірінші теңдеуге x пен y-тің орнына 1, 2, 3, 4, 5, 6 сандарын қойсақ.....

Осыдан 32 – 9=23 шығатынын байқаймыз.

Тексереміз:

Парабола және түзумен шектелген әрі боялған фигураның ауданын тиімді тәсілмен табыңыз


Негізгі шығарылу жолы:
![]()

 y
y 


![]()
![]()
![]() 5
5

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 =
=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1 
![]()
![]() -1 2 x
-1 2 x
Тиімді тәсілмен шығарылу жолы:


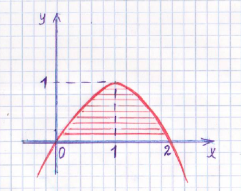
2.а)Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз
Негізгі шығарылу жолы:
Шешуі: Парабола тармағы төмен қарағындықтан және төбесі (1;1) нүктесінде жатқандықтан оның теңдеуі
у=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады, ендеше

 Жауабы:
Жауабы:
Тиімді тәсілмен шығарылу жолы:
S=2*1 =
=
Параболаның төбесінің координатарынан бастап
есептегенде ішкі бөлік ауданы  шаршы бірлікке, ал сыртқы бөлік
ауданы
шаршы бірлікке, ал сыртқы бөлік
ауданы  шаршы бірлікке
тең.
шаршы бірлікке
тең.
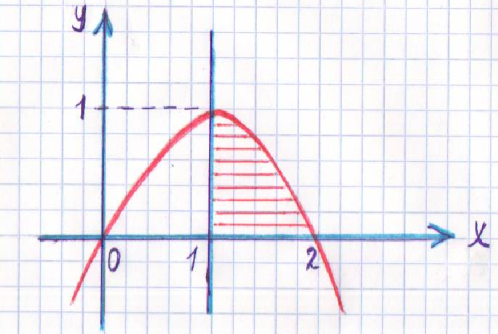
ә)Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз
Негізгі шығарылу жолы:
Шешуі: Парабола тармағы төмен қарағындықтан және төбесі (1;1) нүктесінде жатқандықтан оның теңдеуі
у=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады, ендеше

Жауабы:
Тиімді тәсілмен шығарылу жолы:
S=1*1* =
= , Жауабы:
, Жауабы: 
Тригонометриялық өрнектерді тиімді тәсілмен есептеу.

Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:

Радикалы бар өрнектерді тиімді тәсілмен есептеу.

Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
Өрнектегі екінші санды екіге бөліп көбейткіштерге жіктейміз

Енді осы көбейткіштерді квадраттап қосқанда өрнектегі екінші сан 5 шығу керек.

Жауабы: 



Жауабы:  .
.
Енді осы көбейткіштерді квадраттап қосқанда өрнектегі екінші сан 5 шығу керек.

Жауабы: 
Геометриялық прогрессияны тиімді тәсілмен есептеу.
Кмімелі
геометриялық прогрессияның екінші мүшесі  –ге ал бірінші мен үшінші
мүшелерінің қосындысы
–ге ал бірінші мен үшінші
мүшелерінің қосындысы  тең. Төртінші мен екінші
мүшелерінің көбейтіндісін тап.
тең. Төртінші мен екінші
мүшелерінің көбейтіндісін тап.
Негізгі шығарылу жолы:
 екінші теңдеуді бірінші
теңдеуге бөлеміз
екінші теңдеуді бірінші
теңдеуге бөлеміз 


Егер 
Тиімді тәсілмен шығарылу жолы:

Мәтінді есептерді тиімді тәсілмен есептеу.
1. Құрамында никельдің мөлшері 5% және 40% болатын екі түрлі сорты бар. Құрамындағы никельдің мөлшері 30% болатын 140 тонна болат алу үшін екі сорттың әрқайсысынан неше тоннадан алу керек?
Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
5![]()
![]() % 40% 40% –
30%=10%*4=40
% 40% 40% –
30%=10%*4=40
![]()
![]() 30%
30% – 5%=25%*4=100
30%
30% – 5%=25%*4=100
1![]()
![]()
![]()
![]() 0% 25% 35%
10% + 25%=35%*4=140
0% 25% 35%
10% + 25%=35%*4=140
40 100
140 
2. 40 литр 5% - дық тұз ерітіндісіне қанша су қосып 4% - дық тұз ерітіндісін алуға болады?
Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
5![]()
![]() % 0%
5% – 4%=1%*10=10
% 0%
5% – 4%=1%*10=10
![]()
![]() 4% 4% – 0%=4%*10=40
4% 4% – 0%=4%*10=40
![]()
![]()
![]()
![]() 4% 1% 5% 4% + 1%=5%*10=50
4% 1% 5% 4% + 1%=5%*10=50
40
10 50 
Мәселе есептерді арифметикалық тәсілмен тиімді шешу
1 есеп. Ауладағы қояндар мен тауықтардың саны 17, аяқтарының саны 44 болса, неше тауық, неше қоян бар?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Теңдеу құрып үйренбеген оқушы үшін бұл есепті шешу оңайға соқпасы анық.
Шешімі: Алдымен, ауладағылардың барлығы тауық деп ойлайық. Онда, 17 тауықта 34 аяқ болады (әр тауықта екі аяқтан). Сонда, 10 аяқ (44 – 34 = 10) артылып қалады. Демек, біз бірнеше қоянды тауық деп санап жібердік. Әр қоянның екі аяғы (4 – 2 = 2) саналмай кеткендітен, артылып қалған 10 аяқты екіге бөліп, қоянның санын табамыз. Сонда, 10 : 2 = 5 қоян бар. Және 17 – 5 = 12 тауық бар.
Жауабы: 12 тауық, 5 қоян бар.
2 есеп. Киноға 36 билет сатылып, одан 16900 теңге жиналды. Алдыңғы қатардағы орындардың бағасы 500 теңге, ал артқы қатардағы орындардың бағасы 450 теңге болса, алдыңғы қатардан қанша билет және артқы қатардан қанша билет сатылды?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Шешімі: Сатылған 36 билеттің барлығын артқы орындықтар деп ойлайық. Онда, 16200 теңге (36 * 450 = 16200) жиналады. Сонда, 700 теңге (16900 – 16200 = 700) артық қалады. Демек, біз бірнеше алдыңғы орындықты артқы деп санадық. Әр алдыңғы орындықтан 50 теңге (500 – 450 = 50) саналмай кеткендітен, артылып қалған 700 теңгені 50ге бөліп, алдыңғы орындықтардың санын табамыз. Сонда, 700 : 50 = 14 алдыңғы орындық, 36 – 14 = 22 артқы орындық бар.
Жауабы: 14 алдыңғы, 22 артқы орындық бар.
3 есеп. Оқушы 40 есеп шығару керек еді. Әр шешілмеген есепке 3 ұпайдан жеңіліп отырады, ал әр шешкен есебіне 5 ұпайдан ұтып отырады. Нәтижесінде, ол жеңбеді де, жеңілмеді де. Оқушы қанша есеп шығарған?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Шешімі: Оқушы барлық есепті шешпеді деп ойлайық. Онда, – 120 ұпай (40 * (-3) = - 120) жинаған болар еді. Сонда, 120 ұпай (0 – (-120) = 120) артық қалады. Демек, біз бірнеше шешілген есепті шешілмеді деп санадық. Әр шешілген есептен 8 ұпай (5 – (-3) = 8) саналмай кеткендіктен, артылып қалған 120 ұпайды 8ге бөліп, шешілген есептердің санын табамыз. Сонда, 120 : 8 = 15 есеп шешілген, 40 – 15 = 25 есеп шешілмеген.
Жауабы: 15 есеп шешілген.
Мәселе есептерді логикалық тәсілмен тиімді есептеу.
1 есеп. Екі санның қосындысы 20, бірінші сан екінші саннан 4-ке артық. Осы сандарды табыңдар.
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Бұл есепті арифметикалық тәсілмен шығару үшін үлкен санды кіші санға дейін кішірейту немесе кіші санды үлкен санға дейін арттыру тәсілі қолданылады.
Есептің шартын схема түрінде беруге де болады:
Талқылау.
1-тәсіл. Егер екі санда кіші санға тең болса, онда олардың қосындысы 4-ке кем болар еді, яғни 20-4=16. Сондықтан кіші сан 16:2=8, ал үлкен сан 8+4=12.
2-тәсіл. Егер екі санда үлкен санға тең болса, онда олардың қосындысы 4-ке артық болар еді, яғни 20+4=24. Сондықтан үлкен сан 24:2=12, ал кіші сан 12-4=8.
3-тәсіл. Логикалық тәсіл. Егер екі санның қосындысы мен олардың айырмасын қосатын болсақ, онда екі еселенген үлкен санға тең болады: (а+b)+(a-b)=2a
20+4=24; 24:2=12; 12-4=8
2 есеп. Екі қорапта 20 қарандаш, біреуінде екіншісіне қ
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Есептерді тиімді жолмен шығару
Есептерді тиімді жолмен шығару
250+150+170=400+170=570
360+340+270=700+270=970
580+120+240=700+240=940
390+110+250=500+250=750
230+170+560=400+560=960
270+180+50=450+50=500
Мына есепті тиімді тәсілмен шығару керек?
1) 45*52-52*42+42*51-51*39+39*50-50*36+36*49-49*33 Жауабы: 606 шығу керек
2) 9,3*2,5-2,5*8,9+8,9*2,4-2,4*8,5+8,5*2,3-2,3*8,1+8,1*2,2-2,2*7,7 Жауабы: 3,76 шығу керек
52(45-42)+51(49-39)+50(39-36)+49(36-33) сосын 52*3+51*3+50*3+49*3 шығады бул жерден 3ті жақшанынң сыртына шығарамыз сонда 3(52+51+50+49) әрі қарай 3*202=606 Екінші есептіде осы тәсілмен шығар оны өзің!
Пайызға берілген есептерді 100 –ге балап сызба арқылы тиімді шешу
Негізгі шығарылу жолы:
№2. Квадраттың қабырғалары 25%-ке ұзартылған. Квадраттың ауданы қанша %-ке көбейеді?
Шешуі: Квадраттың бастапқы қабырғасы а 25%-ке ұзартылғаннан кейінгі қабырғасының ұзындығы. Бастапқы ауданы – а2 Ұзартылғаннан кейінгі аудан –
Пропорция: а2 – 100% – х% : х=156,25% 100=56,25 56,25%
Тиімді тәсілмен шығарылу жолы:
100 100 25


 (100)2=10 000
(100)2=10 000
100% 100 125 (125)2=15 625
25 15 625 – 10 000=5625
5625 : 100%=56,25%
Негізгі шығарылу жолы:
8-сынып алгебра, Шыныбеков.
№359. (С тобының есебі)
Әуежайдан бір уақытта ұшып шыққан ұшақтардың біреуі батысқа, ал екіншісі оңтүстікке бет алды. Олар 2 сағ ұшқаннан кейін бір-бірінен 2000 км қашықтықта болды. Егер бір ұшақтың жылдамдығы екіншісінің жылдамдығының 75%-індей болса, онда әрбір ұшақтың жылдамдықтары қандай?
Шешуі:
1-ұшақ – 0,75х км/сағ
2-ұшақ – х км/сағ
2 сағ кейін: 2х 2000км
1-ұшақ – 1,5х км/сағ
2-ұшақ – 2х км/сағ
1,5х
П.т.б.: 2,25х2+4х2=4000000
6,25х2=4000000
х2=640000
х=800 (км/сағ)
Жауабы: 600км/сағ, 800км/сағ.
Тиімді тәсілмен шығарылу жолы:
t=2 сағ
 1002+752=15625=1252
1002+752=15625=1252
2000 км
75 2000 : 125=16
16*75=1200 км 16*100=1600
100 1200 км : 2 сағ=600 км/сағ 1600 км : 2 сағ=800 км/сағ
Көрсеткіштік теңсіздіктерді тиімді тәсілмен шешу.
Негізгі шығарылу жолы:






Жауабы: 
Тиімді тәсілмен шығарылу жолы:




Жауабы:  себебі -2 ден кіші -3 теңсіздікті
қанағаттандырмайды.
себебі -2 ден кіші -3 теңсіздікті
қанағаттандырмайды.
Көрсеткіштік теңдеулер жүйесін тиімді тәсілмен шешу.
Негізгі шығарылу жолы:



Тиімді тәсілмен шығарылу жолы:
Бірінші теңдеуге x пен y-тің орнына 1, 2, 3, 4, 5, 6 сандарын қойсақ.....

Осыдан 32 – 9=23 шығатынын байқаймыз.

Тексереміз:

Парабола және түзумен шектелген әрі боялған фигураның ауданын тиімді тәсілмен табыңыз


Негізгі шығарылу жолы:
![]()

 y
y 


![]()
![]()
![]() 5
5

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 =
=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1 
![]()
![]() -1 2 x
-1 2 x
Тиімді тәсілмен шығарылу жолы:


2.а)Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз

Негізгі шығарылу жолы:
Шешуі: Парабола тармағы төмен қарағындықтан және төбесі (1;1) нүктесінде жатқандықтан оның теңдеуі
у=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады, ендеше

 Жауабы:
Жауабы:
Тиімді тәсілмен шығарылу жолы:
S=2*1 =
=
Параболаның төбесінің координатарынан бастап
есептегенде ішкі бөлік ауданы  шаршы бірлікке, ал сыртқы бөлік
ауданы
шаршы бірлікке, ал сыртқы бөлік
ауданы  шаршы бірлікке
тең.
шаршы бірлікке
тең.
ә)Парабола және түзумен шектелген әрі боялған фигураның ауданын табыңыз

Негізгі шығарылу жолы:
Шешуі: Парабола тармағы төмен қарағындықтан және төбесі (1;1) нүктесінде жатқандықтан оның теңдеуі
у=-(x-1)2 +1==-x2 +2х-1+1=2x-x2 болады, ендеше

Жауабы:
Тиімді тәсілмен шығарылу жолы:
S=1*1* =
= , Жауабы:
, Жауабы: 
Тригонометриялық өрнектерді тиімді тәсілмен есептеу.

Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:

Радикалы бар өрнектерді тиімді тәсілмен есептеу.

Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
Өрнектегі екінші санды екіге бөліп көбейткіштерге жіктейміз

Енді осы көбейткіштерді квадраттап қосқанда өрнектегі екінші сан 5 шығу керек.

Жауабы: 



Жауабы:  .
.
Енді осы көбейткіштерді квадраттап қосқанда өрнектегі екінші сан 5 шығу керек.

Жауабы: 
Геометриялық прогрессияны тиімді тәсілмен есептеу.
Кмімелі
геометриялық прогрессияның екінші мүшесі  –ге ал бірінші мен үшінші
мүшелерінің қосындысы
–ге ал бірінші мен үшінші
мүшелерінің қосындысы  тең. Төртінші мен екінші
мүшелерінің көбейтіндісін тап.
тең. Төртінші мен екінші
мүшелерінің көбейтіндісін тап.
Негізгі шығарылу жолы:
 екінші теңдеуді бірінші
теңдеуге бөлеміз
екінші теңдеуді бірінші
теңдеуге бөлеміз 


Егер 
Тиімді тәсілмен шығарылу жолы:

Мәтінді есептерді тиімді тәсілмен есептеу.
1. Құрамында никельдің мөлшері 5% және 40% болатын екі түрлі сорты бар. Құрамындағы никельдің мөлшері 30% болатын 140 тонна болат алу үшін екі сорттың әрқайсысынан неше тоннадан алу керек?
Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
5![]()
![]() % 40% 40% –
30%=10%*4=40
% 40% 40% –
30%=10%*4=40
![]()
![]() 30%
30% – 5%=25%*4=100
30%
30% – 5%=25%*4=100
1![]()
![]()
![]()
![]() 0% 25% 35%
10% + 25%=35%*4=140
0% 25% 35%
10% + 25%=35%*4=140
40 100
140 
2. 40 литр 5% - дық тұз ерітіндісіне қанша су қосып 4% - дық тұз ерітіндісін алуға болады?
Негізгі шығарылу жолы:


Тиімді тәсілмен шығарылу жолы:
5![]()
![]() % 0%
5% – 4%=1%*10=10
% 0%
5% – 4%=1%*10=10
![]()
![]() 4% 4% – 0%=4%*10=40
4% 4% – 0%=4%*10=40
![]()
![]()
![]()
![]() 4% 1% 5% 4% + 1%=5%*10=50
4% 1% 5% 4% + 1%=5%*10=50
40
10 50 
Мәселе есептерді арифметикалық тәсілмен тиімді шешу
1 есеп. Ауладағы қояндар мен тауықтардың саны 17, аяқтарының саны 44 болса, неше тауық, неше қоян бар?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Теңдеу құрып үйренбеген оқушы үшін бұл есепті шешу оңайға соқпасы анық.
Шешімі: Алдымен, ауладағылардың барлығы тауық деп ойлайық. Онда, 17 тауықта 34 аяқ болады (әр тауықта екі аяқтан). Сонда, 10 аяқ (44 – 34 = 10) артылып қалады. Демек, біз бірнеше қоянды тауық деп санап жібердік. Әр қоянның екі аяғы (4 – 2 = 2) саналмай кеткендітен, артылып қалған 10 аяқты екіге бөліп, қоянның санын табамыз. Сонда, 10 : 2 = 5 қоян бар. Және 17 – 5 = 12 тауық бар.
Жауабы: 12 тауық, 5 қоян бар.
2 есеп. Киноға 36 билет сатылып, одан 16900 теңге жиналды. Алдыңғы қатардағы орындардың бағасы 500 теңге, ал артқы қатардағы орындардың бағасы 450 теңге болса, алдыңғы қатардан қанша билет және артқы қатардан қанша билет сатылды?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Шешімі: Сатылған 36 билеттің барлығын артқы орындықтар деп ойлайық. Онда, 16200 теңге (36 * 450 = 16200) жиналады. Сонда, 700 теңге (16900 – 16200 = 700) артық қалады. Демек, біз бірнеше алдыңғы орындықты артқы деп санадық. Әр алдыңғы орындықтан 50 теңге (500 – 450 = 50) саналмай кеткендітен, артылып қалған 700 теңгені 50ге бөліп, алдыңғы орындықтардың санын табамыз. Сонда, 700 : 50 = 14 алдыңғы орындық, 36 – 14 = 22 артқы орындық бар.
Жауабы: 14 алдыңғы, 22 артқы орындық бар.
3 есеп. Оқушы 40 есеп шығару керек еді. Әр шешілмеген есепке 3 ұпайдан жеңіліп отырады, ал әр шешкен есебіне 5 ұпайдан ұтып отырады. Нәтижесінде, ол жеңбеді де, жеңілмеді де. Оқушы қанша есеп шығарған?
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Шешімі: Оқушы барлық есепті шешпеді деп ойлайық. Онда, – 120 ұпай (40 * (-3) = - 120) жинаған болар еді. Сонда, 120 ұпай (0 – (-120) = 120) артық қалады. Демек, біз бірнеше шешілген есепті шешілмеді деп санадық. Әр шешілген есептен 8 ұпай (5 – (-3) = 8) саналмай кеткендіктен, артылып қалған 120 ұпайды 8ге бөліп, шешілген есептердің санын табамыз. Сонда, 120 : 8 = 15 есеп шешілген, 40 – 15 = 25 есеп шешілмеген.
Жауабы: 15 есеп шешілген.
Мәселе есептерді логикалық тәсілмен тиімді есептеу.
1 есеп. Екі санның қосындысы 20, бірінші сан екінші саннан 4-ке артық. Осы сандарды табыңдар.
Негізгі шығарылу жолы:

Тиімді тәсілмен шығарылу жолы:
Бұл есепті арифметикалық тәсілмен шығару үшін үлкен санды кіші санға дейін кішірейту немесе кіші санды үлкен санға дейін арттыру тәсілі қолданылады.
Есептің шартын схема түрінде беруге де болады:
Талқылау.
1-тәсіл. Егер екі санда кіші санға тең болса, онда олардың қосындысы 4-ке кем болар еді, яғни 20-4=16. Сондықтан кіші сан 16:2=8, ал үлкен сан 8+4=12.
2-тәсіл. Егер екі санда үлкен санға тең болса, онда олардың қосындысы 4-ке артық болар еді, яғни 20+4=24. Сондықтан үлкен сан 24:2=12, ал кіші сан 12-4=8.
3-тәсіл. Логикалық тәсіл. Егер екі санның қосындысы мен олардың айырмасын қосатын болсақ, онда екі еселенген үлкен санға тең болады: (а+b)+(a-b)=2a
20+4=24; 24:2=12; 12-4=8
2 есеп. Екі қорапта 20 қарандаш, біреуінде екіншісіне қ

шағым қалдыра аласыз















