
МАЗМҰНЫ
1.1. Мектептегі геометрия аксиоматикасының қазіргі жағдайы туралы 2
1.2. Жұмыста қаралған мәселе 4
II ТАРАУ. АКСИОМАЛАР СИСТЕМАСЫНА ЖАЛПЫ ШОЛУ 5
2.1. Евклидтен Гильбертке дейінгі геометриялық зерттеулерге жалпы шолу 5
2.2. Геометрияны аксиоматикалық әдіспен құру туралы 7
2.3. Гильберт аксиомалар системасы 11
2.2. Вейль аксиомалар системасы 19
2.2.1. Тұйық және тұйық емес аксиомалар системасы 20
2.2.3. Қайшылықсыздығы мен толықтығы 23
2.2.4. Түзу, жазықтық, кесінді, сәуле және бұрыштың анықталуы 25
2.3. А.В.Погорелов аксиомалар системасы 31
2.4. А.Н.Колмогоров аксиомалар системасы 37
2.5. А.Д.Александров аксиомалар системасы 40
I ТАРАУ КІРІСПЕ
1.1. Мектептегі геометрия аксиоматикасының қазіргі жағдайы туралы
Орта мектепте оқылатын геометрия пәнінде соңғы 50-60 жылда көптеген өзгерістер болды. Кеңес одағында көп уақытқа дейін орта мектепте геометрия Н.Никитиннің [7], содан кейін А.Киселевтің [5] оқулықтарымен оқылған болатын. Бірақ бұл оқулықтарда евклидтік геометрияны аксиоматикалық түрде құруға қатты көңіл бөлінді деп айтуға болмайды. Сонымен қатар бұл оқулықтарда геометриялық фигуралардың кейбір қасиеттері көрнекілік тұрғыдан қарастырылып айқын деп есептеледі де әрі қарай оларды логикалық қатаң тұрғыдан дәлелденбей алынады. Аксиомалар туралы аздаған мәліметтер оқулық соңында қосымша ретінде қысқаша келтіріледі.
Сонымен қатар мектеп оқулықтары сол кездегі математиканың даму деңгейінен едәуір қалыс қалды деп айтуға болады. Математикада кеңінен орын алған жиындық көзқарас тіпті қолданбайтын. Сондай-ақ мектепте оқылатын алгебра курсымен байланысы өте аз болатын.
Ал бұның өзі мектеп оқушылары жоғарғы оқу орындарында оқылатын математикалық пәндерді оқығанда математикаға көзқарасын түбегейлі өзгертуге әкеліп соқты.
1966 жылы Кеңес Одағында мектептегі оқылатын пәндердің мазмұнын анықтау үшін академик А.Колмогоровтың басшылығымен комиссия құрылған болатын. Осы комиссияның жұмысы нәтиежесі мектеп геометриясын оқушыларға баяндау тәсілін өзгерту керек деген қорытындыға келген болатын. Мектеп курсында аксиоматикалық қатаң дедуктивтік түрде геометрияны баяндау керек қажеттілігі айқындалды. Мектептерде жиындар теориясының элементтері кеңінен қолданылатын А.Колмогоровтың аксиомалар системасы енгізілді. Мұнда тек қана геометрияға емес алгебра пәнінде де өзгерістер енгізіліп мектептегі осы екі математикалық пәндердің арасындағы байланыс кеңейтілді.
Мектеп геометриясын А.Колмогровтың басшылығымен жасалған аксиомалар системасына негізделген оқулықпен оқытыла бастады. Мектеп оқытушыларына геометрияны жаңадан жазылған оқулықпен оқыту біраз қиыншылықтарға әкеліп соқты. А.Колмогоровтың аксиомалар системасы математик ғалымдар мен мектеп оқытушылары арасында әртүрлі пікір таласына әкеліп соқты. Мысалы академик Л. Понтрягин «Коммунист» журналында (N14, 1980) бұл системаны қатаң сынға алған болатын. Л. Понтрягинге қарсы, Колмогоров аксиоматикасын қолдап айтылған пікірлер де көп айтылды (мысалы В. Арнольд)
Осы кездерде Кеңес одағында мектепте оқылатын геометрия пәніне арналған аксиомалар системасын құруға конкурс жарияланды. Бұған көптеген математик ғалым-ұстаздар қатысқан болатын (А.Погорелов, А.Александров, Л.Атанасян т.б.). Орыс тілінде жазылған мектеп курсының геометриясының көптеген оқулықтары жарыққа шықты - М. Е. Ващенко-Захарченко, С.Е.Гурьев, А. Ю. Давидов, А.В.Погорелов, В.А.Гусев, Л.С.Атанасян (В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина); А.Д.Александров (А.Л.Вернер, В.И.Рыжик); Г.П.Бевз (В.Г.Бевз, Н.Г.Владимирова); В.Г.Болтянский (М.Б.Волович, А.Д.Семушин); В.М. Клопский (3.А.Скопец, М.И.Ягодовский); А.Н. Колмогоров (А.Ф.Семенович, Р.С.Черкасов); В.Н.Руденко, Г.А.Бахурин, Г.Е.Алимухамбетова және басқалар. Бұл оқулықтардың кейбіреулері Ресей мектептерінде қазір де пайдаланылуда.
Қазіргі кезде Қазақстан мектептерінде А.Погорелов аксиоматикасының негізінде авторлар коллективі (Ж.Қайдасов, И.Бекбоев, А.Абдиев, Г.Досмаганбетов) жазған оқулықтармен геометрия оқытылуда.
Әрбір жаңа оқулық енгізілгенде бұрыннан жұмыс істеп келе жатқан мектеп оқытушылары едәуір қиыншылықтарға кездесіп отырды – қандай себеппен жаңа оқулыққа көшті, қандай ерекшеліктер бар, аксиомалар системасын өзгертуге не себептер болды т.с.с. Жұмыста мектеп оқытушыларының осы сұрақтарына жауап беру мәселесі де қарастырылды.
1.2. Жұмыста қаралған мәселе
Жұмыста алға қойылған негізгі мақсат – мектеп курсында оқылатын евклидтік геометрияның аксиоматикасына негіз болған Гильберт аксиоматикасын, кезінде мектепте қолданылған Колмогоров аксиоматикасын, қазір қолданылып жүрген Погорелов аксиоматикасының ерекшеліктеріне тоқталып оларды салыстыру. Сонымен қатар Вейль аксиомалар системасы мен Александров аксиомалар системасы олардың кей ерекшеліктеріне байланысты қарастырылады
Жұмыста геометрияны оқыту әдістемелік мәселері қарастырылмайды.
II ТАРАУ. АКСИОМАЛАР СИСТЕМАСЫНА ЖАЛПЫ ШОЛУ
2.1. Евклидтен Гильбертке дейінгі геометриялық зерттеулерге жалпы шолу
Ең алғаш рет геометрияны қатаң логикалық түрде
құруға жасалған сәтті талпыныс Евклидтің «Бастамалар» еңбегі деп
есептеледі. Евклид бұл еңбегінде дәлелденбей алынатын тұжырымдарды
келтіреді, олардың кейбірін аксиомалар деп, ал кейбірін постулаттар
деп атаған. Неге бұлай әртүрлі атағаны белгісіз (математика
тарихымен айналысатын ғалымдар әртүрлі пікір айтады). Сонымен қатар
Евклид барлық ұғымдарды анықтауға тырысқан, бұлай істеу мүмкін
еместігін кейінгі параграфтарда айтамыз. Евклид сонымен қатар
геометриялық фигуралардың былайынша ап-айқын деп есептелетін
қасиеттерін дәлелдеуде көп пайдаланады. Ал математиканы қатаң
дедуктивтік түрде құрғанда бұлай істеуге болмайды. Евклидтің
«Бастамаларында» басқа да кемшіліктер бар. Кейінгі математиктер
Евклидтің ол кемшіліктеріне назар аудармай негізінен Евклидтің
қатесі V постулатты дәлелдемей алуы деп есептеп осы постулатты
дәлелдеуге тырысты.
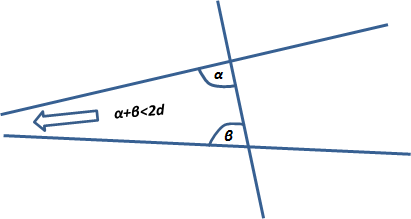
V постулат. Екі түзуді үшінші түзу қиған кезде оның алғашқы екі түзумен жасаған біржақты ішкі бұрыштарының қосындысы екі тік бұрыштан кіші болған кезде алғашқы екі түзу осы біржақты екі бұрыштың қосындысы екі тік бұрыштан кіші болған жақтан қиылысады.
Сонымен Евклидтен кейінгі көптеген математиктер мынандай есеппен айналысты - Евклидтің V постулатын оның қалған аксиомалары мен постулаттарына сүйенбей, V постулатқа эквивалентті тұжырымды қолданбай V постулатты дәлелдеу керек.
V постулатты дәлелдеуге көптеген белгілі математиктер ат салысты:
Ежелгі дүние математиктері – Аристотель, Посидоний, Птоломей, Прокл, Симплиций, Аганис т.б.
Орта ғасыр математиктері – ал-Хазин, ат-Гуси, аш-Шахни, ан-Найризи, Омар Хайиам, ибн ал-Хайсан, Насир-Эд-Дин т.б.
Қайта өрлеу дәуірі мен одан кейінгі математиктер – Клавий, Валлис, Плейфер, Саккери, Ламберт, Лежандр, т.б.
Бұл математиктердің осы постулатты дәлелдеуге арналған еңбектерін Н.Лобачевскийдің өмірбаянын зерттеуші В.Ф.Каган былай сипаттайды - «... Бұны (V постулатты) дәлелдеуге қанша күш жігердің сарп болғанын көз алдымызға елестетудің өзі қиын. Кей адамдар бұны өз өмірлерінің мақсаты етіп қойды, бұған көптеген жылдарын құрбан етті, мистикалық агностицизмге дейін барды, ақыл есінен айрылғандар да болды ...»
Жалпы V постулаттың дәлелденбейтіндігі кейіннен белгілі болды, оның дәлелденбейтіндігін қалай көрсету мәселесін шешетін математикалық әдіс те кейін шықты. Дегенмен V постулатты дәлелдеуге тырысқан ғалымдардың еңбегі зая кеткен жоқ. Олар V постулат пен қалған аксиомалардың арасындағы байланысты анықтады, V постулатқа эквивалентті көптеген тұжырымдар айқындалды. Олардың кейбірін келтіре кетелік:
-
Үшбұрыштың ішкі бұрыштарының қосындысы екі тік бұрышқа тең.
-
Пифагор теоремасы.
-
Жазықтықтағы түзуден бірдей қашықтықта жатқан нүктелердің жиыны түзу болады.
-
Параллель түзулердің ара қашықтығы ақырлы.
-
Кез – келген үшбұрышқа кез-келген ұқсастық коэффициентімен ұқсас үшбұрыштар болады.
-
Бір түзудің бойында жатпайтын үш нүкте арқылы өтетін шеңбер барлық уақытта табылады.
-
Түзуден тысқары жатқан нүкте арқылы оған параллель өтетін түзулер саны біреуден аспайды.
Орыс математигі Н.Лобачевский, неміс математигі К.Гаусс, венгр математигі Я.Бояй V постулат дәлелденбейді деп есептеп оны қарама қарсы тұжырыммен алмастыру арқылы қазір Лобачевскийдің гиперболалық геометриясы деп аталатын жаңа геометрия ашты.
2.2. Геометрияны аксиоматикалық әдіспен құру туралы
Мектепте оқылатын геометрияда математикадағы аксиоматикалық әдіс қолданылады.
Біздің эрамызға дейінгі III ғасырдың басында ежелгі грек дәуірінің ұлы ғалымы Аристотельдің еңбектерінде ғылыми теорияларды құрудың негізгі принциптері бой көрсете бастаған болатын. Осы принциптерді алғаш рет Евклид өзінің «Бастамалар» деген белгілі еңбегінде іске асыруға тырысты. Өзіне дейінгі жинақталған математикалық мәліметтерді талдай отырып дәлелденбей алынатын бірнеше математикалық тұжырымдарды таңдап алып, оларды аксиомалар және постулаттар деп атады (неге бұлай әртүрлі атағаны туралы әртүрлі пікірлер айтылады). Осы дәлелденбей алынған тұжырымдардың салдарлары ретінде теоремаларды дәлелдейді. Евклид осылай құрған система ешқандай елеулі өзгеріссіз біздің дәуіріміздің XIX ғасырына дейін келді. Бірақ Евклид құрған жүйеде көптеген, математика үшін макңызы бар кемшіліктер болды. Тек қана ғасырлар аралығында ғана аксиоматикалық әдістің негізгі принциптері құрылып евклидтік геометрияның логикалық түрде мүлтіксіз аксиоматикалық жүйесі құрылды.
Математикалық теорияны аксиоматикалық түрде құрудың негізгі принциптерін келтірелік:
-
Анықталмай алынатын негізгі (бастапқы) ұғымдардың тізімі келтіріледі. Басқа ұғымдар осы негізгі ұғымдардың және бұрын анықталған басқа ұғымдардың көмегі арқылы анықталуы керек. Бұлай болатын себебі ұғымдардың бәрін бірдей анықтай беру мүмкін емес. Бәрін анықтауға тырыссақ, онда шексіз процесске немесе «логикалық дөңгелекке» тап боламыз.
-
Аксиомалар тізімі келтіріледі. Олар дәлелденбей алынатын тұжырымдар. Тұжырымдарда ұғымдар туралы пікірлер айтылады. Ұғымдар (түптеп келгенде) негізгі ұғымдар осы аксиомаларды қанағаттандыруы керек. Басқаша айтқанда аксиомалар – негізгі ұғымдарға қойылатын талаптар. Сондықтан негізгі ұғымдар аксиомалар арқылы «анықталып тұр» деп те айтады. Қазіргі заманда дәлелденбей алынатын тұжырымдарды аксиомалар және постулаттар деп бөлмейді, негізінен қалыптасқан термин – аксиомалар. Кей ғылым салаларында «постулат» термині де қолданылуы мүмкін.
-
Негізгі ұғымдардың тізімі мен аксиомалар тізімі келтірілгеннен кейін әрбір жаңа енгізілген ұғым қатаң түрде анықталып, әрбір тұжырым қатаң түрде дәлелденіп отыруы керек.Осылай етіп құрылған математикалық теория абстрактылық теория ғана болады. Мысалы негізгі ұғымдар - «нүкте, түзу, арқылы өтеді, т.с.с» болсын.
Құрып отырған теорияда нүкте, түзу, арқылы өтеді, т.с.с деп қандай да бір нақты нәрселер аталып отырған жоқ. Егерде бір нақты объектілер мен олардың арасындағы қатынастар табылып олар теориядағы негізгі ұғымдарға қойылатын талаптарды - аксиомалардың бәрін қанағаттандырса онда оларды осы теорияның интерпретациясы дейді. Интерпретация объектілері мен қатынастары аксиомаларды қанағаттандыратын болғандықтан, олар аксиомалардың салдарлары – теоремаларды қанағаттандырады. Сонымен интерпретацияда негізгі ұғымдарға нақты мағына береміз.
Сонымен біз аксиоматикалық түрде теория құрғанда тек қана абстрактылық объектілермен жұмыс істейміз – тек аксиомалардың логикалық салдарларын зерттейміз.
Әрине осылай етіп абстрактылық теория құрған кезде біздің аксиомалар системасынан бірін бірі жоққа шығаратын тұжырымдар дәлелденбейтініне сенімді болуымыз керек. Аксиомалар системасына қойылатын бұндай талап – аксиомалар системасының қайшылықсыз болуы керек деген талап болады. Геометриялық аксиомалар системасының қайшылықсыздығын нақты сандар арқылы құрылған интерпретация арқылы шешуге болады. Жалпы бұл талап орындалмаса, ондай аксиомалар системасының керегі жоқ, бұл системада кез – келген тұжырымды дәлелдеуге болады. Сондықтан аксиомалар системасын құрғанда бірден қайшылықсыздық мәселесі шешілуі керек.
Аксиомалар системасына қойылатын тағы бір талап – аксиомалар системасының тәуелсіздігі. Бұл талап бойынша әрбір аксиоманы қалған аксиомалардың көмегі арқылы дәлелдеуге болмайтын болу керек. Былайынша айтқанда аксиомалардың ішіне «жасырын теоремалар» кірмеуі керек. Бұны кейде аксиомалар системасының минималдылығы деп те атайды. Бұл талап алдыңғы келтірілген қайшылықсыздық сияқты өте қатаң талап емес. Кейде, әсіресе мектеп курсындағы геометрияда, кей теоремалардың дәлелдеуі оқушыларға түсінікті болуы үшін аксиомалар системасын тәуелді қылып алады. Аксиомалар системасының тәуелсіздігін зерттеуді интерпретациялар құру арқылы шешуге болады. Бұл жерде Евклид құрған аксиомалар системасындағы V постулаттың қалған аксиомалардан тәуелсіздігін шешу мәселесі екі мың жылдай уақыт алғанын айта кеткен жөн (ол кезде аксиомалар системасына қойылатын талаптар, оларды қалай шешу мәселесі, жалпы аксиомалар системасы деген не сияқты сұрақтар математиктер алдына айқын қойылмаған болатын).
Аксиомалар системасына қойылатын тағы бір талап – аксиомалар системасының толықтылығы. Бұл талап бойынша аксиомалар осы теорияның кез – келген тұжырымын дәлелдеуге немесе жоққа шығаруға жеткілікті болуы керек. Кейде неғұрлым «тереңірек» жатқан математикалық байланыстарды зерттеу үшін аксиомалар системасын әдейі толық емес қылып алады. Аксиомалар системасының толықтылығын кей жағдайда аксиомалар системасының жеткіліктілігі деп те атайды.
Бұл дипломдық жұмыста тек қана евклидтік геометрияның аксиомалар системасы туралы айтылады. Сондықтан біз тек қана евклидтік геометрияға қарсы мәселелерді қарастырамыз.
Сонымен геометрияның аксиомалар системасын құрғанда құрушыда негізгі ұғымдар мен аксималарды таңдауда едәуір еркіндік болады екен. Сондықтан да евклидтік геометрияның көптеген ғалымдар құрған аксиомалар системасы бар, олардың көбі мектеп оқушыларына геометрияны оқытқанда олардың түсінуіне жеңіл болсын деген оймен жасалған. Дипломдық жұмыста көп тараған аксиомалар системасына шолу жасалып, олардың ерекшеліктеріне тоқталмақпыз.
XIX ғасырдың ортасына дейін геометрия Евклидтің «Бастамалардағы» келтірілген системаға негізделді деп айтуға болады (аздаған енгізілген өзгерістер онша елеулі бола қойған жоқ). XIX ғасырдың екінші жартысынан бастап жалпы математиканы негіздеу мәселелері өріс алды. Осы кезде геометрияны негіздеу мәселесімен көптеген зерттеулер жүргізілді. Осы кездегі ең көп танымал болған неміс ғалымы Давид Гильберттің 1899 жылы шыққан «Геометрияның негіздері» деген еңбегі болатын. Бұл еңбекте евклидтік геометрия өте қатаң түрде құрылды. Бұл еңбек тұралы кейін толығырақ айтылады.
Гильберттің аксиомалар системасынан басқа 1904 жылы Фридрих Шурдың аксиомалар системасын айта кетелік. Бұл аксиоматиканың идеясын Кеңес Одағының академигі А.Н.Тихонов бастаған математиктер тобы мектеп геометриясын құруда қолданды. Осы кездерде В.Ф.Каган (ара қашықтыққа негізделген), Г.Вейль (векторлық кеңістікке негізделген) аксиомалар системасын келтірді.
Евклидтік геометрияның негізгі үш талапты (қайшылықсыздық, тәуелсіздік, толықтық) қанағаттандыратын аксиомалар системасы құрылғанмен, мектеп оқушыларының жас ерекшеліктеріне, мектепте оқылатын математика және басқа пәндердің деңгейіне сәйкес келетін талаптарды толық қанағаттандыратын «қолайлы» аксиомалар системасы туралы сұрақ толық шешілді деп айту қиындау.
2.3. Гильберт аксиомалар системасы
1899 ж. неміс математигі Д.Гильберттің «Геометрия негіздемелері» атты атақты кітабы басылып шықты.Бұл кітапта тұңғыш рет евклидтік геометрияны логикалық жолмен құруға жеткілікті болатын аксиомалардың тізімі келтірілді.Осы күнгі математикадағы аксиоматикалық әдіс пен математикалық структуралардың қазіргі тұрғыдан қарастырылатын теориясы (яғни Н.Бурбаки тобы қалыптастырған түсініктер) Гильберттің осы «Геометрия негіздемелерінен» басталады деуге болады.
2.1.1. Негізгі ұғымдар
Гильберттің баяндауы бойынша
евклидтік кеңістік структурасының базасы үш жиыннан
–  жиындарынан тұрады.
Бірінші
жиындарынан тұрады.
Бірінші  жиынының
элементтері нүктелер деп аталады
да
жиынының
элементтері нүктелер деп аталады
да  әріптерімен
белгіленеді,
әріптерімен
белгіленеді,  жиынының
элементтері түзулер деп аталады
да
жиынының
элементтері түзулер деп аталады
да  әріптерімен
белгіленеді,
әріптерімен
белгіленеді,  жиынының
элементтері жазықтықтар деп аталады
да
жиынының
элементтері жазықтықтар деп аталады
да  (немесе
(немесе
 ) әріптерімен
белгіленеді.
) әріптерімен
белгіленеді.
Базаның жиындары үстінде «тиісті» (немесе жатады), «арасында жатады» және «конгруэнт» сөздерімен белгіленетін қатынастар болады. Бұл қатынастардың нақты сипаты қандай екендігі елеулі рөл атқармайды,тек сол қатынастар төменде тізімі келтірілетін аксиомаларды қанағаттандыратын болса болғаны.
Сонымен Гильберт бойынша негізгі ұғымдар – нүкте,түзу, жазықтық және олардың арасындағы қатынастар – тиісті, арасында жатады, конгруэнт.
2.1.2. Аксиомалар
Гильберттің негізгі ұғымдарға қойылатын талаптары 20 аксиома түрінде айтылып, олар 5 топқа бөлінген.
I топ. Тиістілік аксиомалары.
«Жатады»,яғни тиістілік
белгісін  таңбасы арқылы белгілейміз.
Бірінші топта мынадай сегіз аксиома бар:
таңбасы арқылы белгілейміз.
Бірінші топта мынадай сегіз аксиома бар:

 ⃓
⃓ 
Мұндай
 түзуі біреу ғана болады
(ол
түзуі біреу ғана болады
(ол деп те
белгіленеді).
деп те
белгіленеді).

 ⃓
⃓ 
 Бір түзуде жатпайтын ең
кем дегенде үш нүкте болады.Егер
Бір түзуде жатпайтын ең
кем дегенде үш нүкте болады.Егер  нүктелері бір түзуде
жатпаса,былай жазып көрсетеді:
нүктелері бір түзуде
жатпаса,былай жазып көрсетеді:  немесе
немесе
 немесе
немесе 

 ⃓
⃓
Мұндай жазықтық біреу ғана
болады (ол ( ) деп те
белгіленеді).
) деп те
белгіленеді).

 ⃓
⃓ 

Бұл жағдайда
« а
түзуі
 жазықтығында жатады»
дейді немесе «
жазықтығында жатады»
дейді немесе « жазықтығы
а
түзуінен өтеді»
дейді.
жазықтығы
а
түзуінен өтеді»
дейді.
 ⃓
⃓
 ⃓
⃓
Бұл аксиомалар бойынша мынадай теореманы дәлелдеуге болады: кез келген жазықтықта бір түзудің бойында жатпайтын үш нүкте болады.
II топ. Рет аксиомалары.
Егер
 нүктесі
нүктесі  және
және
 нүктелерінің арасында
жататын болса,былай жазылады
нүктелерінің арасында
жататын болса,былай жазылады 
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Евклидтік геометрия
Евклидтік геометрия
МАЗМҰНЫ
1.1. Мектептегі геометрия аксиоматикасының қазіргі жағдайы туралы 2
1.2. Жұмыста қаралған мәселе 4
II ТАРАУ. АКСИОМАЛАР СИСТЕМАСЫНА ЖАЛПЫ ШОЛУ 5
2.1. Евклидтен Гильбертке дейінгі геометриялық зерттеулерге жалпы шолу 5
2.2. Геометрияны аксиоматикалық әдіспен құру туралы 7
2.3. Гильберт аксиомалар системасы 11
2.2. Вейль аксиомалар системасы 19
2.2.1. Тұйық және тұйық емес аксиомалар системасы 20
2.2.3. Қайшылықсыздығы мен толықтығы 23
2.2.4. Түзу, жазықтық, кесінді, сәуле және бұрыштың анықталуы 25
2.3. А.В.Погорелов аксиомалар системасы 31
2.4. А.Н.Колмогоров аксиомалар системасы 37
2.5. А.Д.Александров аксиомалар системасы 40
I ТАРАУ КІРІСПЕ
1.1. Мектептегі геометрия аксиоматикасының қазіргі жағдайы туралы
Орта мектепте оқылатын геометрия пәнінде соңғы 50-60 жылда көптеген өзгерістер болды. Кеңес одағында көп уақытқа дейін орта мектепте геометрия Н.Никитиннің [7], содан кейін А.Киселевтің [5] оқулықтарымен оқылған болатын. Бірақ бұл оқулықтарда евклидтік геометрияны аксиоматикалық түрде құруға қатты көңіл бөлінді деп айтуға болмайды. Сонымен қатар бұл оқулықтарда геометриялық фигуралардың кейбір қасиеттері көрнекілік тұрғыдан қарастырылып айқын деп есептеледі де әрі қарай оларды логикалық қатаң тұрғыдан дәлелденбей алынады. Аксиомалар туралы аздаған мәліметтер оқулық соңында қосымша ретінде қысқаша келтіріледі.
Сонымен қатар мектеп оқулықтары сол кездегі математиканың даму деңгейінен едәуір қалыс қалды деп айтуға болады. Математикада кеңінен орын алған жиындық көзқарас тіпті қолданбайтын. Сондай-ақ мектепте оқылатын алгебра курсымен байланысы өте аз болатын.
Ал бұның өзі мектеп оқушылары жоғарғы оқу орындарында оқылатын математикалық пәндерді оқығанда математикаға көзқарасын түбегейлі өзгертуге әкеліп соқты.
1966 жылы Кеңес Одағында мектептегі оқылатын пәндердің мазмұнын анықтау үшін академик А.Колмогоровтың басшылығымен комиссия құрылған болатын. Осы комиссияның жұмысы нәтиежесі мектеп геометриясын оқушыларға баяндау тәсілін өзгерту керек деген қорытындыға келген болатын. Мектеп курсында аксиоматикалық қатаң дедуктивтік түрде геометрияны баяндау керек қажеттілігі айқындалды. Мектептерде жиындар теориясының элементтері кеңінен қолданылатын А.Колмогоровтың аксиомалар системасы енгізілді. Мұнда тек қана геометрияға емес алгебра пәнінде де өзгерістер енгізіліп мектептегі осы екі математикалық пәндердің арасындағы байланыс кеңейтілді.
Мектеп геометриясын А.Колмогровтың басшылығымен жасалған аксиомалар системасына негізделген оқулықпен оқытыла бастады. Мектеп оқытушыларына геометрияны жаңадан жазылған оқулықпен оқыту біраз қиыншылықтарға әкеліп соқты. А.Колмогоровтың аксиомалар системасы математик ғалымдар мен мектеп оқытушылары арасында әртүрлі пікір таласына әкеліп соқты. Мысалы академик Л. Понтрягин «Коммунист» журналында (N14, 1980) бұл системаны қатаң сынға алған болатын. Л. Понтрягинге қарсы, Колмогоров аксиоматикасын қолдап айтылған пікірлер де көп айтылды (мысалы В. Арнольд)
Осы кездерде Кеңес одағында мектепте оқылатын геометрия пәніне арналған аксиомалар системасын құруға конкурс жарияланды. Бұған көптеген математик ғалым-ұстаздар қатысқан болатын (А.Погорелов, А.Александров, Л.Атанасян т.б.). Орыс тілінде жазылған мектеп курсының геометриясының көптеген оқулықтары жарыққа шықты - М. Е. Ващенко-Захарченко, С.Е.Гурьев, А. Ю. Давидов, А.В.Погорелов, В.А.Гусев, Л.С.Атанасян (В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина); А.Д.Александров (А.Л.Вернер, В.И.Рыжик); Г.П.Бевз (В.Г.Бевз, Н.Г.Владимирова); В.Г.Болтянский (М.Б.Волович, А.Д.Семушин); В.М. Клопский (3.А.Скопец, М.И.Ягодовский); А.Н. Колмогоров (А.Ф.Семенович, Р.С.Черкасов); В.Н.Руденко, Г.А.Бахурин, Г.Е.Алимухамбетова және басқалар. Бұл оқулықтардың кейбіреулері Ресей мектептерінде қазір де пайдаланылуда.
Қазіргі кезде Қазақстан мектептерінде А.Погорелов аксиоматикасының негізінде авторлар коллективі (Ж.Қайдасов, И.Бекбоев, А.Абдиев, Г.Досмаганбетов) жазған оқулықтармен геометрия оқытылуда.
Әрбір жаңа оқулық енгізілгенде бұрыннан жұмыс істеп келе жатқан мектеп оқытушылары едәуір қиыншылықтарға кездесіп отырды – қандай себеппен жаңа оқулыққа көшті, қандай ерекшеліктер бар, аксиомалар системасын өзгертуге не себептер болды т.с.с. Жұмыста мектеп оқытушыларының осы сұрақтарына жауап беру мәселесі де қарастырылды.
1.2. Жұмыста қаралған мәселе
Жұмыста алға қойылған негізгі мақсат – мектеп курсында оқылатын евклидтік геометрияның аксиоматикасына негіз болған Гильберт аксиоматикасын, кезінде мектепте қолданылған Колмогоров аксиоматикасын, қазір қолданылып жүрген Погорелов аксиоматикасының ерекшеліктеріне тоқталып оларды салыстыру. Сонымен қатар Вейль аксиомалар системасы мен Александров аксиомалар системасы олардың кей ерекшеліктеріне байланысты қарастырылады
Жұмыста геометрияны оқыту әдістемелік мәселері қарастырылмайды.
II ТАРАУ. АКСИОМАЛАР СИСТЕМАСЫНА ЖАЛПЫ ШОЛУ
2.1. Евклидтен Гильбертке дейінгі геометриялық зерттеулерге жалпы шолу

Ең алғаш рет геометрияны қатаң логикалық түрде
құруға жасалған сәтті талпыныс Евклидтің «Бастамалар» еңбегі деп
есептеледі. Евклид бұл еңбегінде дәлелденбей алынатын тұжырымдарды
келтіреді, олардың кейбірін аксиомалар деп, ал кейбірін постулаттар
деп атаған. Неге бұлай әртүрлі атағаны белгісіз (математика
тарихымен айналысатын ғалымдар әртүрлі пікір айтады). Сонымен қатар
Евклид барлық ұғымдарды анықтауға тырысқан, бұлай істеу мүмкін
еместігін кейінгі параграфтарда айтамыз. Евклид сонымен қатар
геометриялық фигуралардың былайынша ап-айқын деп есептелетін
қасиеттерін дәлелдеуде көп пайдаланады. Ал математиканы қатаң
дедуктивтік түрде құрғанда бұлай істеуге болмайды. Евклидтің
«Бастамаларында» басқа да кемшіліктер бар. Кейінгі математиктер
Евклидтің ол кемшіліктеріне назар аудармай негізінен Евклидтің
қатесі V постулатты дәлелдемей алуы деп есептеп осы постулатты
дәлелдеуге тырысты.
V постулат. Екі түзуді үшінші түзу қиған кезде оның алғашқы екі түзумен жасаған біржақты ішкі бұрыштарының қосындысы екі тік бұрыштан кіші болған кезде алғашқы екі түзу осы біржақты екі бұрыштың қосындысы екі тік бұрыштан кіші болған жақтан қиылысады.
Сонымен Евклидтен кейінгі көптеген математиктер мынандай есеппен айналысты - Евклидтің V постулатын оның қалған аксиомалары мен постулаттарына сүйенбей, V постулатқа эквивалентті тұжырымды қолданбай V постулатты дәлелдеу керек.
V постулатты дәлелдеуге көптеген белгілі математиктер ат салысты:
Ежелгі дүние математиктері – Аристотель, Посидоний, Птоломей, Прокл, Симплиций, Аганис т.б.
Орта ғасыр математиктері – ал-Хазин, ат-Гуси, аш-Шахни, ан-Найризи, Омар Хайиам, ибн ал-Хайсан, Насир-Эд-Дин т.б.
Қайта өрлеу дәуірі мен одан кейінгі математиктер – Клавий, Валлис, Плейфер, Саккери, Ламберт, Лежандр, т.б.
Бұл математиктердің осы постулатты дәлелдеуге арналған еңбектерін Н.Лобачевскийдің өмірбаянын зерттеуші В.Ф.Каган былай сипаттайды - «... Бұны (V постулатты) дәлелдеуге қанша күш жігердің сарп болғанын көз алдымызға елестетудің өзі қиын. Кей адамдар бұны өз өмірлерінің мақсаты етіп қойды, бұған көптеген жылдарын құрбан етті, мистикалық агностицизмге дейін барды, ақыл есінен айрылғандар да болды ...»
Жалпы V постулаттың дәлелденбейтіндігі кейіннен белгілі болды, оның дәлелденбейтіндігін қалай көрсету мәселесін шешетін математикалық әдіс те кейін шықты. Дегенмен V постулатты дәлелдеуге тырысқан ғалымдардың еңбегі зая кеткен жоқ. Олар V постулат пен қалған аксиомалардың арасындағы байланысты анықтады, V постулатқа эквивалентті көптеген тұжырымдар айқындалды. Олардың кейбірін келтіре кетелік:
-
Үшбұрыштың ішкі бұрыштарының қосындысы екі тік бұрышқа тең.
-
Пифагор теоремасы.
-
Жазықтықтағы түзуден бірдей қашықтықта жатқан нүктелердің жиыны түзу болады.
-
Параллель түзулердің ара қашықтығы ақырлы.
-
Кез – келген үшбұрышқа кез-келген ұқсастық коэффициентімен ұқсас үшбұрыштар болады.
-
Бір түзудің бойында жатпайтын үш нүкте арқылы өтетін шеңбер барлық уақытта табылады.
-
Түзуден тысқары жатқан нүкте арқылы оған параллель өтетін түзулер саны біреуден аспайды.
Орыс математигі Н.Лобачевский, неміс математигі К.Гаусс, венгр математигі Я.Бояй V постулат дәлелденбейді деп есептеп оны қарама қарсы тұжырыммен алмастыру арқылы қазір Лобачевскийдің гиперболалық геометриясы деп аталатын жаңа геометрия ашты.
2.2. Геометрияны аксиоматикалық әдіспен құру туралы
Мектепте оқылатын геометрияда математикадағы аксиоматикалық әдіс қолданылады.
Біздің эрамызға дейінгі III ғасырдың басында ежелгі грек дәуірінің ұлы ғалымы Аристотельдің еңбектерінде ғылыми теорияларды құрудың негізгі принциптері бой көрсете бастаған болатын. Осы принциптерді алғаш рет Евклид өзінің «Бастамалар» деген белгілі еңбегінде іске асыруға тырысты. Өзіне дейінгі жинақталған математикалық мәліметтерді талдай отырып дәлелденбей алынатын бірнеше математикалық тұжырымдарды таңдап алып, оларды аксиомалар және постулаттар деп атады (неге бұлай әртүрлі атағаны туралы әртүрлі пікірлер айтылады). Осы дәлелденбей алынған тұжырымдардың салдарлары ретінде теоремаларды дәлелдейді. Евклид осылай құрған система ешқандай елеулі өзгеріссіз біздің дәуіріміздің XIX ғасырына дейін келді. Бірақ Евклид құрған жүйеде көптеген, математика үшін макңызы бар кемшіліктер болды. Тек қана ғасырлар аралығында ғана аксиоматикалық әдістің негізгі принциптері құрылып евклидтік геометрияның логикалық түрде мүлтіксіз аксиоматикалық жүйесі құрылды.
Математикалық теорияны аксиоматикалық түрде құрудың негізгі принциптерін келтірелік:
-
Анықталмай алынатын негізгі (бастапқы) ұғымдардың тізімі келтіріледі. Басқа ұғымдар осы негізгі ұғымдардың және бұрын анықталған басқа ұғымдардың көмегі арқылы анықталуы керек. Бұлай болатын себебі ұғымдардың бәрін бірдей анықтай беру мүмкін емес. Бәрін анықтауға тырыссақ, онда шексіз процесске немесе «логикалық дөңгелекке» тап боламыз.
-
Аксиомалар тізімі келтіріледі. Олар дәлелденбей алынатын тұжырымдар. Тұжырымдарда ұғымдар туралы пікірлер айтылады. Ұғымдар (түптеп келгенде) негізгі ұғымдар осы аксиомаларды қанағаттандыруы керек. Басқаша айтқанда аксиомалар – негізгі ұғымдарға қойылатын талаптар. Сондықтан негізгі ұғымдар аксиомалар арқылы «анықталып тұр» деп те айтады. Қазіргі заманда дәлелденбей алынатын тұжырымдарды аксиомалар және постулаттар деп бөлмейді, негізінен қалыптасқан термин – аксиомалар. Кей ғылым салаларында «постулат» термині де қолданылуы мүмкін.
-
Негізгі ұғымдардың тізімі мен аксиомалар тізімі келтірілгеннен кейін әрбір жаңа енгізілген ұғым қатаң түрде анықталып, әрбір тұжырым қатаң түрде дәлелденіп отыруы керек.Осылай етіп құрылған математикалық теория абстрактылық теория ғана болады. Мысалы негізгі ұғымдар - «нүкте, түзу, арқылы өтеді, т.с.с» болсын.
Құрып отырған теорияда нүкте, түзу, арқылы өтеді, т.с.с деп қандай да бір нақты нәрселер аталып отырған жоқ. Егерде бір нақты объектілер мен олардың арасындағы қатынастар табылып олар теориядағы негізгі ұғымдарға қойылатын талаптарды - аксиомалардың бәрін қанағаттандырса онда оларды осы теорияның интерпретациясы дейді. Интерпретация объектілері мен қатынастары аксиомаларды қанағаттандыратын болғандықтан, олар аксиомалардың салдарлары – теоремаларды қанағаттандырады. Сонымен интерпретацияда негізгі ұғымдарға нақты мағына береміз.
Сонымен біз аксиоматикалық түрде теория құрғанда тек қана абстрактылық объектілермен жұмыс істейміз – тек аксиомалардың логикалық салдарларын зерттейміз.
Әрине осылай етіп абстрактылық теория құрған кезде біздің аксиомалар системасынан бірін бірі жоққа шығаратын тұжырымдар дәлелденбейтініне сенімді болуымыз керек. Аксиомалар системасына қойылатын бұндай талап – аксиомалар системасының қайшылықсыз болуы керек деген талап болады. Геометриялық аксиомалар системасының қайшылықсыздығын нақты сандар арқылы құрылған интерпретация арқылы шешуге болады. Жалпы бұл талап орындалмаса, ондай аксиомалар системасының керегі жоқ, бұл системада кез – келген тұжырымды дәлелдеуге болады. Сондықтан аксиомалар системасын құрғанда бірден қайшылықсыздық мәселесі шешілуі керек.
Аксиомалар системасына қойылатын тағы бір талап – аксиомалар системасының тәуелсіздігі. Бұл талап бойынша әрбір аксиоманы қалған аксиомалардың көмегі арқылы дәлелдеуге болмайтын болу керек. Былайынша айтқанда аксиомалардың ішіне «жасырын теоремалар» кірмеуі керек. Бұны кейде аксиомалар системасының минималдылығы деп те атайды. Бұл талап алдыңғы келтірілген қайшылықсыздық сияқты өте қатаң талап емес. Кейде, әсіресе мектеп курсындағы геометрияда, кей теоремалардың дәлелдеуі оқушыларға түсінікті болуы үшін аксиомалар системасын тәуелді қылып алады. Аксиомалар системасының тәуелсіздігін зерттеуді интерпретациялар құру арқылы шешуге болады. Бұл жерде Евклид құрған аксиомалар системасындағы V постулаттың қалған аксиомалардан тәуелсіздігін шешу мәселесі екі мың жылдай уақыт алғанын айта кеткен жөн (ол кезде аксиомалар системасына қойылатын талаптар, оларды қалай шешу мәселесі, жалпы аксиомалар системасы деген не сияқты сұрақтар математиктер алдына айқын қойылмаған болатын).
Аксиомалар системасына қойылатын тағы бір талап – аксиомалар системасының толықтылығы. Бұл талап бойынша аксиомалар осы теорияның кез – келген тұжырымын дәлелдеуге немесе жоққа шығаруға жеткілікті болуы керек. Кейде неғұрлым «тереңірек» жатқан математикалық байланыстарды зерттеу үшін аксиомалар системасын әдейі толық емес қылып алады. Аксиомалар системасының толықтылығын кей жағдайда аксиомалар системасының жеткіліктілігі деп те атайды.
Бұл дипломдық жұмыста тек қана евклидтік геометрияның аксиомалар системасы туралы айтылады. Сондықтан біз тек қана евклидтік геометрияға қарсы мәселелерді қарастырамыз.
Сонымен геометрияның аксиомалар системасын құрғанда құрушыда негізгі ұғымдар мен аксималарды таңдауда едәуір еркіндік болады екен. Сондықтан да евклидтік геометрияның көптеген ғалымдар құрған аксиомалар системасы бар, олардың көбі мектеп оқушыларына геометрияны оқытқанда олардың түсінуіне жеңіл болсын деген оймен жасалған. Дипломдық жұмыста көп тараған аксиомалар системасына шолу жасалып, олардың ерекшеліктеріне тоқталмақпыз.
XIX ғасырдың ортасына дейін геометрия Евклидтің «Бастамалардағы» келтірілген системаға негізделді деп айтуға болады (аздаған енгізілген өзгерістер онша елеулі бола қойған жоқ). XIX ғасырдың екінші жартысынан бастап жалпы математиканы негіздеу мәселелері өріс алды. Осы кезде геометрияны негіздеу мәселесімен көптеген зерттеулер жүргізілді. Осы кездегі ең көп танымал болған неміс ғалымы Давид Гильберттің 1899 жылы шыққан «Геометрияның негіздері» деген еңбегі болатын. Бұл еңбекте евклидтік геометрия өте қатаң түрде құрылды. Бұл еңбек тұралы кейін толығырақ айтылады.
Гильберттің аксиомалар системасынан басқа 1904 жылы Фридрих Шурдың аксиомалар системасын айта кетелік. Бұл аксиоматиканың идеясын Кеңес Одағының академигі А.Н.Тихонов бастаған математиктер тобы мектеп геометриясын құруда қолданды. Осы кездерде В.Ф.Каган (ара қашықтыққа негізделген), Г.Вейль (векторлық кеңістікке негізделген) аксиомалар системасын келтірді.
Евклидтік геометрияның негізгі үш талапты (қайшылықсыздық, тәуелсіздік, толықтық) қанағаттандыратын аксиомалар системасы құрылғанмен, мектеп оқушыларының жас ерекшеліктеріне, мектепте оқылатын математика және басқа пәндердің деңгейіне сәйкес келетін талаптарды толық қанағаттандыратын «қолайлы» аксиомалар системасы туралы сұрақ толық шешілді деп айту қиындау.
2.3. Гильберт аксиомалар системасы
1899 ж. неміс математигі Д.Гильберттің «Геометрия негіздемелері» атты атақты кітабы басылып шықты.Бұл кітапта тұңғыш рет евклидтік геометрияны логикалық жолмен құруға жеткілікті болатын аксиомалардың тізімі келтірілді.Осы күнгі математикадағы аксиоматикалық әдіс пен математикалық структуралардың қазіргі тұрғыдан қарастырылатын теориясы (яғни Н.Бурбаки тобы қалыптастырған түсініктер) Гильберттің осы «Геометрия негіздемелерінен» басталады деуге болады.
2.1.1. Негізгі ұғымдар
Гильберттің баяндауы бойынша
евклидтік кеңістік структурасының базасы үш жиыннан
–  жиындарынан тұрады.
Бірінші
жиындарынан тұрады.
Бірінші  жиынының
элементтері нүктелер деп аталады
да
жиынының
элементтері нүктелер деп аталады
да  әріптерімен
белгіленеді,
әріптерімен
белгіленеді,  жиынының
элементтері түзулер деп аталады
да
жиынының
элементтері түзулер деп аталады
да  әріптерімен
белгіленеді,
әріптерімен
белгіленеді,  жиынының
элементтері жазықтықтар деп аталады
да
жиынының
элементтері жазықтықтар деп аталады
да  (немесе
(немесе
 ) әріптерімен
белгіленеді.
) әріптерімен
белгіленеді.
Базаның жиындары үстінде «тиісті» (немесе жатады), «арасында жатады» және «конгруэнт» сөздерімен белгіленетін қатынастар болады. Бұл қатынастардың нақты сипаты қандай екендігі елеулі рөл атқармайды,тек сол қатынастар төменде тізімі келтірілетін аксиомаларды қанағаттандыратын болса болғаны.
Сонымен Гильберт бойынша негізгі ұғымдар – нүкте,түзу, жазықтық және олардың арасындағы қатынастар – тиісті, арасында жатады, конгруэнт.
2.1.2. Аксиомалар
Гильберттің негізгі ұғымдарға қойылатын талаптары 20 аксиома түрінде айтылып, олар 5 топқа бөлінген.
I топ. Тиістілік аксиомалары.
«Жатады»,яғни тиістілік
белгісін  таңбасы арқылы белгілейміз.
Бірінші топта мынадай сегіз аксиома бар:
таңбасы арқылы белгілейміз.
Бірінші топта мынадай сегіз аксиома бар:

 ⃓
⃓ 
Мұндай
 түзуі біреу ғана болады
(ол
түзуі біреу ғана болады
(ол деп те
белгіленеді).
деп те
белгіленеді).

 ⃓
⃓ 
 Бір түзуде жатпайтын ең
кем дегенде үш нүкте болады.Егер
Бір түзуде жатпайтын ең
кем дегенде үш нүкте болады.Егер  нүктелері бір түзуде
жатпаса,былай жазып көрсетеді:
нүктелері бір түзуде
жатпаса,былай жазып көрсетеді:  немесе
немесе
 немесе
немесе 

 ⃓
⃓
Мұндай жазықтық біреу ғана
болады (ол ( ) деп те
белгіленеді).
) деп те
белгіленеді).

 ⃓
⃓ 

Бұл жағдайда
« а
түзуі
 жазықтығында жатады»
дейді немесе «
жазықтығында жатады»
дейді немесе « жазықтығы
а
түзуінен өтеді»
дейді.
жазықтығы
а
түзуінен өтеді»
дейді.
 ⃓
⃓
 ⃓
⃓
Бұл аксиомалар бойынша мынадай теореманы дәлелдеуге болады: кез келген жазықтықта бір түзудің бойында жатпайтын үш нүкте болады.
II топ. Рет аксиомалары.
Егер
 нүктесі
нүктесі  және
және
 нүктелерінің арасында
жататын болса,былай жазылады
нүктелерінің арасында
жататын болса,былай жазылады 

шағым қалдыра аласыз

















