
Дата: _____________________
Тема урока: Физический и геометрический смысл производной. Касательная к графику функции.
Тип урока: урок изучения нового материала.
Цели урока:
Учащиеся должны знать:
-
что называется угловым коэффициентом прямой;
-
углом между прямой и осью Ох;
-
в чем состоит геометрический смысл производной;
-
уравнение касательной к графику функции;
-
способ построения касательной к параболе;
-
уметь применять теоретические знания на практике.
Задачи урока:
Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями механический и геометрический смысл производной.
Воспитательные: формировать у учащихся научное мировоззрение.
Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.
Методы организации учебно-познавательной деятельности:
-
наглядные;
-
практические;
-
по мыслительной деятельности: индуктивный;
-
по усвоению материала: частично-поисковый, репродуктивный;
-
стимулирующие: поощрения;
-
контроля: устный фронтальный опрос.
План урока
-
Устные упражнения (найти производную)
-
Изучение нового материала
-
Решение заданий.
-
Подведение итогов урока.
Оборудование: карточки
Ход урока
“Человек лишь там чего – то добивается, где он верит в свои силы”
Л. Фейербах
I. Организационный момент.
Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.
Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.
Устный счет
1. Найдите производные:
(![]() ) ' (
) ' (![]() ) ' (
) ' (![]() )'
)'
![]() ',
(
',
(![]() )' , (4sin
x)', (cos2x)', (tg x)',
)' , (4sin
x)', (cos2x)', (tg x)', ![]() '
'
2. Логический тест.
а) Вставить пропущенное выражение.
|
5х3-6х |
15х2-6 |
30х |
|
2sinx |
2cosx … |
|
|
cos2x |
… … |
|
II. Изучение нового материала.
Пойдем по пути Ньютона и Лейбница и посмотрим, каким способом можно анализировать процесс, рассматривая его как функцию времени.
Введем несколько понятий, которые помогут нам в дальнейшем.
Графиком линей ной функции
y=kx+ b является прямая, число k называют угловым коэффициентом
прямой k=tg![]() , где
, где ![]() – угол прямой, то есть угол между
этой прямой и положительным направлением оси Ох.
– угол прямой, то есть угол между
этой прямой и положительным направлением оси Ох.
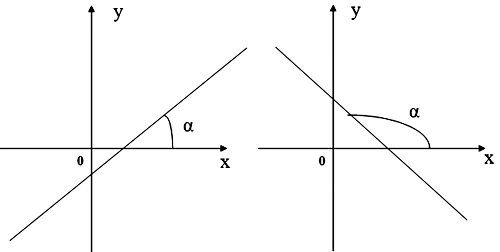
Рисунок 1

Рассмотрим график функции у=f(х). Проведем секущую через любые две точки, например, секущую АМ. (Рис.2)
Угловой коэффициент секущей
k=tg![]() . В прямоугольном треугольнике
АМС (объясните почему?). Тогда tg
. В прямоугольном треугольнике
АМС (объясните почему?). Тогда tg![]() =
= ![]() =
= ![]() , что с точки зрения физики есть
величина средней скорости протекания любого процесса на данном
промежутке времени, например, скорости изменения расстояния в
механике.
, что с точки зрения физики есть
величина средней скорости протекания любого процесса на данном
промежутке времени, например, скорости изменения расстояния в
механике.
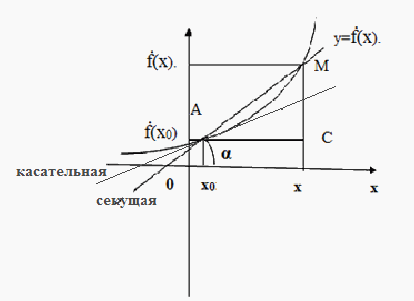
Рисунок 2
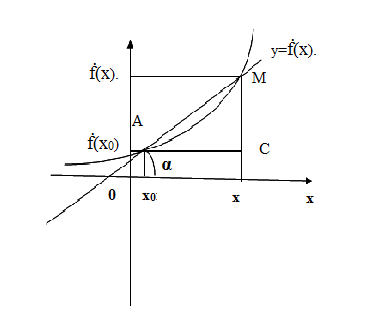
Рисунок 3
Сам термин “скорость” характеризует зависимость изменения одной величины от изменения другой, и последняя необязательно должна быть временем.
Итак, тангенс угла наклона
секущей tg![]() =
= ![]() .
.
Нас интересует зависимость
изменения величин в более короткий промежуток времени. Устремим
приращение аргумента к нулю. Тогда правая часть формулы –
производная функции в точке А (объясните почему).
Если ![]() х – 0, то точка М движется по
графику к точке А, значит прямая АМ приближается к некоторой прямой
АВ, которая является касательной к графику функции у = f(х)
в точке А.
(Рис.3)
х – 0, то точка М движется по
графику к точке А, значит прямая АМ приближается к некоторой прямой
АВ, которая является касательной к графику функции у = f(х)
в точке А.
(Рис.3)
Угол наклона секущей стремится к углу наклона касательной.
Геометрический смысл производной состоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в точке.
Механический смысл производной.
Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, то есть новая характеристика изучаемого процесса. Эту величину Лейбниц назвал производной, а Ньютон говорил, что производной называется сама мгновенная скорость.
III. Решение заданий.
-
Показать на доске.
Угловой коэффициент касательной к кривой f(х) = х3 в точке х0 – 1 есть значение производной этой функции при х = 1. f’(1) = 3х2; f’(1) = 3.
Ответ: 3.
№ 159, № 161 – у доски.
Вопросы к классу:
-
Каков физический смысл производной перемещения? (Скорость).
-
Можно ли найти производную скорости? Используется ли эта величина в физике? Как она называется? (Ускорение).
-
Мгновенная скорость равна нулю. Что можно сказать о движении тела в это момент? (Это момент остановки).
-
Каков физический смысл следующих высказываний: производная движения равна нулю в точке t0; при переходе через точку t0 производная меняет знак? ( Тело останавливается; меняется направление движения на противоположное).
IV. Подведение итогов урока
1) В чем состоит геометрический
смысл производной?
2) В чем состоит механический смысл производной?
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Физический и геометрический смысл производной. Касательная к графику функции.
Физический и геометрический смысл производной. Касательная к графику функции.
Дата: _____________________
Тема урока: Физический и геометрический смысл производной. Касательная к графику функции.
Тип урока: урок изучения нового материала.
Цели урока:
Учащиеся должны знать:
-
что называется угловым коэффициентом прямой;
-
углом между прямой и осью Ох;
-
в чем состоит геометрический смысл производной;
-
уравнение касательной к графику функции;
-
способ построения касательной к параболе;
-
уметь применять теоретические знания на практике.
Задачи урока:
Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями механический и геометрический смысл производной.
Воспитательные: формировать у учащихся научное мировоззрение.
Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.
Методы организации учебно-познавательной деятельности:
-
наглядные;
-
практические;
-
по мыслительной деятельности: индуктивный;
-
по усвоению материала: частично-поисковый, репродуктивный;
-
стимулирующие: поощрения;
-
контроля: устный фронтальный опрос.
План урока
-
Устные упражнения (найти производную)
-
Изучение нового материала
-
Решение заданий.
-
Подведение итогов урока.
Оборудование: карточки
Ход урока
“Человек лишь там чего – то добивается, где он верит в свои силы”
Л. Фейербах
I. Организационный момент.
Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.
Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.
Устный счет
1. Найдите производные:
(![]() ) ' (
) ' (![]() ) ' (
) ' (![]() )'
)'
![]() ',
(
',
(![]() )' , (4sin
x)', (cos2x)', (tg x)',
)' , (4sin
x)', (cos2x)', (tg x)', ![]() '
'
2. Логический тест.
а) Вставить пропущенное выражение.
|
5х3-6х |
15х2-6 |
30х |
|
2sinx |
2cosx … |
|
|
cos2x |
… … |
|
II. Изучение нового материала.
Пойдем по пути Ньютона и Лейбница и посмотрим, каким способом можно анализировать процесс, рассматривая его как функцию времени.
Введем несколько понятий, которые помогут нам в дальнейшем.
Графиком линей ной функции
y=kx+ b является прямая, число k называют угловым коэффициентом
прямой k=tg![]() , где
, где ![]() – угол прямой, то есть угол между
этой прямой и положительным направлением оси Ох.
– угол прямой, то есть угол между
этой прямой и положительным направлением оси Ох.

Рисунок 1

Рассмотрим график функции у=f(х). Проведем секущую через любые две точки, например, секущую АМ. (Рис.2)
Угловой коэффициент секущей
k=tg![]() . В прямоугольном треугольнике
АМС (объясните почему?). Тогда tg
. В прямоугольном треугольнике
АМС (объясните почему?). Тогда tg![]() =
= ![]() =
= ![]() , что с точки зрения физики есть
величина средней скорости протекания любого процесса на данном
промежутке времени, например, скорости изменения расстояния в
механике.
, что с точки зрения физики есть
величина средней скорости протекания любого процесса на данном
промежутке времени, например, скорости изменения расстояния в
механике.

Рисунок 2
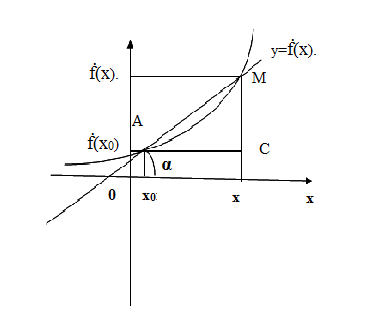
Рисунок 3
Сам термин “скорость” характеризует зависимость изменения одной величины от изменения другой, и последняя необязательно должна быть временем.
Итак, тангенс угла наклона
секущей tg![]() =
= ![]() .
.
Нас интересует зависимость
изменения величин в более короткий промежуток времени. Устремим
приращение аргумента к нулю. Тогда правая часть формулы –
производная функции в точке А (объясните почему).
Если ![]() х – 0, то точка М движется по
графику к точке А, значит прямая АМ приближается к некоторой прямой
АВ, которая является касательной к графику функции у = f(х)
в точке А.
(Рис.3)
х – 0, то точка М движется по
графику к точке А, значит прямая АМ приближается к некоторой прямой
АВ, которая является касательной к графику функции у = f(х)
в точке А.
(Рис.3)
Угол наклона секущей стремится к углу наклона касательной.
Геометрический смысл производной состоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в точке.
Механический смысл производной.
Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, то есть новая характеристика изучаемого процесса. Эту величину Лейбниц назвал производной, а Ньютон говорил, что производной называется сама мгновенная скорость.
III. Решение заданий.
-
Показать на доске.
Угловой коэффициент касательной к кривой f(х) = х3 в точке х0 – 1 есть значение производной этой функции при х = 1. f’(1) = 3х2; f’(1) = 3.
Ответ: 3.
№ 159, № 161 – у доски.
Вопросы к классу:
-
Каков физический смысл производной перемещения? (Скорость).
-
Можно ли найти производную скорости? Используется ли эта величина в физике? Как она называется? (Ускорение).
-
Мгновенная скорость равна нулю. Что можно сказать о движении тела в это момент? (Это момент остановки).
-
Каков физический смысл следующих высказываний: производная движения равна нулю в точке t0; при переходе через точку t0 производная меняет знак? ( Тело останавливается; меняется направление движения на противоположное).
IV. Подведение итогов урока
1) В чем состоит геометрический
смысл производной?
2) В чем состоит механический смысл производной?

шағым қалдыра аласыз















