
Тақырыбы:
Тема: Угол между прямыми и пространстве. Перпендикулярность прямых. Перпендикулярность прямой и плоскости
Сабақтың түрі:
Тип урока: Урок формирования ЗУН
Метод урока: Наглядно-иллюстрированный
Сабақ мақсаты:
Цели урока:
Образовательные: рассмотреть взаимное расположение 2-х прямых в пространстве. Ввести понятие параллельных и скрещивающихся прямых;
Развивающие: доказать теоремы о параллельности прямых и параллельности 3-х прямых
Воспитательные: воспитание на уроке воли и упорства для достижения конечных результатов, активномти, уважительного отношения друг к другу.
Пәнаралық байланыс:
Межпредметные связи: черчение
Көрнекі құралдар,жабдықтар,үлестірмелі қағаздар:
Нагладные пособия,оборудование,раздочный материал: Чертежные принадлежности, учебники
САБАҚ БАРЫСЫ / ХОД УРОКА
Ұйымдастыру кезеңі:
Организационная часть: 5 минут
Өткен тақырыпты қайталау:
Опрос и проверка
пройденного материала:  10 вопросы упр 4 стр
41
10 вопросы упр 4 стр
41
ЖОСПАР/ ПЛАН
Жаңа тақырыпты оқыту:
Изучение нового матертале:
Определение. Две прямые называются перпендикулярными, если угол между ними равен 90°.
Обозначение. ![]() .
.
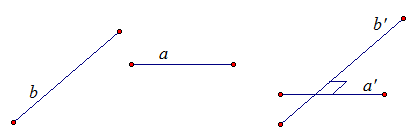
Рис. 1.
Рассмотрим
прямые а и b. Прямые могут пересекаться, скрещиваться, быть
параллельными. Для того, чтобы построить угол между ними нужно
выбрать точку и через нее провести
прямую ![]() , параллельную
прямой а, и
прямую
, параллельную
прямой а, и
прямую ![]() ,
параллельную прямойb. Прямые
,
параллельную прямойb. Прямые ![]() и
и ![]() пересекаются. Угол между ними и есть угол
между прямыми а и b. Если угол равен 90°, то
прямые а и b перпендикулярны.
пересекаются. Угол между ними и есть угол
между прямыми а и b. Если угол равен 90°, то
прямые а и b перпендикулярны.
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Доказательство:
Пусть даны две параллельные
прямые а и b, и прямая с,причем ![]() . Нужно доказать,
что
. Нужно доказать,
что ![]() .
.
Возьмем произвольную
точку М. Через
точку М проведем
прямую ![]() , параллельную
прямой а и
прямую
, параллельную
прямой а и
прямую ![]() ,
параллельную прямой c (рис. 2). Тогда
угол АМС равен 90°.
,
параллельную прямой c (рис. 2). Тогда
угол АМС равен 90°.
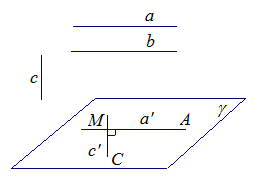
Рис. 2.
Прямая b параллельна
прямой а по условию,
прямая ![]() параллельна
прямой а по построению. Значит,
прямые
параллельна
прямой а по построению. Значит,
прямые ![]() и b параллельны.
и b параллельны.
Имеем, прямые ![]() и b параллельны,
прямые с и
и b параллельны,
прямые с и ![]() параллельны по построению. Значит, угол
между прямыми b и с – это угол между
прямыми
параллельны по построению. Значит, угол
между прямыми b и с – это угол между
прямыми ![]() и
и![]() , то есть
угол АМС, равный 90°. Значит,
прямые b и с перпендикулярны, что и требовалось
доказать.
, то есть
угол АМС, равный 90°. Значит,
прямые b и с перпендикулярны, что и требовалось
доказать.
Определение перпендикулярности прямой и плоскости
Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Обозначение. ![]() .
.
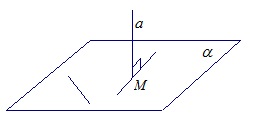
Рис. 3.
Если ![]() ,
то
,
то ![]() . (пересечение а и
. (пересечение а и ![]() )
)
Доказательство:
Напоминание. Прямая и плоскость или пересекаются в одной точке, или параллельны, или прямая лежит в плоскости.
Если
прямая а параллельна
плоскости![]() (рис. 4), то в
плоскости
(рис. 4), то в
плоскости ![]() можно провести прямую
можно провести прямую ![]() ,
параллельную прямой а. Получаем
противоречие с определением перпендикулярности прямой и
плоскости.
,
параллельную прямой а. Получаем
противоречие с определением перпендикулярности прямой и
плоскости.
Если
прямая а лежит в
плоскости![]() (рис. 5), то в
плоскости
(рис. 5), то в
плоскости ![]() можно провести прямую
можно провести прямую ![]() ,
параллельную прямой а. Опять получаем
противоречие с определением перпендикулярности прямой и
плоскости.
,
параллельную прямой а. Опять получаем
противоречие с определением перпендикулярности прямой и
плоскости.
Значит, если
прямая а перпендикулярна
плоскости ![]() ,
то она пересекается с ней.
,
то она пересекается с ней.
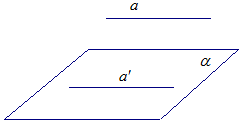
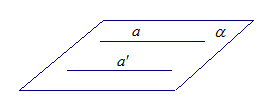
Рис. 4
Рис. 5
Теорема
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перепедикуляная к этой плоскости.
Доказательство.
Пусть
прямая а параллельна
прямой а1.
Прямая а перепендикулярна
плоскости![]() . Докажем, что и
прямая а1перепендикулярна плоскости
. Докажем, что и
прямая а1перепендикулярна плоскости![]() .
.
Прямая а перпендикулярна
плоскости ![]() .
Значит, она перпендикулярна любой прямой, лежащей в этой плоскости.
Прямая х лежит в
плоскости
.
Значит, она перпендикулярна любой прямой, лежащей в этой плоскости.
Прямая х лежит в
плоскости ![]() ,
значит,
,
значит, ![]() (см. рис. 6).
(см. рис. 6).
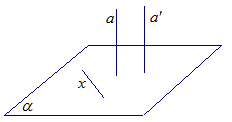
Рис 6.
Прямая а перпендикулярна
прямой х, а
прямая а1 параллельна прямой а. Значит,
прямая а1 перпендикулярна прямой х по лемме.
Прямую х мы выбирали
произвольно. Значит, прямая а1 перпендикулярна любой прямой в
плоскости ![]() ,
то есть прямая х перпендикулярна
плоскости
,
то есть прямая х перпендикулярна
плоскости ![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Нығайту:
Закрепление нового материала:
Дан
параллелепипед ABCDA1B1C1D1 (рис. 9).
Докажите, что ![]() и
и ![]() ,
если
,
если ![]() .
.
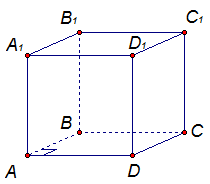
Рис. 9.
Доказательство.
ABCD – прямоугольник, так
как в параллелограмме ABCD угол ![]() .
.
Прямая В1С1 параллельна прямой ВС, а прямая ВС перпендикулярна прямой DС. Значит, по лемме, прямая DС перпендикулярна В1С1.
Прямая АВ перпендикулярна прямой ВС, а ВС параллельна прямой A1D1. Значит, по лемме, прямая АВ перпендикулярна A1D1. Задача доказана.
Рассмотрим другое доказательство факта,
что ![]() .
.
Угол DCB равен углу между прямыми DC и В1С1. Угол DCB – прямой. Значит, прямые DС и В1С1 перпендикулярны.
Задача 2
В тетраэдре ABCD
- ![]() . Докажите,
что
. Докажите,
что ![]() ,
где М и N середины
ребер АВ и АС.
,
где М и N середины
ребер АВ и АС.
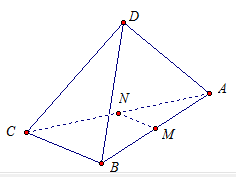
Рис. 10.
Доказательство.
MN – средняя линия треугольника АВС. По свойству средней линии, ВС параллельна MN.
Прямые ВС и MN параллельны, а прямые ВС и AD перпендикулярны. Значит, по лемме, прямые AD и MN перпендикулярны, что и требовалось доказать.
Бағалау
Выставления оценок
Үй тапсырмасы:
Домашнее задание: §10. упр 4 стр
41
Өздік жұмысы:
Самостоятельная работа:
№ 1,2,3,5,6 , 1
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Геометрия. Угол между прямыми и пространстве. Перпендикулярность прямых. Перпендикулярность прямой и плоскости
Геометрия. Угол между прямыми и пространстве. Перпендикулярность прямых. Перпендикулярность прямой и плоскости
Тақырыбы:
Тема: Угол между прямыми и пространстве. Перпендикулярность прямых. Перпендикулярность прямой и плоскости
Сабақтың түрі:
Тип урока: Урок формирования ЗУН
Метод урока: Наглядно-иллюстрированный
Сабақ мақсаты:
Цели урока:
Образовательные: рассмотреть взаимное расположение 2-х прямых в пространстве. Ввести понятие параллельных и скрещивающихся прямых;
Развивающие: доказать теоремы о параллельности прямых и параллельности 3-х прямых
Воспитательные: воспитание на уроке воли и упорства для достижения конечных результатов, активномти, уважительного отношения друг к другу.
Пәнаралық байланыс:
Межпредметные связи: черчение
Көрнекі құралдар,жабдықтар,үлестірмелі қағаздар:
Нагладные пособия,оборудование,раздочный материал: Чертежные принадлежности, учебники
САБАҚ БАРЫСЫ / ХОД УРОКА
Ұйымдастыру кезеңі:
Организационная часть: 5 минут
Өткен тақырыпты қайталау:
Опрос и проверка
пройденного материала:  10 вопросы упр 4 стр
41
10 вопросы упр 4 стр
41
ЖОСПАР/ ПЛАН
Жаңа тақырыпты оқыту:
Изучение нового матертале:
Определение. Две прямые называются перпендикулярными, если угол между ними равен 90°.
Обозначение. ![]() .
.

Рис. 1.
Рассмотрим
прямые а и b. Прямые могут пересекаться, скрещиваться, быть
параллельными. Для того, чтобы построить угол между ними нужно
выбрать точку и через нее провести
прямую ![]() , параллельную
прямой а, и
прямую
, параллельную
прямой а, и
прямую ![]() ,
параллельную прямойb. Прямые
,
параллельную прямойb. Прямые ![]() и
и ![]() пересекаются. Угол между ними и есть угол
между прямыми а и b. Если угол равен 90°, то
прямые а и b перпендикулярны.
пересекаются. Угол между ними и есть угол
между прямыми а и b. Если угол равен 90°, то
прямые а и b перпендикулярны.
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Доказательство:
Пусть даны две параллельные
прямые а и b, и прямая с,причем ![]() . Нужно доказать,
что
. Нужно доказать,
что ![]() .
.
Возьмем произвольную
точку М. Через
точку М проведем
прямую ![]() , параллельную
прямой а и
прямую
, параллельную
прямой а и
прямую ![]() ,
параллельную прямой c (рис. 2). Тогда
угол АМС равен 90°.
,
параллельную прямой c (рис. 2). Тогда
угол АМС равен 90°.

Рис. 2.
Прямая b параллельна
прямой а по условию,
прямая ![]() параллельна
прямой а по построению. Значит,
прямые
параллельна
прямой а по построению. Значит,
прямые ![]() и b параллельны.
и b параллельны.
Имеем, прямые ![]() и b параллельны,
прямые с и
и b параллельны,
прямые с и ![]() параллельны по построению. Значит, угол
между прямыми b и с – это угол между
прямыми
параллельны по построению. Значит, угол
между прямыми b и с – это угол между
прямыми ![]() и
и![]() , то есть
угол АМС, равный 90°. Значит,
прямые b и с перпендикулярны, что и требовалось
доказать.
, то есть
угол АМС, равный 90°. Значит,
прямые b и с перпендикулярны, что и требовалось
доказать.
Определение перпендикулярности прямой и плоскости
Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Обозначение. ![]() .
.

Рис. 3.
Если ![]() ,
то
,
то ![]() . (пересечение а и
. (пересечение а и ![]() )
)
Доказательство:
Напоминание. Прямая и плоскость или пересекаются в одной точке, или параллельны, или прямая лежит в плоскости.
Если
прямая а параллельна
плоскости![]() (рис. 4), то в
плоскости
(рис. 4), то в
плоскости ![]() можно провести прямую
можно провести прямую ![]() ,
параллельную прямой а. Получаем
противоречие с определением перпендикулярности прямой и
плоскости.
,
параллельную прямой а. Получаем
противоречие с определением перпендикулярности прямой и
плоскости.
Если
прямая а лежит в
плоскости![]() (рис. 5), то в
плоскости
(рис. 5), то в
плоскости ![]() можно провести прямую
можно провести прямую ![]() ,
параллельную прямой а. Опять получаем
противоречие с определением перпендикулярности прямой и
плоскости.
,
параллельную прямой а. Опять получаем
противоречие с определением перпендикулярности прямой и
плоскости.
Значит, если
прямая а перпендикулярна
плоскости ![]() ,
то она пересекается с ней.
,
то она пересекается с ней.


Рис. 4
Рис. 5
Теорема
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перепедикуляная к этой плоскости.
Доказательство.
Пусть
прямая а параллельна
прямой а1.
Прямая а перепендикулярна
плоскости![]() . Докажем, что и
прямая а1перепендикулярна плоскости
. Докажем, что и
прямая а1перепендикулярна плоскости![]() .
.
Прямая а перпендикулярна
плоскости ![]() .
Значит, она перпендикулярна любой прямой, лежащей в этой плоскости.
Прямая х лежит в
плоскости
.
Значит, она перпендикулярна любой прямой, лежащей в этой плоскости.
Прямая х лежит в
плоскости ![]() ,
значит,
,
значит, ![]() (см. рис. 6).
(см. рис. 6).

Рис 6.
Прямая а перпендикулярна
прямой х, а
прямая а1 параллельна прямой а. Значит,
прямая а1 перпендикулярна прямой х по лемме.
Прямую х мы выбирали
произвольно. Значит, прямая а1 перпендикулярна любой прямой в
плоскости ![]() ,
то есть прямая х перпендикулярна
плоскости
,
то есть прямая х перпендикулярна
плоскости ![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Нығайту:
Закрепление нового материала:
Дан
параллелепипед ABCDA1B1C1D1 (рис. 9).
Докажите, что ![]() и
и ![]() ,
если
,
если ![]() .
.

Рис. 9.
Доказательство.
ABCD – прямоугольник, так
как в параллелограмме ABCD угол ![]() .
.
Прямая В1С1 параллельна прямой ВС, а прямая ВС перпендикулярна прямой DС. Значит, по лемме, прямая DС перпендикулярна В1С1.
Прямая АВ перпендикулярна прямой ВС, а ВС параллельна прямой A1D1. Значит, по лемме, прямая АВ перпендикулярна A1D1. Задача доказана.
Рассмотрим другое доказательство факта,
что ![]() .
.
Угол DCB равен углу между прямыми DC и В1С1. Угол DCB – прямой. Значит, прямые DС и В1С1 перпендикулярны.
Задача 2
В тетраэдре ABCD
- ![]() . Докажите,
что
. Докажите,
что ![]() ,
где М и N середины
ребер АВ и АС.
,
где М и N середины
ребер АВ и АС.

Рис. 10.
Доказательство.
MN – средняя линия треугольника АВС. По свойству средней линии, ВС параллельна MN.
Прямые ВС и MN параллельны, а прямые ВС и AD перпендикулярны. Значит, по лемме, прямые AD и MN перпендикулярны, что и требовалось доказать.
Бағалау
Выставления оценок
Үй тапсырмасы:
Домашнее задание: §10. упр 4 стр
41
Өздік жұмысы:
Самостоятельная работа:
№ 1,2,3,5,6 , 1

шағым қалдыра аласыз















