
Геометриялық емес есептердің геометриялық шешімдері
Мектеп бағдарламасы математикасында жоқ теңдеулер жүйесін геометриялық әдіспен шешуді ұсынамыз.
Мысал
1.  теңдеулер жүйесін
шешіп,
теңдеулер жүйесін
шешіп,  мәнін
тап.
мәнін
тап.
Шешуі. 1-ші және 2-ші теңдеулерді
қосып,  аламыз. 3-ші
теңдеудегі
аламыз. 3-ші
теңдеудегі  -тің мәнін алмастырып, 2-ші
теңдеуге қоямыз, яғни
-тің мәнін алмастырып, 2-ші
теңдеуге қоямыз, яғни  . Сонымен
. Сонымен
 тең болады.
Егер
тең болады.
Егер  болса, онда 1-ші теңдеуге
алмастырып қойғанда
болса, онда 1-ші теңдеуге
алмастырып қойғанда  аламыз. Әрі қарай теңдеуді
шешіп,
аламыз. Әрі қарай теңдеуді
шешіп,  екенін анықтаймыз.
Бұдан
екенін анықтаймыз.
Бұдан  және
және
 болатынын табамыз.
Сонда
болатынын табамыз.
Сонда  . [1]
. [1]
Бірақ бұл жүйені шығармай
және  өрнегінің мәнін таппай-ақ
шешімін табуға болатынын көрсетейік.
өрнегінің мәнін таппай-ақ
шешімін табуға болатынын көрсетейік.
Пифагор теоремасына кері
теорема бойынша  және 3 сандары
сәйкесінше
және 3 сандары
сәйкесінше  үшбұрышының каттеттері мен
гипотенузасы болсын (мұндағы
үшбұрышының каттеттері мен
гипотенузасы болсын (мұндағы  -тік
бұрыш).
-тік
бұрыш).
Онда екінші теңдеуді
қарастыратын болсақ,  және 4 сандары
сәйкесінше
және 4 сандары
сәйкесінше  үшбұрышының катеттері мен
гипотенузасы болсын (мұндағы
үшбұрышының катеттері мен
гипотенузасы болсын (мұндағы  -тік
бұрыш).
-тік
бұрыш).
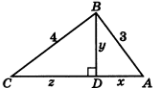
1.1- сурет.
Жүйенің үшінші
теңдеуіндегі  саны
саны
 және
және  сандарының пропорционалдық
ортасы. Онда тік бұрышты үшбұрыштың пропорционалдық кесінділері
туралы теорема бойынша
сандарының пропорционалдық
ортасы. Онда тік бұрышты үшбұрыштың пропорционалдық кесінділері
туралы теорема бойынша  үшбұрышы тік бұрышты үшбұрыш
болады. Енді
үшбұрышы тік бұрышты үшбұрыш
болады. Енді  өрнегін
қарастырайық. [1]
өрнегін
қарастырайық. [1]

Жауабы: 12
Мысал
2.  өрнегінің мәнін тап,
егер
өрнегінің мәнін тап,
егер  ,
,
 ,
,
 және
және  болса.
болса.
Шешуі. Біріншіден,  және
және
 . Шындығында,
егер
. Шындығында,
егер  немесе
немесе
 болса,
онда
болса,
онда  . Алайда, 1 және 0 сандар
жұбы
. Алайда, 1 және 0 сандар
жұбы  теңдеуін қанағаттандырмайды.
Сәйкесінше, 0 және 2 сандар жұбы
теңдеуін қанағаттандырмайды.
Сәйкесінше, 0 және 2 сандар жұбы  теңдеуін
қанағаттандырмайды.
теңдеуін
қанағаттандырмайды.
Екіншіден,  және
және
 шарттары
үшін
шарттары
үшін  және
және
 теңдеулерін
сәйкесінше
теңдеулерін
сәйкесінше
 және
және 
түрде түрлендіруге болады. [1], [4]
Үшіншіден, алдыңғы мысалдың шешу әдісін пайдаланатын болсақ, онда

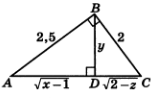
1.2 - сурет
Жауабы: 5
Мысал
3.  және
және
 оң сандары
үшін,
оң сандары
үшін,  ,
,
 ,
,
 шарттарымен
берілген
шарттарымен
берілген  өрнегінің мәнін
тап.
өрнегінің мәнін
тап.
Шешуі. Есептің берілген үш шартын жүйеге келтіреміз:

Пифагор теоремасына кері
теорема бойынша  ,
,
 және 5 сандары тік
бұрышы
және 5 сандары тік
бұрышы  болатын
болатын
 үшбұрышының сәйкесінше
катеттері мен гипотенузасы болсын ал,
үшбұрышының сәйкесінше
катеттері мен гипотенузасы болсын ал,
 ,
,
 және 13 сандары
бұрышы
және 13 сандары
бұрышы  болатын
болатын
 үшбұрышының қабырғалары
болсын. Сондай-ақ,
үшбұрышының қабырғалары
болсын. Сондай-ақ,  ,
,
 және 12 сандары
бұрышы
және 12 сандары
бұрышы  болатын
болатын
 үшбұрышының қабырғалары
болсын.
үшбұрышының қабырғалары
болсын.
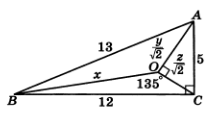
1.3 – сурет
 болғандықтан,
болғандықтан,  үшбұрышында
үшбұрышында  .
.




 өрнегі
берілген
өрнегі
берілген  үшбұрышының төрт еселенген
мәніне тең, яғни
үшбұрышының төрт еселенген
мәніне тең, яғни  .
.
Жауабы: 120.
Мысал
4.  және
және
 оң сандары
үшін,
оң сандары
үшін,  ,
,
 ,
,
 теңдеулер жүйесінің
мәнін таппай,
теңдеулер жүйесінің
мәнін таппай,  өрнегінің мәнін
тап.
өрнегінің мәнін
тап.
Шешуі.

 .
.
 үшбұрышының ауданы 6-ға
тең болғандықтан,
үшбұрышының ауданы 6-ға
тең болғандықтан,  .
.
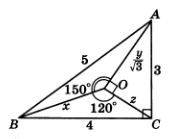
1.4-сурет
Мысал
5.  теңдеулер жүйесін
шешіңіз.
теңдеулер жүйесін
шешіңіз.
Шешуі. Егер
 ,
,
 және
және  болса,
онда
болса,
онда  және
және
 - катеттері,
ал
- катеттері,
ал  - гипотенузасы, сонымен
қатар
- гипотенузасы, сонымен
қатар  бұрышы тік
болатындай
бұрышы тік
болатындай  үшбұрышы бар
болады.
үшбұрышы бар
болады.
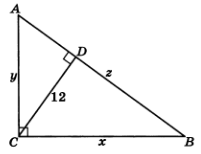
1.5-сурет
Берілген үшбұрыштың периметрі 60 см, ал тік бұрышынан жүргізілген биіктік 12 см.
Бірінші
теңдеуден  , ал екінші және үшінші
теңдеулерден
, ал екінші және үшінші
теңдеулерден  аламыз. Соңғы теңдеулердің оң
жақ бөліктерін теңестіру арқылы
аламыз. Соңғы теңдеулердің оң
жақ бөліктерін теңестіру арқылы  , яғни
, яғни
 болатынын
байқаймыз. [5]
болатынын
байқаймыз. [5]
Бұдан бастапқы берілген жүйеден келесі жүйені аламыз:

Бұл жүйенің шешімі 15 және 20. Демек бастапқы жүйенің шешімі (15; 20;25) және (20; 15; 25).
Мысал
6.  теңдеулер жүйесін
шеш.
теңдеулер жүйесін
шеш.
Шешуі.  болғандықтан,
болғандықтан,  ,
,
 және
және  сандары
тік
бұрышы
сандары
тік
бұрышы  болатындай
болатындай  үшбұрышының сәйкес катеттері
мен гипотенузасы болып табылады. Бұл үшбұрыштың ауданы 24
см2, ал периметрі 24 см.
Онда
үшбұрышының сәйкес катеттері
мен гипотенузасы болып табылады. Бұл үшбұрыштың ауданы 24
см2, ал периметрі 24 см.
Онда  үшбұрышына іштей сызылған
шеңбердің радиусы 2-ге тең. Екінші
теңдеуден
үшбұрышына іштей сызылған
шеңбердің радиусы 2-ге тең. Екінші
теңдеуден  аламыз.
Демек,
аламыз.
Демек,  немесе
немесе
 .
.
Жауабы. (10;6), (10;8)
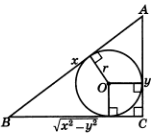
1.6-сурет
Мысал
7.  теңдеулер жүйесін
шеш.
теңдеулер жүйесін
шеш.
Шешуі.  ,
,
 ,
,
 екені анық.
Қабырғаларының ұзындығы берілген жүйені қанағаттандыратын үшбұрыш
бар болсын. Бірінші теңдеуден
екені анық.
Қабырғаларының ұзындығы берілген жүйені қанағаттандыратын үшбұрыш
бар болсын. Бірінші теңдеуден  табамыз.
табамыз.
Сонда екінші теңдеудің түрі:
 (1)
(1)
Берілген теңдеуді
түрлендіріп,  - қа қатысты квадрат теңдеуді
аламыз:
- қа қатысты квадрат теңдеуді
аламыз:
 .
.
Бұл теңдеудің
дискриминанты  тең. Онда
тең. Онда
 .
Теңсіздік
.
Теңсіздік  болғанда орынды болады. (1)
теңдеуді
болғанда орынды болады. (1)
теңдеуді  -ке қатысты түрлендірсек,
онда
-ке қатысты түрлендірсек,
онда  . Бірінші
теңдеуден
. Бірінші
теңдеуден  екені
табылады.
екені
табылады.
Жауабы.
 .
.
Қорытынды
Математика басқа ғылымдар сияқты ілгері жылжиды. Қоғамның дамуымен қатар заман көзқарастары мен сұраныстары өзгереді, жаңа ойлар мен жаңа жобалар пайда болады.
Берілген есептердің шешімі визуалды турде, яғни сызбамен көрсетіледі. Есептердің шешімін табудың дәстүрлі емес әдістері оқушылардың ғылыми ізденістерін, шығармашылық қабілеттерін арттырады.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Геометриялық емес есептердің геометриялық шешімдері
Геометриялық емес есептердің геометриялық шешімдері
Геометриялық емес есептердің геометриялық шешімдері
Мектеп бағдарламасы математикасында жоқ теңдеулер жүйесін геометриялық әдіспен шешуді ұсынамыз.
Мысал
1.  теңдеулер жүйесін
шешіп,
теңдеулер жүйесін
шешіп,  мәнін
тап.
мәнін
тап.
Шешуі. 1-ші және 2-ші теңдеулерді
қосып,  аламыз. 3-ші
теңдеудегі
аламыз. 3-ші
теңдеудегі  -тің мәнін алмастырып, 2-ші
теңдеуге қоямыз, яғни
-тің мәнін алмастырып, 2-ші
теңдеуге қоямыз, яғни  . Сонымен
. Сонымен
 тең болады.
Егер
тең болады.
Егер  болса, онда 1-ші теңдеуге
алмастырып қойғанда
болса, онда 1-ші теңдеуге
алмастырып қойғанда  аламыз. Әрі қарай теңдеуді
шешіп,
аламыз. Әрі қарай теңдеуді
шешіп,  екенін анықтаймыз.
Бұдан
екенін анықтаймыз.
Бұдан  және
және
 болатынын табамыз.
Сонда
болатынын табамыз.
Сонда  . [1]
. [1]
Бірақ бұл жүйені шығармай
және  өрнегінің мәнін таппай-ақ
шешімін табуға болатынын көрсетейік.
өрнегінің мәнін таппай-ақ
шешімін табуға болатынын көрсетейік.
Пифагор теоремасына кері
теорема бойынша  және 3 сандары
сәйкесінше
және 3 сандары
сәйкесінше  үшбұрышының каттеттері мен
гипотенузасы болсын (мұндағы
үшбұрышының каттеттері мен
гипотенузасы болсын (мұндағы  -тік
бұрыш).
-тік
бұрыш).
Онда екінші теңдеуді
қарастыратын болсақ,  және 4 сандары
сәйкесінше
және 4 сандары
сәйкесінше  үшбұрышының катеттері мен
гипотенузасы болсын (мұндағы
үшбұрышының катеттері мен
гипотенузасы болсын (мұндағы  -тік
бұрыш).
-тік
бұрыш).

1.1- сурет.
Жүйенің үшінші
теңдеуіндегі  саны
саны
 және
және  сандарының пропорционалдық
ортасы. Онда тік бұрышты үшбұрыштың пропорционалдық кесінділері
туралы теорема бойынша
сандарының пропорционалдық
ортасы. Онда тік бұрышты үшбұрыштың пропорционалдық кесінділері
туралы теорема бойынша  үшбұрышы тік бұрышты үшбұрыш
болады. Енді
үшбұрышы тік бұрышты үшбұрыш
болады. Енді  өрнегін
қарастырайық. [1]
өрнегін
қарастырайық. [1]

Жауабы: 12
Мысал
2.  өрнегінің мәнін тап,
егер
өрнегінің мәнін тап,
егер  ,
,
 ,
,
 және
және  болса.
болса.
Шешуі. Біріншіден,  және
және
 . Шындығында,
егер
. Шындығында,
егер  немесе
немесе
 болса,
онда
болса,
онда  . Алайда, 1 және 0 сандар
жұбы
. Алайда, 1 және 0 сандар
жұбы  теңдеуін қанағаттандырмайды.
Сәйкесінше, 0 және 2 сандар жұбы
теңдеуін қанағаттандырмайды.
Сәйкесінше, 0 және 2 сандар жұбы  теңдеуін
қанағаттандырмайды.
теңдеуін
қанағаттандырмайды.
Екіншіден,  және
және
 шарттары
үшін
шарттары
үшін  және
және
 теңдеулерін
сәйкесінше
теңдеулерін
сәйкесінше
 және
және 
түрде түрлендіруге болады. [1], [4]
Үшіншіден, алдыңғы мысалдың шешу әдісін пайдаланатын болсақ, онда


1.2 - сурет
Жауабы: 5
Мысал
3.  және
және
 оң сандары
үшін,
оң сандары
үшін,  ,
,
 ,
,
 шарттарымен
берілген
шарттарымен
берілген  өрнегінің мәнін
тап.
өрнегінің мәнін
тап.
Шешуі. Есептің берілген үш шартын жүйеге келтіреміз:

Пифагор теоремасына кері
теорема бойынша  ,
,
 және 5 сандары тік
бұрышы
және 5 сандары тік
бұрышы  болатын
болатын
 үшбұрышының сәйкесінше
катеттері мен гипотенузасы болсын ал,
үшбұрышының сәйкесінше
катеттері мен гипотенузасы болсын ал,
 ,
,
 және 13 сандары
бұрышы
және 13 сандары
бұрышы  болатын
болатын
 үшбұрышының қабырғалары
болсын. Сондай-ақ,
үшбұрышының қабырғалары
болсын. Сондай-ақ,  ,
,
 және 12 сандары
бұрышы
және 12 сандары
бұрышы  болатын
болатын
 үшбұрышының қабырғалары
болсын.
үшбұрышының қабырғалары
болсын.

1.3 – сурет
 болғандықтан,
болғандықтан,  үшбұрышында
үшбұрышында  .
.




 өрнегі
берілген
өрнегі
берілген  үшбұрышының төрт еселенген
мәніне тең, яғни
үшбұрышының төрт еселенген
мәніне тең, яғни  .
.
Жауабы: 120.
Мысал
4.  және
және
 оң сандары
үшін,
оң сандары
үшін,  ,
,
 ,
,
 теңдеулер жүйесінің
мәнін таппай,
теңдеулер жүйесінің
мәнін таппай,  өрнегінің мәнін
тап.
өрнегінің мәнін
тап.
Шешуі.

 .
.
 үшбұрышының ауданы 6-ға
тең болғандықтан,
үшбұрышының ауданы 6-ға
тең болғандықтан,  .
.

1.4-сурет
Мысал
5.  теңдеулер жүйесін
шешіңіз.
теңдеулер жүйесін
шешіңіз.
Шешуі. Егер
 ,
,
 және
және  болса,
онда
болса,
онда  және
және
 - катеттері,
ал
- катеттері,
ал  - гипотенузасы, сонымен
қатар
- гипотенузасы, сонымен
қатар  бұрышы тік
болатындай
бұрышы тік
болатындай  үшбұрышы бар
болады.
үшбұрышы бар
болады.

1.5-сурет
Берілген үшбұрыштың периметрі 60 см, ал тік бұрышынан жүргізілген биіктік 12 см.
Бірінші
теңдеуден  , ал екінші және үшінші
теңдеулерден
, ал екінші және үшінші
теңдеулерден  аламыз. Соңғы теңдеулердің оң
жақ бөліктерін теңестіру арқылы
аламыз. Соңғы теңдеулердің оң
жақ бөліктерін теңестіру арқылы  , яғни
, яғни
 болатынын
байқаймыз. [5]
болатынын
байқаймыз. [5]
Бұдан бастапқы берілген жүйеден келесі жүйені аламыз:

Бұл жүйенің шешімі 15 және 20. Демек бастапқы жүйенің шешімі (15; 20;25) және (20; 15; 25).
Мысал
6.  теңдеулер жүйесін
шеш.
теңдеулер жүйесін
шеш.
Шешуі.  болғандықтан,
болғандықтан,  ,
,
 және
және  сандары
тік
бұрышы
сандары
тік
бұрышы  болатындай
болатындай  үшбұрышының сәйкес катеттері
мен гипотенузасы болып табылады. Бұл үшбұрыштың ауданы 24
см2, ал периметрі 24 см.
Онда
үшбұрышының сәйкес катеттері
мен гипотенузасы болып табылады. Бұл үшбұрыштың ауданы 24
см2, ал периметрі 24 см.
Онда  үшбұрышына іштей сызылған
шеңбердің радиусы 2-ге тең. Екінші
теңдеуден
үшбұрышына іштей сызылған
шеңбердің радиусы 2-ге тең. Екінші
теңдеуден  аламыз.
Демек,
аламыз.
Демек,  немесе
немесе
 .
.
Жауабы. (10;6), (10;8)

1.6-сурет
Мысал
7.  теңдеулер жүйесін
шеш.
теңдеулер жүйесін
шеш.
Шешуі.  ,
,
 ,
,
 екені анық.
Қабырғаларының ұзындығы берілген жүйені қанағаттандыратын үшбұрыш
бар болсын. Бірінші теңдеуден
екені анық.
Қабырғаларының ұзындығы берілген жүйені қанағаттандыратын үшбұрыш
бар болсын. Бірінші теңдеуден  табамыз.
табамыз.
Сонда екінші теңдеудің түрі:
 (1)
(1)
Берілген теңдеуді
түрлендіріп,  - қа қатысты квадрат теңдеуді
аламыз:
- қа қатысты квадрат теңдеуді
аламыз:
 .
.
Бұл теңдеудің
дискриминанты  тең. Онда
тең. Онда
 .
Теңсіздік
.
Теңсіздік  болғанда орынды болады. (1)
теңдеуді
болғанда орынды болады. (1)
теңдеуді  -ке қатысты түрлендірсек,
онда
-ке қатысты түрлендірсек,
онда  . Бірінші
теңдеуден
. Бірінші
теңдеуден  екені
табылады.
екені
табылады.
Жауабы.
 .
.
Қорытынды
Математика басқа ғылымдар сияқты ілгері жылжиды. Қоғамның дамуымен қатар заман көзқарастары мен сұраныстары өзгереді, жаңа ойлар мен жаңа жобалар пайда болады.
Берілген есептердің шешімі визуалды турде, яғни сызбамен көрсетіледі. Есептердің шешімін табудың дәстүрлі емес әдістері оқушылардың ғылыми ізденістерін, шығармашылық қабілеттерін арттырады.

шағым қалдыра аласыз















