
Геометриялық емес есептердің тригонометриялық шешімдері
Соңғы онжылдықта тригонометрия дербес пән ретінде жойылып, негізгі мектеп курсының алгебра және геометриясына ғана емес, сондай – ақ алгебра және анализ бастамалары пәндеріне енгізілген. [1]
Тригонометриялық есептерге мысалдар келтірейік.
Мысал
1. Есептеңіз:  .
.
Шешуі. 9 сынып оқулығында қосудың формуласын пайдалана отырып, берілген есепті былайша шығаруға болады:
 .
.
Бірақ 8 сыныпта бұл есептің шешімін табу көп уақытты кажет етпейді.

 теңбүйірлі үшбұрышын
қарастырайық. Мұнда
теңбүйірлі үшбұрышын
қарастырайық. Мұнда  . Берілген
үшбұрыштың
. Берілген
үшбұрыштың  және
және
 биіктіктерін
жүргізейік.
биіктіктерін
жүргізейік.  .
.
 .
Егер
.
Егер  болса,
онда
болса,
онда  және
және
 .
Демек,
.
Демек,  .
.
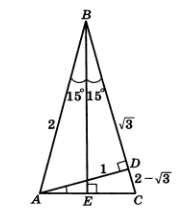
1.7-сурет
Жауабы.
 .
.
Мысал
2. Дәлелдеңіз: .
.
Шешуі. 
 тік бұрышты үшбұрышын
қарастырайық. Мұнда
тік бұрышты үшбұрышын
қарастырайық. Мұнда  гипотенузасы 1-ге тең.
Онда
гипотенузасы 1-ге тең.
Онда  және
және
 болсын. Пифагор
теоремасы бойынша
болсын. Пифагор
теоремасы бойынша  .
.
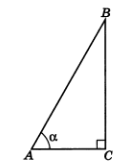
1.8-сурет
Мысал
3. Дәлелдеңіз: 
Дәлелдеуі. Егер
 үшбұрышында
үшбұрышында  катеті 1-ге тең болса,
онда
катеті 1-ге тең болса,
онда  және
және
 . Демек, Пифагор
теоремасы бойынша
. Демек, Пифагор
теоремасы бойынша  .
.
Мысал
4. Дәлелдеңіз: 
Дәлелдеуі.  үшбұрышында
үшбұрышында  ,
,
 ,
сондай-ақ
,
сондай-ақ  және
және
 биіктіктері
берілсін.
биіктіктері
берілсін.
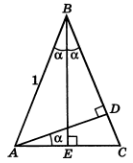
1.9-сурет
Сурет
бойынша  ,
,
 ,
,
 .
.
 және
және  үшбұрыштары ұқсас
болғандықтан, онда
үшбұрыштары ұқсас
болғандықтан, онда  ,
яғни
,
яғни
 .
.
Демек,
 .
.
Мысал
5. Дәлелдеңіз:  .
.
Дәлелдеуі. 1.9 – сурет
бойынша  ,
,
 ,
,
 болсын.
болсын.  және
және
 үшбұрыштарының
ұқсастығына байланысты
үшбұрыштарының
ұқсастығына байланысты  екені анық,
яғни
екені анық,
яғни  .
Демек,
.
Демек,

Мысал
6. Дәлелдеңіз:  .
.
Дәлелдеуі.  үшбұрышын
қарастырайық.
үшбұрышын
қарастырайық.  ,
,
 және
және  болсын. Есептің шарты
бойынша
болсын. Есептің шарты
бойынша  және
және
 бұрыштары сүйір болса,
онда
бұрыштары сүйір болса,
онда  нүктесі
нүктесі
 кесіндісінің бойынан
алынған нүкте.
кесіндісінің бойынан
алынған нүкте.  ,
,
 ,
,
 және
және  деп белгілеулер
енгізейік.
деп белгілеулер
енгізейік.
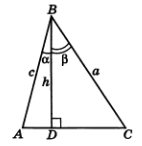
1.10-сурет
 ,
,
 .
.
 .
.
 .
.
Демек,
 .
.
Мысал
7. Есептеңдер:  .
.
Шешуі. Егер тік бұрышты үшбұрыштың сүйір бұрышының косинусы мен котангенсі, Пифагор теоремасы және бұрыштың биссектрисасы ұғымдарын пайдалансақ, есеп лезде шығарылады. [1]
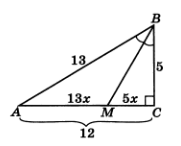
1.11-сурет
Суретте
 үшбұрышы
кескінделген.
үшбұрышы
кескінделген.  ,
,
 ,
,
 және
және  -
-
 бұрышының
биссектрисасы.
бұрышының
биссектрисасы.
Онда
 ,
,
 және
және  , яғни
, яғни
 .
.
 .
.
Жауабы. 1,5.
Қорытынды
Жұмыста стандарт емес есептерді, соның ішінде геометриялық емес есептердің тригонометриялық шешімдерін табу қарастырылады.
Жұмыста берілген есептерді шешу күнделікті мектеп бағдарламасында шығарып жүрген есептерден ерекшеленеді. Берілген есептердің шешімі визуалды турде, яғни сызбамен көрсетіледі. Есептердің шешімін табудың дәстүрлі емес әдістері оқушылардың ғылыми ізденістерін, шығармашылық қабілеттерін арттырады. Кейбір есептердің шешімін салыстыруға бірнеше мысалдар қарастырылған. Қарастырылатын мысалдардың кебіреулері күрделі болып көрінгенімен, оларды негізгі мектеп курсындағы оқушылар да шығара алады.
11
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Геометриялық емес есептердің тригонометриялық шешімдері
Геометриялық емес есептердің тригонометриялық шешімдері
Геометриялық емес есептердің тригонометриялық шешімдері
Соңғы онжылдықта тригонометрия дербес пән ретінде жойылып, негізгі мектеп курсының алгебра және геометриясына ғана емес, сондай – ақ алгебра және анализ бастамалары пәндеріне енгізілген. [1]
Тригонометриялық есептерге мысалдар келтірейік.
Мысал
1. Есептеңіз:  .
.
Шешуі. 9 сынып оқулығында қосудың формуласын пайдалана отырып, берілген есепті былайша шығаруға болады:
 .
.
Бірақ 8 сыныпта бұл есептің шешімін табу көп уақытты кажет етпейді.

 теңбүйірлі үшбұрышын
қарастырайық. Мұнда
теңбүйірлі үшбұрышын
қарастырайық. Мұнда  . Берілген
үшбұрыштың
. Берілген
үшбұрыштың  және
және
 биіктіктерін
жүргізейік.
биіктіктерін
жүргізейік.  .
.
 .
Егер
.
Егер  болса,
онда
болса,
онда  және
және
 .
Демек,
.
Демек,  .
.

1.7-сурет
Жауабы.
 .
.
Мысал
2. Дәлелдеңіз: .
.
Шешуі. 
 тік бұрышты үшбұрышын
қарастырайық. Мұнда
тік бұрышты үшбұрышын
қарастырайық. Мұнда  гипотенузасы 1-ге тең.
Онда
гипотенузасы 1-ге тең.
Онда  және
және
 болсын. Пифагор
теоремасы бойынша
болсын. Пифагор
теоремасы бойынша  .
.

1.8-сурет
Мысал
3. Дәлелдеңіз: 
Дәлелдеуі. Егер
 үшбұрышында
үшбұрышында  катеті 1-ге тең болса,
онда
катеті 1-ге тең болса,
онда  және
және
 . Демек, Пифагор
теоремасы бойынша
. Демек, Пифагор
теоремасы бойынша  .
.
Мысал
4. Дәлелдеңіз: 
Дәлелдеуі.  үшбұрышында
үшбұрышында  ,
,
 ,
сондай-ақ
,
сондай-ақ  және
және
 биіктіктері
берілсін.
биіктіктері
берілсін.

1.9-сурет
Сурет
бойынша  ,
,
 ,
,
 .
.
 және
және  үшбұрыштары ұқсас
болғандықтан, онда
үшбұрыштары ұқсас
болғандықтан, онда  ,
яғни
,
яғни
 .
.
Демек,
 .
.
Мысал
5. Дәлелдеңіз:  .
.
Дәлелдеуі. 1.9 – сурет
бойынша  ,
,
 ,
,
 болсын.
болсын.  және
және
 үшбұрыштарының
ұқсастығына байланысты
үшбұрыштарының
ұқсастығына байланысты  екені анық,
яғни
екені анық,
яғни  .
Демек,
.
Демек,

Мысал
6. Дәлелдеңіз:  .
.
Дәлелдеуі.  үшбұрышын
қарастырайық.
үшбұрышын
қарастырайық.  ,
,
 және
және  болсын. Есептің шарты
бойынша
болсын. Есептің шарты
бойынша  және
және
 бұрыштары сүйір болса,
онда
бұрыштары сүйір болса,
онда  нүктесі
нүктесі
 кесіндісінің бойынан
алынған нүкте.
кесіндісінің бойынан
алынған нүкте.  ,
,
 ,
,
 және
және  деп белгілеулер
енгізейік.
деп белгілеулер
енгізейік.

1.10-сурет
 ,
,
 .
.
 .
.
 .
.
Демек,
 .
.
Мысал
7. Есептеңдер:  .
.
Шешуі. Егер тік бұрышты үшбұрыштың сүйір бұрышының косинусы мен котангенсі, Пифагор теоремасы және бұрыштың биссектрисасы ұғымдарын пайдалансақ, есеп лезде шығарылады. [1]

1.11-сурет
Суретте
 үшбұрышы
кескінделген.
үшбұрышы
кескінделген.  ,
,
 ,
,
 және
және  -
-
 бұрышының
биссектрисасы.
бұрышының
биссектрисасы.
Онда
 ,
,
 және
және  , яғни
, яғни
 .
.
 .
.
Жауабы. 1,5.
Қорытынды
Жұмыста стандарт емес есептерді, соның ішінде геометриялық емес есептердің тригонометриялық шешімдерін табу қарастырылады.
Жұмыста берілген есептерді шешу күнделікті мектеп бағдарламасында шығарып жүрген есептерден ерекшеленеді. Берілген есептердің шешімі визуалды турде, яғни сызбамен көрсетіледі. Есептердің шешімін табудың дәстүрлі емес әдістері оқушылардың ғылыми ізденістерін, шығармашылық қабілеттерін арттырады. Кейбір есептердің шешімін салыстыруға бірнеше мысалдар қарастырылған. Қарастырылатын мысалдардың кебіреулері күрделі болып көрінгенімен, оларды негізгі мектеп курсындағы оқушылар да шығара алады.
11

шағым қалдыра аласыз















