Геометрияның пайда болу тарихы.
"Геометрия" сөзі гректің "гео" — жер және "метрия" — Өлшем сөздерінен шыққан.
Е желгі
мәдениеттер өздерінің күнделікті өмірінің ажырамас бөлігі ретінде
геометрияның едәуір мөлшерін практикалық өлшем ретінде және
храмдар, сарайлар мен азаматтық құрылыс салу үшін әртүрлі түрлердің
формаларын бөлу және біріктіру ережелері ретінде білді. Күнделікті
практикалық мақсаттары үшін адамдар "тегіс" жерде өмір сүрді. "Түзу
сызық" тығыз тартылған арқан болды және шеңберді бекітілген
нүктенің айналасында сызу арқылы салуға
болады.
желгі
мәдениеттер өздерінің күнделікті өмірінің ажырамас бөлігі ретінде
геометрияның едәуір мөлшерін практикалық өлшем ретінде және
храмдар, сарайлар мен азаматтық құрылыс салу үшін әртүрлі түрлердің
формаларын бөлу және біріктіру ережелері ретінде білді. Күнделікті
практикалық мақсаттары үшін адамдар "тегіс" жерде өмір сүрді. "Түзу
сызық" тығыз тартылған арқан болды және шеңберді бекітілген
нүктенің айналасында сызу арқылы салуға
болады.
Бұл халықтар туралы білімнің көп бөлігі Жерорта теңізінде белгілі болды және грек өркениеті б.з. д. 4 ғасырда өзін жариялай бастағанда, Аристотель сияқты философтар (б. з. д. 384-322 жж.) қатысушылардан өз дәлелдерінің негізін мүмкіндігінше нақты көрсетуді талап ететін талқылау тәсілі. Бұл атмосферада грек логикасы дүниеге келді.
О сы кезеңде
Александрия грек тілін үйренудің маңызды орталықтарының біріне
айналды және біздің эрамызға дейінгі 300 жылы Евклидтің "математика
элементтері" жазылған. Аристотельдің принциптеріне сүйене отырып,
Евклид өзінің математикасын нүктелер, түзулер, беттер, бұрыштар,
шеңберлер мен үшбұрыштар және аксиомалар (немесе постулаттар)
сияқты негізгі объектілердің бірқатар анықтамаларына негіздеді. Бұл
оның математиканы дамытуының келісілген бастапқы нүктелері
болды.
сы кезеңде
Александрия грек тілін үйренудің маңызды орталықтарының біріне
айналды және біздің эрамызға дейінгі 300 жылы Евклидтің "математика
элементтері" жазылған. Аристотельдің принциптеріне сүйене отырып,
Евклид өзінің математикасын нүктелер, түзулер, беттер, бұрыштар,
шеңберлер мен үшбұрыштар және аксиомалар (немесе постулаттар)
сияқты негізгі объектілердің бірқатар анықтамаларына негіздеді. Бұл
оның математиканы дамытуының келісілген бастапқы нүктелері
болды.
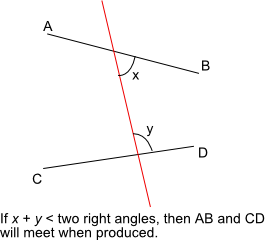
Не істеуге болатыны туралы алғашқы үш постулат, келесісі тік бұрыштардың теңдігі туралы, ал соңғы тұжырым екі түзудің кездесетінін анықтау үшін екі тік бұрыштың қосындысын пайдаланады:
Кез келген нүктеден кез келген басқа нүктеге түзу сызық сызыңыз.
Соңғы түзуді түзу сызық бойымен үздіксіз жасаңыз (ұзартыңыз).
Кез келген центрі мен қашықтығы бар шеңберді сипаттаңыз.
Барлық тік бұрыштар бір-біріне тең.
Егер екі түзуге түсетін түзу бір жағынан екі түзуден кіші ішкі бұрыштарды құраса, онда егер екі түзу шексіз түзілсе, онда олар бұрыштары екі түзу бұрыштан кіші жағында кездеседі.
 Евклид қаламды қойғаннан кейін
математиктер мен философтар бесінші постулатта қиындықтарға тап
болды. Алғашқы төртеудің қысқаша тұжырымдарынан айырмашылығы,
бесіншісі аксиома емес, теорема болуы керек сияқты көрінді, яғни
оны басқа аксиомалардан шығару керек. Біз мұны басқа математиктер
жазған әртүрлі логикалық талдаулардан білеміз. Біздің заманымыздың
бесінші ғасырында Проклус (б. з. 411-485 жж.) бесінші постулаттың
қарапайым нұсқасын берді:
Евклид қаламды қойғаннан кейін
математиктер мен философтар бесінші постулатта қиындықтарға тап
болды. Алғашқы төртеудің қысқаша тұжырымдарынан айырмашылығы,
бесіншісі аксиома емес, теорема болуы керек сияқты көрінді, яғни
оны басқа аксиомалардан шығару керек. Біз мұны басқа математиктер
жазған әртүрлі логикалық талдаулардан білеміз. Біздің заманымыздың
бесінші ғасырында Проклус (б. з. 411-485 жж.) бесінші постулаттың
қарапайым нұсқасын берді:
Т үзу сызықта
жатпайтын түзу мен нүктенің көмегімен осы нүкте арқылы түзуге
параллель дәл бір түзу сызуға болады.
үзу сызықта
жатпайтын түзу мен нүктенің көмегімен осы нүкте арқылы түзуге
параллель дәл бір түзу сызуға болады.
Бүгінде бұл белгілі Плейфер аксиомасы, 1795 жылы Евклид туралы маңызды жұмыс жазған ағылшын математигі Джон Плейфердің құрметіне, бірақ бұл аксиома 1200 жылдан астам уақыт бойы белгілі болды!
Араб математиктері грек шығармаларын зерттеп, бесінші постулаттың салыстырмалы түрде күрделі тұжырымын логикалық тұрғыдан талдап, өз нұсқаларын жасады.
Абул Вафа Әл-Бузжани (940-998)
 Абул Вафа тригонометрияның
кейбір маңызды идеяларын дамытты және жұлдыздардың ауытқуын дәл
өлшеу үшін қабырға квадрантын ойлап тапты дейді. Ол сондай-ақ
тангенс, секант және косекант функцияларын енгізді және
тригонометриялық кестелерді 15° аралықпен және үтірден кейін 8
таңбаға дейін есептеу әдістерін жетілдірді. Мұның бәрі оның "ай
теорияларында" айдың орбитасын зерттеу аясында жасалды . Оның
есімі-Абу л-Вафа кратері.
Абул Вафа тригонометрияның
кейбір маңызды идеяларын дамытты және жұлдыздардың ауытқуын дәл
өлшеу үшін қабырға квадрантын ойлап тапты дейді. Ол сондай-ақ
тангенс, секант және косекант функцияларын енгізді және
тригонометриялық кестелерді 15° аралықпен және үтірден кейін 8
таңбаға дейін есептеу әдістерін жетілдірді. Мұның бәрі оның "ай
теорияларында" айдың орбитасын зерттеу аясында жасалды . Оның
есімі-Абу л-Вафа кратері.
Т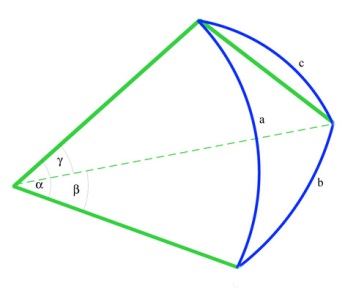 ригонометриялық зерттеулерінің нәтижесінде ол сфералық үшбұрыштар
туралы кейбір есептерді шешу жолдарын ойлап
тапты.
ригонометриялық зерттеулерінің нәтижесінде ол сфералық үшбұрыштар
туралы кейбір есептерді шешу жолдарын ойлап
тапты.
Омар Хайям (1048-1131)
Поэзиясымен танымал Омар Хайям
сонымен қатар Евклид кітабының қиын постулаттарына түсініктеме
жазған көрнекті астроном және математик болды . Ол бесінші
постулатты дәлелдеуге тырысты және фигуралардың кейбір евклидтік
емес қасиеттерін тапқанын анықтады.
Омар Хайям Евклидтің бесінші постулатын қалған төртеуінен шығаруға болатындығын дәлелдеу үшін суретте көрсетілген төртбұрыш тұрғызды. Ол AB-ге перпендикуляр AD және BC тең сегменттерін құрудан бастады. Егер ол төртбұрыштың жоғарғы жағындағы ішкі бұрыштардың түзу екенін дәлелдей алса, онда ол AB-ге параллель екенін көрсетер еді. Ол шыңның ішкі бұрыштары тең екенін көрсеткенімен (өзіңіз көріңіз), олардың түзу екенін дәлелдей алмады
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Геометрияның пайда болу тарихы.
Геометрияның пайда болу тарихы.
Геометрияның пайда болу тарихы.
"Геометрия" сөзі гректің "гео" — жер және "метрия" — Өлшем сөздерінен шыққан.
Е желгі
мәдениеттер өздерінің күнделікті өмірінің ажырамас бөлігі ретінде
геометрияның едәуір мөлшерін практикалық өлшем ретінде және
храмдар, сарайлар мен азаматтық құрылыс салу үшін әртүрлі түрлердің
формаларын бөлу және біріктіру ережелері ретінде білді. Күнделікті
практикалық мақсаттары үшін адамдар "тегіс" жерде өмір сүрді. "Түзу
сызық" тығыз тартылған арқан болды және шеңберді бекітілген
нүктенің айналасында сызу арқылы салуға
болады.
желгі
мәдениеттер өздерінің күнделікті өмірінің ажырамас бөлігі ретінде
геометрияның едәуір мөлшерін практикалық өлшем ретінде және
храмдар, сарайлар мен азаматтық құрылыс салу үшін әртүрлі түрлердің
формаларын бөлу және біріктіру ережелері ретінде білді. Күнделікті
практикалық мақсаттары үшін адамдар "тегіс" жерде өмір сүрді. "Түзу
сызық" тығыз тартылған арқан болды және шеңберді бекітілген
нүктенің айналасында сызу арқылы салуға
болады.
Бұл халықтар туралы білімнің көп бөлігі Жерорта теңізінде белгілі болды және грек өркениеті б.з. д. 4 ғасырда өзін жариялай бастағанда, Аристотель сияқты философтар (б. з. д. 384-322 жж.) қатысушылардан өз дәлелдерінің негізін мүмкіндігінше нақты көрсетуді талап ететін талқылау тәсілі. Бұл атмосферада грек логикасы дүниеге келді.
О сы кезеңде
Александрия грек тілін үйренудің маңызды орталықтарының біріне
айналды және біздің эрамызға дейінгі 300 жылы Евклидтің "математика
элементтері" жазылған. Аристотельдің принциптеріне сүйене отырып,
Евклид өзінің математикасын нүктелер, түзулер, беттер, бұрыштар,
шеңберлер мен үшбұрыштар және аксиомалар (немесе постулаттар)
сияқты негізгі объектілердің бірқатар анықтамаларына негіздеді. Бұл
оның математиканы дамытуының келісілген бастапқы нүктелері
болды.
сы кезеңде
Александрия грек тілін үйренудің маңызды орталықтарының біріне
айналды және біздің эрамызға дейінгі 300 жылы Евклидтің "математика
элементтері" жазылған. Аристотельдің принциптеріне сүйене отырып,
Евклид өзінің математикасын нүктелер, түзулер, беттер, бұрыштар,
шеңберлер мен үшбұрыштар және аксиомалар (немесе постулаттар)
сияқты негізгі объектілердің бірқатар анықтамаларына негіздеді. Бұл
оның математиканы дамытуының келісілген бастапқы нүктелері
болды.
Не істеуге болатыны туралы алғашқы үш постулат, келесісі тік бұрыштардың теңдігі туралы, ал соңғы тұжырым екі түзудің кездесетінін анықтау үшін екі тік бұрыштың қосындысын пайдаланады:
Кез келген нүктеден кез келген басқа нүктеге түзу сызық сызыңыз.
Соңғы түзуді түзу сызық бойымен үздіксіз жасаңыз (ұзартыңыз).
Кез келген центрі мен қашықтығы бар шеңберді сипаттаңыз.
Барлық тік бұрыштар бір-біріне тең.
Егер екі түзуге түсетін түзу бір жағынан екі түзуден кіші ішкі бұрыштарды құраса, онда егер екі түзу шексіз түзілсе, онда олар бұрыштары екі түзу бұрыштан кіші жағында кездеседі.
 Евклид қаламды қойғаннан кейін
математиктер мен философтар бесінші постулатта қиындықтарға тап
болды. Алғашқы төртеудің қысқаша тұжырымдарынан айырмашылығы,
бесіншісі аксиома емес, теорема болуы керек сияқты көрінді, яғни
оны басқа аксиомалардан шығару керек. Біз мұны басқа математиктер
жазған әртүрлі логикалық талдаулардан білеміз. Біздің заманымыздың
бесінші ғасырында Проклус (б. з. 411-485 жж.) бесінші постулаттың
қарапайым нұсқасын берді:
Евклид қаламды қойғаннан кейін
математиктер мен философтар бесінші постулатта қиындықтарға тап
болды. Алғашқы төртеудің қысқаша тұжырымдарынан айырмашылығы,
бесіншісі аксиома емес, теорема болуы керек сияқты көрінді, яғни
оны басқа аксиомалардан шығару керек. Біз мұны басқа математиктер
жазған әртүрлі логикалық талдаулардан білеміз. Біздің заманымыздың
бесінші ғасырында Проклус (б. з. 411-485 жж.) бесінші постулаттың
қарапайым нұсқасын берді:
Т үзу сызықта
жатпайтын түзу мен нүктенің көмегімен осы нүкте арқылы түзуге
параллель дәл бір түзу сызуға болады.
үзу сызықта
жатпайтын түзу мен нүктенің көмегімен осы нүкте арқылы түзуге
параллель дәл бір түзу сызуға болады.
Бүгінде бұл белгілі Плейфер аксиомасы, 1795 жылы Евклид туралы маңызды жұмыс жазған ағылшын математигі Джон Плейфердің құрметіне, бірақ бұл аксиома 1200 жылдан астам уақыт бойы белгілі болды!
Араб математиктері грек шығармаларын зерттеп, бесінші постулаттың салыстырмалы түрде күрделі тұжырымын логикалық тұрғыдан талдап, өз нұсқаларын жасады.
Абул Вафа Әл-Бузжани (940-998)
 Абул Вафа тригонометрияның
кейбір маңызды идеяларын дамытты және жұлдыздардың ауытқуын дәл
өлшеу үшін қабырға квадрантын ойлап тапты дейді. Ол сондай-ақ
тангенс, секант және косекант функцияларын енгізді және
тригонометриялық кестелерді 15° аралықпен және үтірден кейін 8
таңбаға дейін есептеу әдістерін жетілдірді. Мұның бәрі оның "ай
теорияларында" айдың орбитасын зерттеу аясында жасалды . Оның
есімі-Абу л-Вафа кратері.
Абул Вафа тригонометрияның
кейбір маңызды идеяларын дамытты және жұлдыздардың ауытқуын дәл
өлшеу үшін қабырға квадрантын ойлап тапты дейді. Ол сондай-ақ
тангенс, секант және косекант функцияларын енгізді және
тригонометриялық кестелерді 15° аралықпен және үтірден кейін 8
таңбаға дейін есептеу әдістерін жетілдірді. Мұның бәрі оның "ай
теорияларында" айдың орбитасын зерттеу аясында жасалды . Оның
есімі-Абу л-Вафа кратері.
Т ригонометриялық зерттеулерінің нәтижесінде ол сфералық үшбұрыштар
туралы кейбір есептерді шешу жолдарын ойлап
тапты.
ригонометриялық зерттеулерінің нәтижесінде ол сфералық үшбұрыштар
туралы кейбір есептерді шешу жолдарын ойлап
тапты.
Омар Хайям (1048-1131)
Поэзиясымен танымал Омар Хайям
сонымен қатар Евклид кітабының қиын постулаттарына түсініктеме
жазған көрнекті астроном және математик болды . Ол бесінші
постулатты дәлелдеуге тырысты және фигуралардың кейбір евклидтік
емес қасиеттерін тапқанын анықтады.
Омар Хайям Евклидтің бесінші постулатын қалған төртеуінен шығаруға болатындығын дәлелдеу үшін суретте көрсетілген төртбұрыш тұрғызды. Ол AB-ге перпендикуляр AD және BC тең сегменттерін құрудан бастады. Егер ол төртбұрыштың жоғарғы жағындағы ішкі бұрыштардың түзу екенін дәлелдей алса, онда ол AB-ге параллель екенін көрсетер еді. Ол шыңның ішкі бұрыштары тең екенін көрсеткенімен (өзіңіз көріңіз), олардың түзу екенін дәлелдей алмады

шағым қалдыра аласыз