Бекітілді: Қысқа мерзімді
жоспар
|
Бөлім: 5.3В Ондық бөлшектер және оларға амалдар қолдану |
Мектеп: Әл – Фараби атындағы №21 мамандандырылған гимназия |
|||||
|
Күні: |
Мұғалімнің аты-жөні: Шокпытова В.Р |
|||||
|
Сынып: 5 |
Қатысқан оқушы саны: |
Қатыспаған оқушы саны: |
||||
|
Сабақтың тақырыбы |
Жиындар арасындағы қатынастар. Ішкі жиын |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
5.4.1.4 ішкі жиын ұғымын меңгеру; 5.4.1.5 жиындар арасындағы қатынастардың сипаттамасын анықтау (қиылысатын және қиылыспайтын жиындар); |
|||||
|
Сабақтың мақсаты: |
- Жиындар арасындағы қатынастарды сипаттамасын анықтайды және ішкі жиынды ажыратады. |
|||||
|
Құндылықтарды дамыту |
«АР-ҰЯТ»: Әдеп нормаларын ұстану, өзін отбасының, сыныптың, мектептің, қоғамның, Отанның бір мүшесі екендігін сезіну; адал еңбекті құрметтеу |
|||||
|
Сабақ барысы |
||||||
|
Сабақ кезеңі |
Педагогтің әрекеті |
Оқушы әрекеті |
Бағалау |
Ресурстар |
||
|
Сабақтың басы 5 минут |
I. Ұйымдастыру сәті - Оқушылармен сәлемдесу, түгендеу - Үй жұмысын топта талқылау арқылы тексеру - Сабаққа дайындығын байқау, оқушылармен әңгімелесу. |
Жаңа сабаққа дайындық |
Мұғалім бағалауы мадақтау |
|
||
|
Сабақтың ортасы 30 минут |
I Сурет бойынша оқушылар адам аттарын жиындарға біріктіреді
мысалы:
|
Білу |
Мұғалім бағалауы |
Қосымша |
||
|
Мағынаны тану III. Анықтама: Егер В жиынының әрбір элементі А жиынына тиісті болса, онда В жиыны А жиынының ішкі жиыны деп аталады.(1.3 - сурет) Математикада ХІХ ғасырдың еінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Г. Кантор. М Жиындардың байланыстары арақатынастары Эйлер дөңгелектері ( алғаш рет ХҮІІІ ғасырда өмір сүрген швейцариялық белгілі математик Леонард Эйлер пайдаланған.) В жиыны А жиынының ішкі жиыны екені Эйлер дөңгелектері арқылы кескінделген. Ж Мысал:
А мен В жиыны қиылысқанда, мынандай жиын пайда болады: (7;13). Екі жиынның қиылысуы Эйлер дөңгелектері арқылы кескінделген. |
Түсіну
|
Өзін өзі бағалау |
Қосымша |
|||
|
|
Жалпысыныптық жұмыс Тапсырма: L = {3, 6, 9, 12, 15, 18} жиыны берілген.
|
Білу. Түсіну Қолдану |
Өзін өзі бағалау |
Ауызша тапсырмалар |
||
|
Мына жиындардың қайсысы ішкі жиын болады? 1. А – музыканттар жиыны: 2. L – еліміздегі қалалар жиыны В – скрипкашылар жиыны K – облыс орталықтары қалаларының жиыны
|
|
|
|
|||
|
I .оқушы басқа оқушының жұмысын тексеру арқылы өз жұмысын тексеру дағдысын қалыптастыру Бұл тапсырмаларды бағалау критерийі: -берілген жиынға тиісті элементтер арқылы ішкі жинды анықтайды |
Талдау Дәптерге жазылым жұмысын орындау |
Бірін бірі бағалау |
Қосымша Таратпа материалдар |
|||
|
|
V. Қалыптастырушы бағалау. Жеке жұмыс. Тұжырымдардың ақиқаттығын анықтаңыз.
|
Жинақтау |
Мұғалім бағалауы |
Таратпа материалдар |
||
|
Сабақтың соңы 5 мин |
VI. Бекіту сұрақтары
|
|
|
|
||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жиындар арасындағы қатынастар. Ішкі жиын
Жиындар арасындағы қатынастар. Ішкі жиын
Бекітілді: Қысқа мерзімді
жоспар
|
Бөлім: 5.3В Ондық бөлшектер және оларға амалдар қолдану |
Мектеп: Әл – Фараби атындағы №21 мамандандырылған гимназия |
|||||
|
Күні: |
Мұғалімнің аты-жөні: Шокпытова В.Р |
|||||
|
Сынып: 5 |
Қатысқан оқушы саны: |
Қатыспаған оқушы саны: |
||||
|
Сабақтың тақырыбы |
Жиындар арасындағы қатынастар. Ішкі жиын |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
5.4.1.4 ішкі жиын ұғымын меңгеру; 5.4.1.5 жиындар арасындағы қатынастардың сипаттамасын анықтау (қиылысатын және қиылыспайтын жиындар); |
|||||
|
Сабақтың мақсаты: |
- Жиындар арасындағы қатынастарды сипаттамасын анықтайды және ішкі жиынды ажыратады. |
|||||
|
Құндылықтарды дамыту |
«АР-ҰЯТ»: Әдеп нормаларын ұстану, өзін отбасының, сыныптың, мектептің, қоғамның, Отанның бір мүшесі екендігін сезіну; адал еңбекті құрметтеу |
|||||
|
Сабақ барысы |
||||||
|
Сабақ кезеңі |
Педагогтің әрекеті |
Оқушы әрекеті |
Бағалау |
Ресурстар |
||
|
Сабақтың басы 5 минут |
I. Ұйымдастыру сәті - Оқушылармен сәлемдесу, түгендеу - Үй жұмысын топта талқылау арқылы тексеру - Сабаққа дайындығын байқау, оқушылармен әңгімелесу. |
Жаңа сабаққа дайындық |
Мұғалім бағалауы мадақтау |
|
||
|
Сабақтың ортасы 30 минут |
I Сурет бойынша оқушылар адам аттарын жиындарға біріктіреді
мысалы:
|
Білу |
Мұғалім бағалауы |
Қосымша |
||
|
Мағынаны тану III. Анықтама: Егер В жиынының әрбір элементі А жиынына тиісті болса, онда В жиыны А жиынының ішкі жиыны деп аталады.(1.3 - сурет) Математикада ХІХ ғасырдың еінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Г. Кантор. М Жиындардың байланыстары арақатынастары Эйлер дөңгелектері ( алғаш рет ХҮІІІ ғасырда өмір сүрген швейцариялық белгілі математик Леонард Эйлер пайдаланған.) В жиыны А жиынының ішкі жиыны екені Эйлер дөңгелектері арқылы кескінделген. Ж Мысал:
А мен В жиыны қиылысқанда, мынандай жиын пайда болады: (7;13). Екі жиынның қиылысуы Эйлер дөңгелектері арқылы кескінделген. |
Түсіну
|
Өзін өзі бағалау |
Қосымша |
|||
|
|
Жалпысыныптық жұмыс Тапсырма: L = {3, 6, 9, 12, 15, 18} жиыны берілген.
|
Білу. Түсіну Қолдану |
Өзін өзі бағалау |
Ауызша тапсырмалар |
||
|
Мына жиындардың қайсысы ішкі жиын болады? 1. А – музыканттар жиыны: 2. L – еліміздегі қалалар жиыны В – скрипкашылар жиыны K – облыс орталықтары қалаларының жиыны
|
|
|
|
|||
|
I .оқушы басқа оқушының жұмысын тексеру арқылы өз жұмысын тексеру дағдысын қалыптастыру Бұл тапсырмаларды бағалау критерийі: -берілген жиынға тиісті элементтер арқылы ішкі жинды анықтайды |
Талдау Дәптерге жазылым жұмысын орындау |
Бірін бірі бағалау |
Қосымша Таратпа материалдар |
|||
|
|
V. Қалыптастырушы бағалау. Жеке жұмыс. Тұжырымдардың ақиқаттығын анықтаңыз.
|
Жинақтау |
Мұғалім бағалауы |
Таратпа материалдар |
||
|
Сабақтың соңы 5 мин |
VI. Бекіту сұрақтары
|
|
|
|
||

шағым қалдыра аласыз


 I. «Ой
қозғау»
I. «Ой
қозғау»  ысалы; А= (
1;2;3;4;5;6;7) осы жиынға тиісті жұп сандар жиыны А жиынының ішкі
жиыны деп аталады. Осы жиынға тиісті жұп сандар жиыны А жиынының
ішкі жиыны деп аталады. В=
(2;4;6)
ысалы; А= (
1;2;3;4;5;6;7) осы жиынға тиісті жұп сандар жиыны А жиынының ішкі
жиыны деп аталады. Осы жиынға тиісті жұп сандар жиыны А жиынының
ішкі жиыны деп аталады. В=
(2;4;6)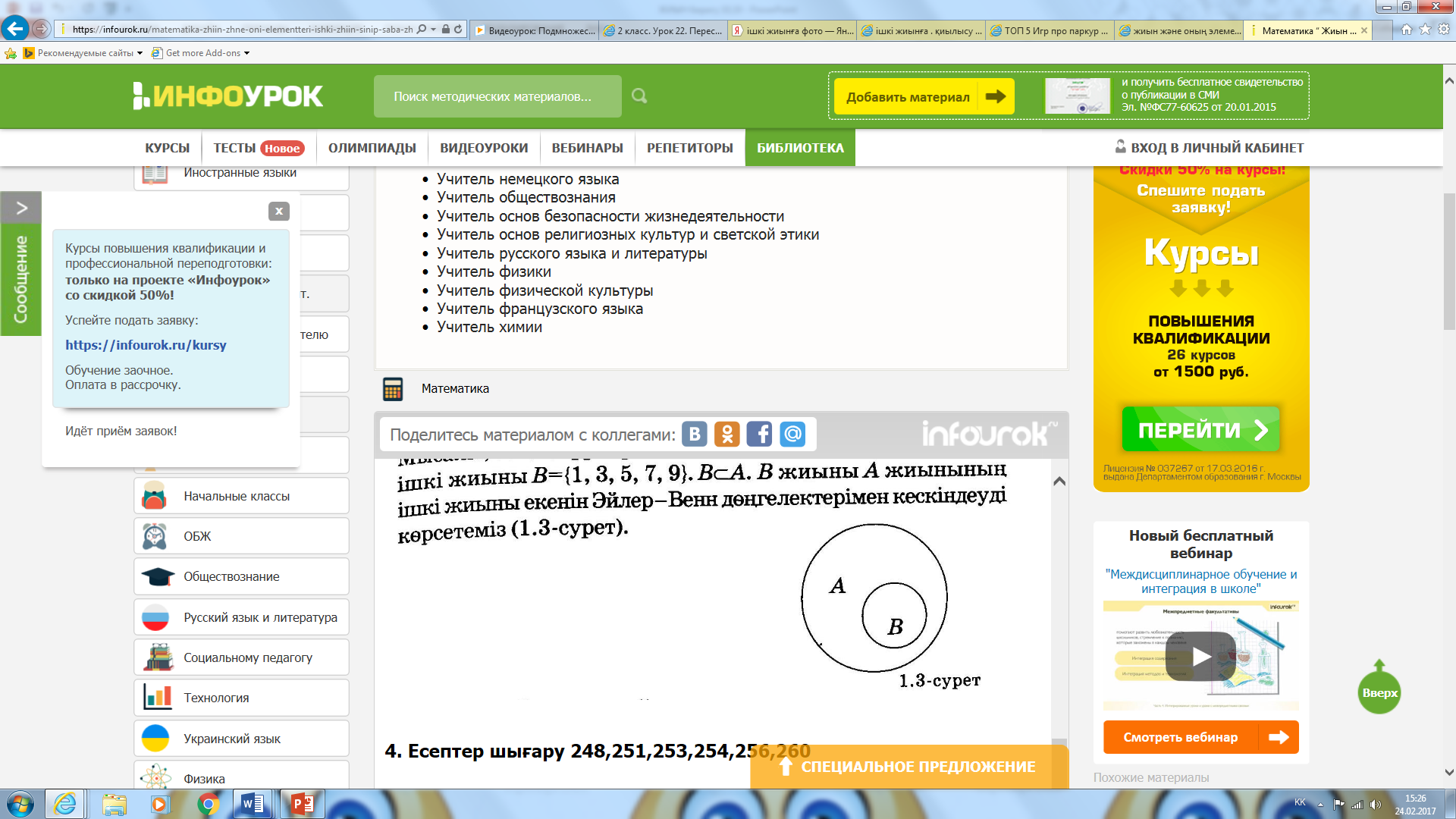 иындардың
қиылысуы. Екі жиынның
қиылысуы.
иындардың
қиылысуы. Екі жиынның
қиылысуы.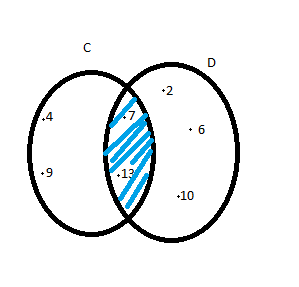 А
А V. «Ойлан,
жұптас, бөліс!» Жұптық жұмыс. Сурет бойынша ішкі жиын аттарын
анықтау
V. «Ойлан,
жұптас, бөліс!» Жұптық жұмыс. Сурет бойынша ішкі жиын аттарын
анықтау