
ЖОҒАРЫ МАТЕМАТИКА КУРСЫНДА MAPLE ПРОГРАММАЛАУ ОРТАСЫН ҚОЛДАНУ
. Ш.Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті Мақалада оқу үрдісінде жаңа педагогикалық бағдарламалық өнімдерге жаңа ақпараттық технологияларды – жоғарғы математика курсында Maple программалау ортасын қолдануға байланысты сұрақтар мен кейбір есептердің Maple-да шешу жолдары қарастырылған.
Түйін
сөздер: Математикалық қалта, жоғары
математика, есептер, пәрмендер. Сапалы білім беру қазіргі уақытта,
білім алушылардың жұмысын ұйымдастыруда жаңа әдістер мен
технологияларды кеңінен пайдалануды, білім беруді ақпараттандыруды
талап етеді [1]. Ақпараттық технологияларды пайдалану-бұрыннан
пайдаланатын жүйелерге қосымша болғанда емес, дәстүрлі жүйелермен
тұрақты байланыста, оқыту процесінде қатысушыларға жаңа
мүмкіндіктерімен ұйымдастырылғанда ғана тиімді [2]. Компьютерлік
оқыту дегеніміз - оқытудың техникалық құралдарының бірі компьютер
мүмкіндіктерін қолдану болып табылады. Жоғары математиканы оқыту
кезінде математикалық жүйелердің мүмкіндіктерін пайдалану да
компьютерлік оқытуға жатады. Мысалы: Maple жүйесі барлық қарапайым
функциялармен бірге математикалық физиканың арнайы стандартты
функцияларын есептеуге мүмкіндік береді. Бұл функциялар әртүрлі
математикалық физика есептерінде кездесіп және кейбір
дифференциалдық теңдеулердің шешімі болып табылады. Maple - 1984
жылдан бстап программалар шығаратын Waterloo Maple Inc
компаниясының өнімі. Maple - компьютер үшін құрамында екі мыңға
жуық командасы арқылы алгебра, геометрия, математикалық талдау,
дифференцалдық теңдеу, статистика, математикалық физика есептерін
шешуге арналған математикалық қалта. Негізгі объектілері формула
және оларды қолдану болып табылады.
Оның
артықшылығы – аналитикалық сондай-ақ
дербес математикалық есептерді шешу мүмкіндігі, қолданбалы
бағдарлама мен приложения жасау мүмкіндігі, керемет екі өлшемді
және үш өлшемді графика сызу мүмкіндігі. Сол
себептен Maple математикалық пакетін
алып, онымен жақынырақ танысып, жүйелі жұмыс жүргізілді. Атап
айтқанда жоғарғы математикның векторлы алгебра, матрица және оларға
амлдар қолдану тақырыптарын алып Maple математикалық қалтасында
нақты мысалдармен есептелінді. Есептеу барысында Maple-дің қалай
жұмыс істейтіндігі, оның ішінде қандай кітапханалар бар екендігін
меңгеріліп, жоғарғы математика есептерін шешу мүмкіндіктері
қарастырылды. Mapl-де жұмыс істеу режимі пайдаланушы пәрмендерді
(өрнектерді, түрлендірулерді) енгізгеннен бастап Maple оны өңдеп,
есептейді. Жұмыс аймағын үш бөлікке бөлінеді: 1)Енгізу аймағы –
пәрмендерден тұрады. Пәрмен «>» сиволынан соң енгізіледі;
2)Шығару аймағы – өңделген команда нәтижесін алгебралық өрнектер,
графикалық объект немесе қателік туралы ескерту түрлерін береді;
3)Коментарий бар мәтін аймағы есептеліп отырған команда жайында кез
келген мәлімет береді. Мәтінде жолдар Maple - да қабылданбайды және
өңделмейді.[3] Жүйеден шықпай жаңа есептеулерді орындау үшін
restart, яғни жаңарту пәрмені орындалады. Maple – математикалық
қалтасына with(кітапхана аты) командасымен орындалатын көптеген
кітапханалар енеді. Ал қарастырылған тақырыпқа сызықты алгебра
операцияларын қабылдайтын LinearAlgebra қалтасы қарастырылған.
Мысалы, қрапайым матрицаны экранға шығаруды
matrix(n, m,
[[a11,a12,…,a1n], [a21,a22,…,
]) пәрменімен
орындасақ,
diag, evalm(A+B), multiply(A,B)
пәрмендері арқылы матрицаларды
қосуға, көбейтуге, диагональ матрианы табуға болады. Сонымен қатар
мұнда: а) матрица тақырыбында: матрицаға амалдар қолдану,
матрицаның анықтауышын, рангін, экспонентасын, ядросын табу,
матрицаға кері матрица табу, сызықтық теңдеулер жүйесін кері
матрицалық әдіспен, Гаусс-Жордано және Крамер әдістерімен шешу,
матрицаның графиг түрінде берілу есептері; ә) векторлы алгебра
элементтеерінде: векторға амалдар қолдану, вектордың нормасын табу,
векторладың скаляр көбейтіндісі,вектордың ұзындығын табу,
Грамма-Шмидт процедурасы қарастырылған. 1-мысал: Теңдеулер жүйесін
Гаусс-Жордана әдісімен шешу: 
-
restart:with(linalg): A:=matrix(3,4,[2,1,-3,-5,1,-2,2,17,1,1,3,4]);
-
gaussjord(A);(1-сурет)
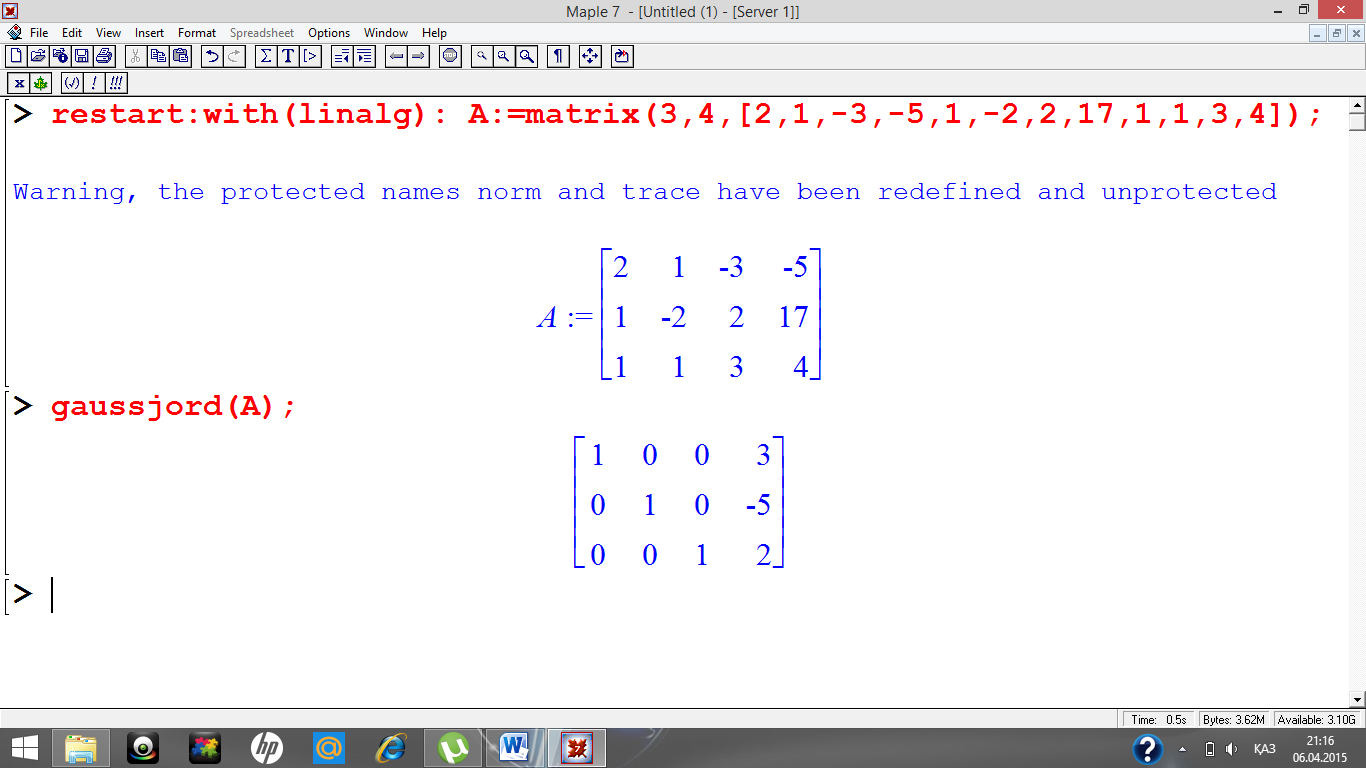
1-сурет Гаусс-Жордана әдісінің көрінісі
|
|
2-мысал: а1=(1,2,2,-1), а2=(1,1,-5,3), а3=(3,2,8,7), а4=(0,1,7,-4), а5=(2,1,12,-10 ) берілген векторлар жүйесінен Грамма-Шмидт процедурусы арқылы базисі мен ортогональін есепте: > restart; with(linalg): a1:=vector([1,2,2,-1]): a2:=vector([1,1,-5,3]): a3:=vector([3,2,8,7]): a4:=vector([0,1,7,-4]): a5:=vector([2,1,12,-10]): g:=basis([a1,a2,a3,a4,a5]); > GramSchmidt(g);(2-сурет)
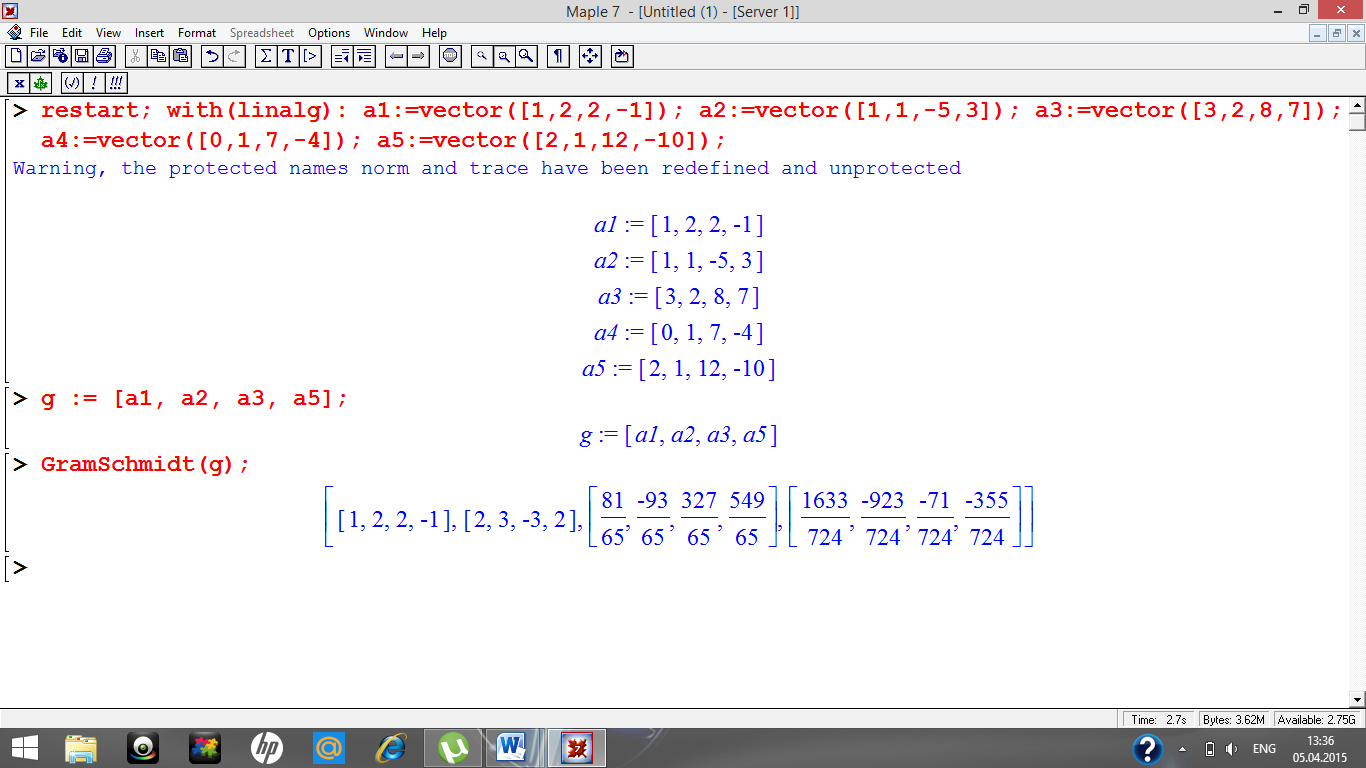
2-сурет Грамм-Шмидт процедурасының көрінісі
Maple жүйесінің графикалық мүмкіндіктері MathCad жүйесіне қарағанда жоғары. Ол жұмыстың көп бөлігін өзі атқарады. Онда кез келген функцияның графигін салу үшін команданы білсеңіз болғаны. Бір басқару жолы арқылы бір математикалық функцияның графигін бірден құра аласыз және оны декарттық координаталар жүйесінде, полярлық жүйеде, үшөлшемді кеңістікте де бейнелей аласыз. Графикті көркемдеуге, түсін өзгертуге, айналдыруға болады. Maple жүйесінің графикалық мүмкіндіктері қуатты және әртүрлі болып келеді. Оларды көбінесе жоғары деңгейлі графика деп атайды. Maple жүйесіндегі жоғары деңгейлі графика әр түрлі графиктерді нақты салумен ерекшеленеді және салу жеңіл көрнекі. Жоғары математиканы оқыту кезінде жаңа ақпараттық технологияларды пайдалануға компьютерленген оқулықтарды және есептер жинағын, мүмкіндіктері жоғары математикалық пакеттерді қолдану арқылы оқыту жүйесіне жаңалық енгізуге болады [4]. Математикалық қалта - программалау деңгейі жоғары математикалық жүйер болып табылады. Бұл жүйелер сандық, символдық, графикалық есептеулер және жоғары деңгейдегі программалау қосымшасымен қатар компьютерлік оқулықтың қабықшасының жасайтын барлық элементтерімен жабдықталған. Сондықтан математикалық қалталарды пайдалана отырып студент төмендегідей нәтижелерге жетеді:
Оқытудың көркемділігі артады, яғни қиын да күрделі материалдарды көрнекі түрде түсіндіруге қол жеткеді;
Оқытудың тиімділігі жоғарлайды және оқыту материалын түсіндіру мүмкіндігі арттырады;
Ғылыми-дүниетанымдық көзқарастарын қалыптастыра отырып, олардың білімге құштарлығын, табиғи сұранысын қанағаттандырады;
Оқытушыны техникалық жұмыстан босата отырып, үнемденген уақытта олардың шығармашылықпен жұмыс істеуіне жағдай жасайды.
Қорыта айтқанда, қазіргі кезде ақпараттық технологиялар даму барысында, ендеше аталған математикалық пакеттер де оқу үрдісінде елеулі орын алуда. Бұл жүйелер математика мен информатика пәнін байланыстырып ғана қоймай, сонымен бірге компьютерлендіру мақсатында математика сабағын жеңілдетіп, көмекші құрал ретінде пайдасын тигізе отыра уақытын үнемдеуге септігін тигізеді. Компьютердің мүмкіндіктерін пайдалана отырып жоғары математика сабағында көрсету, түсіндіру, жаттықтыру, түзету және бағалауды жүзеге асыруға болады. Оқытушы педагогикалық жұмыста белгілі бір нәтижеге жетуді көздеп, компьютерлік техниканы жоғары математика пәнін оқытуда тиімді пайдаланып, сабақ өтсе сапалы білім беруге қол жеткізуге болатындығы айқын.
Әдебиет
-
Симонович С. «Новейший самоучитель работы на компьютере». – Москва. – 1999г. – Б. 15-17
-
Шәдиев Қ. Компьютерді қолданудың педагогикалық мәселелері // Қазақстан мектебі. – №5. - 2006. – Б.7-9
-
Мочанова Л.А. Введение в Maple.- Владивосток. - 2006г.- Б.3-4
-
Әбілқасымова А. Е., Садықов Т. С. «Жоғары мектепте білім берудің дидактикалық негіздері». – Алматы: Ғылым, 2003. – Б. 5-13
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ЖОҒАРЫ МАТЕМАТИКА КУРСЫНДА MAPLE ПРОГРАММАЛАУ ОРТАСЫН ҚОЛДАНУ мақала
ЖОҒАРЫ МАТЕМАТИКА КУРСЫНДА MAPLE ПРОГРАММАЛАУ ОРТАСЫН ҚОЛДАНУ мақала
ЖОҒАРЫ МАТЕМАТИКА КУРСЫНДА MAPLE ПРОГРАММАЛАУ ОРТАСЫН ҚОЛДАНУ
. Ш.Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті Мақалада оқу үрдісінде жаңа педагогикалық бағдарламалық өнімдерге жаңа ақпараттық технологияларды – жоғарғы математика курсында Maple программалау ортасын қолдануға байланысты сұрақтар мен кейбір есептердің Maple-да шешу жолдары қарастырылған.
Түйін
сөздер: Математикалық қалта, жоғары
математика, есептер, пәрмендер. Сапалы білім беру қазіргі уақытта,
білім алушылардың жұмысын ұйымдастыруда жаңа әдістер мен
технологияларды кеңінен пайдалануды, білім беруді ақпараттандыруды
талап етеді [1]. Ақпараттық технологияларды пайдалану-бұрыннан
пайдаланатын жүйелерге қосымша болғанда емес, дәстүрлі жүйелермен
тұрақты байланыста, оқыту процесінде қатысушыларға жаңа
мүмкіндіктерімен ұйымдастырылғанда ғана тиімді [2]. Компьютерлік
оқыту дегеніміз - оқытудың техникалық құралдарының бірі компьютер
мүмкіндіктерін қолдану болып табылады. Жоғары математиканы оқыту
кезінде математикалық жүйелердің мүмкіндіктерін пайдалану да
компьютерлік оқытуға жатады. Мысалы: Maple жүйесі барлық қарапайым
функциялармен бірге математикалық физиканың арнайы стандартты
функцияларын есептеуге мүмкіндік береді. Бұл функциялар әртүрлі
математикалық физика есептерінде кездесіп және кейбір
дифференциалдық теңдеулердің шешімі болып табылады. Maple - 1984
жылдан бстап программалар шығаратын Waterloo Maple Inc
компаниясының өнімі. Maple - компьютер үшін құрамында екі мыңға
жуық командасы арқылы алгебра, геометрия, математикалық талдау,
дифференцалдық теңдеу, статистика, математикалық физика есептерін
шешуге арналған математикалық қалта. Негізгі объектілері формула
және оларды қолдану болып табылады.
Оның
артықшылығы – аналитикалық сондай-ақ
дербес математикалық есептерді шешу мүмкіндігі, қолданбалы
бағдарлама мен приложения жасау мүмкіндігі, керемет екі өлшемді
және үш өлшемді графика сызу мүмкіндігі. Сол
себептен Maple математикалық пакетін
алып, онымен жақынырақ танысып, жүйелі жұмыс жүргізілді. Атап
айтқанда жоғарғы математикның векторлы алгебра, матрица және оларға
амлдар қолдану тақырыптарын алып Maple математикалық қалтасында
нақты мысалдармен есептелінді. Есептеу барысында Maple-дің қалай
жұмыс істейтіндігі, оның ішінде қандай кітапханалар бар екендігін
меңгеріліп, жоғарғы математика есептерін шешу мүмкіндіктері
қарастырылды. Mapl-де жұмыс істеу режимі пайдаланушы пәрмендерді
(өрнектерді, түрлендірулерді) енгізгеннен бастап Maple оны өңдеп,
есептейді. Жұмыс аймағын үш бөлікке бөлінеді: 1)Енгізу аймағы –
пәрмендерден тұрады. Пәрмен «>» сиволынан соң енгізіледі;
2)Шығару аймағы – өңделген команда нәтижесін алгебралық өрнектер,
графикалық объект немесе қателік туралы ескерту түрлерін береді;
3)Коментарий бар мәтін аймағы есептеліп отырған команда жайында кез
келген мәлімет береді. Мәтінде жолдар Maple - да қабылданбайды және
өңделмейді.[3] Жүйеден шықпай жаңа есептеулерді орындау үшін
restart, яғни жаңарту пәрмені орындалады. Maple – математикалық
қалтасына with(кітапхана аты) командасымен орындалатын көптеген
кітапханалар енеді. Ал қарастырылған тақырыпқа сызықты алгебра
операцияларын қабылдайтын LinearAlgebra қалтасы қарастырылған.
Мысалы, қрапайым матрицаны экранға шығаруды
matrix(n, m,
[[a11,a12,…,a1n], [a21,a22,…,
]) пәрменімен
орындасақ,
diag, evalm(A+B), multiply(A,B)
пәрмендері арқылы матрицаларды
қосуға, көбейтуге, диагональ матрианы табуға болады. Сонымен қатар
мұнда: а) матрица тақырыбында: матрицаға амалдар қолдану,
матрицаның анықтауышын, рангін, экспонентасын, ядросын табу,
матрицаға кері матрица табу, сызықтық теңдеулер жүйесін кері
матрицалық әдіспен, Гаусс-Жордано және Крамер әдістерімен шешу,
матрицаның графиг түрінде берілу есептері; ә) векторлы алгебра
элементтеерінде: векторға амалдар қолдану, вектордың нормасын табу,
векторладың скаляр көбейтіндісі,вектордың ұзындығын табу,
Грамма-Шмидт процедурасы қарастырылған. 1-мысал: Теңдеулер жүйесін
Гаусс-Жордана әдісімен шешу: 
-
restart:with(linalg): A:=matrix(3,4,[2,1,-3,-5,1,-2,2,17,1,1,3,4]);
-
gaussjord(A);(1-сурет)

1-сурет Гаусс-Жордана әдісінің көрінісі
|
|
2-мысал: а1=(1,2,2,-1), а2=(1,1,-5,3), а3=(3,2,8,7), а4=(0,1,7,-4), а5=(2,1,12,-10 ) берілген векторлар жүйесінен Грамма-Шмидт процедурусы арқылы базисі мен ортогональін есепте: > restart; with(linalg): a1:=vector([1,2,2,-1]): a2:=vector([1,1,-5,3]): a3:=vector([3,2,8,7]): a4:=vector([0,1,7,-4]): a5:=vector([2,1,12,-10]): g:=basis([a1,a2,a3,a4,a5]); > GramSchmidt(g);(2-сурет)

2-сурет Грамм-Шмидт процедурасының көрінісі
Maple жүйесінің графикалық мүмкіндіктері MathCad жүйесіне қарағанда жоғары. Ол жұмыстың көп бөлігін өзі атқарады. Онда кез келген функцияның графигін салу үшін команданы білсеңіз болғаны. Бір басқару жолы арқылы бір математикалық функцияның графигін бірден құра аласыз және оны декарттық координаталар жүйесінде, полярлық жүйеде, үшөлшемді кеңістікте де бейнелей аласыз. Графикті көркемдеуге, түсін өзгертуге, айналдыруға болады. Maple жүйесінің графикалық мүмкіндіктері қуатты және әртүрлі болып келеді. Оларды көбінесе жоғары деңгейлі графика деп атайды. Maple жүйесіндегі жоғары деңгейлі графика әр түрлі графиктерді нақты салумен ерекшеленеді және салу жеңіл көрнекі. Жоғары математиканы оқыту кезінде жаңа ақпараттық технологияларды пайдалануға компьютерленген оқулықтарды және есептер жинағын, мүмкіндіктері жоғары математикалық пакеттерді қолдану арқылы оқыту жүйесіне жаңалық енгізуге болады [4]. Математикалық қалта - программалау деңгейі жоғары математикалық жүйер болып табылады. Бұл жүйелер сандық, символдық, графикалық есептеулер және жоғары деңгейдегі программалау қосымшасымен қатар компьютерлік оқулықтың қабықшасының жасайтын барлық элементтерімен жабдықталған. Сондықтан математикалық қалталарды пайдалана отырып студент төмендегідей нәтижелерге жетеді:
Оқытудың көркемділігі артады, яғни қиын да күрделі материалдарды көрнекі түрде түсіндіруге қол жеткеді;
Оқытудың тиімділігі жоғарлайды және оқыту материалын түсіндіру мүмкіндігі арттырады;
Ғылыми-дүниетанымдық көзқарастарын қалыптастыра отырып, олардың білімге құштарлығын, табиғи сұранысын қанағаттандырады;
Оқытушыны техникалық жұмыстан босата отырып, үнемденген уақытта олардың шығармашылықпен жұмыс істеуіне жағдай жасайды.
Қорыта айтқанда, қазіргі кезде ақпараттық технологиялар даму барысында, ендеше аталған математикалық пакеттер де оқу үрдісінде елеулі орын алуда. Бұл жүйелер математика мен информатика пәнін байланыстырып ғана қоймай, сонымен бірге компьютерлендіру мақсатында математика сабағын жеңілдетіп, көмекші құрал ретінде пайдасын тигізе отыра уақытын үнемдеуге септігін тигізеді. Компьютердің мүмкіндіктерін пайдалана отырып жоғары математика сабағында көрсету, түсіндіру, жаттықтыру, түзету және бағалауды жүзеге асыруға болады. Оқытушы педагогикалық жұмыста белгілі бір нәтижеге жетуді көздеп, компьютерлік техниканы жоғары математика пәнін оқытуда тиімді пайдаланып, сабақ өтсе сапалы білім беруге қол жеткізуге болатындығы айқын.
Әдебиет
-
Симонович С. «Новейший самоучитель работы на компьютере». – Москва. – 1999г. – Б. 15-17
-
Шәдиев Қ. Компьютерді қолданудың педагогикалық мәселелері // Қазақстан мектебі. – №5. - 2006. – Б.7-9
-
Мочанова Л.А. Введение в Maple.- Владивосток. - 2006г.- Б.3-4
-
Әбілқасымова А. Е., Садықов Т. С. «Жоғары мектепте білім берудің дидактикалық негіздері». – Алматы: Ғылым, 2003. – Б. 5-13

шағым қалдыра аласыз















