
Сабақтың тақырыбы: Көпжақты бұрыш. Үшжақты бұрыш.Геометриялық дене.Көпжақтар.
Сабақтың мақсаты:
1. Көп жақтар және олардың беттерінің аудандарын табудағы білімдерін жүйелеу және жалпылау;
2. Есеп шығару дағдыларын арттыру, ой-өрісін дамыту, жаңашылдық, ғылым мен техниканың жетістіктерін пайдалана білуге үйрету;
3. Еңбекке баулу, сыйластыққа және ұйымшылдыққа, алдарына қойған мақсатқа жетуге тәрбиелеу;
Сабақтыңтипі: өткен тақырыптарды пысықтау, қорытындылау.
Сабақтыңтүрі: жарыс сабағы.
Сабақтыңкөрнекілігі: интерактивті тақта, плакат, үлестірмелі қима қағаздары, кестелер.
Сабақтың барысы.
1. Үй жұмысы. Әр топ өз презентацияларын ұсынады және қорғайды «Бізді қоршаған әлемдегі көпжақтар» тақырыбында. Пирамида, Призма және Дұрыс көпжақтар топтары.
2) Формулаларды жалғастыр:
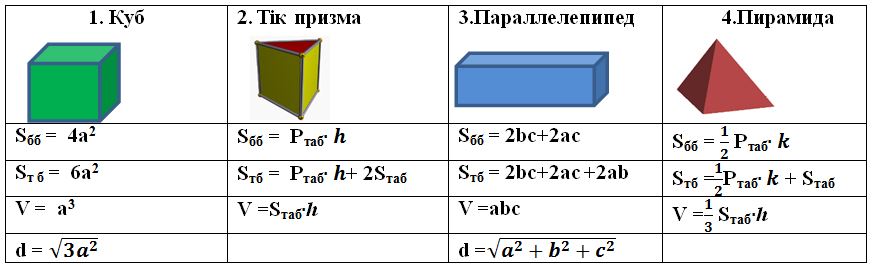
Жаңа
сабақты түсіндіру 1) Ортақ бір О нүктесінен шығатын а,
в, с сәулелерін алайық. а, б, с сәулелері қос –қостан үш доғамен
бөліп көрсетілген α, β, γ бұрыштарын анықтайды. Осы үш бұрыштан және кеңістіктің осы
жазық бұрыштарымен шектелген бөлігінен тұратын
фигураны үшжақты бұрыш деп атайды. 2) Үшжақты бұрышты құрастыру үшін бір
нүктеден шығатын үш сәулені алдық. Сәулелер санын 4, 5, 6,.., n деп
алсақ, көпжақты бұрыш шығады. 3) Анықтама. Егер көпжақты бұрыш өзінің жағын
қамтитын әрбәр жазықтыққа қараған дасол жазықтықтың бір жағында
орналасса, онда ол дөңес көпжақты бұрыш деп аталады.
1-теорема. Үшжақты бұрыштың әрбір жазық бұрышы
қалған екі жазық бұрышының қосындысынан кіші болады.
2-теорема. Дөңес көпжақты бұрыштың барлық жазық
бұрыштарының қосындысы 360º-тан кіші болады.
Геометриялық денелер дегеніміз кеңістіктің
немесе жазықтықтың қисық беттерімен шектелген тұйықталған
бөлігі. Барлық геометриялық
денелер екі топқа бөлінеді, олар: көпжақтылар (текше, призма,
параллелипепед, прирамида) және айналу денелері (цилиндр, кону,
шар)
«Призма»
тобы:
1. Сегіз жақты дұрыс көпжақтын атауы...
2. Ромбтың ауданын табатын формула...
3. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы деп..
4. Көпбұрыштың барлық бұрыштарының қосындысын анықтайтын формула...
5. Шеңбер ұзындығын табатын формула...
«Дұрыс көпжақтар» тобы:
1. Параллелограмның ауданын табатын формула...
2. Барлық қырлары тең болатын үшбұрышты пирамиданың атауы...
3. Пирамиданың бүйір жағының биіктігі деп...
4. Тікбұрышты үшбұрыштың сүйір бұрышының синусы деп..
4) Кім жылдам?
1. Кубтың диагоналі 6 см-ге тең. Кубтың қырын табыңдар? (√12)
2. Тікбұрышты параллелепипедтің өлшемдері 8см, 10см және 13 см. Диагоналін табыңдар? Көлемі?
3. Параллелепипедтің үш жағының аудандары сәйкесінше 20 см2, 30 см2 және 40 см2. Параллелепипедтың толық беті неге тең?
4. Кубтың қыры 9 см. Оның толық беті нешеге тең? Бүйір бетінің ауданы? Көлемі?
5) Көпжақтардың қималарын салу:
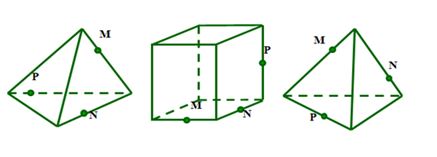
7) Сабақты қорытындылау. Синквейн.
СИНКВЕЙН әдісі - ақпаратты түйіндеу, күрделі ойларды бірнеше маңызды сөздермен, кең және қысқа сөйлемдермен жеткізу.
— Бірінші жолда- тақырып бір сөзбен беріледі (зат есім)
— Екінші жолда- тақырып екі сөзбен сипаттау (сын есім)
— Үшінші жолда- тақырыпқа қатысты қимыл атауынан үш сөз жазу. (етістік)
— Төртінші жолда-4 сөзден тұратын бір сөйлем.
8) Бағалау. Рефлексия.
6) Есептерді шығару.
 1. Бейбітшілік және Келісім
сарайы – архитектуралық құрылыс
кешені, сәулет өнерінің бірегей туындысы.
Қазақстан халықтары ассамблеясы, ұлтаралық және дінаралық
келісім орталығы болып келеді. Бұл ғимарат дұрыс пирамида түрінде
салынған. Оның табанының қабырғасы 62 метр, биіктігі де 62
метрін құрайды, яғни «Фибоначчидің алтын қимасы»
қағидаттарына сай тұрғызылған. Осы ғажайып құрылыстың бүйір бетінің
ауданын анықтау қажет?(15376 м2)
1. Бейбітшілік және Келісім
сарайы – архитектуралық құрылыс
кешені, сәулет өнерінің бірегей туындысы.
Қазақстан халықтары ассамблеясы, ұлтаралық және дінаралық
келісім орталығы болып келеді. Бұл ғимарат дұрыс пирамида түрінде
салынған. Оның табанының қабырғасы 62 метр, биіктігі де 62
метрін құрайды, яғни «Фибоначчидің алтын қимасы»
қағидаттарына сай тұрғызылған. Осы ғажайып құрылыстың бүйір бетінің
ауданын анықтау қажет?(15376 м2)
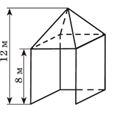
2. Жаздық шатырдың құрылысы тікбұрышты параллелепипедтің 3 бүйір жағынан тұрады және төбесінде дұрыс төртбұрышты пирамида. Оның табанының диагоналі 6√2 м. Осы шатырдың сыртын қаптауға неше квадрат метр мата керектігін анықтау керек? (240 м2)
 3. Бөлменің ұзындығы 10
м, ені 5м және биіктігі 4м. Толық бетінің ауданының
10%-ын есік пен терезе құрайды. Ақталуға тиісті
бөліктің ауданың анықтау
қажет?
3. Бөлменің ұзындығы 10
м, ені 5м және биіктігі 4м. Толық бетінің ауданының
10%-ын есік пен терезе құрайды. Ақталуға тиісті
бөліктің ауданың анықтау
қажет?
7) Сабақты қорытындылау. Синквейн.
СИНКВЕЙН әдісі - ақпаратты түйіндеу, күрделі ойларды бірнеше маңызды сөздермен, кең және қысқа сөйлемдермен жеткізу.
— Бірінші жолда- тақырып бір сөзбен беріледі (зат есім)
— Екінші жолда- тақырып екі сөзбен сипаттау (сын есім)
— Үшінші жолда- тақырыпқа қатысты қимыл атауынан үш сөз жазу. (етістік)
— Төртінші жолда-4 сөзден тұратын бір сөйлем.
8) Оқушыларды бағалау. Рефлексия.
Пән мұғалімі: Ельжанова Г.Х.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Көпжақтар туралы түсінік
Көпжақтар туралы түсінік
Сабақтың тақырыбы: Көпжақты бұрыш. Үшжақты бұрыш.Геометриялық дене.Көпжақтар.
Сабақтың мақсаты:
1. Көп жақтар және олардың беттерінің аудандарын табудағы білімдерін жүйелеу және жалпылау;
2. Есеп шығару дағдыларын арттыру, ой-өрісін дамыту, жаңашылдық, ғылым мен техниканың жетістіктерін пайдалана білуге үйрету;
3. Еңбекке баулу, сыйластыққа және ұйымшылдыққа, алдарына қойған мақсатқа жетуге тәрбиелеу;
Сабақтыңтипі: өткен тақырыптарды пысықтау, қорытындылау.
Сабақтыңтүрі: жарыс сабағы.
Сабақтыңкөрнекілігі: интерактивті тақта, плакат, үлестірмелі қима қағаздары, кестелер.
Сабақтың барысы.
1. Үй жұмысы. Әр топ өз презентацияларын ұсынады және қорғайды «Бізді қоршаған әлемдегі көпжақтар» тақырыбында. Пирамида, Призма және Дұрыс көпжақтар топтары.
2) Формулаларды жалғастыр:

Жаңа
сабақты түсіндіру 1) Ортақ бір О нүктесінен шығатын а,
в, с сәулелерін алайық. а, б, с сәулелері қос –қостан үш доғамен
бөліп көрсетілген α, β, γ бұрыштарын анықтайды. Осы үш бұрыштан және кеңістіктің осы
жазық бұрыштарымен шектелген бөлігінен тұратын
фигураны үшжақты бұрыш деп атайды. 2) Үшжақты бұрышты құрастыру үшін бір
нүктеден шығатын үш сәулені алдық. Сәулелер санын 4, 5, 6,.., n деп
алсақ, көпжақты бұрыш шығады. 3) Анықтама. Егер көпжақты бұрыш өзінің жағын
қамтитын әрбәр жазықтыққа қараған дасол жазықтықтың бір жағында
орналасса, онда ол дөңес көпжақты бұрыш деп аталады.
1-теорема. Үшжақты бұрыштың әрбір жазық бұрышы
қалған екі жазық бұрышының қосындысынан кіші болады.
2-теорема. Дөңес көпжақты бұрыштың барлық жазық
бұрыштарының қосындысы 360º-тан кіші болады.
Геометриялық денелер дегеніміз кеңістіктің
немесе жазықтықтың қисық беттерімен шектелген тұйықталған
бөлігі. Барлық геометриялық
денелер екі топқа бөлінеді, олар: көпжақтылар (текше, призма,
параллелипепед, прирамида) және айналу денелері (цилиндр, кону,
шар)
«Призма»
тобы:
1. Сегіз жақты дұрыс көпжақтын атауы...
2. Ромбтың ауданын табатын формула...
3. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы деп..
4. Көпбұрыштың барлық бұрыштарының қосындысын анықтайтын формула...
5. Шеңбер ұзындығын табатын формула...
«Дұрыс көпжақтар» тобы:
1. Параллелограмның ауданын табатын формула...
2. Барлық қырлары тең болатын үшбұрышты пирамиданың атауы...
3. Пирамиданың бүйір жағының биіктігі деп...
4. Тікбұрышты үшбұрыштың сүйір бұрышының синусы деп..
4) Кім жылдам?
1. Кубтың диагоналі 6 см-ге тең. Кубтың қырын табыңдар? (√12)
2. Тікбұрышты параллелепипедтің өлшемдері 8см, 10см және 13 см. Диагоналін табыңдар? Көлемі?
3. Параллелепипедтің үш жағының аудандары сәйкесінше 20 см2, 30 см2 және 40 см2. Параллелепипедтың толық беті неге тең?
4. Кубтың қыры 9 см. Оның толық беті нешеге тең? Бүйір бетінің ауданы? Көлемі?
5) Көпжақтардың қималарын салу:

7) Сабақты қорытындылау. Синквейн.
СИНКВЕЙН әдісі - ақпаратты түйіндеу, күрделі ойларды бірнеше маңызды сөздермен, кең және қысқа сөйлемдермен жеткізу.
— Бірінші жолда- тақырып бір сөзбен беріледі (зат есім)
— Екінші жолда- тақырып екі сөзбен сипаттау (сын есім)
— Үшінші жолда- тақырыпқа қатысты қимыл атауынан үш сөз жазу. (етістік)
— Төртінші жолда-4 сөзден тұратын бір сөйлем.
8) Бағалау. Рефлексия.
6) Есептерді шығару.
 1. Бейбітшілік және Келісім
сарайы – архитектуралық құрылыс
кешені, сәулет өнерінің бірегей туындысы.
Қазақстан халықтары ассамблеясы, ұлтаралық және дінаралық
келісім орталығы болып келеді. Бұл ғимарат дұрыс пирамида түрінде
салынған. Оның табанының қабырғасы 62 метр, биіктігі де 62
метрін құрайды, яғни «Фибоначчидің алтын қимасы»
қағидаттарына сай тұрғызылған. Осы ғажайып құрылыстың бүйір бетінің
ауданын анықтау қажет?(15376 м2)
1. Бейбітшілік және Келісім
сарайы – архитектуралық құрылыс
кешені, сәулет өнерінің бірегей туындысы.
Қазақстан халықтары ассамблеясы, ұлтаралық және дінаралық
келісім орталығы болып келеді. Бұл ғимарат дұрыс пирамида түрінде
салынған. Оның табанының қабырғасы 62 метр, биіктігі де 62
метрін құрайды, яғни «Фибоначчидің алтын қимасы»
қағидаттарына сай тұрғызылған. Осы ғажайып құрылыстың бүйір бетінің
ауданын анықтау қажет?(15376 м2)

2. Жаздық шатырдың құрылысы тікбұрышты параллелепипедтің 3 бүйір жағынан тұрады және төбесінде дұрыс төртбұрышты пирамида. Оның табанының диагоналі 6√2 м. Осы шатырдың сыртын қаптауға неше квадрат метр мата керектігін анықтау керек? (240 м2)
 3. Бөлменің ұзындығы 10
м, ені 5м және биіктігі 4м. Толық бетінің ауданының
10%-ын есік пен терезе құрайды. Ақталуға тиісті
бөліктің ауданың анықтау
қажет?
3. Бөлменің ұзындығы 10
м, ені 5м және биіктігі 4м. Толық бетінің ауданының
10%-ын есік пен терезе құрайды. Ақталуға тиісті
бөліктің ауданың анықтау
қажет?
7) Сабақты қорытындылау. Синквейн.
СИНКВЕЙН әдісі - ақпаратты түйіндеу, күрделі ойларды бірнеше маңызды сөздермен, кең және қысқа сөйлемдермен жеткізу.
— Бірінші жолда- тақырып бір сөзбен беріледі (зат есім)
— Екінші жолда- тақырып екі сөзбен сипаттау (сын есім)
— Үшінші жолда- тақырыпқа қатысты қимыл атауынан үш сөз жазу. (етістік)
— Төртінші жолда-4 сөзден тұратын бір сөйлем.
8) Оқушыларды бағалау. Рефлексия.
Пән мұғалімі: Ельжанова Г.Х.

шағым қалдыра аласыз















