«Логорифмдік жəне көрсеткіштік өрнектер»
11 сынып
Авторлық бағдарлама

Құрастырған: Джилбаева Гульназ Кураловна
математика пәнінің мұғалімі


2021 жыл

Түсініктеме хат
Оқушылардық функционалдық сауаттылығын дамыту жөніндегі 2012 – 2016 жылдарға арналған Ұлттық іс-қимыл жоспары оқушылардың функциялық сауаттылығын дамыту процесін мазмұндық, оқу-əдістемелік, материалдық- техникалық қамтамасыз ету жөніндегі іс-шаралар кешенін қамтиды.
Мектеп оқушыларының функционалдық сауаттылығын дамыту қазіргі 11 жылдық сияқты 12 жылдық мектептің Мемлекеттік жалпыға міндетті білім беру стандартын (МЖБС) жаңарту шеңберінде білім берудің басым мақсаттарының бірі ретінде айқындалады.
Бұл ретте функционалдық сауаттылықты дамыту нəтижесі білім алушылардың жастарға алған білімдерін практикалық жағдайларда тиімді жəне əлеуметтік бейімделу процесінде сəтті пайдалануға мүмкіндік беретін негізгі құзыреттіліктер жүйесін меңгеруі болып табылады. Негізгі құзыреттілік – бұл мемлекеттің орта мектепті бітіруші тұлғаның сапасына МЖБС-да жəне оқу бағдарламаларында көрсетілген білім беру нəтижелері түрінде қоятын талаптары.
Оқу бағдарламалары, сондай-ақ, мектеп оқушыларының функционалдық сауаттылығын дамытуға жəне негізгі, пəндік құзыреттіліктерге қол жеткізуге оқу үдерісін жұмылдыру арқылы, тəжірибе-бағдарлық мазмұндағы тапсырмалармен қоса жүйелі шешу əдістері арқылы бағдарланады. Бұл бағдарлама 11 сынып оқушылары үшін (барлығы 34 сағат, аптасына
1 сағат) оқуға арналған, ҚР-ның бастауыш, негізгі орта, жалпы орта білім беру мемлекеттік жалпыға міндетті білім беру стандарты негізінде жасалған (ҚР МЖБС, Астана, ҚР БҒМ 2012, Ы.Алтынсарин атындағы ұлттық білім беру академиясы, 23.08.2012 жылғы № 1080 бұйрығымен бекітілген).
ҚР БҒМ мен Ы.Алтынсарин атындағы ұлттық білім беру академиясының оқу бағдарламасы (Астана 2013, ҚР Білім жəне ғылым министрінің 23.08.2020жылғы № 115 бұйрығымен бекітілген). «Қазақстан Республикасының 2013-2014 оқу жылындағы жалпыға білім беру мекемелерінде ғылым негіздерін оқыту ерекшеліктері туралы» əдістемелік нұсқау хаты (ҚР БҒМ, Ы.Алтынсарин атындағы ұлттық білім беру академиясының ғылыми кеңесінде ұсынылған 25 мамыр 2013 жылғы №5 хаттамасы).
Бұл оқушылардың білімін кеңейтуге бағытталған, жоғары сынып оқушыларына қиындықтар туғызатын математикалық тақырыптар бойынша есептер шығару арқылы математикадан дайындық деңгейін көтеру, қосымша əдістермен жəне стандарттық емес тəсілдермен оқушыларды таныстыру, сондай-ақ шешу тəсілдерін жүйелеу, ҚЖСБ 2012 сəйкес тапсырмаларды шешу ғана емес тиімдісі, теңдеулер тапсырмаларын шешу де тиімді.
Математиканы оқытудың негізгі тапсырмалары мен міндеті – оқушылардың математикадан білім, біліктілік жүйесін саналы жəне тиянақты меңгеруін қамтамасыз ету. Бұл курс пəнге деген қызығушылықты қалыптастыруды қарастырады, математикалық қабілеттілікті дамыту жəне көрсету, мамандыққа бағыт беру, бір сөзбен айтқанда математикамен тығыз байланысты жүргізіледі. Оқушыларда негізгі жəне пəндік құзыреттіліктерді дифференциалды деңгейлеу, ынтымақтастық технологиясы, жобалау технологиясы, АКТ пайдалану,тірек конспектісі,материалды ірі блоктармен пайдаланып дамыту.
Бағдарламаның мақсаты: жоғарғы мектеп математикасының негізгі бөлімдері бойынша оқушылардың білім мен біліктерін кеңейту жəне тереңдету, жүйелеуге мүмкіндік жасау.
Бағдарламаның тапсырмалары:
-
Орта мектеп бітірушілердің пəндік жəне негізгі құзыреттілігін жетілдіруге мүмкіндік жасау;
-
Проблемалық жəне стандартты емес жағдайда білімдерін пайдалана білу;
-
Оқушыларда жекелей жəне топтық жұмыс істеу дағдысын дамыту;
-
Кітаптағы қиындығы жоғары есептерді шығармашылықпен шығару дағдысын дамыту;
-
Оқушылардың өзіндік бақылау мен өзара бақылау, рефлексия біліктерін дамыту;
Бағдарламаны меңгерту кезіндегі нұсқаулық:
-
Оқушыларда негізгі жəне пəндік құзыреттілігін дифференциалды деңгейлеу, ынтымақтастық технологиясы, жобалау технологиясы, АКТ пайдалану,тірек конспектісі,материалды ірі блоктармен пайдаланып дамыту.
-
Оқушылардың дайындық деңгейін оқу материалына сəйкес бейімдеу.
-
Оқылған материалдың практикалық бағытын бағдарлауды жүзеге асыру;
-
Қазіргі уақыттағы əртүрлі ақпараттар көзін пайдаланып өзара қарым- қатынас əдістерімен қамтамасыз ету.
Оқушылардың білімдерін қалыптастыру жəне дамыту:
-
Есептердің мағынасын ажырата білу.
-
Негізгі бағыттарды іздеуге ,анықтауға үйрету.
-
Жүйелі түрде есептердің дұрыс шешімдерін табуға бағыттау.
-
Есеп шығаруда дəстүрлі жолдарын таба білу.
-
Логикалық, аналогтық жəне жүйелі ойлауын дамыту
-
Есеп шығаруда тиімді тəсілдерді таба білу.
Бағдарламаның ерекшеліктері:
-
Қосымша əдебиеттер мен тірек конспектілермен жұмыс;
-
Оқушылардың зерттеу жұмыстары;
-
Электронды оқулық пен əдістемеліктер көмегімен жұмыс;
-
Оқушылардың теорияны меңгерудегі өздік жұмысы;
-
Практикалық блок:
-
Сыныптағы практикалық жұмыс (есептер жəне ең қиын бақылау сұрақтары);
-
Өз бетімен шешу;
-
Тест тапсырмаларын шешу;
-
Орындалған тапсырмаларды өзіндік жəне өзара тексеру
-
Соңғы жылдардағы тестер жинағынан қиындық тудыратын тест тапсырмаларын жинақтау;
-
ББД бақылау жəне бағалау.
-
Сынақ тапсыру ,конспект бойынша ауызша сұрау;
-
Кескін жұмыстары;
-
Өзара жұптық жəне топтық тексеру;
-
Өзара тексеру;
-
Тестілеу;
Сабақта мақсатты меңгерту үшін төмендегі форма ұсынылады: Лекция, практикалық семинарлар, модельдеу, өзара оқыту сабақтары, жоба қорғау сабақтары.
Оқушылардың білім, білік, дағдыларына қойылатын талаптар.
Оқушылардың ба5дарламаны оқу барысында білуі тиіс:
-курстың негізгі жоспарындағы формулалар мен негізгі түсініктер;
-дəрежені төмендету формуласы, үш аргументті бұрыштың формуласы, универсалды ауыстыру;
-
Безу теоремасы, Горнер схемасы;
-
полярлық жəне тікбұрышты координата жүйесінде жазық фигуралардың беттері аудандарын есептеу формулалары;
-
«күрделі экспонент» түсінігін беру;
-
симметриялық, кері жəне біртекті теңдеулердің жалпы түрлері;
-
параметрі бар теңдеулер тен теңсіздіктердің классификациясы;
-
логарифмдік өрнектерді түрлендіруге қосымша формулалар.
Қолдана білу:
-
функцияларды зерттеуге бірінші жəне екінші ретті туындылар;
-
күрделі салуларға көмекші əдістер;
-
функциялардың графиктері;
-
күрделі экспонент немесе негізінде айнымалысы бар логарифмді теңдеулер тен теңсіздіктердің шешу əдістері;
-
аркфункция белгісінің ішінде айнымалысы бар трансценденттік өрнектерді эквивалентті түрлендіру тəселдері;
-
графиктік интерпретация əдісін кірістіре параметр, модуль белгісі бар теңдеулер тен теңсіздіктердің шешу əдістері;
-
біртектес жəне қайтымды,симметриялы, жоғарғы дəрежелі теңдеулерді шешу əдістері;
-
логарифмдік өрнектерді түрлендіруге стандарт емес əдістер жəне қосымша формулалар;
-тригонометриялық жəне иррационалдық өрнектері бар теңдеулердің түбірлерін іріктеу тəсілдері əдісі;
-
интеграл табуда айнымалыны ауыстыру əдісі;
-логарифмдік жəне көрсеткіштік функциялардың монотондылық қасиеттері;
-логарифмдік жəне көрсеткіштік теңдеулер тен теңсіздіктердің шешудегі экстремалдық функциялар қасиеттері жəне интервалдар əдісіндегі стандарт емес ауыстырулар;
-
полярлық жəне тікбұрышты координата жүйесінде жазық фигуралардың беттері аудандарын есептеуге анықталған интеграл , айналу денелерінің көлемін есептеу;
-
геометриялық есептерді шешудің қосымша əдістері.
Пайдалана алу
Тапсырманы орындап білімді ары қарай жалғастыруда, өзіндік жұмыстар процесі мен практикалық іс-əрекетте білім мен білікті игеру
-
Практикалық есептер жəне формула бойынша түрлендіру, кіргізілген формулалар, дəрежесі бар, радикалдар, логарифмдер, тригонометриялық функциялар, туынды, алғашқы функция, керек болған кезде қосымша формулаларды қолдану, курстың негізгі жоспарындағы тəсілдер, əдістер, анықтамалық материалдар жəне қарапайым есептеу құрылғылары;
-
графиктік, графиктерді интерпретациялап көрсетуде əртүрлі байланыстарды функциялардың көмегімен беру;
-
физикалық жəне əлеуметтік-экономикалық мағынадағы қолдаңбалы есептерді шешу; қарапайым математикалық моделді салу мен зерттеу. Жəне фигурлар қасиеттері мен оқып білген формулалар негізінде қиын емес практикалық ситуацияларды зерттеу(моделдеу);
-
кеңістік денелерінің беттері аудандары мен көлемдерін есептеуге арналған практикалық есептерді шешуде қажет болса анықтамалық материалдар жəне қарапайым есептеу құрылғыларын пайдалану.
Білу:
-
есеп шешудің стратегиясын немесе жемісті əдісін таңдау, есеп шешуді орындағанда өзіндік тексеруді іске асыру жəне толық негіздеуді жүргізу;
-
əртүрлі моделдер (мысалы, диаграммалар, кестелер, схемалар немесе графиктер) пайдаланып математикалық ақпарат жəне берілгенін ұсыну;
-
есеп шешуге сəйкес модель (мысалы , теңдеу, диаграмма, график) ойластыру;
-
болжам жасау, сараптау, тарату;
-
комбинация/нəтиже алуға əртүрлі əдістерді ұйғару;
-таза математикалық немесе нақты өмірдегі ситуациялармен байланысты стандарт емес есептерді шешу;
-қиын немесе таныс емес ситуацияларға математикалық əдістерді қолдану;
-Интернет жəне əртүрлі ақпарат көздерін пайдалану.
Құзіреттіліктерді меңгеру:
-
оқу–танымдық,
-
бағдарлы – мақсатты,
-
рефлексивті,
-
коммуникативті,
-
ақпараттық,
-
еңбек –əлеуметтік:
Бағдарламаның мазмұны
Тақырып:«Өрнектерді түрлендіруге қосымша тригонометриялық формулаларды қолдану».
Мақсаты:Тригонометриялық өрнектерді түрлендіруге теориялық материалды қолдана білу білігі жəне білу, білімді жүйелеу (дəрежені төмендету формуласы, үшбұрыштың формуласы, универсалды ауыстыру).
Тақырып: «Күрделі функциялар графиктерін салуға көмекші тəсілдер». Мақсаты:Күрделі функциялардың графиктерін салуды неғұрлым тереңдетуді қамтиды жəне модуль таңбасы бар функциялардың графиктерін салуды жүйелеуді қарастыру.
Тақырып: «Геометриялық есептерді шешудің əдістері».
Мақсаты: білімді жүйелеу, геометриялық есептерді шешуге қосымша теориялық материалды қолдана білу білігі мен білуі, алған білімді практикада қолдану. Оқушылардың математикалық деңгейін көтеруді дамыту.
Тақырып:«Айнымалылары аркфункция таңбасының ішінде болатын трансценденттік өрнектерді эквивалентті түрлендіру».
Мақсаты: Кері тригонометриялық функциялар кездесетін өрнектерді түрлендіруде стандартты емес тəсілдерді қолдана білуді қалыптастыру.Тепе- теңдіктерді түрлендіруді оқуда мысалдарды қолданып шешу білімін жүйелеу.
Тақырып: «Тригонометриялық теңдеулер мен тіңсіздіктерді шешу əдістерін жүйелеу».
Мақсаты: Тригонометриялық теңдеулер мен теңсіздіктерді шешу- көбейткіштерге жіктеуде стандартты емес тəсілдерді қолдана білу мен білігін қалыптастыру, жаңа айнымалы еңгізу, графикалық тəсіл, квадраттық теңдеу мен теңсіздікке келтіру.
Тақырып: «Жоғарғы дəрежелі теңдеулер мен теңсіздіктерді шешу». Мақсаты: Жоғарғы дəрежелі теңдеулер мен теңсіздіктерді шешуге стандартты емес тəсілдерді қолдана білуді қалыптастыру: көбейткіштерге жіктеуде , жаңа айнымалы еңгізу, графикалық тəсіл, , квадраттық теңдеу мен теңсіздікке келтіру, Безу теоремасын қолдануда анықталмаған коэффициенттер əдісі, Горнер схемасы.
Тақырып: «Айнымалылары модуль таңбасының ішінде болатын теңдеулер мен теңсіздіктерді шешудің əдістері».
Мақсаты: Айнымалылары модуль таңбасының ішінде болатын теңдеулер мен теңсіздіктерді шешуде стандартты емес тəсілдерді қолдана білуді қалыптастыру, тақырып бойынша білімді тереңдету.
Тақырып: «Қолданбалы есептерді шешуге дифференциалды есептеуді ұсыну».
Мақсаты :Математика жəне физикадағы практикалық есептерде теориялық материалды қолдана білу білігі жəне білу, білімді жүйелеу.
Тақырып: «Логикалық есептерді шешу».
Мақсаты: Кеңістікті сезіне білуін дамыту есептерін, практикалық – бағдарлау есептерін, қабілетті комбинациялауды дамыту, ықтималдықты статистикалық анықтау, таңдау, шеңбер бойымен қозғалу есептерін, арифметикалық есептерді шешуде функциональдық сауаттылықты дамыту.
11 сынып қолданбалы курсының күнтізбелік-тақырыптық жоспары.
|
№ саб ақ |
Мазмұны |
Сағат саны |
теория |
практика |
Өткізу |
Білім берудің нəтижесі |
Дидактикалы қ қамтылуы |
|
1. Қолданбалы есептерді шешуде дифференциалды есептеулерді қолдану. (3 сағат). |
|||||||
|
1,2 |
Бірінші жəне екінші ретті туындыны функцияны зерттеуде қолдану. |
2 |
0,5 |
1,5 |
Лекция |
тірек конспектісі, есеп шығаруүлгілері |
1 қосымш а |
|
3 |
Геометрии, физика и химияда дифференциалды есептеулер элементтерин қолдану. |
1 |
0 |
1 |
2 қосымша |
||
|
2. Қолданбалы есептерде интеграл мен алғашқы функция. (3 сағат) |
|||||||
|
4 |
Интегралды тура интегралдау əдісімен шешу . |
1 |
0,5 |
0,5 |
Фронталды, |
тірек конспектісі, |
3 қосым ша |
|
5 |
Физикалық есептерді шешуде интегралды пайдалану. |
1 |
0 |
1 |
4 қосым ша |
||
|
6 |
Тік бұрышты жəне полярлық координат жүйесінде жазық фигуранын ауданын есептеу.Айналу денесінің көлемін есептеу. |
1 |
0,5 |
0,5 |
|
|
5 қосымша |
|
3.Теңдеулер мен теңсіздіктерді шешуде жəне өрнекті өзгертуде радикалдың қасиетін қолдану (5сағат) . |
|||||||
|
7 |
Радикалдың негізгі қасиеті.Радикалдарды түрлендіру. Ұқсас радикалдар. |
1 |
0,5 |
0,5 |
Лекция, фронталды, топтық |
тірек конспектісі, есеп шығару үлгілері |
6 қосымша |
|
8- 11 |
Құрамында түбір астындағы айнымалысы бар теңсіздіктер мен теңдеулерді шешу. Тригонометриялық жəне ирационалдық өрнегі бар теңдеулердің түбірін табу. |
4 |
0,5 |
3,5 |
7 қосымша |
||
|
4. Тестік жəне логикалық есептер (8 сағат). |
|||||||
|
12- 15 |
Мəтінмен берілген есептердің түрлері мен шығару тəсілдері
|
4 |
0,5 |
3,5 |
Фронталды, жекелей, топтық, |
Создание базы заданий по соответствующим темам |
қосымша8 |
|
16- 17 |
Логикалық есептер. |
2 |
0,5 |
1,5 |
9 қосым ша |
||
|
18 |
Функциональды сауаттылықты дамытуға есептер |
1 |
0 |
1 |
|
|
10 қосым ша |
|
19 |
Ойлау кеңістігін дамытуға есептер. |
1 |
0 |
1 |
11қосымша |
||
|
5.Практикалық бағыттағы есептердегі көрсеткіштік функция. Əр түрлі функциялардың графиктерин жəне туындыларының графигин зерттеу. (3 сағат). |
|||||||
|
20 |
Əртүрлі функциялар графигін жəне туындысының графигін зерттеуге есептер. |
1 |
0 |
1 |
Лекция, |
тірек конспектісі, есеп шығару үлгілері |
12 қосымша |
|
21- 22 |
Практикалық бағыттағы есепті шешуде көрсеткіштік функцияны қолдану (экономикада, өндірісте, географияда, химияда, биологияда). |
2 |
0,5 |
1,5 |
13 қосымша |
||
|
6.Логорифмдік жəне көрсеткіштік өрнектердің қасиеттерін қолдану. (6 сағат). |
|||||||
|
23 |
Логарифмдік өрнектерді түрлендіруде стандартты емес əдістерді пайдану. |
1 |
0 |
1 |
Лекция, |
Тірек схемаларды құру алгоритмін дайындау |
14 қосымша |
|
24 |
Логарифмдер теориясын пайдаланып физикалық есептерді шығару. |
1 |
0 |
1 |
15 қосымша |
||
|
25 |
Логаримдеу əдісін пайдаланып |
1 |
0,5 |
0,5 |
16 қо сы |
||
|
|
көрсеткіштік теңдеулерді шешу. |
|
|
|
|
|
|
|
26 |
Күрделі экспонента.Негізі тұрақсыз логорифм. Күрделі экспонент немесе негізі тұрақсыз логорифмі бар теңдеулер мен теңсіздіктерді шешу. |
1 |
0,5 |
0,5 |
17 қосымша |
||
|
27- 28 |
Логарифмдік жəне көрсеткіштік теңдеулер мен теңсіздіктерді шешуде логарифмдік жəне корсеткіштік функция монотондылығы,функцияның экстремал қасиетін жəне инетегралды ауыстыруды əдісін колдану. |
2 |
0,5 |
1,5 |
18 қосымша |
||
|
7.Əр түрлі теңдеулер мен теңсіздіктерді шешуге мəндес ауысым. (6 сағат) |
|||||||
|
29- 30 |
Симметриялы, қайтымды жəне біртекті теңдеу |
2 |
0,5 |
1,5 |
Лекция, |
Тірек схемаларды құру алгоритмін дайындау |
19 қосым ша |
|
31- 32 |
Модуль белгісі бар теңдеулер жəне теңсіздіктер шешу: əдіс- тəсілдері, бірмəнді ауыссым. |
2 |
0,5 |
1,5 |
20 қосымша |
||
|
33- 34 |
Теңдеулер жəне теңсіздіктер қасиеттер: əдіс-тəсілдері, бірмəнді ауыссым. Графикалық интерпритация тəсілі. |
2 |
0,5 |
1,5 |
21 қосым ша |
||
Көрсеткіштік және логарифмдік теңдеулер, олардың жүйелері.
Көрсеткіштік және логарифмдік теңдеулерді шешу үшін көрсеткіштік функциясы мен логарифмдік функцияларының қасиеттерін білу керек.
1 –Теорема. Егер болса, онда теңдеуі теңдеуімен мәндес.
Көрсеткіштік теңдеудің көпшілігі теңдеудің екі жақ бөлігін бірдей негізге келтіру әдісімен шешіледі. Негізгі екі әдісті: 1) теңдеуінен теңдеуіне келтіру; 2) Жаңа айнымалы енгізу әдістері пайдаланылады. Кейбір жағдайда жасанды әдіспен шешуге тура келеді.
теңдеуін шешу, – пен ауыстырып, оған мәндес жай көрсеткіштік теңдеулер жиынтығы
шешуге келтіріледі, мұндағы теңдеуінің барлық түбірлері.
сандар, теңдеуі оған мәндес теңдеулер жиынтығын шешуге келтіреді, мұндағы - теңдеуінің түбірелері.
-
теңдеуін шешу теңдеуін шешуге келтіреді. -
( – нақты сандар, – функция, ал негіздері үшін, орындалады).
теңдеулер жиынтығын шешуге келеді.
- теңдеуінің түбірлері.
теңдеуінің
-
және болғанда бір ғана түбір болады; -
және болғанда бірге тең емес, кез келген оң сан шешімі; -
және болғанда шешімі болмайды.
Ауыстыруға болады, осыны есептер шығаруда
пайдаланады.
Көрсеткіштік және логарифмдік теңдеулер жүйесін шешуде алгебралық
теңдеулер жүйесін шешу барысында әдістер пайдаланылады.Теңдеулер
жүйесін түрлендіруде жүйенің әрбір теңдеуі қарапайым түрге
келтірілуін қадағалау керек.
1.Жүйені шешіңдер:
Шешуі: АО:
Жауабы:
3.Жүйені шешіңдер
Шешуі: бұл теңдікболғанда болуы мүмкін.
Олай болса
Жауабы:
Рационал теңсіздіктерді шешу
VIII-дәріс
V.Бұрын, біз қарапайым сандық функцияларға VI.
Көпмүшесін және екі көпмүшенің қатынасын қарастырайық
1-анықтама. Егер a саны функциясының нөлі, немесе көпмүшенің түбірі деп аталады.
Көпмүшенің түбірі оның дәрежесінен артық емес
2-анықтама. Рационал функциялардан тұратын теңсіздікті рационал теңсіздіктер деп атайды.немесе ,немесе теңсіздіктері рационал теңсіздіктер
Рационал теңсіздіктерді аралық (интервалдар) әдісімен шешу тиімді
Рационал теңсіздіктерді шешу үшін :
1.Функцияны канондық түрде көбейткіштерге жіктеу керек( яғни х-тің барлық коэффиценттері оң сан)
2. Функцияның барлық нөлдерін (түбірлерін тауып, оны сан осіне өсу ретімен белгілеп,салу керек)
3.Функцияның таңбасы әр уақытта оң жоғарғы жағынан басталады (толқын түрінде) және функцияның түбірінен өткенде кезекпен алмасып тұрады.
4.Егер функцияның көбейткіштерге жіктелуі
канондық түрде болмаса ,онда функция таңбасы оң төменгі жағынан
басталады және функция түбірінен өткенде таңба кезекпен ауысып
отырады.
5.Егер функцияның оң мәндерін білу керек болса, онда сан өсінің
жоғарғы жағындағы аралықтарды жазамыз. Ал,егер функцияның мәндерін
білу үшін сан өсінің төменгі жағындағы аралықтарды
жазамыз.
6. Қайталама түбірді анықтаймыз: егер функцияның жұп рет қайталама түбірі болса, онда функция өзінің таңбасын осы түбірден өткенде екі рет қарсы таңбаға өзгертеді, егер қайталама түбір тақ рет болса, осы түбірден өткенде функция таңбасын қарама-қарсы таңбаға алмастырады.
1.Теңсіздікті шеш:
Шешуі:
қайталама түбір, екі рет
қайлайды.
Жауабы:
Модуль таңбасына тәуелді теңсіздіктерді шешу
үшін, алдымен модульдің анықтамасын еске
түсірейік.
X нақты санның
модулі, немесе
абсолюттік шамасы деп болғанда х санының өзін айтады, егер болса
(-х) санын айтады, оны деп белгілейді.
Сонымен
Модуль таңбасына тәуелді теңсіздіктерді шешуде
тиімді қасеттерді атап өтейік.
Логарифм (грекше logos — қатынас және arіthmos — сан). Логарифм белгіленуі: log. Логарифмнің жалпы түрі: Logab . Логарифм түрлері: ондық lg және ln натурал логарифм жайлы да айтуға болады. е саны иррационал сан, e≈2.718.
Аңықтама.
b санының a негізі бойынша логарифмі деп x санын атаймыз және бұл санды loga b деп белгілейміз:
ax =b, x= loga b.
23=8 теңдігінде 3 дәреже көрсеткіш, ал 8 шығу үшін негізі екіні үш дәрежеге шығару керектігін білдіреді.
Мысал:
50=0 (1/3)2=1/9 3-2=1/9
Анықтама: N санының а негізі бойынша логарифмі деп N саны табылатындай а санының дәреже көрсеткішін айтады. Негізі а болғандағы а санының логарифмі loga N символымен белгіленеді.
Негізі 10 болғанда log10 N=lgN - ондық логарифм деп аталады.
е болғанда loge M=lgM - натурал логарифм деп аталады.
Логарифмдердің қасиеттері:
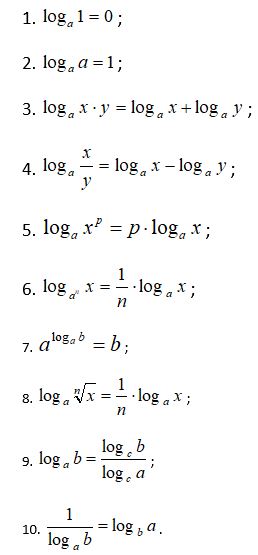
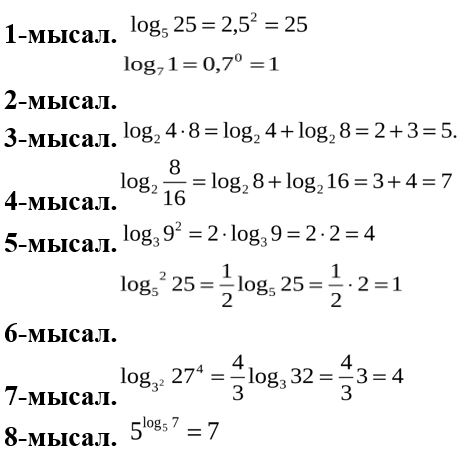
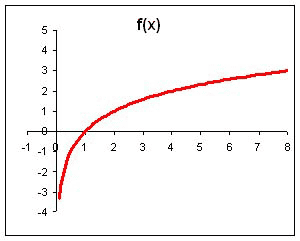
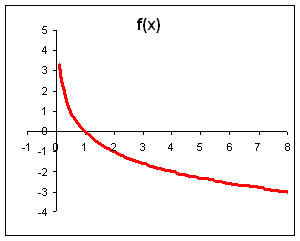
Логарифмдік функция және оның қасиеті мен графигі.
Анықтама: y=logax (a>0, a≠1) формуласымен берілген функцияны логарифмдік функция деп аталады.
Логарифмдік функцияның негізгі қасиеттері:
1. Логарифмдік функцияның анықталу облысы - барлық оң сандар жиыны R+, яғни D(loga)=R+
Шынында да алдыңғыда атап көрсетілгендей, әрбір оң x санының а негізі бойынша логарифмі бар болады.
2. Логарифмдік функцияның мәндерінің облысы – барлық нақты сандар жиыны.
Шынында да, логарифмнің анықтамасы бойынша кез келген нақты y үшін мына теңдік орындалады:
loga(ay)=y
яғни y=logax функциясы x0=ay0 нүктесінде y0 мәнін қабылдайды.
3. Логарифмдік функция бүкіл анықталу облысында өседі,(a>1 болғанда), не кемиді (0<a<1 болғанда)
Логарифмдік функциялардың қасиеттері қолданылатын мысалдар.
1-мысал. Мына функцияның анықталу облысын табайық: f(x)=log8(4-5x)
Логарифмдік функцияның анықталу облысы R+ - жиыны. Сондықтан берілген функция тек 4-5x>0 шарты орындалатындай x мәндерінде анықталған, яғни x<0.8. Олай болса, берілген функцияның анықталу облысы (-∾, 0.8) интервалы.
2-мысал. Мына функцияның анықталу облысын табайық. f(x)=log2(x2-3x-4)
Алдыңғы мысалдағы сияқты, f функциясы x2-3x-4>0 шарты орындалатындай барлық x мәндерінде анықталған. Осы квадрат теңсіздікті шешіп, D(f) дегеніміз (-∾,-1)Ú(4,+∾) интервалдарының бірігуі екенін табамыз.
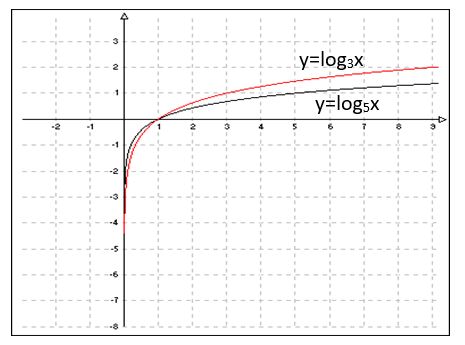
Мысалы: y=log3x және y=log5x функцияларының графигін салу керек.
Шешуі:
1) y=log3x
|
х |
1/9 |
1/3 |
1 |
3 |
9 |
|
у |
-2 |
-1 |
0 |
1 |
2 |
2) y=log5x
|
х |
1/25 |
1/5 |
1 |
5 |
25 |
|
у |
-2 |
-1 |
0 |
1 |
2 |
Логарифмдік теңдеулер мен теңсіздіктер және оларды шешу.
Анықтама: Айнымалысы логарифм белгісінің ішінде болатын теңднуді логарифмдік теңдеу деп атаймыз. Ең қарапайым логарифмдік теңдеуді қарастырайық logax=b. Логарифмдік функция (0,∾) аралығында өседі (не кемиді) және осы аралықта барлық нақты мәндерді қабылдайды. Түбір туралы теорема бойынша кез келген b үшін берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады. Санның логарифмінің анықтамасы бойынша ab саны сол шешім екендігі бірден табылады. Логарифмдік теңдеулерді шешудің бірнеше әдістері бар:
1. Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер.
Мысал - .
logx(x3-5x+10)=3 теңдеуін шешейік.
Шешуі: Логарифмнің анықтамасы бойынша x3-5x+10=x3, онда бұл
теңдеудің шешімі x=2.
Табылған айнымалының мәнін теңдеуге қойып тексереміз:
log2(23-5*2+10)=log28=log223=3log22=3
Демек, x=3 мәні теңдеуді қанағаттандырады.
Жауабы: x=2.
2. Потенциалдауды қолдану арқылы логарифмдік теңдеулерді шешу. Жаңа айнымалы енгізу әдісі. Мүшелеп логарифмдеу әдісі.
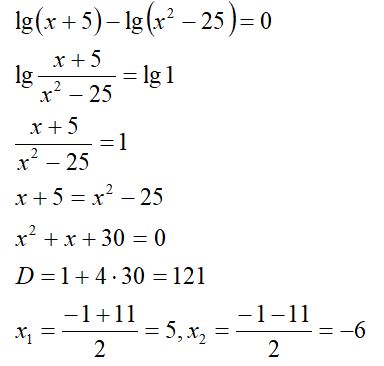
3. Жаңа айнымалы енгізу әдісі.
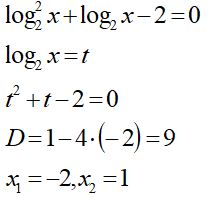
4. Мүшелеп логарифмдеу әдісі.
xlog2x-2=8 теңдеуін шешейік.
Шешуі:
Берілген теңдеуді былай жазайық: xlog2x*x-2=8 немесе xlog2x=8x2
Шыққан теңдеуді негізін 2 – ге тең етіп логарифмдейік:
log2x*log2x=log28+log2x2
log22x=3+2log2x
log22x-2log2x-3=0
Демек,
1) log2x=3, осыдан x1=8
2) log2x=-1, осыдан x2=1/2.
Тексеру:
1) 8log28-2=8 немесе 83-2=8, 8=8.
2) (1/2)log2(1/2)-2=8 немесе (1/2)-3=8, 8=8.
Жауабы: x1=8; x2=1/2.
|
Оқу мақсаттары (оқу бағдарламасына сілтеме) |
АУ 10.3 қарапайым логарифмдік теңдеулерді шешеді. Мысалы: 2log4x – 3 = 0, (log_2 (x+1) = log_2 6–log_2 x). |
|
Сабақ мақсаттары |
Логарифм ұғымын меңгеру және оны қолдана білу. Білу және түсіну Логарифм анықтамасы мен қасиеттерін негізге ала отырып, қарапайым логарифмдік теңдеулерді шешу алгоритмін біледі. Білімін қолдану
|
|
Тілдік мақсаттар |
Оқушылар: Күнделікті өмірде логарифмнің қолданысы туралы талқылайды және әңгімелей алады. Логарифм – Логарифмдік функция – Дәреже көрсеткіші – Негізгі түрлендірулер – Иррационал сан – Логарифм қасиеттері – Логарифмдік тепе-теңдіктер – Шынайы өмірде көрсеткіштік функция көп жерде қолданылады. Логарифмдерді түсіну үшін маңызды. Инженерлер логарифмнің қолданысын білуі қажет. Калькулятор болмағанда логарифмдерді білу . . . қатысты болды. Химиядаға pH келесіге негізделген. Көрсеткіштік функцияларды түсіну астрономдар үшін маңызды. |
|
Құндылықтарды дарыту |
Сыни тұрғыдан ойлау арқылы білімге деген сүйіспеншілікті қалыптастыру. |
|
Пәнаралық байланыстар |
Астрономия, химия, информатика. |
|
АКТ қолдану дағдылары |
Презентация |
|
Бастапқы білім |
Натурал көрсеткішті дәреже, бүтін көрсеткішті дәреже, дәреженің қасиеттері. |
Сабақ барысы
|
Сабақ кезеңдері |
Жоспарланған іс-әрекет |
Ресурстар |
|
Басы (3 минут) |
І. Ұйымдастыру. Амандасу. Көңіл күйлерін смайликтер арқылы білу. |
|
|
Басы (2 минут) |
І. Үй тапсырмаларын тексеру. 1. Теңдеулер түрлерін ата 2. Логарифмнің дамуына көп үлес қосқан ғалым? |
Презентация бойынша өткен тақырып бойынша тапсырмалар. |
|
Ортасы (20 минут) |
ІІ. Ауызша есептейік. «Кім жүйрік?» 1. (log_3sqrt{3} ) 2. Log71 3. (log_5 frac{1}{625})Log51 4. Log211 - Log244 ІІІ. Ауызша тест.
IV. “Кім жылдам?”
V. «Кім тапқыр?»
Логарифмдік теңдеулер 5. Log3( 243 * 729) |
Презентация бойынша өткен тақырып бойынша тапсырмалар. |
|
Жаңа сабақ |
Жаңа сабақ: Логарифмдік теңдеулер. Анықтама Логарифм белгісі астында немесе (және) оның негізінде белгісізді қамтитын теңдеу логарифмдік теңдеу деп аталады. Қарапайым логарифмдік теңдеу деп logax=b түріндегі теңдеу атаймыз. Тұжырым 1. Егер a > 0, a ≠1 теңдеу кез келген нақты b кезінде x = ab деген бір ғана шешімі болады. Логарифмдік теңдеуді шешудің тәсілдері. 1. Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер. Логарифмнің анықтамасы бойынша: logax=b түріндегі теңдеулер былай шешіледі. logax=b⟺x=ab Мысал: log3(x2 + 4x + 12) = 2. 2. Потенцирлеу әдісін қолдану үшін логарифмдік теңдеуді logaƒ(x) = logag(x) түріне келтіру. log2(x2 + 7x – 5) = log2(4x – 1). 3. Жаңа айнымалы енгізу тәсілі. Логарифмдік теңдеулерді жаңа белгіні қолданып, шешуге болады. Бастапқы теңдеуге жаңа белгіні қойғаннан кейін, жаңа, барынша қарапайым теңдеу аламыз, оны шешкеннен кейін, алмастыруға қайта оралып, бастапқы теңдеудің түбірлерін табамыз. 4. Мүшелеп логарифмдеу тәсілі. Берілген әдіс потенцирлеу әдісіне “кері” болып келеді, яғни логарифмдері жоқ теңдеулерден оларды қамтитын теңдеулерге көшеміз. ƒ(x) = g(x) Бұл әдіс әдетте егер теңдеуде көрсеткіштік функциялар болса қолданылады, логарифмдер көрсеткіште. 5. Бір негізден екінші негізге көшу. Егер теңдеуде әртүрлі негізді логарифмдер болса, онда ең алдымен ауысу формуласын қолданып, барлық логарифмдерді бір негізге келтіру қажет. logax = (frac{log_{b}x}{log_{b}a}) https://bilimland.kz/kk/courses/math-kz/analiz-bastamalary/korsetkishtik-zhane-logarifmdik-funkcziyalar/lesson/logarifmdik-tengdeulerdi-sheshu-adisteri сайты бойынша түсіндіру. |
|
|
Жалпы сыныппен жұмыс (15 минут) |
Жалпы сыныппен жұмыс. 1-жаттығу Теңдеуді шешіңіз: log3(2x + 1) = 2. 7-жаттығу log3(2x − 1) + log3(x + 3) = 2 теңдеуін шешіңіз. 8-жаттығу logx + 4(x2 − 1)= logx + 4(5 − x) теңдеуін шешіңіз. 9-жаттығу Теңдеуді шешіңіз: log24 x + (frac{1}{2})log4 (sqrt{x}) - 1,5 = 0. 13-жаттығу Теңдеуді шешіңіз: log2 x + log3 x = 1. 17-жаттығу Теңдеуді шешіңіз: xlgx - 1 = 100. |
https://bilimland.kz/kk/courses/math-kz/analiz-bastamalary/korsetkishtik-zhane-logarifmdik-funkcziyalar/lesson/logarifmdik-tengdeulerdi-sheshu-adisteri сайтындағы есептерді шығару |
|
Жұптық жұмыс |
Жұптық жұмыс http://itest.kz/lekciya_logarifmdik_tengdeuler_men_tengsizdikteri_sheshuding_adisteri сайты есебін жұптық жұмыста орындайды және бір-бірін тексереді. Жұп 1 Теңдеуді шешіңіз: (log_{sqrt{2}})x+ log2x = 1,5. Теңдеуді шешіңіз: log7x = 2log73 + 4log492. Жұп 2 Теңдеуді шешіңіз: (log_4)x + log16x + log64x = (frac{11}{12}). Теңдеуді шешіңіз: log25x2 + (log_sqrt{5} )x = 3. Жұп 3 Теңдеуді шешіңіз: (log_5)x • log7x = 4log57x. Теңдеуді шешіңіз: log5x + (logsqrt{5} )x + (log_{frac{1}{5}})x = 6. Жұп 4 Теңдеуді шешіңіз: (log_{8-x})11 = (frac{1}{2}). Теңдеуді шешіңіз: (log_{x^2+4x+4})3 = (frac{1}{2}). Жұп 5 Теңдеуді шешіңіз: (lg_{(8-x)})+ lg(x–3) = 1 – lg5. Теңдеуді шешіңіз: log2x + log8x = 8. VIII. Рефлексия - нені білдім, нені үйрендім. - нені толық түсінбедім. - немен жұмысты жалғастыру қажет. Үйге: itest.kz сайтынан есеп беріледі. Теңдеуді шешіңіз: log2(x + 2) = log2(x2 + x – 7) Теңдеуді шешіңіз: logx-6(x – 4) = 2. Теңдеуді шешіңіз: log3(0,5 + x) = log30,5 – log3x |
|
Логарифдік функция және оның қасиеттері, графиктері, өрнектерді түрлендіру.
1.Санның логарифмінің
ұғымы.у=ax көрсеткіштік
функция берілсін (a>0,a 1).Бұл бірсарынды функция. Сондықтан тек
аргументтің (х) әр мәніне функцияның бір ғана мәні сәйкес келіп
қоймай, керісінше,функцияның алдын ала берілген әр мәніне х-тің бір
ғана мәні сәйкес келеді.
1).Бұл бірсарынды функция. Сондықтан тек
аргументтің (х) әр мәніне функцияның бір ғана мәні сәйкес келіп
қоймай, керісінше,функцияның алдын ала берілген әр мәніне х-тің бір
ғана мәні сәйкес келеді.
aх=b теңдеуін
қарастырайық. b 0 болғанда теңдеудің түбірі болмайды.Егер
b>0болса, онда теңдеудің бір ғана түбірі
болады.
0 болғанда теңдеудің түбірі болмайды.Егер
b>0болса, онда теңдеудің бір ғана түбірі
болады.
Графикте көрсетейік y=ax функциясының графигін сызамыз: y=b (b>0)
Түзуін жүргіземіз.
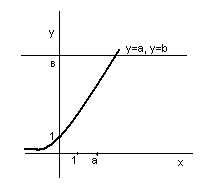
![]()
![]()
Осы екі
графиктердің қиылысу нүктесінің абциссасы, яғни
x= -ax=b теңдеунің іздеп
отырған түбірі болады. Сонымен ax=b
(a
-ax=b теңдеунің іздеп
отырған түбірі болады. Сонымен ax=b
(a 1,
1,
a>0, b>0). ax=b теңдеуінің b санының а негізді логарифмі деп аталады.
Анықтама.b оң санының
бірден өзгеше, оң а негізді логарифмі деп,b санын алу үшін а
санының дәреже көрсеткіші болатын  санын айтады:
санын айтады: =Iogab.Оқылуы:
«
=Iogab.Оқылуы:
« дегеніміз b санының а негізді логарифмі
».
дегеніміз b санының а негізді логарифмі
».
 =Igb,яғни 10 саны
негіз болып жазылмайды.Мұндай логарифмдер
-ондық логарифм деп
аталады.
=Igb,яғни 10 саны
негіз болып жазылмайды.Мұндай логарифмдер
-ондық логарифм деп
аталады.
Сонымен,a 1,a>0, b>0 болғанда
аа=b теңдеуінен
анықтама бойынша
1,a>0, b>0 болғанда
аа=b теңдеуінен
анықтама бойынша  =Iogab теңдігі шығады.
Соңғы теңдеудегі
=Iogab теңдігі шығады.
Соңғы теңдеудегі  -ның орнына мәнін
қойсақ,аIogab=b
(a>1,b>0,a
-ның орнына мәнін
қойсақ,аIogab=b
(a>1,b>0,a 1).Бұл теңдік негізгі
логарифмдік тепе-теңдік деп
аталады.
1).Бұл теңдік негізгі
логарифмдік тепе-теңдік деп
аталады.
IY. Логарифмдік функцияның графигі
y=ax функциясы
бірсарынды. Демек, әрбір х  (-
(- ;+
;+ ) мәніне бір y
) мәніне бір y (0;
(0; )
)
сәйкес келеді, керісінше, әрбір
у (0;
(0;  ) мәніне бір ғана x
) мәніне бір ғана x  (-
(- ; +
; + ) мәні сәйкес келеді, яғни
y=Iogax кері функциясы
бар болады: D(y)=(0;+
) мәні сәйкес келеді, яғни
y=Iogax кері функциясы
бар болады: D(y)=(0;+ ).
).
y=Iogax және
y=Iog x функцияларының графиктерін
салайық.
x функцияларының графиктерін
салайық.
a=2 және a= болғандағы y=Iogax функциясының
графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге
болады. a>1 болғанда : 1) функцияның анықталу облысы оң нақты
сандар жиыны: D(Iogax)=R+.
болғандағы y=Iogax функциясының
графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге
болады. a>1 болғанда : 1) функцияның анықталу облысы оң нақты
сандар жиыны: D(Iogax)=R+.
2) функция мәндерінің жиыны барлық нақты сандар жиыны: Е(Iogax)=R.
3) Функция бүкіл анықталу облысы бойында өседі: x2>x1 болғанда, Iogax2>Iogax1.
4) x (0;1) болғанда Iogx <0; x=1 болғанда Iogx=0;
x
(0;1) болғанда Iogx <0; x=1 болғанда Iogx=0;
x (1;
(1; ) болғанда Iogax>0.
) болғанда Iogax>0.
0<a<1 болғанда :
1) функцияның анықталу облысы барлық оң нақты сандар жиыны:D(Iogax)=R+ .
2) функция мәндерінің жиыны барлық нақты сандар жиыны: Е(Iogax)=R.
3) функция бүкіл анықталу облысы бойынша кемиді: x2>x1 болғанда Iogax2<Iogax1.
4) x (0;1) болғанда Iogax >0; x=1
болғанда Iogax=0;
x
(0;1) болғанда Iogax >0; x=1
болғанда Iogax=0;
x (1;
(1; ) болғанда Iogax<0.
) болғанда Iogax<0.
y=Iogax логарифмдік функциясының маңызды қасиеті – оның бүкіл анықталу облысы бойында үзіліссіздігі.
М ы с а
л.. 1.Log28.
Егер Iog28= десек,онда 2а=8=>2a=23.
десек,онда 2а=8=>2a=23. 10Ig
10Ig .
. ∙ 10Ig
∙ 10Ig .=
.=
 =7.
=7.
2.Логарифмдердің
қасиеттері.1-т е о р е м а.. Екі оң санның
көбейтіндісінің  (a>0,a
(a>0,a 1) негізді логарифмі көбейткіштердің сол негізді
логарифмдердің қосындысына тең:loga(x1x2)=logax1+logax2 (x1>0
x2>0).
1) негізді логарифмі көбейткіштердің сол негізді
логарифмдердің қосындысына тең:loga(x1x2)=logax1+logax2 (x1>0
x2>0).
М ы с а л.log37=a, log34=b.log328-? log328=log3(7∙ 4)=log327+log34=a+b.
2-т е о р е м а. Екі санының
қатынасының  (a>0,a
(a>0,a 1) нкгізді логарифмі оның алымы мен бөлімінің сол
негізді логарифмдерінің айырымына тең:
1) нкгізді логарифмі оның алымы мен бөлімінің сол
негізді логарифмдерінің айырымына тең:
loga =logax1-logax2 (x1>0
=logax1-logax2 (x1>0 x2>0).
x2>0).
М ы с а л..log315=a.log35-?
log35=log3( )=log315-log33=a-1.
)=log315-log33=a-1.
3-т е о р е м а . Дәреженің a негізді
логарифмі көрсеткішті дәреже негізінің логарифміне (а негізді )
көбейткенге тең:Iogaxa= Iogax
(x>0).
Iogax
(x>0).
Дәлелдеуі. logax=y, сонда
х=ay.Осы теңдіктің екі
жағын  дәрежеге шығарайық:х
дәрежеге шығарайық:х =aay.Логарифмнің
анықтамасы бойынша logaxa=
=aay.Логарифмнің
анықтамасы бойынша logaxa= y=
y= logax.
logax.
М ы с а л..log327-?.log33=3log33=3*1=3:
4-т е о р е м а.Оң санның берілген негізді
логарифмі осы санның басқа бір негізді логарифмі мен берілген
негіздің жаңа негізді логарифмінің қатынасына
тең:logax=l
(x>0,a>0,b>0;a 1,b
1,b 1,logba
1,logba 0).
0).
Дәлелдеуі.Негізгі логарифмдік тепе-теңдікті b
негізбен логарифмдейік:аlogax=x=>logaxlogaa=logax=>logax= .Соңғы қатынас а негізді логарифмнен b негізді
логарифмге көшу формуласы деп аталады.
.Соңғы қатынас а негізді логарифмнен b негізді
логарифмге көшу формуласы деп аталады.
Сонымен логарифмнің мынадай қасиеттері бар:
10.alogab=b (b>0, a>0,a 1).
1).
20.loga(x1x2)=logax1+logax2 (x1>0,x2>0,a>0,a 1).
1).
30.loga =logax1-logax2 (x1>0,x2>0,a>0,a
=logax1-logax2 (x1>0,x2>0,a>0,a 1).
1).
40.logaxp=plogax (x>0,a>0,a 1).
1).
50.logax= (Iogba
(Iogba 0,x>0,a
0,x>0,a 1,b>0,b
1,b>0,b 1).
1).
60.logax= (a>0,a
(a>0,a 1,x>0,x
1,x>0,x 1).
1).
70.logaax= logax,logax=loga
logax,logax=loga x
x (x>0,
(x>0,
 0,a>0,a
0,a>0,a 1
1
|
Сабақтың тақырыбы |
Логарифмдік теңдеулерге есептер шығару. |
||||||||||||||||||||||||||||||||||||
|
Сабақтың мақсаты |
Білімділік – логарифмдік теңдеулерді шешуге логарифм қасиеттерін тиімді қолдана білуге үйрету. Дамытушылық – теориялық білімін практикада ұштастыра отырып , ауызша , жазбаша есептеу дағдыларын жетілдіру , топпен , өз бетінше жұмыс жасауға дағдыландыру. Тәрбиелік - оқуға саналы көзқарасқа , өз мүмкіндігіне жете білуге , өз еңбегін бағалай білуге үйрету. Оқушыларды ұқыптылыққа , жауапкершілікке , ұжым намысын қорғауға , мақсатқа жете білуге тәрбиелеу. |
||||||||||||||||||||||||||||||||||||
|
Негізгі идея |
Логарифмнің негізгі қасиеттерін толық меңгерту , логарифмдік теңдеулерді шеше білуге үйрету. |
||||||||||||||||||||||||||||||||||||
|
Табыс критерийі |
Оқушылар логарифмдік теңдеулерді шешуде логарифм қасиеттерін қолдана білуді үйренеді , логарифмдік өрнектері бар тапсырмаларды түрлендіріп есептеуді үйренеді. Логикалық ойлау дағдысын , өз ойын жинақтап , жүйелі жеткізе біледі. |
||||||||||||||||||||||||||||||||||||
|
Модульдер |
СТО |
||||||||||||||||||||||||||||||||||||
|
Әдістер |
Топтық , жұптық , жеке жұмыстар түртіп алу. |
||||||||||||||||||||||||||||||||||||
|
Дерек көзі |
Оқулық , постер , түрлі түсті қағаздар, сызғыш, карандаш, формула т.б. |
||||||||||||||||||||||||||||||||||||
|
Сабақтың барысы |
Мұғалім іс-әрекеті |
Оқушы іс-әрекеті |
|||||||||||||||||||||||||||||||||||
|
Ұйымдастыру кезеңі |
Оқушылармен сәлемдесу Оқушыларды түгелдеу Оқу құралын тексеру Топқа бөлу. Стикер алу арқылы.
Бүгінгі сабақта жақсы нәтижеге жету үшін әрбір кезеңдер ұпаймен есептеледі. Бағалау парағына топ басшылар топ мүшелерін бағалайды. |
Мұғаліммен сәлемдеседі. Оқу құралын алу. Топқа бөліну. |
|||||||||||||||||||||||||||||||||||
|
Миға шабуыл |
Үй жұмысын тексеру сұрақ – жауап арқылы: / № 292/ Өткен сабаққа шолу І- топ. Сәйкестендіру тестімен жұмыс.
№ 1. қосымша ІІ-топ. Балама жауапты тест.
ІІІ- топ.
|
Үй жұмысын тексеру, қойылған сұрақтарға жауап беру. |
|||||||||||||||||||||||||||||||||||
|
Тапсырма |
Есептер шығару. «Домино» ойыны
|
Дәптерге күнді жазады. 1. Х1=-1 , X2 =4 2.Х1=-3 , X2 =-1 3.Х1=-1 4.Х1=1,5, X2 =3 5.Х1=4 6.Х1=1 , 7.Х1=3 8.X=4 9.X=1000, X=1/10 10.X=4, Y=2 |
|||||||||||||||||||||||||||||||||||
|
Топпен жұмыс |
«Жасырын сөзді » табу кезеңі Кестедегі жауаптың тұсына оған сәйкес әріпті қойыңдар.
І-топ.
Lg25+2lg2 2 К Log8(3x-1)=1 x=3 С ІІ-топ. Log212+log25/3+log24/5 4 П Log6(4x+1)<1 (-0,25; 1,25) О (log4243)(log364) 15 7 ІІІ-топ. Lnx=1 e 2 Log3(tgx)=0
Жасырын сөз ЭКСПО-2017 . |
Топ оқушылары жұптасып есепті шығарады. |
|||||||||||||||||||||||||||||||||||
|
Сергіту |
Болашақ кілті білімде. «Білімді болу деген –жаңалық ашуға қабілетті болу» (Әл-Фараби) Арифметика математиканың, ал математика ғылымдарының патшасы (К.Гаусс) Әр ғалым математика дамығанда ғана дами алады. Ғылым нәтижесі ең жаңа заманауи технологиялар мен олардың жұмыс істеу принциптері ЭКСПО-2017 көрмесінде көрсетіледі. «ЭКСПО»- деген не? Бұл – бүкіләлемдік көрме. Индустрияландырудың белгісі және техникалық һәм технологиялық жетістіктерді көрсететін мүмкіндік. «ЭКСПО-2017» 10 маусымда басталып, 10 қыркүйекте аяқталады. Астанадағы көрме «Болашақтың энергиясы» деген атпен өтеді. Ұйымдастырушылар Әлемнің түкпірінен бес миллионға жуық адам келіп қатысады деген болжам жасалып отыр. «ЭКСПО-2017» Дүниежүзілік көрмесінің мақсаты Қазақстанда қайта қалпына келетін энергетиканың алдыңғы қатарлы технологияларын шоғырландыру болып табылады. |
|
|||||||||||||||||||||||||||||||||||
|
Ойлан , бөліс, талқыла |
Логарифмдік өрнектің мәнін есептеніз:
|
Өрнекті есептеудің екі жолын көрсетеді. |
|||||||||||||||||||||||||||||||||||
|
Логикалық тапсырма |
«ҚЫРЫҚ» сөзін неше рет оқуға болады? Қ Ы Р Ы Қ Ы Ы Р Ы Ы Р Р Р Р Р Ы Ы Р Ы Ы Қ Ы Р Ы Қ |
|
|||||||||||||||||||||||||||||||||||
|
Рефлексия |
Кері байланыс: Не білдім? Не ұнады? Не қызықты болды? Не білгім келеді? |
Сабақтан алған әсерін стикерге жазу арқылы әр оқушы өз пікірін білдіреді. (ағашқа іледі) |
|||||||||||||||||||||||||||||||||||
|
Үйге тапсырма |
Келесі өтілетін сабаққа сілтеме № 299 № 230 |
Үйге берілген тапсырманы орындап, келесі сабаққа дайындалып келеді. |
|||||||||||||||||||||||||||||||||||
|
Бағалау |
Бағалау парағы арқылы:
|
Оқушылар алған бағаларын күнделікке қойдырады. |
|||||||||||||||||||||||||||||||||||
Дәреженің және түбірдің логарифмі
Т е о р е м а -1.а негізіндегі хn санының логарифмі n Ioga x-ке тең:
Iog axn = nIogax (мұндағы x>0). Мысалы Iog425=Iog452=2Iog45.
Т е о р е м а -2. а негізіндегі
 санының логарифмі өрнектің
логарифмін
санының логарифмі өрнектің
логарифмін  санына көбейткенге тең:
санына көбейткенге тең:
Мысалы: log2 =
= log2
log2 ; log2
; log2 =
= log227.
log227.
aIogab=b ( мұнда a>0,
a 1, b>0) теңсіздігін логарифм
жөніндегі негізгі теңбе-теңдікке сүйеніп дәлелдейді.
log ab=
1, b>0) теңсіздігін логарифм
жөніндегі негізгі теңбе-теңдікке сүйеніп дәлелдейді.
log ab= теңдігі тура болады.(басқа негізге ауысу
формуласы деп аталады).
теңдігі тура болады.(басқа негізге ауысу
формуласы деп аталады).
Мысалы: log56= ; Cалдар: logab=
; Cалдар: logab= яғни,log813=
яғни,log813= =
= .
.
3.Логарифмдеу және потенциалдау.Жоғарыда көрсетілген теоремалардың негізінде төмендегі екі өзара кері түрлендірулер шығады.
Логарифмдеу-белгісіз айнымалылары бар өрнектердің логарифмін осы айнымалылардың логарифмдерінің қосындыларына түрлендіру.Логарифмдердің қосындылары мен қосындының логарифмін айыра білген жөн.Логарифмдердің қосындысы көбейтіндінің логарифміне тең,ал қосындының логарифмі үшін формула жоқ.
Потенциалдау_- айнымалылардың логарифмдерінің қосындыларын немесе айырымдарын айнымалысы бар өрнектің логарифміне түрлендіру.Потенциалдау – логарифмдеуге кері түрлендіру.
М ы с а
л.1.lgx=4lga-5lgb+( )lgc (a>0,b>0,c>0) x-ті табу
керек.Потенциалдаймыз:lgx=lga4-lgb5+lgc
)lgc (a>0,b>0,c>0) x-ті табу
керек.Потенциалдаймыз:lgx=lga4-lgb5+lgc =lg
=lg ; x=
; x= .
.
"Логарифмдік функция, оның қасиеттері мен графигі"
Мақсаты: логарифмдік функцияның қасиеттері мен графигін зерттеу.
y = ax (a 0, a =/= 1) функциясы a1 монотонды артады; 0 a y мәндері үшін анықталу облысынан аргументтің жалғыз x мәні сәйкес келеді.
|
y = ax, a 1
|
y = ax, 0 a
|
a оң, бірге тең емес сан болсын. Әрбір оң x санына х санының негізі а логарифмі болып табылатын y саны сәйкес келеді, яғни y = logax.
Анықтама. y = logax, (a 0, a =/= 1) функциясы логарифмдік функция деп аталады.
Осылайша:
|
g(x) = ax, a 0, a =/= 1 |
f(x) = logax, a 0, a =/= 1 |
|
D(g) = R |
D(f) =
(0; |
|
E(g) =(
0; |
E(f) = R |
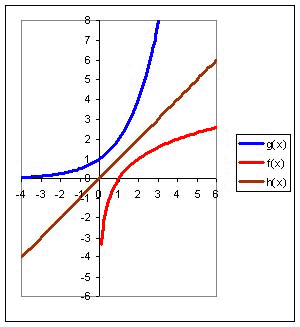
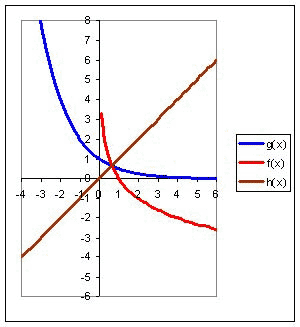
Функцияның анықтамасы бойынша g(x) = ax, a 0, a =/= 1 және f(x) = logax, a 0, a =/= 1 өзара кері болып табылады. Олардың графиктері h(x) = x түзуіне қарағанда симметриялы.
|
|
|
Функциялардың графигін саламыз: f(x) = log2 x, f(x) = log1/2 x.
|
х
|
|
||||||||||||||||||
|
|
||||||||||||||||||
|
|
и |
|
|||||||||||||||||
Логарифмдік функциялардың қасиеттері
|
|
Функцияның қасиеттері |
a 1 |
0 a |
|
1. |
Анықталу облысы |
(0; |
|
|
2. |
Мәндернің жиыны |
(– |
|
|
3. |
Жұп, тақтылығы |
Функция жұп та, тақ та емес |
|
|
4. |
Функция нольдері |
x = 1 болғанда, y = 0 |
|
|
5. |
Таңба тұрақтылығы аралықтары |
x x |
x |
|
6. |
Экстремумы |
Функцияның экстремумдары жоқ |
|
|
7. |
x |
Функция өседі |
Функция кемиді |
|
8. |
Асимптота |
x = 0 |
|
Кестені толтыруда мына тапсырмаларды орындаймыз.
№ 1 тапсырма. Функция үшін х аргументінің мәні мүмкін болады ма?
|
y = logax, a 0, a =/= 1 |
D(y) |
|
y = log5(–x) |
(– |
|
y = log3(x)1/2 |
(0; |
|
y = log2x(x–1) |
(1; |
|
y = log0,5(x2–1) |
(– |
|
y = logx+2(x2 + 1) |
(–2;–1) U(–1; |
|
y = log 0,7 | x | |
(–? ;0) U(0; |
№ 2 тапсырма (таңба тұрақтылығының аралықтары).
y = logax болсын
|
a 1
және x 1 |
y 0 |
|
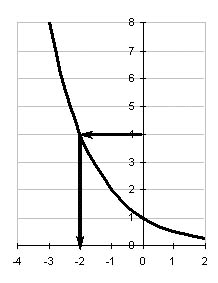
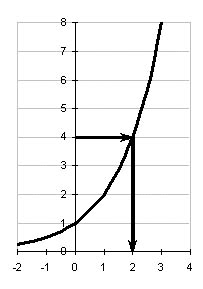
a 1 и 0 x 0 a x 1 |
y |
1 қорытынды. Егер сан мен логарифмнің негізі бірліктен бір жағында жатса, логарифмдік функцияның мәні оң болады.
2 қорытынды. Егер сан мен логарифмнің негізі бірліктің екі жағында жатса, логарифмдік функцияның мәні теріс болады.
Санның таңбасын анықтаймыз.
|
log23 0 |
2 1 және 3 1 |
|
log50,1 |
5 1 және 0 |
|
log0,31,8 |
0 1 |
|
log0,20,8 0 |
0 |
m санын бірлікпен салыстырамыз, егер:
|
log0,5 m = – 0,5 |
m 1 |
0 |
|
log3 m = 1,5 |
m 1 |
3 1 және 1,5 0 |
|
log0,2 m = 5 |
0 m |
0 0 |
|
log2,4 m = – 0,2 |
0 m |
2,4 1 және – 0,2 |
№ 3 тапсырма. (Монотондылығын зерттеу үшін).
Функциялардың қайсысы өспелі, қайсысы кемімелі болады?
|
y = log2x |
өспелі |
2 1 |
|
y = log0,5(2x + 5) |
кемімелі |
0 |
|
y = lg (x)1/2 |
Өспелі |
10 1 |
|
y = ln(x + 2) |
Өспелі |
e 1 |
а санын бірлікпен салыстырамыз, егер:
|
loga0,2 = 3 |
0 a |
0 0 |
|
loga0,5 loga0,4 |
a 1 |
0,5 0,4 |
|
loga0,8 = – 5 |
a 1 |
0 |
|
loga 2/3 loga1,5 |
0 a |
2/3 |
m және n араларына немесе
|
log0,5 m log0,5 n |
m |
0 |
|
log8 m log8 n |
m n |
8 1 |
|
log2,5 m 2,5 n |
m |
2,5 1 |
|
log0,2 m 0,2 n |
m n |
0 |
Кестені толтырғаннан кейін мына тапсырмаларды қолданамыз.
№ 1 тапсырма.
Мына функциялардың графиктерін бір координаталар жазықтығына салыңдар: g(x) = ln x, h(x) = log5x, f(x)=lg x. Функция графиктерінің координаталар остеріне қатысты орналасуы туралы қорытындылар жасаймыз.
Қорытынды. a 1 болғанда, логарифмдік функцияның негізі неғұрлым үлкен болса, соғұрлым график координата осіне жақын орналасады.
№ 2 тапсырма.
Мына функциялардың графиктерін бір координаталар жазықтығына салыңдар: f(x) = log0,1x, g(x) = log0,3x, h(x) = log0,5x.
Қорытынды.0 a
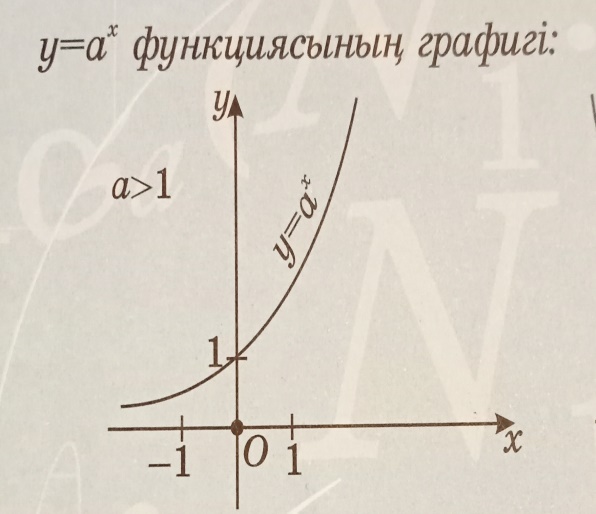
Сабақтың тақырыбы: Көрсеткіштік функция, оның қасиеттері және графигі
Анықтама.
y=ах, а>0, а≠1 (1)
формуласы арқылы берілген функцияны көрсеткіштік функция деп аталады.
Мұнда а саны көрсеткіштік функцияның негізі, ал тәуелсіз айнымалы х – дәреженің көрсеткіші.
Көрсеткіштік функциясының негізгі қасиеттері:
1) анықталу облысы – барлық оң нақты сандар жиыны, яғни x ϵ R;
2) мәндер жиыны – барлық оң нақты сандар жиыны, яғни y ϵ R;
3) негізі а>1 болғанда, функция – қатаң кемімелі функция;
өспелі, ал 0< а< 1 болғанда, функция – қатаң кемімелі функция;
4) барлық нақты сандар жиынында, яғни х ϵ R-де y=ах( а>0, а≠1) функция үзіліссіз.
Көрсеткіштік функция үшін х және у-тің кез келгеннақты мәндерінде келесі теңдіктер орындалады:
aх ∙
ау ꞊ах+у ау ; ![]() ꞊
ах-у;
(ab)x ꞊aх ∙
bx;
꞊
ах-у;
(ab)x ꞊aх ∙
bx; ![]() ꞊
꞊ ![]() ;
(ах)у꞊аху .
;
(ах)у꞊аху .
Бұл формулалар дәрежелеудің негізгі қасиеттері деп аталады.
Функцияның жоғарыда аталған қасиеттерін дәлелдейік.
Дәлелдеу.
1) негеізі а > 0 болғанда, х-тің кез келген мәні үшін аx дәрежесін есептеуге болады. Олай болса, у꞊ах функциясының анықталуы облысы – нақты сандар жиыны.
2) y=ах а>0, а≠1функциясының мәні кез келген х нқты саны үшін оң сан. Демек, y=ах функциясының мәндер жиыны барлық он нақты сандар жиыны болады.
3) Ox осінің бойынан кез келеген х1 және х2 (х1 < х2) нүктелерін (сандарын) алайық. Сонда осы екі нүктеге сәйкес келетін функция мына мәндерді қабылдайды: у1 ꞊ ах1 , у2 ꞊ах2.
а>1 жағдайында кіші аргументке функцияның кіші мәні, үлкен аргументке функцияның үлкен мәні сәйкес болғандықтан, ах1< ах2.
Осы заңдылық функцияның анықталу облысының жиынындағы кез келген екі нүктесі үшін орындалады, Олай болса, y=ах функциясы а>1 болғанда,қатаң өспелі функция.
Көрсеткіштік функцияның негізі 0 < a < 1 болғанда, жоғарыда айтылған заңдылық керісінше орындалады, кіші аргіментке функцияның үлкен мәні, үокен аргументке функцияның кіші мәні сәйкес болғандықтан, ах1 >ах2. Демек 0 < a < 1аралығында y=ах функциясы – қатаң кемімелі функция.
Мысал ретінде y=3х және у ꞊ функцияларының графиктерін қарастырайық.
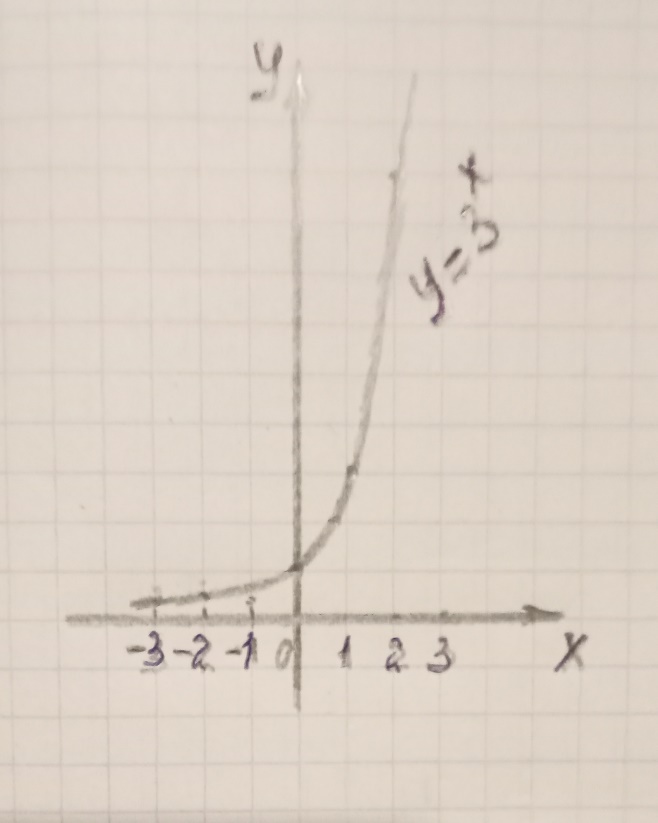
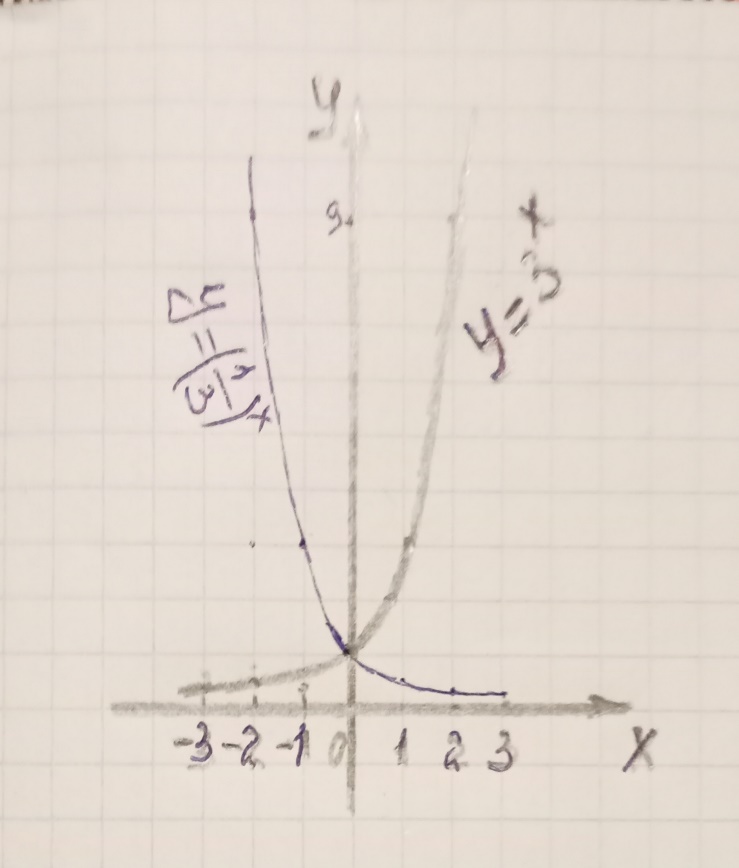
I. y=3х функциясының графигін салу үшін келесі кестені құрамыз:
|
Х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y=3х |
|
|
|
1 |
3 |
9 |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-сурет
(-3; ![]() )
,(-2;
)
,(-2; ![]() )
,(-1;
)
,(-1; ![]() ), (0; 1),
(1;3),(2;9), (3; 27) нүктелерін координаталық жазықтыққа
түсіргеннен кейін, оларды қоссақ, y=3х функциясының
графигіналамыз (1-сурет)
), (0; 1),
(1;3),(2;9), (3; 27) нүктелерін координаталық жазықтыққа
түсіргеннен кейін, оларды қоссақ, y=3х функциясының
графигіналамыз (1-сурет)
Графигтен берілген функцияның қатаң өспелі функция екені көрініп тұр.
ІІ.
y= ![]() фунуциясының
графигін салу үшін келесі кестені құрамыз:
фунуциясының
графигін салу үшін келесі кестені құрамыз:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y= |
27 |
9 |
3 |
1 |
|
|
|
(-3;27), (-2;9),
(-1;3), (0;1), (1; ![]() ),
(2;
),
(2; ![]() ),
(3;
),
(3; ![]() ) нүктелерін
координаталық жазықтыққа түсіріп және оларды қоссақ,
y=
) нүктелерін
координаталық жазықтыққа түсіріп және оларды қоссақ,
y= ![]() функциясының
графигін аламыз (2-сурет)
функциясының
графигін аламыз (2-сурет)
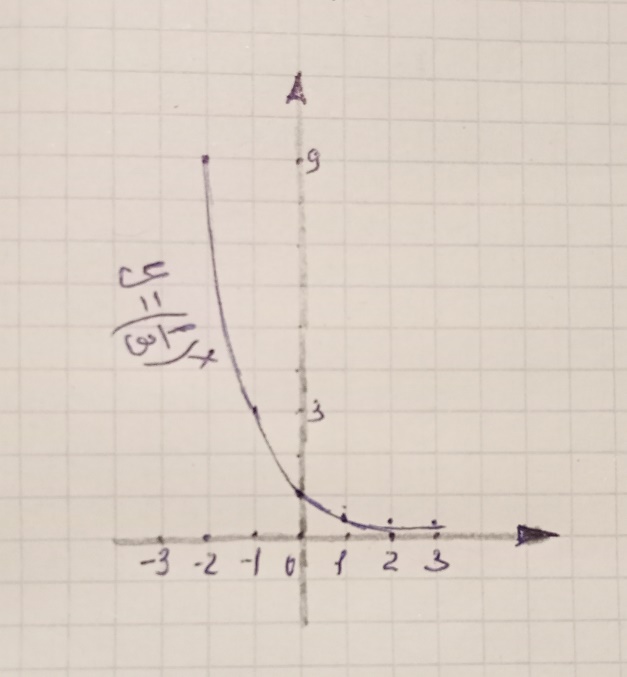
2-сурет
y= ![]()
Графигтен берілген функцияның анықталу облысында қатаң кемімелі екенін көреміз.
Енді y=ах а>0, а≠1 функциясының графигін жалпы түрде берейік.
а>1 болғандағы y=ах а>0, а≠1 функциясының графигі 3 – суретте, ал
0 < a < 1болғандағы – 4-суретте көрсетілген.
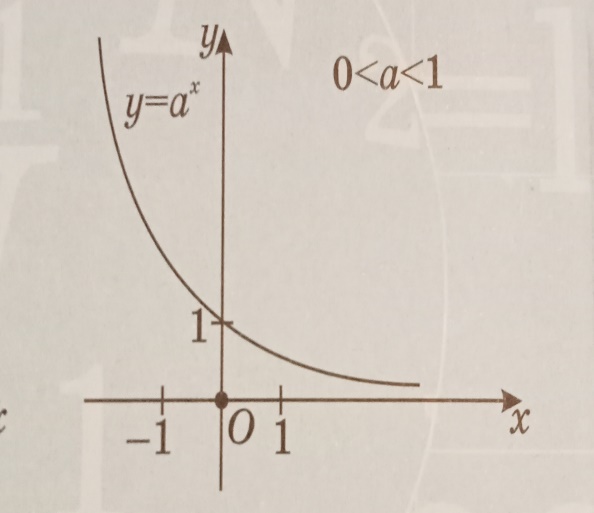
y=ах y=ах
3 – сурет 4-сурет
y=3х және
y= ![]() көрсеткіштік
функцияларының графиктерін бір координаталық жазықтаққа салайық
(5-сурет).
көрсеткіштік
функцияларының графиктерін бір координаталық жазықтаққа салайық
(5-сурет).
![]()
 y=3х
y=3х
|
|
|
|
|
|
суреттен аталған функциялардың графиктері Оу осіне қарағанда симметриялы екені көрініп тұр . Осыдан келесі тұжырымды аламыз: егер екі көрсеткіштік функцияның негіздері өзара кері сандар болса, онда ол функциялардың графиктері Оу осіне қарағанда симметриялы.
4) Көрсеткіштік функцияның үзіліссіздігі дәлелдейік y=ах, а>0, а≠1 функциясы берілген. Аргумент х – ке ∆х өсімше берейік, онда аргумент өсімшесіне сәйкес функция да өсімше қабылдайды:
∆ ах+∆х - ах ∙ а∆х - ах = ах(а∆х -1 ).
![]() Енді осы өсімшенің ∆х 0 ұмтылғандағы
шегін анықтайық:
Енді осы өсімшенің ∆х 0 ұмтылғандағы
шегін анықтайық:
![]() ∆у ах ∙а0-1)
꞊0.
∆у ах ∙а0-1)
꞊0.
Аргументтің шексіз фз өсімшесіне функцияның да шексіз аз өсімшесі сәйкес келеді. Осы заңдылық y=ах функциясы өзінің анықталу облысының кез келген нүктесінде үзіліссіз.
1- м ы с а л. y=5х-1 +1 функциясының графигін салайық.
Шешуі. Алдымен y=5х функциясының графигін салу керек.Ол үшін
а ꞊ 5>1 екенін ескеріп, 26,1-суреті бойынша барлық нақты сандар диынында өспелі функцияның графигін жүргіземіз. Одан кейін салынған графигі Ох осі бойымен бір бірлікке оң бағытта параллель көшіреміз. Шыққан графикті Оу осі бойымен бір бірлікке жоғары параллель көшіреміз (6-сурет).
2 – м ы с а л. 0,274 және 0,2710 сандарын салыстырайық .
Шешуі. Берілген сандардың негізгідері бірдей және 0,27-ге тең. Осы негіздерді бір санымен салыстырамыз: 0,27 <1, бұл жағдайда көрсеткіштік функция кемімелі. Демек , кіші аргументке функцияның үлкен мәні сәйкес. Сондықтан 0,274 >0,2710 .
Жауабы: 0,274 >0,2710 .
3- м ы с а л. y=2х және y=х2 функцияларының графиктері неше нүктеде қиылысатынын анықтайық.
Шешуі. Ол үшін бір координаталық жазықтыққа y=2х және y=х2 функцияларының графигін саламыз. бірінші функция көрсеткіштік функция және негізі 1-ден үлкен . Демек y=2х және y=х2 функцияның графигі (0;1) нүктесі арқылы өтетін және -де өспелі қисық. Ал y=х2 функциясының графигі төбесі (0;0) нүктесі болатын , тармақтары жоғары бағытталған парабола. Графигтер А және В нүктелерінде қиылысады (28-сурет).
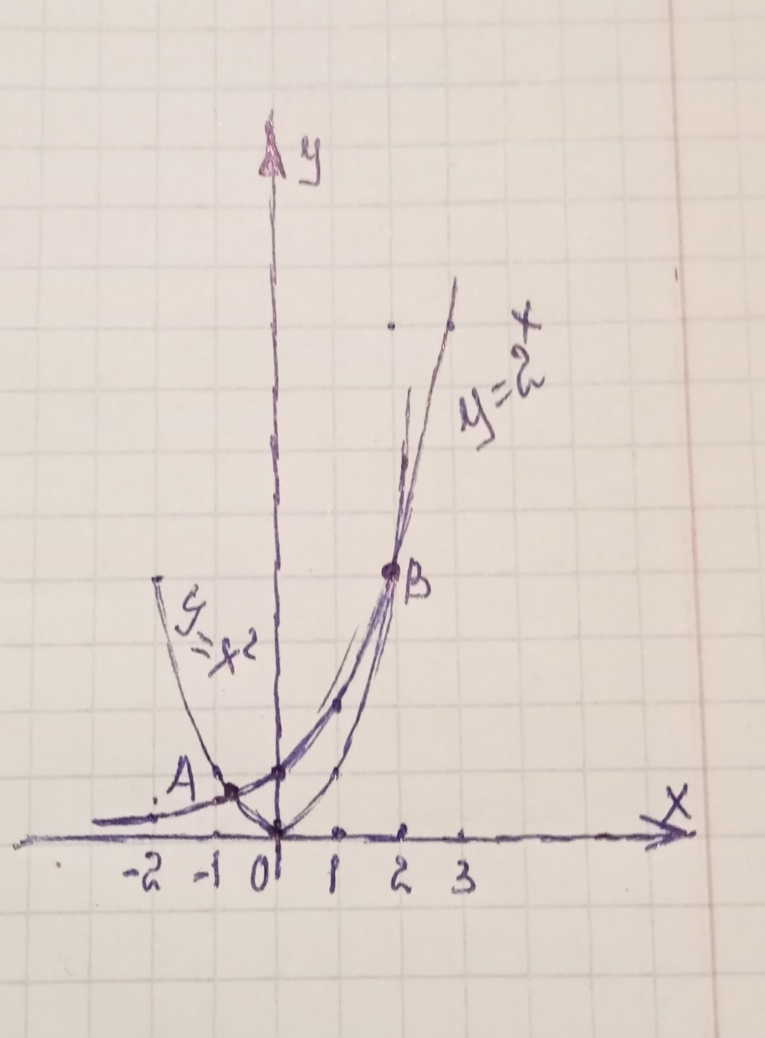
Жауабы: екі нүктеде қиылысады
Жаттығулар
А
у ꞊ f(x) функциясының графигін салыңдар (150-151):
1. 1) f(x) ꞊5х ; 2) f(x)꞊1,5х ;
3) f(x)
꞊0,85х 4)
f(x)꞊ ![]() .
.
2. 1)
f(x)꞊ ![]() ; 2)
f(x)꞊
; 2)
f(x)꞊ ![]() ;
;
3)
f(x)꞊ ![]() ; 4) f(x)꞊
135х.
; 4) f(x)꞊
135х.
3. у ꞊ f(x) функциясының мәндер жиынын табыңдар:
1)
f(x)꞊0,24х + 3; 2)
f(x)꞊ ![]() - 2
;
- 2
;
3) f(x)꞊-7х +1; 4) f(x)꞊36х -4.
4. Сандарды салыстырыңдар:
1) 1,83 және 23; 2) 0,82 және 0,54;
3) 0,53 және 0,577; 4) 3,21,6 және 3,21,7;
5) 0,2√2 және 0,21,4 ; 6) 3π және 33,149.
5. 1; 8; 32; 0,25; 0,0625 сандарын 2 санының дәрежересі ретінде жазыңдар.
6.Есептеңдер:
1)
4 1 -
3√2 ∙ 64√2 –
1 ; 2)( ![]() √3)√3;
√3)√3;
3)
49√7 : ![]() ;
4)
;
4) ![]() + 1
:36√5 .
+ 1
:36√5 .
7. Ықшамдаңдар:
1) ![]() ∙
а √3+2 ; 2)
(а√6) ∙
(а√+1 :а √3)
;
∙
а √3+2 ; 2)
(а√6) ∙
(а√+1 :а √3)
;
3)b3.5:
(b√b3) 4)
b √5 ∙b1.4 : ![]() .
.
8. у ꞊ f(x) және у ꞊ g(x) функцияларының графиктері неше нүктеде қиылысатынын анықтаңдар:
1)
f(x)꞊3х және
g(x)꞊3х ; 2)
f(x)꞊ ![]() және
g(x)꞊х2 ;
және
g(x)꞊х2 ;
3)
f(x)꞊7х және g(x)
꞊ ![]() ; 4)
f(x)꞊
; 4)
f(x)꞊ ![]() және
g(x)꞊х3 .
және
g(x)꞊х3 .
В
9. y=ах функциясының графигіне қарапайым түрлендірулер қолданып,
у ꞊ g(x) функциясының графигін салыңдар:
1)
g(x)꞊ ![]() - 2 ; 2)
g(x)꞊ 4х +
3;
- 2 ; 2)
g(x)꞊ 4х +
3;
3) g(x)꞊(2,5)х -1 + 2; 4) g(x)꞊(2,25)х +3 - 4.
10. у ꞊ f(x) функциясның мәндер жиынын табыңдар:
1) f(x)꞊ 4х – 5,6; 2) f(x)꞊(0,35)х + 3;
3) f(x)꞊ 1- 3х .
11. Салыстырыңдар:
1) ((√3)√2)√2 және 3 1,5 ;
2) ![]() және
6-2,25;
және
6-2,25;
3) (7 - 4√3)-3,5 және (7 - 4√3)3,5;
4) (5+2√6)3,3 және (5+2√6)-3,1 .
13. у ꞊ g(x) функциясының ең үлкен және ең кіші мәндерін анықтаңдар:
1) g(x )꞊ 3cosx ; 2) g(x)= 2sinx;
3)
g(x)= ![]() ; 4) g(x)= 4
– 16
; 4) g(x)= 4
– 16 ![]() .
.
14. Егер:
1) b=5 болса,
онда ![]() ∙
∙ ![]() ;
;
2) b꞊ 3 болса ,
онда ![]() ∙
∙ ![]() ;
;
3) b꞊ 2 болса ,
онда ![]() ∙
∙ ![]() ;
;
4) b꞊ 4 болса ,
онда ![]() ∙
∙ ![]() өрнегінің
мәнін табыңдар.
өрнегінің
мәнін табыңдар.
15. у ꞊ f(x) және у ꞊ g(x) функцияларының графиктері неше нүктеде қиылысатынын анықтаңдар:
1) f(x)꞊ 5х және g(x) ꞊6 –х;
2)
f(x)꞊ ![]() және g(x) ꞊3
–х;
және g(x) ꞊3
–х;
3) f(x)꞊ 2х - 2 және g(x) ꞊1 –х;
4) f(x)꞊
3х және g(x)
꞊ ![]() .
.
4.11
Мұғалімдерге арналған əдебиеттер:
-
«Қазақстан Республикасы жалпы орта білім берудің стандарты»
-
Математикадан 5-11 сыныптарға арналған мемлекеттік бағдарлама
-
Тердікбай Күшай «Математика олимпиадасының дайындық курстары» 6- 11 сынып оқу əдістемелік құралы. Астана 2010ж.
-
О.С. Беркімбаев, А.О.Беркімбаева. Арифметика есптері, Алматы
«Рауан», 1996
-
П. Т. Досанбай «Математикалық логика » Алматы «Дəуір» 2011 ж
-
Ə.Н Шыныбеков «Алгебра жəне анализ бастамалары» 10-11 сыныптар
-
И.Ф. Шарыгин, К.О. Бүкүбаева 10-11 сыныптарға арналған оқулық Алматы 2004
-
В.ВЛокоть Параметрі бар теңдеулер.Көрсеткіштік жəне логарифмдік теңдеулер,теңсіздіктер олардың жүйелері. Москва 2005ж
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10- сыныбына арналған оқулық,Алматы. “Мектеп”,2010.
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11- сыныбына арналған оқулық,Алматы. “Мектеп”,2011.
-
М.Л. Галицкий «Углубленное изучение алгебры и математического анализа».- Москва: Просвещение, 1997
-
И.П.Рустюмова, С.Т.Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике»; Алматы 2007;
-
Б.М., Ивлев, А.М Абрамов, Ю.П.Дудницын, С.И. Шварцбурд «Задачи повышенной трудности по алгебре и началам анализа», Москва 1990
-
И.Л. Никольская, В.В. Фирсов, Методика факультативных занятий в 9-10
классах. Избранные вопросы математики. Москва, 1983
-
М.И. Сканави «Полный сборник решений задач для поступающих в вузы. Группа повышенной сложности».- Москва,1999.
-
И.А.Терешин, Т.Н. Терешина «2000 задач по алгебре и началам анализа
10 класс», Москва, 1999
-
И.П.Рустюмова,С.Т.В. Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике» Алматы 2007г; 2011 г, 2013.
-
И.П.Рустюмова,С.Т.В. Рустюмова «Тренажер для подготовки к единому национальному тестированию (ЕНТ) по математике» Алматы 2007; 2011 , 2013.
-
В. Кривоногов «Нестандартные задания по математике».
-
М.И. Абрамович, М.Т. Стародубцев «Математика»
-
И.Ф.Шарыгин, В.И. Голубев «Факультативный курс по математике»
-
М.И. Сканави «Сборник задач по математике для поступающих во ВТУЗы
-
И.Ф.Шарыгин, В.И.Голубев Факультативный курс по математике. Решение задач, Москва: Просвещение, 1991
-
С. И. Колесникова «Математика. Решение сложных задач ЕГЭ» М. Айрис-пресс, 2007
Оқушыларға арналған əдебиеттер:
-
В.ВЛокоть Параметрі бар теңдеулер.Көрсеткіштік жəне логарифмдік теңдеулер,теңсіздіктер олардың жүйелері. Москва 2005ж
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10- сыныбына арналған оқулық,Алматы. “Мектеп”,2010.
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11- сыныбына арналған оқулық,Алматы. “Мектеп”,2011
-
И.П.Рустюмова, С.Т.Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике»; Алматы 2007; 2011
, 2013.
-
И.П.Рустюмова, С.Т. Рустюмова «Тренажер для подготовки к единому национальному тестированию (ЕНТ) по математике» 2011 , 2013.
-
В.С. Крамор «Повторяем и систематизируем школьный курс алгебры и начал анализа». Москва, 1990
-
В.В. Прасолов «Задачи по планиметрии», Москва: МЦНМ.
-
М.И. Шабунин «Пособие по математике для поступающих в вузы».- Москва: Лаборатория Базовых Знаний, 2000.
-
А.Д.Александров, Геометрия 11 сынып. Математиканы тереңдетіп оқитын сыныптар мен мектептердегі оқушыларға арналған оқу құралы.- Москва, Просвещение, 2000.
-
Н.Я. Виленкин Алгебра жəне анализ бастамалары.11сынып. Математиканы тереңдетіп оқитын сыныптар мен мектептердегі оқушыларға арналған оқу құралы ,Москва.:Просвещение,2000.
-
О.Б.Епишева, В.И. Крупич «Учить школьников учиться математике». Москва, 1990г
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Көрсеткіштік және логарифмдік өрнектер
Көрсеткіштік және логарифмдік өрнектер

«Логорифмдік жəне көрсеткіштік өрнектер»
11 сынып
Авторлық бағдарлама

Құрастырған: Джилбаева Гульназ Кураловна
математика пәнінің мұғалімі


2021 жыл

Түсініктеме хат
Оқушылардық функционалдық сауаттылығын дамыту жөніндегі 2012 – 2016 жылдарға арналған Ұлттық іс-қимыл жоспары оқушылардың функциялық сауаттылығын дамыту процесін мазмұндық, оқу-əдістемелік, материалдық- техникалық қамтамасыз ету жөніндегі іс-шаралар кешенін қамтиды.
Мектеп оқушыларының функционалдық сауаттылығын дамыту қазіргі 11 жылдық сияқты 12 жылдық мектептің Мемлекеттік жалпыға міндетті білім беру стандартын (МЖБС) жаңарту шеңберінде білім берудің басым мақсаттарының бірі ретінде айқындалады.
Бұл ретте функционалдық сауаттылықты дамыту нəтижесі білім алушылардың жастарға алған білімдерін практикалық жағдайларда тиімді жəне əлеуметтік бейімделу процесінде сəтті пайдалануға мүмкіндік беретін негізгі құзыреттіліктер жүйесін меңгеруі болып табылады. Негізгі құзыреттілік – бұл мемлекеттің орта мектепті бітіруші тұлғаның сапасына МЖБС-да жəне оқу бағдарламаларында көрсетілген білім беру нəтижелері түрінде қоятын талаптары.
Оқу бағдарламалары, сондай-ақ, мектеп оқушыларының функционалдық сауаттылығын дамытуға жəне негізгі, пəндік құзыреттіліктерге қол жеткізуге оқу үдерісін жұмылдыру арқылы, тəжірибе-бағдарлық мазмұндағы тапсырмалармен қоса жүйелі шешу əдістері арқылы бағдарланады. Бұл бағдарлама 11 сынып оқушылары үшін (барлығы 34 сағат, аптасына
1 сағат) оқуға арналған, ҚР-ның бастауыш, негізгі орта, жалпы орта білім беру мемлекеттік жалпыға міндетті білім беру стандарты негізінде жасалған (ҚР МЖБС, Астана, ҚР БҒМ 2012, Ы.Алтынсарин атындағы ұлттық білім беру академиясы, 23.08.2012 жылғы № 1080 бұйрығымен бекітілген).
ҚР БҒМ мен Ы.Алтынсарин атындағы ұлттық білім беру академиясының оқу бағдарламасы (Астана 2013, ҚР Білім жəне ғылым министрінің 23.08.2020жылғы № 115 бұйрығымен бекітілген). «Қазақстан Республикасының 2013-2014 оқу жылындағы жалпыға білім беру мекемелерінде ғылым негіздерін оқыту ерекшеліктері туралы» əдістемелік нұсқау хаты (ҚР БҒМ, Ы.Алтынсарин атындағы ұлттық білім беру академиясының ғылыми кеңесінде ұсынылған 25 мамыр 2013 жылғы №5 хаттамасы).
Бұл оқушылардың білімін кеңейтуге бағытталған, жоғары сынып оқушыларына қиындықтар туғызатын математикалық тақырыптар бойынша есептер шығару арқылы математикадан дайындық деңгейін көтеру, қосымша əдістермен жəне стандарттық емес тəсілдермен оқушыларды таныстыру, сондай-ақ шешу тəсілдерін жүйелеу, ҚЖСБ 2012 сəйкес тапсырмаларды шешу ғана емес тиімдісі, теңдеулер тапсырмаларын шешу де тиімді.
Математиканы оқытудың негізгі тапсырмалары мен міндеті – оқушылардың математикадан білім, біліктілік жүйесін саналы жəне тиянақты меңгеруін қамтамасыз ету. Бұл курс пəнге деген қызығушылықты қалыптастыруды қарастырады, математикалық қабілеттілікті дамыту жəне көрсету, мамандыққа бағыт беру, бір сөзбен айтқанда математикамен тығыз байланысты жүргізіледі. Оқушыларда негізгі жəне пəндік құзыреттіліктерді дифференциалды деңгейлеу, ынтымақтастық технологиясы, жобалау технологиясы, АКТ пайдалану,тірек конспектісі,материалды ірі блоктармен пайдаланып дамыту.
Бағдарламаның мақсаты: жоғарғы мектеп математикасының негізгі бөлімдері бойынша оқушылардың білім мен біліктерін кеңейту жəне тереңдету, жүйелеуге мүмкіндік жасау.
Бағдарламаның тапсырмалары:
-
Орта мектеп бітірушілердің пəндік жəне негізгі құзыреттілігін жетілдіруге мүмкіндік жасау;
-
Проблемалық жəне стандартты емес жағдайда білімдерін пайдалана білу;
-
Оқушыларда жекелей жəне топтық жұмыс істеу дағдысын дамыту;
-
Кітаптағы қиындығы жоғары есептерді шығармашылықпен шығару дағдысын дамыту;
-
Оқушылардың өзіндік бақылау мен өзара бақылау, рефлексия біліктерін дамыту;
Бағдарламаны меңгерту кезіндегі нұсқаулық:
-
Оқушыларда негізгі жəне пəндік құзыреттілігін дифференциалды деңгейлеу, ынтымақтастық технологиясы, жобалау технологиясы, АКТ пайдалану,тірек конспектісі,материалды ірі блоктармен пайдаланып дамыту.
-
Оқушылардың дайындық деңгейін оқу материалына сəйкес бейімдеу.
-
Оқылған материалдың практикалық бағытын бағдарлауды жүзеге асыру;
-
Қазіргі уақыттағы əртүрлі ақпараттар көзін пайдаланып өзара қарым- қатынас əдістерімен қамтамасыз ету.
Оқушылардың білімдерін қалыптастыру жəне дамыту:
-
Есептердің мағынасын ажырата білу.
-
Негізгі бағыттарды іздеуге ,анықтауға үйрету.
-
Жүйелі түрде есептердің дұрыс шешімдерін табуға бағыттау.
-
Есеп шығаруда дəстүрлі жолдарын таба білу.
-
Логикалық, аналогтық жəне жүйелі ойлауын дамыту
-
Есеп шығаруда тиімді тəсілдерді таба білу.
Бағдарламаның ерекшеліктері:
-
Қосымша əдебиеттер мен тірек конспектілермен жұмыс;
-
Оқушылардың зерттеу жұмыстары;
-
Электронды оқулық пен əдістемеліктер көмегімен жұмыс;
-
Оқушылардың теорияны меңгерудегі өздік жұмысы;
-
Практикалық блок:
-
Сыныптағы практикалық жұмыс (есептер жəне ең қиын бақылау сұрақтары);
-
Өз бетімен шешу;
-
Тест тапсырмаларын шешу;
-
Орындалған тапсырмаларды өзіндік жəне өзара тексеру
-
Соңғы жылдардағы тестер жинағынан қиындық тудыратын тест тапсырмаларын жинақтау;
-
ББД бақылау жəне бағалау.
-
Сынақ тапсыру ,конспект бойынша ауызша сұрау;
-
Кескін жұмыстары;
-
Өзара жұптық жəне топтық тексеру;
-
Өзара тексеру;
-
Тестілеу;
Сабақта мақсатты меңгерту үшін төмендегі форма ұсынылады: Лекция, практикалық семинарлар, модельдеу, өзара оқыту сабақтары, жоба қорғау сабақтары.
Оқушылардың білім, білік, дағдыларына қойылатын талаптар.
Оқушылардың ба5дарламаны оқу барысында білуі тиіс:
-курстың негізгі жоспарындағы формулалар мен негізгі түсініктер;
-дəрежені төмендету формуласы, үш аргументті бұрыштың формуласы, универсалды ауыстыру;
-
Безу теоремасы, Горнер схемасы;
-
полярлық жəне тікбұрышты координата жүйесінде жазық фигуралардың беттері аудандарын есептеу формулалары;
-
«күрделі экспонент» түсінігін беру;
-
симметриялық, кері жəне біртекті теңдеулердің жалпы түрлері;
-
параметрі бар теңдеулер тен теңсіздіктердің классификациясы;
-
логарифмдік өрнектерді түрлендіруге қосымша формулалар.
Қолдана білу:
-
функцияларды зерттеуге бірінші жəне екінші ретті туындылар;
-
күрделі салуларға көмекші əдістер;
-
функциялардың графиктері;
-
күрделі экспонент немесе негізінде айнымалысы бар логарифмді теңдеулер тен теңсіздіктердің шешу əдістері;
-
аркфункция белгісінің ішінде айнымалысы бар трансценденттік өрнектерді эквивалентті түрлендіру тəселдері;
-
графиктік интерпретация əдісін кірістіре параметр, модуль белгісі бар теңдеулер тен теңсіздіктердің шешу əдістері;
-
біртектес жəне қайтымды,симметриялы, жоғарғы дəрежелі теңдеулерді шешу əдістері;
-
логарифмдік өрнектерді түрлендіруге стандарт емес əдістер жəне қосымша формулалар;
-тригонометриялық жəне иррационалдық өрнектері бар теңдеулердің түбірлерін іріктеу тəсілдері əдісі;
-
интеграл табуда айнымалыны ауыстыру əдісі;
-логарифмдік жəне көрсеткіштік функциялардың монотондылық қасиеттері;
-логарифмдік жəне көрсеткіштік теңдеулер тен теңсіздіктердің шешудегі экстремалдық функциялар қасиеттері жəне интервалдар əдісіндегі стандарт емес ауыстырулар;
-
полярлық жəне тікбұрышты координата жүйесінде жазық фигуралардың беттері аудандарын есептеуге анықталған интеграл , айналу денелерінің көлемін есептеу;
-
геометриялық есептерді шешудің қосымша əдістері.
Пайдалана алу
Тапсырманы орындап білімді ары қарай жалғастыруда, өзіндік жұмыстар процесі мен практикалық іс-əрекетте білім мен білікті игеру
-
Практикалық есептер жəне формула бойынша түрлендіру, кіргізілген формулалар, дəрежесі бар, радикалдар, логарифмдер, тригонометриялық функциялар, туынды, алғашқы функция, керек болған кезде қосымша формулаларды қолдану, курстың негізгі жоспарындағы тəсілдер, əдістер, анықтамалық материалдар жəне қарапайым есептеу құрылғылары;
-
графиктік, графиктерді интерпретациялап көрсетуде əртүрлі байланыстарды функциялардың көмегімен беру;
-
физикалық жəне əлеуметтік-экономикалық мағынадағы қолдаңбалы есептерді шешу; қарапайым математикалық моделді салу мен зерттеу. Жəне фигурлар қасиеттері мен оқып білген формулалар негізінде қиын емес практикалық ситуацияларды зерттеу(моделдеу);
-
кеңістік денелерінің беттері аудандары мен көлемдерін есептеуге арналған практикалық есептерді шешуде қажет болса анықтамалық материалдар жəне қарапайым есептеу құрылғыларын пайдалану.
Білу:
-
есеп шешудің стратегиясын немесе жемісті əдісін таңдау, есеп шешуді орындағанда өзіндік тексеруді іске асыру жəне толық негіздеуді жүргізу;
-
əртүрлі моделдер (мысалы, диаграммалар, кестелер, схемалар немесе графиктер) пайдаланып математикалық ақпарат жəне берілгенін ұсыну;
-
есеп шешуге сəйкес модель (мысалы , теңдеу, диаграмма, график) ойластыру;
-
болжам жасау, сараптау, тарату;
-
комбинация/нəтиже алуға əртүрлі əдістерді ұйғару;
-таза математикалық немесе нақты өмірдегі ситуациялармен байланысты стандарт емес есептерді шешу;
-қиын немесе таныс емес ситуацияларға математикалық əдістерді қолдану;
-Интернет жəне əртүрлі ақпарат көздерін пайдалану.
Құзіреттіліктерді меңгеру:
-
оқу–танымдық,
-
бағдарлы – мақсатты,
-
рефлексивті,
-
коммуникативті,
-
ақпараттық,
-
еңбек –əлеуметтік:
Бағдарламаның мазмұны
Тақырып:«Өрнектерді түрлендіруге қосымша тригонометриялық формулаларды қолдану».
Мақсаты:Тригонометриялық өрнектерді түрлендіруге теориялық материалды қолдана білу білігі жəне білу, білімді жүйелеу (дəрежені төмендету формуласы, үшбұрыштың формуласы, универсалды ауыстыру).
Тақырып: «Күрделі функциялар графиктерін салуға көмекші тəсілдер». Мақсаты:Күрделі функциялардың графиктерін салуды неғұрлым тереңдетуді қамтиды жəне модуль таңбасы бар функциялардың графиктерін салуды жүйелеуді қарастыру.
Тақырып: «Геометриялық есептерді шешудің əдістері».
Мақсаты: білімді жүйелеу, геометриялық есептерді шешуге қосымша теориялық материалды қолдана білу білігі мен білуі, алған білімді практикада қолдану. Оқушылардың математикалық деңгейін көтеруді дамыту.
Тақырып:«Айнымалылары аркфункция таңбасының ішінде болатын трансценденттік өрнектерді эквивалентті түрлендіру».
Мақсаты: Кері тригонометриялық функциялар кездесетін өрнектерді түрлендіруде стандартты емес тəсілдерді қолдана білуді қалыптастыру.Тепе- теңдіктерді түрлендіруді оқуда мысалдарды қолданып шешу білімін жүйелеу.
Тақырып: «Тригонометриялық теңдеулер мен тіңсіздіктерді шешу əдістерін жүйелеу».
Мақсаты: Тригонометриялық теңдеулер мен теңсіздіктерді шешу- көбейткіштерге жіктеуде стандартты емес тəсілдерді қолдана білу мен білігін қалыптастыру, жаңа айнымалы еңгізу, графикалық тəсіл, квадраттық теңдеу мен теңсіздікке келтіру.
Тақырып: «Жоғарғы дəрежелі теңдеулер мен теңсіздіктерді шешу». Мақсаты: Жоғарғы дəрежелі теңдеулер мен теңсіздіктерді шешуге стандартты емес тəсілдерді қолдана білуді қалыптастыру: көбейткіштерге жіктеуде , жаңа айнымалы еңгізу, графикалық тəсіл, , квадраттық теңдеу мен теңсіздікке келтіру, Безу теоремасын қолдануда анықталмаған коэффициенттер əдісі, Горнер схемасы.
Тақырып: «Айнымалылары модуль таңбасының ішінде болатын теңдеулер мен теңсіздіктерді шешудің əдістері».
Мақсаты: Айнымалылары модуль таңбасының ішінде болатын теңдеулер мен теңсіздіктерді шешуде стандартты емес тəсілдерді қолдана білуді қалыптастыру, тақырып бойынша білімді тереңдету.
Тақырып: «Қолданбалы есептерді шешуге дифференциалды есептеуді ұсыну».
Мақсаты :Математика жəне физикадағы практикалық есептерде теориялық материалды қолдана білу білігі жəне білу, білімді жүйелеу.
Тақырып: «Логикалық есептерді шешу».
Мақсаты: Кеңістікті сезіне білуін дамыту есептерін, практикалық – бағдарлау есептерін, қабілетті комбинациялауды дамыту, ықтималдықты статистикалық анықтау, таңдау, шеңбер бойымен қозғалу есептерін, арифметикалық есептерді шешуде функциональдық сауаттылықты дамыту.
11 сынып қолданбалы курсының күнтізбелік-тақырыптық жоспары.
|
№ саб ақ |
Мазмұны |
Сағат саны |
теория |
практика |
Өткізу |
Білім берудің нəтижесі |
Дидактикалы қ қамтылуы |
|
1. Қолданбалы есептерді шешуде дифференциалды есептеулерді қолдану. (3 сағат). |
|||||||
|
1,2 |
Бірінші жəне екінші ретті туындыны функцияны зерттеуде қолдану. |
2 |
0,5 |
1,5 |
Лекция |
тірек конспектісі, есеп шығаруүлгілері |
1 қосымш а |
|
3 |
Геометрии, физика и химияда дифференциалды есептеулер элементтерин қолдану. |
1 |
0 |
1 |
2 қосымша |
||
|
2. Қолданбалы есептерде интеграл мен алғашқы функция. (3 сағат) |
|||||||
|
4 |
Интегралды тура интегралдау əдісімен шешу . |
1 |
0,5 |
0,5 |
Фронталды, |
тірек конспектісі, |
3 қосым ша |
|
5 |
Физикалық есептерді шешуде интегралды пайдалану. |
1 |
0 |
1 |
4 қосым ша |
||
|
6 |
Тік бұрышты жəне полярлық координат жүйесінде жазық фигуранын ауданын есептеу.Айналу денесінің көлемін есептеу. |
1 |
0,5 |
0,5 |
|
|
5 қосымша |
|
3.Теңдеулер мен теңсіздіктерді шешуде жəне өрнекті өзгертуде радикалдың қасиетін қолдану (5сағат) . |
|||||||
|
7 |
Радикалдың негізгі қасиеті.Радикалдарды түрлендіру. Ұқсас радикалдар. |
1 |
0,5 |
0,5 |
Лекция, фронталды, топтық |
тірек конспектісі, есеп шығару үлгілері |
6 қосымша |
|
8- 11 |
Құрамында түбір астындағы айнымалысы бар теңсіздіктер мен теңдеулерді шешу. Тригонометриялық жəне ирационалдық өрнегі бар теңдеулердің түбірін табу. |
4 |
0,5 |
3,5 |
7 қосымша |
||
|
4. Тестік жəне логикалық есептер (8 сағат). |
|||||||
|
12- 15 |
Мəтінмен берілген есептердің түрлері мен шығару тəсілдері
|
4 |
0,5 |
3,5 |
Фронталды, жекелей, топтық, |
Создание базы заданий по соответствующим темам |
қосымша8 |
|
16- 17 |
Логикалық есептер. |
2 |
0,5 |
1,5 |
9 қосым ша |
||
|
18 |
Функциональды сауаттылықты дамытуға есептер |
1 |
0 |
1 |
|
|
10 қосым ша |
|
19 |
Ойлау кеңістігін дамытуға есептер. |
1 |
0 |
1 |
11қосымша |
||
|
5.Практикалық бағыттағы есептердегі көрсеткіштік функция. Əр түрлі функциялардың графиктерин жəне туындыларының графигин зерттеу. (3 сағат). |
|||||||
|
20 |
Əртүрлі функциялар графигін жəне туындысының графигін зерттеуге есептер. |
1 |
0 |
1 |
Лекция, |
тірек конспектісі, есеп шығару үлгілері |
12 қосымша |
|
21- 22 |
Практикалық бағыттағы есепті шешуде көрсеткіштік функцияны қолдану (экономикада, өндірісте, географияда, химияда, биологияда). |
2 |
0,5 |
1,5 |
13 қосымша |
||
|
6.Логорифмдік жəне көрсеткіштік өрнектердің қасиеттерін қолдану. (6 сағат). |
|||||||
|
23 |
Логарифмдік өрнектерді түрлендіруде стандартты емес əдістерді пайдану. |
1 |
0 |
1 |
Лекция, |
Тірек схемаларды құру алгоритмін дайындау |
14 қосымша |
|
24 |
Логарифмдер теориясын пайдаланып физикалық есептерді шығару. |
1 |
0 |
1 |
15 қосымша |
||
|
25 |
Логаримдеу əдісін пайдаланып |
1 |
0,5 |
0,5 |
16 қо сы |
||
|
|
көрсеткіштік теңдеулерді шешу. |
|
|
|
|
|
|
|
26 |
Күрделі экспонента.Негізі тұрақсыз логорифм. Күрделі экспонент немесе негізі тұрақсыз логорифмі бар теңдеулер мен теңсіздіктерді шешу. |
1 |
0,5 |
0,5 |
17 қосымша |
||
|
27- 28 |
Логарифмдік жəне көрсеткіштік теңдеулер мен теңсіздіктерді шешуде логарифмдік жəне корсеткіштік функция монотондылығы,функцияның экстремал қасиетін жəне инетегралды ауыстыруды əдісін колдану. |
2 |
0,5 |
1,5 |
18 қосымша |
||
|
7.Əр түрлі теңдеулер мен теңсіздіктерді шешуге мəндес ауысым. (6 сағат) |
|||||||
|
29- 30 |
Симметриялы, қайтымды жəне біртекті теңдеу |
2 |
0,5 |
1,5 |
Лекция, |
Тірек схемаларды құру алгоритмін дайындау |
19 қосым ша |
|
31- 32 |
Модуль белгісі бар теңдеулер жəне теңсіздіктер шешу: əдіс- тəсілдері, бірмəнді ауыссым. |
2 |
0,5 |
1,5 |
20 қосымша |
||
|
33- 34 |
Теңдеулер жəне теңсіздіктер қасиеттер: əдіс-тəсілдері, бірмəнді ауыссым. Графикалық интерпритация тəсілі. |
2 |
0,5 |
1,5 |
21 қосым ша |
||
Көрсеткіштік және логарифмдік теңдеулер, олардың жүйелері.
Көрсеткіштік және логарифмдік теңдеулерді шешу үшін көрсеткіштік функциясы мен логарифмдік функцияларының қасиеттерін білу керек.
1 –Теорема. Егер болса, онда теңдеуі теңдеуімен мәндес.
Көрсеткіштік теңдеудің көпшілігі теңдеудің екі жақ бөлігін бірдей негізге келтіру әдісімен шешіледі. Негізгі екі әдісті: 1) теңдеуінен теңдеуіне келтіру; 2) Жаңа айнымалы енгізу әдістері пайдаланылады. Кейбір жағдайда жасанды әдіспен шешуге тура келеді.
теңдеуін шешу, – пен ауыстырып, оған мәндес жай көрсеткіштік теңдеулер жиынтығы
шешуге келтіріледі, мұндағы теңдеуінің барлық түбірлері.
сандар, теңдеуі оған мәндес теңдеулер жиынтығын шешуге келтіреді, мұндағы - теңдеуінің түбірелері.
-
теңдеуін шешу теңдеуін шешуге келтіреді. -
( – нақты сандар, – функция, ал негіздері үшін, орындалады).
теңдеулер жиынтығын шешуге келеді.
- теңдеуінің түбірлері.
теңдеуінің
-
және болғанда бір ғана түбір болады; -
және болғанда бірге тең емес, кез келген оң сан шешімі; -
және болғанда шешімі болмайды.
Ауыстыруға болады, осыны есептер шығаруда
пайдаланады.
Көрсеткіштік және логарифмдік теңдеулер жүйесін шешуде алгебралық
теңдеулер жүйесін шешу барысында әдістер пайдаланылады.Теңдеулер
жүйесін түрлендіруде жүйенің әрбір теңдеуі қарапайым түрге
келтірілуін қадағалау керек.
1.Жүйені шешіңдер:
Шешуі: АО:
Жауабы:
3.Жүйені шешіңдер
Шешуі: бұл теңдікболғанда болуы мүмкін.
Олай болса
Жауабы:
Рационал теңсіздіктерді шешу
VIII-дәріс
V.Бұрын, біз қарапайым сандық функцияларға VI.
Көпмүшесін және екі көпмүшенің қатынасын қарастырайық
1-анықтама. Егер a саны функциясының нөлі, немесе көпмүшенің түбірі деп аталады.
Көпмүшенің түбірі оның дәрежесінен артық емес
2-анықтама. Рационал функциялардан тұратын теңсіздікті рационал теңсіздіктер деп атайды.немесе ,немесе теңсіздіктері рационал теңсіздіктер
Рационал теңсіздіктерді аралық (интервалдар) әдісімен шешу тиімді
Рационал теңсіздіктерді шешу үшін :
1.Функцияны канондық түрде көбейткіштерге жіктеу керек( яғни х-тің барлық коэффиценттері оң сан)
2. Функцияның барлық нөлдерін (түбірлерін тауып, оны сан осіне өсу ретімен белгілеп,салу керек)
3.Функцияның таңбасы әр уақытта оң жоғарғы жағынан басталады (толқын түрінде) және функцияның түбірінен өткенде кезекпен алмасып тұрады.
4.Егер функцияның көбейткіштерге жіктелуі
канондық түрде болмаса ,онда функция таңбасы оң төменгі жағынан
басталады және функция түбірінен өткенде таңба кезекпен ауысып
отырады.
5.Егер функцияның оң мәндерін білу керек болса, онда сан өсінің
жоғарғы жағындағы аралықтарды жазамыз. Ал,егер функцияның мәндерін
білу үшін сан өсінің төменгі жағындағы аралықтарды
жазамыз.
6. Қайталама түбірді анықтаймыз: егер функцияның жұп рет қайталама түбірі болса, онда функция өзінің таңбасын осы түбірден өткенде екі рет қарсы таңбаға өзгертеді, егер қайталама түбір тақ рет болса, осы түбірден өткенде функция таңбасын қарама-қарсы таңбаға алмастырады.
1.Теңсіздікті шеш:
Шешуі:
қайталама түбір, екі рет
қайлайды.
Жауабы:
Модуль таңбасына тәуелді теңсіздіктерді шешу
үшін, алдымен модульдің анықтамасын еске
түсірейік.
X нақты санның
модулі, немесе
абсолюттік шамасы деп болғанда х санының өзін айтады, егер болса
(-х) санын айтады, оны деп белгілейді.
Сонымен
Модуль таңбасына тәуелді теңсіздіктерді шешуде
тиімді қасеттерді атап өтейік.
Логарифм (грекше logos — қатынас және arіthmos — сан). Логарифм белгіленуі: log. Логарифмнің жалпы түрі: Logab . Логарифм түрлері: ондық lg және ln натурал логарифм жайлы да айтуға болады. е саны иррационал сан, e≈2.718.
Аңықтама.
b санының a негізі бойынша логарифмі деп x санын атаймыз және бұл санды loga b деп белгілейміз:
ax =b, x= loga b.
23=8 теңдігінде 3 дәреже көрсеткіш, ал 8 шығу үшін негізі екіні үш дәрежеге шығару керектігін білдіреді.
Мысал:
50=0 (1/3)2=1/9 3-2=1/9
Анықтама: N санының а негізі бойынша логарифмі деп N саны табылатындай а санының дәреже көрсеткішін айтады. Негізі а болғандағы а санының логарифмі loga N символымен белгіленеді.
Негізі 10 болғанда log10 N=lgN - ондық логарифм деп аталады.
е болғанда loge M=lgM - натурал логарифм деп аталады.
Логарифмдердің қасиеттері:
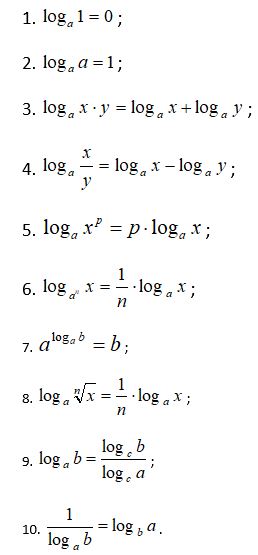
Логарифмдік функция және оның қасиеті мен графигі.
Анықтама: y=logax (a>0, a≠1) формуласымен берілген функцияны логарифмдік функция деп аталады.
Логарифмдік функцияның негізгі қасиеттері:
1. Логарифмдік функцияның анықталу облысы - барлық оң сандар жиыны R+, яғни D(loga)=R+
Шынында да алдыңғыда атап көрсетілгендей, әрбір оң x санының а негізі бойынша логарифмі бар болады.
2. Логарифмдік функцияның мәндерінің облысы – барлық нақты сандар жиыны.
Шынында да, логарифмнің анықтамасы бойынша кез келген нақты y үшін мына теңдік орындалады:
loga(ay)=y
яғни y=logax функциясы x0=ay0 нүктесінде y0 мәнін қабылдайды.
3. Логарифмдік функция бүкіл анықталу облысында өседі,(a>1 болғанда), не кемиді (0<a<1 болғанда)
Логарифмдік функциялардың қасиеттері қолданылатын мысалдар.
1-мысал. Мына функцияның анықталу облысын табайық: f(x)=log8(4-5x)
Логарифмдік функцияның анықталу облысы R+ - жиыны. Сондықтан берілген функция тек 4-5x>0 шарты орындалатындай x мәндерінде анықталған, яғни x<0.8. Олай болса, берілген функцияның анықталу облысы (-∾, 0.8) интервалы.
2-мысал. Мына функцияның анықталу облысын табайық. f(x)=log2(x2-3x-4)
Алдыңғы мысалдағы сияқты, f функциясы x2-3x-4>0 шарты орындалатындай барлық x мәндерінде анықталған. Осы квадрат теңсіздікті шешіп, D(f) дегеніміз (-∾,-1)Ú(4,+∾) интервалдарының бірігуі екенін табамыз.
Мысалы: y=log3x және y=log5x функцияларының графигін салу керек.
Шешуі:
1) y=log3x
|
х |
1/9 |
1/3 |
1 |
3 |
9 |
|
у |
-2 |
-1 |
0 |
1 |
2 |
2) y=log5x
|
х |
1/25 |
1/5 |
1 |
5 |
25 |
|
у |
-2 |
-1 |
0 |
1 |
2 |

Логарифмдік теңдеулер мен теңсіздіктер және оларды шешу.
Анықтама: Айнымалысы логарифм белгісінің ішінде болатын теңднуді логарифмдік теңдеу деп атаймыз. Ең қарапайым логарифмдік теңдеуді қарастырайық logax=b. Логарифмдік функция (0,∾) аралығында өседі (не кемиді) және осы аралықта барлық нақты мәндерді қабылдайды. Түбір туралы теорема бойынша кез келген b үшін берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады. Санның логарифмінің анықтамасы бойынша ab саны сол шешім екендігі бірден табылады. Логарифмдік теңдеулерді шешудің бірнеше әдістері бар:
1. Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер.
Мысал - .
logx(x3-5x+10)=3 теңдеуін шешейік.
Шешуі: Логарифмнің анықтамасы бойынша x3-5x+10=x3, онда бұл
теңдеудің шешімі x=2.
Табылған айнымалының мәнін теңдеуге қойып тексереміз:
log2(23-5*2+10)=log28=log223=3log22=3
Демек, x=3 мәні теңдеуді қанағаттандырады.
Жауабы: x=2.
2. Потенциалдауды қолдану арқылы логарифмдік теңдеулерді шешу. Жаңа айнымалы енгізу әдісі. Мүшелеп логарифмдеу әдісі.
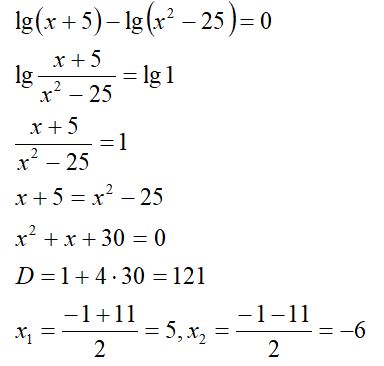
3. Жаңа айнымалы енгізу әдісі.
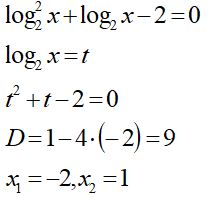
4. Мүшелеп логарифмдеу әдісі.
xlog2x-2=8 теңдеуін шешейік.
Шешуі:
Берілген теңдеуді былай жазайық: xlog2x*x-2=8 немесе xlog2x=8x2
Шыққан теңдеуді негізін 2 – ге тең етіп логарифмдейік:
log2x*log2x=log28+log2x2
log22x=3+2log2x
log22x-2log2x-3=0
Демек,
1) log2x=3, осыдан x1=8
2) log2x=-1, осыдан x2=1/2.
Тексеру:
1) 8log28-2=8 немесе 83-2=8, 8=8.
2) (1/2)log2(1/2)-2=8 немесе (1/2)-3=8, 8=8.
Жауабы: x1=8; x2=1/2.
|
Оқу мақсаттары (оқу бағдарламасына сілтеме) |
АУ 10.3 қарапайым логарифмдік теңдеулерді шешеді. Мысалы: 2log4x – 3 = 0, (log_2 (x+1) = log_2 6–log_2 x). |
|
Сабақ мақсаттары |
Логарифм ұғымын меңгеру және оны қолдана білу. Білу және түсіну Логарифм анықтамасы мен қасиеттерін негізге ала отырып, қарапайым логарифмдік теңдеулерді шешу алгоритмін біледі. Білімін қолдану
|
|
Тілдік мақсаттар |
Оқушылар: Күнделікті өмірде логарифмнің қолданысы туралы талқылайды және әңгімелей алады. Логарифм – Логарифмдік функция – Дәреже көрсеткіші – Негізгі түрлендірулер – Иррационал сан – Логарифм қасиеттері – Логарифмдік тепе-теңдіктер – Шынайы өмірде көрсеткіштік функция көп жерде қолданылады. Логарифмдерді түсіну үшін маңызды. Инженерлер логарифмнің қолданысын білуі қажет. Калькулятор болмағанда логарифмдерді білу . . . қатысты болды. Химиядаға pH келесіге негізделген. Көрсеткіштік функцияларды түсіну астрономдар үшін маңызды. |
|
Құндылықтарды дарыту |
Сыни тұрғыдан ойлау арқылы білімге деген сүйіспеншілікті қалыптастыру. |
|
Пәнаралық байланыстар |
Астрономия, химия, информатика. |
|
АКТ қолдану дағдылары |
Презентация |
|
Бастапқы білім |
Натурал көрсеткішті дәреже, бүтін көрсеткішті дәреже, дәреженің қасиеттері. |
Сабақ барысы
|
Сабақ кезеңдері |
Жоспарланған іс-әрекет |
Ресурстар |
|
Басы (3 минут) |
І. Ұйымдастыру. Амандасу. Көңіл күйлерін смайликтер арқылы білу. |
|
|
Басы (2 минут) |
І. Үй тапсырмаларын тексеру. 1. Теңдеулер түрлерін ата 2. Логарифмнің дамуына көп үлес қосқан ғалым? |
Презентация бойынша өткен тақырып бойынша тапсырмалар. |
|
Ортасы (20 минут) |
ІІ. Ауызша есептейік. «Кім жүйрік?» 1. (log_3sqrt{3} ) 2. Log71 3. (log_5 frac{1}{625})Log51 4. Log211 - Log244 ІІІ. Ауызша тест.
IV. “Кім жылдам?”
V. «Кім тапқыр?»
Логарифмдік теңдеулер 5. Log3( 243 * 729) |
Презентация бойынша өткен тақырып бойынша тапсырмалар. |
|
Жаңа сабақ |
Жаңа сабақ: Логарифмдік теңдеулер. Анықтама Логарифм белгісі астында немесе (және) оның негізінде белгісізді қамтитын теңдеу логарифмдік теңдеу деп аталады. Қарапайым логарифмдік теңдеу деп logax=b түріндегі теңдеу атаймыз. Тұжырым 1. Егер a > 0, a ≠1 теңдеу кез келген нақты b кезінде x = ab деген бір ғана шешімі болады. Логарифмдік теңдеуді шешудің тәсілдері. 1. Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер. Логарифмнің анықтамасы бойынша: logax=b түріндегі теңдеулер былай шешіледі. logax=b⟺x=ab Мысал: log3(x2 + 4x + 12) = 2. 2. Потенцирлеу әдісін қолдану үшін логарифмдік теңдеуді logaƒ(x) = logag(x) түріне келтіру. log2(x2 + 7x – 5) = log2(4x – 1). 3. Жаңа айнымалы енгізу тәсілі. Логарифмдік теңдеулерді жаңа белгіні қолданып, шешуге болады. Бастапқы теңдеуге жаңа белгіні қойғаннан кейін, жаңа, барынша қарапайым теңдеу аламыз, оны шешкеннен кейін, алмастыруға қайта оралып, бастапқы теңдеудің түбірлерін табамыз. 4. Мүшелеп логарифмдеу тәсілі. Берілген әдіс потенцирлеу әдісіне “кері” болып келеді, яғни логарифмдері жоқ теңдеулерден оларды қамтитын теңдеулерге көшеміз. ƒ(x) = g(x) Бұл әдіс әдетте егер теңдеуде көрсеткіштік функциялар болса қолданылады, логарифмдер көрсеткіште. 5. Бір негізден екінші негізге көшу. Егер теңдеуде әртүрлі негізді логарифмдер болса, онда ең алдымен ауысу формуласын қолданып, барлық логарифмдерді бір негізге келтіру қажет. logax = (frac{log_{b}x}{log_{b}a}) https://bilimland.kz/kk/courses/math-kz/analiz-bastamalary/korsetkishtik-zhane-logarifmdik-funkcziyalar/lesson/logarifmdik-tengdeulerdi-sheshu-adisteri сайты бойынша түсіндіру. |
|
|
Жалпы сыныппен жұмыс (15 минут) |
Жалпы сыныппен жұмыс. 1-жаттығу Теңдеуді шешіңіз: log3(2x + 1) = 2. 7-жаттығу log3(2x − 1) + log3(x + 3) = 2 теңдеуін шешіңіз. 8-жаттығу logx + 4(x2 − 1)= logx + 4(5 − x) теңдеуін шешіңіз. 9-жаттығу Теңдеуді шешіңіз: log24 x + (frac{1}{2})log4 (sqrt{x}) - 1,5 = 0. 13-жаттығу Теңдеуді шешіңіз: log2 x + log3 x = 1. 17-жаттығу Теңдеуді шешіңіз: xlgx - 1 = 100. |
https://bilimland.kz/kk/courses/math-kz/analiz-bastamalary/korsetkishtik-zhane-logarifmdik-funkcziyalar/lesson/logarifmdik-tengdeulerdi-sheshu-adisteri сайтындағы есептерді шығару |
|
Жұптық жұмыс |
Жұптық жұмыс http://itest.kz/lekciya_logarifmdik_tengdeuler_men_tengsizdikteri_sheshuding_adisteri сайты есебін жұптық жұмыста орындайды және бір-бірін тексереді. Жұп 1 Теңдеуді шешіңіз: (log_{sqrt{2}})x+ log2x = 1,5. Теңдеуді шешіңіз: log7x = 2log73 + 4log492. Жұп 2 Теңдеуді шешіңіз: (log_4)x + log16x + log64x = (frac{11}{12}). Теңдеуді шешіңіз: log25x2 + (log_sqrt{5} )x = 3. Жұп 3 Теңдеуді шешіңіз: (log_5)x • log7x = 4log57x. Теңдеуді шешіңіз: log5x + (logsqrt{5} )x + (log_{frac{1}{5}})x = 6. Жұп 4 Теңдеуді шешіңіз: (log_{8-x})11 = (frac{1}{2}). Теңдеуді шешіңіз: (log_{x^2+4x+4})3 = (frac{1}{2}). Жұп 5 Теңдеуді шешіңіз: (lg_{(8-x)})+ lg(x–3) = 1 – lg5. Теңдеуді шешіңіз: log2x + log8x = 8. VIII. Рефлексия - нені білдім, нені үйрендім. - нені толық түсінбедім. - немен жұмысты жалғастыру қажет. Үйге: itest.kz сайтынан есеп беріледі. Теңдеуді шешіңіз: log2(x + 2) = log2(x2 + x – 7) Теңдеуді шешіңіз: logx-6(x – 4) = 2. Теңдеуді шешіңіз: log3(0,5 + x) = log30,5 – log3x |
|
Логарифдік функция және оның қасиеттері, графиктері, өрнектерді түрлендіру.
1.Санның логарифмінің
ұғымы.у=ax көрсеткіштік
функция берілсін (a>0,a 1).Бұл бірсарынды функция. Сондықтан тек
аргументтің (х) әр мәніне функцияның бір ғана мәні сәйкес келіп
қоймай, керісінше,функцияның алдын ала берілген әр мәніне х-тің бір
ғана мәні сәйкес келеді.
1).Бұл бірсарынды функция. Сондықтан тек
аргументтің (х) әр мәніне функцияның бір ғана мәні сәйкес келіп
қоймай, керісінше,функцияның алдын ала берілген әр мәніне х-тің бір
ғана мәні сәйкес келеді.
aх=b теңдеуін
қарастырайық. b 0 болғанда теңдеудің түбірі болмайды.Егер
b>0болса, онда теңдеудің бір ғана түбірі
болады.
0 болғанда теңдеудің түбірі болмайды.Егер
b>0болса, онда теңдеудің бір ғана түбірі
болады.
Графикте көрсетейік y=ax функциясының графигін сызамыз: y=b (b>0)
Түзуін жүргіземіз.
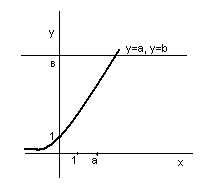
![]()
![]()
Осы екі
графиктердің қиылысу нүктесінің абциссасы, яғни
x= -ax=b теңдеунің іздеп
отырған түбірі болады. Сонымен ax=b
(a
-ax=b теңдеунің іздеп
отырған түбірі болады. Сонымен ax=b
(a 1,
1,
a>0, b>0). ax=b теңдеуінің b санының а негізді логарифмі деп аталады.
Анықтама.b оң санының
бірден өзгеше, оң а негізді логарифмі деп,b санын алу үшін а
санының дәреже көрсеткіші болатын  санын айтады:
санын айтады: =Iogab.Оқылуы:
«
=Iogab.Оқылуы:
« дегеніміз b санының а негізді логарифмі
».
дегеніміз b санының а негізді логарифмі
».
 =Igb,яғни 10 саны
негіз болып жазылмайды.Мұндай логарифмдер
-ондық логарифм деп
аталады.
=Igb,яғни 10 саны
негіз болып жазылмайды.Мұндай логарифмдер
-ондық логарифм деп
аталады.
Сонымен,a 1,a>0, b>0 болғанда
аа=b теңдеуінен
анықтама бойынша
1,a>0, b>0 болғанда
аа=b теңдеуінен
анықтама бойынша  =Iogab теңдігі шығады.
Соңғы теңдеудегі
=Iogab теңдігі шығады.
Соңғы теңдеудегі  -ның орнына мәнін
қойсақ,аIogab=b
(a>1,b>0,a
-ның орнына мәнін
қойсақ,аIogab=b
(a>1,b>0,a 1).Бұл теңдік негізгі
логарифмдік тепе-теңдік деп
аталады.
1).Бұл теңдік негізгі
логарифмдік тепе-теңдік деп
аталады.
IY. Логарифмдік функцияның графигі
y=ax функциясы
бірсарынды. Демек, әрбір х  (-
(- ;+
;+ ) мәніне бір y
) мәніне бір y (0;
(0; )
)
сәйкес келеді, керісінше, әрбір
у (0;
(0;  ) мәніне бір ғана x
) мәніне бір ғана x  (-
(- ; +
; + ) мәні сәйкес келеді, яғни
y=Iogax кері функциясы
бар болады: D(y)=(0;+
) мәні сәйкес келеді, яғни
y=Iogax кері функциясы
бар болады: D(y)=(0;+ ).
).
y=Iogax және
y=Iog x функцияларының графиктерін
салайық.
x функцияларының графиктерін
салайық.
a=2 және a= болғандағы y=Iogax функциясының
графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге
болады. a>1 болғанда : 1) функцияның анықталу облысы оң нақты
сандар жиыны: D(Iogax)=R+.
болғандағы y=Iogax функциясының
графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге
болады. a>1 болғанда : 1) функцияның анықталу облысы оң нақты
сандар жиыны: D(Iogax)=R+.
2) функция мәндерінің жиыны барлық нақты сандар жиыны: Е(Iogax)=R.
3) Функция бүкіл анықталу облысы бойында өседі: x2>x1 болғанда, Iogax2>Iogax1.
4) x (0;1) болғанда Iogx <0; x=1 болғанда Iogx=0;
x
(0;1) болғанда Iogx <0; x=1 болғанда Iogx=0;
x (1;
(1; ) болғанда Iogax>0.
) болғанда Iogax>0.
0<a<1 болғанда :
1) функцияның анықталу облысы барлық оң нақты сандар жиыны:D(Iogax)=R+ .
2) функция мәндерінің жиыны барлық нақты сандар жиыны: Е(Iogax)=R.
3) функция бүкіл анықталу облысы бойынша кемиді: x2>x1 болғанда Iogax2<Iogax1.
4) x (0;1) болғанда Iogax >0; x=1
болғанда Iogax=0;
x
(0;1) болғанда Iogax >0; x=1
болғанда Iogax=0;
x (1;
(1; ) болғанда Iogax<0.
) болғанда Iogax<0.
y=Iogax логарифмдік функциясының маңызды қасиеті – оның бүкіл анықталу облысы бойында үзіліссіздігі.
М ы с а
л.. 1.Log28.
Егер Iog28= десек,онда 2а=8=>2a=23.
десек,онда 2а=8=>2a=23. 10Ig
10Ig .
. ∙ 10Ig
∙ 10Ig .=
.=
 =7.
=7.
2.Логарифмдердің
қасиеттері.1-т е о р е м а.. Екі оң санның
көбейтіндісінің  (a>0,a
(a>0,a 1) негізді логарифмі көбейткіштердің сол негізді
логарифмдердің қосындысына тең:loga(x1x2)=logax1+logax2 (x1>0
x2>0).
1) негізді логарифмі көбейткіштердің сол негізді
логарифмдердің қосындысына тең:loga(x1x2)=logax1+logax2 (x1>0
x2>0).
М ы с а л.log37=a, log34=b.log328-? log328=log3(7∙ 4)=log327+log34=a+b.
2-т е о р е м а. Екі санының
қатынасының  (a>0,a
(a>0,a 1) нкгізді логарифмі оның алымы мен бөлімінің сол
негізді логарифмдерінің айырымына тең:
1) нкгізді логарифмі оның алымы мен бөлімінің сол
негізді логарифмдерінің айырымына тең:
loga =logax1-logax2 (x1>0
=logax1-logax2 (x1>0 x2>0).
x2>0).
М ы с а л..log315=a.log35-?
log35=log3( )=log315-log33=a-1.
)=log315-log33=a-1.
3-т е о р е м а . Дәреженің a негізді
логарифмі көрсеткішті дәреже негізінің логарифміне (а негізді )
көбейткенге тең:Iogaxa= Iogax
(x>0).
Iogax
(x>0).
Дәлелдеуі. logax=y, сонда
х=ay.Осы теңдіктің екі
жағын  дәрежеге шығарайық:х
дәрежеге шығарайық:х =aay.Логарифмнің
анықтамасы бойынша logaxa=
=aay.Логарифмнің
анықтамасы бойынша logaxa= y=
y= logax.
logax.
М ы с а л..log327-?.log33=3log33=3*1=3:
4-т е о р е м а.Оң санның берілген негізді
логарифмі осы санның басқа бір негізді логарифмі мен берілген
негіздің жаңа негізді логарифмінің қатынасына
тең:logax=l
(x>0,a>0,b>0;a 1,b
1,b 1,logba
1,logba 0).
0).
Дәлелдеуі.Негізгі логарифмдік тепе-теңдікті b
негізбен логарифмдейік:аlogax=x=>logaxlogaa=logax=>logax= .Соңғы қатынас а негізді логарифмнен b негізді
логарифмге көшу формуласы деп аталады.
.Соңғы қатынас а негізді логарифмнен b негізді
логарифмге көшу формуласы деп аталады.
Сонымен логарифмнің мынадай қасиеттері бар:
10.alogab=b (b>0, a>0,a 1).
1).
20.loga(x1x2)=logax1+logax2 (x1>0,x2>0,a>0,a 1).
1).
30.loga =logax1-logax2 (x1>0,x2>0,a>0,a
=logax1-logax2 (x1>0,x2>0,a>0,a 1).
1).
40.logaxp=plogax (x>0,a>0,a 1).
1).
50.logax= (Iogba
(Iogba 0,x>0,a
0,x>0,a 1,b>0,b
1,b>0,b 1).
1).
60.logax= (a>0,a
(a>0,a 1,x>0,x
1,x>0,x 1).
1).
70.logaax= logax,logax=loga
logax,logax=loga x
x (x>0,
(x>0,
 0,a>0,a
0,a>0,a 1
1
|
Сабақтың тақырыбы |
Логарифмдік теңдеулерге есептер шығару. |
||||||||||||||||||||||||||||||||||||
|
Сабақтың мақсаты |
Білімділік – логарифмдік теңдеулерді шешуге логарифм қасиеттерін тиімді қолдана білуге үйрету. Дамытушылық – теориялық білімін практикада ұштастыра отырып , ауызша , жазбаша есептеу дағдыларын жетілдіру , топпен , өз бетінше жұмыс жасауға дағдыландыру. Тәрбиелік - оқуға саналы көзқарасқа , өз мүмкіндігіне жете білуге , өз еңбегін бағалай білуге үйрету. Оқушыларды ұқыптылыққа , жауапкершілікке , ұжым намысын қорғауға , мақсатқа жете білуге тәрбиелеу. |
||||||||||||||||||||||||||||||||||||
|
Негізгі идея |
Логарифмнің негізгі қасиеттерін толық меңгерту , логарифмдік теңдеулерді шеше білуге үйрету. |
||||||||||||||||||||||||||||||||||||
|
Табыс критерийі |
Оқушылар логарифмдік теңдеулерді шешуде логарифм қасиеттерін қолдана білуді үйренеді , логарифмдік өрнектері бар тапсырмаларды түрлендіріп есептеуді үйренеді. Логикалық ойлау дағдысын , өз ойын жинақтап , жүйелі жеткізе біледі. |
||||||||||||||||||||||||||||||||||||
|
Модульдер |
СТО |
||||||||||||||||||||||||||||||||||||
|
Әдістер |
Топтық , жұптық , жеке жұмыстар түртіп алу. |
||||||||||||||||||||||||||||||||||||
|
Дерек көзі |
Оқулық , постер , түрлі түсті қағаздар, сызғыш, карандаш, формула т.б. |
||||||||||||||||||||||||||||||||||||
|
Сабақтың барысы |
Мұғалім іс-әрекеті |
Оқушы іс-әрекеті |
|||||||||||||||||||||||||||||||||||
|
Ұйымдастыру кезеңі |
Оқушылармен сәлемдесу Оқушыларды түгелдеу Оқу құралын тексеру Топқа бөлу. Стикер алу арқылы.
Бүгінгі сабақта жақсы нәтижеге жету үшін әрбір кезеңдер ұпаймен есептеледі. Бағалау парағына топ басшылар топ мүшелерін бағалайды. |
Мұғаліммен сәлемдеседі. Оқу құралын алу. Топқа бөліну. |
|||||||||||||||||||||||||||||||||||
|
Миға шабуыл |
Үй жұмысын тексеру сұрақ – жауап арқылы: / № 292/ Өткен сабаққа шолу І- топ. Сәйкестендіру тестімен жұмыс.
№ 1. қосымша ІІ-топ. Балама жауапты тест.
ІІІ- топ.
|
Үй жұмысын тексеру, қойылған сұрақтарға жауап беру. |
|||||||||||||||||||||||||||||||||||
|
Тапсырма |
Есептер шығару. «Домино» ойыны
|
Дәптерге күнді жазады. 1. Х1=-1 , X2 =4 2.Х1=-3 , X2 =-1 3.Х1=-1 4.Х1=1,5, X2 =3 5.Х1=4 6.Х1=1 , 7.Х1=3 8.X=4 9.X=1000, X=1/10 10.X=4, Y=2 |
|||||||||||||||||||||||||||||||||||
|
Топпен жұмыс |
«Жасырын сөзді » табу кезеңі Кестедегі жауаптың тұсына оған сәйкес әріпті қойыңдар.
І-топ.
Lg25+2lg2 2 К Log8(3x-1)=1 x=3 С ІІ-топ. Log212+log25/3+log24/5 4 П Log6(4x+1)<1 (-0,25; 1,25) О (log4243)(log364) 15 7 ІІІ-топ. Lnx=1 e 2 Log3(tgx)=0
Жасырын сөз ЭКСПО-2017 . |
Топ оқушылары жұптасып есепті шығарады. |
|||||||||||||||||||||||||||||||||||
|
Сергіту |
Болашақ кілті білімде. «Білімді болу деген –жаңалық ашуға қабілетті болу» (Әл-Фараби) Арифметика математиканың, ал математика ғылымдарының патшасы (К.Гаусс) Әр ғалым математика дамығанда ғана дами алады. Ғылым нәтижесі ең жаңа заманауи технологиялар мен олардың жұмыс істеу принциптері ЭКСПО-2017 көрмесінде көрсетіледі. «ЭКСПО»- деген не? Бұл – бүкіләлемдік көрме. Индустрияландырудың белгісі және техникалық һәм технологиялық жетістіктерді көрсететін мүмкіндік. «ЭКСПО-2017» 10 маусымда басталып, 10 қыркүйекте аяқталады. Астанадағы көрме «Болашақтың энергиясы» деген атпен өтеді. Ұйымдастырушылар Әлемнің түкпірінен бес миллионға жуық адам келіп қатысады деген болжам жасалып отыр. «ЭКСПО-2017» Дүниежүзілік көрмесінің мақсаты Қазақстанда қайта қалпына келетін энергетиканың алдыңғы қатарлы технологияларын шоғырландыру болып табылады. |
|
|||||||||||||||||||||||||||||||||||
|
Ойлан , бөліс, талқыла |
Логарифмдік өрнектің мәнін есептеніз:
|
Өрнекті есептеудің екі жолын көрсетеді. |
|||||||||||||||||||||||||||||||||||
|
Логикалық тапсырма |
«ҚЫРЫҚ» сөзін неше рет оқуға болады? Қ Ы Р Ы Қ Ы Ы Р Ы Ы Р Р Р Р Р Ы Ы Р Ы Ы Қ Ы Р Ы Қ |
|
|||||||||||||||||||||||||||||||||||
|
Рефлексия |
Кері байланыс: Не білдім? Не ұнады? Не қызықты болды? Не білгім келеді? |
Сабақтан алған әсерін стикерге жазу арқылы әр оқушы өз пікірін білдіреді. (ағашқа іледі) |
|||||||||||||||||||||||||||||||||||
|
Үйге тапсырма |
Келесі өтілетін сабаққа сілтеме № 299 № 230 |
Үйге берілген тапсырманы орындап, келесі сабаққа дайындалып келеді. |
|||||||||||||||||||||||||||||||||||
|
Бағалау |
Бағалау парағы арқылы:
|
Оқушылар алған бағаларын күнделікке қойдырады. |
|||||||||||||||||||||||||||||||||||
Дәреженің және түбірдің логарифмі
Т е о р е м а -1.а негізіндегі хn санының логарифмі n Ioga x-ке тең:
Iog axn = nIogax (мұндағы x>0). Мысалы Iog425=Iog452=2Iog45.
Т е о р е м а -2. а негізіндегі
 санының логарифмі өрнектің
логарифмін
санының логарифмі өрнектің
логарифмін  санына көбейткенге тең:
санына көбейткенге тең:
Мысалы: log2 =
= log2
log2 ; log2
; log2 =
= log227.
log227.
aIogab=b ( мұнда a>0,
a 1, b>0) теңсіздігін логарифм
жөніндегі негізгі теңбе-теңдікке сүйеніп дәлелдейді.
log ab=
1, b>0) теңсіздігін логарифм
жөніндегі негізгі теңбе-теңдікке сүйеніп дәлелдейді.
log ab= теңдігі тура болады.(басқа негізге ауысу
формуласы деп аталады).
теңдігі тура болады.(басқа негізге ауысу
формуласы деп аталады).
Мысалы: log56= ; Cалдар: logab=
; Cалдар: logab= яғни,log813=
яғни,log813= =
= .
.
3.Логарифмдеу және потенциалдау.Жоғарыда көрсетілген теоремалардың негізінде төмендегі екі өзара кері түрлендірулер шығады.
Логарифмдеу-белгісіз айнымалылары бар өрнектердің логарифмін осы айнымалылардың логарифмдерінің қосындыларына түрлендіру.Логарифмдердің қосындылары мен қосындының логарифмін айыра білген жөн.Логарифмдердің қосындысы көбейтіндінің логарифміне тең,ал қосындының логарифмі үшін формула жоқ.
Потенциалдау_- айнымалылардың логарифмдерінің қосындыларын немесе айырымдарын айнымалысы бар өрнектің логарифміне түрлендіру.Потенциалдау – логарифмдеуге кері түрлендіру.
М ы с а
л.1.lgx=4lga-5lgb+( )lgc (a>0,b>0,c>0) x-ті табу
керек.Потенциалдаймыз:lgx=lga4-lgb5+lgc
)lgc (a>0,b>0,c>0) x-ті табу
керек.Потенциалдаймыз:lgx=lga4-lgb5+lgc =lg
=lg ; x=
; x= .
.
"Логарифмдік функция, оның қасиеттері мен графигі"
Мақсаты: логарифмдік функцияның қасиеттері мен графигін зерттеу.
y = ax (a 0, a =/= 1) функциясы a1 монотонды артады; 0 a y мәндері үшін анықталу облысынан аргументтің жалғыз x мәні сәйкес келеді.
|
y = ax, a 1
|
y = ax, 0 a
|
a оң, бірге тең емес сан болсын. Әрбір оң x санына х санының негізі а логарифмі болып табылатын y саны сәйкес келеді, яғни y = logax.
Анықтама. y = logax, (a 0, a =/= 1) функциясы логарифмдік функция деп аталады.
Осылайша:
|
g(x) = ax, a 0, a =/= 1 |
f(x) = logax, a 0, a =/= 1 |
|
D(g) = R |
D(f) =
(0; |
|
E(g) =(
0; |
E(f) = R |
Функцияның анықтамасы бойынша g(x) = ax, a 0, a =/= 1 және f(x) = logax, a 0, a =/= 1 өзара кері болып табылады. Олардың графиктері h(x) = x түзуіне қарағанда симметриялы.
|
|
|
Функциялардың графигін саламыз: f(x) = log2 x, f(x) = log1/2 x.
|
х
|
|
||||||||||||||||||
|
|
||||||||||||||||||
|
|
и |
|
|||||||||||||||||
Логарифмдік функциялардың қасиеттері
|
|
Функцияның қасиеттері |
a 1 |
0 a |
|
1. |
Анықталу облысы |
(0; |
|
|
2. |
Мәндернің жиыны |
(– |
|
|
3. |
Жұп, тақтылығы |
Функция жұп та, тақ та емес |
|
|
4. |
Функция нольдері |
x = 1 болғанда, y = 0 |
|
|
5. |
Таңба тұрақтылығы аралықтары |
x x |
x |
|
6. |
Экстремумы |
Функцияның экстремумдары жоқ |
|
|
7. |
x |
Функция өседі |
Функция кемиді |
|
8. |
Асимптота |
x = 0 |
|
Кестені толтыруда мына тапсырмаларды орындаймыз.
№ 1 тапсырма. Функция үшін х аргументінің мәні мүмкін болады ма?
|
y = logax, a 0, a =/= 1 |
D(y) |
|
y = log5(–x) |
(– |
|
y = log3(x)1/2 |
(0; |
|
y = log2x(x–1) |
(1; |
|
y = log0,5(x2–1) |
(– |
|
y = logx+2(x2 + 1) |
(–2;–1) U(–1; |
|
y = log 0,7 | x | |
(–? ;0) U(0; |
№ 2 тапсырма (таңба тұрақтылығының аралықтары).
y = logax болсын
|
a 1
және x 1 |
y 0 |
|
a 1 и 0 x 0 a x 1 |
y |
1 қорытынды. Егер сан мен логарифмнің негізі бірліктен бір жағында жатса, логарифмдік функцияның мәні оң болады.
2 қорытынды. Егер сан мен логарифмнің негізі бірліктің екі жағында жатса, логарифмдік функцияның мәні теріс болады.
Санның таңбасын анықтаймыз.
|
log23 0 |
2 1 және 3 1 |
|
log50,1 |
5 1 және 0 |
|
log0,31,8 |
0 1 |
|
log0,20,8 0 |
0 |
m санын бірлікпен салыстырамыз, егер:
|
log0,5 m = – 0,5 |
m 1 |
0 |
|
log3 m = 1,5 |
m 1 |
3 1 және 1,5 0 |
|
log0,2 m = 5 |
0 m |
0 0 |
|
log2,4 m = – 0,2 |
0 m |
2,4 1 және – 0,2 |
№ 3 тапсырма. (Монотондылығын зерттеу үшін).
Функциялардың қайсысы өспелі, қайсысы кемімелі болады?
|
y = log2x |
өспелі |
2 1 |
|
y = log0,5(2x + 5) |
кемімелі |
0 |
|
y = lg (x)1/2 |
Өспелі |
10 1 |
|
y = ln(x + 2) |
Өспелі |
e 1 |
а санын бірлікпен салыстырамыз, егер:
|
loga0,2 = 3 |
0 a |
0 0 |
|
loga0,5 loga0,4 |
a 1 |
0,5 0,4 |
|
loga0,8 = – 5 |
a 1 |
0 |
|
loga 2/3 loga1,5 |
0 a |
2/3 |
m және n араларына немесе
|
log0,5 m log0,5 n |
m |
0 |
|
log8 m log8 n |
m n |
8 1 |
|
log2,5 m 2,5 n |
m |
2,5 1 |
|
log0,2 m 0,2 n |
m n |
0 |
Кестені толтырғаннан кейін мына тапсырмаларды қолданамыз.
№ 1 тапсырма.
Мына функциялардың графиктерін бір координаталар жазықтығына салыңдар: g(x) = ln x, h(x) = log5x, f(x)=lg x. Функция графиктерінің координаталар остеріне қатысты орналасуы туралы қорытындылар жасаймыз.
Қорытынды. a 1 болғанда, логарифмдік функцияның негізі неғұрлым үлкен болса, соғұрлым график координата осіне жақын орналасады.
№ 2 тапсырма.
Мына функциялардың графиктерін бір координаталар жазықтығына салыңдар: f(x) = log0,1x, g(x) = log0,3x, h(x) = log0,5x.
Қорытынды.0 a
Сабақтың тақырыбы: Көрсеткіштік функция, оның қасиеттері және графигі
Анықтама.
y=ах, а>0, а≠1 (1)
формуласы арқылы берілген функцияны көрсеткіштік функция деп аталады.
Мұнда а саны көрсеткіштік функцияның негізі, ал тәуелсіз айнымалы х – дәреженің көрсеткіші.
Көрсеткіштік функциясының негізгі қасиеттері:
1) анықталу облысы – барлық оң нақты сандар жиыны, яғни x ϵ R;
2) мәндер жиыны – барлық оң нақты сандар жиыны, яғни y ϵ R;
3) негізі а>1 болғанда, функция – қатаң кемімелі функция;
өспелі, ал 0< а< 1 болғанда, функция – қатаң кемімелі функция;
4) барлық нақты сандар жиынында, яғни х ϵ R-де y=ах( а>0, а≠1) функция үзіліссіз.
Көрсеткіштік функция үшін х және у-тің кез келгеннақты мәндерінде келесі теңдіктер орындалады:
aх ∙
ау ꞊ах+у ау ; ![]() ꞊
ах-у;
(ab)x ꞊aх ∙
bx;
꞊
ах-у;
(ab)x ꞊aх ∙
bx; ![]() ꞊
꞊ ![]() ;
(ах)у꞊аху .
;
(ах)у꞊аху .
Бұл формулалар дәрежелеудің негізгі қасиеттері деп аталады.
Функцияның жоғарыда аталған қасиеттерін дәлелдейік.
Дәлелдеу.
1) негеізі а > 0 болғанда, х-тің кез келген мәні үшін аx дәрежесін есептеуге болады. Олай болса, у꞊ах функциясының анықталуы облысы – нақты сандар жиыны.
2) y=ах а>0, а≠1функциясының мәні кез келген х нқты саны үшін оң сан. Демек, y=ах функциясының мәндер жиыны барлық он нақты сандар жиыны болады.
3) Ox осінің бойынан кез келеген х1 және х2 (х1 < х2) нүктелерін (сандарын) алайық. Сонда осы екі нүктеге сәйкес келетін функция мына мәндерді қабылдайды: у1 ꞊ ах1 , у2 ꞊ах2.
а>1 жағдайында кіші аргументке функцияның кіші мәні, үлкен аргументке функцияның үлкен мәні сәйкес болғандықтан, ах1< ах2.
Осы заңдылық функцияның анықталу облысының жиынындағы кез келген екі нүктесі үшін орындалады, Олай болса, y=ах функциясы а>1 болғанда,қатаң өспелі функция.
Көрсеткіштік функцияның негізі 0 < a < 1 болғанда, жоғарыда айтылған заңдылық керісінше орындалады, кіші аргіментке функцияның үлкен мәні, үокен аргументке функцияның кіші мәні сәйкес болғандықтан, ах1 >ах2. Демек 0 < a < 1аралығында y=ах функциясы – қатаң кемімелі функция.
Мысал ретінде y=3х және у ꞊ функцияларының графиктерін қарастырайық.
I. y=3х функциясының графигін салу үшін келесі кестені құрамыз:
|
Х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y=3х |
|
|
|
1 |
3 |
9 |
27 |
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
1-сурет
(-3; ![]() )
,(-2;
)
,(-2; ![]() )
,(-1;
)
,(-1; ![]() ), (0; 1),
(1;3),(2;9), (3; 27) нүктелерін координаталық жазықтыққа
түсіргеннен кейін, оларды қоссақ, y=3х функциясының
графигіналамыз (1-сурет)
), (0; 1),
(1;3),(2;9), (3; 27) нүктелерін координаталық жазықтыққа
түсіргеннен кейін, оларды қоссақ, y=3х функциясының
графигіналамыз (1-сурет)
Графигтен берілген функцияның қатаң өспелі функция екені көрініп тұр.
ІІ.
y= ![]() фунуциясының
графигін салу үшін келесі кестені құрамыз:
фунуциясының
графигін салу үшін келесі кестені құрамыз:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y= |
27 |
9 |
3 |
1 |
|
|
|
(-3;27), (-2;9),
(-1;3), (0;1), (1; ![]() ),
(2;
),
(2; ![]() ),
(3;
),
(3; ![]() ) нүктелерін
координаталық жазықтыққа түсіріп және оларды қоссақ,
y=
) нүктелерін
координаталық жазықтыққа түсіріп және оларды қоссақ,
y= ![]() функциясының
графигін аламыз (2-сурет)
функциясының
графигін аламыз (2-сурет)

2-сурет
y= ![]()
Графигтен берілген функцияның анықталу облысында қатаң кемімелі екенін көреміз.
Енді y=ах а>0, а≠1 функциясының графигін жалпы түрде берейік.
а>1 болғандағы y=ах а>0, а≠1 функциясының графигі 3 – суретте, ал
0 < a < 1болғандағы – 4-суретте көрсетілген.

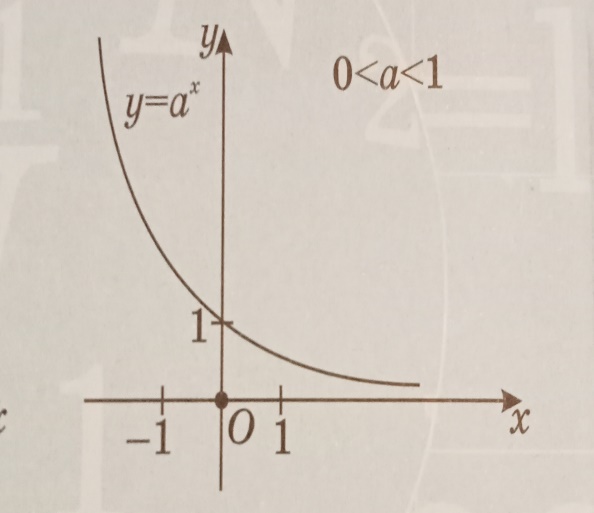
y=ах y=ах
3 – сурет 4-сурет
y=3х және
y= ![]() көрсеткіштік
функцияларының графиктерін бір координаталық жазықтаққа салайық
(5-сурет).
көрсеткіштік
функцияларының графиктерін бір координаталық жазықтаққа салайық
(5-сурет).
![]()
 y=3х
y=3х
|
|
|
|
|
|
суреттен аталған функциялардың графиктері Оу осіне қарағанда симметриялы екені көрініп тұр . Осыдан келесі тұжырымды аламыз: егер екі көрсеткіштік функцияның негіздері өзара кері сандар болса, онда ол функциялардың графиктері Оу осіне қарағанда симметриялы.
4) Көрсеткіштік функцияның үзіліссіздігі дәлелдейік y=ах, а>0, а≠1 функциясы берілген. Аргумент х – ке ∆х өсімше берейік, онда аргумент өсімшесіне сәйкес функция да өсімше қабылдайды:
∆ ах+∆х - ах ∙ а∆х - ах = ах(а∆х -1 ).
![]() Енді осы өсімшенің ∆х 0 ұмтылғандағы
шегін анықтайық:
Енді осы өсімшенің ∆х 0 ұмтылғандағы
шегін анықтайық:
![]() ∆у ах ∙а0-1)
꞊0.
∆у ах ∙а0-1)
꞊0.
Аргументтің шексіз фз өсімшесіне функцияның да шексіз аз өсімшесі сәйкес келеді. Осы заңдылық y=ах функциясы өзінің анықталу облысының кез келген нүктесінде үзіліссіз.
1- м ы с а л. y=5х-1 +1 функциясының графигін салайық.
Шешуі. Алдымен y=5х функциясының графигін салу керек.Ол үшін
а ꞊ 5>1 екенін ескеріп, 26,1-суреті бойынша барлық нақты сандар диынында өспелі функцияның графигін жүргіземіз. Одан кейін салынған графигі Ох осі бойымен бір бірлікке оң бағытта параллель көшіреміз. Шыққан графикті Оу осі бойымен бір бірлікке жоғары параллель көшіреміз (6-сурет).
2 – м ы с а л. 0,274 және 0,2710 сандарын салыстырайық .
Шешуі. Берілген сандардың негізгідері бірдей және 0,27-ге тең. Осы негіздерді бір санымен салыстырамыз: 0,27 <1, бұл жағдайда көрсеткіштік функция кемімелі. Демек , кіші аргументке функцияның үлкен мәні сәйкес. Сондықтан 0,274 >0,2710 .
Жауабы: 0,274 >0,2710 .
3- м ы с а л. y=2х және y=х2 функцияларының графиктері неше нүктеде қиылысатынын анықтайық.
Шешуі. Ол үшін бір координаталық жазықтыққа y=2х және y=х2 функцияларының графигін саламыз. бірінші функция көрсеткіштік функция және негізі 1-ден үлкен . Демек y=2х және y=х2 функцияның графигі (0;1) нүктесі арқылы өтетін және -де өспелі қисық. Ал y=х2 функциясының графигі төбесі (0;0) нүктесі болатын , тармақтары жоғары бағытталған парабола. Графигтер А және В нүктелерінде қиылысады (28-сурет).

Жауабы: екі нүктеде қиылысады
Жаттығулар
А
у ꞊ f(x) функциясының графигін салыңдар (150-151):
1. 1) f(x) ꞊5х ; 2) f(x)꞊1,5х ;
3) f(x)
꞊0,85х 4)
f(x)꞊ ![]() .
.
2. 1)
f(x)꞊ ![]() ; 2)
f(x)꞊
; 2)
f(x)꞊ ![]() ;
;
3)
f(x)꞊ ![]() ; 4) f(x)꞊
135х.
; 4) f(x)꞊
135х.
3. у ꞊ f(x) функциясының мәндер жиынын табыңдар:
1)
f(x)꞊0,24х + 3; 2)
f(x)꞊ ![]() - 2
;
- 2
;
3) f(x)꞊-7х +1; 4) f(x)꞊36х -4.
4. Сандарды салыстырыңдар:
1) 1,83 және 23; 2) 0,82 және 0,54;
3) 0,53 және 0,577; 4) 3,21,6 және 3,21,7;
5) 0,2√2 және 0,21,4 ; 6) 3π және 33,149.
5. 1; 8; 32; 0,25; 0,0625 сандарын 2 санының дәрежересі ретінде жазыңдар.
6.Есептеңдер:
1)
4 1 -
3√2 ∙ 64√2 –
1 ; 2)( ![]() √3)√3;
√3)√3;
3)
49√7 : ![]() ;
4)
;
4) ![]() + 1
:36√5 .
+ 1
:36√5 .
7. Ықшамдаңдар:
1) ![]() ∙
а √3+2 ; 2)
(а√6) ∙
(а√+1 :а √3)
;
∙
а √3+2 ; 2)
(а√6) ∙
(а√+1 :а √3)
;
3)b3.5:
(b√b3) 4)
b √5 ∙b1.4 : ![]() .
.
8. у ꞊ f(x) және у ꞊ g(x) функцияларының графиктері неше нүктеде қиылысатынын анықтаңдар:
1)
f(x)꞊3х және
g(x)꞊3х ; 2)
f(x)꞊ ![]() және
g(x)꞊х2 ;
және
g(x)꞊х2 ;
3)
f(x)꞊7х және g(x)
꞊ ![]() ; 4)
f(x)꞊
; 4)
f(x)꞊ ![]() және
g(x)꞊х3 .
және
g(x)꞊х3 .
В
9. y=ах функциясының графигіне қарапайым түрлендірулер қолданып,
у ꞊ g(x) функциясының графигін салыңдар:
1)
g(x)꞊ ![]() - 2 ; 2)
g(x)꞊ 4х +
3;
- 2 ; 2)
g(x)꞊ 4х +
3;
3) g(x)꞊(2,5)х -1 + 2; 4) g(x)꞊(2,25)х +3 - 4.
10. у ꞊ f(x) функциясның мәндер жиынын табыңдар:
1) f(x)꞊ 4х – 5,6; 2) f(x)꞊(0,35)х + 3;
3) f(x)꞊ 1- 3х .
11. Салыстырыңдар:
1) ((√3)√2)√2 және 3 1,5 ;
2) ![]() және
6-2,25;
және
6-2,25;
3) (7 - 4√3)-3,5 және (7 - 4√3)3,5;
4) (5+2√6)3,3 және (5+2√6)-3,1 .
13. у ꞊ g(x) функциясының ең үлкен және ең кіші мәндерін анықтаңдар:
1) g(x )꞊ 3cosx ; 2) g(x)= 2sinx;
3)
g(x)= ![]() ; 4) g(x)= 4
– 16
; 4) g(x)= 4
– 16 ![]() .
.
14. Егер:
1) b=5 болса,
онда ![]() ∙
∙ ![]() ;
;
2) b꞊ 3 болса ,
онда ![]() ∙
∙ ![]() ;
;
3) b꞊ 2 болса ,
онда ![]() ∙
∙ ![]() ;
;
4) b꞊ 4 болса ,
онда ![]() ∙
∙ ![]() өрнегінің
мәнін табыңдар.
өрнегінің
мәнін табыңдар.
15. у ꞊ f(x) және у ꞊ g(x) функцияларының графиктері неше нүктеде қиылысатынын анықтаңдар:
1) f(x)꞊ 5х және g(x) ꞊6 –х;
2)
f(x)꞊ ![]() және g(x) ꞊3
–х;
және g(x) ꞊3
–х;
3) f(x)꞊ 2х - 2 және g(x) ꞊1 –х;
4) f(x)꞊
3х және g(x)
꞊ ![]() .
.
4.11
Мұғалімдерге арналған əдебиеттер:
-
«Қазақстан Республикасы жалпы орта білім берудің стандарты»
-
Математикадан 5-11 сыныптарға арналған мемлекеттік бағдарлама
-
Тердікбай Күшай «Математика олимпиадасының дайындық курстары» 6- 11 сынып оқу əдістемелік құралы. Астана 2010ж.
-
О.С. Беркімбаев, А.О.Беркімбаева. Арифметика есптері, Алматы
«Рауан», 1996
-
П. Т. Досанбай «Математикалық логика » Алматы «Дəуір» 2011 ж
-
Ə.Н Шыныбеков «Алгебра жəне анализ бастамалары» 10-11 сыныптар
-
И.Ф. Шарыгин, К.О. Бүкүбаева 10-11 сыныптарға арналған оқулық Алматы 2004
-
В.ВЛокоть Параметрі бар теңдеулер.Көрсеткіштік жəне логарифмдік теңдеулер,теңсіздіктер олардың жүйелері. Москва 2005ж
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10- сыныбына арналған оқулық,Алматы. “Мектеп”,2010.
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11- сыныбына арналған оқулық,Алматы. “Мектеп”,2011.
-
М.Л. Галицкий «Углубленное изучение алгебры и математического анализа».- Москва: Просвещение, 1997
-
И.П.Рустюмова, С.Т.Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике»; Алматы 2007;
-
Б.М., Ивлев, А.М Абрамов, Ю.П.Дудницын, С.И. Шварцбурд «Задачи повышенной трудности по алгебре и началам анализа», Москва 1990
-
И.Л. Никольская, В.В. Фирсов, Методика факультативных занятий в 9-10
классах. Избранные вопросы математики. Москва, 1983
-
М.И. Сканави «Полный сборник решений задач для поступающих в вузы. Группа повышенной сложности».- Москва,1999.
-
И.А.Терешин, Т.Н. Терешина «2000 задач по алгебре и началам анализа
10 класс», Москва, 1999
-
И.П.Рустюмова,С.Т.В. Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике» Алматы 2007г; 2011 г, 2013.
-
И.П.Рустюмова,С.Т.В. Рустюмова «Тренажер для подготовки к единому национальному тестированию (ЕНТ) по математике» Алматы 2007; 2011 , 2013.
-
В. Кривоногов «Нестандартные задания по математике».
-
М.И. Абрамович, М.Т. Стародубцев «Математика»
-
И.Ф.Шарыгин, В.И. Голубев «Факультативный курс по математике»
-
М.И. Сканави «Сборник задач по математике для поступающих во ВТУЗы
-
И.Ф.Шарыгин, В.И.Голубев Факультативный курс по математике. Решение задач, Москва: Просвещение, 1991
-
С. И. Колесникова «Математика. Решение сложных задач ЕГЭ» М. Айрис-пресс, 2007
Оқушыларға арналған əдебиеттер:
-
В.ВЛокоть Параметрі бар теңдеулер.Көрсеткіштік жəне логарифмдік теңдеулер,теңсіздіктер олардың жүйелері. Москва 2005ж
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10- сыныбына арналған оқулық,Алматы. “Мектеп”,2010.
-
А.Е.Əбілқасымова жəне т.б. “Алгебра жəне анализ бастамалары”. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11- сыныбына арналған оқулық,Алматы. “Мектеп”,2011
-
И.П.Рустюмова, С.Т.Рустюмова «Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике»; Алматы 2007; 2011
, 2013.
-
И.П.Рустюмова, С.Т. Рустюмова «Тренажер для подготовки к единому национальному тестированию (ЕНТ) по математике» 2011 , 2013.
-
В.С. Крамор «Повторяем и систематизируем школьный курс алгебры и начал анализа». Москва, 1990
-
В.В. Прасолов «Задачи по планиметрии», Москва: МЦНМ.
-
М.И. Шабунин «Пособие по математике для поступающих в вузы».- Москва: Лаборатория Базовых Знаний, 2000.
-
А.Д.Александров, Геометрия 11 сынып. Математиканы тереңдетіп оқитын сыныптар мен мектептердегі оқушыларға арналған оқу құралы.- Москва, Просвещение, 2000.
-
Н.Я. Виленкин Алгебра жəне анализ бастамалары.11сынып. Математиканы тереңдетіп оқитын сыныптар мен мектептердегі оқушыларға арналған оқу құралы ,Москва.:Просвещение,2000.
-
О.Б.Епишева, В.И. Крупич «Учить школьников учиться математике». Москва, 1990г

шағым қалдыра аласыз


 =1-log34
=1-log34

 Э
Э