
Түркістан облысы
Ордабасы ауданы
«Ынтымақ» жалпы білім беретін мектеп»
коммуналдық мемлекеттік мекемесі
Тақырыбы: Рубик текшесінің математикасы
Бағыты: Қолданбалы математика
Орындаушы: Арысбек Мирас
8 сынып оқушысы «Ынтымақ» мектебі
Ордабасы ауданы Түркістан облысы
Жұмыстың жетекшісі: Мырзалиева Нургул Даулетовна «Ынтымақ» жалпы білім беретін мектептің математика пәні мұғалімі
Жұмыс орындалған жыл: 2023-2024 жыл
2024ж
Мазмұны
Аңдатпа
I.Кіріспе
II.Негізгі бөлім
2.1 Рубик текшесі дегеніміз не?
2.2 Рубик текшесінің тарихы
2.3 Рубик текшесін құрастыру әдістері
2.4 Рубик текшесі бойынша өткізілген жарыстар
2.5 Олимпиадалық есептерді шешуде Рубик текшесін қолдану
III. Практикалық бөлім
Қорытынды
IV.Пайдаланылған әдебиеттер
Аңдатпа
Рубик текшесі-әлемдегі ең танымал басқатырғыштардың бірі, ол тек қызықты ғана емес, сонымен қатар бай математикалық әлеуетке ие. Бұл ғылыми жоба топ теориясын, комбинаториканы және оңтайландыруды қоса алғанда, Рубик текшесінің артындағы математиканы зерттейді.
Жоба Рубик текшесімен байланысты негізгі математикалық ұғымдарды қарастырады, мысалы:
Айналдыру және ауыстыру топтары
Шешім алгоритмдері (қабатты қалпына келтіру әдісі, алгебралық әдістер)
Шешілмейтін конфигурациялар мен парадокстар
Алгоритмдерді оңтайландыру және шешімдерді ең аз қозғалыста табу
Жоба сонымен қатар Рубик текшесі математикасының практикалық қосымшаларын зерттейді, мысалы:
Математиканы оқыту және насихаттау
Рубик текшесінің математикасына терең талдау жасай отырып, бұл жоба осы қызықты басқатырғышты түсінуді тереңдетуге және оның пәнаралық сипатын көрсетуге тырысады. Зерттеу жаңа математикалық білім беріп қана қоймайды, сонымен қатар көптеген пәндер бойынша болашақ зерттеулер мен қосымшаларды шабыттандырады.
Аннотация
Кубик Рубика — одна из самых популярных головоломок в мире, которая не только увлекательна, но и содержит богатый математический потенциал. Этот научный проект исследует математику, лежащую в основе кубика Рубика, включая теорию групп, комбинаторику и оптимизацию.
В проекте рассматриваются основные математические концепции, связанные с кубиком Рубика, такие как:
Группы вращений и перестановок
Алгоритмы решения (метод послойного восстановления, алгебраические методы)
Нерешаемые конфигурации и парадоксы
Оптимизация алгоритмов и поиск решений в минимальном количестве ходов
Проект также изучает практические приложения математики кубика Рубика в областях, таких как:
Образование и популяризация математики
Проводя углубленный анализ математики кубика Рубика, этот проект стремится углубить понимание этой увлекательной головоломки и продемонстрировать ее междисциплинарный характер. Исследование не только предоставит новые математические знания, но и вдохновит будущие исследования и применения в широком спектре дисциплин.
Annotation
Rubik's cube is one of the most popular puzzles in the world, which is not only fascinating, but also contains a rich mathematical potential. This research project explores the mathematics behind the Rubik's cube, including group theory, combinatorics, and optimization.
The project examines the basic mathematical concepts related to the Rubik's cube, such as:
Groups of rotations and permutations
Solution algorithms (layer-by-layer reconstruction method, algebraic methods)
Unsolvable configurations and paradoxes
Optimization of algorithms and search for solutions in a minimum number of moves
The project also explores the practical applications of Rubik's cube mathematics in areas such as:
Education and popularization of mathematics
By conducting an in-depth analysis of the mathematics of the Rubik's cube, this project aims to deepen understanding of this fascinating puzzle and demonstrate its interdisciplinary nature. The research will not only provide new mathematical knowledge, but also inspire future research and applications in a wide range of disciplines.
Кіріспе
1974 жылы Венгр мүсіншісі және сәулет профессоры Эрне Рубик ойлап тапқан Рубик текшесі-әлемдегі ең танымал басқатырғыштардың бірі. Ол үш осьтің айналасында айналатын 26 кіші текшеден тұратын үш өлшемді текше. Пазлдың мақсаты-текшені алты Жақтың әрқайсысы бірдей түсті болатындай етіп жинау.
Рубик текшесінің математикасы-бұл математиканың топ теориясы, комбинаторика және алгоритмдер сияқты салаларына әсер ететін күрделі және қызықты зерттеу саласы. Бұл жұмыста біз Рубик текшесінің кейбір математикалық аспектілерін қарастырамыз, соның ішінде:
Рубик текшесінің ықтимал комбинацияларының саны;
Рубик текшесінің симметриясын сипаттайтын математикалық топтар;
Рубик текшесін шешуге арналған Алгоритмдер;
Басқа салалардағы рубик текшесінің математикасының қосымшалары.
Рубик текшесінің математикасын үйрену бізге басқатырғыштың өзін ғана емес, сонымен қатар нақты әлемдегі көптеген басқа объектілер мен құбылыстардың негізінде жатқан негізгі математикалық принциптерді тереңірек түсінуге мүмкіндік береді.
Өзектілігі:Рубик текшесі-барлық жастағы адамдардың назарын аударатын әлемдегі ең танымал басқатырғыштардың бірі. Рубик текшесі өзінің ойын-сауық сипатынан басқа, математикалық зерттеулердің қызықты нысаны болып табылады. Рубик текшесінің математикасын үйрену бізге басқатырғыштың өзін тереңірек түсінуге ғана емес, сонымен қатар нақты әлемдегі көптеген басқа объектілер мен құбылыстардың негізінде жатқан негізгі математикалық принциптерге мүмкіндік береді.
Бұл ғылыми жобаның мақсаты-Рубик текшесінің математикалық аспектілерін зерттеу, соның ішінде:
Рубик текшесінің ықтимал комбинацияларының саны;
Рубик текшесінің симметриясын сипаттайтын математикалық топтар;
Рубик текшесін шешуге арналған Алгоритмдер;
Басқа салалардағы Рубик текшесінің математикасының қосымшалары.
Міндеттері:
-
Мақсатқа жету үшін келесі міндеттерді шешу қажет:
-
Рубик текшесінің математикасындағы бар теориялық нәтижелерді зерттеу;
-
Өз зерттеулеріңізді жасаңыз және жаңа нәтижелерге қол жеткізіңіз;
-
Рубик текшесінің математикасының практикалық қосымшаларын жасаңыз;
-
Зерттеу нәтижелері бойынша ғылыми жарияланымдар мен баяндамалар дайындау.
Гипотеза:Біз рубик текшесінің математикасын ғылым мен техниканың әртүрлі салаларындағы басқа күрделі есептер мен мәселелерді шешу үшін қолдануға болады деп болжаймыз.
Жаңалық:Бұл ғылыми жоба түпнұсқа болып табылады және рубик текшесінің математикасын зерттеуге жаңа үлес қосады. Атап айтқанда, біз жоспарлап отырмыз:
Рубик текшесін шешудің жаңа алгоритмдерін жасау;
Рубик текшесінің жаңа математикалық қасиеттерін зерттеу;
Практикалық маңыздылығы:Осы ғылыми жобаның нәтижелері келесі салаларда практикалық маңызға ие болуы мүмкін:
-
Күрделі есептерді шешудің жаңа алгоритмдері мен әдістерін әзірлеу;
-
Жаңа басқатырғыштар мен ойындар жасау;
-
Математиканы танымал ету және оны зерттеуге жастарды тарту.
Зерттеу әдісі:Қойылған мақсаттарға қол жеткізу және зерттеу міндеттерін шешу үшін мынадай әдістер пайдаланылатын болады:
Теориялық зерттеу: рубик текшесінің математикасындағы бар теориялық нәтижелерді зерттеу, өз зерттеулеріңізді жүргізу және жаңа нәтижелер алу.
Эксперименттік зерттеу: гипотезаларды тексеру және жаңа алгоритмдерді әзірлеу үшін рубик текшесімен эксперименттер жүргізу.
Негізгі бөлім
Рубик текшесі дегеніміз не?
Рубик текшесі, бастапқыда "Сиқырлы текше" деп аталды — 1974 жылы Венгр мүсіншісі және сәулет мұғалімі Эрне Рубик ойлап тапқан механикалық басқатырғыш.
Пазл-бұл 54 көрінетін түсті беттері бар 3×3×3 пластикалық текше (бастапқы нұсқада). Үлкен текшенің беттері текшенің 3 ішкі осінің айналасында айнала алады. Алты беттің әрқайсысы тоғыз шаршыдан тұрады және алты түстің біріне боялған, бір — біріне қарама — қарсы жұпта орналасқан жалпы бояу нұсқаларының бірі: қызыл — қызғылт сары, ақ-сары, көк-жасыл. Бет бұрылыстары түрлі-түсті квадраттарды әртүрлі тәсілдермен қайта реттеуге мүмкіндік береді. Ойыншының міндеті - "Рубик текшесін жинау": текшенің беттерін бұру, оны бастапқы күйіне қайтару, мұнда беттердің әрқайсысы бірдей түсті квадраттардан тұрады.
Рубик текшесінің тарихы
Өнертапқыш бастапқыда қағаз, картон және пластик текшелермен тәжірибе жасады. Инженер 26 элементтен тұратын біртұтас механизм құру міндетін біраз уақыт бойы шешті, онда жеке элементтер құрылымның бірлігіне зиян келтірмей айналады.
Көптеген тапқыр өнертабыстар сияқты, рубик текшесінің де қызықты аңызы бар. Эрне Рубик Дунай жағалауында отырғанда өзеннің су ағындары қиыршық тастарды жылжытатын, қиыршық тастарды бір-біріне соқтығысатын процеске назар аударды, содан кейін олар жаңа пішінге ие болды. Рубик оны таң қалдырды, содан кейін ол эксперименттік текшелерді қайрай бастады.
26 текшеде 156 бет бар. Өнертапқыш олардың жүзден астамын кесіп тастады, болашақ басқатырғыш ойыншықта барлығы 54 қалды. Алты орталық текшеде бір ғана, он екі бүйір текшеде екі, ал сегіз бұрышта 3 бар. Ішкі механизм цилиндр тәрізді. Айналу кезінде механизм Рубик текшесін құрастырумен бірге жүретін ерекше дағдарыс тудырады. Бастапқыда өнертапқыш ойыншықтардың шеттерінде сандар мен сызбаларды бейнелеуді ойлады, бірақ соңында әртүрлі түстерге тоқталды.
Алдымен ғалымның өзі текшені жинады, оған басқатырғышты шешуге шамамен бір ай қажет болды. Енді текшені бүкіл әлем бойынша миллиондаған адамдар жинайды.
1975 жылы 30 қаңтарда Эрне Рубик өзінің өнертабысы "Сиқырлы текше" (Bűvös kocka) үшін Венгр патентін (HU170062) алды.
Рубик текшелерінің алғашқы партиялары 1977 жылдың соңында Будапешт ойыншықтар дүкені үшін шығарылды.
1979 жылы қыркүйекте Будапешттегі келіссөздерде АҚШ-қа миллион текше жеткізу үшін АҚШ-тың ірі ideal Toy Corporation компаниясымен келісім жасалды.
Кеңес Одағында рубик текшесі 1981 жылы пайда болды.
Ол кезде 100 миллионға жуық "заңды текшелер" және одан да көп жалған заттар шығарылды. 80-ші жылдары өркениетті әлемнің әрбір оныншы тұрғыны рубик текшесінің жұмбағын шешті. Оқушылар оны сабақ кезінде парта астында жинады. Мектептерде жылдамдық бойынша "жабық" чемпионаттар өтті. Алғашқы жылдарында оны бір минутта жинай алған аңызға айналған тұлғалар болды.
Көп ұзамай рубик текшесінің басқатырғышына деген қызығушылық күлді.
Бір қызығы, көптеген куберлер текшені беттердің 30-дан аз бұрылыстарымен жинай алады, бірақ математиктер текшені кез-келген бастапқы позициядан 22-ден аспайтын қозғалыспен жеңуге болатын күн келеді деп сенді.
1985 жылы Кремерге тиесілі Seven Towns ағылшын фирмасы текше құқығын сатып алып, 1991 жылы бұл басқатырғышты қайта шығара бастады. 1996 жылы АҚШ-та 300 мың текше сатылды, ал Ұлыбританияда бір жылдан кейін 100 мың текше сатылды.
90-шы жылдары текше Екінші тыныс алды — дербес компьютерлердің пайда болуымен Windows үшін виртуалды Рубик текшесі пайда болды. Компьютерде текше ойнауға мүмкіндік туды. Алайда, рубиктің тірі, нақты, қолтаңбасы сықырлаған текшесі, тіпті бүгінгі күні де сирек кездеседі.
Рубик текшесін құрастыру әдістері
Балалар мен ересектер үшін кейде 3х3 рубик текшесін қалай жинау керектігі қиын болып көрінуі мүмкін.
Қалай "қалай болды"? Ең алдымен, сіз түсінуіңіз керек: кішкентай текшелердің "қарым-қатынасы" ерікті емес, бірақ қатаң тәртіпке негізделген. Текшелердің қатарлары бір — біріне қатысты қанша болса да, бұрыштық текшелер әрқашан бұрыштық, бүйір сүйектері борттық, ал орталық сүйектері орталық болып қалады. Орталық текшелерді орнынан жылжыту мүмкін емес, сондықтан олар ұмтылатын тиісті беттің бастапқы түсін анықтайды.
Бұл мәселеде жаңадан бастаушыларға арналған сурет схемасы-негізгі көмекшілердің бірі.
Рубик текшесін жинау тәжірибесінің алғашқы кезеңдерінде мен бірдей крест әдісін қолдандым. Осы кезде мен беттердің орналасуын және олардың текше жазықтығында қозғалуын дұрыс анықтауды үйрендім. Текшені құрастыру әдістері әртүрлі. Жаңадан бастаушыларға арналған схема 7 кезеңнен тұрады. Бұл басқатырғышты шешкен кезде мен құрастыру процесін сипаттайтын суреттерге сүйендім.
Үлкен текшеде 8 түрлі жерде болуы мүмкін тек 8 бұрыштық текше бар. Біз олардың орналасқан 8 жерін анықтай аламыз, мүмкін болатын тәсілдермен (бірінші текшені 8 бос орынның біріне, екіншісін қалған 7 орынның біріне қою және т. б 8*7*6*5*4*3*2*1=8!)
8 бұрыштық текшенің әрқайсысын 3 жолдың бірімен бұруға болады, тек 38 нұсқа бар.
Осылайша, бұрыштық текшелердің ықтимал орналасуының жалпы саны (8!) (38), бұл 264 539 520-ға тең
"Төрт" деп аталатын бірінші формула:
Біз бірінші бетте сары крест жинаймыз:
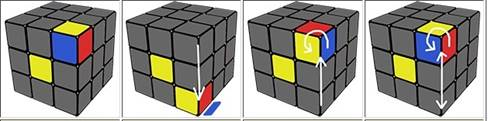
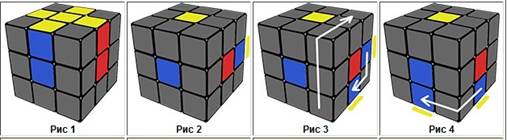
1 сурет 2 сурет 3 сурет 4 сурет
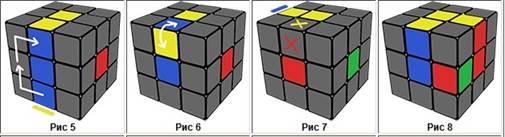
5 сурет 6 сурет 7 сурет 8 сурет
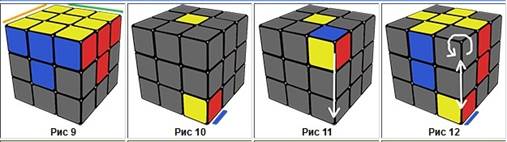
9 сурет 10 сурет 11 сурет 12 сурет
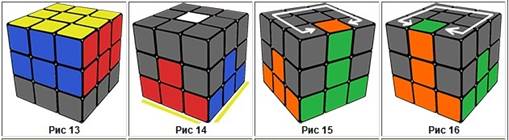
13 сурет 14 сурет 15 сурет 16 сурет

17 сурет 18 сурет 19 сурет 20 сурет
Рубик текшесін бастапқы кресттен жинау принципі онша күрделі емес. Мұнда беттердің орналасуын дұрыс зерттеу керек.
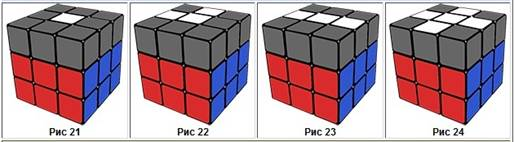
21 сурет 22 сурет 23 сурет 24 сурет
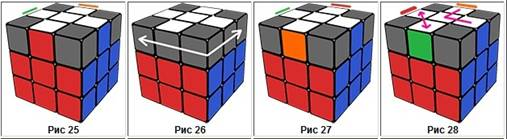
25 сурет 26 сурет 27 сурет 28 сурет
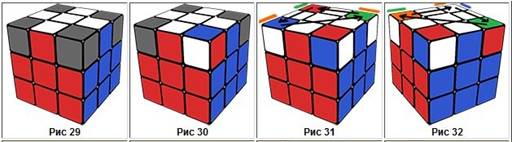
29 сурет 30 сурет 31 сурет 32 сурет
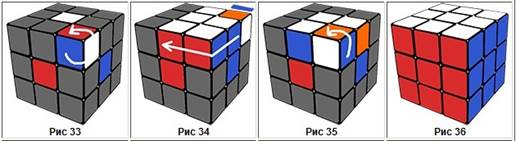
33 сурет 34 сурет 35 сурет 36 сурет
Басқатырғышты шешудің оңтайлы жолы-басқатырғышты шешу үшін ең қысқа қимылдар тізбегін көрсету. Бірнеше оңтайлы шешімдер болуы мүмкін.
Рубик текшесін ерікті конфигурациядан ақырғы конфигурацияға ауыстыруға арналған көптеген алгоритмдер бар (жиналған, барлық беттер бір түсті).
Рубик текшесінің математикасы-бұл текшені құрастыру алгоритмдерін зерттеуге және бағалауға арналған математикалық әдістердің жиынтығы.
Құрастыру алгоритмдері, комбинаторика және ықтималдық
3x3x3 Рубик текшесінің әрқайсысының түсі әртүрлі алты беті бар.
Бірдей түстер әрқашан бір – біріне қарама – қарсы орналасады; стандартты текшеде ақ түс сарыға, қызыл түс қызғылт сарыға, көк түс жасылға қарама-қарсы. Математик және комбинаториктер Рубик текшесін араластырудың жалпы тәсілдерін анықтады: 43 252 003 274 489 856 000. Математикалық формула ретінде бұл санды келесідей көрсетуге болады:
(3 8 8!)(2 12 12!)/12. Бұл формула қалай алынады? Бірінші элемент, 3 8, сегіз бұрыштық текшенің айналуының мүмкін нұсқаларының санын анықтайды.
Бұрыштық текшені үш түрлі жолмен бұруға болатын ойыққа салуға болады. Яғни сегіз бұрыштық текшенің әрқайсысы үшін мультипликатор 3-ке тең. Әрі қарай, біз әр бұрыштық текшенің қозғалысын ескереміз. Барлығы сегіз бұрыштық ойық бар, сондықтан бірінші бұрыштық текшеде сегіз нұсқа. Екінші бұрыштық текшеде жеті нұсқа қалады, сол жақтағы келесі сүйекте алты нұсқа бар және т.б., соңғы бұрыштық текшеге дейін, ол соңғы бұрыштық ойыққа енуі керек.
Бұл 8 факториалды береді!. Осылайша, 3 8 мәні – бұрыштық текшелердің бағыты, ал 8! - олардың жағдайы. Формуланың келесі бөлігінде (2 12 12!)
дәл осы қағида қолданылады, бірақ қазір қабырғалар үшін. Қабырғалардың тек екі бағыты бар, сондықтан 12 қабырғада барлығы 2 12 бағыт болуы мүмкін. Барлығы 12 ереже бар, сондықтан 12! бұл текшелерді осындай позицияларға орналастыруға болатын тәсілдердің санын білдіреді. 12-ге бөлудің қайдан келетінін түсіну үшін Рубик текшесі құрамдас бөліктерге бөлінгенін елестету керек, содан кейін олар кездейсоқ түрде жиналып, барлық текшелерді кездейсоқ ойықтарға қайта енгізеді (бұрыштық текшелерді тек бұрыштарға, ал бүйір текшелерді тек шеттерге орнатуға болады). Біз әдеттегідей көрінетін құрылымды аралас текшені аламыз
және осы сәтте біз осылайша жасалған текшенің барлық мүмкін комбинацияларын есептедік: (3 8 8!)(2 12 12!). Әрекет кезінде
мұндай текшені жинау үшін сіз төмендегі комбинациялардың бірін аласыз.

Көріп отырғаныңыздай, дәл осындай комбинациялар 12. Осылайша, текшені бөлшектеу және текшелерді кездейсоқ жинау ықтималдығы
басқатырғышты шешуге болады, ол 12-ден 1-ге дейін болады. Сондықтан комбинациялардың жалпы санын 12 - ге бөлу керек ,яғни (3 8 8!)(2 12 12!)/12.
Рубик текшесі бойынша өткізілген жарыстар
Рубик текшесін жылдам құрастыруды ұнататын адамдар спидкуберлер деп аталады. Ал жылдамдықты құрастырудың өзі-спидкубинг.
1982 жылы 5 маусымда Будапешт қаласында Рубик кубогын жылдам құрастыру бойынша бірінші дүниежүзілік әлем чемпионаты өтті.
Жеңімпаздар үш әрекеттің ең жақсы уақытын көрсеткендерден анықталды. Олар: АҚШ - тан келген Михн шай бірінші орын-22,95 секунд, екінші орын
бұл орынды Нидерландыдан келген Разоух Шилтс жеңіп алды, ол 24,32 секунд.
Кубикті жылдам құрастыру бойынша бірінші дүниежүзілік чемпионаттың жеңімпаздары Рубиказолтан Лабас Венгриядан 24,49 ұпаймен үшінші орында. Әрине, бұл қазіргі заманғы спидкуберлердің рекордтарынан айтарлықтай ерекшеленеді, бірақ сол кезде және сол Рубик текшелерінің техникалық мүмкіндіктерін ескере отырып, бұл ең жақсы нәтижелер болды.
Рубик текшесін жылдам құрастыру бойынша ресми жарыстарды Дүниежүзілік куб қауымдастығы — World Cube Association (WCA) үнемі өткізеді. Жыл сайын Еуропа чемпионаты немесе Әлем чемпионаты өтеді.
WCA ережелеріне сәйкес, текшелерді жинамас бұрын араластыру керек. Бұл жағдайда барлық қатысушылардың аралас текшенің бастапқы позициялары бірдей болуы керек. Жеңімпаз бірлік құрастыру нәтижесі бойынша емес, 5 әрекеттің орташа уақыты бойынша анықталады, ал ең жақсы және нашар әрекеттер есепке алынбайды, бірақ қалған 3 әрекеттің орташа мәні есептеледі.
2010 жылғы 1-3 қазан аралығында Будапештте Еуропа чемпионаты өтті, оған түрлі пәндер бойынша жарысқа қатысқан қатысушылар жиналды. 3×3×3 классикалық текшені құрастыруда Еуропа чемпионы финалда бұрынғы рекордшы Эрик Аккерсдейкті қоса алғанда,
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Кубик рубиктің математикасы
Кубик рубиктің математикасы
Түркістан облысы
Ордабасы ауданы
«Ынтымақ» жалпы білім беретін мектеп»
коммуналдық мемлекеттік мекемесі
Тақырыбы: Рубик текшесінің математикасы
Бағыты: Қолданбалы математика
Орындаушы: Арысбек Мирас
8 сынып оқушысы «Ынтымақ» мектебі
Ордабасы ауданы Түркістан облысы
Жұмыстың жетекшісі: Мырзалиева Нургул Даулетовна «Ынтымақ» жалпы білім беретін мектептің математика пәні мұғалімі
Жұмыс орындалған жыл: 2023-2024 жыл
2024ж
Мазмұны
Аңдатпа
I.Кіріспе
II.Негізгі бөлім
2.1 Рубик текшесі дегеніміз не?
2.2 Рубик текшесінің тарихы
2.3 Рубик текшесін құрастыру әдістері
2.4 Рубик текшесі бойынша өткізілген жарыстар
2.5 Олимпиадалық есептерді шешуде Рубик текшесін қолдану
III. Практикалық бөлім
Қорытынды
IV.Пайдаланылған әдебиеттер
Аңдатпа
Рубик текшесі-әлемдегі ең танымал басқатырғыштардың бірі, ол тек қызықты ғана емес, сонымен қатар бай математикалық әлеуетке ие. Бұл ғылыми жоба топ теориясын, комбинаториканы және оңтайландыруды қоса алғанда, Рубик текшесінің артындағы математиканы зерттейді.
Жоба Рубик текшесімен байланысты негізгі математикалық ұғымдарды қарастырады, мысалы:
Айналдыру және ауыстыру топтары
Шешім алгоритмдері (қабатты қалпына келтіру әдісі, алгебралық әдістер)
Шешілмейтін конфигурациялар мен парадокстар
Алгоритмдерді оңтайландыру және шешімдерді ең аз қозғалыста табу
Жоба сонымен қатар Рубик текшесі математикасының практикалық қосымшаларын зерттейді, мысалы:
Математиканы оқыту және насихаттау
Рубик текшесінің математикасына терең талдау жасай отырып, бұл жоба осы қызықты басқатырғышты түсінуді тереңдетуге және оның пәнаралық сипатын көрсетуге тырысады. Зерттеу жаңа математикалық білім беріп қана қоймайды, сонымен қатар көптеген пәндер бойынша болашақ зерттеулер мен қосымшаларды шабыттандырады.
Аннотация
Кубик Рубика — одна из самых популярных головоломок в мире, которая не только увлекательна, но и содержит богатый математический потенциал. Этот научный проект исследует математику, лежащую в основе кубика Рубика, включая теорию групп, комбинаторику и оптимизацию.
В проекте рассматриваются основные математические концепции, связанные с кубиком Рубика, такие как:
Группы вращений и перестановок
Алгоритмы решения (метод послойного восстановления, алгебраические методы)
Нерешаемые конфигурации и парадоксы
Оптимизация алгоритмов и поиск решений в минимальном количестве ходов
Проект также изучает практические приложения математики кубика Рубика в областях, таких как:
Образование и популяризация математики
Проводя углубленный анализ математики кубика Рубика, этот проект стремится углубить понимание этой увлекательной головоломки и продемонстрировать ее междисциплинарный характер. Исследование не только предоставит новые математические знания, но и вдохновит будущие исследования и применения в широком спектре дисциплин.
Annotation
Rubik's cube is one of the most popular puzzles in the world, which is not only fascinating, but also contains a rich mathematical potential. This research project explores the mathematics behind the Rubik's cube, including group theory, combinatorics, and optimization.
The project examines the basic mathematical concepts related to the Rubik's cube, such as:
Groups of rotations and permutations
Solution algorithms (layer-by-layer reconstruction method, algebraic methods)
Unsolvable configurations and paradoxes
Optimization of algorithms and search for solutions in a minimum number of moves
The project also explores the practical applications of Rubik's cube mathematics in areas such as:
Education and popularization of mathematics
By conducting an in-depth analysis of the mathematics of the Rubik's cube, this project aims to deepen understanding of this fascinating puzzle and demonstrate its interdisciplinary nature. The research will not only provide new mathematical knowledge, but also inspire future research and applications in a wide range of disciplines.
Кіріспе
1974 жылы Венгр мүсіншісі және сәулет профессоры Эрне Рубик ойлап тапқан Рубик текшесі-әлемдегі ең танымал басқатырғыштардың бірі. Ол үш осьтің айналасында айналатын 26 кіші текшеден тұратын үш өлшемді текше. Пазлдың мақсаты-текшені алты Жақтың әрқайсысы бірдей түсті болатындай етіп жинау.
Рубик текшесінің математикасы-бұл математиканың топ теориясы, комбинаторика және алгоритмдер сияқты салаларына әсер ететін күрделі және қызықты зерттеу саласы. Бұл жұмыста біз Рубик текшесінің кейбір математикалық аспектілерін қарастырамыз, соның ішінде:
Рубик текшесінің ықтимал комбинацияларының саны;
Рубик текшесінің симметриясын сипаттайтын математикалық топтар;
Рубик текшесін шешуге арналған Алгоритмдер;
Басқа салалардағы рубик текшесінің математикасының қосымшалары.
Рубик текшесінің математикасын үйрену бізге басқатырғыштың өзін ғана емес, сонымен қатар нақты әлемдегі көптеген басқа объектілер мен құбылыстардың негізінде жатқан негізгі математикалық принциптерді тереңірек түсінуге мүмкіндік береді.
Өзектілігі:Рубик текшесі-барлық жастағы адамдардың назарын аударатын әлемдегі ең танымал басқатырғыштардың бірі. Рубик текшесі өзінің ойын-сауық сипатынан басқа, математикалық зерттеулердің қызықты нысаны болып табылады. Рубик текшесінің математикасын үйрену бізге басқатырғыштың өзін тереңірек түсінуге ғана емес, сонымен қатар нақты әлемдегі көптеген басқа объектілер мен құбылыстардың негізінде жатқан негізгі математикалық принциптерге мүмкіндік береді.
Бұл ғылыми жобаның мақсаты-Рубик текшесінің математикалық аспектілерін зерттеу, соның ішінде:
Рубик текшесінің ықтимал комбинацияларының саны;
Рубик текшесінің симметриясын сипаттайтын математикалық топтар;
Рубик текшесін шешуге арналған Алгоритмдер;
Басқа салалардағы Рубик текшесінің математикасының қосымшалары.
Міндеттері:
-
Мақсатқа жету үшін келесі міндеттерді шешу қажет:
-
Рубик текшесінің математикасындағы бар теориялық нәтижелерді зерттеу;
-
Өз зерттеулеріңізді жасаңыз және жаңа нәтижелерге қол жеткізіңіз;
-
Рубик текшесінің математикасының практикалық қосымшаларын жасаңыз;
-
Зерттеу нәтижелері бойынша ғылыми жарияланымдар мен баяндамалар дайындау.
Гипотеза:Біз рубик текшесінің математикасын ғылым мен техниканың әртүрлі салаларындағы басқа күрделі есептер мен мәселелерді шешу үшін қолдануға болады деп болжаймыз.
Жаңалық:Бұл ғылыми жоба түпнұсқа болып табылады және рубик текшесінің математикасын зерттеуге жаңа үлес қосады. Атап айтқанда, біз жоспарлап отырмыз:
Рубик текшесін шешудің жаңа алгоритмдерін жасау;
Рубик текшесінің жаңа математикалық қасиеттерін зерттеу;
Практикалық маңыздылығы:Осы ғылыми жобаның нәтижелері келесі салаларда практикалық маңызға ие болуы мүмкін:
-
Күрделі есептерді шешудің жаңа алгоритмдері мен әдістерін әзірлеу;
-
Жаңа басқатырғыштар мен ойындар жасау;
-
Математиканы танымал ету және оны зерттеуге жастарды тарту.
Зерттеу әдісі:Қойылған мақсаттарға қол жеткізу және зерттеу міндеттерін шешу үшін мынадай әдістер пайдаланылатын болады:
Теориялық зерттеу: рубик текшесінің математикасындағы бар теориялық нәтижелерді зерттеу, өз зерттеулеріңізді жүргізу және жаңа нәтижелер алу.
Эксперименттік зерттеу: гипотезаларды тексеру және жаңа алгоритмдерді әзірлеу үшін рубик текшесімен эксперименттер жүргізу.
Негізгі бөлім
Рубик текшесі дегеніміз не?
Рубик текшесі, бастапқыда "Сиқырлы текше" деп аталды — 1974 жылы Венгр мүсіншісі және сәулет мұғалімі Эрне Рубик ойлап тапқан механикалық басқатырғыш.
Пазл-бұл 54 көрінетін түсті беттері бар 3×3×3 пластикалық текше (бастапқы нұсқада). Үлкен текшенің беттері текшенің 3 ішкі осінің айналасында айнала алады. Алты беттің әрқайсысы тоғыз шаршыдан тұрады және алты түстің біріне боялған, бір — біріне қарама — қарсы жұпта орналасқан жалпы бояу нұсқаларының бірі: қызыл — қызғылт сары, ақ-сары, көк-жасыл. Бет бұрылыстары түрлі-түсті квадраттарды әртүрлі тәсілдермен қайта реттеуге мүмкіндік береді. Ойыншының міндеті - "Рубик текшесін жинау": текшенің беттерін бұру, оны бастапқы күйіне қайтару, мұнда беттердің әрқайсысы бірдей түсті квадраттардан тұрады.
Рубик текшесінің тарихы
Өнертапқыш бастапқыда қағаз, картон және пластик текшелермен тәжірибе жасады. Инженер 26 элементтен тұратын біртұтас механизм құру міндетін біраз уақыт бойы шешті, онда жеке элементтер құрылымның бірлігіне зиян келтірмей айналады.
Көптеген тапқыр өнертабыстар сияқты, рубик текшесінің де қызықты аңызы бар. Эрне Рубик Дунай жағалауында отырғанда өзеннің су ағындары қиыршық тастарды жылжытатын, қиыршық тастарды бір-біріне соқтығысатын процеске назар аударды, содан кейін олар жаңа пішінге ие болды. Рубик оны таң қалдырды, содан кейін ол эксперименттік текшелерді қайрай бастады.
26 текшеде 156 бет бар. Өнертапқыш олардың жүзден астамын кесіп тастады, болашақ басқатырғыш ойыншықта барлығы 54 қалды. Алты орталық текшеде бір ғана, он екі бүйір текшеде екі, ал сегіз бұрышта 3 бар. Ішкі механизм цилиндр тәрізді. Айналу кезінде механизм Рубик текшесін құрастырумен бірге жүретін ерекше дағдарыс тудырады. Бастапқыда өнертапқыш ойыншықтардың шеттерінде сандар мен сызбаларды бейнелеуді ойлады, бірақ соңында әртүрлі түстерге тоқталды.
Алдымен ғалымның өзі текшені жинады, оған басқатырғышты шешуге шамамен бір ай қажет болды. Енді текшені бүкіл әлем бойынша миллиондаған адамдар жинайды.
1975 жылы 30 қаңтарда Эрне Рубик өзінің өнертабысы "Сиқырлы текше" (Bűvös kocka) үшін Венгр патентін (HU170062) алды.
Рубик текшелерінің алғашқы партиялары 1977 жылдың соңында Будапешт ойыншықтар дүкені үшін шығарылды.
1979 жылы қыркүйекте Будапешттегі келіссөздерде АҚШ-қа миллион текше жеткізу үшін АҚШ-тың ірі ideal Toy Corporation компаниясымен келісім жасалды.
Кеңес Одағында рубик текшесі 1981 жылы пайда болды.
Ол кезде 100 миллионға жуық "заңды текшелер" және одан да көп жалған заттар шығарылды. 80-ші жылдары өркениетті әлемнің әрбір оныншы тұрғыны рубик текшесінің жұмбағын шешті. Оқушылар оны сабақ кезінде парта астында жинады. Мектептерде жылдамдық бойынша "жабық" чемпионаттар өтті. Алғашқы жылдарында оны бір минутта жинай алған аңызға айналған тұлғалар болды.
Көп ұзамай рубик текшесінің басқатырғышына деген қызығушылық күлді.
Бір қызығы, көптеген куберлер текшені беттердің 30-дан аз бұрылыстарымен жинай алады, бірақ математиктер текшені кез-келген бастапқы позициядан 22-ден аспайтын қозғалыспен жеңуге болатын күн келеді деп сенді.
1985 жылы Кремерге тиесілі Seven Towns ағылшын фирмасы текше құқығын сатып алып, 1991 жылы бұл басқатырғышты қайта шығара бастады. 1996 жылы АҚШ-та 300 мың текше сатылды, ал Ұлыбританияда бір жылдан кейін 100 мың текше сатылды.
90-шы жылдары текше Екінші тыныс алды — дербес компьютерлердің пайда болуымен Windows үшін виртуалды Рубик текшесі пайда болды. Компьютерде текше ойнауға мүмкіндік туды. Алайда, рубиктің тірі, нақты, қолтаңбасы сықырлаған текшесі, тіпті бүгінгі күні де сирек кездеседі.
Рубик текшесін құрастыру әдістері
Балалар мен ересектер үшін кейде 3х3 рубик текшесін қалай жинау керектігі қиын болып көрінуі мүмкін.
Қалай "қалай болды"? Ең алдымен, сіз түсінуіңіз керек: кішкентай текшелердің "қарым-қатынасы" ерікті емес, бірақ қатаң тәртіпке негізделген. Текшелердің қатарлары бір — біріне қатысты қанша болса да, бұрыштық текшелер әрқашан бұрыштық, бүйір сүйектері борттық, ал орталық сүйектері орталық болып қалады. Орталық текшелерді орнынан жылжыту мүмкін емес, сондықтан олар ұмтылатын тиісті беттің бастапқы түсін анықтайды.
Бұл мәселеде жаңадан бастаушыларға арналған сурет схемасы-негізгі көмекшілердің бірі.
Рубик текшесін жинау тәжірибесінің алғашқы кезеңдерінде мен бірдей крест әдісін қолдандым. Осы кезде мен беттердің орналасуын және олардың текше жазықтығында қозғалуын дұрыс анықтауды үйрендім. Текшені құрастыру әдістері әртүрлі. Жаңадан бастаушыларға арналған схема 7 кезеңнен тұрады. Бұл басқатырғышты шешкен кезде мен құрастыру процесін сипаттайтын суреттерге сүйендім.
Үлкен текшеде 8 түрлі жерде болуы мүмкін тек 8 бұрыштық текше бар. Біз олардың орналасқан 8 жерін анықтай аламыз, мүмкін болатын тәсілдермен (бірінші текшені 8 бос орынның біріне, екіншісін қалған 7 орынның біріне қою және т. б 8*7*6*5*4*3*2*1=8!)
8 бұрыштық текшенің әрқайсысын 3 жолдың бірімен бұруға болады, тек 38 нұсқа бар.
Осылайша, бұрыштық текшелердің ықтимал орналасуының жалпы саны (8!) (38), бұл 264 539 520-ға тең
"Төрт" деп аталатын бірінші формула:
Біз бірінші бетте сары крест жинаймыз:


1 сурет 2 сурет 3 сурет 4 сурет

5 сурет 6 сурет 7 сурет 8 сурет

9 сурет 10 сурет 11 сурет 12 сурет

13 сурет 14 сурет 15 сурет 16 сурет

17 сурет 18 сурет 19 сурет 20 сурет
Рубик текшесін бастапқы кресттен жинау принципі онша күрделі емес. Мұнда беттердің орналасуын дұрыс зерттеу керек.

21 сурет 22 сурет 23 сурет 24 сурет

25 сурет 26 сурет 27 сурет 28 сурет

29 сурет 30 сурет 31 сурет 32 сурет

33 сурет 34 сурет 35 сурет 36 сурет
Басқатырғышты шешудің оңтайлы жолы-басқатырғышты шешу үшін ең қысқа қимылдар тізбегін көрсету. Бірнеше оңтайлы шешімдер болуы мүмкін.
Рубик текшесін ерікті конфигурациядан ақырғы конфигурацияға ауыстыруға арналған көптеген алгоритмдер бар (жиналған, барлық беттер бір түсті).
Рубик текшесінің математикасы-бұл текшені құрастыру алгоритмдерін зерттеуге және бағалауға арналған математикалық әдістердің жиынтығы.
Құрастыру алгоритмдері, комбинаторика және ықтималдық
3x3x3 Рубик текшесінің әрқайсысының түсі әртүрлі алты беті бар.
Бірдей түстер әрқашан бір – біріне қарама – қарсы орналасады; стандартты текшеде ақ түс сарыға, қызыл түс қызғылт сарыға, көк түс жасылға қарама-қарсы. Математик және комбинаториктер Рубик текшесін араластырудың жалпы тәсілдерін анықтады: 43 252 003 274 489 856 000. Математикалық формула ретінде бұл санды келесідей көрсетуге болады:
(3 8 8!)(2 12 12!)/12. Бұл формула қалай алынады? Бірінші элемент, 3 8, сегіз бұрыштық текшенің айналуының мүмкін нұсқаларының санын анықтайды.
Бұрыштық текшені үш түрлі жолмен бұруға болатын ойыққа салуға болады. Яғни сегіз бұрыштық текшенің әрқайсысы үшін мультипликатор 3-ке тең. Әрі қарай, біз әр бұрыштық текшенің қозғалысын ескереміз. Барлығы сегіз бұрыштық ойық бар, сондықтан бірінші бұрыштық текшеде сегіз нұсқа. Екінші бұрыштық текшеде жеті нұсқа қалады, сол жақтағы келесі сүйекте алты нұсқа бар және т.б., соңғы бұрыштық текшеге дейін, ол соңғы бұрыштық ойыққа енуі керек.
Бұл 8 факториалды береді!. Осылайша, 3 8 мәні – бұрыштық текшелердің бағыты, ал 8! - олардың жағдайы. Формуланың келесі бөлігінде (2 12 12!)
дәл осы қағида қолданылады, бірақ қазір қабырғалар үшін. Қабырғалардың тек екі бағыты бар, сондықтан 12 қабырғада барлығы 2 12 бағыт болуы мүмкін. Барлығы 12 ереже бар, сондықтан 12! бұл текшелерді осындай позицияларға орналастыруға болатын тәсілдердің санын білдіреді. 12-ге бөлудің қайдан келетінін түсіну үшін Рубик текшесі құрамдас бөліктерге бөлінгенін елестету керек, содан кейін олар кездейсоқ түрде жиналып, барлық текшелерді кездейсоқ ойықтарға қайта енгізеді (бұрыштық текшелерді тек бұрыштарға, ал бүйір текшелерді тек шеттерге орнатуға болады). Біз әдеттегідей көрінетін құрылымды аралас текшені аламыз
және осы сәтте біз осылайша жасалған текшенің барлық мүмкін комбинацияларын есептедік: (3 8 8!)(2 12 12!). Әрекет кезінде
мұндай текшені жинау үшін сіз төмендегі комбинациялардың бірін аласыз.

Көріп отырғаныңыздай, дәл осындай комбинациялар 12. Осылайша, текшені бөлшектеу және текшелерді кездейсоқ жинау ықтималдығы
басқатырғышты шешуге болады, ол 12-ден 1-ге дейін болады. Сондықтан комбинациялардың жалпы санын 12 - ге бөлу керек ,яғни (3 8 8!)(2 12 12!)/12.
Рубик текшесі бойынша өткізілген жарыстар
Рубик текшесін жылдам құрастыруды ұнататын адамдар спидкуберлер деп аталады. Ал жылдамдықты құрастырудың өзі-спидкубинг.
1982 жылы 5 маусымда Будапешт қаласында Рубик кубогын жылдам құрастыру бойынша бірінші дүниежүзілік әлем чемпионаты өтті.
Жеңімпаздар үш әрекеттің ең жақсы уақытын көрсеткендерден анықталды. Олар: АҚШ - тан келген Михн шай бірінші орын-22,95 секунд, екінші орын
бұл орынды Нидерландыдан келген Разоух Шилтс жеңіп алды, ол 24,32 секунд.
Кубикті жылдам құрастыру бойынша бірінші дүниежүзілік чемпионаттың жеңімпаздары Рубиказолтан Лабас Венгриядан 24,49 ұпаймен үшінші орында. Әрине, бұл қазіргі заманғы спидкуберлердің рекордтарынан айтарлықтай ерекшеленеді, бірақ сол кезде және сол Рубик текшелерінің техникалық мүмкіндіктерін ескере отырып, бұл ең жақсы нәтижелер болды.
Рубик текшесін жылдам құрастыру бойынша ресми жарыстарды Дүниежүзілік куб қауымдастығы — World Cube Association (WCA) үнемі өткізеді. Жыл сайын Еуропа чемпионаты немесе Әлем чемпионаты өтеді.
WCA ережелеріне сәйкес, текшелерді жинамас бұрын араластыру керек. Бұл жағдайда барлық қатысушылардың аралас текшенің бастапқы позициялары бірдей болуы керек. Жеңімпаз бірлік құрастыру нәтижесі бойынша емес, 5 әрекеттің орташа уақыты бойынша анықталады, ал ең жақсы және нашар әрекеттер есепке алынбайды, бірақ қалған 3 әрекеттің орташа мәні есептеледі.
2010 жылғы 1-3 қазан аралығында Будапештте Еуропа чемпионаты өтті, оған түрлі пәндер бойынша жарысқа қатысқан қатысушылар жиналды. 3×3×3 классикалық текшені құрастыруда Еуропа чемпионы финалда бұрынғы рекордшы Эрик Аккерсдейкті қоса алғанда,

шағым қалдыра аласыз















