
«Математика мұғалімдерінің пәндік құзыреттерін дамыту»
біліктілікті арттыру курсы бойынша
ҚОРЫТЫНДЫ ЖҰМЫС
Математика мұғалімдеріне арналған
ӘДІСТЕМЕЛІК МАТЕРИАЛ
Бағалау критерийлері:
-
Есептер оқу мақсатына/мақсаттарына сәйкес.
-
Есептер практикалық мазмұнды.
-
Есептердің дұрыс шығару жолы берілген.
-
Есептердің жауабы көрсетілген.
-
Есептерді сабақта пайдалану бойынша әдістемелік ұсыныс берілген.
Математика мұғалімдеріне арналған
ӘДІСТЕМЕЛІК МАТЕРИАЛ
Бұл жинақта курстың оқу жоспары бойынша пәннің оқу бағдарламасындағы оқу мақсаттарын жүзеге асыруға мүмкіндік беретін есептер, оларды шығару және сабақта қолдану тәсілдері туралы мұғалімге арналған ұсыныстар берілген.
Орындаған:
1. Иманова Жанар Алиевна – С.Н.Имашев атындағы жалпы орта мектебінің математика пән мұғалімі.
2. Жубанаева Гульмира Каратаевна- Қадір Мырза Әли атындағы жалпы орта мектебінің математика пән мұғалімі.
3. Мажитова Айгуль Рахметовна- М.Ауезов атындағы жалпы орта мектебінің математика пән мұғалімі.
4. Мажитова Аксулу Сериковна- Ғ.Мүсірепов атындағы жалпы орта мектебінің математика, физика пән мұғалімі.
5. Мәлік Гүлімай Мұқанбедуллақызы- С.Н.Имашев атындағы жалпы орта мектебінің математика пән мұғалімі.
6.Касимова Анаргуль Бахтибекқызы – Қадір Мырза Әли атындағы жалпы орта мектебінің математика пән мұғалімі.
2
|
МАЗМҰНЫ
|
бет |
|
Мәтінді есептерді шығару тәсілдері |
5-7 |
|
Мәтінді есептерді пропорцияның көмегімен шығару. Масштаб, шеңбердің ұзындығын, дөңгелектің ауданын табуға арналған есептер |
|
|
Мәтінді есептерді теңдеу мен теңсіздіктердің көмегімен шығару |
|
|
Негізгі мектептегі статистика және ықтималдықтар теориясы бойынша есептерді шығару әдістері |
8-9 |
|
Комбинаторика элементтері. Комбинаторика формулаларын қолдану арқылы есептер шығару. Ньютон биномы және оның қасиеттері |
|
|
Оқиғалар мен ықтималдыққа байланысты есептерді шығару әдістері. Геометриялық ықтималдықты есеп шығаруда қолдану |
|
|
Математикалық статистика элементтері. Вариациялық қатар. Статистикалық кесте, жиілік алқабы және гистограммамен берілген ақпаратты талдау |
|
|
Математикалық модельдеу және анализ бойынша қолданбалы есептер |
10 |
|
Квадраттық функцияны зерттеумен байланысты қолданбалы есептер |
|
|
Прогрессиямен байланысты мәтінді есептерді шығару тәсілдері |
|
|
Оңтайландырумен байланысты қолданбалы есептер. Теңсіздіктер жүйесін графиктік тәсілмен шешу |
|
|
Планиметрия есептерін шығару |
11 |
|
Үшбұрыштарды шешу. Геометриядағы практикалық есептер |
|
|
Жазықтықтағы векторлар. Векторды қолданып геометриялық есептер шығару |
|
|
Жазықтықтағы түрлендірулер. Жазықтықтағы түрлендіруді қолданып есептер шығару |
|
|
Стереометрия есептерін шығару |
12 |
|
Кеңістік фигураларының бүйір беті мен толық бетінің ауданын табу есептерін шығару тәсілдері. Графикалық редактордың көмегімен көпжақтың жазықтықпен қимасын салу |
|
|
Айналу денелерінің элементтері мен көлемін табуға арналған есептерді шығару әдістері |
|
|
Комплекс сандар. Алгебраның негізгі теоремасы |
13 |
|
Комплекс сандар. Комплекс сандарға арифметикалық амалдар қолдану |
|
|
Комплекс сандар жазықтығы. Комплекс санның модулі |
|
|
Квадрат теңдеулерді комплекс сандар жиынында шешу. Алгебраның негізгі теоремасы |
|
|
Жоғары сыныпта теңдеулер мен теңсіздіктерді шешу әдістері |
14 |
|
Жоғары дәрежелі теңдеулерді шешу әдістері. Үшінші дәрежелі көпмүшеге жалпыланған Виет теоремасын қолдану |
|
|
Иррационал теңдеулер мен теңсіздіктерді шешу әдістері |
|
|
Тригонометриялық теңдеулер мен теңсіздіктерді шешу әдістері |
|
|
Көрсеткіштік және логарифмдік теңдеулер мен теңсіздіктерді шешу |
|
|
Жоғары сыныптағы статистика және ықтималдықтар теориясы |
15-17 |
|
Оқиға ықтималдығы және оның қасиеттері. Ықтималдықтарды қосу және көбейту ережелері |
|
|
Комбинаторика формулаларын қолданып, ықтималдықты табуға есептер шығару. Жуықтап есептеу үшін Ньютон биномын қолдану |
|
|
Толық ықтималдық формуласы. Байес формуласын есеп шығаруда қолдану. Бернулли формуласы мен оның салдарларын есеп шығаруда қолдану |
|
|
Математикалық модельдеу және анализ бойынша жоғары сыныптағы қолданбалы есептер |
18-20 |
|
Туындының физикалық және геометриялық мағынасын пайдаланып қолданбалы есептерді шығару тәсілдері |
|
|
Функцияның ең үлкен (ең кіші) мәнін табуға байланысты қолданбалы есептер |
|
|
Анықталған интегралды жұмыс пен арақашықтықты есептеуге берілген физикалық есептерді шығару үшін қолдану |
|
|
Қолданбалы есептерді шығаруда дифференциалдық теңдеулерді қолдану |
|
|
Қолданылған әдебиеттер |
|
|
Қосымша |
|
Мәтінді есептерді шығару тәсілдері
Тапсырма 1.1
|
Тақырып |
Мәтін есептерді шығару |
|
Оқу мақсаты |
6.1.2.5 пропорцияның негізгі өасиетін білу және қолдану; 6.1.1.2 қандай шамалар тура пропорционалды болатынын түсіну және оларға мысалдар келтіру,есептер шығару; 6.1.1.3 қандай шамалар кері пропорционалды болатынын түсіну және оларға мысалдар келтіру,есептер шығару; 6.5.1.1шамалары тура және кері пропорционалдықпен байланысты есептерді ажырату және шығару; 6.1.2.23 тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру |
|
Есептің шарты |
Құрылыс жүргізу үшін алаңды тазалау керек. Егер осындай алаңды 4 бульдозер 9 сағ-та тазаласа, онда осы алаңды 6 бульдозер қанша сағатта тазалайды? |
|
Есепті шығару жолы |
4 бульд --------9 сағ 6 бульд--------х сағат
Алаңды тазалауға жұмсалатын уақыт бульдозер санына кері пропорционал. Сонда: 4/6 = x/9 x= (4·9):6 = 36:6=6 сағат
Пропорция көмегімен 6 бульдозер 6 сіатта тазалайды |
|
Жауабы |
6 сағат |
|
Әдістемелік Ұсыныс |
Теорияны практикамен байланыстыру.Талдау,нақтылау,ашық сұрақтар арқылы есептің шартын жазу,жауабын анықтау. |
5
Тапсырма 1.2
|
Тема: |
Длина окружности. Площади круга.Шар.Сфера |
|
Цель обучения: |
6.3.3.4 знать и применять формулу площади круга. |
|
Условие задачи: |
Длина радиуса большей окружности равна 21см, длина радиуса меньшей окружности – 16см. Вычислите площадь кольца, образованного этими окружностями. |
|
Решение: |
Допустим, что радиус большей окружности -R2, радиус меньшей окружности-R1. Как мы знаем, формула площади кольца равна
S= то, подставляя все известные нам значения, получим S=
|
|
Ответ: |
185 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО. Можно применять в ГР, ПР. |
6
Тапсырма 1.3
|
Тақырып: |
Санның пайызын табуға мәтінді есептерді шығару |
||||||||||
|
Оқу мақсаты: |
5.5.1.6 пайызға байланысты мәтінді есептерді шығару; |
||||||||||
|
Есептің шарты: |
Есеп 1: Алма ағашы Арманның үйіндегі бақшада алма ағашы өсіп тұр. Сол алма ағашы жылына 20 кг жеміс береді. Арманның ата-анасы Арманға осы алма ағашындағы жемісті өзі пайдалануына рұқсат берді Сұрақ 1: Арман алма ағашындағы жемісті 4 күнде жинап бітірді. Арман бірінші күні күні 3 кг алма, екінші күні барлық теру керек алманың 20%-ын, үшінші күні 25%-ын терді. Берілген кестеге Арманның күніне неше кг алма тергенін жазыңыз. Арман екінші, үшінші және төртінші күндері неше кг алма тергенін анықтаңыз
Сұрақ 2. Арман терілген жемісті сатып өзіне велосипед сатып алмақшы. Магазинде велосипед 17000 теңге, бірақ Арманда 50% жеңілдік бар. Арман велосипед алуы үшін алманың килограмын кем дегенде қанша теңгеге сатуы қажет?
А) 450
|
||||||||||
|
Есепті шығару жолы: |
Сұрақ
1:
20 20-(3+4+5)=8 кг ( төртінші күні)
Сұрақ
2: 17000 8500тг:20=425тг (Алманың 1 кг бағасы) |
||||||||||
|
Жауабы: |
Сұрақ 1: 4кг,5кг, 8 кг Сұрақ 2: 425тг |
||||||||||
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Жұптық, топтық жұмыстарда қолдану |
7
Негізгі мектептегі статистика және ықтималдықтар теориясы бойынша есептерді шығару әдістері
Тапсырма 2.1
|
Тема: |
Элементы комбинаторики и их применение для нахождения вероятности событий. |
|
Цель обучения: |
10.3.1.3 решать задачи, применяя формулы комбинаторики для вычисления числа перестановок, размещений, сочетания без повторений; |
|
Условие задачи: |
Выбирают актив класса из 6 человек, который должен состоять как минимум из 4 девочек и 1 мальчика, выбор производится из 10 девочек и 9 мальчиков. Как много различных вариантов состава актива класс можно предложить? |
|
Решение: |
|
|
Ответ: |
9828 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО. Можно применять в ПР. |
8
Тапсырма 2.2
|
Тақырып: |
Статистикалық деректерді көрсету тәсілдері |
|
Оқу мақсаты: |
5.4.3.3 кесте немесе диаграмма түрінде берілген статистикалық ақпаратты алу |
|
Есептің шарты: |
Жылдық есеп» тапсырмасы. Нұржан айына өзіне есеп береді, яғни барлық шығындары мен тапқан ақшасын есептейді. Ол 2023 жыл бойынша өзіне есеп берді, әр айда тапқан пайдасын тізіп жазды ( төменде көрсетілген). Сұрақ 1: Нұржанның орташа айлық табысы қанша тг? Тапқан табысының өзгеріс ауқымы қанша тг? 215000 283000 255000 257000 301000 213000 277000 242000 263000 252000 315000 289000 Сұрақ 2: Нұржан өзінің айлық шығынын 40 пайызға азайтуды ойлады. Берілген графикте Нұржанның ақшасы қайда жұмсалғаны көрсетілген. Графикті пайдаланып Нұржанға шығынын азайтуға көмектесіңіз
|
|
Есепті шығару жолы: |
Сұрақ 1: (215000+283000+255000+301000+213000+277000+242000+263000+252000+ +315000+289000):12= 263500тг Өзгеріс ауқымы: 315000-213000=102000тг Сұрақ 2: Шығындардың қажеттілігіне қарай отырып, ойын- сауық пен ақылы телеканалдарға шығынды азайтуға болатынын байқауға болады. |
|
Жауабы: |
Сұрақ 1: Орташа айлық табыс: 263500тг, өзгеріс ауқымы: 102000тг. Сұрақ 2: Ойын- сауық пен ақылы телеканалдарға шығын шығармау. |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Топтық және жұптық тапсырма ретінде. |
9
Математикалық модельдеу және анализ бойынша қолданбалы есептер
Тапсырма3.1
|
Тема: |
Текстовые задачи на прогрессии |
|
Цель обучения: |
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями. |
|
Условие задачи: |
Бригада маляров красит забор длиной 640 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 140 метров забора. Определите, сколько дней бригада маляров красила весь забор. |
|
Решение: |
В задаче
фигурирует арифметическая
прогрессия (назовем ее {а
Итак, нам известно:
{ а
Требуется найти n
Воспользуемся формулой
суммы
630=
n=9 |
|
Ответ: |
9 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО . Можно применять в ГР. |
10
Планиметрия есептерін шығару
Тапсырма4.1
|
Тема: |
Решение треугольников Определение синуса, косинуса, тангенса и котангенса |
|
Цель обучения: |
Цели обучения: 8.1.3.2 знать определения синуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике; 8.1.3.24 находить значения sinα, cosα, tgα, ctgα по данному значению одного из них; 8.1.3.21. выводить формулу sin2 + cos2 = 1, используя теорему Пифагора и применять при решении задач; |
|
Условие задачи: |
Вычислите значения синуса, косинуса, тангенса и котангенса отмеченных углов.
b a c |
|
Решение: |
Гипотенуза данного прямоугольного треугольника
равна с=
Найдём искомые тригонометрические
функции:
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно использовать для закрепления темы, также для ФО, СОР |
11
Стереометрия есептерін шығару
Тапсырма 5.1
|
Тема: |
Пирамида |
|
Цель обучения: |
11.1.4 - знать определение пирамиды, ее элементов, виды пирамид; уметь изображать их на плоскости; 11.2.4 - определять расположение проекции вершины пирамиды на плоскость основания; 11.3.3 - решать задачи на нахождение элементов многогранников; |
|
Условие задачи: |
Основанием пирамиды является прямоугольник со
сторонами 3см и 4см. Ее объем равен 16см3. Найдите высоту этой
пирамиды. |
|
Решение: |
Из формулы объема находим
высоту Нам неизвестен площадь основания.S=AB*BC=3*4=12см3
SO= |
|
Ответ: |
4 см |
|
Методические рекомендации по использованию на уроке: |
Задачу можно применять для формативного оценивания после изучения темы. |
12
Комплекс сандар. Алгебраның негізгі теоремасы
Тапсырма 6.1
|
Тема: |
Извлечение квадратного корня из комплексного числа |
|
Цель обучения: |
Цели обучения: 11.1.2.3 - уметь извлекать квадратный корень из комплексного числа;
|
|
Условие задачи: |
Вычислите корень |
|
Решение: |
Преобразуем выражение:
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно предложить на ФО. Для закрепления новой темы. |
13
Жоғары сыныпта теңдеулер мен теңсіздіктерді шешу әдістері
Тапсырма 7.1
|
Тема: |
Методы решения тригонометрических уравнений и неравенств |
|
Цель обучения: |
10.2.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики; 10.2.3.9 - уметь решать тригонометрические уравнения с помощью разложения на множители; 10.2.3.11 - уметь решать тригонометрические уравнения с использованием тригонометрических формул; |
|
Условие задачи: |
Решить уравнение: cos 2 x + sin x · cos x = 1. |
|
Решение: |
Перенесём все члены уравнения влево и преобразуем: cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 , sin x · cos x – sin 2 x = 0 , sin x · ( cos x – sin x ) = 0 ,
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно решать при закреплении темы или ФО. |
Тапсырма 7.2
|
Тақырып: |
Иррационал теңдеулер мен теңсіздіктерді шешу әдістері |
|
Оқу мақсаты: |
11.2.2.2 - теңдеудің екі жағын бірдей n-ші дәрежеге шығару әдісі арқылы иррационал теңдеулерді шеше алу; |
|
Есептің шарты: |
√2х − 1= −2*5 |
|
Есепті шығару жолы: |
Теңдеудің екі жағын бесінші дәрежеге шығарамыз: 2x-1=-32; 2x=-31; x=-15,5. |
|
Жауабы: |
Жауабы: х= -15,5. |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Денгейлік тапсырма ретіңде қолдануға болады |
14
Жоғары сыныптағы статистика және ықтималдықтар теориясы
Тапсырма 8.1
|
Тема: |
Применение бинома Ньютона для приближённых вычислений |
|
Цель обучения: |
10.3.1.5 - применять Бином Ньютона для приближённых вычислений (с натуральным показателем) |
|
Условие задачи: |
Используя формулу бинома Ньютона,
вычислить |
|
Решение: |
По формуле имеем:
остальные слагаемые еще меньше. Поэтому все слагаемые, начиная с третьего, можно отбросить. Тогда
|
|
Ответ: |
1.009 |
|
Методические рекомендации по использованию на уроке: |
Задачу можно предложить для индивидуальной работы . |
15
Тапсырма 8.2
|
Тақырып: |
Ықтималдықтарды қосу және көбейту ережелері |
|
Оқу мақсаты: |
10.2.1.3 - ықтималдықтарды қосу және көбейту ережелерін: * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); түсіну және қолдану; |
|
Есептің шарты: |
Егер 4-тен төмен емес баға алса, курсант ату бойынша сынақты тапсырады. Егер оқ атқаны үшін 0,3 ықтималдықпен 5-ті және 0,6 ықтималдықпен 4-ті алатыны белгілі болса, курсанттың сынақты тапсыру ықтималдығы қандай? |
|
Есепті шығару жолы: |
Бұл тәжірибеде курсант мылтық атып, сол бойынша баға алады. А - «оқ ату бойынша курсант 5 бағасын алды» және В - «оқ ату бойынша курсант 4 бағасын алды» оқиғаларын белгілейміз. Бұл оқиғалар өзара үйлесімсіз оқиғалар. «Сынақ тапсырылды» оқиғасы олардың қосындысы C = A + B болып табылады. Есеп шарты бойынша P(A) = 0,3 және P(B) = 0,6 болады. Онда: Р (?) = ? (? + ?) = ? (?) + ? (?) = 0,3 + 0, 6 = 0,9 |
|
Жауабы: |
0,9 |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Тақырыпты бекітуде қолдануға ұсынылады. |
16
Тапсырма 8.3
|
Тақырып: |
Толық ықтималдық формуласы. Байес формуласын қолданып есеп шығару. Бернулли формуласы мен оның салдарларын есеп шығаруда қолдану |
|
Оқу мақсаты: |
10.3.2.5 - толық ықтималдық формуласын білу және оны есептер шығаруда қолдану; 10.3.2.6 - Байес формуласын білу және оны есептер шығаруда қолдану; 10.3.2.8 - Бернулли формуласы мен оның салдарларын есептер шығаруда қолдану |
|
Есептің шарты: |
. Аспап қалыпты және төтенше жағдайда екі режимде жұмыс істейді. Аспапты пайдалану барысында 80% қалыпты режимде, 20% төтенше режимде жұмыс жасайтыны байқалды. Аспаптың қалыпты жағдайда жұмыс істегенде қандай да бір t уақытта істен шығып қалу ықтималдығы 0,1, ал төтенше жағдайда – 0,7. Аспаптың t уақытта істен шығу ықтималдығын табыңыз. |
|
Есепті шығару жолы: |
Аспаптың істен шығу оқиғасын A арқылы белгілейміз. ?1 − қалыпты жағдайда жұмыс істеу, ?2 − төтенше жағдайда жұмыс істеу. Есептің шарты бойынша ?(?1) = 0,8 , (?(?2) = 0,2 А оқиғасының ықтималдығы (яғни, аспаптың істен шығуы) бірінші оқиғаға (қалыпты режимге) байланысты 0,1-ге тең (?(?/?1 = 0,1); екінші оқиғаға (төтенше режимге) байланысты – 0,7-ге тең (?(?/?2 = 0,7). Осы мәндерді толық ықтималдық формуласына қоямыз: ?(?) = ?(??)?(?/??) + ?(??)?(?/??) ?(?) = 0,8 ∙ 0,1 + 0,2 ∙ 0,7 = 0,22 |
|
Жауабы: |
Жауабы: 0,22 |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Тақырыпты бекітуде қолдануға болады |
17
Тапсырма 9.1
Математикалық модельдеу және анализ бойынша жоғары сыныптағы қолданбалы есептер
|
Тема: |
Предел и непрерывность |
|
Цель обучения: |
10.4.1.11 - находить пределы числовых последовательностей, применяя свойства предела функции на бесконечности; |
|
Условие задачи: |
Найти предел: |
|
Решение: |
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно применить для закрепления новой темы, для СОР. |
18
Тапсырма 9.2
|
Тақырып: |
Айнымалылары ажыратылатын бірінші ретті дифференциалдық теңдеулер |
|
Оқу мақсаты: |
11.3.3.1-физикалық есептерді шығаруда дифференциалдық теңдеулерді қолдану |
|
Есептің шарты: |
Жартылай ыдырау периоды 27 жыл болатын, 8 кг радиактивті цезийден 135 жылдан кейін қалған атомдардың массасы. |
|
Есепті шығару жолы: |
Берілгені: Шешуі:
t= 135 жыл Радиактивті ыдырау заңы мына формуламен анықталады . Мұндағы: N0- бастапқы мезеттегі ядролар саны. N-t мезеттегі ядорлар саны. Т-жартылай ыдырау периоды. Олай болса (1) формуланы мына түрде жазуға болады.
Масса мен электрон саны
бір-біріне пропорционал
болғандықтан:
|
|
Жауабы: |
|
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Дифференциалдық теңдеулер нақты өмірдегі көптеген процестерді сипаттауға қолданылады.Жоғарғы математика курсында дифференциалдық теңдеулерді қарастыру қазіргі таңдағы маманды дайындауға теориялық және қолданбалы негізі бар. |
Тапсырма 9.3
|
Тақырып: |
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы |
|
Оқу мақсаты: |
11.4.2.1. – анықталған интегралды жұмыс пен арақашықтықты есептеуге берілген физикалық есептерді шығару үшін қолдану; |
|
Есептің шарты: |
Серіппе 10 Н күштің әсерінен 0,005 метрге сығылады. Оны 0,03 метрге дейін сығуға жұмсалатын жұмысты табыңыз. |
|
Есепті шығару жолы: |
Гук заңы бойынша F серпімділік күші, х созылуына пропорционал, яғни ? = ??, мұндағы k – пропорционалдық коэффициенті. Шарт бойынша ? = 10Н серіппені ? = 0,005 м созады. 10 = ? ∙ 0,005 ⇒ ? = 2000. Сонда ? = ?? = 2000?. Жұмысты есептейік: 0,03 ? = ∫ 2000??? = 1000?² = 1000 ∙ 0,03² = 0,9Дж 0 |
|
Жауабы: |
0,9 Дж |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Топтық жұмыста физика пәнімен байланыстырып, оқушыларға тапсырманы беруге болады. |
20
Литература:
1. Алгебра и начала анализа 1, 2 часть 10класс ЕМ
А.Е. Абылкасымова , Т.П.Кучер, В.Е., В.Е.Корчевский, З.А.Жумагулова 2019 г
2. Алгебра и начала анализа 11класс ЕМ
А.Е. Абылкасымова , В.Е., В.Е.Корчевский, З.А.Жумагулова 2020г
3. Макарычев Ю. Н., Миндюк Н.Г. Алгебра: элементы статистики и теории вероятностей: учебное пособие для 7-9 классов общеобразовательных учреждений / под ред. С.А. Теляковского. – М.: Просвещение, 2003
4.Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы/ авт. – сост. И.И.Зубарева, А.Г.Мордкович. – М. : Мнемозина, 2007. – 64 с.
5.Алгебра. 9 класс. Задачник для учащихся общеобразовательных учреждений/ под редакцией А.Г.Мордковича. – 11-е изд., стер. – М.: Мнемозина, 2009. – 223с.
6.Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений/ под редакцией А.Г.Мордковича. – 11-е изд., стер. – М.: Мнемозина, 2009. – 224с.
21
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математика мұғалімдеріне арналған ӘДІСТЕМЕЛІК МАТЕРИАЛ. Функционалды сауаттылық тапсырмалары жауаптарымен
Математика мұғалімдеріне арналған ӘДІСТЕМЕЛІК МАТЕРИАЛ. Функционалды сауаттылық тапсырмалары жауаптарымен
«Математика мұғалімдерінің пәндік құзыреттерін дамыту»
біліктілікті арттыру курсы бойынша
ҚОРЫТЫНДЫ ЖҰМЫС
Математика мұғалімдеріне арналған
ӘДІСТЕМЕЛІК МАТЕРИАЛ
Бағалау критерийлері:
-
Есептер оқу мақсатына/мақсаттарына сәйкес.
-
Есептер практикалық мазмұнды.
-
Есептердің дұрыс шығару жолы берілген.
-
Есептердің жауабы көрсетілген.
-
Есептерді сабақта пайдалану бойынша әдістемелік ұсыныс берілген.
Математика мұғалімдеріне арналған
ӘДІСТЕМЕЛІК МАТЕРИАЛ
Бұл жинақта курстың оқу жоспары бойынша пәннің оқу бағдарламасындағы оқу мақсаттарын жүзеге асыруға мүмкіндік беретін есептер, оларды шығару және сабақта қолдану тәсілдері туралы мұғалімге арналған ұсыныстар берілген.
Орындаған:
1. Иманова Жанар Алиевна – С.Н.Имашев атындағы жалпы орта мектебінің математика пән мұғалімі.
2. Жубанаева Гульмира Каратаевна- Қадір Мырза Әли атындағы жалпы орта мектебінің математика пән мұғалімі.
3. Мажитова Айгуль Рахметовна- М.Ауезов атындағы жалпы орта мектебінің математика пән мұғалімі.
4. Мажитова Аксулу Сериковна- Ғ.Мүсірепов атындағы жалпы орта мектебінің математика, физика пән мұғалімі.
5. Мәлік Гүлімай Мұқанбедуллақызы- С.Н.Имашев атындағы жалпы орта мектебінің математика пән мұғалімі.
6.Касимова Анаргуль Бахтибекқызы – Қадір Мырза Әли атындағы жалпы орта мектебінің математика пән мұғалімі.
2
|
МАЗМҰНЫ
|
бет |
|
Мәтінді есептерді шығару тәсілдері |
5-7 |
|
Мәтінді есептерді пропорцияның көмегімен шығару. Масштаб, шеңбердің ұзындығын, дөңгелектің ауданын табуға арналған есептер |
|
|
Мәтінді есептерді теңдеу мен теңсіздіктердің көмегімен шығару |
|
|
Негізгі мектептегі статистика және ықтималдықтар теориясы бойынша есептерді шығару әдістері |
8-9 |
|
Комбинаторика элементтері. Комбинаторика формулаларын қолдану арқылы есептер шығару. Ньютон биномы және оның қасиеттері |
|
|
Оқиғалар мен ықтималдыққа байланысты есептерді шығару әдістері. Геометриялық ықтималдықты есеп шығаруда қолдану |
|
|
Математикалық статистика элементтері. Вариациялық қатар. Статистикалық кесте, жиілік алқабы және гистограммамен берілген ақпаратты талдау |
|
|
Математикалық модельдеу және анализ бойынша қолданбалы есептер |
10 |
|
Квадраттық функцияны зерттеумен байланысты қолданбалы есептер |
|
|
Прогрессиямен байланысты мәтінді есептерді шығару тәсілдері |
|
|
Оңтайландырумен байланысты қолданбалы есептер. Теңсіздіктер жүйесін графиктік тәсілмен шешу |
|
|
Планиметрия есептерін шығару |
11 |
|
Үшбұрыштарды шешу. Геометриядағы практикалық есептер |
|
|
Жазықтықтағы векторлар. Векторды қолданып геометриялық есептер шығару |
|
|
Жазықтықтағы түрлендірулер. Жазықтықтағы түрлендіруді қолданып есептер шығару |
|
|
Стереометрия есептерін шығару |
12 |
|
Кеңістік фигураларының бүйір беті мен толық бетінің ауданын табу есептерін шығару тәсілдері. Графикалық редактордың көмегімен көпжақтың жазықтықпен қимасын салу |
|
|
Айналу денелерінің элементтері мен көлемін табуға арналған есептерді шығару әдістері |
|
|
Комплекс сандар. Алгебраның негізгі теоремасы |
13 |
|
Комплекс сандар. Комплекс сандарға арифметикалық амалдар қолдану |
|
|
Комплекс сандар жазықтығы. Комплекс санның модулі |
|
|
Квадрат теңдеулерді комплекс сандар жиынында шешу. Алгебраның негізгі теоремасы |
|
|
Жоғары сыныпта теңдеулер мен теңсіздіктерді шешу әдістері |
14 |
|
Жоғары дәрежелі теңдеулерді шешу әдістері. Үшінші дәрежелі көпмүшеге жалпыланған Виет теоремасын қолдану |
|
|
Иррационал теңдеулер мен теңсіздіктерді шешу әдістері |
|
|
Тригонометриялық теңдеулер мен теңсіздіктерді шешу әдістері |
|
|
Көрсеткіштік және логарифмдік теңдеулер мен теңсіздіктерді шешу |
|
|
Жоғары сыныптағы статистика және ықтималдықтар теориясы |
15-17 |
|
Оқиға ықтималдығы және оның қасиеттері. Ықтималдықтарды қосу және көбейту ережелері |
|
|
Комбинаторика формулаларын қолданып, ықтималдықты табуға есептер шығару. Жуықтап есептеу үшін Ньютон биномын қолдану |
|
|
Толық ықтималдық формуласы. Байес формуласын есеп шығаруда қолдану. Бернулли формуласы мен оның салдарларын есеп шығаруда қолдану |
|
|
Математикалық модельдеу және анализ бойынша жоғары сыныптағы қолданбалы есептер |
18-20 |
|
Туындының физикалық және геометриялық мағынасын пайдаланып қолданбалы есептерді шығару тәсілдері |
|
|
Функцияның ең үлкен (ең кіші) мәнін табуға байланысты қолданбалы есептер |
|
|
Анықталған интегралды жұмыс пен арақашықтықты есептеуге берілген физикалық есептерді шығару үшін қолдану |
|
|
Қолданбалы есептерді шығаруда дифференциалдық теңдеулерді қолдану |
|
|
Қолданылған әдебиеттер |
|
|
Қосымша |
|
Мәтінді есептерді шығару тәсілдері
Тапсырма 1.1
|
Тақырып |
Мәтін есептерді шығару |
|
Оқу мақсаты |
6.1.2.5 пропорцияның негізгі өасиетін білу және қолдану; 6.1.1.2 қандай шамалар тура пропорционалды болатынын түсіну және оларға мысалдар келтіру,есептер шығару; 6.1.1.3 қандай шамалар кері пропорционалды болатынын түсіну және оларға мысалдар келтіру,есептер шығару; 6.5.1.1шамалары тура және кері пропорционалдықпен байланысты есептерді ажырату және шығару; 6.1.2.23 тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру |
|
Есептің шарты |
Құрылыс жүргізу үшін алаңды тазалау керек. Егер осындай алаңды 4 бульдозер 9 сағ-та тазаласа, онда осы алаңды 6 бульдозер қанша сағатта тазалайды? |
|
Есепті шығару жолы |
4 бульд --------9 сағ 6 бульд--------х сағат
Алаңды тазалауға жұмсалатын уақыт бульдозер санына кері пропорционал. Сонда: 4/6 = x/9 x= (4·9):6 = 36:6=6 сағат
Пропорция көмегімен 6 бульдозер 6 сіатта тазалайды |
|
Жауабы |
6 сағат |
|
Әдістемелік Ұсыныс |
Теорияны практикамен байланыстыру.Талдау,нақтылау,ашық сұрақтар арқылы есептің шартын жазу,жауабын анықтау. |
5
Тапсырма 1.2
|
Тема: |
Длина окружности. Площади круга.Шар.Сфера |
|
Цель обучения: |
6.3.3.4 знать и применять формулу площади круга. |
|
Условие задачи: |
Длина радиуса большей окружности равна 21см, длина радиуса меньшей окружности – 16см. Вычислите площадь кольца, образованного этими окружностями. |
|
Решение: |
Допустим, что радиус большей окружности -R2, радиус меньшей окружности-R1. Как мы знаем, формула площади кольца равна
S= то, подставляя все известные нам значения, получим S=
|
|
Ответ: |
185 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО. Можно применять в ГР, ПР. |
6
Тапсырма 1.3
|
Тақырып: |
Санның пайызын табуға мәтінді есептерді шығару |
||||||||||
|
Оқу мақсаты: |
5.5.1.6 пайызға байланысты мәтінді есептерді шығару; |
||||||||||
|
Есептің шарты: |
Есеп 1: Алма ағашы Арманның үйіндегі бақшада алма ағашы өсіп тұр. Сол алма ағашы жылына 20 кг жеміс береді. Арманның ата-анасы Арманға осы алма ағашындағы жемісті өзі пайдалануына рұқсат берді Сұрақ 1: Арман алма ағашындағы жемісті 4 күнде жинап бітірді. Арман бірінші күні күні 3 кг алма, екінші күні барлық теру керек алманың 20%-ын, үшінші күні 25%-ын терді. Берілген кестеге Арманның күніне неше кг алма тергенін жазыңыз. Арман екінші, үшінші және төртінші күндері неше кг алма тергенін анықтаңыз
Сұрақ 2. Арман терілген жемісті сатып өзіне велосипед сатып алмақшы. Магазинде велосипед 17000 теңге, бірақ Арманда 50% жеңілдік бар. Арман велосипед алуы үшін алманың килограмын кем дегенде қанша теңгеге сатуы қажет?
А) 450
|
||||||||||
|
Есепті шығару жолы: |
Сұрақ
1:
20 20-(3+4+5)=8 кг ( төртінші күні)
Сұрақ
2: 17000 8500тг:20=425тг (Алманың 1 кг бағасы) |
||||||||||
|
Жауабы: |
Сұрақ 1: 4кг,5кг, 8 кг Сұрақ 2: 425тг |
||||||||||
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Жұптық, топтық жұмыстарда қолдану |
7
Негізгі мектептегі статистика және ықтималдықтар теориясы бойынша есептерді шығару әдістері
Тапсырма 2.1
|
Тема: |
Элементы комбинаторики и их применение для нахождения вероятности событий. |
|
Цель обучения: |
10.3.1.3 решать задачи, применяя формулы комбинаторики для вычисления числа перестановок, размещений, сочетания без повторений; |
|
Условие задачи: |
Выбирают актив класса из 6 человек, который должен состоять как минимум из 4 девочек и 1 мальчика, выбор производится из 10 девочек и 9 мальчиков. Как много различных вариантов состава актива класс можно предложить? |
|
Решение: |
|
|
Ответ: |
9828 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО. Можно применять в ПР. |
8
Тапсырма 2.2
|
Тақырып: |
Статистикалық деректерді көрсету тәсілдері |
|
Оқу мақсаты: |
5.4.3.3 кесте немесе диаграмма түрінде берілген статистикалық ақпаратты алу |
|
Есептің шарты: |
Жылдық есеп» тапсырмасы. Нұржан айына өзіне есеп береді, яғни барлық шығындары мен тапқан ақшасын есептейді. Ол 2023 жыл бойынша өзіне есеп берді, әр айда тапқан пайдасын тізіп жазды ( төменде көрсетілген). Сұрақ 1: Нұржанның орташа айлық табысы қанша тг? Тапқан табысының өзгеріс ауқымы қанша тг? 215000 283000 255000 257000 301000 213000 277000 242000 263000 252000 315000 289000 Сұрақ 2: Нұржан өзінің айлық шығынын 40 пайызға азайтуды ойлады. Берілген графикте Нұржанның ақшасы қайда жұмсалғаны көрсетілген. Графикті пайдаланып Нұржанға шығынын азайтуға көмектесіңіз
|
|
Есепті шығару жолы: |
Сұрақ 1: (215000+283000+255000+301000+213000+277000+242000+263000+252000+ +315000+289000):12= 263500тг Өзгеріс ауқымы: 315000-213000=102000тг Сұрақ 2: Шығындардың қажеттілігіне қарай отырып, ойын- сауық пен ақылы телеканалдарға шығынды азайтуға болатынын байқауға болады. |
|
Жауабы: |
Сұрақ 1: Орташа айлық табыс: 263500тг, өзгеріс ауқымы: 102000тг. Сұрақ 2: Ойын- сауық пен ақылы телеканалдарға шығын шығармау. |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Топтық және жұптық тапсырма ретінде. |
9
Математикалық модельдеу және анализ бойынша қолданбалы есептер
Тапсырма3.1
|
Тема: |
Текстовые задачи на прогрессии |
|
Цель обучения: |
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями. |
|
Условие задачи: |
Бригада маляров красит забор длиной 640 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 140 метров забора. Определите, сколько дней бригада маляров красила весь забор. |
|
Решение: |
В задаче
фигурирует арифметическая
прогрессия (назовем ее {а
Итак, нам известно:
{ а
Требуется найти n
Воспользуемся формулой
суммы
630=
n=9 |
|
Ответ: |
9 |
|
Методические рекомендации по использованию на уроке: |
Применяем как задание ФО . Можно применять в ГР. |
10
Планиметрия есептерін шығару
Тапсырма4.1
|
Тема: |
Решение треугольников Определение синуса, косинуса, тангенса и котангенса |
|
Цель обучения: |
Цели обучения: 8.1.3.2 знать определения синуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике; 8.1.3.24 находить значения sinα, cosα, tgα, ctgα по данному значению одного из них; 8.1.3.21. выводить формулу sin2 + cos2 = 1, используя теорему Пифагора и применять при решении задач; |
|
Условие задачи: |
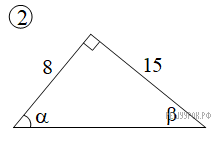
Вычислите значения синуса, косинуса, тангенса и котангенса отмеченных углов.
b a c |
|
Решение: |
Гипотенуза данного прямоугольного треугольника
равна с=
Найдём искомые тригонометрические
функции:
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно использовать для закрепления темы, также для ФО, СОР |
11
Стереометрия есептерін шығару
Тапсырма 5.1
|
Тема: |
Пирамида |
|
Цель обучения: |
11.1.4 - знать определение пирамиды, ее элементов, виды пирамид; уметь изображать их на плоскости; 11.2.4 - определять расположение проекции вершины пирамиды на плоскость основания; 11.3.3 - решать задачи на нахождение элементов многогранников; |
|
Условие задачи: |
Основанием пирамиды является прямоугольник со
сторонами 3см и 4см. Ее объем равен 16см3. Найдите высоту этой
пирамиды. |
|
Решение: |
Из формулы объема находим
высоту Нам неизвестен площадь основания.S=AB*BC=3*4=12см3
SO= |
|
Ответ: |
4 см |
|
Методические рекомендации по использованию на уроке: |
Задачу можно применять для формативного оценивания после изучения темы. |
12
Комплекс сандар. Алгебраның негізгі теоремасы
Тапсырма 6.1
|
Тема: |
Извлечение квадратного корня из комплексного числа |
|
Цель обучения: |
Цели обучения: 11.1.2.3 - уметь извлекать квадратный корень из комплексного числа;
|
|
Условие задачи: |
Вычислите корень |
|
Решение: |
Преобразуем выражение:
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно предложить на ФО. Для закрепления новой темы. |
13
Жоғары сыныпта теңдеулер мен теңсіздіктерді шешу әдістері
Тапсырма 7.1
|
Тема: |
Методы решения тригонометрических уравнений и неравенств |
|
Цель обучения: |
10.2.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики; 10.2.3.9 - уметь решать тригонометрические уравнения с помощью разложения на множители; 10.2.3.11 - уметь решать тригонометрические уравнения с использованием тригонометрических формул; |
|
Условие задачи: |
Решить уравнение: cos 2 x + sin x · cos x = 1. |
|
Решение: |
Перенесём все члены уравнения влево и преобразуем: cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 , sin x · cos x – sin 2 x = 0 , sin x · ( cos x – sin x ) = 0 ,
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно решать при закреплении темы или ФО. |
Тапсырма 7.2
|
Тақырып: |
Иррационал теңдеулер мен теңсіздіктерді шешу әдістері |
|
Оқу мақсаты: |
11.2.2.2 - теңдеудің екі жағын бірдей n-ші дәрежеге шығару әдісі арқылы иррационал теңдеулерді шеше алу; |
|
Есептің шарты: |
√2х − 1= −2*5 |
|
Есепті шығару жолы: |
Теңдеудің екі жағын бесінші дәрежеге шығарамыз: 2x-1=-32; 2x=-31; x=-15,5. |
|
Жауабы: |
Жауабы: х= -15,5. |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Денгейлік тапсырма ретіңде қолдануға болады |
14
Жоғары сыныптағы статистика және ықтималдықтар теориясы
Тапсырма 8.1
|
Тема: |
Применение бинома Ньютона для приближённых вычислений |
|
Цель обучения: |
10.3.1.5 - применять Бином Ньютона для приближённых вычислений (с натуральным показателем) |
|
Условие задачи: |
Используя формулу бинома Ньютона,
вычислить |
|
Решение: |
По формуле имеем:
остальные слагаемые еще меньше. Поэтому все слагаемые, начиная с третьего, можно отбросить. Тогда
|
|
Ответ: |
1.009 |
|
Методические рекомендации по использованию на уроке: |
Задачу можно предложить для индивидуальной работы . |
15
Тапсырма 8.2
|
Тақырып: |
Ықтималдықтарды қосу және көбейту ережелері |
|
Оқу мақсаты: |
10.2.1.3 - ықтималдықтарды қосу және көбейту ережелерін: * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); түсіну және қолдану; |
|
Есептің шарты: |
Егер 4-тен төмен емес баға алса, курсант ату бойынша сынақты тапсырады. Егер оқ атқаны үшін 0,3 ықтималдықпен 5-ті және 0,6 ықтималдықпен 4-ті алатыны белгілі болса, курсанттың сынақты тапсыру ықтималдығы қандай? |
|
Есепті шығару жолы: |
Бұл тәжірибеде курсант мылтық атып, сол бойынша баға алады. А - «оқ ату бойынша курсант 5 бағасын алды» және В - «оқ ату бойынша курсант 4 бағасын алды» оқиғаларын белгілейміз. Бұл оқиғалар өзара үйлесімсіз оқиғалар. «Сынақ тапсырылды» оқиғасы олардың қосындысы C = A + B болып табылады. Есеп шарты бойынша P(A) = 0,3 және P(B) = 0,6 болады. Онда: Р (?) = ? (? + ?) = ? (?) + ? (?) = 0,3 + 0, 6 = 0,9 |
|
Жауабы: |
0,9 |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Тақырыпты бекітуде қолдануға ұсынылады. |
16
Тапсырма 8.3
|
Тақырып: |
Толық ықтималдық формуласы. Байес формуласын қолданып есеп шығару. Бернулли формуласы мен оның салдарларын есеп шығаруда қолдану |
|
Оқу мақсаты: |
10.3.2.5 - толық ықтималдық формуласын білу және оны есептер шығаруда қолдану; 10.3.2.6 - Байес формуласын білу және оны есептер шығаруда қолдану; 10.3.2.8 - Бернулли формуласы мен оның салдарларын есептер шығаруда қолдану |
|
Есептің шарты: |
. Аспап қалыпты және төтенше жағдайда екі режимде жұмыс істейді. Аспапты пайдалану барысында 80% қалыпты режимде, 20% төтенше режимде жұмыс жасайтыны байқалды. Аспаптың қалыпты жағдайда жұмыс істегенде қандай да бір t уақытта істен шығып қалу ықтималдығы 0,1, ал төтенше жағдайда – 0,7. Аспаптың t уақытта істен шығу ықтималдығын табыңыз. |
|
Есепті шығару жолы: |
Аспаптың істен шығу оқиғасын A арқылы белгілейміз. ?1 − қалыпты жағдайда жұмыс істеу, ?2 − төтенше жағдайда жұмыс істеу. Есептің шарты бойынша ?(?1) = 0,8 , (?(?2) = 0,2 А оқиғасының ықтималдығы (яғни, аспаптың істен шығуы) бірінші оқиғаға (қалыпты режимге) байланысты 0,1-ге тең (?(?/?1 = 0,1); екінші оқиғаға (төтенше режимге) байланысты – 0,7-ге тең (?(?/?2 = 0,7). Осы мәндерді толық ықтималдық формуласына қоямыз: ?(?) = ?(??)?(?/??) + ?(??)?(?/??) ?(?) = 0,8 ∙ 0,1 + 0,2 ∙ 0,7 = 0,22 |
|
Жауабы: |
Жауабы: 0,22 |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Тақырыпты бекітуде қолдануға болады |
17
Тапсырма 9.1
Математикалық модельдеу және анализ бойынша жоғары сыныптағы қолданбалы есептер
|
Тема: |
Предел и непрерывность |
|
Цель обучения: |
10.4.1.11 - находить пределы числовых последовательностей, применяя свойства предела функции на бесконечности; |
|
Условие задачи: |
Найти предел: |
|
Решение: |
|
|
Ответ: |
|
|
Методические рекомендации по использованию на уроке: |
Задачу можно применить для закрепления новой темы, для СОР. |
18
Тапсырма 9.2
|
Тақырып: |
Айнымалылары ажыратылатын бірінші ретті дифференциалдық теңдеулер |
|
Оқу мақсаты: |
11.3.3.1-физикалық есептерді шығаруда дифференциалдық теңдеулерді қолдану |
|
Есептің шарты: |
Жартылай ыдырау периоды 27 жыл болатын, 8 кг радиактивті цезийден 135 жылдан кейін қалған атомдардың массасы. |
|
Есепті шығару жолы: |
Берілгені: Шешуі:
t= 135 жыл Радиактивті ыдырау заңы мына формуламен анықталады . Мұндағы: N0- бастапқы мезеттегі ядролар саны. N-t мезеттегі ядорлар саны. Т-жартылай ыдырау периоды. Олай болса (1) формуланы мына түрде жазуға болады.
Масса мен электрон саны
бір-біріне пропорционал
болғандықтан:
|
|
Жауабы: |
|
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Дифференциалдық теңдеулер нақты өмірдегі көптеген процестерді сипаттауға қолданылады.Жоғарғы математика курсында дифференциалдық теңдеулерді қарастыру қазіргі таңдағы маманды дайындауға теориялық және қолданбалы негізі бар. |
Тапсырма 9.3
|
Тақырып: |
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы |
|
Оқу мақсаты: |
11.4.2.1. – анықталған интегралды жұмыс пен арақашықтықты есептеуге берілген физикалық есептерді шығару үшін қолдану; |
|
Есептің шарты: |
Серіппе 10 Н күштің әсерінен 0,005 метрге сығылады. Оны 0,03 метрге дейін сығуға жұмсалатын жұмысты табыңыз. |
|
Есепті шығару жолы: |
Гук заңы бойынша F серпімділік күші, х созылуына пропорционал, яғни ? = ??, мұндағы k – пропорционалдық коэффициенті. Шарт бойынша ? = 10Н серіппені ? = 0,005 м созады. 10 = ? ∙ 0,005 ⇒ ? = 2000. Сонда ? = ?? = 2000?. Жұмысты есептейік: 0,03 ? = ∫ 2000??? = 1000?² = 1000 ∙ 0,03² = 0,9Дж 0 |
|
Жауабы: |
0,9 Дж |
|
Сабақта пайдалану бойынша әдістемелік ұсыныс: |
Топтық жұмыста физика пәнімен байланыстырып, оқушыларға тапсырманы беруге болады. |
20
Литература:
1. Алгебра и начала анализа 1, 2 часть 10класс ЕМ
А.Е. Абылкасымова , Т.П.Кучер, В.Е., В.Е.Корчевский, З.А.Жумагулова 2019 г
2. Алгебра и начала анализа 11класс ЕМ
А.Е. Абылкасымова , В.Е., В.Е.Корчевский, З.А.Жумагулова 2020г
3. Макарычев Ю. Н., Миндюк Н.Г. Алгебра: элементы статистики и теории вероятностей: учебное пособие для 7-9 классов общеобразовательных учреждений / под ред. С.А. Теляковского. – М.: Просвещение, 2003
4.Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы/ авт. – сост. И.И.Зубарева, А.Г.Мордкович. – М. : Мнемозина, 2007. – 64 с.
5.Алгебра. 9 класс. Задачник для учащихся общеобразовательных учреждений/ под редакцией А.Г.Мордковича. – 11-е изд., стер. – М.: Мнемозина, 2009. – 223с.
6.Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений/ под редакцией А.Г.Мордковича. – 11-е изд., стер. – М.: Мнемозина, 2009. – 224с.
21

шағым қалдыра аласыз



 21
21 см2
см2




 }), так как бригада ежедневно
увеличивала норму покраски на одно и то же число
метров. Индекс
}), так как бригада ежедневно
увеличивала норму покраски на одно и то же число
метров. Индекс  =140
=140 сумма первых n членов арифметической
прогрессии.
сумма первых n членов арифметической
прогрессии.
 ;
; 

 = 17 (по теореме
Пифагора).
= 17 (по теореме
Пифагора).









 .
.
 см.
см.


 2)
2) 



 Оценим третье слагаемое в
этой сумме.
Оценим третье слагаемое в
этой сумме.












 )
)
 )
т
)
т

















