Баяндама
Тақырыбы: Математика сабақтарында «Geogebra» бағдарламасын қолданудың тиімділігі
Геогебра» бағдарламасы туралы түсініктер:
Геогебра – Тегін таратылатын математикалық , (www.geogebra.org) геометрия және алгебраны байланыстыратын компьютерлік интерактивті бағдарлама. Қазіргі таңда әлем бойынша ең көп таралған математикалық бағдарлама ретінде танылып отыр. 149 елде қолданылып жатыр, 49 тілге аударылған. Авторы – австриялық математик Маркус Хохенвартер. 2009 бұл бағдарлама үшін арнайы байқаудың жеңімпазы атанды. Сол жылдың тамызында оның үш өлшемді нұсқасы шықты. Бұл бағдарлама әлем бойынша кең таралған. Орталығы Австрия мемлекетінде орналасқан. Геогебраның басқа мемлекеттерде дамыту жергілікті мұғалімдер арқылы жүзеге асырылады: бағдарлама жергілікті тілге аударылады, Геогебра институттары ашылып, сол институттар арқылы бағдарлама әрі қарай дамытылып, интерактивті нұсқалар дайындалады, үйретуші бейнекөріністер жазылады, қолданушы кітапшалары жазылады, әрі басқа елдердегі
мұғалімдермен Геогебра бағдарламасы бойынша тәжірибе алмасу іске асырылады.Қазіргі уақытта Геогебраны қазақ тіліне аударып жүрген Қостанайлық математик Талғат Байназаров .
Қазақ интернетінің дамуына үлес қосып жүрген Талғат Байназаров Қостанай қаласындағы С. Мәуленов атындағы гимназияның математика пәні мұғалімі.Ғаламторда «Математика және мультимедия» атты блог жүргізеді.
Мен сіздерге өзім қолданып жүрген сабақтардан бірнеше мысалдар келтірейін.
Геогебраның негізгі терезелеріне тоқтала кетсек,бағдарламаны ашып алғаннан кейін кез-келген терезені ашып алып,(төменде көрсетілгендей) керекті есепті шеше аламыз.
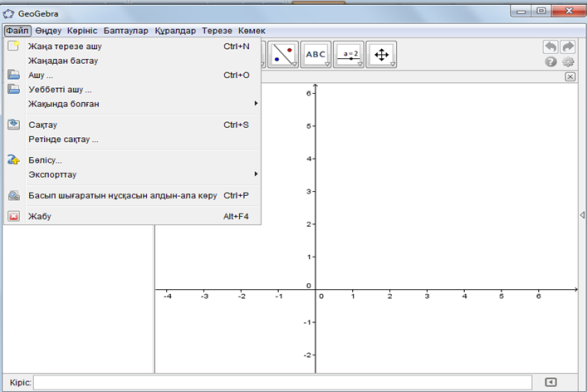
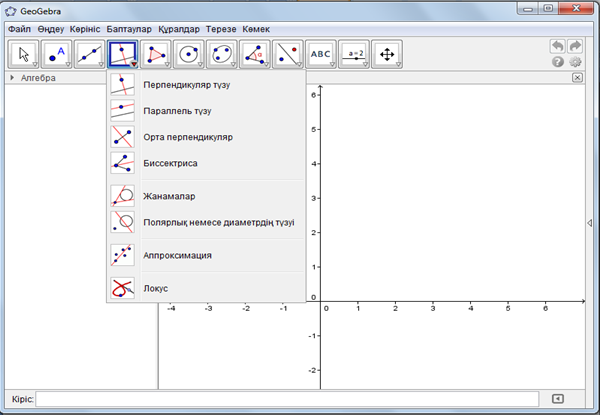
1-мысал:Теңдеулер жүйесін ГеоГебрада шешу.
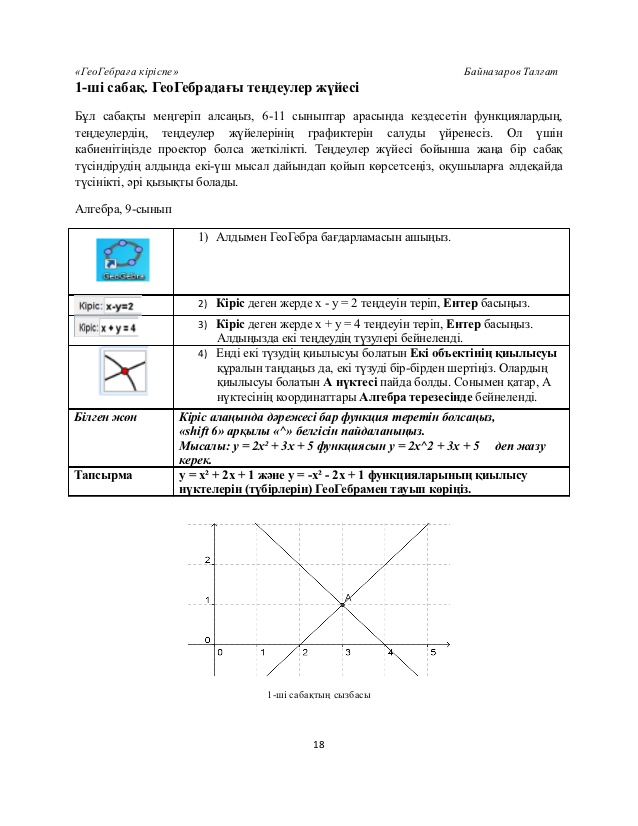
Бұл сабақты меңгеру арқылы сіз 6-11 сыныптардағы теңдеулер мен теңдеулер жүйесін, сол сияқты олардың графиктерін салуды үйренесіз.Теңдеулер жүйесі бойынша жаңа сабақ түсіндірмес бұрын алдында бір-екі мысал дайындап қойып «ойнау» батырмасымен көрсетсеңіз, оқушыларға әлдеқайда түсінікті әрі қызықты болады.Мысал келтірейік:Алгебра 9 сынып.
|
|
|
|
Кіріс: х-у=3 |
2)Кіріс деген жерде х-у=2теңдеуін жазып, Ентер басыңыз. |
|
Кіріс: х+у=4 |
3) Кіріс деген жерде х+у=4 теңдеуін жазып, Ентер басыңыз. |
|
|
3)Енді екі түзудің қиылысуы болатын Екі объектінің қиылысуы құралын таңдаңыз да, екі түзуді бәр-бірден шертіңіз.Олардың қиылысуы болатын А нүктесі пайда болады.Сонымен қатар А нүктесінің координаталары Алгебра терезесінде көрінеді. |
|
Ескерту
|
Кіріс алаңына кез-келген функцияны теруүшін Көрініс терезесінен Пернетақта құралын пайдаланған дұрыс. |
2-мысал:Графиктерді түрлендіруді ГеоГебрада орындау.
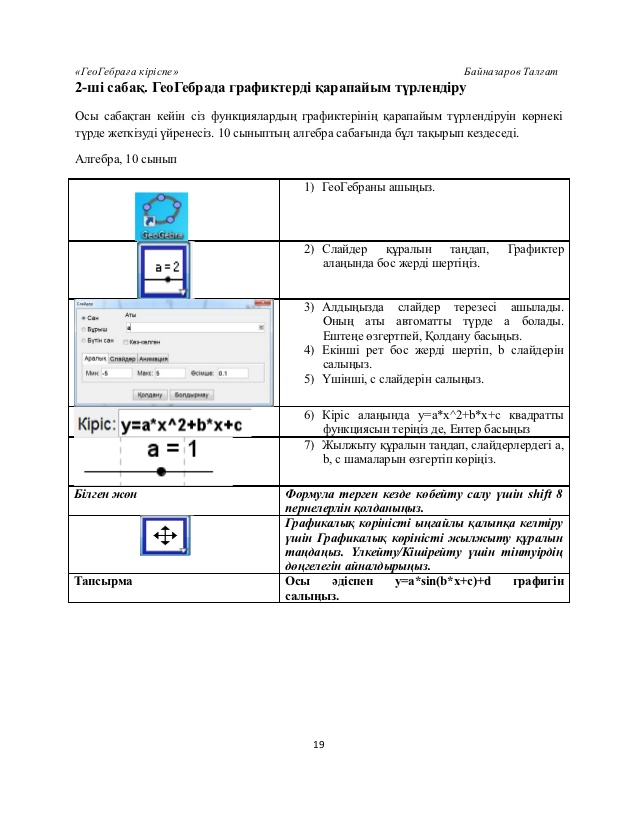
Бұл сабақта сіз функциялардың графиктерін қарапайым түрлендіруді үйренесіз. 10 сыныптың алгебрасында кездесетін тақырыпты игеруге балаларға көмегін көп тигізеді.Ескерту: а,в,с айнымалының орнына бірден сан мәнін енгізу керек.
|
|
Алдымен ГеоГебра бағдарламасын ашыңыз. |
|
|
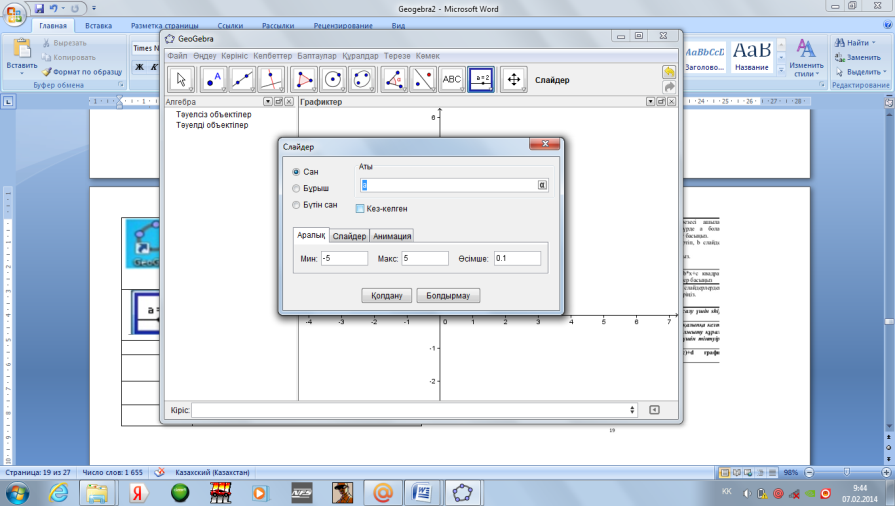
2)Слайдер құралын таңдап, Графиктер алаңындағы бос жерге шертіңіз. |
|
|
3)Алдыңызда Слайдер терезесі ашылды.Оның аты автоматты түрде а болады. Ештеңені өзгертпей Қолдануды басыңыз.4)Екінші рет бос жерді шертіп, в слайдерін 5)Үшінші рет бос жерді шертіп ,с слайдерін салыңыз. |
|
Кіріс:y=a*x^2+bx+c |
6) Кіріс алаңына y=a*x^2+bx+c квадрат функциясын теріңіз де, Ентер басыңыз. |
|
|
7)Жылжыту құралын таңдап, слайдерлерден а,в,с шамаларын өзгертіп көріңіз. |
|
|
Сызбаны ыңғайлы қалыпқа келтіру үшін Графикалық объектіні жылжыту құралын таңдаңыз.Үлкейту, кішірейту үшін тінтуірдің дөңгелегін айналдырыңыз. |
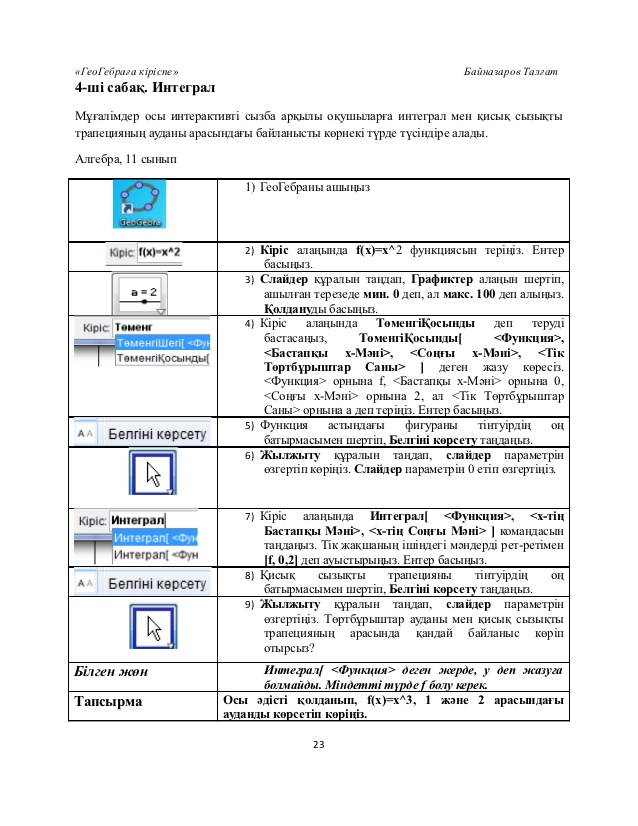
3-мысал:Интегралды ГеоГебрада есептеу,сызбасын салу.Оқушылар осы сызба арқылы интеграл мен қисық сызықты трапеция ауданы арасындағы байланысты көрнекі түрде көре алады.Алгебра 11 сынып.
|
|
1)Алдымен ГеоГебра бағдарламасын ашыңыз |
|
Кіріс:f(x)=x^2 |
2)Кіріс алаңына f(x)=x^2 функциясын теріңіз. Ентер басыңыз. |
|
|
3)Слайдер құралын таңдап,Графиктер алаңын шертіп,ашылған терезеде мин.0деп,ал макс.100деп алып, Қолдануды басыңыз. |
|
|
4)Кіріс алаңында ТөменгіҚосынды деп теребастасаңыз, [«Функция» , «Бастапқых-Мәні», «Соңғы х-Мәні», «Тік Төртбұрыштыр саны»]деген жазу көресіз. Осылардың әрқайсысының орнына f,0,2,a деп теріңіз. |
|
|
5)Функция астындағы фигураны тінтуірдің оңжағын шертіп, Белгіні көрсету таңдаңыз. |
|
|
6)Жылжыту құралын таңдап,слайдер параметрін өзгертіп,Слайдер параметрін 0деп өзгертіңіз. |
|
Кіріс : Интеграл |
7) Кіріс алаңында Интеграл «Функция», «х-тің Бастапқы мәні» «х-тің соңғы мәні» командасын таңдаңыз.[f,0,2] деп ауыстырыңыз.Ентер басыңыз |
|
|
8)Қисық сызықты трапецияны тінтуірдің оң батырмасымен шертіп,Белгіні көрсету таңдаңыз. |
|
|
9) Жылжыту құралын таңдап,слайдер параметрін өзгертіңіз.Төртбұрыштар ауданы мен қисық сызықты трапецияның арасында қандай байланыс көріп отырсыз? |
4-мысал:Тригонометриялық функциялардың туындыларының
графиктерін сызуды ГеоГебрада орындау. Алгебра 10 сынып.
|
|
1)Алдымен ГеоГебра бағдарламасын ашыңыз |
|
Кіріс:y=cos(x) |
|
|
|
3)Жаңа нүкте құралын таңдап, косинус графигінің бойынан бір нүкте таңдаңыз.Ол А деп аталады. |
|
|
4)Жылжыту құралын таңдап,А нүктесін жылжытып көріңіз. |
|
|
5)Жанама құралын таңдап,алдымен Анүктесін,содан косинус графигін шертіңіз.Сонда функцияның жанама сызығы сызылады. |
|
|
6)Бұрыштық коэффициент құралын таңдап,А нүктесін бір рет шертіңіз. |
|
|
7) Жылжыту құралын таңдап,А нүктесін жылжытып көріңіз. |
|
Кіріс:В=(x(A),m) |
8) Кіріс алаңына В=(x(A),m)жаңа нүкте салыңыз.Бұл жердегі у координатасыА нүктесі арқылы өткен жанаманың бұрыштық коэффициенті. |
|
|
9)Тінтуірдің оң жағын шертіп,Із бар таңдаңыз. |
|
|
10) Анүктесін жылжытып көріңіз.А нүктесі орнын өзгеоткен сайын, В нүктесі де өзгереді, артынан із қалдырады.Бұл із-косинус функциясының туындысы болатын синус графигі |
Сонымен қатар, 3Д көрінісін таңдау арқылы кеңістіктегі фигураларды және олардың жазбаларын салып, көрсетуге болады.Кубтың жазбасын алу үшін құралдар терезесінен жазба батырмасын таңдап алып , кубтың үстін шертсек, кубтың жазбасы шығады. Бұл жерде кубтың жазбасы «Жазықтық» және «Кеңістік» терезелерінің екеуінен де көрініп тұрады.
5-мысал:.Куб салу ережесі. Құралдар терезесінен кеңістік терезесін ашып алып, одан екі нүктенің орнын шертеміз, онда куб салынғанын көреміз.
о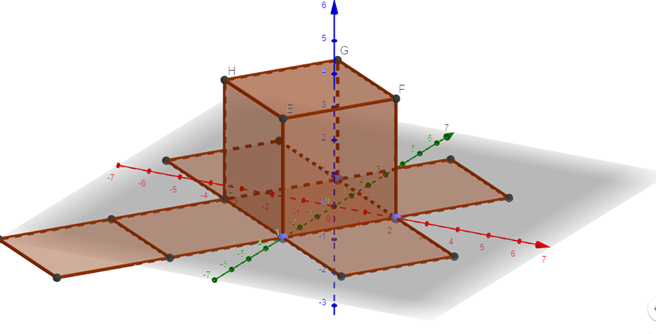 ның жазбасы
мына түрде көрінеді:
ның жазбасы
мына түрде көрінеді:
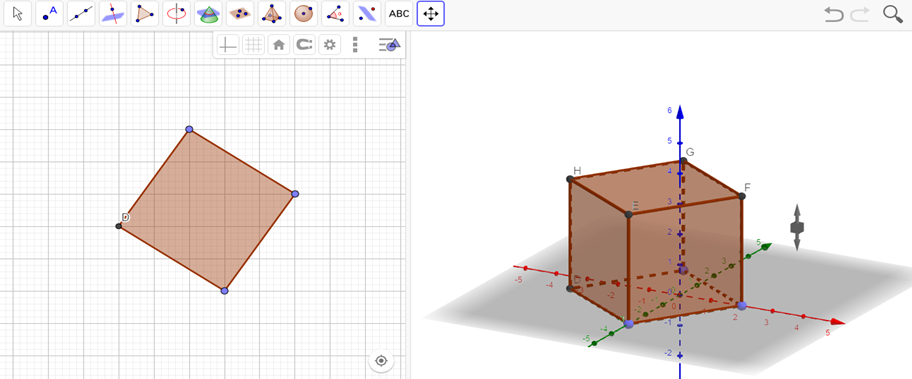
6-мысал: Пирамида салу ережесі. Пирамида салу және оның жазбасын алу дәл жоғарыдағы ережелермен орындалады.
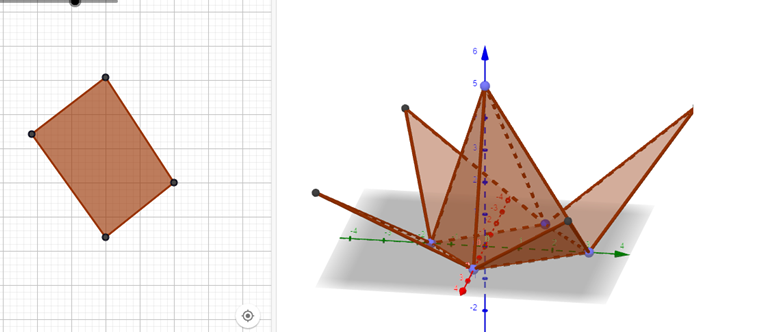
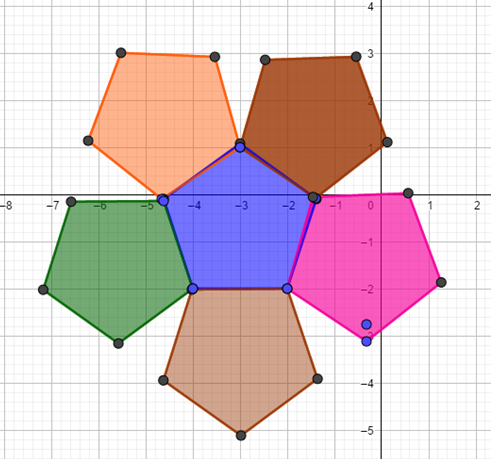
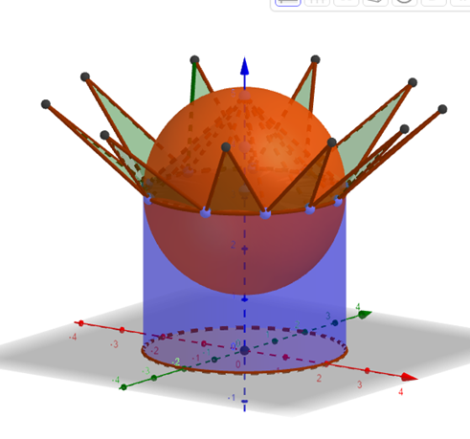
Осы фигураларды сала отырып, оқушылар шығармашылығын да арттыруға болады, мысалы , төменгі сынып оқушыларына мынадай мозайкалар және бәйтерек салып көрсетуге болады.
Шығыс Қазақстан облысы
Тарбағатай ауданы
Үштөбе ауылы
«Өкпеті» орта мектебінің жоғары
санатты математика пәні мұғалімі
Кенжекова Мейрамкүл Қайсақызы
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математика сабақтарында «Geogebra» бағдарламасын қолданудың тиімділігі
Математика сабақтарында «Geogebra» бағдарламасын қолданудың тиімділігі
Баяндама
Тақырыбы: Математика сабақтарында «Geogebra» бағдарламасын қолданудың тиімділігі
Геогебра» бағдарламасы туралы түсініктер:
Геогебра – Тегін таратылатын математикалық , (www.geogebra.org) геометрия және алгебраны байланыстыратын компьютерлік интерактивті бағдарлама. Қазіргі таңда әлем бойынша ең көп таралған математикалық бағдарлама ретінде танылып отыр. 149 елде қолданылып жатыр, 49 тілге аударылған. Авторы – австриялық математик Маркус Хохенвартер. 2009 бұл бағдарлама үшін арнайы байқаудың жеңімпазы атанды. Сол жылдың тамызында оның үш өлшемді нұсқасы шықты. Бұл бағдарлама әлем бойынша кең таралған. Орталығы Австрия мемлекетінде орналасқан. Геогебраның басқа мемлекеттерде дамыту жергілікті мұғалімдер арқылы жүзеге асырылады: бағдарлама жергілікті тілге аударылады, Геогебра институттары ашылып, сол институттар арқылы бағдарлама әрі қарай дамытылып, интерактивті нұсқалар дайындалады, үйретуші бейнекөріністер жазылады, қолданушы кітапшалары жазылады, әрі басқа елдердегі
мұғалімдермен Геогебра бағдарламасы бойынша тәжірибе алмасу іске асырылады.Қазіргі уақытта Геогебраны қазақ тіліне аударып жүрген Қостанайлық математик Талғат Байназаров .
Қазақ интернетінің дамуына үлес қосып жүрген Талғат Байназаров Қостанай қаласындағы С. Мәуленов атындағы гимназияның математика пәні мұғалімі.Ғаламторда «Математика және мультимедия» атты блог жүргізеді.
Мен сіздерге өзім қолданып жүрген сабақтардан бірнеше мысалдар келтірейін.
Геогебраның негізгі терезелеріне тоқтала кетсек,бағдарламаны ашып алғаннан кейін кез-келген терезені ашып алып,(төменде көрсетілгендей) керекті есепті шеше аламыз.


1-мысал:Теңдеулер жүйесін ГеоГебрада шешу.
Бұл сабақты меңгеру арқылы сіз 6-11 сыныптардағы теңдеулер мен теңдеулер жүйесін, сол сияқты олардың графиктерін салуды үйренесіз.Теңдеулер жүйесі бойынша жаңа сабақ түсіндірмес бұрын алдында бір-екі мысал дайындап қойып «ойнау» батырмасымен көрсетсеңіз, оқушыларға әлдеқайда түсінікті әрі қызықты болады.Мысал келтірейік:Алгебра 9 сынып.
|
|
|
|
Кіріс: х-у=3 |
2)Кіріс деген жерде х-у=2теңдеуін жазып, Ентер басыңыз. |
|
Кіріс: х+у=4 |
3) Кіріс деген жерде х+у=4 теңдеуін жазып, Ентер басыңыз. |
|
|
3)Енді екі түзудің қиылысуы болатын Екі объектінің қиылысуы құралын таңдаңыз да, екі түзуді бәр-бірден шертіңіз.Олардың қиылысуы болатын А нүктесі пайда болады.Сонымен қатар А нүктесінің координаталары Алгебра терезесінде көрінеді. |
|
Ескерту
|
Кіріс алаңына кез-келген функцияны теруүшін Көрініс терезесінен Пернетақта құралын пайдаланған дұрыс. |
2-мысал:Графиктерді түрлендіруді ГеоГебрада орындау.
Бұл сабақта сіз функциялардың графиктерін қарапайым түрлендіруді үйренесіз. 10 сыныптың алгебрасында кездесетін тақырыпты игеруге балаларға көмегін көп тигізеді.Ескерту: а,в,с айнымалының орнына бірден сан мәнін енгізу керек.
|
|
Алдымен ГеоГебра бағдарламасын ашыңыз. |
|
|
2)Слайдер құралын таңдап, Графиктер алаңындағы бос жерге шертіңіз. |
|
|
3)Алдыңызда Слайдер терезесі ашылды.Оның аты автоматты түрде а болады. Ештеңені өзгертпей Қолдануды басыңыз.4)Екінші рет бос жерді шертіп, в слайдерін 5)Үшінші рет бос жерді шертіп ,с слайдерін салыңыз. |
|
Кіріс:y=a*x^2+bx+c |
6) Кіріс алаңына y=a*x^2+bx+c квадрат функциясын теріңіз де, Ентер басыңыз. |
|
|
7)Жылжыту құралын таңдап, слайдерлерден а,в,с шамаларын өзгертіп көріңіз. |
|
|
Сызбаны ыңғайлы қалыпқа келтіру үшін Графикалық объектіні жылжыту құралын таңдаңыз.Үлкейту, кішірейту үшін тінтуірдің дөңгелегін айналдырыңыз. |
3-мысал:Интегралды ГеоГебрада есептеу,сызбасын салу.Оқушылар осы сызба арқылы интеграл мен қисық сызықты трапеция ауданы арасындағы байланысты көрнекі түрде көре алады.Алгебра 11 сынып.
|
|
1)Алдымен ГеоГебра бағдарламасын ашыңыз |
|
Кіріс:f(x)=x^2 |
2)Кіріс алаңына f(x)=x^2 функциясын теріңіз. Ентер басыңыз. |
|
|
3)Слайдер құралын таңдап,Графиктер алаңын шертіп,ашылған терезеде мин.0деп,ал макс.100деп алып, Қолдануды басыңыз. |
|
|
4)Кіріс алаңында ТөменгіҚосынды деп теребастасаңыз, [«Функция» , «Бастапқых-Мәні», «Соңғы х-Мәні», «Тік Төртбұрыштыр саны»]деген жазу көресіз. Осылардың әрқайсысының орнына f,0,2,a деп теріңіз. |
|
|
5)Функция астындағы фигураны тінтуірдің оңжағын шертіп, Белгіні көрсету таңдаңыз. |
|
|
6)Жылжыту құралын таңдап,слайдер параметрін өзгертіп,Слайдер параметрін 0деп өзгертіңіз. |
|
Кіріс : Интеграл |
7) Кіріс алаңында Интеграл «Функция», «х-тің Бастапқы мәні» «х-тің соңғы мәні» командасын таңдаңыз.[f,0,2] деп ауыстырыңыз.Ентер басыңыз |
|
|
8)Қисық сызықты трапецияны тінтуірдің оң батырмасымен шертіп,Белгіні көрсету таңдаңыз. |
|
|
9) Жылжыту құралын таңдап,слайдер параметрін өзгертіңіз.Төртбұрыштар ауданы мен қисық сызықты трапецияның арасында қандай байланыс көріп отырсыз? |
4-мысал:Тригонометриялық функциялардың туындыларының
графиктерін сызуды ГеоГебрада орындау. Алгебра 10 сынып.
|
|
1)Алдымен ГеоГебра бағдарламасын ашыңыз |
|
Кіріс:y=cos(x) |
|
|
|
3)Жаңа нүкте құралын таңдап, косинус графигінің бойынан бір нүкте таңдаңыз.Ол А деп аталады. |
|
|
4)Жылжыту құралын таңдап,А нүктесін жылжытып көріңіз. |
|
|
5)Жанама құралын таңдап,алдымен Анүктесін,содан косинус графигін шертіңіз.Сонда функцияның жанама сызығы сызылады. |
|
|
6)Бұрыштық коэффициент құралын таңдап,А нүктесін бір рет шертіңіз. |
|
|
7) Жылжыту құралын таңдап,А нүктесін жылжытып көріңіз. |
|
Кіріс:В=(x(A),m) |
8) Кіріс алаңына В=(x(A),m)жаңа нүкте салыңыз.Бұл жердегі у координатасыА нүктесі арқылы өткен жанаманың бұрыштық коэффициенті. |
|
|
9)Тінтуірдің оң жағын шертіп,Із бар таңдаңыз. |
|
|
10) Анүктесін жылжытып көріңіз.А нүктесі орнын өзгеоткен сайын, В нүктесі де өзгереді, артынан із қалдырады.Бұл із-косинус функциясының туындысы болатын синус графигі |
Сонымен қатар, 3Д көрінісін таңдау арқылы кеңістіктегі фигураларды және олардың жазбаларын салып, көрсетуге болады.Кубтың жазбасын алу үшін құралдар терезесінен жазба батырмасын таңдап алып , кубтың үстін шертсек, кубтың жазбасы шығады. Бұл жерде кубтың жазбасы «Жазықтық» және «Кеңістік» терезелерінің екеуінен де көрініп тұрады.
5-мысал:.Куб салу ережесі. Құралдар терезесінен кеңістік терезесін ашып алып, одан екі нүктенің орнын шертеміз, онда куб салынғанын көреміз.
о ның жазбасы
мына түрде көрінеді:
ның жазбасы
мына түрде көрінеді:

6-мысал: Пирамида салу ережесі. Пирамида салу және оның жазбасын алу дәл жоғарыдағы ережелермен орындалады.

Осы фигураларды сала отырып, оқушылар шығармашылығын да арттыруға болады, мысалы , төменгі сынып оқушыларына мынадай мозайкалар және бәйтерек салып көрсетуге болады.


Шығыс Қазақстан облысы
Тарбағатай ауданы
Үштөбе ауылы
«Өкпеті» орта мектебінің жоғары
санатты математика пәні мұғалімі
Кенжекова Мейрамкүл Қайсақызы

шағым қалдыра аласыз