
МАТЕМАТИКАЛЫҚ ҚҰРАЛДАР МЕН МОДЕЛЬДЕУ
3.1 Анықтауыштар мен матрицалар негіздері.
-
Мысал. Жүйені есептеңіз:

Шешімі: Бас анықтауышын есептейміз
 =
=
 =2(-1)-(-3)1=
-2+3=1
=2(-1)-(-3)1=
-2+3=1
 және
және
 анықтауыштарын
есептейміз:
анықтауыштарын
есептейміз:
 =
=
 =4(-1)-5(-3)=11,
=4(-1)-5(-3)=11,  =
= =10-4=6
=10-4=6
(1.4) формуласын қолданып, белгісіз х және у анықтаймыз:

-
Мысал. Анықтауышты есептеңдер:

Мұнда а11=2, а12=-1, а13=3, а21=1, а22=2, а23=-1, а31=0, а32=1, а33=1. Сонда (1.5) формула бойынша


-
Мысал:
 анықтауышты
есептеңдер.
анықтауышты
есептеңдер.
Сарриус әдісін қолданамыз:

3) Анықтауышты жолы немесе баған элементтері арқылы жіктеп есептеу әдісі.
Анықтауыштың қандай болса да жолының (бағанның) элементтерін сәйкес алгебралық толықтауыштарына көбейтіп, қосқаннан шыққан қосынды анықтауыштың шамасына тең болады. Немесе
 (бірінші жолы бойынша
жіктеу).
(бірінші жолы бойынша
жіктеу).
 (бірінші баған бойынша
жіктеу).
(бірінші баған бойынша
жіктеу).
Мысал: Бірінші жолдың элементтері арқылы жіктеп анықтауышты есептеңдер.

-
Анықтауыштарды есептеу әдістері.
-
Сараптау әдісі (Sarrus ережесі)
Бұл әдіс 3x3 өлшемді анықтауыштарды есептеу үшін қолданылады.
Мысал 1:
Берілген матрица:
A = 
Анықтауыш:
det(A)=2⋅5⋅3+3⋅2⋅1+1⋅4⋅0−(1⋅5⋅1+3⋅4⋅3+2⋅0⋅2)
Есептейміз:
det(A)=30+6+0−(5+36+0)=36−41=−5
Жауабы: det(A)=−5
2. Минорлар және алгебралық толықтауыш әдісі
Бұл әдіс n×n өлшемді матрицалардың анықтауыштарын есептеу үшін қолданылады.
Мысал
2:
Берілген матрица:
В
=

Минорлар және алгебралық толықтауышты қолданамыз:
det(B)
=
1
⋅
 ⋅
⋅
 +
3 ⋅
+
3 ⋅ 
Минорларды есептейміз:
 =
1⋅0 – 2
⋅
4
= - 8
=
1⋅0 – 2
⋅
4
= - 8
 =
3⋅2 – 5
⋅
1
= 1
=
3⋅2 – 5
⋅
1
= 1
Толық анықтауыш:
det(C)=2⋅(−8)+0⋅(...)+1⋅1=−16+1=−15
Жауабы: det(C)=−15
-
Матрицалармен жұмыс істеу. 1 сағат
1. Матрицаларды көбейту
Мысал 1:
Берілген матрицалар:
A
=  ,
В =
,
В = 
Көбейту нәтижесі:
C=A⋅B
=
 =
=  =
=

Жауабы:
С
= 
2. Квадрат матрицаның анықтауышын есептеу
Мысал
2:
Берілген матрица:
D
= 
Анықтауышты есептейміз:
det(D) =
 =
4⋅1-3⋅2 = 4-6 = - 2
=
4⋅1-3⋅2 = 4-6 = - 2
Жауабы:
detD)=−2
3. Кері матрицаны табу және сызықтық теңдеулер жүйесін шешу
Мысал
3:
Сызықтық теңдеулер жүйесі:
2x+y=5x−y=1
x - y &= 1
Матрицалық түрде жазамыз:
 ⋅
⋅  =
=

a) Анықтауышты есептейміз:
det(A) =
 2⋅(-1) - 1⋅1 = -2-1 = - 3
2⋅(-1) - 1⋅1 = -2-1 = - 3
b)
Кері матрицаны табу:
Формула:
A-1 =
 ⋅
⋅

.
A-1 =
 ⋅
⋅
 =
=

c) Шешімді табу:
 A-1 ⋅
A-1 ⋅

 ⋅
⋅ 
Есептейміз:
x=
 ⋅
5
+
⋅
5
+  ⋅
1
=
⋅
1
=  +
+
 =
2
=
2
y=
 ⋅
5
-
⋅
5
-  ⋅
1
=
⋅
1
=  -
-
 =
1
=
1
Жауабы:
x=2, y=1
-
Матрицалармен операциялар. 1 сағат.
1. Матрицаларды қосу және азайту
Мысал 1:
Берілген матрицалар:
A
=  ,
В =
,
В = 
a) Матрицаларды қосу:
A+B=  =
=

b) Матрицаларды азайту:
A−B
=  =
=

2. Матрицаларды транспонирлеу және скалярмен көбейту
Мысал 2:
Берілген матрица:
C=

-
Транспонирлеу:
CТ = 
-
Скалярмен көбейту (k=3 ):
k⋅
C =
3 ⋅
 =
=
 =
= 
-
Анықтауыштардың бизнесте қолданылуы. 2 сағат
Мысал-1. Аяқ киім фабрикасы үшін экономикалық есепті қарастырамыз
|
Шикі зат |
Бір парға шартты бірлік кететін норма |
1 күнде кететін |
||
|
түрлері |
|
|
|
шикі зат |
|
Аяқ киім |
Х1 |
Х2 |
Х3 |
шартты бірлігі |
|
түрлерінің |
|
|
|
|
|
көлемі |
|
|
|
|
|
S1 |
5 |
3 |
4 |
2700 |
|
S2 |
2 |
1 |
1 |
900 |
|
S3 |
3 |
2 |
2 |
1600 |
Аяқ киімнің əр түрінен күнделікті қанша көлемде шығарылуын, яғни х1, х2, х3 – терді табу керек.
Келесі жүйені құрастырамыз:
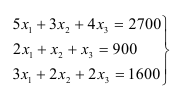
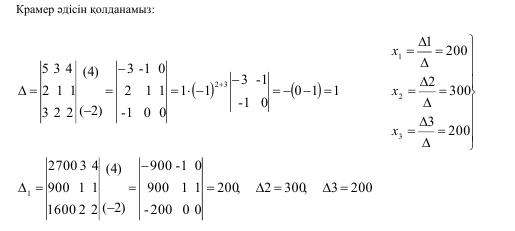
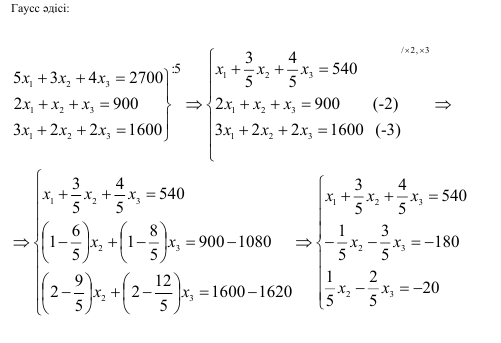

Жауабы:
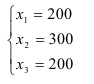
1. Крамер ережесі арқылы сызықтық теңдеулер жүйесін шешу
Мысал
1:
Сызықтық теңдеулер жүйесі:
2x+y=5x−3y=−7
x - 3y &= -7
а) Матрицалық түрде жазамыз:
 ,
,
 ,
,
,
,  =
=

b) Анықтауышты есептейміз:
det(A) =
 2⋅(-3) - 1⋅1 = -6-1 = - 7
2⋅(-3) - 1⋅1 = -6-1 = - 7
с) Крамер ережесі бойынша:
x=  , у =
, у =

 ,
,

 =
=  =
=
 5⋅(-3) - 1⋅(-7) = -15 + 7 = - 8
5⋅(-3) - 1⋅(-7) = -15 + 7 = - 8
 =
=  =
=
 2⋅(-7) - 5⋅1 = -14 - 5 = - 19
2⋅(-7) - 5⋅1 = -14 - 5 = - 19
-
Айнымалыларды табамыз:
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
МАТЕМАТИКАЛЫҚ ҚҰРАЛДАР МЕН МОДЕЛЬДЕУ
МАТЕМАТИКАЛЫҚ ҚҰРАЛДАР МЕН МОДЕЛЬДЕУ
МАТЕМАТИКАЛЫҚ ҚҰРАЛДАР МЕН МОДЕЛЬДЕУ
3.1 Анықтауыштар мен матрицалар негіздері.
-
Мысал. Жүйені есептеңіз:

Шешімі: Бас анықтауышын есептейміз
 =
=
 =2(-1)-(-3)1=
-2+3=1
=2(-1)-(-3)1=
-2+3=1
 және
және
 анықтауыштарын
есептейміз:
анықтауыштарын
есептейміз:
 =
=
 =4(-1)-5(-3)=11,
=4(-1)-5(-3)=11,  =
= =10-4=6
=10-4=6
(1.4) формуласын қолданып, белгісіз х және у анықтаймыз:

-
Мысал. Анықтауышты есептеңдер:

Мұнда а11=2, а12=-1, а13=3, а21=1, а22=2, а23=-1, а31=0, а32=1, а33=1. Сонда (1.5) формула бойынша


-
Мысал:
 анықтауышты
есептеңдер.
анықтауышты
есептеңдер.
Сарриус әдісін қолданамыз:

3) Анықтауышты жолы немесе баған элементтері арқылы жіктеп есептеу әдісі.
Анықтауыштың қандай болса да жолының (бағанның) элементтерін сәйкес алгебралық толықтауыштарына көбейтіп, қосқаннан шыққан қосынды анықтауыштың шамасына тең болады. Немесе
 (бірінші жолы бойынша
жіктеу).
(бірінші жолы бойынша
жіктеу).
 (бірінші баған бойынша
жіктеу).
(бірінші баған бойынша
жіктеу).
Мысал: Бірінші жолдың элементтері арқылы жіктеп анықтауышты есептеңдер.

-
Анықтауыштарды есептеу әдістері.
-
Сараптау әдісі (Sarrus ережесі)
Бұл әдіс 3x3 өлшемді анықтауыштарды есептеу үшін қолданылады.
Мысал 1:
Берілген матрица:
A = 
Анықтауыш:
det(A)=2⋅5⋅3+3⋅2⋅1+1⋅4⋅0−(1⋅5⋅1+3⋅4⋅3+2⋅0⋅2)
Есептейміз:
det(A)=30+6+0−(5+36+0)=36−41=−5
Жауабы: det(A)=−5
2. Минорлар және алгебралық толықтауыш әдісі
Бұл әдіс n×n өлшемді матрицалардың анықтауыштарын есептеу үшін қолданылады.
Мысал
2:
Берілген матрица:
В
=

Минорлар және алгебралық толықтауышты қолданамыз:
det(B)
=
1
⋅
 ⋅
⋅
 +
3 ⋅
+
3 ⋅ 
Минорларды есептейміз:
 =
1⋅0 – 2
⋅
4
= - 8
=
1⋅0 – 2
⋅
4
= - 8
 =
3⋅2 – 5
⋅
1
= 1
=
3⋅2 – 5
⋅
1
= 1
Толық анықтауыш:
det(C)=2⋅(−8)+0⋅(...)+1⋅1=−16+1=−15
Жауабы: det(C)=−15
-
Матрицалармен жұмыс істеу. 1 сағат
1. Матрицаларды көбейту
Мысал 1:
Берілген матрицалар:
A
=  ,
В =
,
В = 
Көбейту нәтижесі:
C=A⋅B
=
 =
=  =
=

Жауабы:
С
= 
2. Квадрат матрицаның анықтауышын есептеу
Мысал
2:
Берілген матрица:
D
= 
Анықтауышты есептейміз:
det(D) =
 =
4⋅1-3⋅2 = 4-6 = - 2
=
4⋅1-3⋅2 = 4-6 = - 2
Жауабы:
detD)=−2
3. Кері матрицаны табу және сызықтық теңдеулер жүйесін шешу
Мысал
3:
Сызықтық теңдеулер жүйесі:
2x+y=5x−y=1
x - y &= 1
Матрицалық түрде жазамыз:
 ⋅
⋅  =
=

a) Анықтауышты есептейміз:
det(A) =
 2⋅(-1) - 1⋅1 = -2-1 = - 3
2⋅(-1) - 1⋅1 = -2-1 = - 3
b)
Кері матрицаны табу:
Формула:
A-1 =
 ⋅
⋅

.
A-1 =
 ⋅
⋅
 =
=

c) Шешімді табу:
 A-1 ⋅
A-1 ⋅

 ⋅
⋅ 
Есептейміз:
x=
 ⋅
5
+
⋅
5
+  ⋅
1
=
⋅
1
=  +
+
 =
2
=
2
y=
 ⋅
5
-
⋅
5
-  ⋅
1
=
⋅
1
=  -
-
 =
1
=
1
Жауабы:
x=2, y=1
-
Матрицалармен операциялар. 1 сағат.
1. Матрицаларды қосу және азайту
Мысал 1:
Берілген матрицалар:
A
=  ,
В =
,
В = 
a) Матрицаларды қосу:
A+B=  =
=

b) Матрицаларды азайту:
A−B
=  =
=

2. Матрицаларды транспонирлеу және скалярмен көбейту
Мысал 2:
Берілген матрица:
C=

-
Транспонирлеу:
CТ = 
-
Скалярмен көбейту (k=3 ):
k⋅
C =
3 ⋅
 =
=
 =
= 
-
Анықтауыштардың бизнесте қолданылуы. 2 сағат
Мысал-1. Аяқ киім фабрикасы үшін экономикалық есепті қарастырамыз
|
Шикі зат |
Бір парға шартты бірлік кететін норма |
1 күнде кететін |
||
|
түрлері |
|
|
|
шикі зат |
|
Аяқ киім |
Х1 |
Х2 |
Х3 |
шартты бірлігі |
|
түрлерінің |
|
|
|
|
|
көлемі |
|
|
|
|
|
S1 |
5 |
3 |
4 |
2700 |
|
S2 |
2 |
1 |
1 |
900 |
|
S3 |
3 |
2 |
2 |
1600 |
Аяқ киімнің əр түрінен күнделікті қанша көлемде шығарылуын, яғни х1, х2, х3 – терді табу керек.
Келесі жүйені құрастырамыз:
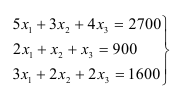
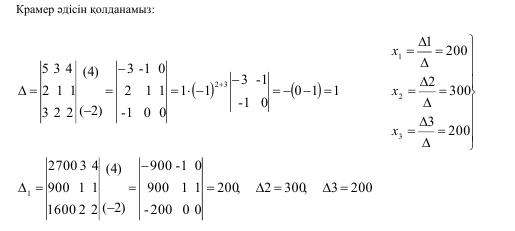
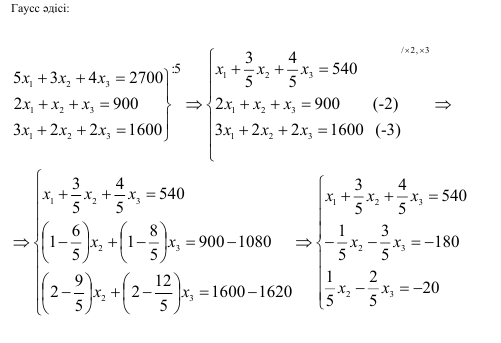

Жауабы:
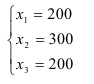
1. Крамер ережесі арқылы сызықтық теңдеулер жүйесін шешу
Мысал
1:
Сызықтық теңдеулер жүйесі:
2x+y=5x−3y=−7
x - 3y &= -7
а) Матрицалық түрде жазамыз:
 ,
,
 ,
,
,
,  =
=

b) Анықтауышты есептейміз:
det(A) =
 2⋅(-3) - 1⋅1 = -6-1 = - 7
2⋅(-3) - 1⋅1 = -6-1 = - 7
с) Крамер ережесі бойынша:
x=  , у =
, у =

 ,
,

 =
=  =
=
 5⋅(-3) - 1⋅(-7) = -15 + 7 = - 8
5⋅(-3) - 1⋅(-7) = -15 + 7 = - 8
 =
=  =
=
 2⋅(-7) - 5⋅1 = -14 - 5 = - 19
2⋅(-7) - 5⋅1 = -14 - 5 = - 19
-
Айнымалыларды табамыз:

шағым қалдыра аласыз















