Введение

Если задана функция y (x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоемко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра, или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно.

Функция у(х) может участвовать в каких-либо физико-технических или чисто математических расчетах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближенной формулой, т. е. подобрать некоторую функцию φ (х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)   φ(х). Близость получают введением в аппроксимирующую функцию свободных параметров а={а₁, а₂, …, а_n} и соответствующим их выбором. В этом случае используются такие понятия как, аппроксимация и интерполяция.

ИНТЕРПОЛЯЦИЯ (от лат. interpolatio — изменение, переделка) - отыскание промежуточных значений величины по некоторым известным ее значениям. Например, отыскание значений функции f( x) в точках x, лежащих между точками x₀ по известным значениям y_i = f( x_i) (где i = 0,1,..., n). Если x лежит вне интервала ( x₀,x_n), аналогичная процедура называется экстраполяцией.

Основная цель интерполяции – получить быстрый (экономичный) алгоритм вычисления значений f(x) для значений х, не содержащихся в таблице.

АППРОКСИМАЦИЯ (от лат. approximo — приближаюсь) - замена одних математических объектов (например, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (например, кривых линий близкими к ним ломаными).

1. Методы графической обработки экспериментальных данных

Табличный способ записи экспериментальных данных является наиболее простым и широко распространенным, полностью воспроизводит полученные результаты. Однако табличный способ менее наглядный по сравнению с графическим.

Графический метод позволяет наглядно оценить изменения переменных величин, установить характер этого изменения, а также с помощью этого метода можно без особых вычислений найти промежуточные значения переменных величин.

Кроме этого, графические методы обработки экспериментальных данных помогают вывести эмпирическую формулу в тех случаях, когда исследуемые процессы не подчиняются уже известным теоретическим законам. Тогда по экспериментальным данным устанавливается вид формулы и постоянные коэффициенты.

Табличный способ записи. В исследованиях по технологии бетона часто приходится определять зависимость между отдельными переменными величинами. При наличии возможности свободно задаваться численными значениями независимых переменных все опыты должны разбиваться на ряд серий с таким расчетом, чтобы в каждой серии одна из независимых переменных оставалась постоянной величиной. Например, необходимо найти зависимость между тремя переменными, из которых -искомая, В/Ц — изменение переменных в следующих пределах:

Для равномерного распределения значений переменных и В/Ц можно записать: для 5 значений, а для В/Ц — 7 значений.

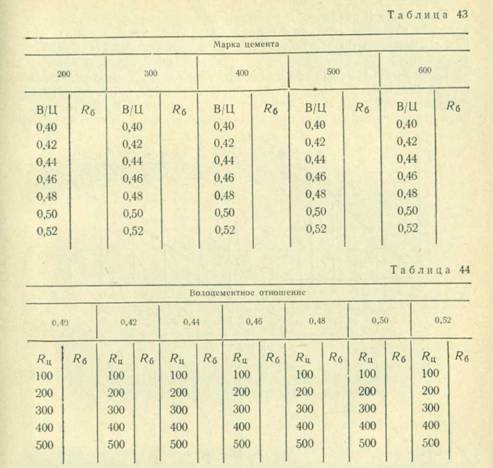
Форма записи по переменной #ц будет иметь вид, приведенный в табл. 43.

Форма записи по перемещенной В/Ц будет иметь вид, приведенный в табл. 44.

Таким образом получили пять серий опытов, каждая при своем постоянном значении переменной, и семь опытов в каждой серии. При наличии таблицы можно на одном графике построить кривые зависимости неизвестной величины от переменной В/Ц при частных значениях переменной. При наличии таблицы легко построить график зависимости неизвестной от переменной при частных значениях переменной В/Ц. При наличии таких графиков легче подыскать и вывести зависимость между тремя переменными.

Выбор масштаба шкалы при построении графиков. При построении графической зависимости переменных величин пользуются равномерными и неравномерными шкалами. Равномерной шкалой при изображении функции в прямоугольных координатах называют такую, на которой расстояния между двумя делениями, соответствующими изменению переменной на одну и ту же величину, равны.

Если расстояния между двумя делениями, соответствующими изменению переменной на одну и ту же величину, не равны, такую шкалу называют неравномерной (логарифмической квадратичной шкалой и т. д.).

Масштабы по осям координат для равномерных шкал обычно принимают равными. Однако в некоторых случаях при значительной разнице в пределах изменения переменных величин не удается применить равные масштабы, тогда на осях координат применяют различные масштабы шкал, но обязательно с таким расчетом, чтобы построенные на этом графике кривые были наглядными и сам график получился бы наиболее компактным.

Применение различных масштабов шкал не сказывается на точности отсчетов, если на графике получается прямая линия, так как с изменением масштабов изменится лишь только ее наклон (рис. № 1).

Если же на графике получается кривая линия, то в этом случае при применении различных масштабов кривая будет искажаться, что может привести к снижению точности отсчетов и ввести в заблуждение исследователя при составлении выводов. Если на графике зависимости двух переменных величин получается кривая линия, следует пользоваться на обеих осях шкалами с равными масштабами.

Построение логарифмической шкалы основано на свойстве логарифмов, заключающемся в том,- что если любое число увеличить в 10, 100 и т. д. раз, то полученный логарифм нового числа, сохраняя свою мантиссу, увеличит только характеристику этого числа соответственно на 1, 2, 3 и т. д. Так, если 6 = 0,78, а 60= 1,78, то для получения отрезка, отвечающего 1д60, т. е. 1,78, нужно на оси отложить отрезок, равный 0,78, так как длина шкалы для значений х от 1 до 10 принимается равной единице (lg 10=1).

Для построения логарифмической шкалы берут две параллельные прямые и на одной из них (верхней) строят равномерную шкалу от 0 до 1. Затем определяют значения логарифмов целых чисел от 1 до 10, отмечают на верхней шкале точки, отвечающие значениям gx и переносят их на нижнюю прямую, записывая каждой перенесенной точке соответствующее значение х (рис № 2). Логарифмическая шкала на осях координат позволяет спрямить получаемые кривые зависимости исследуемых величин и упрощает построение некоторых уравнений.

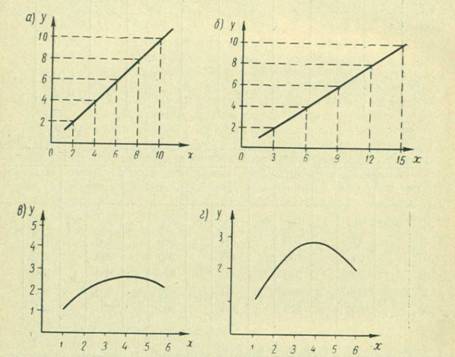
Рисунок 1 - Построение графика зависимости в прямоугольных координатах:

А — с равными масштабами шкал для прямой; б -с различными масштабами шкал для прямой; в — с равными масштабами шкал для кривой; г — с разными масштабами шкал для кривой

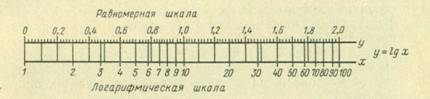
Рисунок 2- Построение логарифмической шкалы функции длиной в два модуля

Под интерполяцией подразумевается нахождение промежуточных значений функций (внутри опытного ряда).

Наиболее простым является метод линейной интерполяции. Когда функция на данном отрезке линейна или близка к линейной, то этот метод точен. Если не требуется высокая точность, то его можно применить и к нелинейным функциям. Этот метод заключается в следующем: имеем таблицу 3 с данными аргумента и функции.

Функций может быть несколько, то есть эту таблицу можно продлить. Например, мы хотим в таблице заменить значение у₃, которое исключили при анализе статистических данных, новым, найденным линейной интерполяцией. Берем разность между соседними данными у₂ и у₄, то есть

Таблица 3 Таблица данных аргумента (х) и функции (у)

Между значениями у₄ и у₂ два промежутка. Предполагая пропорциональность , где - шаг аргумента, получаем:

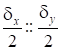
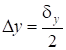
Это значит, что аргумент х₃ соответствует поправке к функции.

Знак + выбирается в зависимости от возрастания или убывания функции. Если функция возрастает сверху вниз ставится знак плюс, если убывает сверху вниз - знак минус.

В сущности методы табличного и графического сглаживания методом наименьших квадратов (МНК и разностного сглаживания) экспериментальных данных можно отнести к методам первичной линейной интерполяции. Более точным оказывается применение интерполяционных формул Ньютона, Лагранжа, итерационно-интерполяционных способов (процесс Эйткена). Необходимо обратить внимание на то, что понятия «интерполяция» и «аппроксимация» являются родственными. Но в контексте излагаемого можно понимать аппроксимацию несколько шире, чем интерполяцию, т.е. не только сглаживание результатов наблюдений, но и получение аппроксимационной эмпирической зависимости с учетом получения случайных результатов наблюдений ПФЭ. В то время, как интерполяция предусматривает только нахождение промежуточного значения функций, а в случае применения интерполяционных формул Ньютона и Лагранжа, так же получение интерполяционного полинома применяются для приближения вычислений значений функций. Это наиболее частый способ применения или для приближенного решения уравнений, содержащих нерешаемые аналитические функции (например, нелинейного уравнения, когда задана в точках в окрестности искомого корня).

Интерполяция и аппроксимация данных

Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем.

Интерполяция и экстраполяция данных

Задача интерполяции экспериментальных данных сводится к тому, чтобы предсказать в промежуточных точках значение функции заданной таблично. То есть исходные данные можно представить в виде таблицы, куда сводятся дискретных экспериментальные значения, полученные в некоторых точках наблюдений или в определенные интервалы времени.

Рассмотрим метод нахождения интерполяционной функции F(x) в виде канонического полинома P_n(x) степени n:

F(x)=P_n(x)= a₀ + a₁x+ a₂x²+…+ a_n-1x^n-1+ a_nx^т

Выбор многочлена P_n(x) степени n, основан на том, что через n + 1 точку проходит единственная кривая, описываемая полиномом P_n(x). Для нахождения значений коэффициентов полинома P_n(x): a₀, a₁, a₂, …, a_n-1, a_n необходимо решить систему линейных уравнений вида.

Решая эту систему уравнений относительно переменных a₀, a₁, a₂, …, a_n-1, a_n находятся коэффициенты интерполяционного полинома P_n(x).

Полином Лагранжа представляет полином вида

где – функция, удовлетворяющая в узлах x_k следующему свойству:

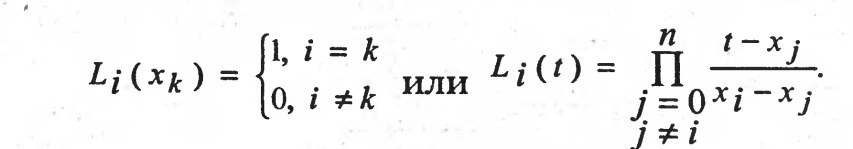
Таким образом, полином Лагранжа выражается следующей формулой

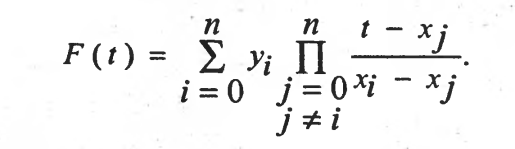
Реализация методов интерполяции и экстраполяции в Mathcad

В Mathcad можно соединять табличные точки прямой линией (линейная интерполяция), либо отрезками кубического полинома (кубическая сплайн-интерполяция). Линейная интерполяция реализуется посредством функции linterp(vx,vy,x), где vx, vy - векторы данных. Причём данные должны быть упорядочены по возрастанию; x - аргумент, для которого возвращается значение y.

Гораздо лучшие результаты интерполяции по сравнению с линейной дает сплайн-интерполяция, еоторая позволяет провести через набор точек гладкую кривую так, чтобы в этих точках были непрерывны первая и вторая производные. Интерполяция осуществляется двумя функциями. Вначале вычисляется вектор вторых производных в рассматриваемых точках, затем вычисляется значение функции в точке x  interp(vs,vx,vy,x). Для построения вектора вторых производных в Mathcad имеется набор из 3-х функций, предназначенных для вычисления вторых производных сплайн – функций:

- cspline(vx,vy) – возвращает вектор VS вторых производных с последующим построением сплайна по кубическому полиному;

- pspline(vx,vy) - возвращает вектор VS вторых производных с последующим построением сплайна по параболической кривой;

lspline(vx,vy) . возвращает вектор VS вторых производных с последующим построением сплайна по линейной зависимости.

Функция interp(vs,vx,vy,x) возвращает значения самой интерполяционной функции y(x) для заданных и вычисленных векторов VS, vx,vy.

Под экстраполяцией как уже пояснялось оанее понимают предсказание поведения функции за пределами области ее определения. Для предсказания (экстраполяции) поведения функции вне интервала задания его значений в MathCad предназначена функция predict(v,m,n). Эта функция использует линейный алгоритм предсказания. Здесь v - вектор эмпирических значений, m - количество ближайших к правой границе точек, на основе которых производится экстраполяция, n - количество точек, в которых производится экстраполяция данных. Результаты, получаемые на основе функции predict(v,m,n), в в значительной мере зависят от параметра m.

Этапы выполнения интерполяции и экстраполяции данных в Mathcad

1. Ввести экспериментальные данные (x_i , y_i , i∊[0,n]).

2. Отобразить графически распределение экспериментальных данных.

3. Выполнить интерполяцию согласно заданного варианта.

4. Проверить результаты интерполяции для 1 –ой , n/2-ой и n-ой точки с координатами x₁, x_n/2, x_n.

5. Провести расчеты значений для 2 новых точек с координатами
   .

6. Выполнить экстраполяцию данных для 3-х новых точек с координатами x_n+1, x_n+2 и x_n+3, используя: 3 последние точки ( x_n, x_n-1 и x_n-2); 5 последних точек; 7 последних точек.

7. Результаты интерполяции и экстраполяции отобразить графически.

Интерполяция и экстраполяция данных в Mathcad

Выполнить интерполяцию и экстраполяцию данных в Mathcad на основе представленных в таблице данных, методами, указанными в колонке «методы интерполяции».

Первоначально необходимо упорядочить данные в колонке «х» по возрастанию.

Дальнейшие пункты задания, выполненные в Mathcad, отображены на листинге, представленном ниже.

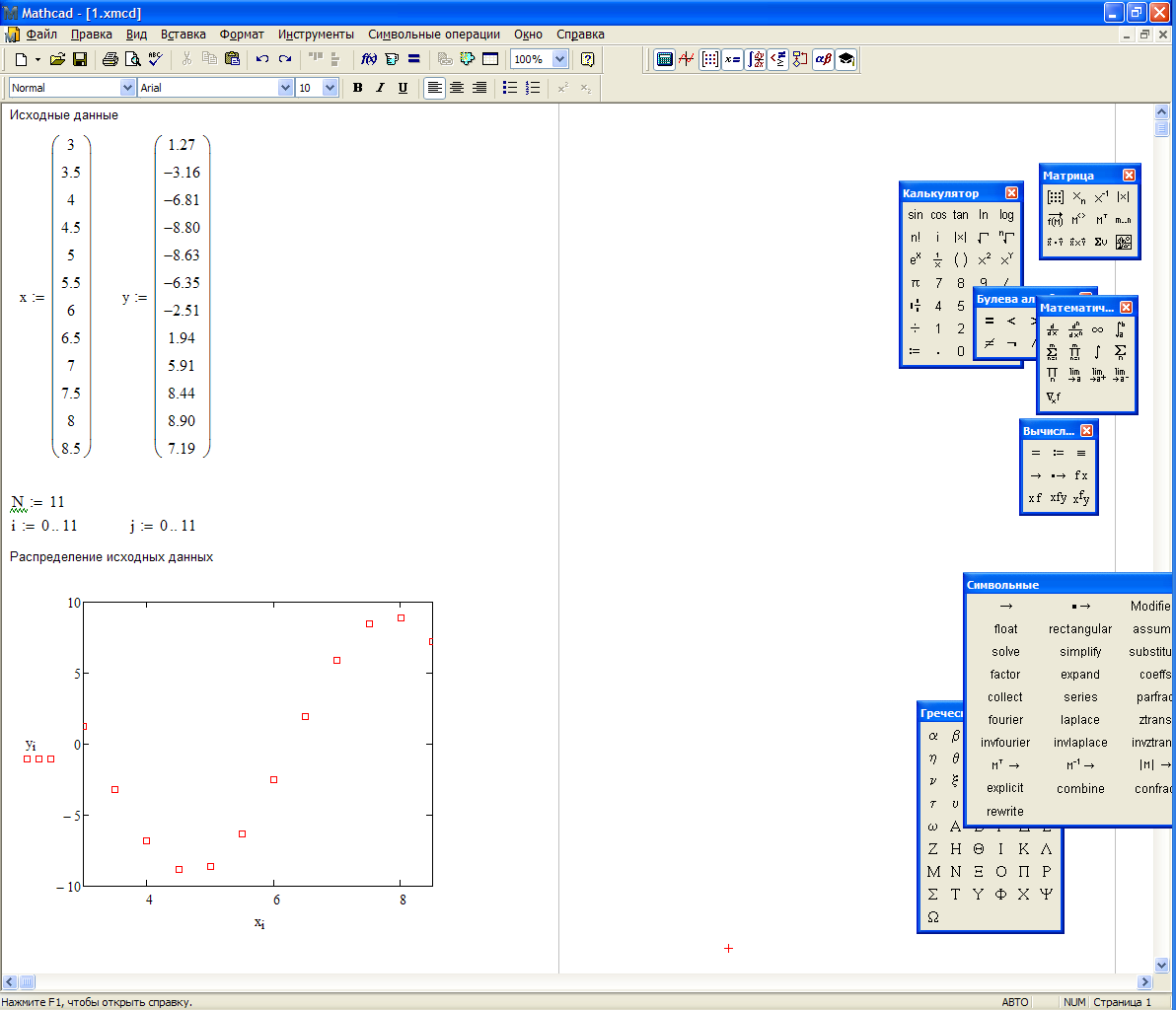
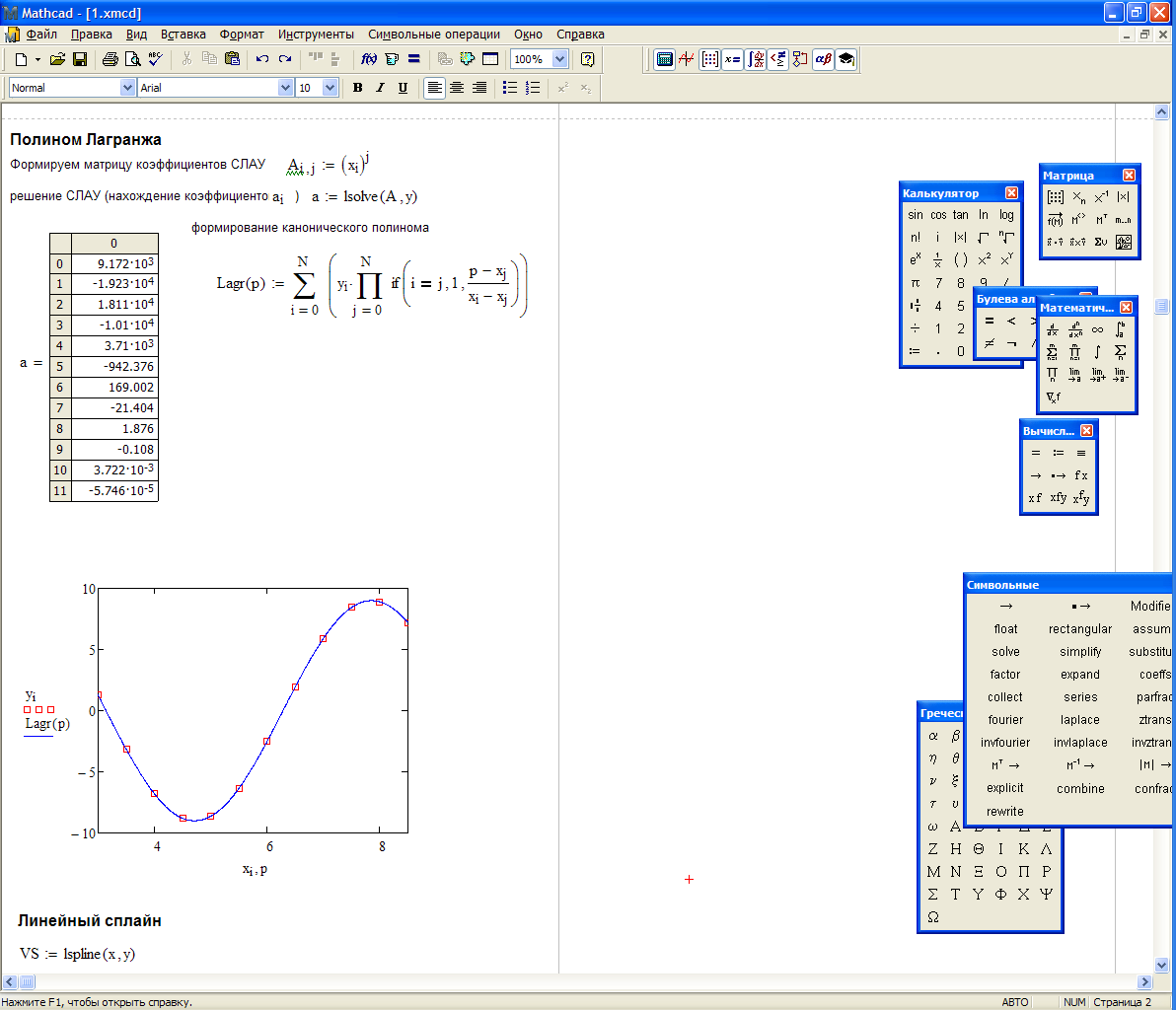
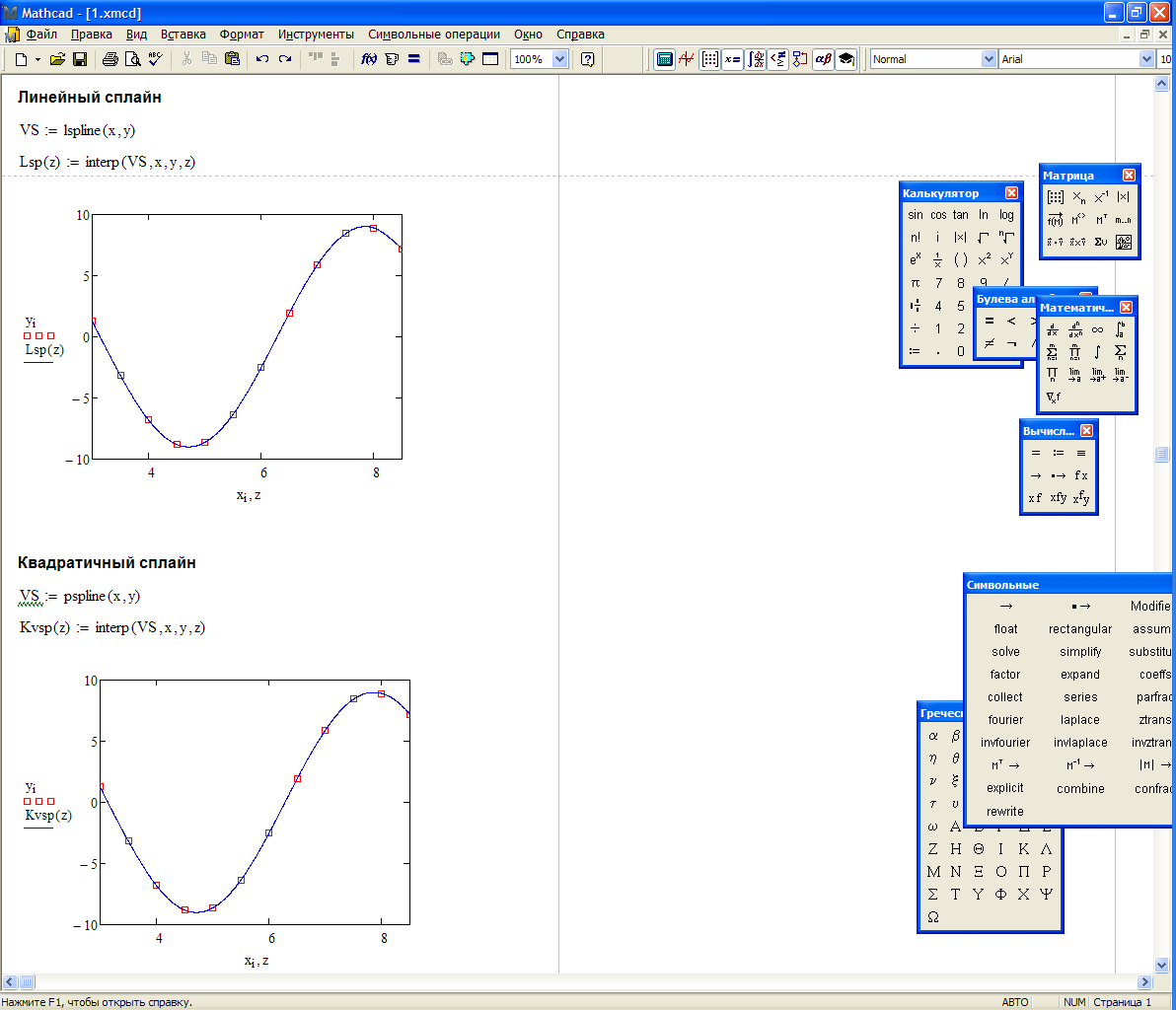
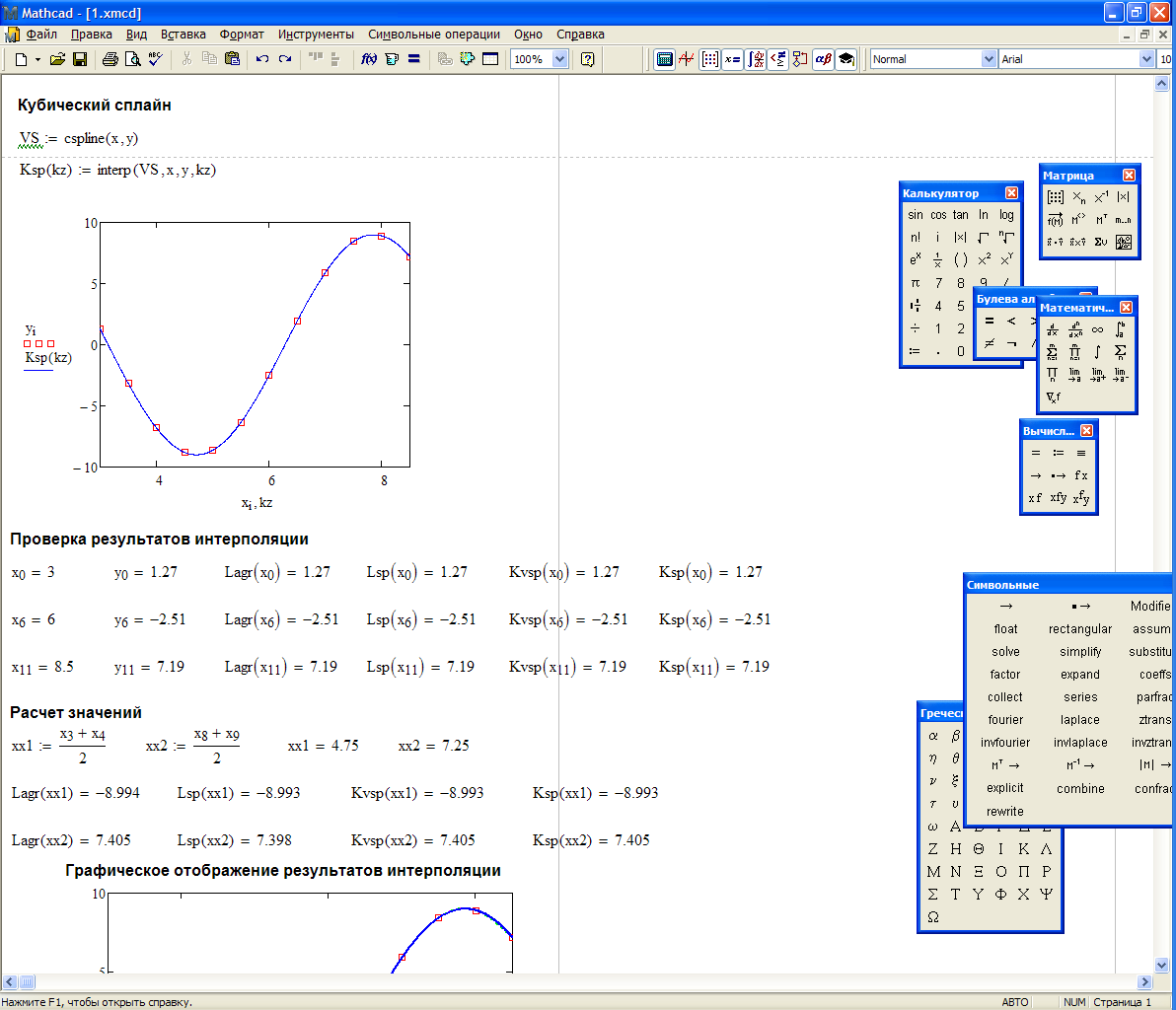
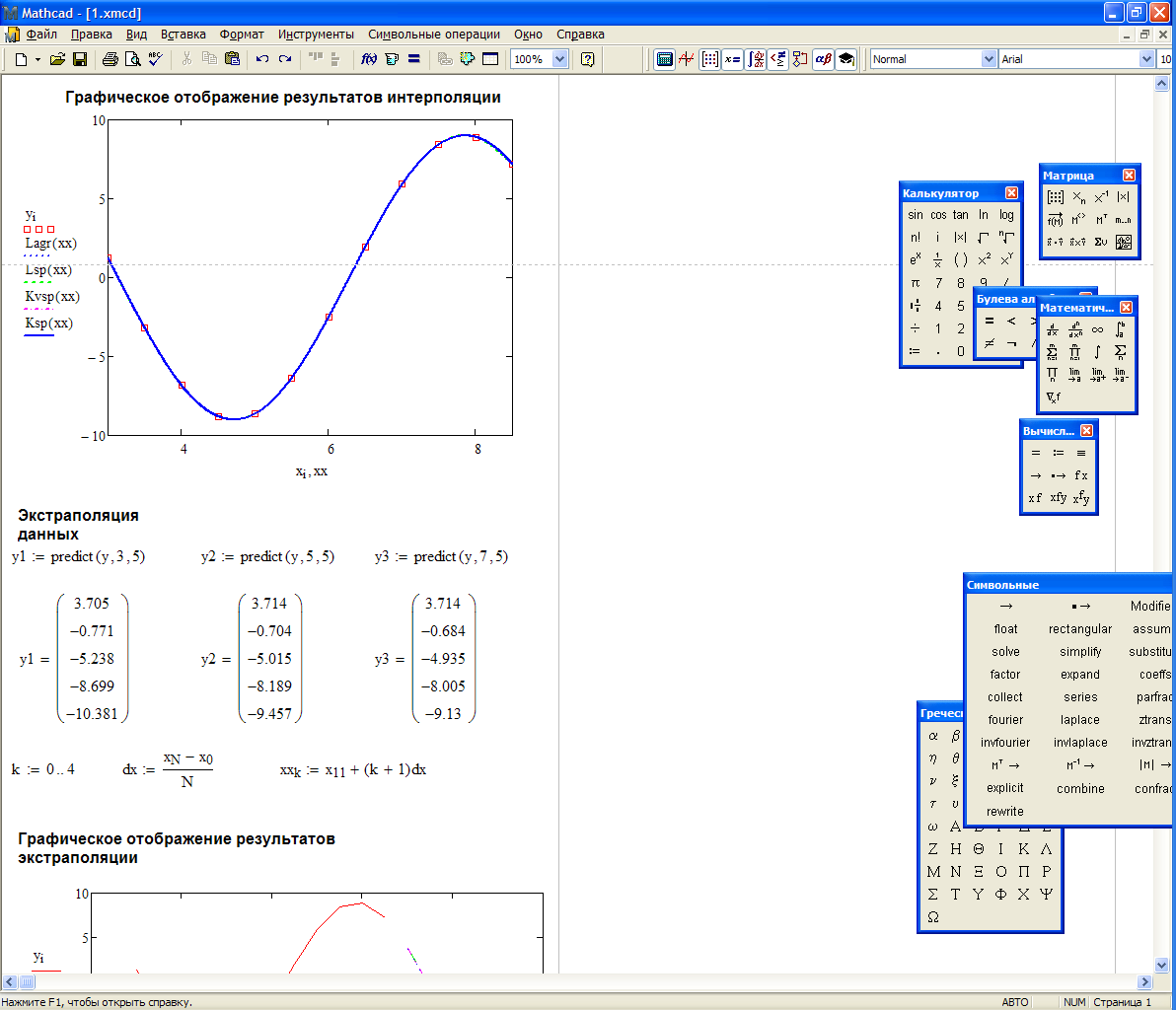
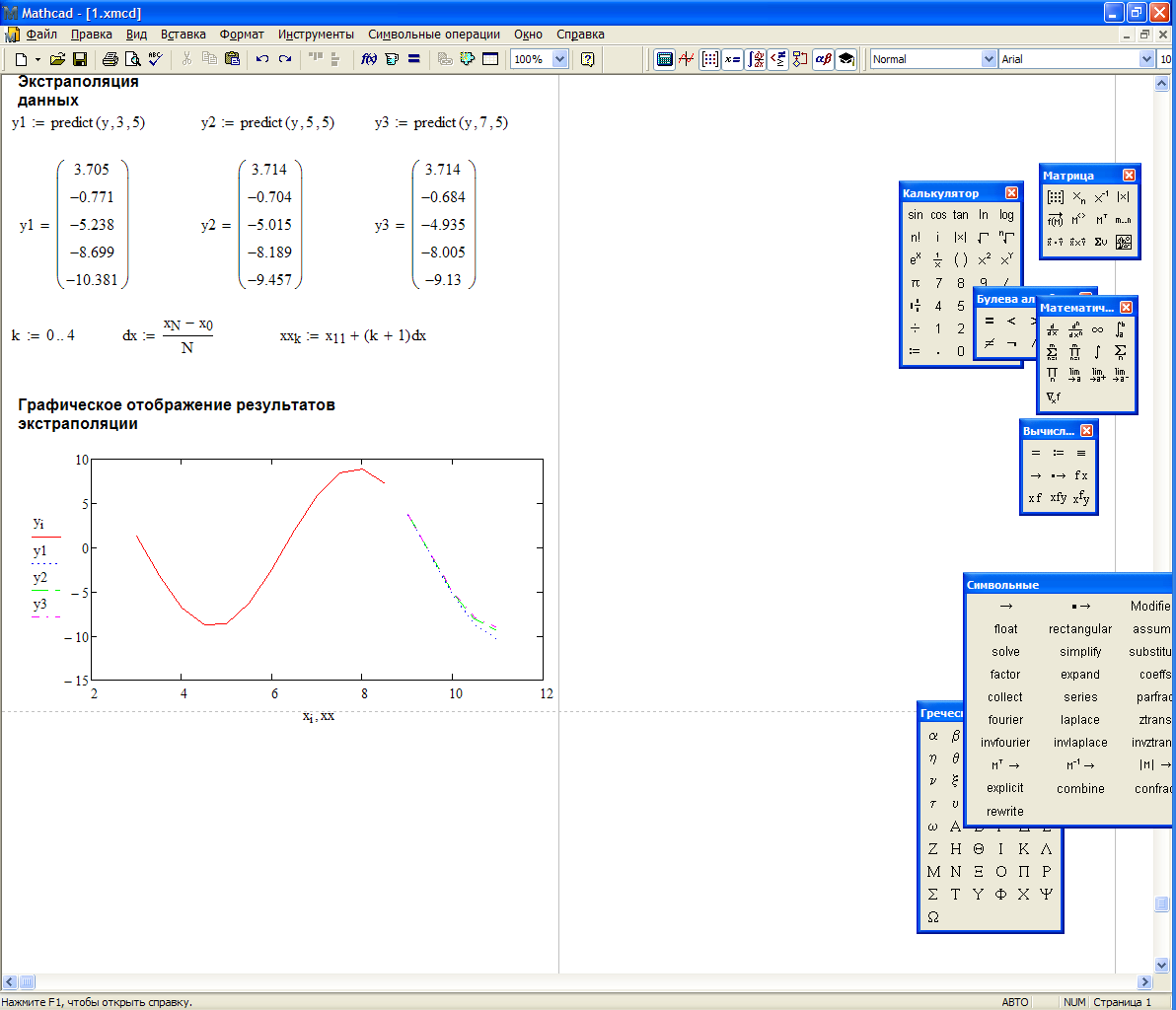
Подбор в MathCAD и Microsoft Excel подходящей эмпирической формулы для аппроксимации экспериментальных данных

Задача отыскания параметров эмпирической формулы является одной из наиболее важных задач, встречающихся при обработке результатов наблюдений, различных экспериментов и т.п. Ее суть в следующем.

Имеется m точек, заданных координатами в декартовой системе координат (x_i,y_i), i=1,…,m. Требуется найти такую функцию y=f(x), значения которой в точках x_i как можно более точно совпадают с y_i., т. е. y_if(x_i).

Слова «наилучшее приближение к имеющимся данным» могут пониматься по-разному. Наиболее часто используется так называемый принцип наименьших квадратов. Он основан на том, что из заданного множества формул вида y=f(x) наилучшей является та функция, для которой сумма квадратов отклонений вычисленных значений f(x_i) от наблюдаемых значений y_i является наименьшей. Подбор параметров функции f(x), основанный на этом принципе, называют методом наименьших квадратов.

Рассмотрим метод наименьших квадратов на примере эмпирической формулы, которая линейно зависит от 2-х параметров и имеет вид:

f(x)=(x, a, b)=a(x)+b(x). (1)

Заметим, что линейная зависимость формулы от параметров взята не случайно. В этом случае метод наименьших квадратов имеет наиболее простую и изящную реализацию. Что касается двух параметров, то это не принципиально, с двумя параметрами проще.

Введем в рассмотрение функцию, представляющую сумму квадратов отклонений:

. (2)

В соответствии с принятым подходом, параметры a и b необходимо подобрать таким образом, чтобы значение F(x,a,b) было минимальным:

. (3)

Как известно из курса высшей математики, точка минимума (a,b) необходимо удовлетворяет условиям:

(4)

Подставляя в систему (4) функцию (1), получаем:

(5)

После несложных преобразований приходим к системе уравнений

(5)

Решив систему (5), найдем значения параметров a и b, которые являются решением задачи (2).

Использование функций Microsoft Excel и Mathcad для решения задачи

При решении задачи в Microsoft Excel после вычисления коэффициентов линейного уравнения и элементов вектора свободных членов для решения системы линейных алгебраических уравнений необходимо использование матричных функций.

Электронная таблица Excel не имеет функций для решения систем уравнений, формулы для вычисления матриц необходимо формировать самостоятельно, используя известные методы, например метод Крамера или метод Гаусса (метод исключения переменных). Однако задача облегчается тем, что Excel имеет ряд функций для работы с матрицами:

МОПРЕД(массив) – вычисление определителя матрицы;

МОБР(массив) – вычисление обратной матрицы;

МУМНОЖ(массив; массив) – умножение матриц.

Это позволяет решать системы уравнений с использованием обратной матрицы: .

Этапы выполнения задания

1. Ввести экспериментальные данные (x_i , y_i , i [0,n]).

2. Отобразить график функции y_i = f(x_i), i [0,n].

3. Проанализировать графический вид функциональной зависимости y_i=f(x_i), i [0,n] и из предлагаемого набора графиков подобрать подходящую эмпирическую формулу.

4. Используя метод наименьших квадратов, найти значения параметров, от которых зависит формула.

5. Отобразить на графике исходные данные и данные, полученные на основе расчетной эмпирической формулы.

6. Выполнить расчеты, согласно пунктам 1 – 5 первоначально в Mathcad, затем в Microsoft Excel.

Интерполяция и экстраполяция данных в Mathcad

Имеются данные:

Построив с помощью Excel график заданной зависимости, получаем:

Рис. 2. График зависимости

Графическое представление зависимости позволяет предположить, что зависимость может задаваться следующей формулой:

, где a>0.

Параметры этой зависимости находятся из системы:

Ниже приводится рабочий лист Excel, на котором выполнен расчет коэффициентов системы и найдены параметры зависимости.

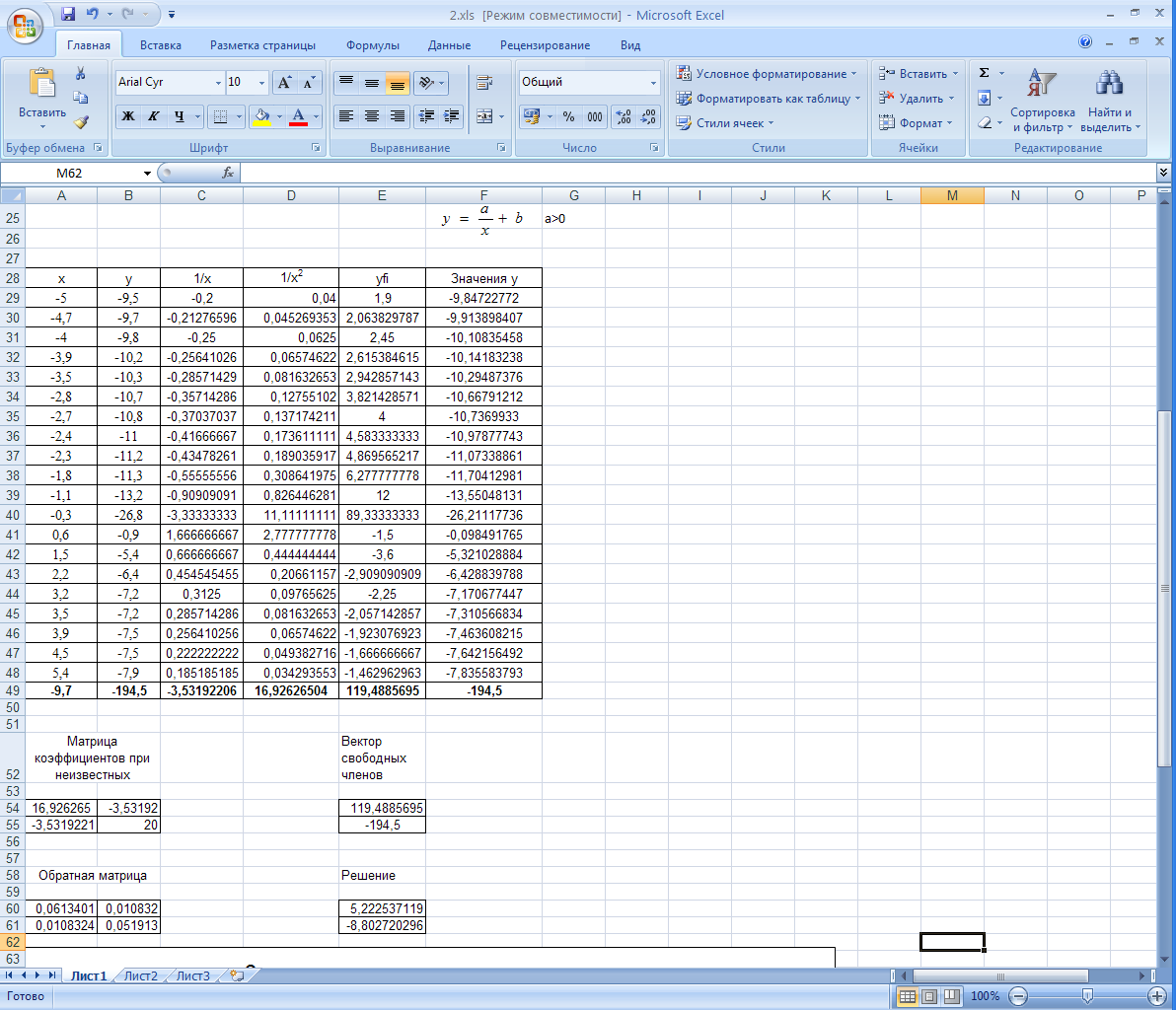
В системе MathCad подбор параметров искомой зависимости может быть выполнен следующим образом:

Аппроксимация данных в Mathcad и Micrrosoft Excel

Реализация методов аппроксимации в Microsoft Excel и Mathcad

В Mathcad существует набор функций, позволяющих осуществлять аппроксимацию. В таблице 1 представлены функции, используемые для аппроксимации с использованием различных регрессионных моделей.

Рассмотрим суть параметров, используемых в качестве аргументов в функциях. В каждой функции используются два вектора исходных данных, vx - вектор независимых переменных, vy - вектор зависимых переменных. Количество элементов вектора vx и vy должно быть одинаково. Функции regress и loess используются только совместно с функцией interp. Сами функции regress и loess вычисляют только вектор, требуемый функцией interp для определения самого полинома. Параметр span функции loess определяет величину области, на которой строится конкретный фрагмент полинома 2-ой степени. Оптимальное значение span, предлагаемое справочной системой Mathcad, равно 0.75, но в каждом конкретном случае рекомендуется путем вариантных расчетов подобрать наилучшее значение span. Параметр g является вектором начальных приближений для неизвестных функции регрессии. После определения регрессионных зависимостей, актуальным является выбор из их совокупности наилучшей функции, с точки зрения адекватности описания исходных экспериментальных данных. В качестве критерия, позволяющего выбрать наилучшую модель, предлагается использовать коэффициент детерминации, численно равный коэффициенту корреляции в квадрате. Значение коэффициента корреляции в MathCad позволяет рассчитать функция corr(A,B), где A и B – два вектора значений.

Другим способом определение коэффициентов функциональных зависимостей является использование функция Microsoft Excel или блок «ПОИСК РЕШЕНИЯ» Microsoft Excel.

Этапы выполнения задания

1. Ввести экспериментальные данные (x_i , y_i , i [0 ,n]).

2. Определить функциональные зависимости для аппроксимации экспериментальных данных на основе функций Mathcad, приведенных в таблице 1.

3. Вычислить в Mathcad значение коэффициента детерминации для каждой функциональной зависимости.

4. Отобразить графически в Mathcad исходные данные и полученные функциональные зависимости.

5. На основе вычисленных в Mathcad значений коэффициента детерминации обосновать выбор наилучшей функциональной зависимости. Для указанной функциональной зависимости, используя «Поиск решения» Microsoft Excel, определить значения коэффициентов этой функциональной зависимости, а затем сравнить их значения со значениями, полученных в Mathcad.

Выполнение аппроксимации данных в Microsoft Excel и MathCAD

Задание согласно номеру варианта:

Листинг решения в MathCAD:

Л и н е й н а я м о д е л ь

П о л и н о м и а л ь н а я 4-й с т е п е н и

Ф р а г м е н т ы п о л и н о м о в 2-й с т е п е н и

Э к с п о н е н ц и а л ь н а я м о д е л ь

С р а в н е н и е м о д е л е й

Из приведенных расчетов можно сделать вывод, что наилучшей функцией является полиномиальная 4-й степени, полученная с помощью функции regress(), так как значение коэффициента детерминации для нее имеет максимальное значение = 0,854.

Решение задачи в Microsoft Excel с помощью надстройки «Поиск решения».

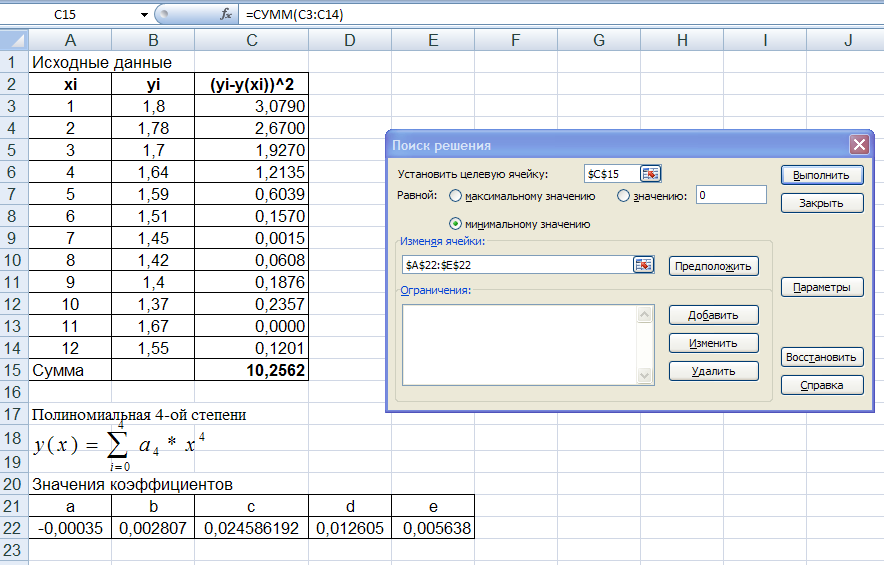
Сравним результаты, полученные в MathCAD и Excel.

(в MathCAD)

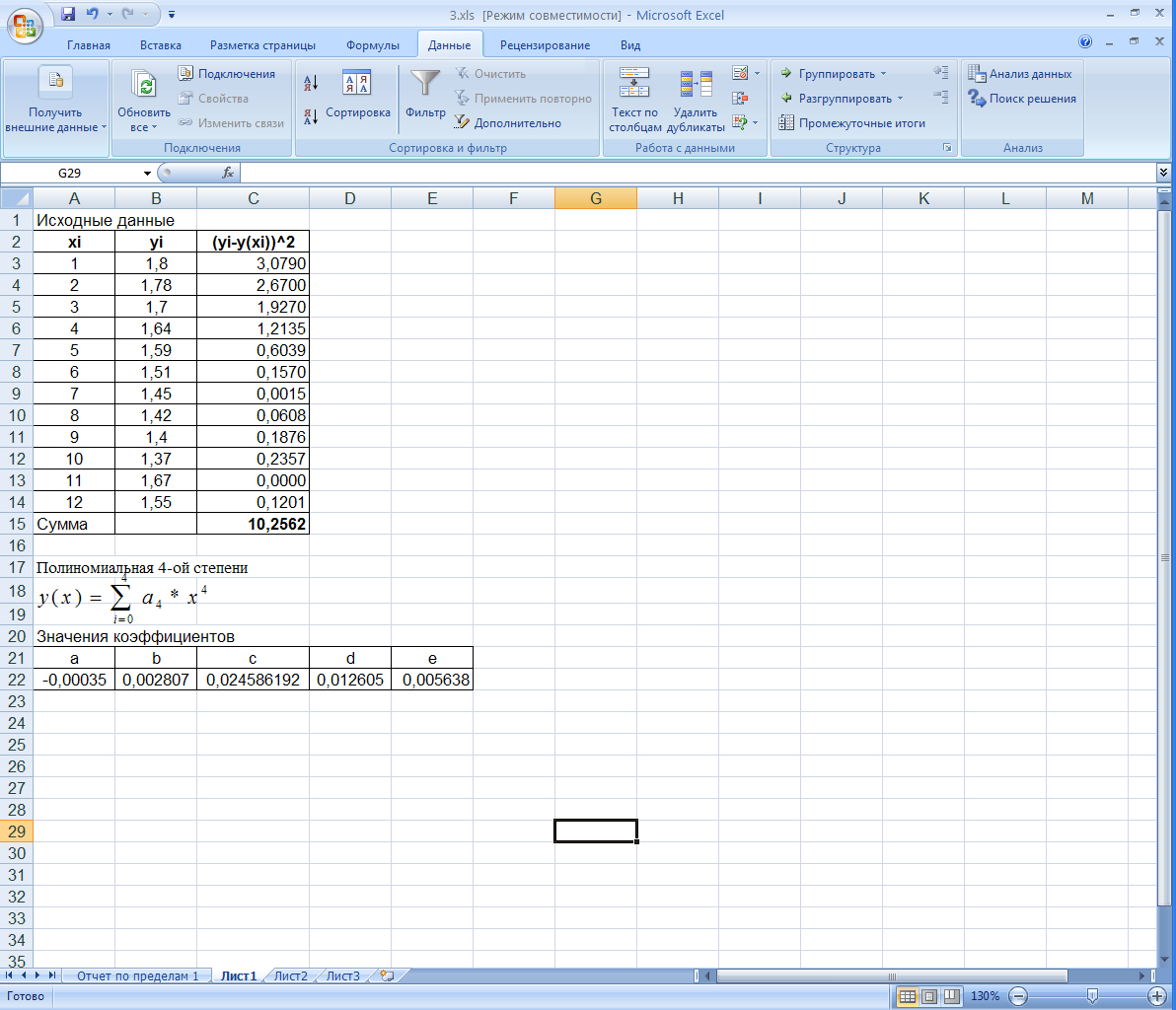(в Excel)

Значения коэффициентов для полиномиальной 4-й степени зависимости отличаются. Скорее всего, из-за различных алгоритмов в MathCAD и Excel.

Литература

1. Гловацкая А.П. Методы и алгоритмы вычислительной математики. Уч.пос. для ВУЗОВ.-М. Радио и связь, 1999.-408с.

2. Данченко В. П., Кондакова Е. Н. Чебышевский альтернанс при аппроксимации констант наипростейшими дробями // Тр. МИАН. — 2010. Т. 270. - С. 86-96.

3. Фрянцев А. В. О численной аппроксимации дифференциальных полиномов // Изв. Саратов, ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2007. - Т. 7, № 2. - С. 39-

4. Чунаев П. В. Об одном нетрадиционном методе аппроксимации // Дифференциальные уравнения и динамические системы: Сб. статей. Тр. МИАН. 2010. - Т. 270. - С. 281-287.

5. Macintyre A. J., Fuchs W.H.J. Iniqualities for the logarithmic derivatives of a polynomial //J. London Math. Soc. — 1940. — V. 15. — P. 162-168.

6. Демидович Б. П., Марон И. А. Основы вычислительной математики. — М.: Физматгиз, 1963. — 660 с.

7. Фихтенгольц Г. М. Основы математического анализа. — СПб., М., Краснодар: Лань, 2005 г.

8. Кондакова Е. Н. Об интерполяции наипростейшими дробями // Между нар. конференция по дифференциальным уравнениям и динамическим системам. — Суздаль, 2008. — С. 138-139.

9. Данченко В. П., Кондакова Е. Н. Об интерполяции наипростейшими дробями // Современные методы теории краевых задач: материалы Воронеж, весен, матем. шк. "Понтрягинские чтения XX". — Воронеж, 2009. - С. 46-47.

10. Данченко В. И., Кондакова E. Н. Критерий возникновения особых узлов в задаче интерполяции наипростейшими дробями// Современные проблемы теории функций и их приложения: материалы 16-й зим. шк. — Саратов, 2012. — С. 62-63.