|
Ұзақмерзімдіжоспарбөлімі: Тікбұрышты үшбұрыштың қабырғалары мен бұрыштары арасындағы қатыстар |
Мектеп: “Damu school “ |
||
|
Күні: |
Мұғалімніңаты-жөні: Іздік Ақерке |
||
|
Класс: 8 а |
Қатысқандар саны: |
Қатыспағандар саны: |
|
|
Сабақтақырыбы |
Негізгі тригонометриялық тепе-теңдіктер |
||
|
Осысабақтақолжеткізілетіноқумақсаттары (оқубағдарламасынасілтеме) |
8.1.3.21Пифагор теоремасын
пайдаланып,
|
||
|
Сабақтыңмақсаттары |
Оқушылар: біледі:
қолдана алады:
|
||
|
Бағалаукритерийлері |
Оқушылар: біледі:
қолдана алады:
|
||
|
Тілдікмақсаттар |
Оқушылар:
Пәндік лексика және терминология:
|
||
|
Құндылықтардыдарыту |
Оқушыларды ашықтыққа үйрету - оқушылардың өздеңгейлерін нақты бағалауды және оқу мақсаттарын қаншалықты игергендігін дәл айқындауды дағдыларын ұштайды. |
||
|
Пәнаралықбайланыс |
Практикалық тапсырмаларды орындау арқылы шынайы өмірмен байланыстыру. |
||
|
Бастапқы білім |
Пифагор теоремасы, тік бұрышты үшбұрыш, ондағы қарапайым тригонометриялық қатынастар |
||
Сабақбарысы:
|
Сабақтыңжоспарланғанкезеңдері |
Сабақтағыжоспарланғаніс-әрекет |
Ресурстар |
||
|
Сабақтың басы 1-3минут |
Ұйымдастыру кезеңі.Тірек білімдерді белсендендіру Ауызша сұрақтар қою:
Сөйтіп, оқушылармен бірлесе отырып сабақ мақсатына сәйкес бағалау критерийлері және дамудың жақын аймағын айқындау. |
№3-4слайдтар |
||
|
Сабақтыңортасы
4-28 минут |
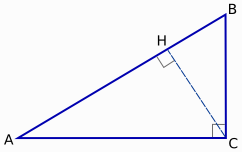
Тікбұрышты үшбұрыштың бір бұрышының синусы мен косинусының квадраттарының қосындысы1-ге тең. sin2α + cos2α = 1 негізгі тригонометриялық теңбе-теңдікдеп аталады. Дәлелдеу:ABC (∠C = 90º)тікүшбұрышыберілген. CHгипотенузғажүргізілгенбиіктік.
ABCүшбұрышыныңкатеттерін косинус
арқылыбелгілейік:
ЕндіACH үшбұрышын
қарастырамыз. Ол да тік,
яғни
Онда
Бұданмынаныаламыз: AH:
AC кесіндісін ABC үшбұрышының А бұрышының синусы арқылы белгілейміз. Сонда шығатыны:
ЕндіBCH қарастырамыз.
Онда
BH белгілеп, ВС
ныоныңмәндеріарқылыөрнектейміз: ABC:
ABкесіндісіAHжәнеBH
қабырғаларының қосындысына тең: AHжәнеBHкесінділерінолардыңкосинустарыарқылыбелгілейік:
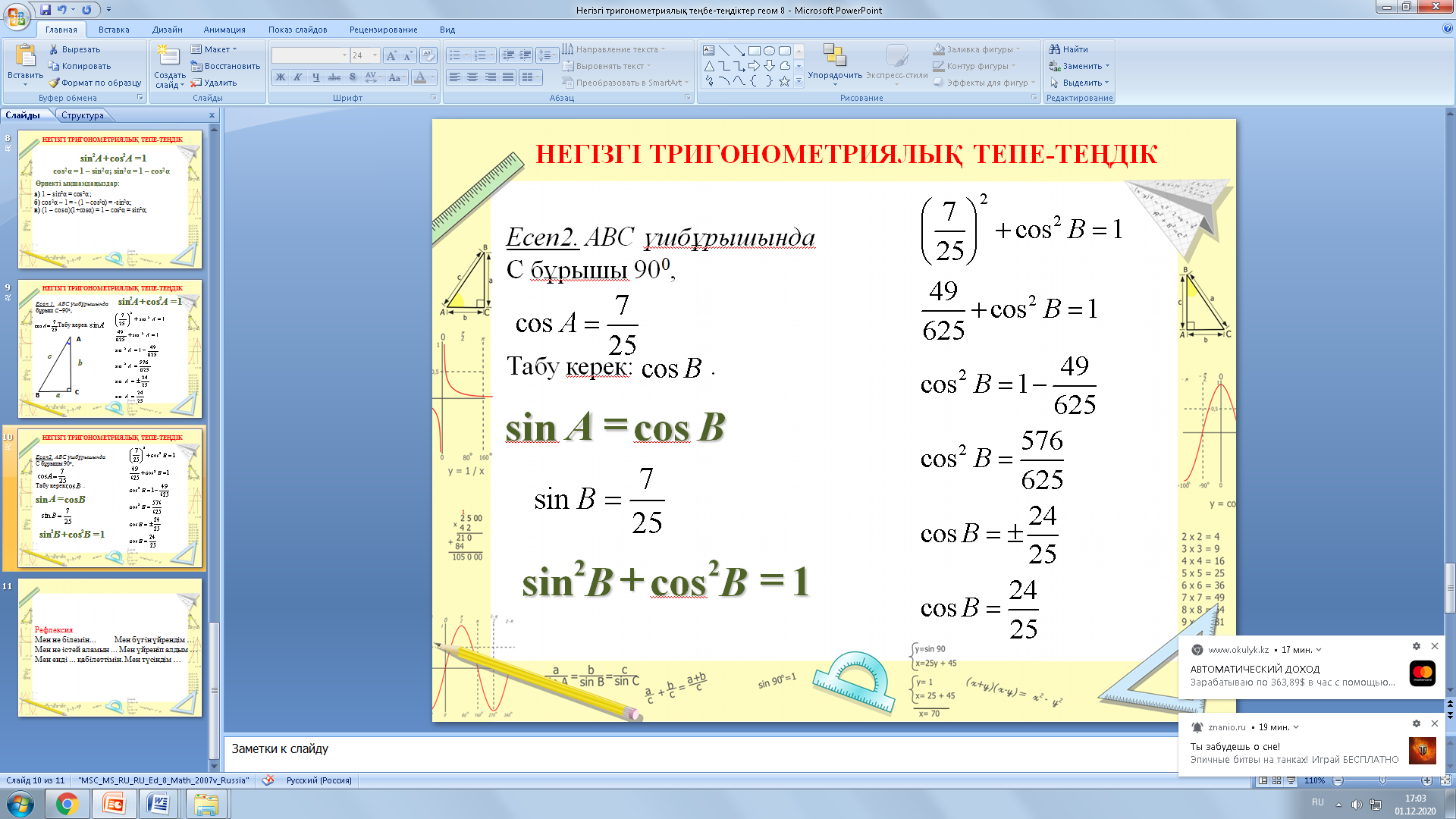
Тікбұрыштыүшбұрыштыңсүйірбұрышының синусы мен осы
үшбұрыштыңекіншісүйірбұрышының косинусы теңекенібелгілі.
Бұлжағдайда:
Сәйкесінше,
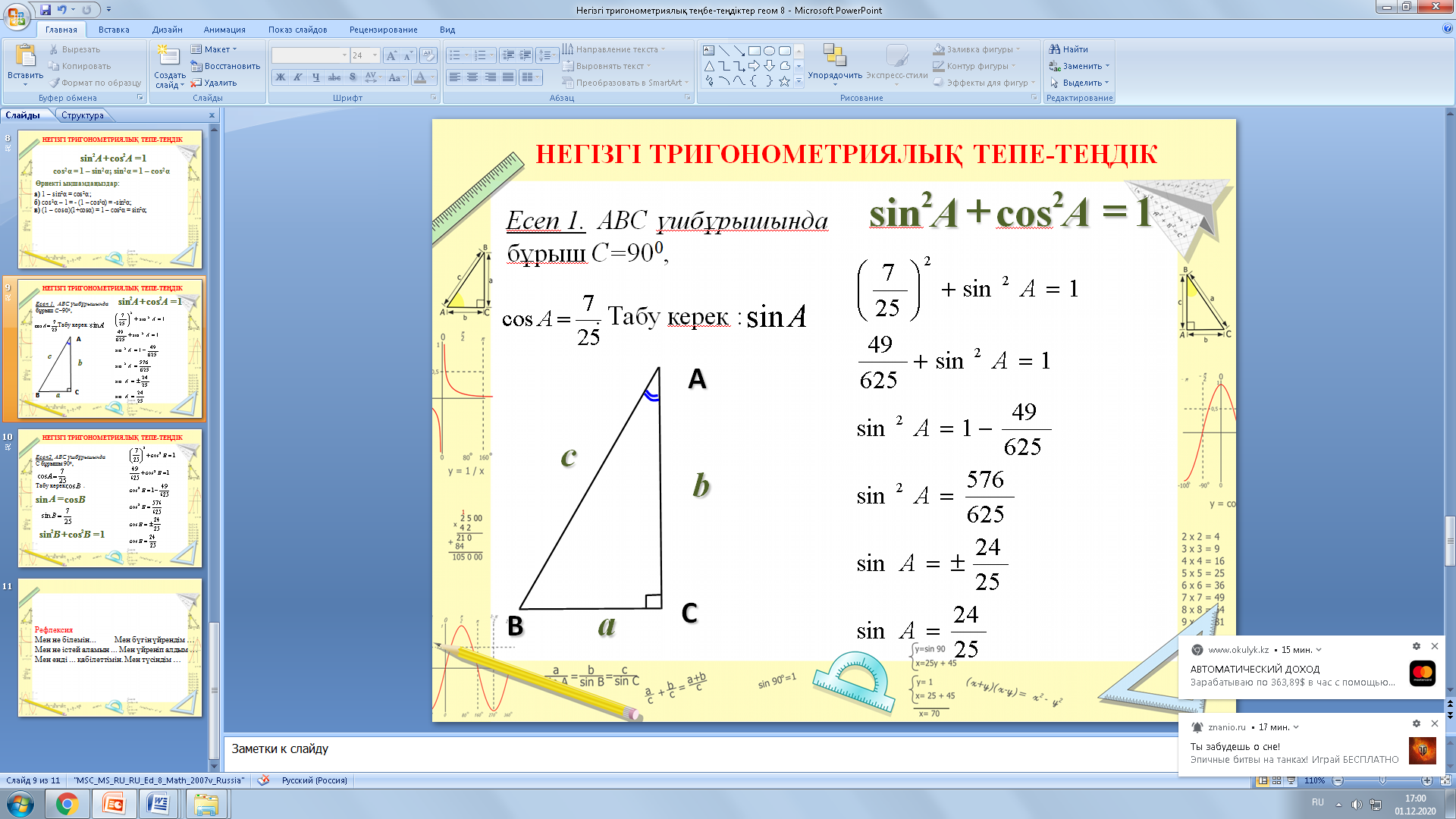
Сөйтіп, тікбұрышты үшбұрыштың бір бұрышының синусы мен косинусының квадраттарының қосындысы 1-ге тең екендігі шығады. sin2α + cos2α = 1 пайдаланып өрнекті ықшамдаңыз а)1 – sin2α; б)cos2α – 1; в)(1 – cosα)(1+cosα);
|
№ 5-7слайд №8 слайд №9-10 слайд |
||
|
|
||||
|
Сабақтыңсоңы 28 - 30 мин |
Рефлексия. Мен не білемін... Мен бүгін үйрендім … Мен не істей аламын ... Мен үйреніп алдым … Мен енді ... қабілеттімін. Мен түсіндім … |
\ |
||
|
Саралау –оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілетіжоғарыоқушыларғақандайміндетқоюдыжоспарлапотырсыз? |
Бағалау – оқушылардыңматериалдымеңгерудеңгейінқалайтексерудіжоспарлайсыз? |
Денсаулықжәнеқауіпсіздіктехникасыныңсақталуы |
||
|
Сабақтаоқытудыңсаралауәдісіәрдеңгейлітпотарғабөлуарқылыкөріністабады. Оқушыларжұппенжұмысжасаукезіндетапсырмалардыкүрделілікдеңгейінебайлыныстыөздерітаңдайды. |
Теориялықбілімдерінбағалаукезіндеоқушыларөзінөзітексеруәдісінқолданады, соныменбіргеөздікжұмыстарынтексерудебірінбірібағалайды. Топтықжұмыскезіндеоқушылардыңтеоремалардыдәлелдеубарысындаүшбұрыштардыңтеңдігінқолданудағдылары да тексеріледі. |
Сабақбарысындасызуқұралдарынқолданудақауіпсіздікережелерінқадағалау.Оқушылардыңтікотыруынқадағалау. |
||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Негізгі тригонометриялық тепе-теңдіктер
Негізгі тригонометриялық тепе-теңдіктер
|
Ұзақмерзімдіжоспарбөлімі: Тікбұрышты үшбұрыштың қабырғалары мен бұрыштары арасындағы қатыстар |
Мектеп: “Damu school “ |
||
|
Күні: |
Мұғалімніңаты-жөні: Іздік Ақерке |
||
|
Класс: 8 а |
Қатысқандар саны: |
Қатыспағандар саны: |
|
|
Сабақтақырыбы |
Негізгі тригонометриялық тепе-теңдіктер |
||
|
Осысабақтақолжеткізілетіноқумақсаттары (оқубағдарламасынасілтеме) |
8.1.3.21Пифагор теоремасын
пайдаланып,
|
||
|
Сабақтыңмақсаттары |
Оқушылар: біледі:
қолдана алады:
|
||
|
Бағалаукритерийлері |
Оқушылар: біледі:
қолдана алады:
|
||
|
Тілдікмақсаттар |
Оқушылар:
Пәндік лексика және терминология:
|
||
|
Құндылықтардыдарыту |
Оқушыларды ашықтыққа үйрету - оқушылардың өздеңгейлерін нақты бағалауды және оқу мақсаттарын қаншалықты игергендігін дәл айқындауды дағдыларын ұштайды. |
||
|
Пәнаралықбайланыс |
Практикалық тапсырмаларды орындау арқылы шынайы өмірмен байланыстыру. |
||
|
Бастапқы білім |
Пифагор теоремасы, тік бұрышты үшбұрыш, ондағы қарапайым тригонометриялық қатынастар |
||
Сабақбарысы:
|
Сабақтыңжоспарланғанкезеңдері |
Сабақтағыжоспарланғаніс-әрекет |
Ресурстар |
||
|
Сабақтың басы 1-3минут |
Ұйымдастыру кезеңі.Тірек білімдерді белсендендіру Ауызша сұрақтар қою:
Сөйтіп, оқушылармен бірлесе отырып сабақ мақсатына сәйкес бағалау критерийлері және дамудың жақын аймағын айқындау. |
№3-4слайдтар |
||
|
Сабақтыңортасы
4-28 минут |
Тікбұрышты үшбұрыштың бір бұрышының синусы мен косинусының квадраттарының қосындысы1-ге тең. sin2α + cos2α = 1 негізгі тригонометриялық теңбе-теңдікдеп аталады. Дәлелдеу:ABC (∠C = 90º)тікүшбұрышыберілген. CHгипотенузғажүргізілгенбиіктік.
ABCүшбұрышыныңкатеттерін косинус
арқылыбелгілейік:
ЕндіACH үшбұрышын
қарастырамыз. Ол да тік,
яғни
Онда
Бұданмынаныаламыз: AH:
AC кесіндісін ABC үшбұрышының А бұрышының синусы арқылы белгілейміз. Сонда шығатыны:
ЕндіBCH қарастырамыз.
Онда
BH белгілеп, ВС
ныоныңмәндеріарқылыөрнектейміз: ABC:
ABкесіндісіAHжәнеBH
қабырғаларының қосындысына тең: AHжәнеBHкесінділерінолардыңкосинустарыарқылыбелгілейік:
Тікбұрыштыүшбұрыштыңсүйірбұрышының синусы мен осы
үшбұрыштыңекіншісүйірбұрышының косинусы теңекенібелгілі.
Бұлжағдайда:
Сәйкесінше,
Сөйтіп, тікбұрышты үшбұрыштың бір бұрышының синусы мен косинусының квадраттарының қосындысы 1-ге тең екендігі шығады. sin2α + cos2α = 1 пайдаланып өрнекті ықшамдаңыз а)1 – sin2α; б)cos2α – 1; в)(1 – cosα)(1+cosα);
|
№ 5-7слайд №8 слайд №9-10 слайд |
||
|
|
||||
|
Сабақтыңсоңы 28 - 30 мин |
Рефлексия. Мен не білемін... Мен бүгін үйрендім … Мен не істей аламын ... Мен үйреніп алдым … Мен енді ... қабілеттімін. Мен түсіндім … |
\ |
||
|
Саралау –оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілетіжоғарыоқушыларғақандайміндетқоюдыжоспарлапотырсыз? |
Бағалау – оқушылардыңматериалдымеңгерудеңгейінқалайтексерудіжоспарлайсыз? |
Денсаулықжәнеқауіпсіздіктехникасыныңсақталуы |
||
|
Сабақтаоқытудыңсаралауәдісіәрдеңгейлітпотарғабөлуарқылыкөріністабады. Оқушыларжұппенжұмысжасаукезіндетапсырмалардыкүрделілікдеңгейінебайлыныстыөздерітаңдайды. |
Теориялықбілімдерінбағалаукезіндеоқушыларөзінөзітексеруәдісінқолданады, соныменбіргеөздікжұмыстарынтексерудебірінбірібағалайды. Топтықжұмыскезіндеоқушылардыңтеоремалардыдәлелдеубарысындаүшбұрыштардыңтеңдігінқолданудағдылары да тексеріледі. |
Сабақбарысындасызуқұралдарынқолданудақауіпсіздікережелерінқадағалау.Оқушылардыңтікотыруынқадағалау. |
||

шағым қалдыра аласыз