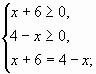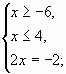Краткосрочный план урока
|
КГУ «Технологический колледж города Алтай» Управления образования Восточно-Казахстанской области |
||||
|
Наименование модуля |
ООД 01 |
|||
|
Поурочный план по предмету |
Математика |
|||
|
Раздел |
Степени и корни |
|||
|
Дата урока |
"27" октябрь 2021 год |
|||
|
Урок № |
45-46 |
|||
|
Тема занятия |
Иррациональные уравнения |
|||
|
Подготовил педагог |
Омырбаева Жанар Муратовна |
|||
|
Общие сведения |
||||
|
Курс, группы |
|
|||
|
Тип занятия |
комбинированный |
|||
|
Цели обучения (в соответствии с УП) |
Знает определение иррационального уравнения; Умеет применять алгоритм решения иррациональных уравнений |
|||
|
Цель урока |
Научить решению иррациональных уравнений, возведением обеих частей в одну и ту же степень |
|||
|
Языковые цели |
Студенты понимают и используют математические термины для описания решения иррациональных уравнений. Развитие навыков речи: дает полные устные/письменные ответы по содержанию. Применяемые тематические слова: степень (возведение в степень), число, левая и правая части уравнения, уравнения, корень уравнения, посторонний корень уравнения, ОДЗ. |
|||
|
Критерии оценивания |
1) Объясняет содержание определения иррационального уравнения и находит область допустимых значений иррационального уравнения; 2) Решает иррациональные уравнения и неравенства методом возведения обеих частей уравнения в n-ую степень; 3) Решает иррациональные уравнения и неравенства и методом замены переменной. |
|||
|
Привитие ценностей |
Создать условия для формирования у студентов умений решать иррациональные уравнения; для развития алгоритмического мышления, памяти, внимательности, умения излагать мысли, делать выводы, обобщать; для усиления познавательной мотивации осознанием студента своей значимости в учебном процессе; для воспитания у студентов самостоятельности. |
|||
|
Межпредметные связи |
Физика, химия |
|||
|
Предварительные знания |
Решение линейных и квадратных уравнений. |
|||
|
Оснащение занятия |
||||
|
Учебно-методическое оснащение, справочная литература (учебник, справочник) |
А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жумагулова, «Алгебра и начала анализа» Учебник для 10 классов естественно- математического направления обшеобразовательных школ 1-2 часть. Алматы: Мектеп, 2019 г. |
|||
|
Техническое оснащение, материалы (ТСО, дидакттика) |
Маршрутный лист урока 45-46, карточки с дифференцированными заданиями, карточки с тестовыми заданиями, картинки для рефлексии |
|||
|
Ход урока |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Начало урока |
Организационный этап: - приветствие, - проверка готовности студентов к занятию, - проверка посещаемости. Проверка домашнего задания Свойства арифметического корня натуральной степени: Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:
Примеры:
Примеры:
Пример:
Пример:
Повторение пройденной темы Примеры решения линейного и квадратного уравнений:
Актуализация знаний Нам известно, что в математике одним из важнейших умений является умение решать уравнения. С понятием уравнения вы уже знакомы со школы. Научились решать линейные и квадратные уравнения. Сегодня на уроке мы продолжим работу в этом направлении и рассмотрим еще один вид уравнений. Даны уравнения, посмотрите внимательно и определите, какие уравнения вы знаете и умеете решать, а какие вам не знакомы и вызывают затруднения. 1) 2) 3) 4) 5) 6) 7) 8) Что объединяет уравнения 1, 2, 6, 8? (неизвестная переменная находится под знаком корня). Правильно. Такие уравнения называются иррациональными. Итак, тема нашего урока «Иррациональные уравнения». Давайте мы вместе сформулируем цель нашего урока. (узнать какие уравнения называются иррациональными и научиться решать иррациональные уравнения) А теперь составим план урока. На доске даны формулировки плана. Ваша задача расставить их в правильном порядке.
Сегодня на уроке мы все вместе постараемся реализовать поставленные цели. У всех возник вопрос: зачем нам изучать решение иррациаональных уравнений. Ответ простой: иррациональным уравнением выражаются формулы, описывающие многие физические процессы: равноускоренное движение, первая и вторая космические скорости, среднее значение скорости теплового движения молекул, период радиоктивного полураспада и другие. Эйнштейн говорил так: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения по – моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно». Вот мы и займемся сегодня уравнениями. |
Маршрутный лист |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Середина урока |
Изучение новой темы Определение. Уравнения, в которых под знаком корня содержится переменная, называют иррациональными. Существует множество методов решения иррациональных уравнений. Методы:
Решим данные иррациональные уравнения № 1.
ОДЗ: 3х+1>0 3x> - 1 x> - 1/3
Возведём обе части уравнения в квадрат, получим:
Д= 81-32=49 Х1 = 1, Х2 = 8 Проверка: Если 5 = 1 -–неверно. 8 = 8 -–верно. Значит, Ответ: Следующие уравнения студенты решают самостоятельно (студент у доски) с последующей проверкой. № 2.
Возведём обе части уравнения в квадрат, получим:
Проверка: Если 10=10-верно. 10=10-верно. Значит, Ответ. -3;3. № 3.
Ответ. Вывод: 1) Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путём возведения в степень обеих частей уравнения. 2) При возведении обеих частей уравнения в чётную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение. Метод решения иррациональных уравнений заключается в следующем:
Физпауза А теперь, ребята, встать Руки медленно поднять Пальцы сжать, потом разжать Руки вниз и так стоять Наклонитесь вправо, влево И беритесь вновь за дело! |
Маршрутный лист |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Конец урока |
Закрепление новой темы «Аукцион идей» (студентам предлагаются разноуровневые задания на отдельных карточках, цвет карточки определяет уровень задания) Красный – 100 % Зеленый – 75 % Желтый – 50 % Задания:
ЖИ арқылы жасау
ЖИ арқылы жасау
Бөлісу 1 - айлық Материал тарифі-96% жеңілдік 00 05 00 ҚМЖ
Ашық сабақ
Тәрбие сағаты
Презентация
БЖБ, ТЖБ тесттер
Көрнекіліктер
Балабақшаға арнарлған құжаттар
Мақала, Эссе
Дидактикалық ойындар
және тағы басқа 400 000 материал
Барлық 400 000 материалдарды шексіз жүктеу мүмкіндігіне ие боласыз 1 990 ₸ 49 000₸ 1 айға қосылу Материалға шағымдану Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз Жариялаған: Омырбаева Жанар МуратовнаШағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз открытый урок "Иррациональные уравнения"
Тақырып бойынша 11 материал табылды
открытый урок "Иррациональные уравнения"Материал туралы қысқаша түсінік
Создать условия для формирования у студентов умений решать иррациональные уравнения; для развития алгоритмического мышления, памяти, внимательности, умения излагать мысли, делать выводы, обобщать; для усиления познавательной мотивации осознанием студента своей значимости в учебном процессе; для воспитания у студентов самостоятельности.
Материалдың қысқаша нұсқасы Краткосрочный план урока
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


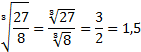 .
.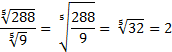 .
.