|
Раздел: 8.3А |
8.3А Площади. |
|
|
ФИО педагога: |
Расулметова М.А |
|
|
Дата: |
21.02.2025г |
|
|
Класс: 8 «Б» |
Количество присутствующих: |
Количество отсутствующих: |
|
Тема урока: |
Площади четырёхугольников и треугольников. |
|
|
Цели обучения в соответствии с учебной программой. |
8.1.3.13 выводить и применять формулы площади трапеции |
|
|
Цели урока: |
Применяет формулы площади трапеции для решения задач |
|
|
Привитие ценностей |
навыки использования различных познавательных инструментов, сбора знаний об окружающем мире (языке, культуре чтения, информации, цифровой среде). |
|
|
|
|
|
|
Этапы урока |
Действия педагога |
Действия ученика |
Оценивание Рубрика |
Ресурсы |
|
Начало урока |
Приветствие.
Проверка домашнего задания.
Проверьте как верно вы решили домашние задачи по слайдам и поставьте баллы в лист оценивания.
1) Высота трапеции равна 16 см, а площадь 4 дм2. Найдите длину средней линии.
2) Площадь трапеции равна 288 см2, основания относятся как 4:5, высота – 3,2 дм. Вычислите основания.
3) Меньше основание равнобедренной трапеции равно боковой стороне. Высота равна 8 см, периметр – 52 см, а площадь – 128 см2. Найдите длины сторон трапеции.
Поставьте в лист оценивания баллы за решение домашнего задания согласно дескрипторам и решениям, приведённым на слайдах. |
Приветствие.
1)
О
2)
4х=8, 5х=10 Ответ: 8 см, 10 см.
3)
P=a+a+a+b=52, 2a+32=52 a=10, b=32-10=22 Ответ: 10 см, 10 см,10 см,22 см.
|
Дескрипторы 1: 1б выполнен чертёж 1б записана формула длины средней линии 1б применена формула площади трапеции 1б выполнен перевод единиц измерения 1б выполнено деление числа площади на высоту 1б записан ответ
Дескрипторы 2: 1б обозначены основания 4х и 5х 1б применена формула площади трапеции 1б приведено решение уравнения 1б вычислено значение х 1б вычислены длины оснований 1б записан ответ
Дескрипторы3: 1б выполнен чертёж 1б отмечены данные 1б применены формулы Р и S 1б вычислена сумма оснований 1б вычислена длина меньшего основания 1б вычислена длина большего основания 1б записан ответ |
Слайды с решением задач Листы оценивания каждому
|
|
Середина урока |
Вы можете назвать ещё формулы для вычисления площади трапеции? Обсуждайте с соседом по парте. Работа в парах.
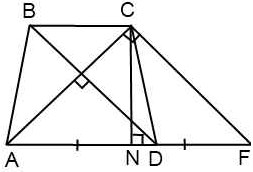
В Существуют ещё формулы? Верно. Поставьте себе баллы в лист оценивания. Рассмотрим равнобедренную трапецию ABCDс высотой BH и средней линией MN. Длина отрезка HD равна длине средней линии. Подумайте, почему это так?
Верно. Поставьте себе баллы в лист оценивания. Тогда формула площади трапеции примет вид
Если диагонали равнобедренной трапеции
будут перпендикулярны, то средняя линия равна её высоте и формула,
для вычисления площади такой трапеции будет иметь
вид: Подумайте, почему средняя линия равна высоте, если в равнобедренной трапеции диагонали перпендикулярны? На этот раз обсудите вопрос в группах, в которых вы работали на прошлом уроке. 5 мин на обсуждение. Предложите ваши решения.
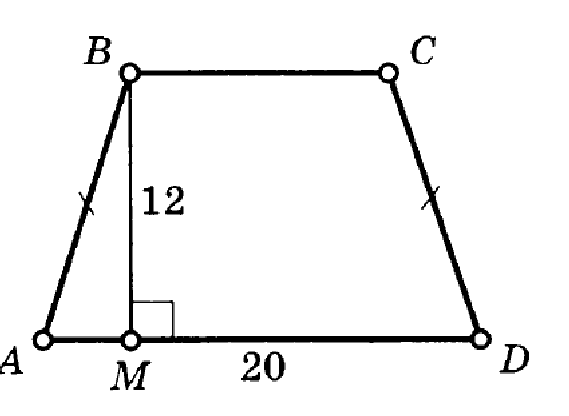
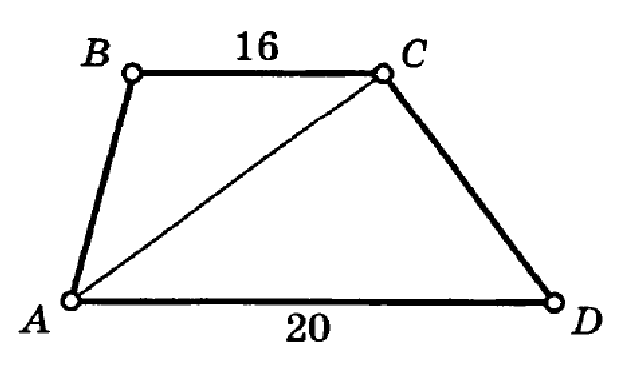
Посмотрите на слайд с ответом на наш вопрос. Поставьте баллы в лист оценивания согласно дескрипторам. Теперь вы знаете 6 формул для вычисления площади трапеции. В конце нашего урока примените знания, полученные о площади трапеции, решая две задачи. Работаем индивидуально. 1) Найти площадь трапеции, если её высота равна 12 см, а длина отрезка MD=20 см. 2) Найти площадь трапеции, если её большее основание равно 20, меньшее – 16. Площадь треугольника ACD=60. Рисунки на карточках есть. 7 мин у вас на это задание.
Проверьте ваши решения по слайдам и поставьте баллы согласно дескрипторам. |
П DBCF – параллелограмм, BC=DF, CF=BD=AC, так как в равнобедренной трапеции диагонали равны. Треугольник ACF –
равнобедренный и прямоугольный, так
как
Проведём высоту
CN.
Она будет и медианой. То есть высота трапеции равна её средней линии.
1)
2) Высота трапеции есть высота треугольника ACD.
|
Дескрипторы: 1б записывает формулу 1б даёт пояснения
Дескрипторы: 1б записывает формулу 1б даёт пояснения
Дескрипторы: 1б проводят вторую высоту
1б 1б поясняет равенства 1б делает вывод HD=MN
Дескрипторы: 1б выполняют чертёж
1б проводят 1бBC=DF, CF=BD=AC
1б равнобедренный и прямоугольный 1б проводят высоту CN
1б получают 1б участвует в работе группы 1б активно участвует в работе группы 1б является лидером группы Дескрипторы 1: 1б выбирают способ решения 1б применяют соответствующую формулу 1б проводят вычисления и получают ответ Дескрипторы 2:
1б отождествляют высоту трапеции с
высотой 1б применяют формулу площади треугольника 1б вычисляют высоту 1б применяют формулу площади трапеции 1б вычисляют площадь трапеции |
Слайды с формулами
Слайды с решениями
Карточки с заданиями. Слайды с решениями.
|
|
Конец урока |
Подведём итоги урока. Вы записали в листе оценивания баллы, которые вы получили за домашнюю работу, работу в парах и группах и индивидуальную работу. Подсчитайте сумму баллов, полученных вами на уроке и процент, исходя из того, что 44 балла составляют 100%. Поместите смайлик, содержащий ваш процент на лестницу успеха. Домашняя работа на следующий урок на карточках. (Приложение 3) Прочтите первую задачу. Как вы думаете её решать?
Очень хорошо. Как решать вторую задачу? Да, вот и пригодилось то, что сегодня изучили. Как решить третью задачу? Совершенно верно. Молодцы! Урок закончен. |
Подсчитывают баллы и проценты. Прикрепляют смайлики на лестницу успеха на доске.
1) Основания трапеции равны 6 и 2 дм, боковые стороны – 0,13 и 0,37 м. Найдите площадь трапеции. 2) Диагонали равнобедренной трапеции взаимно перпендикулярны. Основания равны 24 и 40 см. Вычислите её площадь. 3) Определите площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны, а высота равна h. Надо вычислить высоту трапеции. Можно вычислить длину из прямоугольных треугольников, образованных высотами. Обозначить за х часть большего основания с гипотенузой 0,13 м, середина будет равна 2 дм, а часть большего основания с гипотенузой – боковой стороной 0,37 м тогда будет 4-х. Потом приравнять эти два равных выражения и вычислить х, и вычислить высоту. Диагонали равнобедренной трапеции взаимно перпендикулярны, высота равна средней линии, значит, вычислим длину средней линии и возведём в квадрат. По той же формуле, только возвести в квадрат высоту. |
|
Карточки с домашним заданием. Чертёж лестницы успеха на доске с уровнями достижений согласно баллов( низкий – до 39%, средний - до 84% и высокий - до 100% |
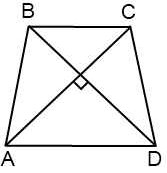
Приложение 1Групповая работа
Подумайте, почему средняя линия равна высоте, если в равнобедренной трапеции диагонали перпендикулярны?
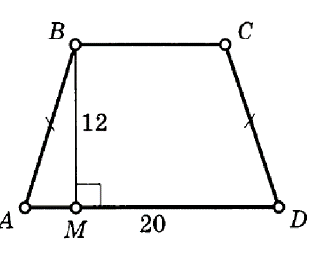
Приложение 2Индивидуальная работа
1)
Найти площадь трапеции, если её высота равна 12 см, а длина
отрезка MD=20
см.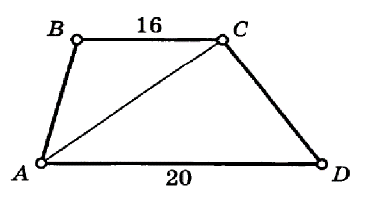
2) Найти площадь трапеции, если её большее основание равно 20, меньшее – 16. Площадь треугольника ACD=60.
Приложение 3 Домашнее задание
1) Основания трапеции равны 6 и 2 дм, боковые стороны – 0,13 и 0,37 м. Найдите площадь трапеции.
2) Диагонали равнобедренной трапеции взаимно перпендикулярны. Основания равны 24 и 40 см. Вычислите её площадь.
3) Определите площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны, а высота равна h.
Лист оценивания
|
Этап урока |
Критерий оценивания/ дескриптор |
Максимальное количество баллов |
Получено |
|
Начало урока Проверка домашнего задания
|
Дескрипторы 1: 1б выполнен чертёж 1б записана формула длины средней линии 1б применена формула площади трапеции 1б выполнен перевод единиц измерения 1б выполнено деление числа площади на высоту 1б записан ответ Дескрипторы 2: 1б обозначены основания 4х и 5х 1б применена формула площади трапеции 1б приведено решение уравнения 1б вычислено значение х 1б вычислены длины оснований 1б записан ответ Дескрипторы3: 1б выполнен чертёж 1б отмечены данные 1б применены формулы Р и S 1б вычислена сумма оснований 1б вычислена длина меньшего основания 1б вычислена длина большего основания 1б записан ответ |
19 |
|
|
Середина урока Работа в парах
Групповая работа
Индивидуальная работа |
Дескрипторы 1: 1б записывает формулу 1б даёт пояснения
Дескрипторы 2: 1б записывает формулу 1б даёт пояснения
Дескрипторы 3: 1б проводят вторую высоту
1б 1б поясняет равенства 1б делает вывод HD=MN
Дескрипторы: 1б выполняют чертёж
1б проводят 1бBC=DF, CF=BD=AC
1б равнобедренный и прямоугольный 1б проводят высоту CN
1б получают 1б участвует в работе группы 1б активно участвует в работе группы 1б является лидером группы
Дескрипторы 1: 1б выбирают способ решения 1б применяют соответствующую формулу 1б проводят вычисления и получают ответ
Дескрипторы 2:
1б отождествляют высоту трапеции с
высотой 1б применяют формулу площади треугольника 1б вычисляют высоту 1б применяют формулу площади трапеции 1б вычисляют площадь трапеции |
25 |
|
|
Итого: |
|
44 |
|
|
Проценты: |
|
100 |
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Площади четырёхугольников и треугольников.
Площади четырёхугольников и треугольников.
|
Раздел: 8.3А |
8.3А Площади. |
|
|
ФИО педагога: |
Расулметова М.А |
|
|
Дата: |
21.02.2025г |
|
|
Класс: 8 «Б» |
Количество присутствующих: |
Количество отсутствующих: |
|
Тема урока: |
Площади четырёхугольников и треугольников. |
|
|
Цели обучения в соответствии с учебной программой. |
8.1.3.13 выводить и применять формулы площади трапеции |
|
|
Цели урока: |
Применяет формулы площади трапеции для решения задач |
|
|
Привитие ценностей |
навыки использования различных познавательных инструментов, сбора знаний об окружающем мире (языке, культуре чтения, информации, цифровой среде). |
|
|
|
|
|
|
Этапы урока |
Действия педагога |
Действия ученика |
Оценивание Рубрика |
Ресурсы |
|
Начало урока |
Приветствие.
Проверка домашнего задания.
Проверьте как верно вы решили домашние задачи по слайдам и поставьте баллы в лист оценивания.
1) Высота трапеции равна 16 см, а площадь 4 дм2. Найдите длину средней линии.
2) Площадь трапеции равна 288 см2, основания относятся как 4:5, высота – 3,2 дм. Вычислите основания.
3) Меньше основание равнобедренной трапеции равно боковой стороне. Высота равна 8 см, периметр – 52 см, а площадь – 128 см2. Найдите длины сторон трапеции.
Поставьте в лист оценивания баллы за решение домашнего задания согласно дескрипторам и решениям, приведённым на слайдах. |
Приветствие.
1)
О
2)
4х=8, 5х=10 Ответ: 8 см, 10 см.
3)
P=a+a+a+b=52, 2a+32=52 a=10, b=32-10=22 Ответ: 10 см, 10 см,10 см,22 см.
|
Дескрипторы 1: 1б выполнен чертёж 1б записана формула длины средней линии 1б применена формула площади трапеции 1б выполнен перевод единиц измерения 1б выполнено деление числа площади на высоту 1б записан ответ
Дескрипторы 2: 1б обозначены основания 4х и 5х 1б применена формула площади трапеции 1б приведено решение уравнения 1б вычислено значение х 1б вычислены длины оснований 1б записан ответ
Дескрипторы3: 1б выполнен чертёж 1б отмечены данные 1б применены формулы Р и S 1б вычислена сумма оснований 1б вычислена длина меньшего основания 1б вычислена длина большего основания 1б записан ответ |
Слайды с решением задач Листы оценивания каждому
|
|
Середина урока |
Вы можете назвать ещё формулы для вычисления площади трапеции? Обсуждайте с соседом по парте. Работа в парах.
В Существуют ещё формулы? Верно. Поставьте себе баллы в лист оценивания. Рассмотрим равнобедренную трапецию ABCDс высотой BH и средней линией MN. Длина отрезка HD равна длине средней линии. Подумайте, почему это так?
Верно. Поставьте себе баллы в лист оценивания. Тогда формула площади трапеции примет вид
Если диагонали равнобедренной трапеции
будут перпендикулярны, то средняя линия равна её высоте и формула,
для вычисления площади такой трапеции будет иметь
вид: Подумайте, почему средняя линия равна высоте, если в равнобедренной трапеции диагонали перпендикулярны? На этот раз обсудите вопрос в группах, в которых вы работали на прошлом уроке. 5 мин на обсуждение. Предложите ваши решения.
Посмотрите на слайд с ответом на наш вопрос. Поставьте баллы в лист оценивания согласно дескрипторам. Теперь вы знаете 6 формул для вычисления площади трапеции. В конце нашего урока примените знания, полученные о площади трапеции, решая две задачи. Работаем индивидуально. 1) Найти площадь трапеции, если её высота равна 12 см, а длина отрезка MD=20 см. 2) Найти площадь трапеции, если её большее основание равно 20, меньшее – 16. Площадь треугольника ACD=60. Рисунки на карточках есть. 7 мин у вас на это задание.
Проверьте ваши решения по слайдам и поставьте баллы согласно дескрипторам. |
П DBCF – параллелограмм, BC=DF, CF=BD=AC, так как в равнобедренной трапеции диагонали равны. Треугольник ACF –
равнобедренный и прямоугольный, так
как
Проведём высоту
CN.
Она будет и медианой. То есть высота трапеции равна её средней линии.
1)
2) Высота трапеции есть высота треугольника ACD.
|
Дескрипторы: 1б записывает формулу 1б даёт пояснения
Дескрипторы: 1б записывает формулу 1б даёт пояснения
Дескрипторы: 1б проводят вторую высоту
1б 1б поясняет равенства 1б делает вывод HD=MN
Дескрипторы: 1б выполняют чертёж
1б проводят 1бBC=DF, CF=BD=AC
1б равнобедренный и прямоугольный 1б проводят высоту CN
1б получают 1б участвует в работе группы 1б активно участвует в работе группы 1б является лидером группы Дескрипторы 1: 1б выбирают способ решения 1б применяют соответствующую формулу 1б проводят вычисления и получают ответ Дескрипторы 2:
1б отождествляют высоту трапеции с
высотой 1б применяют формулу площади треугольника 1б вычисляют высоту 1б применяют формулу площади трапеции 1б вычисляют площадь трапеции |
Слайды с формулами
Слайды с решениями
Карточки с заданиями. Слайды с решениями.
|
|
Конец урока |
Подведём итоги урока. Вы записали в листе оценивания баллы, которые вы получили за домашнюю работу, работу в парах и группах и индивидуальную работу. Подсчитайте сумму баллов, полученных вами на уроке и процент, исходя из того, что 44 балла составляют 100%. Поместите смайлик, содержащий ваш процент на лестницу успеха. Домашняя работа на следующий урок на карточках. (Приложение 3) Прочтите первую задачу. Как вы думаете её решать?
Очень хорошо. Как решать вторую задачу? Да, вот и пригодилось то, что сегодня изучили. Как решить третью задачу? Совершенно верно. Молодцы! Урок закончен. |
Подсчитывают баллы и проценты. Прикрепляют смайлики на лестницу успеха на доске.
1) Основания трапеции равны 6 и 2 дм, боковые стороны – 0,13 и 0,37 м. Найдите площадь трапеции. 2) Диагонали равнобедренной трапеции взаимно перпендикулярны. Основания равны 24 и 40 см. Вычислите её площадь. 3) Определите площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны, а высота равна h. Надо вычислить высоту трапеции. Можно вычислить длину из прямоугольных треугольников, образованных высотами. Обозначить за х часть большего основания с гипотенузой 0,13 м, середина будет равна 2 дм, а часть большего основания с гипотенузой – боковой стороной 0,37 м тогда будет 4-х. Потом приравнять эти два равных выражения и вычислить х, и вычислить высоту. Диагонали равнобедренной трапеции взаимно перпендикулярны, высота равна средней линии, значит, вычислим длину средней линии и возведём в квадрат. По той же формуле, только возвести в квадрат высоту. |
|
Карточки с домашним заданием. Чертёж лестницы успеха на доске с уровнями достижений согласно баллов( низкий – до 39%, средний - до 84% и высокий - до 100% |

Приложение 1Групповая работа
Подумайте, почему средняя линия равна высоте, если в равнобедренной трапеции диагонали перпендикулярны?

Приложение 2Индивидуальная работа
1)
Найти площадь трапеции, если её высота равна 12 см, а длина
отрезка MD=20
см.
2) Найти площадь трапеции, если её большее основание равно 20, меньшее – 16. Площадь треугольника ACD=60.
Приложение 3 Домашнее задание
1) Основания трапеции равны 6 и 2 дм, боковые стороны – 0,13 и 0,37 м. Найдите площадь трапеции.
2) Диагонали равнобедренной трапеции взаимно перпендикулярны. Основания равны 24 и 40 см. Вычислите её площадь.
3) Определите площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны, а высота равна h.
Лист оценивания
|
Этап урока |
Критерий оценивания/ дескриптор |
Максимальное количество баллов |
Получено |
|
Начало урока Проверка домашнего задания
|
Дескрипторы 1: 1б выполнен чертёж 1б записана формула длины средней линии 1б применена формула площади трапеции 1б выполнен перевод единиц измерения 1б выполнено деление числа площади на высоту 1б записан ответ Дескрипторы 2: 1б обозначены основания 4х и 5х 1б применена формула площади трапеции 1б приведено решение уравнения 1б вычислено значение х 1б вычислены длины оснований 1б записан ответ Дескрипторы3: 1б выполнен чертёж 1б отмечены данные 1б применены формулы Р и S 1б вычислена сумма оснований 1б вычислена длина меньшего основания 1б вычислена длина большего основания 1б записан ответ |
19 |
|
|
Середина урока Работа в парах
Групповая работа
Индивидуальная работа |
Дескрипторы 1: 1б записывает формулу 1б даёт пояснения
Дескрипторы 2: 1б записывает формулу 1б даёт пояснения
Дескрипторы 3: 1б проводят вторую высоту
1б 1б поясняет равенства 1б делает вывод HD=MN
Дескрипторы: 1б выполняют чертёж
1б проводят 1бBC=DF, CF=BD=AC
1б равнобедренный и прямоугольный 1б проводят высоту CN
1б получают 1б участвует в работе группы 1б активно участвует в работе группы 1б является лидером группы
Дескрипторы 1: 1б выбирают способ решения 1б применяют соответствующую формулу 1б проводят вычисления и получают ответ
Дескрипторы 2:
1б отождествляют высоту трапеции с
высотой 1б применяют формулу площади треугольника 1б вычисляют высоту 1б применяют формулу площади трапеции 1б вычисляют площадь трапеции |
25 |
|
|
Итого: |
|
44 |
|
|
Проценты: |
|
100 |
|

шағым қалдыра аласыз




 твет: 2,5
см.
твет: 2,5
см.


 ерно. Поставьте
себе баллы в лист оценивания.
ерно. Поставьте
себе баллы в лист оценивания.
 .
.
 -угол между диагоналями, так как
трапеция является
четырёхугольником.
-угол между диагоналями, так как
трапеция является
четырёхугольником. , так как они являются средними линиями
соответственно треугольников
, так как они являются средними линиями
соответственно треугольников 
 роведём
роведём  ,
, и
и  .
.