
«КГУ «Общеобразовательная школа села Мадениет отдела образования по Сандыктаускому району управления образования Акмолинской области»
Учитель математики Сабитова Айгуль Аманжоловна
Теория вероятностей в задачах.
«Математику уже затем учить надо, что она ум в порядок приводит» - известные слова Михаила Ломоносова. Действительно, математика является основой всех наук, необходимым инструментом для познания окружающих нас процессов. Умение применять математические знания в реальных жизненных ситуациях, является составной частью функциональной грамотности. В школьной математике есть много разделов, в которых мы можем развивать этот навык. Одним из таких разделов является «Теория вероятностей». Стоит сказать, что многие задачи международных исследований функциональной грамотности учащихся относятся к данному разделу. Задачи из раздела «Теория вероятностей» часто вызывают трудности у учащихся, поэтому темы этого раздела я предлагаю изучать на дополнительных занятиях.
За время своей педагогической практики, на протяжении многих лет, я проводила прикладные курсы в 10 и 11 классах, на которых старалась рассмотреть разделы, вызывающие затруднения и темы, необходимые для сдачи ЕНТ. Программы, составленные к ним, объединены в авторском сборнике прикладных курсов по математике для 10-11 классов. В этот сборник входит программа курса «Теория вероятностей в задачах».
В данной статье предлагаю программу курса «Теория вероятностей в задачах» и решение задач из этого курса. Задачи взяты из раздела «Элементы теории вероятностей и комбинаторики» учебника «Алгебра» для 9 класса, автор Шыныбеков А. Н., издательство «Атамұра», 2005 г.
Цель курса:
Учащиеся смогут решать задачи теории вероятностей и комбинаторики, проводить испытания повторяющихся событий и предоставлять результат.
Задачи курса:
-
интеграция знаний по изучению методов решения задач теории вероятностей;
-
формирование навыков и умений проведения эксперимента;
-
повышение информационной и коммуникативной компетентности учащихся;
-
развитие навыков работы учащихся с табличными данными;
-
обеспечение условий для развития творческого потенциала школьника.
Содержание курса
-
Классическое определение вероятности;
-
Элементы теории вероятностей;
-
Элементы комбинаторики;
-
Повторение испытаний. Формула Бернулли;
-
Практический опыт.
Ожидаемые результаты
Учащийся умеет:
-
Определять вероятность событий;
-
Решать задачи комбинаторики;
-
Решать задачи с помощью формулы Бернулли;
-
Проводить испытания повторяющихся событий;
-
Предоставлять результаты испытаний.
Тематическое планирование учебного материала
|
№ п/п |
Тақырып Тема |
Сағат Часы |
Мерзім Дата |
Ескерту Коррект. |
|
|
Классическое определение вероятности |
14 |
|
|
|
1 |
История возникновения науки «Теория вероятностей». |
2 |
|
|
|
2 |
Роль теории вероятностей в различных областях деятельности человека |
2 |
|
|
|
3 |
Понятие вероятности |
2 |
|
|
|
4 |
События. Виды событий |
2 |
|
|
|
5 |
Вероятность событий |
2 |
|
|
|
6 |
Сложение и умножение вероятностей |
2 |
|
|
|
7 |
Решение задач на вероятность событий |
2 |
|
|
|
|
Элементы комбинаторики |
12 |
|
|
|
8 |
Исторические комбинаторные задачи. Задача Дирихле. Для чего нужна комбинаторика |
2 |
|
|
|
9 |
Комбинации элементов |
2 |
|
|
|
10 |
Общие правила комбинаторики |
2 |
|
|
|
11 |
Совокупности без повторений и с повторениями. |
2 |
|
|
|
12 |
Перестановки. Сочетания. Размещения. |
2 |
|
|
|
13 |
Решение задач комбинаторики |
2 |
|
|
|
|
Повторение испытаний |
8 |
|
|
|
14 |
Повторение испытаний. Формула Бернулли |
2 |
|
|
|
15 |
Решение задач с помощью формулы Бернулли |
2 |
|
|
|
16 |
Проведение испытаний - подбрасывание игрального кубика. Обработка и анализ данных |
2 |
|
|
|
17 |
Решение задач |
2 |
|
|
|
|
Всего часов |
34 |
|
|
Основные формулы, необходимые для решения задач:
-
Сложение несовместимых событий: P (A + B) = P (A) + P (B)
Сложение совместимых событий: P (A + B) = P (A) + P (B) — P (A ⋅ B)
-
Умножение событий: P (A * B) = P (A) * P (B)
-
Вероятность события Р =

-
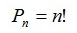
Перестановки
![]()
Размещения без повторений
![]()
Размещения с повторениями
![]()
Сочетания без повторений
![]()
Сочетания с повторениями
P(k) = Cnkpkqn-k, k=0, 1, 2 … n - формула Бернулли
Задача 1(А. 859).
Два стрелка произвели по одному выстрелу по мишени. Один из стрелков может поразить мишень с вероятностью, равной 0,7, а второй – с вероятностью 0,8. Какова вероятность того, что:
-
Оба стрелка попали в мишень;
-
Оба стрелка промахнулись;
-
В мишень попал только один стрелок;
-
В мишень попал, по крайней мере, один стрелок;
-
По крайней мере, один из стрелков промахнулся?
Решение:
Пусть Аn означает событие «n- ый стрелок попал в мишень», n=1,2. Тогда Ᾱn означает «n- ый стрелок не попал в мишень».
Р(А1)= 0,7; Р(А2) = 0,8; Р(Ᾱ1)=1-0,7=0,3; Р(Ᾱ2)=1-0,8=0,2.
А1 А2 – означает «оба стрелка попали в мишень»,
Ᾱ1 Ᾱ2 – «оба стрелка промахнулись»
А1 Ᾱ2- «первый стрелок попал, а второй промахнулся»,
Ᾱ1 А2 – «первый стрелок промахнулся, а второй попал в мишень»
1) оба стрелка попали в мишень: Р (А1 А2) = 0,7*0,8 = 0,56
2) оба стрелка промахнулись: Р (Ᾱ1 Ᾱ2) = 0,3*0,2 = 0,06
3) в мишень попал только один стрелок: Р (А1 Ᾱ2+ Ᾱ1 А2) = 0.7*0.2+0.3*0.8= 0.14+0.24=0,38
4) по крайней мере один попал в мишень Р (А1+ А2) = 0,7+0,8-0,7*0,8= 1,5-0,56=0,94;
5) по крайней мере один промахнулся Р (Ᾱ1 +Ᾱ2) = 0,3+0,2 – 0,3*0,2 = 0,5 – 0,06=0,44;
Задача 2(А. 862).
В среднем одна из 100 лампочек, имеющихся в магазине бывает бракованной. Какова вероятность того, что из двух купленных лампочек:
-
Обе бракованные;
-
Обе не бракованные;
-
Только одна бракованная?
Решение.
1)Аn – «Купленная лампочка бракованная», n=1,2. Р(Аn) = 0,01
Обе бракованные: 0,01*0,01=0,0001
Ᾱn = «купленная лампочка не бракованная», Р (Ᾱ1) = 1-0,01=0,99
2) Обе не бракованные 0,99*0,99 = 0,9801;
3) Только одна бракованная: Р (А1 Ᾱ2+ Ᾱ1 А2) = 0,01*0,99+0,99*0,01=
0,0099+0,0099=0,0198.
Задача 3. (В. 927)
Сколькими способами можно составить четырехзначное число, в котором 1) цифры не повторяются, 2) цифры могут повторяться?
Решение. Всего имеется 10 цифр. Первая цифра не должна быть нулем, поэтому ее можно выбрать 9 способами
-
Если цифры не повторяются, то вторую цифру можно выбрать из оставшихся девяти, третью – из оставшихся восьми и четвертую - из оставшихся 7 цифр. По правилу произведения, без повторения цифр четырехзначное число можно составить 9*9*8*7=6174.
-
Если цифры повторяются, то каждую из остальных трех цифр можно выбрать 10 различными способами и это равно 9*103=9000.
Задача 4(С. 942).
Сколько можно написать четных чисел, меньших, чем 104, с помощью цифр 0; 4 и 5?
Решение:
-
Однозначные – 2 числа, двузначные (4,5) * (0,4) = 2*2=4
-
Трехзначные: (4,5)*(0,4,5)*(0,4) = 2*3*2= 12
-
Четырехзначные: (4,5)*(0,4,5)*(0,4,5)*(0,4)= 2*3*3*2=36
Всего: 2+4+12+36= 54
Задача 5 (В. 866).
На районной математической олимпиаде среди 9 классов 5 из 12 учеников являются отличниками. Какова вероятность того, что все три призера окажутся отличниками? Здесь считается, что все 12 учеников имеют равные возможности.
Решение: первые три места можно распределить А12 3= 12*11*10.
Первые три места среди пяти отличников можно распределить А53=5*4*3.
Р= А53 /А12 3=12*11*10/5*4*3=1/22
Задача 6(В. 960).
Из имеющихся отрезков длиной 2, 5, 6 и 10, случайно отобраны три отрезка. Какова вероятность того, что из отобранных отрезков можно составить треугольник?
Решение: из четырех отрезков три можно выбрать С43= 4!/(3!*1!)=4 способами: (2,5,6), (2,5,10), (2,6,10), (5,6,10) - это число всевозможных исходов. Из них треугольник можно составить из двух троек (2,5,6) и (5,6,10), так как сумма двух сторон треугольника должна быть больше третьей стороны – это число благоприятствующих исходов. Следовательно Р=2/4=0,5
Задача 7(А.915).
Сколькими способами можно посадить 6 человек 1) в один ряд; 2) за круглым столом?
Ответ: 1) 6! =720 ; 2) 5!=120
Задача 8 (С. 966).
За круглым столом случайно расселись 6 учеников. Какова вероятность того, что 2 определенных ученика сядут рядом?
Решение: За круглым столом 6 учеников можно рассадить 5! Способами (см. задача 915). Определенные два человека всегда сидят рядом, поэтому их места можно объединить, считая их два места за одно. В таком случае нужно рассадить не пять человек, а четыре. Тогда число способов =4! Два определенных человека на своих двух соседних местах могут пересаживаться двумя способами. Следовательно, 6 человек можно рассадить так, чтобы определенные два человека всегда сидели рядом, 2*4! способами – это число благоприятствующих исходов. Тогда искомая вероятность равна (2*4!)/5!=2/5=0,4. Ответ: Р=0,4
Задача 9 (В. 958).
Игральная кость подбрасывается три раза. Какова вероятность того, что все три раза выпадут разные очки?
Решение: при трехразовом бросании всего 6*6*6 всевозможных исходов.
Пусть выпали разные очки n, m, k. Число таких различных троек А63=6*5*4.
Р=(6*5*4)/(6*6*6)=5/9
Литература:
1) Учебник «Алгебра» для 9 класса, автор Шыныбеков А. Н., издательство «Атамұра», 2005
2) Решение задач по учебнику «Алгебра» за 9 класс по теме «Теория вероятностей», Кокшетау 2006.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Программа прикладного курса "Теория вероятностей в задачах"
Программа прикладного курса "Теория вероятностей в задачах"
«КГУ «Общеобразовательная школа села Мадениет отдела образования по Сандыктаускому району управления образования Акмолинской области»
Учитель математики Сабитова Айгуль Аманжоловна
Теория вероятностей в задачах.
«Математику уже затем учить надо, что она ум в порядок приводит» - известные слова Михаила Ломоносова. Действительно, математика является основой всех наук, необходимым инструментом для познания окружающих нас процессов. Умение применять математические знания в реальных жизненных ситуациях, является составной частью функциональной грамотности. В школьной математике есть много разделов, в которых мы можем развивать этот навык. Одним из таких разделов является «Теория вероятностей». Стоит сказать, что многие задачи международных исследований функциональной грамотности учащихся относятся к данному разделу. Задачи из раздела «Теория вероятностей» часто вызывают трудности у учащихся, поэтому темы этого раздела я предлагаю изучать на дополнительных занятиях.
За время своей педагогической практики, на протяжении многих лет, я проводила прикладные курсы в 10 и 11 классах, на которых старалась рассмотреть разделы, вызывающие затруднения и темы, необходимые для сдачи ЕНТ. Программы, составленные к ним, объединены в авторском сборнике прикладных курсов по математике для 10-11 классов. В этот сборник входит программа курса «Теория вероятностей в задачах».
В данной статье предлагаю программу курса «Теория вероятностей в задачах» и решение задач из этого курса. Задачи взяты из раздела «Элементы теории вероятностей и комбинаторики» учебника «Алгебра» для 9 класса, автор Шыныбеков А. Н., издательство «Атамұра», 2005 г.
Цель курса:
Учащиеся смогут решать задачи теории вероятностей и комбинаторики, проводить испытания повторяющихся событий и предоставлять результат.
Задачи курса:
-
интеграция знаний по изучению методов решения задач теории вероятностей;
-
формирование навыков и умений проведения эксперимента;
-
повышение информационной и коммуникативной компетентности учащихся;
-
развитие навыков работы учащихся с табличными данными;
-
обеспечение условий для развития творческого потенциала школьника.
Содержание курса
-
Классическое определение вероятности;
-
Элементы теории вероятностей;
-
Элементы комбинаторики;
-
Повторение испытаний. Формула Бернулли;
-
Практический опыт.
Ожидаемые результаты
Учащийся умеет:
-
Определять вероятность событий;
-
Решать задачи комбинаторики;
-
Решать задачи с помощью формулы Бернулли;
-
Проводить испытания повторяющихся событий;
-
Предоставлять результаты испытаний.
Тематическое планирование учебного материала
|
№ п/п |
Тақырып Тема |
Сағат Часы |
Мерзім Дата |
Ескерту Коррект. |
|
|
Классическое определение вероятности |
14 |
|
|
|
1 |
История возникновения науки «Теория вероятностей». |
2 |
|
|
|
2 |
Роль теории вероятностей в различных областях деятельности человека |
2 |
|
|
|
3 |
Понятие вероятности |
2 |
|
|
|
4 |
События. Виды событий |
2 |
|
|
|
5 |
Вероятность событий |
2 |
|
|
|
6 |
Сложение и умножение вероятностей |
2 |
|
|
|
7 |
Решение задач на вероятность событий |
2 |
|
|
|
|
Элементы комбинаторики |
12 |
|
|
|
8 |
Исторические комбинаторные задачи. Задача Дирихле. Для чего нужна комбинаторика |
2 |
|
|
|
9 |
Комбинации элементов |
2 |
|
|
|
10 |
Общие правила комбинаторики |
2 |
|
|
|
11 |
Совокупности без повторений и с повторениями. |
2 |
|
|
|
12 |
Перестановки. Сочетания. Размещения. |
2 |
|
|
|
13 |
Решение задач комбинаторики |
2 |
|
|
|
|
Повторение испытаний |
8 |
|
|
|
14 |
Повторение испытаний. Формула Бернулли |
2 |
|
|
|
15 |
Решение задач с помощью формулы Бернулли |
2 |
|
|
|
16 |
Проведение испытаний - подбрасывание игрального кубика. Обработка и анализ данных |
2 |
|
|
|
17 |
Решение задач |
2 |
|
|
|
|
Всего часов |
34 |
|
|
Основные формулы, необходимые для решения задач:
-
Сложение несовместимых событий: P (A + B) = P (A) + P (B)
Сложение совместимых событий: P (A + B) = P (A) + P (B) — P (A ⋅ B)
-
Умножение событий: P (A * B) = P (A) * P (B)
-
Вероятность события Р =

-
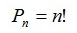
Перестановки
![]()
Размещения без повторений
![]()
Размещения с повторениями
![]()
Сочетания без повторений
![]()
Сочетания с повторениями
P(k) = Cnkpkqn-k, k=0, 1, 2 … n - формула Бернулли
Задача 1(А. 859).
Два стрелка произвели по одному выстрелу по мишени. Один из стрелков может поразить мишень с вероятностью, равной 0,7, а второй – с вероятностью 0,8. Какова вероятность того, что:
-
Оба стрелка попали в мишень;
-
Оба стрелка промахнулись;
-
В мишень попал только один стрелок;
-
В мишень попал, по крайней мере, один стрелок;
-
По крайней мере, один из стрелков промахнулся?
Решение:
Пусть Аn означает событие «n- ый стрелок попал в мишень», n=1,2. Тогда Ᾱn означает «n- ый стрелок не попал в мишень».
Р(А1)= 0,7; Р(А2) = 0,8; Р(Ᾱ1)=1-0,7=0,3; Р(Ᾱ2)=1-0,8=0,2.
А1 А2 – означает «оба стрелка попали в мишень»,
Ᾱ1 Ᾱ2 – «оба стрелка промахнулись»
А1 Ᾱ2- «первый стрелок попал, а второй промахнулся»,
Ᾱ1 А2 – «первый стрелок промахнулся, а второй попал в мишень»
1) оба стрелка попали в мишень: Р (А1 А2) = 0,7*0,8 = 0,56
2) оба стрелка промахнулись: Р (Ᾱ1 Ᾱ2) = 0,3*0,2 = 0,06
3) в мишень попал только один стрелок: Р (А1 Ᾱ2+ Ᾱ1 А2) = 0.7*0.2+0.3*0.8= 0.14+0.24=0,38
4) по крайней мере один попал в мишень Р (А1+ А2) = 0,7+0,8-0,7*0,8= 1,5-0,56=0,94;
5) по крайней мере один промахнулся Р (Ᾱ1 +Ᾱ2) = 0,3+0,2 – 0,3*0,2 = 0,5 – 0,06=0,44;
Задача 2(А. 862).
В среднем одна из 100 лампочек, имеющихся в магазине бывает бракованной. Какова вероятность того, что из двух купленных лампочек:
-
Обе бракованные;
-
Обе не бракованные;
-
Только одна бракованная?
Решение.
1)Аn – «Купленная лампочка бракованная», n=1,2. Р(Аn) = 0,01
Обе бракованные: 0,01*0,01=0,0001
Ᾱn = «купленная лампочка не бракованная», Р (Ᾱ1) = 1-0,01=0,99
2) Обе не бракованные 0,99*0,99 = 0,9801;
3) Только одна бракованная: Р (А1 Ᾱ2+ Ᾱ1 А2) = 0,01*0,99+0,99*0,01=
0,0099+0,0099=0,0198.
Задача 3. (В. 927)
Сколькими способами можно составить четырехзначное число, в котором 1) цифры не повторяются, 2) цифры могут повторяться?
Решение. Всего имеется 10 цифр. Первая цифра не должна быть нулем, поэтому ее можно выбрать 9 способами
-
Если цифры не повторяются, то вторую цифру можно выбрать из оставшихся девяти, третью – из оставшихся восьми и четвертую - из оставшихся 7 цифр. По правилу произведения, без повторения цифр четырехзначное число можно составить 9*9*8*7=6174.
-
Если цифры повторяются, то каждую из остальных трех цифр можно выбрать 10 различными способами и это равно 9*103=9000.
Задача 4(С. 942).
Сколько можно написать четных чисел, меньших, чем 104, с помощью цифр 0; 4 и 5?
Решение:
-
Однозначные – 2 числа, двузначные (4,5) * (0,4) = 2*2=4
-
Трехзначные: (4,5)*(0,4,5)*(0,4) = 2*3*2= 12
-
Четырехзначные: (4,5)*(0,4,5)*(0,4,5)*(0,4)= 2*3*3*2=36
Всего: 2+4+12+36= 54
Задача 5 (В. 866).
На районной математической олимпиаде среди 9 классов 5 из 12 учеников являются отличниками. Какова вероятность того, что все три призера окажутся отличниками? Здесь считается, что все 12 учеников имеют равные возможности.
Решение: первые три места можно распределить А12 3= 12*11*10.
Первые три места среди пяти отличников можно распределить А53=5*4*3.
Р= А53 /А12 3=12*11*10/5*4*3=1/22
Задача 6(В. 960).
Из имеющихся отрезков длиной 2, 5, 6 и 10, случайно отобраны три отрезка. Какова вероятность того, что из отобранных отрезков можно составить треугольник?
Решение: из четырех отрезков три можно выбрать С43= 4!/(3!*1!)=4 способами: (2,5,6), (2,5,10), (2,6,10), (5,6,10) - это число всевозможных исходов. Из них треугольник можно составить из двух троек (2,5,6) и (5,6,10), так как сумма двух сторон треугольника должна быть больше третьей стороны – это число благоприятствующих исходов. Следовательно Р=2/4=0,5
Задача 7(А.915).
Сколькими способами можно посадить 6 человек 1) в один ряд; 2) за круглым столом?
Ответ: 1) 6! =720 ; 2) 5!=120
Задача 8 (С. 966).
За круглым столом случайно расселись 6 учеников. Какова вероятность того, что 2 определенных ученика сядут рядом?
Решение: За круглым столом 6 учеников можно рассадить 5! Способами (см. задача 915). Определенные два человека всегда сидят рядом, поэтому их места можно объединить, считая их два места за одно. В таком случае нужно рассадить не пять человек, а четыре. Тогда число способов =4! Два определенных человека на своих двух соседних местах могут пересаживаться двумя способами. Следовательно, 6 человек можно рассадить так, чтобы определенные два человека всегда сидели рядом, 2*4! способами – это число благоприятствующих исходов. Тогда искомая вероятность равна (2*4!)/5!=2/5=0,4. Ответ: Р=0,4
Задача 9 (В. 958).
Игральная кость подбрасывается три раза. Какова вероятность того, что все три раза выпадут разные очки?
Решение: при трехразовом бросании всего 6*6*6 всевозможных исходов.
Пусть выпали разные очки n, m, k. Число таких различных троек А63=6*5*4.
Р=(6*5*4)/(6*6*6)=5/9
Литература:
1) Учебник «Алгебра» для 9 класса, автор Шыныбеков А. Н., издательство «Атамұра», 2005
2) Решение задач по учебнику «Алгебра» за 9 класс по теме «Теория вероятностей», Кокшетау 2006.

шағым қалдыра аласыз















