|
Тақырыбы: 53-САБАҚ |
Центрлік бұрыш |
||||
|
Күні,айы: |
Мұғалімнің аты-жөні |
||||
|
|
Сабаққа қатысқан оқушылар саны: |
Сабаққа қатыспаған оқушылар саны: |
|||
|
Оқу бағдарламасына сәйкес оқу мақсаты |
7.1.1.31 нүктелердің геометриялық орнының анықтамасын білу; 7.1.1.28 шеңбер мен дөңгелектің және олардың элементтерінің (центр, радиус, диаметр, хорда) анықтамаларын білу; 7.1.1.29 центрлік бұрыштың анықтамасы мен қасиеттерін білу және қолдану; 7.1.1.30 шеңбер диаметрі мен хордасының перпендикулярлығы туралы теоремаларды дәлелдеу және қолдану;; |
||||
|
Сабақ мақсаты |
Барлық оқушылар:
Оқушылар шеңбер
тақырыбы бойынша геометриялық есептерді шығару машықтарын дамытады,
геометрия пәні бойынша алған білімдерін қайталау және білімдерінің
практикалық бағытталуын қадағалау, шығармашылық қабілеттерін
қалыптастырады. Шеңберге іштей сызылған бұрыш, центрлік бұрыш, шеңбер доғасы туралы білімдерін жетілдіреді. Кейбір оқушылар: Танымдық қабілетін дамыту арқылы , пәнге қызығушылығын арттырады. |
||||
|
Сабақтың барысы |
|||||
|
Сабақтың кезеңдері |
Жоспарланған жұмыс |
Ресурстар |
|||
|
Сабақтың басы(2-5 минут) |
(МК) .Сұрақ-жауап әдісі арқылы оқушылармен пікір алмасу
(Сұрақтары:
|
|
|||
|
Сабақтың ортасы (6-40 минут) |
(МК,Ұ)
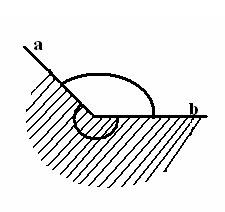
Б Егер бұрыштардың біреуінің градустық өлшемі α – ға тең болса, онда толықтауыш бұрыштың градустық өлшемі 3600- α болады.
Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады.
АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады. Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады. Теореманы дәлелдеу үшін 3 жағдайды қарастырамыз:
1. Бұрыштың бір
қабырғасы шеңбердің центрінен өтеді. АО радиусын жүргізсек,
теңбүйірлі АВО үшбұрышы шығады, мұнда АО=ОВ,
сондықтан 2. Шеңбердің О центрі шеңберге іштей сызылған бұрыш қабырғаларының арасында жатады. ВD диаметрін жүргіземіз, сонда
3. Шеңбердің О
центрі шеңберге іштей сызылған АВС бұрышынан тысқары жатсын. ВD
диаметрін жүргіземіз, сонда Теорема дәлелденді. Есеп шығару кезеңі 1) Шеңберге іштей сызылған бұрыш 220/ - қа тең. Осы бұрыш тірелетін доғаның градустық шамасын есептеңдер. 2) Шеңбер хордаларымен 1:2:3 қатынасында бөлінген. Пайда болған үшбұрыштың бұрыштарын есептеңдер. 3) Іштей сызылған АВС бұрышы АС доғасына тіреледі. АС доғасы 570- қа тең. АВС бұрышы неге тең? 4) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=5 см6 ВЕ=2 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 5) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=7 см, ВЕ=5 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 6) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=8 см6 ВЕ=9 см, СЕ=3,5см. ЕД кесіндісінің ұзындығы есептеңдер. |
Оқулық Аудидиск: №1Жұмыс дәптері |
|||
|
Сабақтың соңы( 41-45мин) |
(Қ) Топтық жұмыс
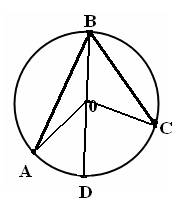
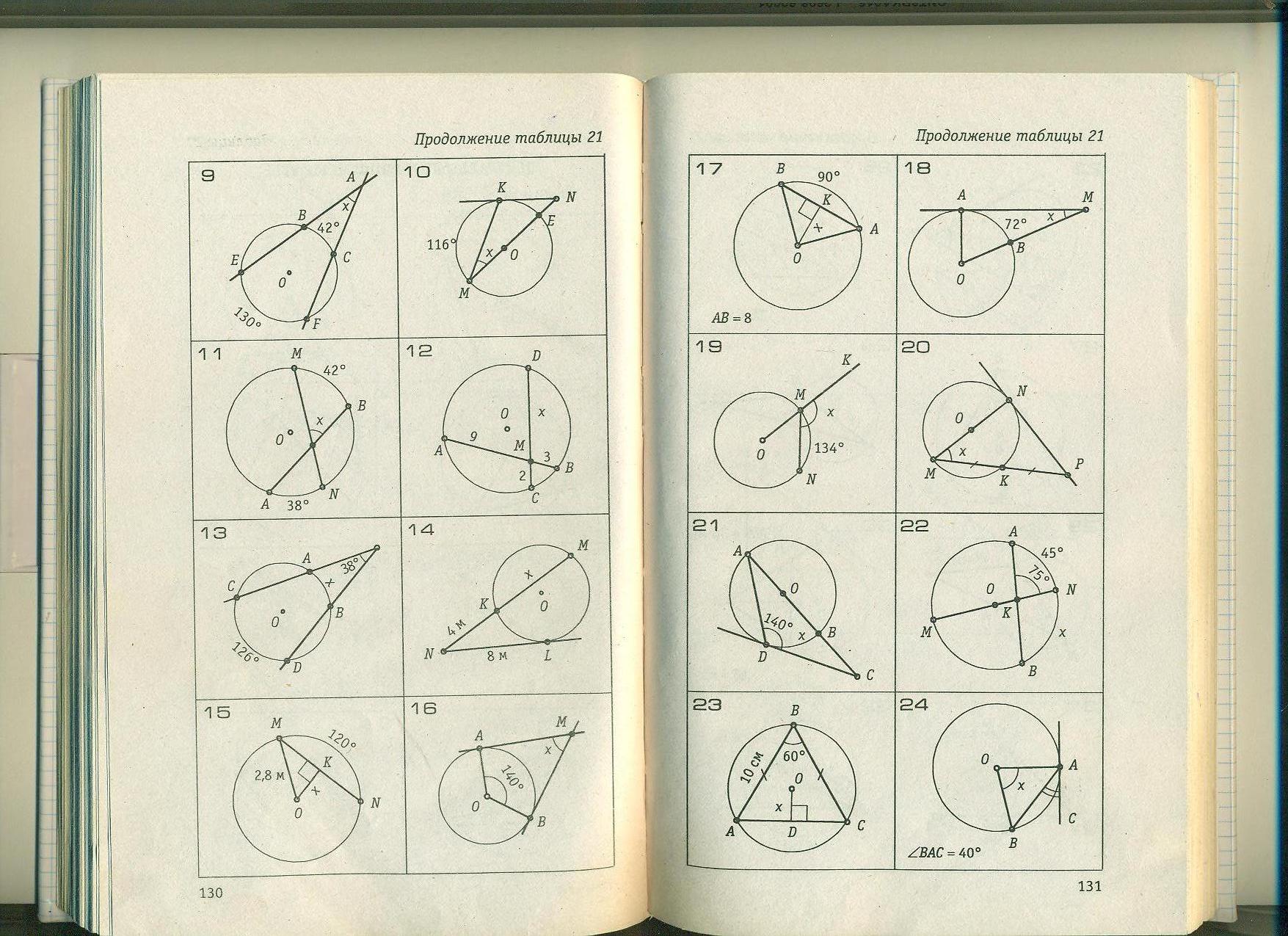
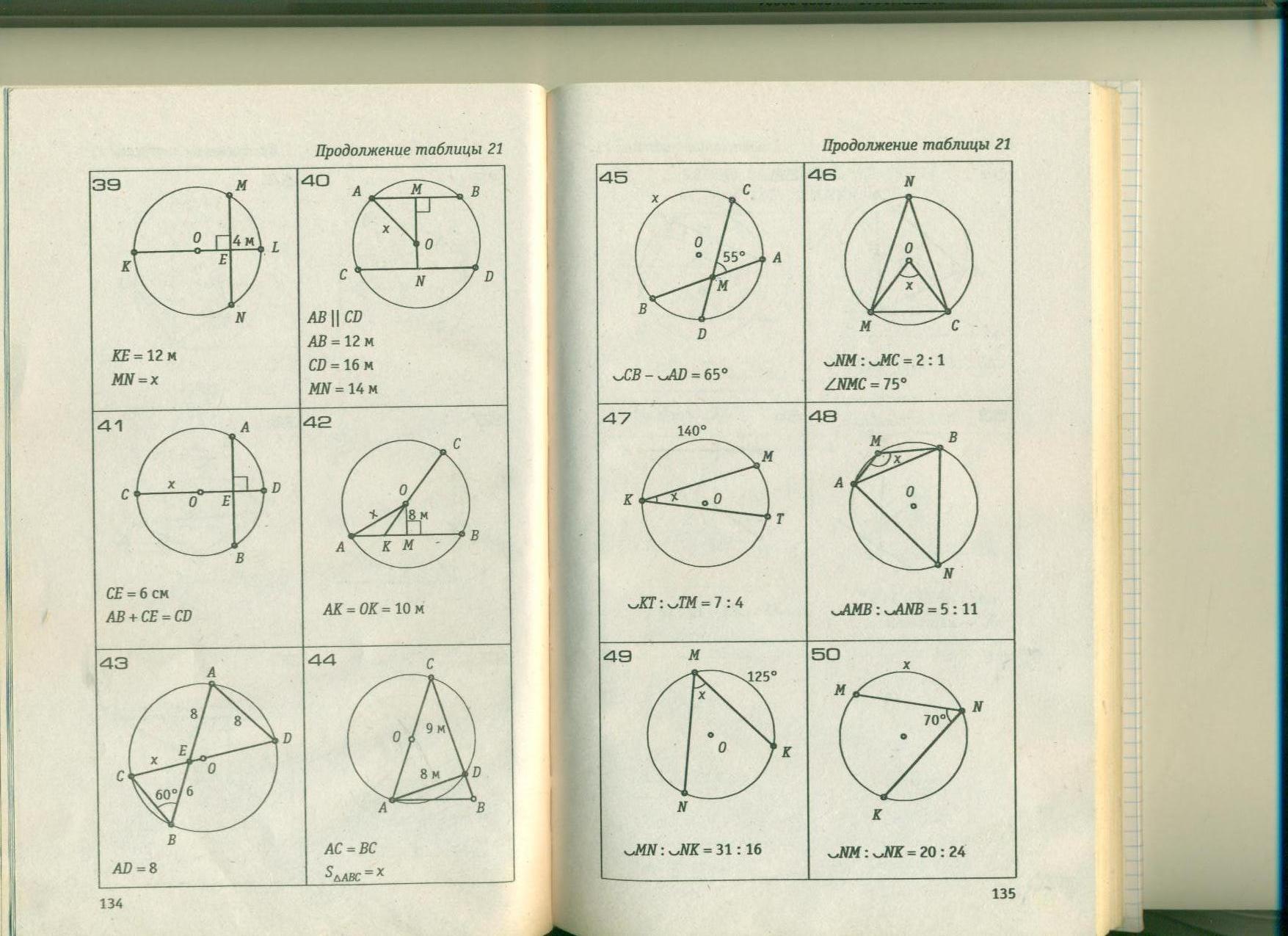
Топбасшыларының критериалды бағалауы. Тапсырма № 1 Табу керек: ∠ АОВ, егер ∠ ВАС = 40°.
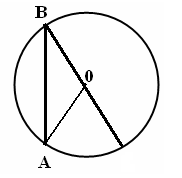
Тапсырма № 2. АВ доғасының градустық шамасын табу керек..
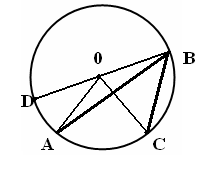
Тапсырма № 3. Табу керек: ∠ МКТ. Пысықтау сұрақтары. 1. Центірлік бұрыш дегеніміз не? 2. Центрлік бұрышқа сәйкес шеңбер доғасы деп қандай доғаны айтады? 3. Шеңбер доғасының градустық өлшемі қалай анықталады? 4. Шеңберге іштей сызылған бұрыш деп қандай бұрышты атайды? 5. Диаметрге тірелетін бұрыш қандай бұрыш болады? 6. Өзара қиылысатын хордалар кесінділерінің қасиеттерін дәлелдеңдер |
||||
|
Қосымша ақпарат |
|||||
|
Қорытындылау |
Төмендегі бөлікті сабағыңыз туралы өз ойыңызды жазуға қолданыңыз.Өз сабағыңыз бойынша сол жақ бағандағы сұрақтарға жауап беріңіз. |
||||
|
1.Сабақ барысында өзгертулер енгіздіңіз бе? 2.Жүргізген жұмыс түрлері қаншалықты тиімді болды? |
|
||||
|
Қорытынды бағалау Ең жақсы өткен екі нәрсе? 1. 2. Қандай екі нәрсе сабақты жақсартар еді? 1. 2. |
|||||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Сабақ жоспары Центрлік бұрыш 7 сынып
Сабақ жоспары Центрлік бұрыш 7 сынып
|
Тақырыбы: 53-САБАҚ |
Центрлік бұрыш |
||||
|
Күні,айы: |
Мұғалімнің аты-жөні |
||||
|
|
Сабаққа қатысқан оқушылар саны: |
Сабаққа қатыспаған оқушылар саны: |
|||
|
Оқу бағдарламасына сәйкес оқу мақсаты |
7.1.1.31 нүктелердің геометриялық орнының анықтамасын білу; 7.1.1.28 шеңбер мен дөңгелектің және олардың элементтерінің (центр, радиус, диаметр, хорда) анықтамаларын білу; 7.1.1.29 центрлік бұрыштың анықтамасы мен қасиеттерін білу және қолдану; 7.1.1.30 шеңбер диаметрі мен хордасының перпендикулярлығы туралы теоремаларды дәлелдеу және қолдану;; |
||||
|
Сабақ мақсаты |
Барлық оқушылар:
Оқушылар шеңбер
тақырыбы бойынша геометриялық есептерді шығару машықтарын дамытады,
геометрия пәні бойынша алған білімдерін қайталау және білімдерінің
практикалық бағытталуын қадағалау, шығармашылық қабілеттерін
қалыптастырады. Шеңберге іштей сызылған бұрыш, центрлік бұрыш, шеңбер доғасы туралы білімдерін жетілдіреді. Кейбір оқушылар: Танымдық қабілетін дамыту арқылы , пәнге қызығушылығын арттырады. |
||||
|
Сабақтың барысы |
|||||
|
Сабақтың кезеңдері |
Жоспарланған жұмыс |
Ресурстар |
|||
|
Сабақтың басы(2-5 минут) |
(МК) .Сұрақ-жауап әдісі арқылы оқушылармен пікір алмасу
(Сұрақтары:
|
|
|||
|
Сабақтың ортасы (6-40 минут) |
(МК,Ұ)
Б Егер бұрыштардың біреуінің градустық өлшемі α – ға тең болса, онда толықтауыш бұрыштың градустық өлшемі 3600- α болады.
Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады.
АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады. Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады. Теореманы дәлелдеу үшін 3 жағдайды қарастырамыз:
1. Бұрыштың бір
қабырғасы шеңбердің центрінен өтеді. АО радиусын жүргізсек,
теңбүйірлі АВО үшбұрышы шығады, мұнда АО=ОВ,
сондықтан 2. Шеңбердің О центрі шеңберге іштей сызылған бұрыш қабырғаларының арасында жатады. ВD диаметрін жүргіземіз, сонда
3. Шеңбердің О
центрі шеңберге іштей сызылған АВС бұрышынан тысқары жатсын. ВD
диаметрін жүргіземіз, сонда Теорема дәлелденді. Есеп шығару кезеңі 1) Шеңберге іштей сызылған бұрыш 220/ - қа тең. Осы бұрыш тірелетін доғаның градустық шамасын есептеңдер. 2) Шеңбер хордаларымен 1:2:3 қатынасында бөлінген. Пайда болған үшбұрыштың бұрыштарын есептеңдер. 3) Іштей сызылған АВС бұрышы АС доғасына тіреледі. АС доғасы 570- қа тең. АВС бұрышы неге тең? 4) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=5 см6 ВЕ=2 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 5) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=7 см, ВЕ=5 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 6) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=8 см6 ВЕ=9 см, СЕ=3,5см. ЕД кесіндісінің ұзындығы есептеңдер. |
Оқулық Аудидиск: №1Жұмыс дәптері |
|||
|
Сабақтың соңы( 41-45мин) |
(Қ) Топтық жұмыс
Топбасшыларының критериалды бағалауы. Тапсырма № 1 Табу керек: ∠ АОВ, егер ∠ ВАС = 40°.
Тапсырма № 2. АВ доғасының градустық шамасын табу керек..
Тапсырма № 3. Табу керек: ∠ МКТ. Пысықтау сұрақтары. 1. Центірлік бұрыш дегеніміз не? 2. Центрлік бұрышқа сәйкес шеңбер доғасы деп қандай доғаны айтады? 3. Шеңбер доғасының градустық өлшемі қалай анықталады? 4. Шеңберге іштей сызылған бұрыш деп қандай бұрышты атайды? 5. Диаметрге тірелетін бұрыш қандай бұрыш болады? 6. Өзара қиылысатын хордалар кесінділерінің қасиеттерін дәлелдеңдер |
||||
|
Қосымша ақпарат |
|||||
|
Қорытындылау |
Төмендегі бөлікті сабағыңыз туралы өз ойыңызды жазуға қолданыңыз.Өз сабағыңыз бойынша сол жақ бағандағы сұрақтарға жауап беріңіз. |
||||
|
1.Сабақ барысында өзгертулер енгіздіңіз бе? 2.Жүргізген жұмыс түрлері қаншалықты тиімді болды? |
|
||||
|
Қорытынды бағалау Ең жақсы өткен екі нәрсе? 1. 2. Қандай екі нәрсе сабақты жақсартар еді? 1. 2. |
|||||

шағым қалдыра аласыз


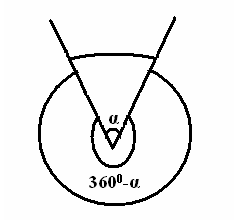 ұрыш жазықтықты
екі бөлікке бөледі. Бұл бөліктердің әр қайсысы
ұрыш жазықтықты
екі бөлікке бөледі. Бұл бөліктердің әр қайсысы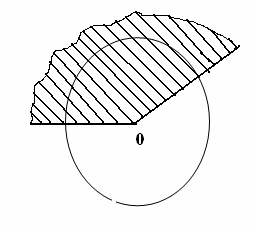 АКВ доғасы
АОВ центрлік бұрышына сәкес. Шеңбер доғасының
АКВ доғасы
АОВ центрлік бұрышына сәкес. Шеңбер доғасының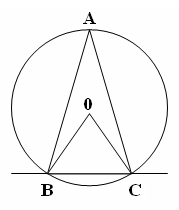 Төбесі
шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін
бұрыш
Төбесі
шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін
бұрыш