
|
Геометрия 8 сынып 23.11.2017 ж Тақырыбы: Үшбұрыштың тамаша нүктелері. Үшбұрыштың биссектрисаларының қиылысу нүктесі. |
|
||||||||||
|
Мақсат: |
|
||||||||||
|
Білімдік |
Жаңа білім |
Үшбұрыштың қанша биссектрисасы бар екендігін анықтайды. Биссектрисаның маңызды қасиеттерін есіне түсіреді. Нүкте мен кесіндінің арасындағы қашықтықты неше түрлі есептеуге болатындығын анықтайды. |
|
||||||||
|
Жаңа түсінік |
Үшбұрыштың тамаша нүктелерін біледі. Үшбұрыштың биссектрисалары тек қана бір жерде қиылысады екендігін түйіндейді. |
|
|||||||||
|
Құзырлылық |
Қолданым әрекеті |
Биссектрисаның қабырғалардан қашықтығы туралы теоремаға кері теорема жазуда, кері теорема түсінігін қолданады. Сол теореманың дұрыстығын есептеп шығарады. |
|
||||||||
|
Талдау әрекеті |
Үшбұрыштың биссектрисаларының бір нүктеде қиылысуын талдайды |
|
|||||||||
|
Шығармашылық әрекет |
Үшбұрыштың биссектрисаларын бір нүктеде қиылысатынын дәлелдеу үшін транспортирді қолданып эксперимент жасайды. |
|
|||||||||
|
Құндылық |
Бағамдау әрекеті |
Биссектриса бұрышты қандай бөліктерге бөлетінін есептейді.Үшбұрыш биссектрисаларының түсіндірмесін береді. Эксперименттің дұрыстығын сынайды. Үшбұрыштың биссектрисалары бір нүктеде қиылысады екендігін түйіндейді. Үшбұрыштың тамаша нүктелерін ерекшелейді. |
|
||||||||
|
Сабақ құрылымы: |
|
||||||||||
|
|
І. Ақпарат алмасу (14 мин.). ІІ. Алғашқы бекіту (4 мин.). ІІІ. Құзырлылық қалыптастыру (16 мин.). ІV. Шығармашылық қалыптастыру (8 мин.). V.Бағамдау - бағалау (3 мин.). |
|
|||||||||
|
Сабақ типі: фронтальді, жұптық |
|
||||||||||
|
Оқыту әдісі: репродуктивті, ішінара ізденушілік. |
|
||||||||||
|
Мұғалім іс-әрекетінің тәсілі: |
|
||||||||||
|
|
Оқушыға жол сілтеу, кей кездері көмектесу және оқушының индивидуалдық қасиеттерін дамыту. |
|
|||||||||
|
Негізгі ұғымдар мен терминдер: Үшбұрыш, үшбұрыштың биссектрисасы, үшбұрыштың биіктігі, үшбұрыштың медианасы, орта перпендикуляр |
|
||||||||||
Тақырып жоспары: 1. Үшбұрыштың тамаша нүктелеріне шолу 2. Үшбұрыштың биссектрисасына анықтама 3. Биссектрисаның қабырғалардан қашықтығы туралы теорема 4. Үшбұрыштың тамаша нүктелерінің біріншісі: биссектрисалардың қиылысу нүктесі |
|
||||||||||
|
|
|||||||||||
|
Үшбұрыштың тамаша нүктелеріне шолу Үшбұрыштың тамаша нүктелері деп төрт нүктені айтамыз. Олар: Үшбұрыштың 1) биссектрисаларының қиылысу нүктесі 2) медианаларының қиылысу нүктесі 3) биіктіктерінің қиылысу нүктесі 4) қабырғаларына жүргізілген орта перпендикулярлардың қиылысу нүктесі |
|||||||||||
|
|
|||||||||||
|
5
АЕ кесіндісі: АВС үшбұрышының биссектрисасы деп аталады. НЕМЕСЕ АВС үшбұрышындағы А бұрышының биссектрисасы деп аталады. |
|||||||||||
|
6 – слайд ЕСКЕРТУ!!!
Мысал: Тікбұрышты үшбұрыштың А төбесінен ВС қабырғасына дейінгі қашықтықты табыңыз Ш |
|
7 – слайд Биссектрисаның қабырғалардан қашықтығы туралы теорема 13 – теорема. Биссектрисаның кез келген нүктесі бұрыш қабырғаларынан бірдей қашықтықта жатады. Д Сонда, үш бұрышы және бір қабырғасы тең болған АВЕ және АСЕ үшбұрыштары тең болып шығады. Осыдан, ВЕ = СЕ. |
|
|
|
8 – слайд Биссектрисаның қабырғалардан қашықтығы туралы теорема МЫСАЛ: ЕВ және ЕС перпендикулярлар және ЕВ=EC. AE биссектриса екенін дәлелде. (Екі тікбұрышты үшбұрыш тең егер бір катеті және гипотенузасы тең болса)
ШЕШУІ: АВС және АСЕ тікбұрышты үшбұрыштар. Ал, тікбұрышты үшбұрыштардың теңдік белгілерін еске салсақ, АЕ екеуіне ортақ гипотенуза, және ЕВ=EС. Яғни АВС және АСЕ тең үшбұрыштар. Осыдан АЕ биссектриса
|
|
|
|
9 – слайд Үшбұрыштың биссектрисалары
Бұл биссектрисалар қанша нүктеде қиылысады? |
|
|
|
10 – слайд Үшбұрыштың биссектрисаларының қиылысу нүктесі 15 – теорема. Үшбұрыштың биссектрисалары бір нүктеде қиылысады Дәлелі: А және В төбелерінен биссектрисалар жүргізейік. Сол екеуінің қиылысу нүктесі арқылы IS, IR, IF перпендикулярларын түсірейік. Сонда, 14-теорема бойынша: IS=IF, IF=IR => IS=IR О Биссектрисалардың қиылысу нүктесін І әрпімен белгілейміз!!! |
|
11 – слайд Үшбұрыштың биссектрисаларының қиылысу нүктесі МЫСАЛ: АВС теңбүйірлі үшбұрыш. АЕ кесіндісі ВС кесіндісіне перпендикуляр екенін дәлелдеңіз.
Ш β = γ Осыдан, АЕВ және АСЕ үшбұрыштарының екі бұрышы тең болады. Ал екі бұрышы тең болса, онда үшінші бұрышы да тең болуы тиіс.
|
|
|
іі. алғашқы бекіту |
|
Мына кестені толтыра отырып сабақтың мазмұны бойынша қорытынды шығар.
|
Үшбұрыштың тамаша нүктелерін жазыңыз |
Үшбұрыштың биссектрисаларын көрсетіңіз |
|
|
|
Қорытынды:___________________________________________________________
|
ііі. құзырлылық қалыптастыру |
|
Деңгейлік тапсырмалар:
І деңгей тапсырмалары
-
Үшбұрыштың қанша биссектрисасы бар?
-
Биссектрисаның ең маңызды қасиетін атаңыз
-
Нүкте мен кесіндінің арасындағы қашықтықты неше түрлі есептеуге болады?
-
А бұрышы 60o-қа тең. Биссектриса сол бұрышты қандай бөліктерге бөледі?
-
Теңқабырғалы үшбұрыштың биссектрисаларын сызыңыз. Пайда болған бұрыштарды табыңыз.
-
Барлық үшбұрыштың биссектрисалары бір нүктеде қиылысады ма?
-
Үшбұрыштың биссектрисалары тек қана үшбұрыш ішінде қиылысады ма?
ІІ деңгей тапсырмалары
1. Биссектрисаның қабырғалардан қашықтығы туралы теоремаға кері теорема жазыңыз
2. Сол теореманы дәлелдеңіз.
ІІІ деңгей тапсырмалары
-
Үшбұрыштың биссектрисаларының бір нүктеде қиылысуы кездейсоқтық па?
|
|
іV. шығармашылық әрекет |
|
Топтық жұмыс.
Сынып оқушылары екі топқа бөлініп келесі тапсырманы орындайды.
І топ
Кез келген үшбұрыштың биіктіктері бір нүктеде қиылысатынын дәлелдеңдер.
ІІ топ
Үшбұрыштың қабырғаларына жүргізілген орта перпендикулярлар бір нүктеде қиылысатынын дәлелдеңдер.
|
|
V. бағамдау-бағалау |
|
Сабақтың мақсатына қалай қол жеткізгендігің туралы эссе жаз.
______________________________________________________________________
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
сабақ жоспары "үшбұрыштың тамаша нүктесі"
сабақ жоспары "үшбұрыштың тамаша нүктесі"
|
Геометрия 8 сынып 23.11.2017 ж Тақырыбы: Үшбұрыштың тамаша нүктелері. Үшбұрыштың биссектрисаларының қиылысу нүктесі. |
|
||||||||||
|
Мақсат: |
|
||||||||||
|
Білімдік |
Жаңа білім |
Үшбұрыштың қанша биссектрисасы бар екендігін анықтайды. Биссектрисаның маңызды қасиеттерін есіне түсіреді. Нүкте мен кесіндінің арасындағы қашықтықты неше түрлі есептеуге болатындығын анықтайды. |
|
||||||||
|
Жаңа түсінік |
Үшбұрыштың тамаша нүктелерін біледі. Үшбұрыштың биссектрисалары тек қана бір жерде қиылысады екендігін түйіндейді. |
|
|||||||||
|
Құзырлылық |
Қолданым әрекеті |
Биссектрисаның қабырғалардан қашықтығы туралы теоремаға кері теорема жазуда, кері теорема түсінігін қолданады. Сол теореманың дұрыстығын есептеп шығарады. |
|
||||||||
|
Талдау әрекеті |
Үшбұрыштың биссектрисаларының бір нүктеде қиылысуын талдайды |
|
|||||||||
|
Шығармашылық әрекет |
Үшбұрыштың биссектрисаларын бір нүктеде қиылысатынын дәлелдеу үшін транспортирді қолданып эксперимент жасайды. |
|
|||||||||
|
Құндылық |
Бағамдау әрекеті |
Биссектриса бұрышты қандай бөліктерге бөлетінін есептейді.Үшбұрыш биссектрисаларының түсіндірмесін береді. Эксперименттің дұрыстығын сынайды. Үшбұрыштың биссектрисалары бір нүктеде қиылысады екендігін түйіндейді. Үшбұрыштың тамаша нүктелерін ерекшелейді. |
|
||||||||
|
Сабақ құрылымы: |
|
||||||||||
|
|
І. Ақпарат алмасу (14 мин.). ІІ. Алғашқы бекіту (4 мин.). ІІІ. Құзырлылық қалыптастыру (16 мин.). ІV. Шығармашылық қалыптастыру (8 мин.). V.Бағамдау - бағалау (3 мин.). |
|
|||||||||
|
Сабақ типі: фронтальді, жұптық |
|
||||||||||
|
Оқыту әдісі: репродуктивті, ішінара ізденушілік. |
|
||||||||||
|
Мұғалім іс-әрекетінің тәсілі: |
|
||||||||||
|
|
Оқушыға жол сілтеу, кей кездері көмектесу және оқушының индивидуалдық қасиеттерін дамыту. |
|
|||||||||
|
Негізгі ұғымдар мен терминдер: Үшбұрыш, үшбұрыштың биссектрисасы, үшбұрыштың биіктігі, үшбұрыштың медианасы, орта перпендикуляр |
|
||||||||||
Тақырып жоспары: 1. Үшбұрыштың тамаша нүктелеріне шолу 2. Үшбұрыштың биссектрисасына анықтама 3. Биссектрисаның қабырғалардан қашықтығы туралы теорема 4. Үшбұрыштың тамаша нүктелерінің біріншісі: биссектрисалардың қиылысу нүктесі |
|
||||||||||
|
|
|||||||||||
|
Үшбұрыштың тамаша нүктелеріне шолу Үшбұрыштың тамаша нүктелері деп төрт нүктені айтамыз. Олар: Үшбұрыштың 1) биссектрисаларының қиылысу нүктесі 2) медианаларының қиылысу нүктесі 3) биіктіктерінің қиылысу нүктесі 4) қабырғаларына жүргізілген орта перпендикулярлардың қиылысу нүктесі |
|||||||||||
|
|
|||||||||||
|
5
АЕ кесіндісі: АВС үшбұрышының биссектрисасы деп аталады. НЕМЕСЕ АВС үшбұрышындағы А бұрышының биссектрисасы деп аталады. |
|||||||||||
|
6 – слайд ЕСКЕРТУ!!!
Мысал: Тікбұрышты үшбұрыштың А төбесінен ВС қабырғасына дейінгі қашықтықты табыңыз Ш |
|
7 – слайд Биссектрисаның қабырғалардан қашықтығы туралы теорема 13 – теорема. Биссектрисаның кез келген нүктесі бұрыш қабырғаларынан бірдей қашықтықта жатады. Д Сонда, үш бұрышы және бір қабырғасы тең болған АВЕ және АСЕ үшбұрыштары тең болып шығады. Осыдан, ВЕ = СЕ. |
|
|
|
8 – слайд Биссектрисаның қабырғалардан қашықтығы туралы теорема МЫСАЛ: ЕВ және ЕС перпендикулярлар және ЕВ=EC. AE биссектриса екенін дәлелде. (Екі тікбұрышты үшбұрыш тең егер бір катеті және гипотенузасы тең болса)
ШЕШУІ: АВС және АСЕ тікбұрышты үшбұрыштар. Ал, тікбұрышты үшбұрыштардың теңдік белгілерін еске салсақ, АЕ екеуіне ортақ гипотенуза, және ЕВ=EС. Яғни АВС және АСЕ тең үшбұрыштар. Осыдан АЕ биссектриса
|
|
|
|
9 – слайд Үшбұрыштың биссектрисалары
Бұл биссектрисалар қанша нүктеде қиылысады? |
|
|
|
10 – слайд Үшбұрыштың биссектрисаларының қиылысу нүктесі 15 – теорема. Үшбұрыштың биссектрисалары бір нүктеде қиылысады Дәлелі: А және В төбелерінен биссектрисалар жүргізейік. Сол екеуінің қиылысу нүктесі арқылы IS, IR, IF перпендикулярларын түсірейік. Сонда, 14-теорема бойынша: IS=IF, IF=IR => IS=IR О Биссектрисалардың қиылысу нүктесін І әрпімен белгілейміз!!! |
|
11 – слайд Үшбұрыштың биссектрисаларының қиылысу нүктесі МЫСАЛ: АВС теңбүйірлі үшбұрыш. АЕ кесіндісі ВС кесіндісіне перпендикуляр екенін дәлелдеңіз.
Ш β = γ Осыдан, АЕВ және АСЕ үшбұрыштарының екі бұрышы тең болады. Ал екі бұрышы тең болса, онда үшінші бұрышы да тең болуы тиіс.
|
|
|
іі. алғашқы бекіту |
|
Мына кестені толтыра отырып сабақтың мазмұны бойынша қорытынды шығар.
|
Үшбұрыштың тамаша нүктелерін жазыңыз |
Үшбұрыштың биссектрисаларын көрсетіңіз |
|
|
|
Қорытынды:___________________________________________________________
|
ііі. құзырлылық қалыптастыру |
|
Деңгейлік тапсырмалар:
І деңгей тапсырмалары
-
Үшбұрыштың қанша биссектрисасы бар?
-
Биссектрисаның ең маңызды қасиетін атаңыз
-
Нүкте мен кесіндінің арасындағы қашықтықты неше түрлі есептеуге болады?
-
А бұрышы 60o-қа тең. Биссектриса сол бұрышты қандай бөліктерге бөледі?
-
Теңқабырғалы үшбұрыштың биссектрисаларын сызыңыз. Пайда болған бұрыштарды табыңыз.
-
Барлық үшбұрыштың биссектрисалары бір нүктеде қиылысады ма?
-
Үшбұрыштың биссектрисалары тек қана үшбұрыш ішінде қиылысады ма?
ІІ деңгей тапсырмалары
1. Биссектрисаның қабырғалардан қашықтығы туралы теоремаға кері теорема жазыңыз
2. Сол теореманы дәлелдеңіз.
ІІІ деңгей тапсырмалары
-
Үшбұрыштың биссектрисаларының бір нүктеде қиылысуы кездейсоқтық па?
|
|
іV. шығармашылық әрекет |
|
Топтық жұмыс.
Сынып оқушылары екі топқа бөлініп келесі тапсырманы орындайды.
І топ
Кез келген үшбұрыштың биіктіктері бір нүктеде қиылысатынын дәлелдеңдер.
ІІ топ
Үшбұрыштың қабырғаларына жүргізілген орта перпендикулярлар бір нүктеде қиылысатынын дәлелдеңдер.
|
|
V. бағамдау-бағалау |
|
Сабақтың мақсатына қалай қол жеткізгендігің туралы эссе жаз.
______________________________________________________________________

шағым қалдыра аласыз


 – слайд Үшбұрыштың
биссектрисасына анықтама
– слайд Үшбұрыштың
биссектрисасына анықтама ешуі: Бұл
тікбұрышты үшбұрыш болғандықтан, АВ кесіндісі ВС кесіндісіне
перпендикуляр. Сондықтан, А төбесінен ВС қабырғасына дейінгі
қашықтық АВ кесіндісінің ұзындығына тең. Яғни, 4
см.
ешуі: Бұл
тікбұрышты үшбұрыш болғандықтан, АВ кесіндісі ВС кесіндісіне
перпендикуляр. Сондықтан, А төбесінен ВС қабырғасына дейінгі
қашықтық АВ кесіндісінің ұзындығына тең. Яғни, 4
см. әлелі:
Бізге А бұрышының биссектрисасы берілген. Сол биссектрисадан бір Е
деген нүкте тандап алайық. Е нүктесі арқылы А бұрышының екі
қабырғасына перпендикуляр түзулер сызайық.
әлелі:
Бізге А бұрышының биссектрисасы берілген. Сол биссектрисадан бір Е
деген нүкте тандап алайық. Е нүктесі арқылы А бұрышының екі
қабырғасына перпендикуляр түзулер сызайық.
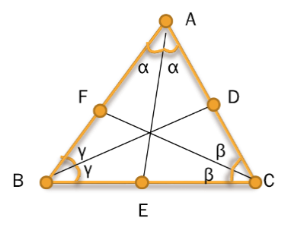 шбұрыштың
ішкі бұрыштарының үш биссектрисасы бар:
шбұрыштың
ішкі бұрыштарының үш биссектрисасы бар: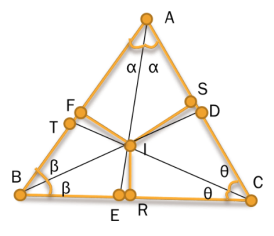 сыдан, І
нүктесі С бұрышының биссектрисасының бойында жатыр. Демек, ІС
кесіндісін ары қарай жалғастырсақ, ол С төбесінен шыққан
биссектриса болады. Яғни, үш биссектриса бір нүктеде
қиылысады.
сыдан, І
нүктесі С бұрышының биссектрисасының бойында жатыр. Демек, ІС
кесіндісін ары қарай жалғастырсақ, ол С төбесінен шыққан
биссектриса болады. Яғни, үш биссектриса бір нүктеде
қиылысады.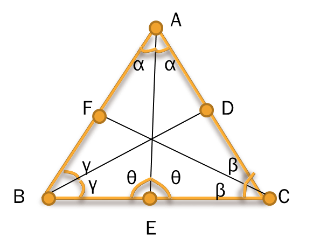 ЕШУІ: АВС
теңбүйірлі болғандықтан, оның екі бүйір қабырғасы тең, яғни, AB=AC.
Сондықтан,
ЕШУІ: АВС
теңбүйірлі болғандықтан, оның екі бүйір қабырғасы тең, яғни, AB=AC.
Сондықтан,














