|
Пән мұғалімі: Жанәділов Азамат Абылайұлы The teacher of the lesson: Zhanadilov Azamat Abylaiuly Күні: Data: |
|||
|
Пәні: Геометрия Сыныбы: 7 «A» Қатысқан оқушы саны: Subject: Geometry Grade:7 «A» Attendant pupils: |
|||
|
Сабақтың тақырыбы The theme of the lesson |
Сәуле, жарты жазықтық, кесінді |
||
|
Сабақтың мақсаты The aim of the lesson |
Оқушыларға сәуле, жарты жазықтық, кесінді анықтамаларын түсіндіру. Кесіндіні өлшеп салу аксиомалар туралы мағлұмат беру және оларды есептер шығаруда қолана білу бейімділіктерін қалыптастыру. Оқушылар сәуле, жарты жазықтық, кесінді ұғымдарын және оларға байланысты есептерді ағылшын тілінде шығара білуге үйрету. |
||
|
Оқып үйренудің нәтижесінде The result of learning |
|
||
|
Үйрену мақсатында бағаны қоса бағалау On the of assessments |
|
||
|
Әдіс-тәсілдер Methods |
|
||
|
Ресурстар Resources |
Оқулық, маркер, дидактикалық материалдар |
||
|
Жоспар |
|||
|
Сабақ кезеңдері During the lesson |
Мұғалімнің іс-әрекеті Teacher's activity |
Оқушының іс-әрекеті Pupil's activity |
|
|
Қызығу- шылықты ояту |
І. Ұйымдастыру кезеңі * оқушылармен амандасу; * оқушыларды түгелдеу; * оқу құралдарын тексеру; * сыныптың тазалығына көңіл бөлу; * оқушылардың зейінін сабаққа аудару; ІІ. Үй тапсырмасын тексеру |
І. * мұғаліммен сәлемдеседі; * оқу құралдарын дайындайды; * зейіндерін сабаққа аударады; ІІ. Оқушылар үйге берілген тапсырманы еске түсіру мақсатында қойылған сұрақтарға жауап береді.
|
|
|
Мағынаны тану
|
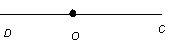
III Геометрияда кесінді және сәуле ұғымдары көп қолданылады. Олар түзудің бөліктері ретінде анықталады. с түзуі берілсін: с түзуінен алынған О нүктесі оны екі бөлікке және екі сәулеге бөледі. Сәуленің символдық бейнелеуі ретінде оның басын бейнелейтін нүктені айқын көрсетіп, түзудің бөлігі алынады, олардың әрқайсысы жарты түзу деп аталады.
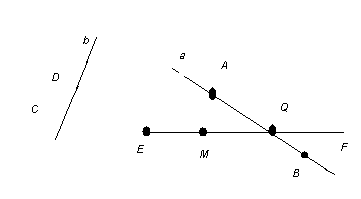
А, В нүктелері жарты түзудің бірінде, ал С, D екіншісінде жатыр. Мұндағы О жарты (мысалы, А, В нүктелерінің немесе C, D нүктелерінің) арасында жатпайтынын байқаймыз. 2) Түзуде жатқан нүкте сол түзуді екі жарты түзуге бөледі. Жарты түзуді сәуле деп те атайды. Суретте көрсетілген жарты түзуді не сәулені екі әріппен белгілейміз. Мысалы, АО және ОС мұнда алдыңғы әріп сәуленің бас нүктесін, ал екіншісі сәуленің бойындағы кез келген нүктені анықтайды. Түзуде жатқан әрбір нүкте түзуді екі сәулеге бөледі. ОА, ОС сәулелері бір- бірін түзуге дейін толықтырып тұрады. Сондықтан олар толықтауыш сәулелер деп аталады. Сәулелер түзудің бөліктері болып есептеледі.
EF сәулесі берілсін: бұл сәуленің бойынан М нүктесін белгілейік. Сонда М нүктесі EF сәулесінде жатыр, ал А нүктесі бұл сәуледе жатпайды. Берілген EF сәулесінде ЕМ кесіндісі де жатыр. Сондықтан ЕМ кесіндісін ЕF сәулесінің бөлігі деп қарастыруға болады. Сәуле ұғымын ағылшын тілінде қарастырайық. Definition: The ray AB is the part of the line AB that contains point A and all the points on the line segment that stretches from point A through point B to infinity. The ray AB is denoted by [AB.
Ray AB or [AB Ray CD or [CD In the diagrams, each ray begins at a point and extends to infinity in one direction. A is the endpoint of [AB, and C is the endpoint of [CD. Жазықтықта кез-келген бір нүктені белгілеп алсақ, онда осы нүктеден бас нүктесі болатын шексіз көп сәуле жүргізуге болады. Жазықтықта жатқан түзу мен нүктелердің өзара орналасуын қарастырайық.
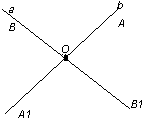
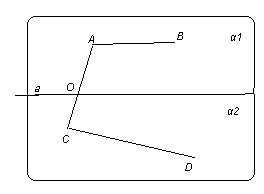
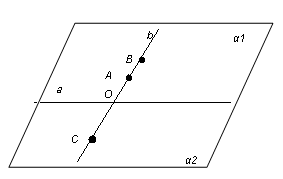
Қандай да бір жазықтық және сол жазықтықта жатқан а түзуі берілсін. а түзуі жазықтықты екі бөлікке бөледі. Бөліктердің әрқайсысы жарты жазықтық деп аталады. Жарты жазықтықтардың біріншісі α1, екіншісін α2 арқылы белгілейік. А, В нүктелері бір жарты жазықтықта жатса, оларды қосатын АВ кесіндісі а түзуімен қиылыспайды. C, D нүктелері мен CD кесіндісі де дәл сол сияқты. Ал, А және С нүктелері әр түрлі жарты жазықтықтарда (α1 және α2) жатыр. Оларды қосатын АС кесіндісі а түзуімен О нүктесінде қиылысады. 3) Түзу жазықтықты екі жарты жазықтыққа бөледі. Жазықтықтағы қиылысқан екі түзудің толықтауыш сәулелері әр түрлі жарты жазықтықтарда жатады. Жазықтықтағы а және b түзулері О нүктесінде қиылыссын. ОА және ОС сәулелері b түзуінің толықтауыш сәулелері.
Егер ОА сәулесінен кез келген
В нүктесін алсақ, О нүктесі А және В нүктелерінің арасында
жатпайды, өйткені О нүктесі ОА сәулесінің бас нүктесі, сондықтан АВ
кесіндісі а түзуімен қиылыспайды. Олай болса, ОА сәулесінде жатқан
кез келген А, В нүктелері жарты жазықтықтарының біреуінде жатады.
ОА сәулесі α1 жарты жазықтығында
жатыр. ОА және ОС сәулелері толықтауыш сәулелер болғандықтан, О
нүктесі А және С нүктелерінің арасында жатыр. Демек,
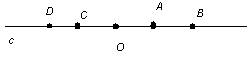
С In mathematics, a plane is a flat, two dimensional surface that extends infinitely far. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with a room's walls extended infinitely far, or they may enjoy an independent existence in their own right, as in the setting of Euclidean geometry. When working exclusively in two-dimensional Euclidean space, the definite article is used, so, the plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory and graphing are performed in a two-dimensional space, or in other words, in the plane. Кесінді Түзудегі үш нүктенің біреуі және тек біреуі ғана басқа екеуінің арасында жатады. «Арасында жатады» деген ұғым кесінді ұғымын анықтауға мүмкіндік береді. Анықтама. Түзудің берілген екі нүктесі мен олардың арасында жатқан барлық нүктелерінен тұратын бөлігін кесінді деп атайды. Берілген екі нүкте кесіндінің ұштары деп аталады.
Кесіндіні АВ немесе ВА арқылы белгілейді. А және В нүктелері – АВ кесіндісінің ұштары түзудің нүктелері шексіз көп болғандықтан, кесіндінің нүктелері де шексіз көп. Кесіндінің символдық бейнеленуі екі ұшы ерекше болған түзудің бөлігінің бейнесі. Кесіндінің ұштары кесіндіге тиісті болады. Енді кесінді ұғымын ағылшын тілінде түсініп көрейік. In geometry, a line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line between its endpoints. Properties:
Property: Using this property, we can conclude that if three points are collinear, then one of them is between the other points.
Point B is between the points A and C.
Термин сөздермен жұмыс: Ray - сәуле, Line segment - кесінді Plane - жазықтық Similarity - ұқсастық Straight line - түзу сызық In one direction - бір бағыт бойынша |
III.Оқушылар жаңа тақырыптағы қажет мәліметтерді дәптерлеріне жазып, сызып отырады.
|
|
|
Ой қозғау
|
ІV. Іс-әрекетке байланысты оқулықтағы №21, №23, №25-есептерді шығарады.
№21 19-сурет бойынша
№23 19-суретте:
№25 Бір түзуде жатпайтын А, В, С нүктелері берілген. Олардың әрбір екеуі арқылы түзу жүргізіңдер.
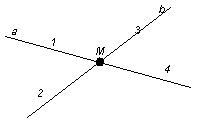
V. Шығармашылық тапсырма. Зеректер әлемі: № 1. М нүктесінде қиылысатын а және b түзулерін салыңдар. Пайда болған жарты түзулерді көрсетіңдер. Шешуі:
№2. Жазықтықта жатқан а түзуі және AB, CD, EF, KL кесінділері берілген. а түзуі берілген
жазықтықты СD және АВ кесінділері бір жазықтықта, KL бір жарты жазықтықта. Қай кесінділер а түзуімен қиылысады және қай кесінділер қиылыспайды? Өзара қиылысатын кесінділер және қиылыспайтын кесінділерді атаңдар. №3 Берілгені: ОС сәулесі жазыңқы бұрыш жасайтын ОD сәулесін жүргіз. Шешуі: Ең алдымен ОС сәулесін
сызамыз. О нүктесінен бастап OD толықтауыш сәулесін
жүргізіп,
№4. а және b түзулері О нүктесінде қиылысады. 1) Неше бұрыш пайда болды? 2) Әрбір бұрышты белгілеп жазыңдар. 3) Жазыңқы бұрышты атаңдар. Шешуі: 6 бұрыш.
|
ІV. Оқушылар оқулықтағы №21, №23, №25-есептерді шығарады. V.Оқушылар шығармашылық тапсырманы өз бетінше орындап, тез жауап беруге тырысады. |
|
|
Қорытын-ды Conclusion |
Оқушылардың жаңа тақырыпты қалай меңгергенін білу үшін «Кім жылдам?» әдісі арқылы төмендегі тапсырмаларды ағылшын тілінде беріліп, жауаптарын ағылшын тілінде айтады. 1. Explain why the concepts of point, line, and plane cannot be defined in geometry. 2. Draw five points on a piece of paper. Draw all the lines passing through these points. How many lines can you draw? 3. Explain the difference between a ray and a half line. 4. At least how many points determine a line? 5. Give examples from daily life to illustrate the concepts of point, line, and plane. 6. Write words to complete the sentences. a. A point has no __________ and no __________. b. Two points determine a ___________. c. d. Two lines that lie in different planes and do not intersect are called ___________ lines. 7. Determine whether the statements are true or false for the given figure.
a. points D and E are not in the line l b. B ∈l c. E ∈l 8. Name all the lines, rays, line segments, and half lines in the given figure.
|
Оқушылар берілген тест тапсырмаларындағы сұрақтарға ойланып, ағылшын тілінде жауап береді. |
|
|
Үйге тапсырма Home work |
Тақырып бойынша қосымша ақпарат жинақтау. Оқулықтан № 26, 27 - есептер |
||
18
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Сәуле, жарты жазықтық және кесінді (Ray, half plane and segment)
Сәуле, жарты жазықтық және кесінді (Ray, half plane and segment)
|
Пән мұғалімі: Жанәділов Азамат Абылайұлы The teacher of the lesson: Zhanadilov Azamat Abylaiuly Күні: Data: |
|||
|
Пәні: Геометрия Сыныбы: 7 «A» Қатысқан оқушы саны: Subject: Geometry Grade:7 «A» Attendant pupils: |
|||
|
Сабақтың тақырыбы The theme of the lesson |
Сәуле, жарты жазықтық, кесінді |
||
|
Сабақтың мақсаты The aim of the lesson |
Оқушыларға сәуле, жарты жазықтық, кесінді анықтамаларын түсіндіру. Кесіндіні өлшеп салу аксиомалар туралы мағлұмат беру және оларды есептер шығаруда қолана білу бейімділіктерін қалыптастыру. Оқушылар сәуле, жарты жазықтық, кесінді ұғымдарын және оларға байланысты есептерді ағылшын тілінде шығара білуге үйрету. |
||
|
Оқып үйренудің нәтижесінде The result of learning |
|
||
|
Үйрену мақсатында бағаны қоса бағалау On the of assessments |
|
||
|
Әдіс-тәсілдер Methods |
|
||
|
Ресурстар Resources |
Оқулық, маркер, дидактикалық материалдар |
||
|
Жоспар |
|||
|
Сабақ кезеңдері During the lesson |
Мұғалімнің іс-әрекеті Teacher's activity |
Оқушының іс-әрекеті Pupil's activity |
|
|
Қызығу- шылықты ояту |
І. Ұйымдастыру кезеңі * оқушылармен амандасу; * оқушыларды түгелдеу; * оқу құралдарын тексеру; * сыныптың тазалығына көңіл бөлу; * оқушылардың зейінін сабаққа аудару; ІІ. Үй тапсырмасын тексеру |
І. * мұғаліммен сәлемдеседі; * оқу құралдарын дайындайды; * зейіндерін сабаққа аударады; ІІ. Оқушылар үйге берілген тапсырманы еске түсіру мақсатында қойылған сұрақтарға жауап береді.
|
|
|
Мағынаны тану
|
III Геометрияда кесінді және сәуле ұғымдары көп қолданылады. Олар түзудің бөліктері ретінде анықталады. с түзуі берілсін: с түзуінен алынған О нүктесі оны екі бөлікке және екі сәулеге бөледі. Сәуленің символдық бейнелеуі ретінде оның басын бейнелейтін нүктені айқын көрсетіп, түзудің бөлігі алынады, олардың әрқайсысы жарты түзу деп аталады.
А, В нүктелері жарты түзудің бірінде, ал С, D екіншісінде жатыр. Мұндағы О жарты (мысалы, А, В нүктелерінің немесе C, D нүктелерінің) арасында жатпайтынын байқаймыз. 2) Түзуде жатқан нүкте сол түзуді екі жарты түзуге бөледі. Жарты түзуді сәуле деп те атайды. Суретте көрсетілген жарты түзуді не сәулені екі әріппен белгілейміз. Мысалы, АО және ОС мұнда алдыңғы әріп сәуленің бас нүктесін, ал екіншісі сәуленің бойындағы кез келген нүктені анықтайды. Түзуде жатқан әрбір нүкте түзуді екі сәулеге бөледі. ОА, ОС сәулелері бір- бірін түзуге дейін толықтырып тұрады. Сондықтан олар толықтауыш сәулелер деп аталады. Сәулелер түзудің бөліктері болып есептеледі.
EF сәулесі берілсін: бұл сәуленің бойынан М нүктесін белгілейік. Сонда М нүктесі EF сәулесінде жатыр, ал А нүктесі бұл сәуледе жатпайды. Берілген EF сәулесінде ЕМ кесіндісі де жатыр. Сондықтан ЕМ кесіндісін ЕF сәулесінің бөлігі деп қарастыруға болады. Сәуле ұғымын ағылшын тілінде қарастырайық. Definition: The ray AB is the part of the line AB that contains point A and all the points on the line segment that stretches from point A through point B to infinity. The ray AB is denoted by [AB.
Ray AB or [AB Ray CD or [CD In the diagrams, each ray begins at a point and extends to infinity in one direction. A is the endpoint of [AB, and C is the endpoint of [CD. Жазықтықта кез-келген бір нүктені белгілеп алсақ, онда осы нүктеден бас нүктесі болатын шексіз көп сәуле жүргізуге болады. Жазықтықта жатқан түзу мен нүктелердің өзара орналасуын қарастырайық.
Қандай да бір жазықтық және сол жазықтықта жатқан а түзуі берілсін. а түзуі жазықтықты екі бөлікке бөледі. Бөліктердің әрқайсысы жарты жазықтық деп аталады. Жарты жазықтықтардың біріншісі α1, екіншісін α2 арқылы белгілейік. А, В нүктелері бір жарты жазықтықта жатса, оларды қосатын АВ кесіндісі а түзуімен қиылыспайды. C, D нүктелері мен CD кесіндісі де дәл сол сияқты. Ал, А және С нүктелері әр түрлі жарты жазықтықтарда (α1 және α2) жатыр. Оларды қосатын АС кесіндісі а түзуімен О нүктесінде қиылысады. 3) Түзу жазықтықты екі жарты жазықтыққа бөледі. Жазықтықтағы қиылысқан екі түзудің толықтауыш сәулелері әр түрлі жарты жазықтықтарда жатады. Жазықтықтағы а және b түзулері О нүктесінде қиылыссын. ОА және ОС сәулелері b түзуінің толықтауыш сәулелері.
Егер ОА сәулесінен кез келген
В нүктесін алсақ, О нүктесі А және В нүктелерінің арасында
жатпайды, өйткені О нүктесі ОА сәулесінің бас нүктесі, сондықтан АВ
кесіндісі а түзуімен қиылыспайды. Олай болса, ОА сәулесінде жатқан
кез келген А, В нүктелері жарты жазықтықтарының біреуінде жатады.
ОА сәулесі α1 жарты жазықтығында
жатыр. ОА және ОС сәулелері толықтауыш сәулелер болғандықтан, О
нүктесі А және С нүктелерінің арасында жатыр. Демек,
С In mathematics, a plane is a flat, two dimensional surface that extends infinitely far. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with a room's walls extended infinitely far, or they may enjoy an independent existence in their own right, as in the setting of Euclidean geometry. When working exclusively in two-dimensional Euclidean space, the definite article is used, so, the plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory and graphing are performed in a two-dimensional space, or in other words, in the plane. Кесінді Түзудегі үш нүктенің біреуі және тек біреуі ғана басқа екеуінің арасында жатады. «Арасында жатады» деген ұғым кесінді ұғымын анықтауға мүмкіндік береді. Анықтама. Түзудің берілген екі нүктесі мен олардың арасында жатқан барлық нүктелерінен тұратын бөлігін кесінді деп атайды. Берілген екі нүкте кесіндінің ұштары деп аталады.
Кесіндіні АВ немесе ВА арқылы белгілейді. А және В нүктелері – АВ кесіндісінің ұштары түзудің нүктелері шексіз көп болғандықтан, кесіндінің нүктелері де шексіз көп. Кесіндінің символдық бейнеленуі екі ұшы ерекше болған түзудің бөлігінің бейнесі. Кесіндінің ұштары кесіндіге тиісті болады. Енді кесінді ұғымын ағылшын тілінде түсініп көрейік. In geometry, a line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line between its endpoints. Properties:
Property: Using this property, we can conclude that if three points are collinear, then one of them is between the other points.
Point B is between the points A and C.
Термин сөздермен жұмыс: Ray - сәуле, Line segment - кесінді Plane - жазықтық Similarity - ұқсастық Straight line - түзу сызық In one direction - бір бағыт бойынша |
III.Оқушылар жаңа тақырыптағы қажет мәліметтерді дәптерлеріне жазып, сызып отырады.
|
|
|
Ой қозғау
|
ІV. Іс-әрекетке байланысты оқулықтағы №21, №23, №25-есептерді шығарады.
№21 19-сурет бойынша
№23 19-суретте:
№25 Бір түзуде жатпайтын А, В, С нүктелері берілген. Олардың әрбір екеуі арқылы түзу жүргізіңдер.
V. Шығармашылық тапсырма. Зеректер әлемі: № 1. М нүктесінде қиылысатын а және b түзулерін салыңдар. Пайда болған жарты түзулерді көрсетіңдер. Шешуі:
№2. Жазықтықта жатқан а түзуі және AB, CD, EF, KL кесінділері берілген. а түзуі берілген
жазықтықты СD және АВ кесінділері бір жазықтықта, KL бір жарты жазықтықта. Қай кесінділер а түзуімен қиылысады және қай кесінділер қиылыспайды? Өзара қиылысатын кесінділер және қиылыспайтын кесінділерді атаңдар. №3 Берілгені: ОС сәулесі жазыңқы бұрыш жасайтын ОD сәулесін жүргіз. Шешуі: Ең алдымен ОС сәулесін
сызамыз. О нүктесінен бастап OD толықтауыш сәулесін
жүргізіп,
№4. а және b түзулері О нүктесінде қиылысады. 1) Неше бұрыш пайда болды? 2) Әрбір бұрышты белгілеп жазыңдар. 3) Жазыңқы бұрышты атаңдар. Шешуі: 6 бұрыш.
|
ІV. Оқушылар оқулықтағы №21, №23, №25-есептерді шығарады. V.Оқушылар шығармашылық тапсырманы өз бетінше орындап, тез жауап беруге тырысады. |
|
|
Қорытын-ды Conclusion |
Оқушылардың жаңа тақырыпты қалай меңгергенін білу үшін «Кім жылдам?» әдісі арқылы төмендегі тапсырмаларды ағылшын тілінде беріліп, жауаптарын ағылшын тілінде айтады. 1. Explain why the concepts of point, line, and plane cannot be defined in geometry. 2. Draw five points on a piece of paper. Draw all the lines passing through these points. How many lines can you draw? 3. Explain the difference between a ray and a half line. 4. At least how many points determine a line? 5. Give examples from daily life to illustrate the concepts of point, line, and plane. 6. Write words to complete the sentences. a. A point has no __________ and no __________. b. Two points determine a ___________. c. d. Two lines that lie in different planes and do not intersect are called ___________ lines. 7. Determine whether the statements are true or false for the given figure.
a. points D and E are not in the line l b. B ∈l c. E ∈l 8. Name all the lines, rays, line segments, and half lines in the given figure.
|
Оқушылар берілген тест тапсырмаларындағы сұрақтарға ойланып, ағылшын тілінде жауап береді. |
|
|
Үйге тапсырма Home work |
Тақырып бойынша қосымша ақпарат жинақтау. Оқулықтан № 26, 27 - есептер |
||
18

шағым қалдыра аласыз


 α
α