СТЕРЕОМЕТРИЯ ЕСЕПТЕРІН КОМПЬЮТЕРЛІК МОДЕЛЬДЕУ

Жоғары мектеп курсының математикасында стереометрия курсы кеңістіктік ойлауды дамыту бойынша маңызды есептердің бірі болып табылады.

Стереометрия курсын теориялық және практикалық тұрғыда оқып үйрену үшін геометриялық денелерді кеңістікте елестете білу қажет.

Қазіргі заманғы бағдарламалық қамтамасыз етілу математика саласында геометриялық объектілерді және олардың нақты қасиеттерін көрнекі жағдайда бағдарламалардың кең ауқымын ұсынады.

Соңғы жылдары математика саласында Maple визуалды бағдарламасы кеңінен қолданылады. Бұл бағдарлама арқылы тіпті анимациялық кескіндерді алуға болады.

Maple жүйесінде екі өлшемді және үш өлшемді кеңістіктерге арналған командалар мен процедуралар жиынтығы бар.

Maple бағдарламалау тілінің ерекшелігін кәсіби маман еместер де меңгере алады.

Мектеп бағдарламасының стереометрия курсында оқушылардың кеңістіктік ойлау қабілетінің дамуының жоғары деңгейін талап ететін проблемалық сипатта кездесетін есептердің қоры мол.

Сондай-ақ, 11 сыныпта «Көлемдер» тақырыбын қарастырған кезде күрделі есептеулер жүргізіледі. Мұндай есептерді шығару кезінде кеңістіктік суреттерді құруда кейбір қиындықтар болуы мүмкін. Сондықтан, оқушының ойлау қабілетін арттыру мақсатында визуалды кеңестер жиынтығы болуы керек.

Maple визуалды бағдарламасында мысал келтірейік.

> with(plots): with(plottools):

A:=plot3d([x,y,3],x=0..2,y=0..1,grid=[2,2]):

B:=plot3d([2,x,y],x=0..1,y=0..3,grid=[2,2]):

C:=plot3d([x,1,y],x=0..2,y=0..3,grid=[2,2]):

DD:=plot3d([x,0,y],x=0..2,y=0..3,grid=[2,2]):

E:=plot3d([x,y,2],x=0..1,y=1..2,grid=[2,2]):

F:=plot3d([0,x,y],x=0..1,y=0..3,grid=[2,2]):

FF:=plot3d([0,x,y],x=2..3,y=2..3, grid=[2,2]):

G:=plot3d([0,x,y],x=1..3,y=0..2,grid=[2,2]):

K:=plot3d([x,y,0],x=0..3,y=1..3,grid=[2,2]):

M:=plot3d([x,y,0],x=0..2,y=0..1,grid=[2,2]):

N:=plot3d([3-2*y,3-2*x,2*y],x=0..1,y=0..1,grid=[2,2]):

P:=plot3d([1-y,3- x,2+y],x=0..1,y=0..1,grid=[2,2]):

T:=plot3d([3- x,3,y],x=0..3,y=0..x,grid=[2,2]):

S:=plot3d([1- x,2,2+y],x=0..1,y=0..x,grid=[2,2]):

SS:=plot3d([3- x,1,y],x=0..1,y=0..x,grid=[2,2]):

ST:=plot3d([1+x,1,2- y],x=0..1,y=0..x,grid=[2,2]):

plots[display]([A,B,C,DD,E,F,FF,G,K,M,N,P,T,S,SS],style=patch,scaling= constrained);

Нәтижесі 2 суретте көрсетілгендей анимациялық үш өлшемді моделі

Мысал 2.

> with(plottools):with(plots):

ff:=PLOT3D(CURVES([[1,1,0],[0,1,0]],COLOR(HUE,0.7),THICKNESS(1)), STYLE(PATCH)):

fff:=PLOT3D(CURVES([[0,0,0],[1,1,1]]),COLOR(HUE,0.9),THICKNESS(3)):

f:=display([ff,fff]): RTS:=[seq(U[k],k=0..40)]:

for k from 0 to 40 do b:=k*0.25*Pi: U[k]:=rotate(f,b,[[0,0,0],[1,1,1]]): end

do:

RRT:=[seq(Y[j],j=0..40)]: for j from 0 to 40 do

RRS:=[seq(T[i],i=0..j)]:

for i from 0 to j do b:=i*0.12*Pi: T[i]:=rotate(f,b,[[0,0,0],[1,1,1]]): end do:

Y[j]:=plots[display](RRS[],scaling=constrained,style=patch):end do:

display(RTS[],RRT[],insequence=true,scaling=constrained,style=patch;

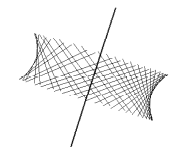
Мысал 3. Көпжақтардан құралған айналу денесі

> with(plottools):with(plots):

f := cu-boid([0,0,0],[1,1,1]):fff:=PLOT3D(CURVES([[0,-

0.5,0],[0,1.5,0]]),COLOR(HUE,0.9),THICKNESS(3)):

f:=display([ff,fff]): RTS:=[seq(U[k],k=0..40)]:

for k from 0 to 40 do b:=k*0.25*Pi: U[k]:=rotate(f,b,[[0,0,0],[0,1,0]]): end do:

RRT:=[seq(Y[j],j=0..15)]: for j from 0 to 15 do

RRS:=[seq(T[i],i=0..j)]: for i from 0 to j do b:=i*0.125*Pi:

T[i]:=rotate(f,b,[[0,0,0],[0,1,0]]): end do:

Y[j]:=plots[display](RRS[],scaling=constrained,style=patch):end do:

display(RTS[],RRT[],insequence=true,scaling=constrained,style=patch;

Айналу денесінің нәтижесі 4 суретте көрсетілген.

Мысал 4.

> with(plottools):with(plots):

ff := cuboid([0,0,0],[1,1,1]): fff:=PLOT3D(CURVES([[-0.5,-0.5,- 0.5],[1.5,1.5,1.5]]),

COLOR(HUE,0.9), THICKNESS(3)):

f:=display([ff,fff]): RTS:=[seq(U[k],k=0..40)]:

for k from 0 to 40 do b:=k*0.25*Pi: U[k]:=rotate(f,b,[[0,0,0],[1,1,1]]): end do:

RRT:=[seq(Y[j],j=0..15)]: for j from 0 to 15 do

RRS:=[seq(T[i],i=0..j)]: for i from 0 to j do b:=i*0.125*Pi:

T[i]:=rotate(f,b,[[0,0,0],[1,1,1]]):

end do: Y[j]:=plots[display](RRS[],scaling=constrained,style=patch):end do:

display(RTS[],RRT[],insequence=true,scaling=constrained,style=patch;

Ізделінді фигуралардың сызбасын оқушылар геометриялық жобалау арқылы өз беттерінше орындай алады.

Мысал 5.

> with(plots):with(plottools):

f:=PLOT3D(POLYGONS([[0,0,0],[1,0,0], [0.5,0.5*sqrt(3.0),0]],

[[1,0,0],[0.5,0.5*sqrt(3.0),0],[0.5,sqrt(3.0)/6,sqrt(6.0)/3]],

[[0,0,0],[1,0,0],[0.5,sqrt(3.0)/6,sqrt(6.0)/3]],

[[0,0,0],[0.5,0.5*sqrt(3.0),0],[0.5,sqrt(3.0)/6,sqrt(6.0)/3]]),

STYLE(PATCH)):

g:=rotate(f,Pi/2,[[0.5,0,0],[0.5,sqrt(3.0)/3,sqrt(6.0)/6]]):

display([f,g],scaling=constrained);

Мысал 6.

> with(plots):with(plottools): f:=PLOT3D(POLYGONS([[0,0,0],

[1,0,0],[1,1,0],[0,1,0]], [[0,0,0],[0,1,0],[0,1,1],[0,0,1]],

[[1,0,0],[1,1,0],[1,1,1],[1,0,1]], [[0,0,0],[1,0,0],[1,0,1],[0,0,1]],

[[0,1,0],[1,1,0],[1,1,1],[0,1,1]], [[0,0,1],[1,0,1],[1,1,1],[0,1,1]]),

TITLE(CUBE),STYLE(PATCH)):

g:=rotate(f,Pi/2,[[0,0,0.5],[1,1,0.5]]):display([f,g],

scaling=constained);

Кеңістіктік ойлау қабілетінің дамуы және компьютерлік технологияны меңгеру стереометрия есептерін зерттеуге үлкен мүмкіндіктер береді.