
Маңғыстау облысы,Жаңаөзен қаласы, 19 орта мектебі
Анықталған интегралды жуықтап есептеу.
Математика пән мұғалімі: Тасбергенова Анар Талғатқызы
Мазмұны
Кіріспе...............................................................................................................3
-
Тіктөртбұрыштар әдісі..............................................................................4
-
Трапеция әдісі............................................................................................8
-
Парабола әдісі........................................................................................12
-
Интегралдау аралығын бөліктеу..........................................................19
-
Есептер..................................................................................................21
Қорытынды........................................................................................................26
Пайдаланылған әдебиеттер............................................................................27
Кіріспе
Анықталған интеграл және оның қасиеттері. Геометриялық және физикалық есептер.
І-есеп. [a,b] кесіндісінде (a мен b-арқылы сандар) үзіліссіз f(x) ≥ 0 функциясы берілсін. y=f(x) қисығы, Ох өсі және x=a мен x=b түзулерімен шенелген фигураның

-
S аудан ұғымын анықтау керек; 2) осы S ауданды табу керек.
Есептегі көрсетілген фигураны қисық сызықты трапеция дейді. Бұл есепті шығару үшін келесі амалды орындаймыз
а) ![]() кесіндіні кез-келген
a=x0<x1<x2<…..<xn
=b
нүктелерімен n бөлікке бөлеміз.
кесіндіні кез-келген
a=x0<x1<x2<…..<xn
=b
нүктелерімен n бөлікке бөлеміз.
![]()
![]() және
және ![]() қисығының
қисығының ![]() j=0,1,2…..,n нүктелерінің
j=0,1,2…..,n нүктелерінің
![]() ординаталарын
тұрғызамыз;
ординаталарын
тұрғызамыз;
б) әрбір ![]() бөлікше кесіндіден кез-келген
бөлікше кесіндіден кез-келген
![]() нүктесін
нүктесін ![]() аламыз және осы нүктелердегі
аламыз және осы нүктелердегі
![]() функция мәндерін тауып,
келесі қосындыны құрамыз
функция мәндерін тауып,
келесі қосындыны құрамыз ![]()
![]()
Анықталған өрнек ![]() функциясының
функциясының ![]() кесіндідегі
интегралдық қосындысы деп аталады. Оның әрбір
кесіндідегі
интегралдық қосындысы деп аталады. Оның әрбір
![]() қосылғышы – табаны
қосылғышы – табаны
![]() , биіктігі
, биіктігі ![]() болатын тік төрбұрыш ауданына
тең, ал Sn
саны
қисықсызықты трапеция ауданын белгілі бір дәлдікпен
жуықтайды: Sn
≈S
. Бұл
жуық теңдік дәлірек болуы үшін барлық
болатын тік төрбұрыш ауданына
тең, ал Sn
саны
қисықсызықты трапеция ауданын белгілі бір дәлдікпен
жуықтайды: Sn
≈S
. Бұл
жуық теңдік дәлірек болуы үшін барлық ![]() , j=0,1,2…..,n-1 , бөлікше кесінділеді мейлінше
ұсақтай түсу керек екені түсінікті;
, j=0,1,2…..,n-1 , бөлікше кесінділеді мейлінше
ұсақтай түсу керек екені түсінікті;
в) ұзындығы ең үлкен бөлікше
кесіндіні нөлге ұмтылдырамыз ![]()
Егерде осыдан
Sn
шамасы
![]() кесіндісін
бөлу
тәсіліне және жәбір бөлікше
кесінділерден алынған
кесіндісін
бөлу
тәсіліне және жәбір бөлікше
кесінділерден алынған ![]() нүктелерін
таңдау
тәсілдеріне тәуелсіз
S нақты санына ұмтылса,
онда S
саны
қисықсызықты трапецияның ауданы
деп
аталады
нүктелерін
таңдау
тәсілдеріне тәуелсіз
S нақты санына ұмтылса,
онда S
саны
қисықсызықты трапецияның ауданы
деп
аталады
 (1)
(1)
Сонымен, І-есептің екі сұрағына да жауап алдық.
1.Тіктөртбұрыштар әдісі
Мынадай жағдайларда кездесуі мүмкін, соңғы түрде табылатын интегралдар үшін жуықтап интегралдау формулаларын қолдану керек болады, бірақ олардың айтылуы қыйынға соғады. Кесте ретінде берілген, құрамында функциялары бар, есептерді шешу кезінде жуықтап интегралдау функциялары әсіресе маңызды болады.
Сандық интегралдауда трапеция және тікбұрыштардың формулалары көбінесе оңай формулалар болып табылады.
Қисық сызықтың көлемін білдіретін, олардың нәтижесі нақты бір интегралдың геометриялық мағынасын қолдануында негізделеді. Кейбір қосымша ұсыныстардан құралған, тікбұрыштардың формуласын интегралдық қосынды деуге болады.
![]() интегралын шығару керек делік,
интегралын шығару керек делік, ![]() интегралдаудың үзіндісін n
бірдей бөліктерге бөліп және функция мағыналары интегралдың
қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына
жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a)/n
бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық
қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен
қатар мынадай жуық теңдеулер аламыз:
интегралдаудың үзіндісін n
бірдей бөліктерге бөліп және функция мағыналары интегралдың
қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына
жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a)/n
бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық
қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен
қатар мынадай жуық теңдеулер аламыз:
![]() (2)
(2)
Мұнда теріс тікбұрыштардың формуласы деп аталады. Осы жерде бұрынғыдай у0,у1,у2,....уn арқылы х0,х1,х2,...хn бөлулердің нүктелерінде y=f(x) функцияның мағыналары белгіленген. Тікбұрыштардың ұқсас формуласы былай да шығарылады: егер интегралдық қосындының функция мағыналарын теріс жақта емес, керісінше, бөлулердің оң жақтан алатын болсақ, сол кезде формула осындай болады:
![]() (3)
(3)
Функция үшін, әр интегралдың қосындысы нақты интегралдың (2) және (3) формулалардың оң жақтарында көрсетілген. Жуықталған мағыналардың арасында қосылған. Сол фактінің геметриялық көркемдеуін 1-суреттен көруге болады.

о
сы жерден әр түрлі қосындыға кіретін, көбеюші функцияны және қосылғандарды алу, пункттер және штрих түсірумен көрстілген.
Осыған орай тікбұрыштардың формулаларының қателіктері туралы көріністі, (2) және (3) формулалары бойынша алынған айырымның нәтижелерін қарастыра білуге болады.
Егер функция интегралдаудың үзіндісінде ақырғы түрде табылатын экстримумдардың санын иеленсе, интегралдаудың үзінділерін бірқалыптылық бөліктерін бөлуге болады. Осылайша тікбұраштар формулаларының қателіктеріне бағалады.
Тік төртбұрыш әдісі.
Мына интегралды жуықтап былайша есептейміз:
 (4)
(4)
мұндағы
![]()
Бұл формуланың геометриялық мағынасы мынандай:
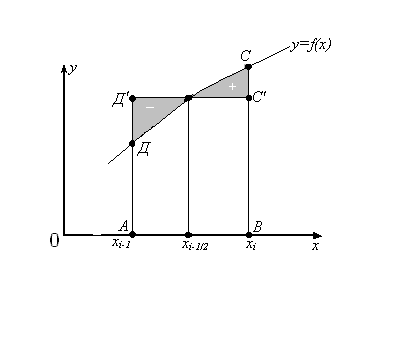 2-сурет
2-сурет
АВСД қисық сызықты трапецияның
ауданы биіктігі ![]() АВД/C/
тік
төртбұрышының ауданымен алмастырылады (2-сурет).
АВД/C/
тік
төртбұрышының ауданымен алмастырылады (2-сурет).
Сондықтан бұл формуланы тік төртбұрыш әдісі дейді.
(4) формуласының дәлдігі
 . (5)
. (5)
Тейлор формуласы арқылы оңай табылады.
Шынында да ![]() ді былайша
жазып
ді былайша
жазып
![]() =
= (6)
(6)
және ![]() +
+![]()

![]()
![]()
![]()
![]() десек, онда (1.10) формуласынан
десек, онда (1.10) формуласынан![]()
 (7)
(7)
формуласын аламыз.
Егер М![]() =
=![]() деп R
деп R![]() -ді жоғарыдан
бағаласақ ,онда
-ді жоғарыдан
бағаласақ ,онда

Яғни ![]() (8)
(8)
болғандықтан, h![]() 0 ұмтылғандағы
дәлдік 0(h
0 ұмтылғандағы
дәлдік 0(h![]() )
болады.
)
болады.
Енді (4) теңдіктің i-дің 1 ден N ге дейінгі қосындысын қарастырсақ
 (9)
(9)
болады. Сондықтан  .
.
Осыдан
 .
.
Егер ![]() десек,
онда
десек,
онда
![]() , (10)
, (10)
яғни тік төртбұрыш әдісінің ![]() кесіндісіндегі
дәлдігі-0(h
кесіндісіндегі
дәлдігі-0(h![]() ).
).
2.Трапеция әдісі
Байқасақ, тіктөртбұрыштардың формуласымен алынған арифметикалық ортасының жуығы қандай да мәнге тең, демек интеграл мағынасының түп мәніне тең болып шығады: қателік 0,05% -ке тең. (2) және (3) формулалары бойынша алынған, интегралдаудың жуықталған мағынасы ретінде орташа арифметикалықтың жуықтаын алуға тура келеді.
Байқасақ, бұл мағыналарды алдын ала шығарып қоюды еш мұхтаждығы жоқ. Өйткені бірден дайын формуламен пайдаланса болады. Шынымен де, (2) және (3)оң формулаларының арифметикалықтың ортасын алсақ, мынаны аламыз:
![]() (11)
(11)
бұл трапециялар формуласы.
(11) трапециялар формуласын былайша оңай алуға да болады, геометриялық мағынасынан шыға тура, a=x0<x1<x2<…<xn-1<xn=b нүктелермен интегралдаудың үзіндісін n-бірдей бөлікке бөліп, бөлулердің барлық нүктелердің ординаталарды жүргіземіз және әр алынған қисық сызықтытыны түзу сызықтыға ауыстырамыз, төмендегі суретте көрсетілген. Әр трапецияның жақтары екі көрші ординаттар болып табылады. Ох сызбаның аймағы, ұзындығы h=(b-a)/n және хордасы қисық.

Сол трапецияның
көлемі ![]() (хі-1,хі)
(хі-1,хі)
Аймақтың үстінде орналасқан, трапецияға сай, мынаны табамыз.
![]() (12)
(12)
1-ден n-ге дейін барлық і-ға (12) көрсетілімдерді қосу, өйткені шеттегіден басқа барлық ординаттар, (12) көрсетілімдердің түрінде екі мәрте қолданылады.
Трапециялық тәсілмен жасалатын сандық интегралдау
ЭЕМ-дағы сандық интегралдау тәсілдерді іске асыруды қажет ететін, нақты бір интегралдың мысалдарын келтірейік.
Мысалы, егерде f(x)-электростанцияғаауырлық болса, квт-уақытта (х-тәуліктің басынан есептелетін, уақыттың саны), тәуліктің ішінде электірлік энергиялық шығыны құрайтын мынау:
![]() (13)
(13)
немесе басқа мысал:
t-уақытта алынған, дисконтталған кірістің көлемі мынаған тең:
![]() (14)
(14)
осы жерде:
t-уақыт
і-пайыздың меншікті нормасы (пайыздар үздіксіз өсе береді)
Сонымен, математикалық тілмен айтқанда нақты бір интегралды жоғарыдағы формулаларды «санға жеткізу» керек.
Сол үшін осы тақырыпта трапециялық тәсілді қолданамыз.
Тәсілдің мәні: интегралдаудың арасы [a, b] n нүктелермен бірнешеге бөлінеді. (n+1) бірдей кішкентай бөліктерге.
Трапеция формуласының көрінісі:
![]() (15)
(15)
f(x) - интегралдың астындағы функциясы;
a, b - интегралдаудың шегі;
n - аралықтың саны;
yi- і нүктеде бөлінетін f(xi) мағынасы
Трапеция
әдісі. (4)
интегралындағы ![]() функциясын
функциясын ![]()
![]() нүктелері
арқылы тұрғызылған
нүктелері
арқылы тұрғызылған
![]()
бір дәрежелі Лагранж көпмүшесімен алмастырсақ, онда
![]()
![]() (16)
(16)
мұндағы![]()
![]()
(16) формуласын ![]() аралығында
интегралдау арқылы
аралығында
интегралдау арқылы

![]() (17)
(17)
теңдігін аламыз. Осыдан
 . Бұл формула трапеция әдісі деп аталады,себебі
. Бұл формула трапеция әдісі деп аталады,себебі ![]()
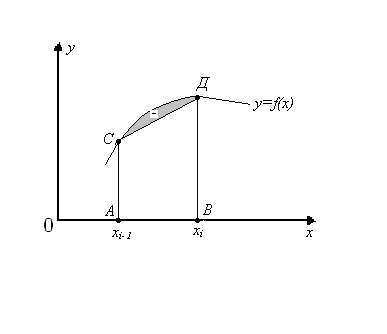
3-сурет
![]() сызықтарымен қоршалған қисық сызықты
трапецияның ауданы
сызықтарымен қоршалған қисық сызықты
трапецияның ауданы ![]() трапециясының ауданымен алмастырылады (3сурет).
трапециясының ауданымен алмастырылады (3сурет).
(17) формуладан бұл әдістің жіберетін қатесі
![]() (18)
(18)
екенін көреміз. Ал жоғарыдан бағаласақ
![]() , (19)
, (19)
![]()
Енді мына интегралды былай есептесек:

![]()
![]() (20)
(20)
Онда
 (21)
(21)
трапеция әдісінің жалпы формуласы шығады.
Ал жіберілетін қате
![]() (22)
(22)
Жоғарыдан бағаласақ
![]() , (23)
, (23)
![]() .
.
Сонымен, трапеция әдісінің ![]() кесіндісіндегі
дәлдігі
кесіндісіндегі
дәлдігі ![]() екенін көреміз.
екенін көреміз.
-
Парабола әдісі
Сандық интегралдың бұл тәсілінде нақты бір интегралдың түрі қарастырылады (4):
![]()
[a, b] интегралдаудың интервалын жұп сан аралығына бөледі демек 2m-ге, демек бөлінетін нүктенің саны 2m+1-ге тең.
Тәсілдің мәні: Трапецияның тәсіліне қарағанда, Симпсон тәсілінде (x0, x1) және (x1, x2) екі көрші аралығында және f(x) қисығын (демек интегралдың астындағы функцияны) параболамен ауыстырады, демек алгебралық көпмүшеліктің түрімен
y=f(x)=A(x- x0)(x- x1)+B(x- x0)(x- x2)+C(x- x1)(x- x2) (24)
осы жерде А,В,С- анықтау керек шама
А,В және С анықталғаннан кейін, парабола формуласының немесе былайша айтқанда Симпсон формуласының берілгені мынау:
![]()
осы жерде yi -0,1,2,..., 2m бөлінген нүктелердегі f(x) интегралдың астындағы функцияларының мағынасы.
Жоғарыдағы қарастырылған трапеция формуласынан да дәлірек формула Симпсон формуласы деп те аталады. Дәл сондай дәлдікке қол жеткізу үшін бұл формулада бөліну аймағының n санын азырақ алып және сәйкесінше үлкен арақашықтық h-деп алу керек. Бірдей арақашықтарда , яғни дәл сондай шешімнің көлемінде, бұл формулада абсолютті және салыстырмалы қателік жіберіледі.
Симпсон формуласын осы уақытқа дейін екі рет қолданған тәсілмен алуға болады.
Аумақты ![]() жұп санды n=2m бөлікке
нүктелермен бөлеміз a= x0
<
x1
<…<
xn-1<
xn=b, ординаттарды бөліну
нүктелерінде y0,
y1,…
yn
арқылы
белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз.
Мысалы, шеткі сол жақтағы a= x0
нүктені
қарастырайық.
жұп санды n=2m бөлікке
нүктелермен бөлеміз a= x0
<
x1
<…<
xn-1<
xn=b, ординаттарды бөліну
нүктелерінде y0,
y1,…
yn
арқылы
белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз.
Мысалы, шеткі сол жақтағы a= x0
нүктені
қарастырайық.

Үш нүкте арқылы қисық сызықты координаталармен параболаны (x0 у0),( x1 у1),( x2 у2) өсімен бірге жүргіземіз. Бұл ось Оу параллель болу керек.Оның теңдеуі былай болады:
y= Ах2 +Вх+С (25)
бірақ А,В,С коэффенцентері әзірше белгісіз болып қала береді:
[x0, x2] аумағында берілген қисық сызықты трапецияның ауданын (1,3,1) параболамен шектелген қисық сызықты трапецияның ауданымен алмастырып, жақындатылған теңдікке келеміз:

жақшаның сыртына жалпы көбейткіштерді x2 – x0 шығарып, содан кейін жалпы бөлгішке әкелемі де, мынадай формуланы аламыз:
![]() (26)
(26)
(25) теңдеуіндегі және (26)
формуласындағы белгісіз А,В,С коэффенценттері
x0,
x1,
x2–ге тең х мағынасындағы
жағдайдан табылады. F(x) функциясы жағдйында сәйкес мағынаға ие
болады. ![]() екендігін
байқасақ, бұл жағдайларды мына түрде жазамыз:
екендігін
байқасақ, бұл жағдайларды мына түрде жазамыз:
![]() (27)
(27)
Екінші теңдікті (27) төртке көбейту арқылы және содан кейін үш теңдікті қатарластыру арқылы мынаны аламыз:
y0+4 y1+ y2=A[x02+ ( x0+ x2)2+ x22]+B[x0+2(x0+ x2)+ x2]+6C=2A(x02+ x0 x2+ x22)+3B(x0+ x2)+6C (28)
(28) теңдеудің оң бөлігінде төрт бұрышты жақшамен сәйес келеді.
(26)-ті (28) теңдеудің оң бөліміне қоя тұра, x2 –x0 =2h ескеріп, жуықталған теңдеуге келеміз
![]() (29)
(29)
Әр ендігі бөлікке тура сондай формула келетіні анық:
![]() (30)
(30)
(29)және (30) теңдеулердің көрінісін барлық аймақ бойынша қоса тұра, мынадай формула аламыз:
![]() (31)
(31)
(31) формуласы бізге керек болған Симпсон формуласы. Формуланың геометриялық мәнін ескере тұра, оны парабола формуласы деп те атайды. Онда барлық ординаттар тақ нөмірмен төртке көбейтіледі, жұп санмен екіге. у0 және у2m шеткі ординаттар коэффенценттері бар формулаға кіреді, олар бірге тең.
(4) интегралын жуықтап есептеу
үшін ![]() функциясын
функциясын ![]() нүктелері арқылы тұрғызылған
нүктелері арқылы тұрғызылған ![]() Лагранж көп
мүшесімен алмастырамыз. Яғни
Лагранж көп
мүшесімен алмастырамыз. Яғни
![]()
![]()
![]() . (32)
. (32)
Осыдан
![]()
![]()
Сонымен мына формуланы –
![]()
![]() (33)
(33)
Симпсон немесе парабола формуласы деп атайды.
Бұл формуланың парабола формуласы деп атайтын себебі
![]() сызықтарымен шектелген қисық сызықты
трапецияның ауданы
сызықтарымен шектелген қисық сызықты
трапецияның ауданы ![]() нүктелері арқылы өтетін парабола және
нүктелері арқылы өтетін парабола және ![]() түзулерімен
шектелген трапецияның ауданымен алмастырылады (4-сурет).
түзулерімен
шектелген трапецияның ауданымен алмастырылады (4-сурет).
Симпсон формуласы ![]() кесіндісінде былайша
жазылады
кесіндісінде былайша
жазылады![]()

![]()
![]()
Бөлшекті индекстерден құтылу үшін
![]() десек,онда Симпсон формуласын былайша
жазамыз:
десек,онда Симпсон формуласын былайша
жазамыз:![]()
![]() . (34)
. (34)
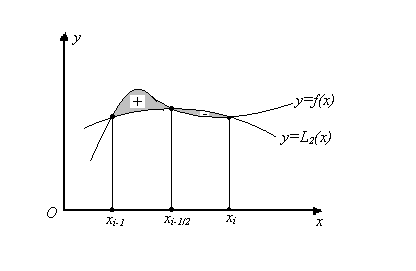
4-сурет
О х у xi-1 xi-1/2 xi y=f(x) y=L2(x) + -
Симпсон формуласының жіберетін қатесін
қарастырардың алдында, оның үш ![]() дәрежелі көпмүше
үшін дәл екенін көрсетейік. Шынында да
дәрежелі көпмүше
үшін дәл екенін көрсетейік. Шынында да
![]() болса, онда
болса, онда
![]()
![]()
![]()
![]()
Осыдан
![]()

![]()
![]()
![]()
Екіншіден
![]()
![]()
екенін ескерсек
![]()
![]()
формуласын аламыз.
Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік.
Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын
![]()
![]()
интерполяциялық Эрмит көпмүшелігін пайдаланамыз .
Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан
 (35)
(35)
Енді ![]()
десек,онда

мұндағы ![]() (36)
(36)
-Эрмит көпмүшесінің жіберетін қатесі.
![]() кесіндісінде
кесіндісінде ![]() көпмүшесі өзінің
таңбасын өзгертпейтін болғандықтан
көпмүшесі өзінің
таңбасын өзгертпейтін болғандықтан

![]()
Сондықтан Симпсон формуласының жіберетін қатесi
 . (37)
. (37)
Hемесе
![]() (38)
(38)
![]()
Симпсон формуласының ![]() кесіндісінде
жіберетін қатесі
кесіндісінде
жіберетін қатесі
![]()
Болғандықтан ![]() (39)
(39)
![]()
Яғни Симпсон әдісінің ![]() кесіндісіндегі
дәлдігі
кесіндісіндегі
дәлдігі ![]() .
.![]()
4.Интегралдау аралығын бөліктеу
Егер ![]() кесіндісінде
үзіліссіз және алғашқы образы-
кесіндісінде
үзіліссіз және алғашқы образы-![]() белгілі болса, онда Ньютон-Лейбниц формуласы
бойынша:
белгілі болса, онда Ньютон-Лейбниц формуласы
бойынша:
 (40)
(40)
Бірақ, көп
жағдайда ![]() функциясын табу өте күрделі мәселе болғандықтан, (40)
формуласы іс жүзінде көп қолданылмайды. Ал кейбір
уақыттарда
функциясын табу өте күрделі мәселе болғандықтан, (40)
формуласы іс жүзінде көп қолданылмайды. Ал кейбір
уақыттарда ![]() функциясы таблица түрінде берілетіндіктен алғашқы образ
деген сөздің өзі мағынасын жоғалтады.
функциясы таблица түрінде берілетіндіктен алғашқы образ
деген сөздің өзі мағынасын жоғалтады.
Сондықтан
 (41)
(41)
интегралын есептеу
үшін ![]() (42)
(42)
ақырғы қосындысы қолданылады.
Мұндағы ![]() -сандық коэффициенті
-сандық коэффициенті ![]() кесіндісінің нүктелері,
кесіндісінің нүктелері, ![]()
Мына жуықтап алынған
теңдік  (43)
(43)
квадратуралық
формула деп аталынады. Ал
(1.3)- квадратуралық
қосынды, ![]() -
квадратуралық формуланың түйіндері
,
-
квадратуралық формуланың түйіндері
, ![]() -kвадратуралық формуланың
коэфициенті деп
аталынады.
-kвадратуралық формуланың
коэфициенті деп
аталынады.
 (44)
(44)
квадратуралық формуланың
дәлдігі делінеді. Квадратуралық
формуланың дәлдігі квадратуралық формуланың
түйіндері-![]() -ның орналасуына, квадратуралық формуланың
коэффициенттері-
-ның орналасуына, квадратуралық формуланың
коэффициенттері-![]() -ның алу жолдарына тікелей байланысты.
-ның алу жолдарына тікелей байланысты.
Енді берілген анықталған
интегралды есептеу үшін ![]() кесіндісін тең
кесіндісін тең ![]() кесіндіге бөлеміз, яғни
кесіндіге бөлеміз, яғни ![]() нүктелер жиынын аламыз да
нүктелер жиынын аламыз да
 (45)
(45)
теңдігін қарастырамыз.
![]() кесіндісіндегі интегралдың мәнін табу
үшін
кесіндісіндегі интегралдың мәнін табу
үшін
 (4)
(4)
интегралының ![]() аралықтағы мәнін
табу жеткілікті, өйткені (1.6) формуласы арқылы интегралдың
аралықтағы мәнін
табу жеткілікті, өйткені (1.6) формуласы арқылы интегралдың
![]() кесіндісіндегі
мәнін табу онша қиындық туғызбайды.
кесіндісіндегі
мәнін табу онша қиындық туғызбайды.
Қорытынды
![]() - анықталмаған интегралын
қарастырамыз, мұндағы
- анықталмаған интегралын
қарастырамыз, мұндағы ![]()
![]() кесіндісінде үзіліссіз
функция. Интеграл астындағы функция «күрделі» болып, яғни
интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру
ыңғайлы болады, яғни
кесіндісінде үзіліссіз
функция. Интеграл астындағы функция «күрделі» болып, яғни
интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру
ыңғайлы болады, яғни![]() делік,
мұндағы
делік,
мұндағы ![]() алынатын
интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап
алынады.
алынатын
интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап
алынады.
Теорема. Егер ![]() интегралында
интегралында
![]() (
(![]() мен
мен
![]() - үзіліссіз функциялар)
ауыстыруын алсақ, онда
- үзіліссіз функциялар)
ауыстыруын алсақ, онда
![]() (1)
(1)
формуласы
орындалады, яғни жаңа ![]() интегралын аламыз, ал ол
кестелік интегралға оңай келуі мүмкін.
интегралын аламыз, ал ол
кестелік интегралға оңай келуі мүмкін.
Дәлелдеу. Сол жағын
![]() бойынша, оң
жағын
бойынша, оң
жағын ![]() бойынша
күрделі функция ретінде дифференциалдаймыз:
бойынша
күрделі функция ретінде дифференциалдаймыз:
![]() ;
;
![]() Оң бөлігі мен сол бөлігінің
теңдігі теореманың дұрыстығын дәлелдейді.
Оң бөлігі мен сол бөлігінің
теңдігі теореманың дұрыстығын дәлелдейді.
Практикалық тәсіл:
![]()
=![]() .
.
Пайдаланылған әдебиеттер
-
Темірғалиев Н. “Математикалық анализ” - Алматы; Мектеп 1987, 288 бет.
-
Ибрашев Х. И., Еркеғұлов Ш. Т. “Математикалық анализ курсы.” – Алматы; Мектеп 2 том, 1970, 527 бет.
-
Кудрявцев А. Д. “Краткий курс математического анализа.” – Москва, Наука, 1989, 735 бет.
-
Фихтенгольц Г. М. “Основы математического анализа.” – Москва, Наука, 1968, ІІ том.
-
“Задачник по курсу математического анализа.” Под редак. Н. Я. Виленкина, Москва, 1971, ч-2.
-
Асинкин А. Г., Бутинов Е. И., Кондратьев А. С. “Краткий физико-математический справочник.” Москва, 1990, 368 стр.
-
Демидович Б. П. “Сборник задачи и упражнений по математическому анализу.” Москва, Наука, 1977.
-
“Егемен Қазақстан” 16 қазан, 2004 жыл.
-
А. Г. Аленкин, Е. И. Бутиков, А. С. Кондратьев. «Краткий физико-математический справочник» М., 1990 г.
-
Шойынбеков К. Д., Әбілқасымов А. Е., Есенова М. И., Тұрлыханова М. А. «Анализ бастамалары» оқу құралы. Алматы, 2002ж., 320 бет.
-
Данко П. Е., Попов А. Г., Кожевникова Т. Я. «Высшая математика в упражнениях и задачах» учебное пособие для студентов вузов. М., Высш.шк., 1926г.
Есептер
Жазық фигуралардың ауданын жуықтап есептеу барысында трапеция әдісін қолдану

![]() анықталған интегралдың
сан мәні дегеніміз – абсцисса өсі, f(x) функциясының қисығы
және x=a, x=b
түзулермен шектелген қисықсызықты трапеци ауданың
шамасы.
анықталған интегралдың
сан мәні дегеніміз – абсцисса өсі, f(x) функциясының қисығы
және x=a, x=b
түзулермен шектелген қисықсызықты трапеци ауданың
шамасы.
Бұл қисық сызықты трапецияның
ауданын табу үшін, ![]() аралығын
әрқайсысының ұзындығы
аралығын
әрқайсысының ұзындығы ![]() –ге тең болатын
–ге тең болатын ![]() n
бөлікке
бөлеміз. Бөліну нүктелерінен қисығымен қиылысқанша
n
бөлікке
бөлеміз. Бөліну нүктелерінен қисығымен қиылысқанша ![]() ординаталарын жүргіземіз де,
олардың қисықсызықпен A,C,D,….B–қиылысу нүктелерін
кесінділерімен қосамыз. Сонда aABb
қисықсызықты трапецияның ауданын шамамен
aACx1,
x1CDx2
, ….,
x1-n
Bb трапецияларының аудандарының
қосындысымен алмастыруға болады. Сөйтіп,
ординаталарын жүргіземіз де,
олардың қисықсызықпен A,C,D,….B–қиылысу нүктелерін
кесінділерімен қосамыз. Сонда aABb
қисықсызықты трапецияның ауданын шамамен
aACx1,
x1CDx2
, ….,
x1-n
Bb трапецияларының аудандарының
қосындысымен алмастыруға болады. Сөйтіп,
![]()
Алынған формула анықталған интегралдың жуық мәнін табу формуласы деп аталады.
Трапеция әдісінен жоғары парабола әдісі (Симпсон әдісі деп те атайды) деп аталатын әдіс те бар. Парабола әдісі бойынша анықталған интегралдың мәні мына формуламен табуға болады:
![]()
Бұл жағдайда ![]() аралығы жұп, яғни 2n бөлікке
бөлінеді.
аралығы жұп, яғни 2n бөлікке
бөлінеді.
Ескерту. Күрделі фигуралар қисық сызықты трапециялардың қосындысы немесе айырмасы түрінде беріледі.
Мысалы, екі қисықпен:
![]() және
x=a,
x=b екі тік сызықпен шектелген
фигураның ауданын табу керек болсын. Бұл жағдайда ізделініп отырған
ауданды екі қисық сызықты трапециялардың аудандарының айырмасы
ретінде қарастыруға болады. Сондықтан да
және
x=a,
x=b екі тік сызықпен шектелген
фигураның ауданын табу керек болсын. Бұл жағдайда ізделініп отырған
ауданды екі қисық сызықты трапециялардың аудандарының айырмасы
ретінде қарастыруға болады. Сондықтан да
![]()
Енді жоғарыда келтірілген әдістерге мысалдар келтіріп, оларды есептеуге арналған программалар құрайық.
Мысал.Интегралдау аралығын
n=20 бөлікке бөліп, ![]() интегралының мәнін трапеция әдісімен табамыз
интегралының мәнін трапеция әдісімен табамыз
Шешілуі:
Алгоритмдік тілде
алг трапеция әдісі (арг нақ a, b, n, арг нәт нақ p)
бер / a, b және бөлік саны n,
тап / интегралдың мәні табылды
басы нақ x, h, бүт i
х:=a;h:=(b-a)/n
р:=y(a)+y(b)
цб үшін і бастап 1 дейін n-1
х:=x+h
р:=p+2*y(x)
цс
р:=p*h/2
соңы
алг нақ у(нақ x)
басы
мән:=1/ln(x)
соңы
SIMPSON Паскаль- бағдарламаның қолдану мысалы:
[1, 3] интегралдаудың аралығын 4 бөлікке бөле тұра, интегралдың мағынасын Симпсон тәсіліі арқылы табу:
![]()
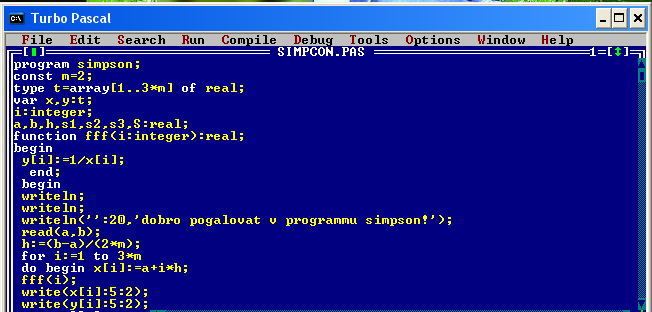
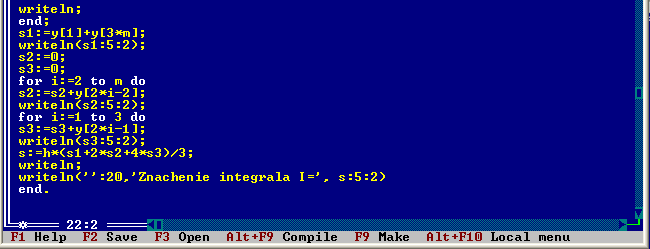
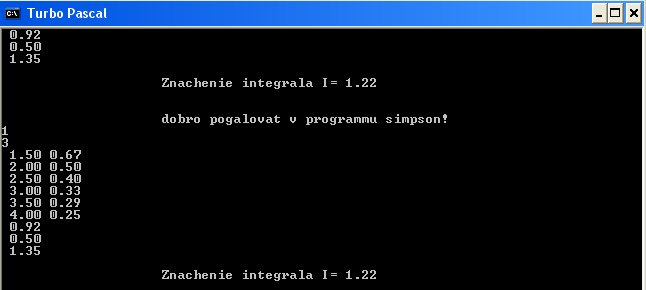
Паскаль-TRAPECIA бағдарламасының қолданылу мысалы: интегралдың аралығын төртке бөліп, трапеция тәсілімен интегралдың мағынасын табу:
![]() [1,3]
аралығын 4 - бөлікке бөлу арқылы интегралдау.
[1,3]
аралығын 4 - бөлікке бөлу арқылы интегралдау.
27
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Тақырыбы: Анықталған интегралды жуықтап есептеу
Тақырыбы: Анықталған интегралды жуықтап есептеу
Маңғыстау облысы,Жаңаөзен қаласы, 19 орта мектебі
Анықталған интегралды жуықтап есептеу.
Математика пән мұғалімі: Тасбергенова Анар Талғатқызы
Мазмұны
Кіріспе...............................................................................................................3
-
Тіктөртбұрыштар әдісі..............................................................................4
-
Трапеция әдісі............................................................................................8
-
Парабола әдісі........................................................................................12
-
Интегралдау аралығын бөліктеу..........................................................19
-
Есептер..................................................................................................21
Қорытынды........................................................................................................26
Пайдаланылған әдебиеттер............................................................................27
Кіріспе
Анықталған интеграл және оның қасиеттері. Геометриялық және физикалық есептер.
І-есеп. [a,b] кесіндісінде (a мен b-арқылы сандар) үзіліссіз f(x) ≥ 0 функциясы берілсін. y=f(x) қисығы, Ох өсі және x=a мен x=b түзулерімен шенелген фигураның

-
S аудан ұғымын анықтау керек; 2) осы S ауданды табу керек.
Есептегі көрсетілген фигураны қисық сызықты трапеция дейді. Бұл есепті шығару үшін келесі амалды орындаймыз
а) ![]() кесіндіні кез-келген
a=x0<x1<x2<…..<xn
=b
нүктелерімен n бөлікке бөлеміз.
кесіндіні кез-келген
a=x0<x1<x2<…..<xn
=b
нүктелерімен n бөлікке бөлеміз.
![]()
![]() және
және ![]() қисығының
қисығының ![]() j=0,1,2…..,n нүктелерінің
j=0,1,2…..,n нүктелерінің
![]() ординаталарын
тұрғызамыз;
ординаталарын
тұрғызамыз;
б) әрбір ![]() бөлікше кесіндіден кез-келген
бөлікше кесіндіден кез-келген
![]() нүктесін
нүктесін ![]() аламыз және осы нүктелердегі
аламыз және осы нүктелердегі
![]() функция мәндерін тауып,
келесі қосындыны құрамыз
функция мәндерін тауып,
келесі қосындыны құрамыз ![]()
![]()
Анықталған өрнек ![]() функциясының
функциясының ![]() кесіндідегі
интегралдық қосындысы деп аталады. Оның әрбір
кесіндідегі
интегралдық қосындысы деп аталады. Оның әрбір
![]() қосылғышы – табаны
қосылғышы – табаны
![]() , биіктігі
, биіктігі ![]() болатын тік төрбұрыш ауданына
тең, ал Sn
саны
қисықсызықты трапеция ауданын белгілі бір дәлдікпен
жуықтайды: Sn
≈S
. Бұл
жуық теңдік дәлірек болуы үшін барлық
болатын тік төрбұрыш ауданына
тең, ал Sn
саны
қисықсызықты трапеция ауданын белгілі бір дәлдікпен
жуықтайды: Sn
≈S
. Бұл
жуық теңдік дәлірек болуы үшін барлық ![]() , j=0,1,2…..,n-1 , бөлікше кесінділеді мейлінше
ұсақтай түсу керек екені түсінікті;
, j=0,1,2…..,n-1 , бөлікше кесінділеді мейлінше
ұсақтай түсу керек екені түсінікті;
в) ұзындығы ең үлкен бөлікше
кесіндіні нөлге ұмтылдырамыз ![]()
Егерде осыдан
Sn
шамасы
![]() кесіндісін
бөлу
тәсіліне және жәбір бөлікше
кесінділерден алынған
кесіндісін
бөлу
тәсіліне және жәбір бөлікше
кесінділерден алынған ![]() нүктелерін
таңдау
тәсілдеріне тәуелсіз
S нақты санына ұмтылса,
онда S
саны
қисықсызықты трапецияның ауданы
деп
аталады
нүктелерін
таңдау
тәсілдеріне тәуелсіз
S нақты санына ұмтылса,
онда S
саны
қисықсызықты трапецияның ауданы
деп
аталады
 (1)
(1)
Сонымен, І-есептің екі сұрағына да жауап алдық.
1.Тіктөртбұрыштар әдісі
Мынадай жағдайларда кездесуі мүмкін, соңғы түрде табылатын интегралдар үшін жуықтап интегралдау формулаларын қолдану керек болады, бірақ олардың айтылуы қыйынға соғады. Кесте ретінде берілген, құрамында функциялары бар, есептерді шешу кезінде жуықтап интегралдау функциялары әсіресе маңызды болады.
Сандық интегралдауда трапеция және тікбұрыштардың формулалары көбінесе оңай формулалар болып табылады.
Қисық сызықтың көлемін білдіретін, олардың нәтижесі нақты бір интегралдың геометриялық мағынасын қолдануында негізделеді. Кейбір қосымша ұсыныстардан құралған, тікбұрыштардың формуласын интегралдық қосынды деуге болады.
![]() интегралын шығару керек делік,
интегралын шығару керек делік, ![]() интегралдаудың үзіндісін n
бірдей бөліктерге бөліп және функция мағыналары интегралдың
қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына
жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a)/n
бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық
қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен
қатар мынадай жуық теңдеулер аламыз:
интегралдаудың үзіндісін n
бірдей бөліктерге бөліп және функция мағыналары интегралдың
қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына
жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a)/n
бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық
қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен
қатар мынадай жуық теңдеулер аламыз:
![]() (2)
(2)
Мұнда теріс тікбұрыштардың формуласы деп аталады. Осы жерде бұрынғыдай у0,у1,у2,....уn арқылы х0,х1,х2,...хn бөлулердің нүктелерінде y=f(x) функцияның мағыналары белгіленген. Тікбұрыштардың ұқсас формуласы былай да шығарылады: егер интегралдық қосындының функция мағыналарын теріс жақта емес, керісінше, бөлулердің оң жақтан алатын болсақ, сол кезде формула осындай болады:
![]() (3)
(3)
Функция үшін, әр интегралдың қосындысы нақты интегралдың (2) және (3) формулалардың оң жақтарында көрсетілген. Жуықталған мағыналардың арасында қосылған. Сол фактінің геметриялық көркемдеуін 1-суреттен көруге болады.

о
сы жерден әр түрлі қосындыға кіретін, көбеюші функцияны және қосылғандарды алу, пункттер және штрих түсірумен көрстілген.
Осыған орай тікбұрыштардың формулаларының қателіктері туралы көріністі, (2) және (3) формулалары бойынша алынған айырымның нәтижелерін қарастыра білуге болады.
Егер функция интегралдаудың үзіндісінде ақырғы түрде табылатын экстримумдардың санын иеленсе, интегралдаудың үзінділерін бірқалыптылық бөліктерін бөлуге болады. Осылайша тікбұраштар формулаларының қателіктеріне бағалады.
Тік төртбұрыш әдісі.
Мына интегралды жуықтап былайша есептейміз:
 (4)
(4)
мұндағы
![]()
Бұл формуланың геометриялық мағынасы мынандай:
 2-сурет
2-сурет
АВСД қисық сызықты трапецияның
ауданы биіктігі ![]() АВД/C/
тік
төртбұрышының ауданымен алмастырылады (2-сурет).
АВД/C/
тік
төртбұрышының ауданымен алмастырылады (2-сурет).
Сондықтан бұл формуланы тік төртбұрыш әдісі дейді.
(4) формуласының дәлдігі
 . (5)
. (5)
Тейлор формуласы арқылы оңай табылады.
Шынында да ![]() ді былайша
жазып
ді былайша
жазып
![]() =
= (6)
(6)
және ![]() +
+![]()

![]()
![]()
![]()
![]() десек, онда (1.10) формуласынан
десек, онда (1.10) формуласынан![]()
 (7)
(7)
формуласын аламыз.
Егер М![]() =
=![]() деп R
деп R![]() -ді жоғарыдан
бағаласақ ,онда
-ді жоғарыдан
бағаласақ ,онда

Яғни ![]() (8)
(8)
болғандықтан, h![]() 0 ұмтылғандағы
дәлдік 0(h
0 ұмтылғандағы
дәлдік 0(h![]() )
болады.
)
болады.
Енді (4) теңдіктің i-дің 1 ден N ге дейінгі қосындысын қарастырсақ
 (9)
(9)
болады. Сондықтан  .
.
Осыдан
 .
.
Егер ![]() десек,
онда
десек,
онда
![]() , (10)
, (10)
яғни тік төртбұрыш әдісінің ![]() кесіндісіндегі
дәлдігі-0(h
кесіндісіндегі
дәлдігі-0(h![]() ).
).
2.Трапеция әдісі
Байқасақ, тіктөртбұрыштардың формуласымен алынған арифметикалық ортасының жуығы қандай да мәнге тең, демек интеграл мағынасының түп мәніне тең болып шығады: қателік 0,05% -ке тең. (2) және (3) формулалары бойынша алынған, интегралдаудың жуықталған мағынасы ретінде орташа арифметикалықтың жуықтаын алуға тура келеді.
Байқасақ, бұл мағыналарды алдын ала шығарып қоюды еш мұхтаждығы жоқ. Өйткені бірден дайын формуламен пайдаланса болады. Шынымен де, (2) және (3)оң формулаларының арифметикалықтың ортасын алсақ, мынаны аламыз:
![]() (11)
(11)
бұл трапециялар формуласы.
(11) трапециялар формуласын былайша оңай алуға да болады, геометриялық мағынасынан шыға тура, a=x0<x1<x2<…<xn-1<xn=b нүктелермен интегралдаудың үзіндісін n-бірдей бөлікке бөліп, бөлулердің барлық нүктелердің ординаталарды жүргіземіз және әр алынған қисық сызықтытыны түзу сызықтыға ауыстырамыз, төмендегі суретте көрсетілген. Әр трапецияның жақтары екі көрші ординаттар болып табылады. Ох сызбаның аймағы, ұзындығы h=(b-a)/n және хордасы қисық.

Сол трапецияның
көлемі ![]() (хі-1,хі)
(хі-1,хі)
Аймақтың үстінде орналасқан, трапецияға сай, мынаны табамыз.
![]() (12)
(12)
1-ден n-ге дейін барлық і-ға (12) көрсетілімдерді қосу, өйткені шеттегіден басқа барлық ординаттар, (12) көрсетілімдердің түрінде екі мәрте қолданылады.
Трапециялық тәсілмен жасалатын сандық интегралдау
ЭЕМ-дағы сандық интегралдау тәсілдерді іске асыруды қажет ететін, нақты бір интегралдың мысалдарын келтірейік.
Мысалы, егерде f(x)-электростанцияғаауырлық болса, квт-уақытта (х-тәуліктің басынан есептелетін, уақыттың саны), тәуліктің ішінде электірлік энергиялық шығыны құрайтын мынау:
![]() (13)
(13)
немесе басқа мысал:
t-уақытта алынған, дисконтталған кірістің көлемі мынаған тең:
![]() (14)
(14)
осы жерде:
t-уақыт
і-пайыздың меншікті нормасы (пайыздар үздіксіз өсе береді)
Сонымен, математикалық тілмен айтқанда нақты бір интегралды жоғарыдағы формулаларды «санға жеткізу» керек.
Сол үшін осы тақырыпта трапециялық тәсілді қолданамыз.
Тәсілдің мәні: интегралдаудың арасы [a, b] n нүктелермен бірнешеге бөлінеді. (n+1) бірдей кішкентай бөліктерге.
Трапеция формуласының көрінісі:
![]() (15)
(15)
f(x) - интегралдың астындағы функциясы;
a, b - интегралдаудың шегі;
n - аралықтың саны;
yi- і нүктеде бөлінетін f(xi) мағынасы
Трапеция
әдісі. (4)
интегралындағы ![]() функциясын
функциясын ![]()
![]() нүктелері
арқылы тұрғызылған
нүктелері
арқылы тұрғызылған
![]()
бір дәрежелі Лагранж көпмүшесімен алмастырсақ, онда
![]()
![]() (16)
(16)
мұндағы![]()
![]()
(16) формуласын ![]() аралығында
интегралдау арқылы
аралығында
интегралдау арқылы

![]() (17)
(17)
теңдігін аламыз. Осыдан
 . Бұл формула трапеция әдісі деп аталады,себебі
. Бұл формула трапеция әдісі деп аталады,себебі ![]()

3-сурет
![]() сызықтарымен қоршалған қисық сызықты
трапецияның ауданы
сызықтарымен қоршалған қисық сызықты
трапецияның ауданы ![]() трапециясының ауданымен алмастырылады (3сурет).
трапециясының ауданымен алмастырылады (3сурет).
(17) формуладан бұл әдістің жіберетін қатесі
![]() (18)
(18)
екенін көреміз. Ал жоғарыдан бағаласақ
![]() , (19)
, (19)
![]()
Енді мына интегралды былай есептесек:

![]()
![]() (20)
(20)
Онда
 (21)
(21)
трапеция әдісінің жалпы формуласы шығады.
Ал жіберілетін қате
![]() (22)
(22)
Жоғарыдан бағаласақ
![]() , (23)
, (23)
![]() .
.
Сонымен, трапеция әдісінің ![]() кесіндісіндегі
дәлдігі
кесіндісіндегі
дәлдігі ![]() екенін көреміз.
екенін көреміз.
-
Парабола әдісі
Сандық интегралдың бұл тәсілінде нақты бір интегралдың түрі қарастырылады (4):
![]()
[a, b] интегралдаудың интервалын жұп сан аралығына бөледі демек 2m-ге, демек бөлінетін нүктенің саны 2m+1-ге тең.
Тәсілдің мәні: Трапецияның тәсіліне қарағанда, Симпсон тәсілінде (x0, x1) және (x1, x2) екі көрші аралығында және f(x) қисығын (демек интегралдың астындағы функцияны) параболамен ауыстырады, демек алгебралық көпмүшеліктің түрімен
y=f(x)=A(x- x0)(x- x1)+B(x- x0)(x- x2)+C(x- x1)(x- x2) (24)
осы жерде А,В,С- анықтау керек шама
А,В және С анықталғаннан кейін, парабола формуласының немесе былайша айтқанда Симпсон формуласының берілгені мынау:
![]()
осы жерде yi -0,1,2,..., 2m бөлінген нүктелердегі f(x) интегралдың астындағы функцияларының мағынасы.
Жоғарыдағы қарастырылған трапеция формуласынан да дәлірек формула Симпсон формуласы деп те аталады. Дәл сондай дәлдікке қол жеткізу үшін бұл формулада бөліну аймағының n санын азырақ алып және сәйкесінше үлкен арақашықтық h-деп алу керек. Бірдей арақашықтарда , яғни дәл сондай шешімнің көлемінде, бұл формулада абсолютті және салыстырмалы қателік жіберіледі.
Симпсон формуласын осы уақытқа дейін екі рет қолданған тәсілмен алуға болады.
Аумақты ![]() жұп санды n=2m бөлікке
нүктелермен бөлеміз a= x0
<
x1
<…<
xn-1<
xn=b, ординаттарды бөліну
нүктелерінде y0,
y1,…
yn
арқылы
белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз.
Мысалы, шеткі сол жақтағы a= x0
нүктені
қарастырайық.
жұп санды n=2m бөлікке
нүктелермен бөлеміз a= x0
<
x1
<…<
xn-1<
xn=b, ординаттарды бөліну
нүктелерінде y0,
y1,…
yn
арқылы
белгілейміз де, көршілес аумақтардың бір-екеуін қарастырамыз.
Мысалы, шеткі сол жақтағы a= x0
нүктені
қарастырайық.

Үш нүкте арқылы қисық сызықты координаталармен параболаны (x0 у0),( x1 у1),( x2 у2) өсімен бірге жүргіземіз. Бұл ось Оу параллель болу керек.Оның теңдеуі былай болады:
y= Ах2 +Вх+С (25)
бірақ А,В,С коэффенцентері әзірше белгісіз болып қала береді:
[x0, x2] аумағында берілген қисық сызықты трапецияның ауданын (1,3,1) параболамен шектелген қисық сызықты трапецияның ауданымен алмастырып, жақындатылған теңдікке келеміз:

жақшаның сыртына жалпы көбейткіштерді x2 – x0 шығарып, содан кейін жалпы бөлгішке әкелемі де, мынадай формуланы аламыз:
![]() (26)
(26)
(25) теңдеуіндегі және (26)
формуласындағы белгісіз А,В,С коэффенценттері
x0,
x1,
x2–ге тең х мағынасындағы
жағдайдан табылады. F(x) функциясы жағдйында сәйкес мағынаға ие
болады. ![]() екендігін
байқасақ, бұл жағдайларды мына түрде жазамыз:
екендігін
байқасақ, бұл жағдайларды мына түрде жазамыз:
![]() (27)
(27)
Екінші теңдікті (27) төртке көбейту арқылы және содан кейін үш теңдікті қатарластыру арқылы мынаны аламыз:
y0+4 y1+ y2=A[x02+ ( x0+ x2)2+ x22]+B[x0+2(x0+ x2)+ x2]+6C=2A(x02+ x0 x2+ x22)+3B(x0+ x2)+6C (28)
(28) теңдеудің оң бөлігінде төрт бұрышты жақшамен сәйес келеді.
(26)-ті (28) теңдеудің оң бөліміне қоя тұра, x2 –x0 =2h ескеріп, жуықталған теңдеуге келеміз
![]() (29)
(29)
Әр ендігі бөлікке тура сондай формула келетіні анық:
![]() (30)
(30)
(29)және (30) теңдеулердің көрінісін барлық аймақ бойынша қоса тұра, мынадай формула аламыз:
![]() (31)
(31)
(31) формуласы бізге керек болған Симпсон формуласы. Формуланың геометриялық мәнін ескере тұра, оны парабола формуласы деп те атайды. Онда барлық ординаттар тақ нөмірмен төртке көбейтіледі, жұп санмен екіге. у0 және у2m шеткі ординаттар коэффенценттері бар формулаға кіреді, олар бірге тең.
(4) интегралын жуықтап есептеу
үшін ![]() функциясын
функциясын ![]() нүктелері арқылы тұрғызылған
нүктелері арқылы тұрғызылған ![]() Лагранж көп
мүшесімен алмастырамыз. Яғни
Лагранж көп
мүшесімен алмастырамыз. Яғни
![]()
![]()
![]() . (32)
. (32)
Осыдан
![]()
![]()
Сонымен мына формуланы –
![]()
![]() (33)
(33)
Симпсон немесе парабола формуласы деп атайды.
Бұл формуланың парабола формуласы деп атайтын себебі
![]() сызықтарымен шектелген қисық сызықты
трапецияның ауданы
сызықтарымен шектелген қисық сызықты
трапецияның ауданы ![]() нүктелері арқылы өтетін парабола және
нүктелері арқылы өтетін парабола және ![]() түзулерімен
шектелген трапецияның ауданымен алмастырылады (4-сурет).
түзулерімен
шектелген трапецияның ауданымен алмастырылады (4-сурет).
Симпсон формуласы ![]() кесіндісінде былайша
жазылады
кесіндісінде былайша
жазылады![]()

![]()
![]()
Бөлшекті индекстерден құтылу үшін
![]() десек,онда Симпсон формуласын былайша
жазамыз:
десек,онда Симпсон формуласын былайша
жазамыз:![]()
![]() . (34)
. (34)

4-сурет
О х у xi-1 xi-1/2 xi y=f(x) y=L2(x) + -
Симпсон формуласының жіберетін қатесін
қарастырардың алдында, оның үш ![]() дәрежелі көпмүше
үшін дәл екенін көрсетейік. Шынында да
дәрежелі көпмүше
үшін дәл екенін көрсетейік. Шынында да
![]() болса, онда
болса, онда
![]()
![]()
![]()
![]()
Осыдан
![]()

![]()
![]()
![]()
Екіншіден
![]()
![]()
екенін ескерсек
![]()
![]()
формуласын аламыз.
Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік.
Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын
![]()
![]()
интерполяциялық Эрмит көпмүшелігін пайдаланамыз .
Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан
 (35)
(35)
Енді ![]()
десек,онда

мұндағы ![]() (36)
(36)
-Эрмит көпмүшесінің жіберетін қатесі.
![]() кесіндісінде
кесіндісінде ![]() көпмүшесі өзінің
таңбасын өзгертпейтін болғандықтан
көпмүшесі өзінің
таңбасын өзгертпейтін болғандықтан

![]()
Сондықтан Симпсон формуласының жіберетін қатесi
 . (37)
. (37)
Hемесе
![]() (38)
(38)
![]()
Симпсон формуласының ![]() кесіндісінде
жіберетін қатесі
кесіндісінде
жіберетін қатесі
![]()
Болғандықтан ![]() (39)
(39)
![]()
Яғни Симпсон әдісінің ![]() кесіндісіндегі
дәлдігі
кесіндісіндегі
дәлдігі ![]() .
.![]()
4.Интегралдау аралығын бөліктеу
Егер ![]() кесіндісінде
үзіліссіз және алғашқы образы-
кесіндісінде
үзіліссіз және алғашқы образы-![]() белгілі болса, онда Ньютон-Лейбниц формуласы
бойынша:
белгілі болса, онда Ньютон-Лейбниц формуласы
бойынша:
 (40)
(40)
Бірақ, көп
жағдайда ![]() функциясын табу өте күрделі мәселе болғандықтан, (40)
формуласы іс жүзінде көп қолданылмайды. Ал кейбір
уақыттарда
функциясын табу өте күрделі мәселе болғандықтан, (40)
формуласы іс жүзінде көп қолданылмайды. Ал кейбір
уақыттарда ![]() функциясы таблица түрінде берілетіндіктен алғашқы образ
деген сөздің өзі мағынасын жоғалтады.
функциясы таблица түрінде берілетіндіктен алғашқы образ
деген сөздің өзі мағынасын жоғалтады.
Сондықтан
 (41)
(41)
интегралын есептеу
үшін ![]() (42)
(42)
ақырғы қосындысы қолданылады.
Мұндағы ![]() -сандық коэффициенті
-сандық коэффициенті ![]() кесіндісінің нүктелері,
кесіндісінің нүктелері, ![]()
Мына жуықтап алынған
теңдік  (43)
(43)
квадратуралық
формула деп аталынады. Ал
(1.3)- квадратуралық
қосынды, ![]() -
квадратуралық формуланың түйіндері
,
-
квадратуралық формуланың түйіндері
, ![]() -kвадратуралық формуланың
коэфициенті деп
аталынады.
-kвадратуралық формуланың
коэфициенті деп
аталынады.
 (44)
(44)
квадратуралық формуланың
дәлдігі делінеді. Квадратуралық
формуланың дәлдігі квадратуралық формуланың
түйіндері-![]() -ның орналасуына, квадратуралық формуланың
коэффициенттері-
-ның орналасуына, квадратуралық формуланың
коэффициенттері-![]() -ның алу жолдарына тікелей байланысты.
-ның алу жолдарына тікелей байланысты.
Енді берілген анықталған
интегралды есептеу үшін ![]() кесіндісін тең
кесіндісін тең ![]() кесіндіге бөлеміз, яғни
кесіндіге бөлеміз, яғни ![]() нүктелер жиынын аламыз да
нүктелер жиынын аламыз да
 (45)
(45)
теңдігін қарастырамыз.
![]() кесіндісіндегі интегралдың мәнін табу
үшін
кесіндісіндегі интегралдың мәнін табу
үшін
 (4)
(4)
интегралының ![]() аралықтағы мәнін
табу жеткілікті, өйткені (1.6) формуласы арқылы интегралдың
аралықтағы мәнін
табу жеткілікті, өйткені (1.6) формуласы арқылы интегралдың
![]() кесіндісіндегі
мәнін табу онша қиындық туғызбайды.
кесіндісіндегі
мәнін табу онша қиындық туғызбайды.
Қорытынды
![]() - анықталмаған интегралын
қарастырамыз, мұндағы
- анықталмаған интегралын
қарастырамыз, мұндағы ![]()
![]() кесіндісінде үзіліссіз
функция. Интеграл астындағы функция «күрделі» болып, яғни
интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру
ыңғайлы болады, яғни
кесіндісінде үзіліссіз
функция. Интеграл астындағы функция «күрделі» болып, яғни
интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру
ыңғайлы болады, яғни![]() делік,
мұндағы
делік,
мұндағы ![]() алынатын
интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап
алынады.
алынатын
интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап
алынады.
Теорема. Егер ![]() интегралында
интегралында
![]() (
(![]() мен
мен
![]() - үзіліссіз функциялар)
ауыстыруын алсақ, онда
- үзіліссіз функциялар)
ауыстыруын алсақ, онда
![]() (1)
(1)
формуласы
орындалады, яғни жаңа ![]() интегралын аламыз, ал ол
кестелік интегралға оңай келуі мүмкін.
интегралын аламыз, ал ол
кестелік интегралға оңай келуі мүмкін.
Дәлелдеу. Сол жағын
![]() бойынша, оң
жағын
бойынша, оң
жағын ![]() бойынша
күрделі функция ретінде дифференциалдаймыз:
бойынша
күрделі функция ретінде дифференциалдаймыз:
![]() ;
;
![]() Оң бөлігі мен сол бөлігінің
теңдігі теореманың дұрыстығын дәлелдейді.
Оң бөлігі мен сол бөлігінің
теңдігі теореманың дұрыстығын дәлелдейді.
Практикалық тәсіл:
![]()
=![]() .
.
Пайдаланылған әдебиеттер
-
Темірғалиев Н. “Математикалық анализ” - Алматы; Мектеп 1987, 288 бет.
-
Ибрашев Х. И., Еркеғұлов Ш. Т. “Математикалық анализ курсы.” – Алматы; Мектеп 2 том, 1970, 527 бет.
-
Кудрявцев А. Д. “Краткий курс математического анализа.” – Москва, Наука, 1989, 735 бет.
-
Фихтенгольц Г. М. “Основы математического анализа.” – Москва, Наука, 1968, ІІ том.
-
“Задачник по курсу математического анализа.” Под редак. Н. Я. Виленкина, Москва, 1971, ч-2.
-
Асинкин А. Г., Бутинов Е. И., Кондратьев А. С. “Краткий физико-математический справочник.” Москва, 1990, 368 стр.
-
Демидович Б. П. “Сборник задачи и упражнений по математическому анализу.” Москва, Наука, 1977.
-
“Егемен Қазақстан” 16 қазан, 2004 жыл.
-
А. Г. Аленкин, Е. И. Бутиков, А. С. Кондратьев. «Краткий физико-математический справочник» М., 1990 г.
-
Шойынбеков К. Д., Әбілқасымов А. Е., Есенова М. И., Тұрлыханова М. А. «Анализ бастамалары» оқу құралы. Алматы, 2002ж., 320 бет.
-
Данко П. Е., Попов А. Г., Кожевникова Т. Я. «Высшая математика в упражнениях и задачах» учебное пособие для студентов вузов. М., Высш.шк., 1926г.
Есептер
Жазық фигуралардың ауданын жуықтап есептеу барысында трапеция әдісін қолдану

![]() анықталған интегралдың
сан мәні дегеніміз – абсцисса өсі, f(x) функциясының қисығы
және x=a, x=b
түзулермен шектелген қисықсызықты трапеци ауданың
шамасы.
анықталған интегралдың
сан мәні дегеніміз – абсцисса өсі, f(x) функциясының қисығы
және x=a, x=b
түзулермен шектелген қисықсызықты трапеци ауданың
шамасы.
Бұл қисық сызықты трапецияның
ауданын табу үшін, ![]() аралығын
әрқайсысының ұзындығы
аралығын
әрқайсысының ұзындығы ![]() –ге тең болатын
–ге тең болатын ![]() n
бөлікке
бөлеміз. Бөліну нүктелерінен қисығымен қиылысқанша
n
бөлікке
бөлеміз. Бөліну нүктелерінен қисығымен қиылысқанша ![]() ординаталарын жүргіземіз де,
олардың қисықсызықпен A,C,D,….B–қиылысу нүктелерін
кесінділерімен қосамыз. Сонда aABb
қисықсызықты трапецияның ауданын шамамен
aACx1,
x1CDx2
, ….,
x1-n
Bb трапецияларының аудандарының
қосындысымен алмастыруға болады. Сөйтіп,
ординаталарын жүргіземіз де,
олардың қисықсызықпен A,C,D,….B–қиылысу нүктелерін
кесінділерімен қосамыз. Сонда aABb
қисықсызықты трапецияның ауданын шамамен
aACx1,
x1CDx2
, ….,
x1-n
Bb трапецияларының аудандарының
қосындысымен алмастыруға болады. Сөйтіп,
![]()
Алынған формула анықталған интегралдың жуық мәнін табу формуласы деп аталады.
Трапеция әдісінен жоғары парабола әдісі (Симпсон әдісі деп те атайды) деп аталатын әдіс те бар. Парабола әдісі бойынша анықталған интегралдың мәні мына формуламен табуға болады:
![]()
Бұл жағдайда ![]() аралығы жұп, яғни 2n бөлікке
бөлінеді.
аралығы жұп, яғни 2n бөлікке
бөлінеді.
Ескерту. Күрделі фигуралар қисық сызықты трапециялардың қосындысы немесе айырмасы түрінде беріледі.
Мысалы, екі қисықпен:
![]() және
x=a,
x=b екі тік сызықпен шектелген
фигураның ауданын табу керек болсын. Бұл жағдайда ізделініп отырған
ауданды екі қисық сызықты трапециялардың аудандарының айырмасы
ретінде қарастыруға болады. Сондықтан да
және
x=a,
x=b екі тік сызықпен шектелген
фигураның ауданын табу керек болсын. Бұл жағдайда ізделініп отырған
ауданды екі қисық сызықты трапециялардың аудандарының айырмасы
ретінде қарастыруға болады. Сондықтан да
![]()
Енді жоғарыда келтірілген әдістерге мысалдар келтіріп, оларды есептеуге арналған программалар құрайық.
Мысал.Интегралдау аралығын
n=20 бөлікке бөліп, ![]() интегралының мәнін трапеция әдісімен табамыз
интегралының мәнін трапеция әдісімен табамыз
Шешілуі:
Алгоритмдік тілде
алг трапеция әдісі (арг нақ a, b, n, арг нәт нақ p)
бер / a, b және бөлік саны n,
тап / интегралдың мәні табылды
басы нақ x, h, бүт i
х:=a;h:=(b-a)/n
р:=y(a)+y(b)
цб үшін і бастап 1 дейін n-1
х:=x+h
р:=p+2*y(x)
цс
р:=p*h/2
соңы
алг нақ у(нақ x)
басы
мән:=1/ln(x)
соңы
SIMPSON Паскаль- бағдарламаның қолдану мысалы:
[1, 3] интегралдаудың аралығын 4 бөлікке бөле тұра, интегралдың мағынасын Симпсон тәсіліі арқылы табу:
![]()



Паскаль-TRAPECIA бағдарламасының қолданылу мысалы: интегралдың аралығын төртке бөліп, трапеция тәсілімен интегралдың мағынасын табу:
![]() [1,3]
аралығын 4 - бөлікке бөлу арқылы интегралдау.
[1,3]
аралығын 4 - бөлікке бөлу арқылы интегралдау.
27

шағым қалдыра аласыз















