ТОПСАЛЫ ТӨРТТИЕКТІ
МЕХАНИЗМНІҢ КОМПЬЮТЕРЛІК МОДЕЛІ
Механиканың есебін шешуде
графикалық әдіс кез келген механизмнің орнын, тиектің жылдамдығы
мен үдеуін анықтауда көрнекті және жан - жақты болып табылады.
Бірақ бұл әдіс аналитикалық шешімнің дәлдігін анықтай алмайды. Ал
соңғы уақытта есептің аналитикалық шешімін алуға мүмкіндік беретін
және экранда бейнелейтін, сондай – ақ шешімнің әр түрлі бастапқы
шарттарында зерттеуге болатын компьютерлің моделі талап
етіледі.
Топсалы төрттиекті механизмді
қарастырайық (1 сурет), мұндағы механизм тиектерінің осі АВСD
контурын құрайды, ал тиектерінің орны
арқылы анықталады.
Аналитикалық зерттеуді векторлық контурлар әдісі арқылы жүргізейік.
Мұндағы 
- модуль вектор бойынша
алынған айнымалы. Механизмнің тиектерінің ұзындығы
және көлбеу бұршышы ,сондай – ақ 1
мен 4 бекітілген топсалары белгілі.
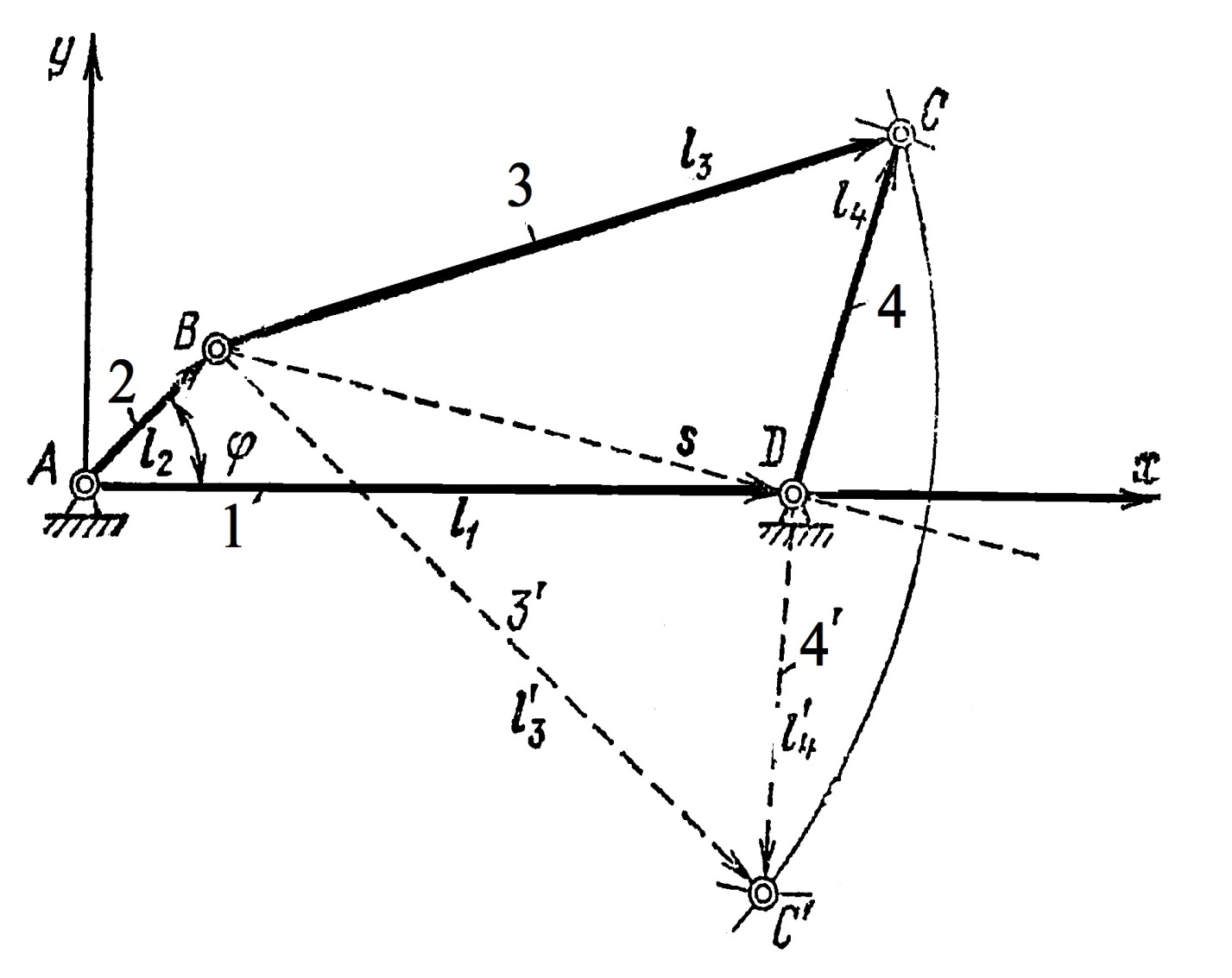
Сурет 1. Екі векторлық
контуры бар топсалы төрттиекті
механизм.
Берілген механизмнің әрбір
элементіне алгоритмін құрайық:
|
№
|
Элемент
|
Delphi-дегі
коды
|
|
1
|
Топса
|
procedure
TForm1.Sharnir(x,y:real);
begin
series1.AddXY(x,y);
series2.AddXY(x,y);
end;
|
|
2
|
Негізі
|
procedure
TForm1.Osnovanie(x,y:real);
begin
series3.AddXY(x,y-1);
series4.AddXY(x,y-3);
end;
|
|
3
|
Тиек
|
procedure
TForm1.zveno(s1,s2:integer);
begin
series5.AddArrow(L[s1,1],L[s1,2],L[s2,1],L[s2,2]);
end;
|
TСhart компонентасы (2 сурет)
берілген түзулерді, векторларды және белгілерді
қамтиды.
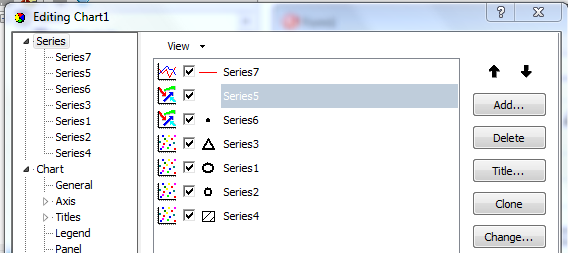
Сурет
2 – TChart
компонентасы
|
№
|
Delphi-дегі
коды
|
Баяндалуы
|
|
1
|
begin
series1.Clear;
series2.Clear;
series3.Clear; series4.Clear;
series5.Clear;
|
Берілгендерді
жою
|
|
2
|
d[1]:=strtofloat(LabeledEdit1.Text);
d[2]:=strtofloat(LabeledEdit2.Text);
d[3]:=strtofloat(LabeledEdit3.Text);
d[4]:=strtofloat(LabeledEdit4.Text);
fi[1]:=strtofloat(LabeledEdit5.Text);
|
Бастапқы шарттарын
алу
|
|
3
|
L[1,1]:=0;
L[1,2]:=0;
|
Бірінші топсаның
координатасы
|
|
4
|
Sharnir(L[1,1],L[1,2]);
Osnovanie(L[1,1],L[1,2]);
|
Бірінші топсаның
бейнесі
|
|
5
|
L[4,1]:=d[1];
L[4,2]:=0;
Sharnir(L[4,1],L[4,2]);
Osnovanie(L[4,1],L[4,2]);
|
4 топсаның координатасы және
оның құрылуы
|
|
6
|
L[2,1]:=d[2]*cos(fi[1]*3.14/180);
L[2,2]:=d[2]*sin(fi[1]*3.14/180);
Sharnir(L[2,1],L[2,2]);
|
2 топсаның ізделінуі және оның
құрылуы
|
|
7
|
zveno(1,2);
|
№2 тиектің
құрылуы
|
|
8
|
S3(L[2,1],L[2,2],d[3],L[4,1],L[4,2],d[4]);
|
3 топсаның координатасының
ізделінуі
|
|
9
|
zveno(2,3);
zveno(3,4);
Sharnir(L[3,1],L[3,2]);
end;
|
Қалған тиектер мен топсаның
құрылуы
|
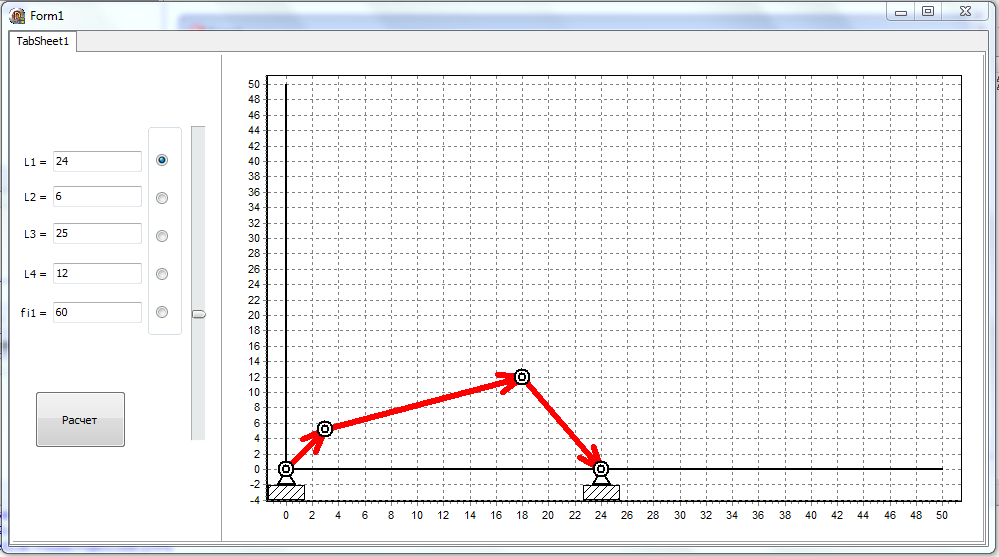
Сурет
3 –
Программа
терезесі.
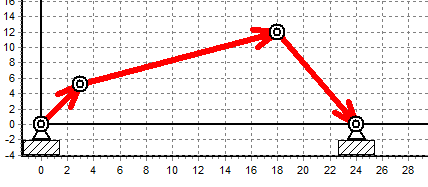
Сурет
4 –
Төрттиекті механизмнің компьютерлік
моделі
Қарастырылған модель автоматты
режимде топсалардың координатасын анықтау арқылы әр түрлі
төрттиекті механизмдердің моделін құруға мүмкіндік
береді.(3-4 сурет).
Екінші топсаның координатасын
анықтау үшін келесі теңдеулер жүйесін шешу
қажет
Ал үшінші
топсаға
жүйесі
шешіледі.
Бұл модель төрттиекті
механизмдердің құрылымын көрсетеді және жазық тұтқалы механизмдерді
зерттеуде қолданылуы болады.
01 Қазан 2018
376
