Таныстым:
Қазақстан Республикасы Оқу-ағарту министрлігі
Момынай жалпы орта білім беретін мектебі
Қысқа мерзімді (сабақ) жоспары
Пәні: Геометрия
Тақырыбы: Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы
|
Бөлім: |
Түзулердің өзара орналасуы |
|
|
Педагогтің Т.А.Ә. |
Алиева Гулжан Аманкулкызы |
|
|
Күні: |
06.02.2024ж |
|
|
Сынып: 7 |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
7.1.1.18 үшбұрыштың сыртқы бұрышының анықтамасын білу және үшбұрыштың сыртқы бұрышы туралы теореманы дәлелдеу; 7.1.1.19 үшбұрыштың сыртқы бұрышы туралы теореманы қолдану; |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурс тар |
||||||||
|
|
Оқушылармен амандасу, түгендеу, назарын сабаққа аудару. Үй тапсырмасын сұрау. Оқушылармен бірге сабақ мақсаттарын / ОМ анықтап алу Оқушылардың «жақын даму аймағын», сабақ соңында күтілетін нәтижелерді анықтау |
Жинақтала ды,сабаққа ынталанады |
Үй жұмысы мадақтау әдісімен бағаланады |
|
||||||||
|
Сабақтың ортасы |
Өткен сабақты пысықтау Анықтама. Үшбұрыштың ішкі бұрышына сыбайлас болатын бұрышты оның сыртқы бұрышы деп атайды. Үшбұрыштың әр төбесінде бір біріне вертикаль екі сыртқы бұрышы бар болады. Яғни, барлық сыртқы бұрыштар саны алтау.
Теорема. Сыртқы бұрыштардың (әр төбесінен бір-бірден алғанда) қосындысы 360°-қа тең. Дәлелдеуі. ∠α′, ∠β′ және ∠γ′ бұрыштары сәйкесінше ∠α, ∠β және ∠γ бұрыштарына сыбайлас сыртқы бұрыштары болса, онда ∠α′ = 180° – ∠α, ∠β′ = 180° – ∠β, ∠γ′ = 180° – ∠γ. Осыдан ∠α′ + ∠β′ + ∠γ′ = 540° – ∠α – ∠β – ∠γ шығады. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша ∠α + ∠β + ∠γ = 180°. Яғни ∠α′ +∠β′ +∠γ′ = 360°. Теорема дәлелденді. Мысал. Егер теңбүйірлі үшбұрыш табан бұрышының сыртқы бұрышы 130°-қа тең болса, онда оның төбесіндегі ішкі және сыртқы бұрыштарын табу керек.
Шешуі. Теорема бойынша теңбүйірлі үшбұрыштың төбесіндегі бұрыштың сыртқы бұрышы 360° – 2 ⋅ 130° = 100°. Олай болса төбесінің ішкі бұрышы 180° – 100° = 80°. Жауабы: төбесіндегі сыртқы бұрыш 100°-қа, ал ішкі бұрыш 80°-қа тең. Тапсырмалар: №1. Үшбұрыштың сыртқы
бұрыштарының бірі оның ішкі бұрыштарының қосындысының
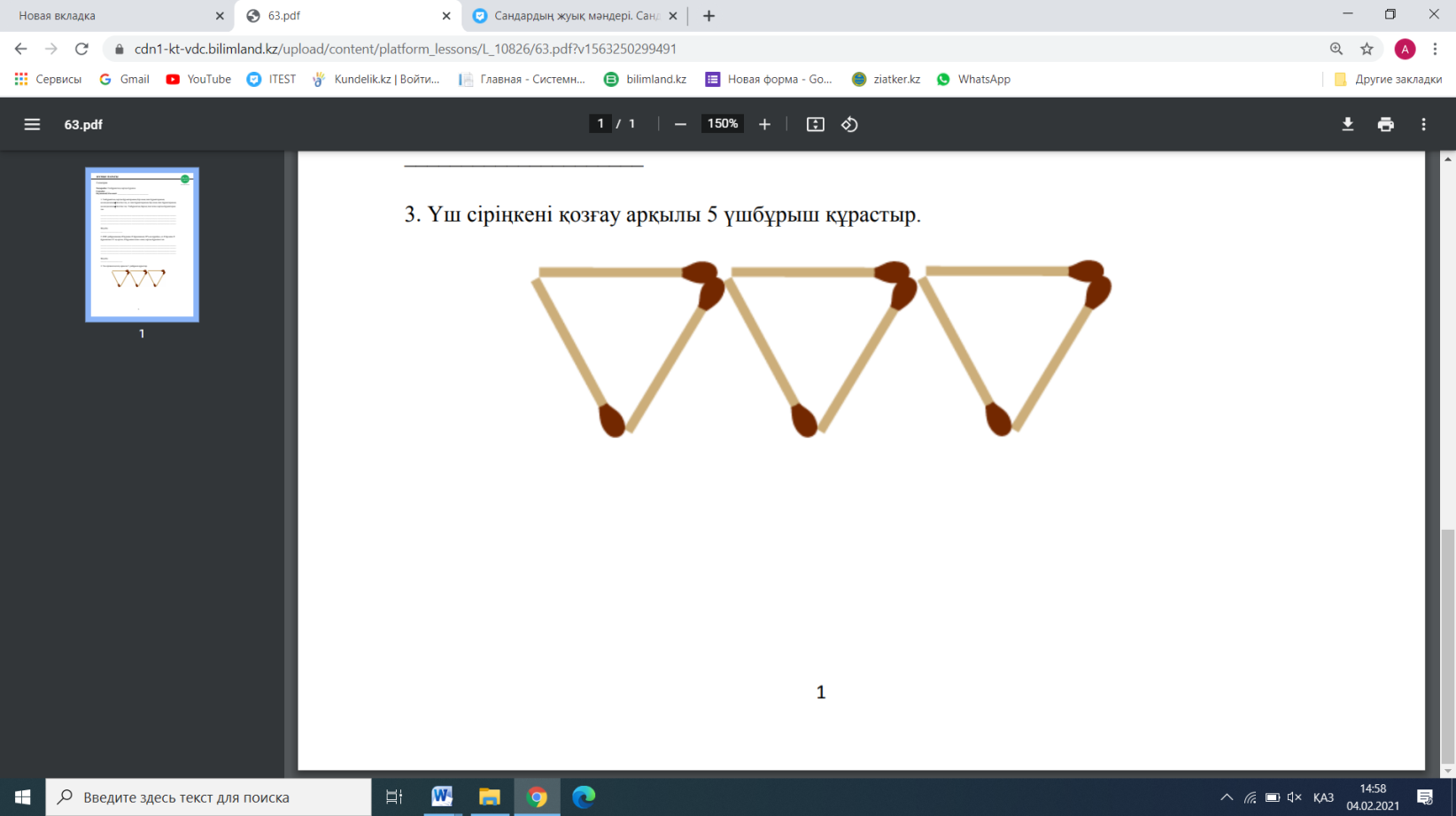
№2. ??? үшбұрышының ? бұрышы ? бұрышының 30%-ын құрайды, ал ? бұрышы ? бұрышынан 19-қа артық. ? бұрышын жəне оның сыртқы бұрышын тап. №3. Үш сіріңкені қозғау арқылы 5 үшбұрыш құрастыр.
Оқулықта берілген тапсырмаларды орындау. |
Алдыңғы сабақта алған білімдерін еске түсіреді. Тапсырмаларды өз бетінше орындайды Сынып бойынша жұмыстар жүргізеді |
Мақтау, мадақтау әдісі арқылы бағаланады. Әр дұрыс жауапқа 1 балл беріледі |
|
||||||||
|
Сабақтың соңы |
Үй жұмысы. № есеп Рефлексия:
|
Үй жұмысымен танысады. Рефлексияны дәптерге орындайды |
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы. ҚМЖ 7 сынып геометрия 3 тоқсан
Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы. ҚМЖ 7 сынып геометрия 3 тоқсан
Таныстым:
Қазақстан Республикасы Оқу-ағарту министрлігі
Момынай жалпы орта білім беретін мектебі
Қысқа мерзімді (сабақ) жоспары
Пәні: Геометрия
Тақырыбы: Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы
|
Бөлім: |
Түзулердің өзара орналасуы |
|
|
Педагогтің Т.А.Ә. |
Алиева Гулжан Аманкулкызы |
|
|
Күні: |
06.02.2024ж |
|
|
Сынып: 7 |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Үшбұрыш бұрыштарының қосындысы. Үшбұрыштың сыртқы бұрышы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
7.1.1.18 үшбұрыштың сыртқы бұрышының анықтамасын білу және үшбұрыштың сыртқы бұрышы туралы теореманы дәлелдеу; 7.1.1.19 үшбұрыштың сыртқы бұрышы туралы теореманы қолдану; |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурс тар |
||||||||
|
|
Оқушылармен амандасу, түгендеу, назарын сабаққа аудару. Үй тапсырмасын сұрау. Оқушылармен бірге сабақ мақсаттарын / ОМ анықтап алу Оқушылардың «жақын даму аймағын», сабақ соңында күтілетін нәтижелерді анықтау |
Жинақтала ды,сабаққа ынталанады |
Үй жұмысы мадақтау әдісімен бағаланады |
|
||||||||
|
Сабақтың ортасы |
Өткен сабақты пысықтау Анықтама. Үшбұрыштың ішкі бұрышына сыбайлас болатын бұрышты оның сыртқы бұрышы деп атайды. Үшбұрыштың әр төбесінде бір біріне вертикаль екі сыртқы бұрышы бар болады. Яғни, барлық сыртқы бұрыштар саны алтау.
Теорема. Сыртқы бұрыштардың (әр төбесінен бір-бірден алғанда) қосындысы 360°-қа тең. Дәлелдеуі. ∠α′, ∠β′ және ∠γ′ бұрыштары сәйкесінше ∠α, ∠β және ∠γ бұрыштарына сыбайлас сыртқы бұрыштары болса, онда ∠α′ = 180° – ∠α, ∠β′ = 180° – ∠β, ∠γ′ = 180° – ∠γ. Осыдан ∠α′ + ∠β′ + ∠γ′ = 540° – ∠α – ∠β – ∠γ шығады. Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша ∠α + ∠β + ∠γ = 180°. Яғни ∠α′ +∠β′ +∠γ′ = 360°. Теорема дәлелденді. Мысал. Егер теңбүйірлі үшбұрыш табан бұрышының сыртқы бұрышы 130°-қа тең болса, онда оның төбесіндегі ішкі және сыртқы бұрыштарын табу керек.
Шешуі. Теорема бойынша теңбүйірлі үшбұрыштың төбесіндегі бұрыштың сыртқы бұрышы 360° – 2 ⋅ 130° = 100°. Олай болса төбесінің ішкі бұрышы 180° – 100° = 80°. Жауабы: төбесіндегі сыртқы бұрыш 100°-қа, ал ішкі бұрыш 80°-қа тең. Тапсырмалар: №1. Үшбұрыштың сыртқы
бұрыштарының бірі оның ішкі бұрыштарының қосындысының
№2. ??? үшбұрышының ? бұрышы ? бұрышының 30%-ын құрайды, ал ? бұрышы ? бұрышынан 19-қа артық. ? бұрышын жəне оның сыртқы бұрышын тап. №3. Үш сіріңкені қозғау арқылы 5 үшбұрыш құрастыр.
Оқулықта берілген тапсырмаларды орындау. |
Алдыңғы сабақта алған білімдерін еске түсіреді. Тапсырмаларды өз бетінше орындайды Сынып бойынша жұмыстар жүргізеді |
Мақтау, мадақтау әдісі арқылы бағаланады. Әр дұрыс жауапқа 1 балл беріледі |
|
||||||||
|
Сабақтың соңы |
Үй жұмысы. № есеп Рефлексия:
|
Үй жұмысымен танысады. Рефлексияны дәптерге орындайды |
|
|

шағым қалдыра аласыз