Алгебра пәні бойынша 7 сынып оқушысының өзіндік жұмысының жоспары

I тоқсан Сабақтың номері : 28

Сабақтың тақырыбы: Сызықтық функция және оның графигі

Мақсаты:

1. түріндегі сызықтық функцияның анықтамасын білу, оның графигін салу және графиктің k және b коэффициенттеріне қатысты орналасуын анықтау;

2. сызықтық функция графигінің координата осьтерімен қиылысу нүктелерін графикті салмай табу;

3. у = kx + b сызықтық функциясының графигінен k және b таңбаларын анықтау;

Бейнеүзіндіhttps://www.youtube.com/watch?v=Uz5s3rZkyzk

https://www.youtube.com/watch?v=OX309b5HEV4

1. Конспект Оқулық: А.Е.Әбілқасымова және басқалары, «Алгебра», 7-сынып, 2Алматы, «Мектеп», 2017,28-32 беттер

Сызықтық функция

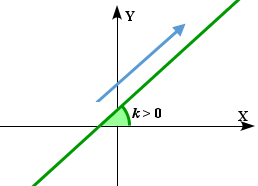
Егер k> О, онда у = kx + b

сызықтық функция өседі

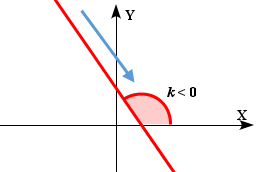
Егер k< О, онда у = kx + b

сызықтық функция кемиді

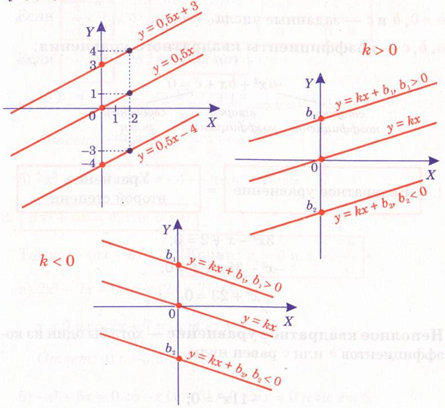
Дербес жағдайдағы функцияның басқа функциялардың айырмашылығын қарап, b- ға қатысты қорытынды шығар:

Мысал 1

Графиктері бойынша функцияларын анықтаңдар

1. Түзу (2;0) және (0,2) нүктелері арқылы өтеді. Сондықтан

0 теңдіктері орындалуы қажет. Осыдан 2 және

2. Түзу (-4;0) және (0,-2) нүктелері арқылы өтеді. Сондықтан

0 теңдіктері орындалуы қажет. Осыдан 2 және

Мысал 2

Координаталық осьтерінде орналасқан нүктелердің координаталары туралы. (Ох осінде, (а; 0), Оу осінде (0; а)).

Функцияның графигін салмай, оның осьтермен қиылысу нүктелерін анықтаныз:

Ох осінде(а; 0), у яғни 3х-7 . Қиылысу нүкте (

Оу осінде (0; а); х Қиылысу нүкте (0; -7)

Тапсырма

№1.

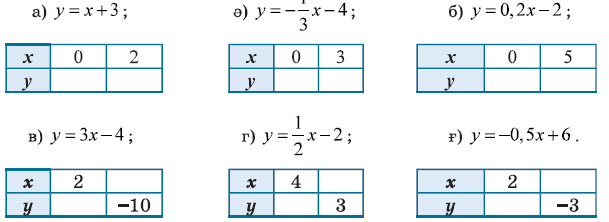
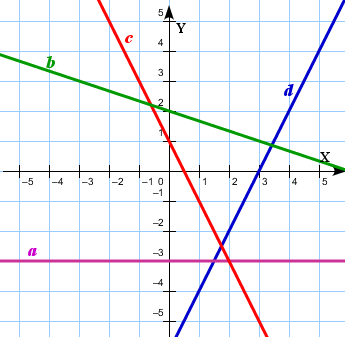
№2. Сызықтық функция графикалық тәсілмен берілген. Аналитикалық тәсілмен берініз.

№3.Графикті салмай, осьтермен қиылысу нүктелерді анықтаныз.

а) ; б) ; в) ;

г) ; д) ;

е) .

Әзірлеуші: Т.Қабылов атындағы орта мектеп -мектепке дейінгі шағын орталығымен» коммуналдық мемлекеттік мекемесі математика пәні мұғалімі. Сайбирова Д

Геометрия пәні бойынша 7 сынып оқушысының өзіндік жұмысының жоспары

Сабақтың номері:

Сабақтың тақырыбы: Үшбұрыштар теңдігінің белгілері

Мақсаты: 1. Үшбұрыштар теңдігінің белгілерін білу және дәлелдеу;

2. Үшбұрыштар теңдігінің белгілерін есептер шығаруда қолдану.

Конспект:

• ABC және A’B’C’ үшбұрыштарының теңдігі былай жазылады:

• ∆ABC=∆A’B’C’.

Мұндағы AB=A’B’, BC=B’C’, AC=A’C’, ∠A=∠A’, ∠B=∠B’, ∠C=∠C’

• Үшбұрыштардың теңдігі орындалуы үшін осы алты шарттың да орындалуын көрсету керек.

• Дегенмен олардың бәрін дәлелдеудің қажеті жоқ.

• Сондықтан арнайы әдіспен үш жағдай таңдалып алынады.

Осы жағдайларды үшбұрыштардың теңдік белгілері дейді.

1-теорема.(Үшбұрыштар теңдігінің 1-ші белгісі). Егер бір үшбұрыштың екі қабырғасы және олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен олардың арасындағы бұрышына тең болса, онда мұндай үшбұрыштар тең болады.

∆ABC=∆A’B’C’берілсін.

AB=A’B’, AC=A’C’, ∠A=∠A’

1 теореманыдәлелдеу

• КесінділертеңдігінесүйенеотырыпABменA’B’кесінділерінбеттестірсек, АменA’, ВменB’нүктелерідәлкеледідеугеболады.

• АВ түзуіне қатысты С нүктесі жатқан жарты жазықтықта АВ сәулесінен бастап ∠A=∠A’ болатын АС сәулесін табуға болады. (5 аксиома)

• АС=A’C’болғандықтан, С’ нүктесі С нүктесімен беттеседі.

• НәтижесіндеBC=B’C’ шығады.

• Солсияқты∠B=∠B’, ∠C=∠C’.

• Ендеше ∆ABC=∆A’B’C’

Теорема дәлелденді.

Бейнеүзінді көру:https://www.youtube.com/watch?v=vZhXRWLJ4XA

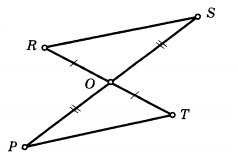
Мысал 1: АВ және CDкесінділері әрқайсысының ортасы болатын О нүктесінде қиылысады. Егер АС=8 м болса, онда BD-ны табыңыз.

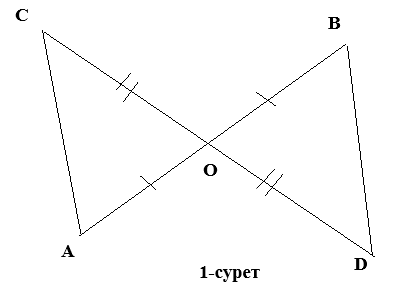
Шешуі:∠AOC = ∠BOD болғандықтан (ветрикаль бұрыштар), үшбұрыштар теңдігінің бірінші белгісі бойынша ∆AОC=∆BOD, себебі

CO=OD

OA=OB

∠COA = ∠BOD(вертикаль бұрыштар)

∆AОC=∆BOD(үшбұрыштар теңдігінің бірінші белігісі бойынша)

Сондықтан BD = AC =8 м (Тең үшбұрыштардың сәйкес қабырғалары өзара тең).

Жауабы:BD = 8 м.

Тапсырма:

№1, №2, №3, №4 есептерден тең үшбұрыштарды тауып, теңдігін дәлелдеңіз.

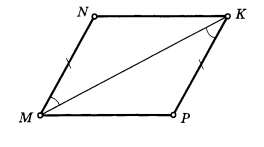
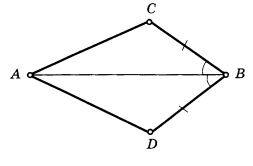№1. №2.

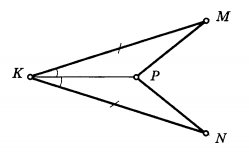
№3. №4.

Әзірлеушілер : Т.Қабылов атындағы орта мектеп -мектепке дейінгі шағын орталығымен» коммуналдық мемлекеттік мекемесі математика пәні мұғалімі. Сайбирова Д

Геометрия пәні бойынша 7 сынып оқушысының өзіндік жұмысының жоспары

Сабақтың номері:

Сабақтың тақырыбы: Үшбұрыштар теңдігінің бірінші белгісі

Мақсаты: 1. Үшбұрыштар теңдігінің бірінші белгісін білу және дәлелдеу;

2. Үшбұрыштар теңдігінің бірінші белгісін есептер шығаруда қолдану.

Конспект:

Бейнеүзінді көру: https://www.youtube.com/watch?v=XDNIOYinr3Q

Мысал 1:

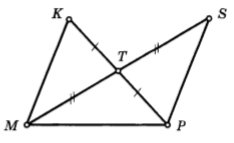Берілгені:

∠MKT =

MK = 10 см

Табу керегі: ∠TPS; PS-?

Шешуі: ∠MKT= ∠STP (вертикаль бұрыш) болғандықтан, үшбұрыштар теңдігінің I– белгісі бойынша .

Сондықтан, ∠MKT = ∠TPS =

MK = PS = 10 см.

Тең үшбұрыштың сәйкес бұрыштары мен сәйкес қабырғалары тең.

Тапсырма:

№1, №2 есептерден тең үшбұрыштарды тауып, теңдігін дәлелдеңіз.

№1. №2.

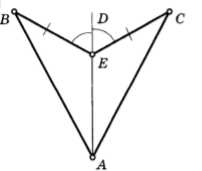
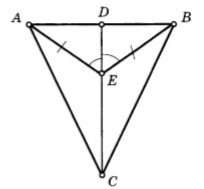
№3. . AB = 5 см, NP = 6 см. АВС үшбұрышының периметрі 18 см. MP-ны табыңыз.

№4. . АС = 8 см, үшбұрышының периметрі 24 см. АВ - ны табыңыз.

Әзірлеушілер : Т.Қабылов атындағы орта мектеп -мектепке дейінгі шағын орталығымен» коммуналдық мемлекеттік мекемесі математика пәні мұғалімі. Сайбирова Д