
Қысқа мерзімді жоспар Тексерілді:_______
|
Ұзақ мерзімді жоспар бөлімі: 9.3B бөлім: Үшбұрыштарды шешу |
|
|
||||||||||||||||||||
|
Күні: |
Мұғалімнің аты-жөні: Джургабаев С.Е. |
|
||||||||||||||||||||
|
Сынып: 9 |
Қатысқандар саны: |
Қатыспағандар саны: |
|
|||||||||||||||||||
|
Сабақ тақырыбы |
Үшбұрыштың медианаларының қасиеттері |
|
||||||||||||||||||||
|
Кәсіби даму мақсаты |
|
|
||||||||||||||||||||
|
Осы сабақта қол жеткізілетін оқу мақсаттары |
9.3.3.7 үшбұрыштың медианаларының қасиеттерін дәлелдейді және қолданады;
|
|
||||||||||||||||||||
|
Сабақ мақсаттары |
Барлығы: Үшбұрыштың медианаларының қасиеттерін біледі і және оны қолданады. Көпшілігі: Үшбұрыштың медианаларының қасиеттерін дәлелдейді Кейбірі: Күрделі есептерді әр түрлі әдістер арқылы шығарады.
|
|
||||||||||||||||||||
|
Бағалау критерийлері |
Оқушылар:
|
|
||||||||||||||||||||
|
Тілдік мақсат |
Пәндік лексика мен терминология
Диалогқа/жазылымға қажетті тіркестер
биссектриса қабырғаны ... бөледі. үшбұрышқа сырттай сызылған шеңбер радиусы ... қатынасына тең;
|
|
||||||||||||||||||||
|
Құндылықтарды дарыту |
Жұптық және топтық жұмыс барысында ынтымақтастықта жұмыс жасай алу дағдысы,академиялық шынайылық қалыптастыру. |
|
||||||||||||||||||||
|
Пәнаралық байланыстар |
Алгебра, физика |
|
||||||||||||||||||||
|
АКТ қолдану дағдылары |
Интербелсенді тақтаны қолдану |
|
||||||||||||||||||||
|
Бастапқы білім
|
үшбұрыштардың түрлерін, үшбұрыштың теңсіздігін,үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатынасты, үшбұрыштың аудан формулаларын білу, тікбұрышты үшбұрыштарды шеше білу. |
|
||||||||||||||||||||
|
Сабақбарысы |
|
|||||||||||||||||||||
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланғаніс-әрекет
|
Ресурстар |
||||||||||||||||||||
|
Сабақтың басы 2 минут |
Оқушылармен амандасу, түгелдеу. Үй тапсырмасын тексеру. |
|
||||||||||||||||||||
|
3мин |
ІІ. Қайталау сұрақтары. Оқушылармен бірге теңқұрамдас фигуралар және теңшамалас фигуралар түсініктерін қайталау.
Сабаққа қатысты термин сөздердің үш тілде айтылуы. |
слайд |
||||||||||||||||||||
|
Топтық жұмыс 10мин Жұптық жұмыс 23мин 2мин |
ІІІ. Оқушыларды үш топқа бөліп, дәлелдеуді ұсыну:
Берілген теореманың қолданылуына есептер шығару.
Бірінші сабақты қортындылау. |
Прикладная программа для исследований медиан: http://www.mathopenreF.com/trianglemedians.html
http://nsportal.ru/sites/default/files/2014/04/19/tsentr_tyazhesti._treug.ppt
|
||||||||||||||||||||
|
Екінші сабақ 10 минут Жеке жұмыс 25мин |
І
1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника. 2. Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.
3. В
треугольника АВС АА1 и СС1 – медианы,
причем АА1=5, 4. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника. 5. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27. |
http://sk.nis.edu.kz/Bank/Show/21529 http://sk.nis.edu.kz/Bank/Show/98026
Карточка |
||||||||||||||||||||
|
Сабақтың соңы 5 минут
|
VI. Рефелексия Үй тапсырмасы: карточка
|
|
||||||||||||||||||||
|
Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз? |
Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз? |
Денсаулық және қауіпсіздік
техникасының сақталуы |
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
Сабақ бойынша рефлексия Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме? Жеткізбесе, неліктен? Сабақта саралау дұрыс жүргізілді ме? Сабақтың уақыттық кезеңдері сақталды ма? Сабақ жоспарынан қандай ауытқулар болды, неліктен? |
Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз. |
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
Есеп 1: SABC = 38см2, Табу керек: SВСK, SABK |
|
|
Есеп 2: SABK = 26 см2 Табу керек: SВСK, SABC |
|
|
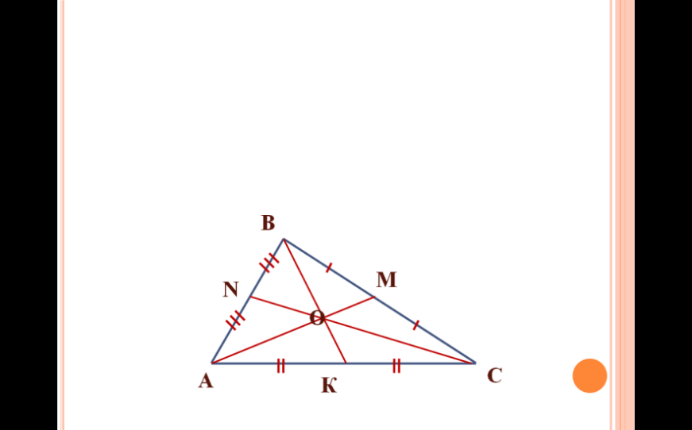
Есеп 3: SBON =12 см2 Табу керек: SВAM, SABC |
|
|
Есеп 4: SBOC = 28 см2 Табу керек: SВKC, SABC |
|
|
Есеп 5: SABE = 28 дм2 , АВ = 7 дм, EB – AEC-ң медианасы, EC – AED-ң медианасы. Табу керек: SECD |
|
|
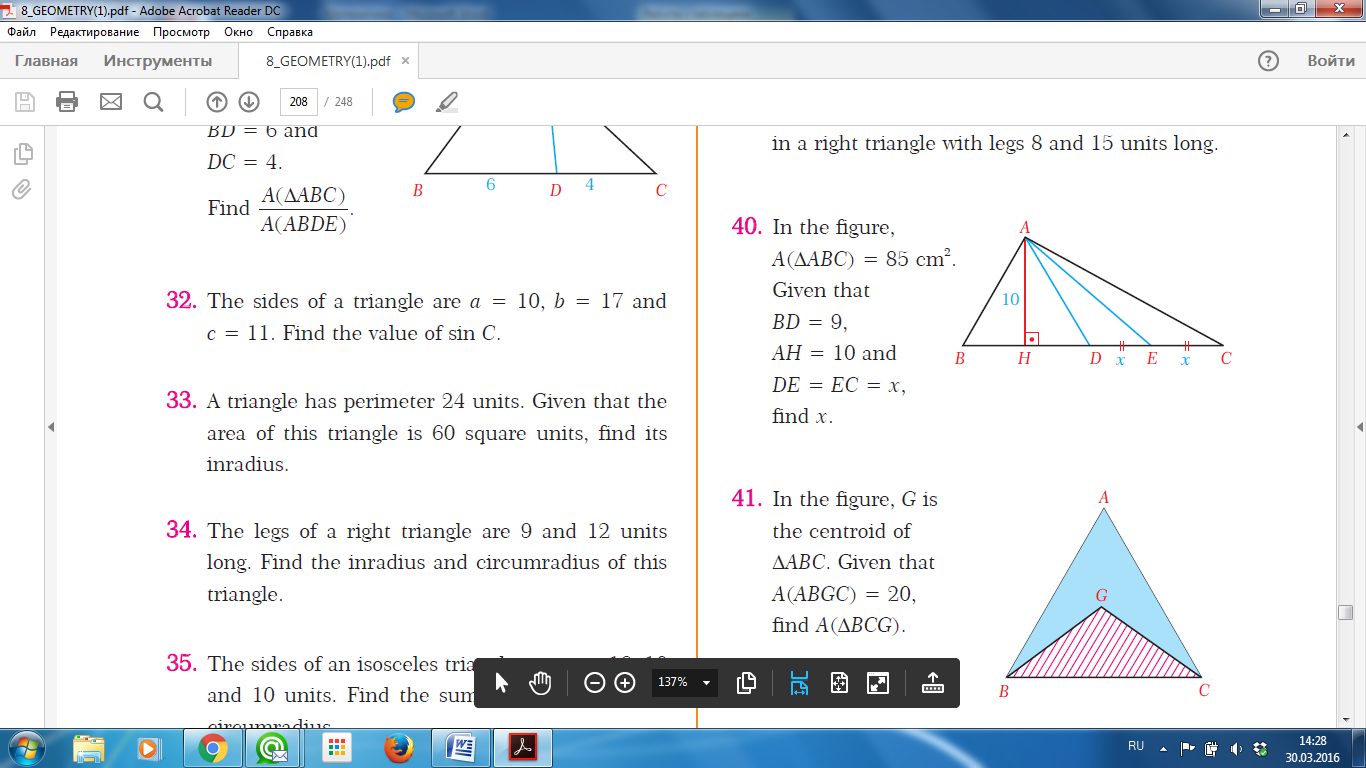
Есеп 6: SABС = 85 см2 BD = 9, AH = 10 DE = EC АD АВС –ң медианасы Табу керек: ЕD |
|
|
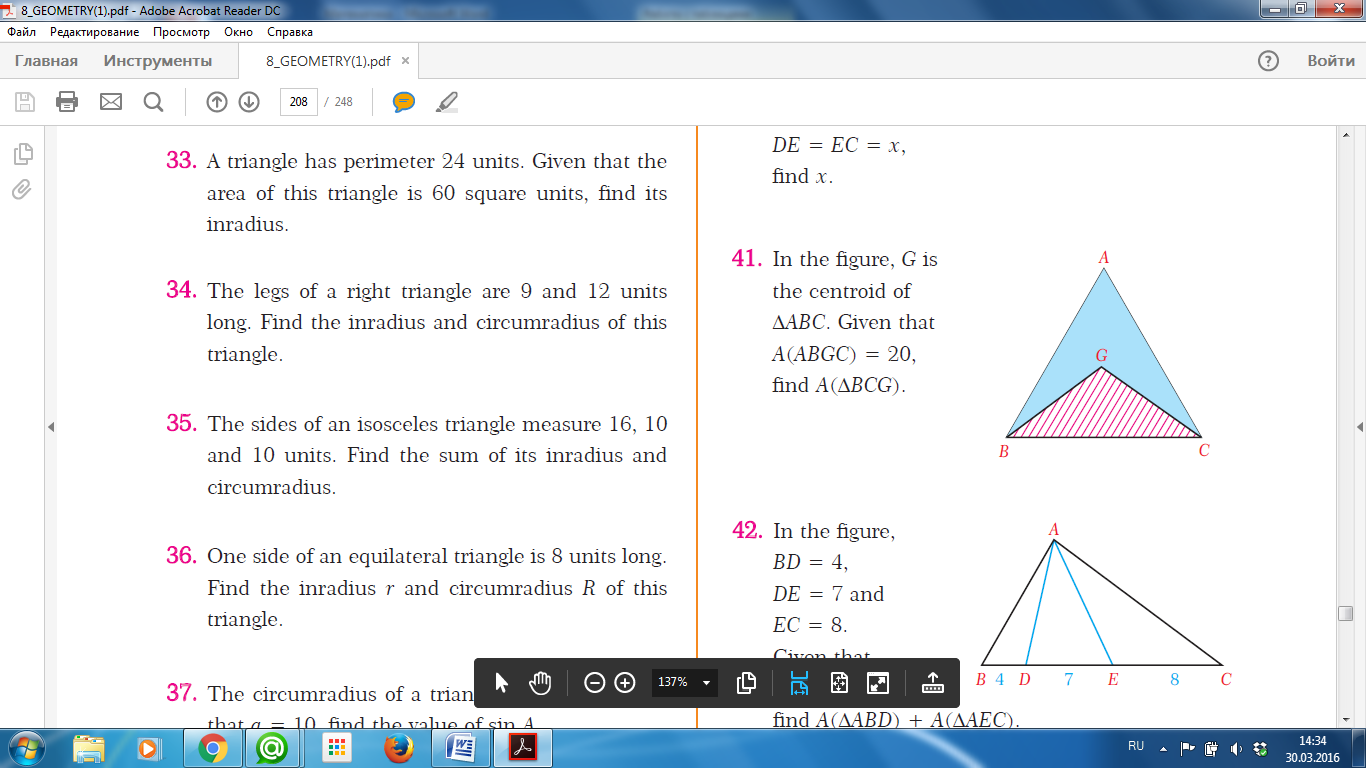
Есеп 7: G нүктесі– медианалардың қиылысу нүктесі, SABGС = 20 см2 Табу керек: SBGС |
|
-
Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.
-
Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.
-
В треугольника АВС АА1 и СС1 – медианы, причем АА1=5,
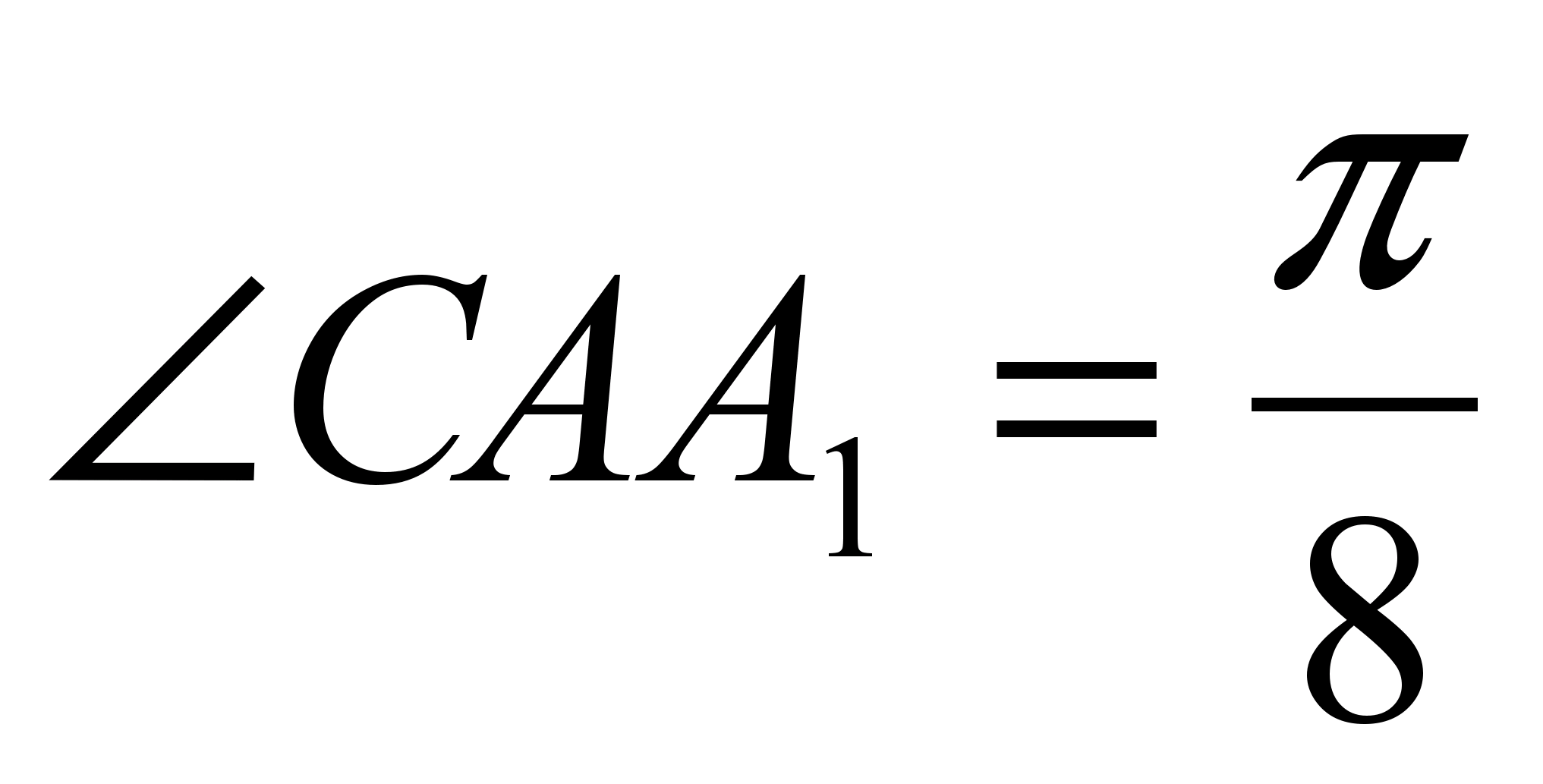 ,
, 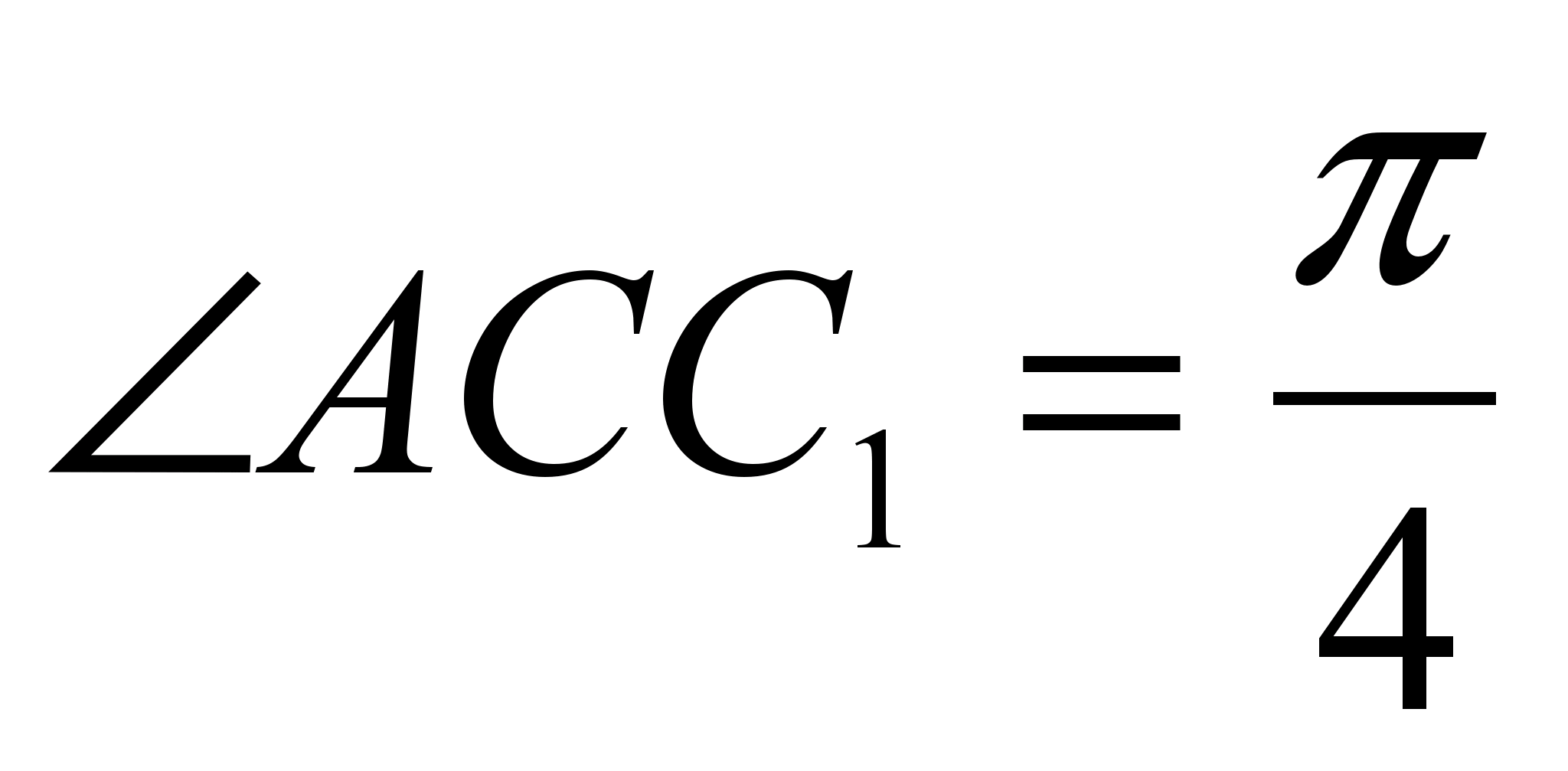 . Найдите площадь
треугольника АВС.
. Найдите площадь
треугольника АВС.
-
Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.
-
Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.
Задачи для самостоятельного решения
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
О т в е т: 8.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
О т в е т: 3.
3. Две медианы равнобедренного
треугольника взаимно перпендикулярны. Боковая сторона
равна ![]() . Найдите площадь
треугольника.
. Найдите площадь
треугольника.
О т в е т: 3.
4. В
треугольнике АВС медианы АD и ВE перпендикулярны, ![]() ,
, ![]() . Чему равен квадрат третьей
стороны?
. Чему равен квадрат третьей
стороны?
О т в е т: 5.
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
О т в е т: 288.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
О т в е т: 14.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
О т в е т: 10.
8. Найдите площадь
треугольника, если две его стороны равны 1
и ![]() , а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т:
, а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т: ![]() .
.
Задачи для самостоятельного решения
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
О т в е т: 8.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
О т в е т: 3.
3. Две медианы равнобедренного
треугольника взаимно перпендикулярны. Боковая сторона
равна ![]() . Найдите площадь
треугольника.
. Найдите площадь
треугольника.
О т в е т: 3.
4. В
треугольнике АВС медианы АD и ВE перпендикулярны, ![]() ,
, ![]() . Чему равен квадрат третьей
стороны?
. Чему равен квадрат третьей
стороны?
О т в е т: 5.
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
О т в е т: 288.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
О т в е т: 14.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
О т в е т: 10.
8. Найдите площадь
треугольника, если две его стороны равны 1
и ![]() , а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т:
, а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т: ![]() .
.
Теорема
(Свойство медиан треугольника)
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
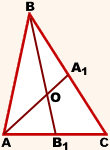 Дано: ABC, AA1, BB1, CC1
— медианы
Дано: ABC, AA1, BB1, CC1
— медианы
Доказать:
![]()
![]()
Доказательство:
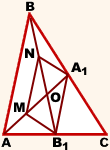 1) Пусть M —
середина отрезка AO, N — середина
BO
1) Пусть M —
середина отрезка AO, N — середина
BO
(то есть AM=OM, BN=ON).
2) Соединим точки M, N, A1 и B1 отрезками.
Тогда MN — средняя линия треугольника AOB и
![]()
3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.
Следовательно, A1B1 — средняя линия треугольника ABC и
![]()
4) Имеем:
![]()
Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).
По свойству диагоналей параллелограмма
![]()
Таким образом,
![]()
![]()
![]()
из чего следует, что
![]()
5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.
Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.
Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.
Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:
![]()
Что и требовалось доказать.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Үшбұрыш медианасының қасиеттері
Үшбұрыш медианасының қасиеттері
Қысқа мерзімді жоспар Тексерілді:_______
|
Ұзақ мерзімді жоспар бөлімі: 9.3B бөлім: Үшбұрыштарды шешу |
|
|
||||||||||||||||||||
|
Күні: |
Мұғалімнің аты-жөні: Джургабаев С.Е. |
|
||||||||||||||||||||
|
Сынып: 9 |
Қатысқандар саны: |
Қатыспағандар саны: |
|
|||||||||||||||||||
|
Сабақ тақырыбы |
Үшбұрыштың медианаларының қасиеттері |
|
||||||||||||||||||||
|
Кәсіби даму мақсаты |
|
|
||||||||||||||||||||
|
Осы сабақта қол жеткізілетін оқу мақсаттары |
9.3.3.7 үшбұрыштың медианаларының қасиеттерін дәлелдейді және қолданады;
|
|
||||||||||||||||||||
|
Сабақ мақсаттары |
Барлығы: Үшбұрыштың медианаларының қасиеттерін біледі і және оны қолданады. Көпшілігі: Үшбұрыштың медианаларының қасиеттерін дәлелдейді Кейбірі: Күрделі есептерді әр түрлі әдістер арқылы шығарады.
|
|
||||||||||||||||||||
|
Бағалау критерийлері |
Оқушылар:
|
|
||||||||||||||||||||
|
Тілдік мақсат |
Пәндік лексика мен терминология
Диалогқа/жазылымға қажетті тіркестер
биссектриса қабырғаны ... бөледі. үшбұрышқа сырттай сызылған шеңбер радиусы ... қатынасына тең;
|
|
||||||||||||||||||||
|
Құндылықтарды дарыту |
Жұптық және топтық жұмыс барысында ынтымақтастықта жұмыс жасай алу дағдысы,академиялық шынайылық қалыптастыру. |
|
||||||||||||||||||||
|
Пәнаралық байланыстар |
Алгебра, физика |
|
||||||||||||||||||||
|
АКТ қолдану дағдылары |
Интербелсенді тақтаны қолдану |
|
||||||||||||||||||||
|
Бастапқы білім
|
үшбұрыштардың түрлерін, үшбұрыштың теңсіздігін,үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатынасты, үшбұрыштың аудан формулаларын білу, тікбұрышты үшбұрыштарды шеше білу. |
|
||||||||||||||||||||
|
Сабақбарысы |
|
|||||||||||||||||||||
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланғаніс-әрекет
|
Ресурстар |
||||||||||||||||||||
|
Сабақтың басы 2 минут |
Оқушылармен амандасу, түгелдеу. Үй тапсырмасын тексеру. |
|
||||||||||||||||||||
|
3мин |
ІІ. Қайталау сұрақтары. Оқушылармен бірге теңқұрамдас фигуралар және теңшамалас фигуралар түсініктерін қайталау.
Сабаққа қатысты термин сөздердің үш тілде айтылуы. |
слайд |
||||||||||||||||||||
|
Топтық жұмыс 10мин Жұптық жұмыс 23мин 2мин |
ІІІ. Оқушыларды үш топқа бөліп, дәлелдеуді ұсыну:
Берілген теореманың қолданылуына есептер шығару.
Бірінші сабақты қортындылау. |
Прикладная программа для исследований медиан: http://www.mathopenreF.com/trianglemedians.html
http://nsportal.ru/sites/default/files/2014/04/19/tsentr_tyazhesti._treug.ppt
|
||||||||||||||||||||
|
Екінші сабақ 10 минут Жеке жұмыс 25мин |
І
1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника. 2. Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.
3. В
треугольника АВС АА1 и СС1 – медианы,
причем АА1=5, 4. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника. 5. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27. |
http://sk.nis.edu.kz/Bank/Show/21529 http://sk.nis.edu.kz/Bank/Show/98026
Карточка |
||||||||||||||||||||
|
Сабақтың соңы 5 минут
|
VI. Рефелексия Үй тапсырмасы: карточка
|
|
||||||||||||||||||||
|
Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз? |
Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз? |
Денсаулық және қауіпсіздік
техникасының сақталуы |
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
Сабақ бойынша рефлексия Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме? Жеткізбесе, неліктен? Сабақта саралау дұрыс жүргізілді ме? Сабақтың уақыттық кезеңдері сақталды ма? Сабақ жоспарынан қандай ауытқулар болды, неліктен? |
Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз. |
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
Есеп 1: SABC = 38см2, Табу керек: SВСK, SABK |
|
|
Есеп 2: SABK = 26 см2 Табу керек: SВСK, SABC |
|
|
Есеп 3: SBON =12 см2 Табу керек: SВAM, SABC |
|
|
Есеп 4: SBOC = 28 см2 Табу керек: SВKC, SABC |
|
|
Есеп 5: SABE = 28 дм2 , АВ = 7 дм, EB – AEC-ң медианасы, EC – AED-ң медианасы. Табу керек: SECD |
|
|
Есеп 6: SABС = 85 см2 BD = 9, AH = 10 DE = EC АD АВС –ң медианасы Табу керек: ЕD |
|
|
Есеп 7: G нүктесі– медианалардың қиылысу нүктесі, SABGС = 20 см2 Табу керек: SBGС |
|
-
Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.
-
Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.
-
В треугольника АВС АА1 и СС1 – медианы, причем АА1=5,
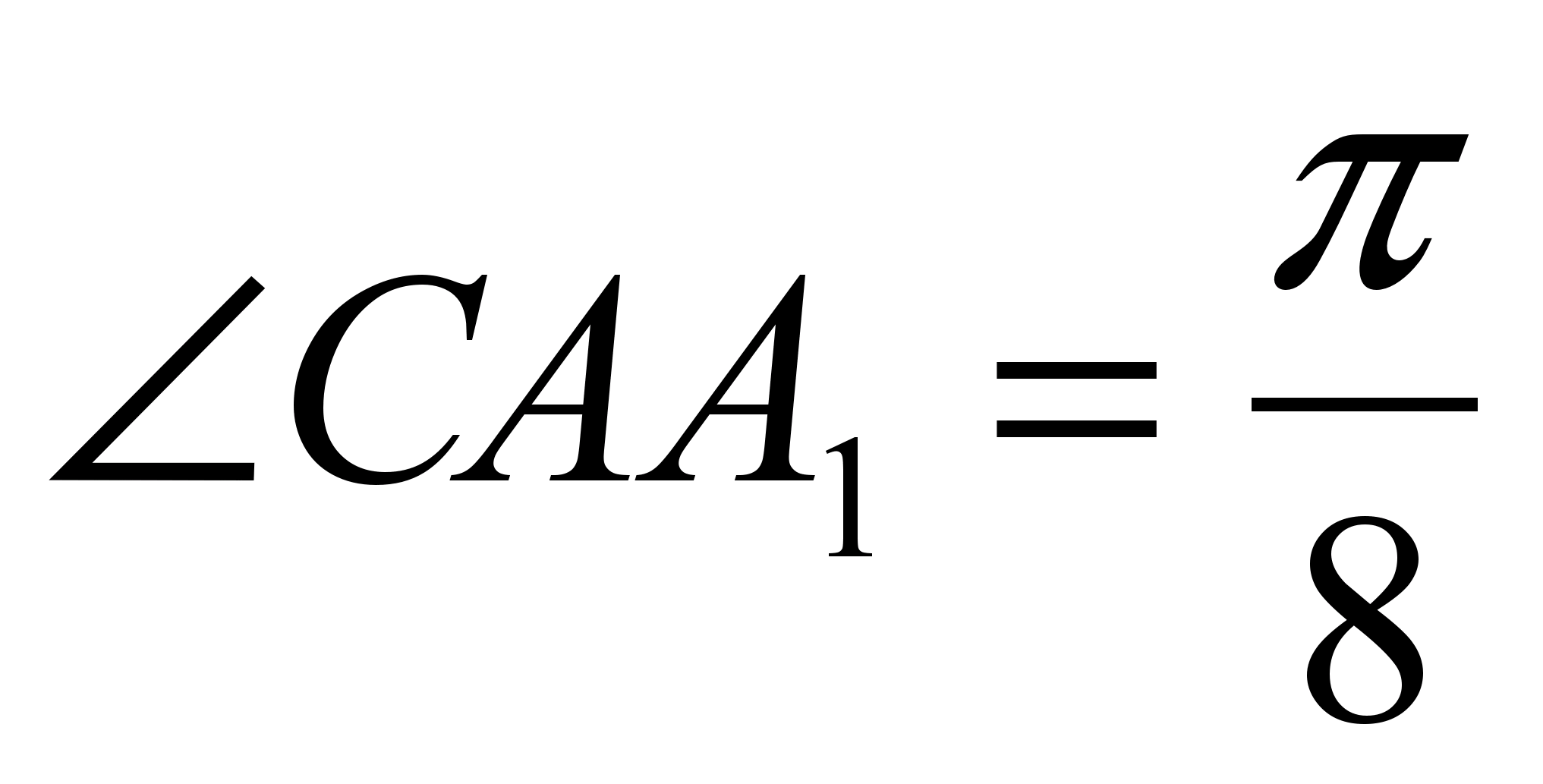 ,
, 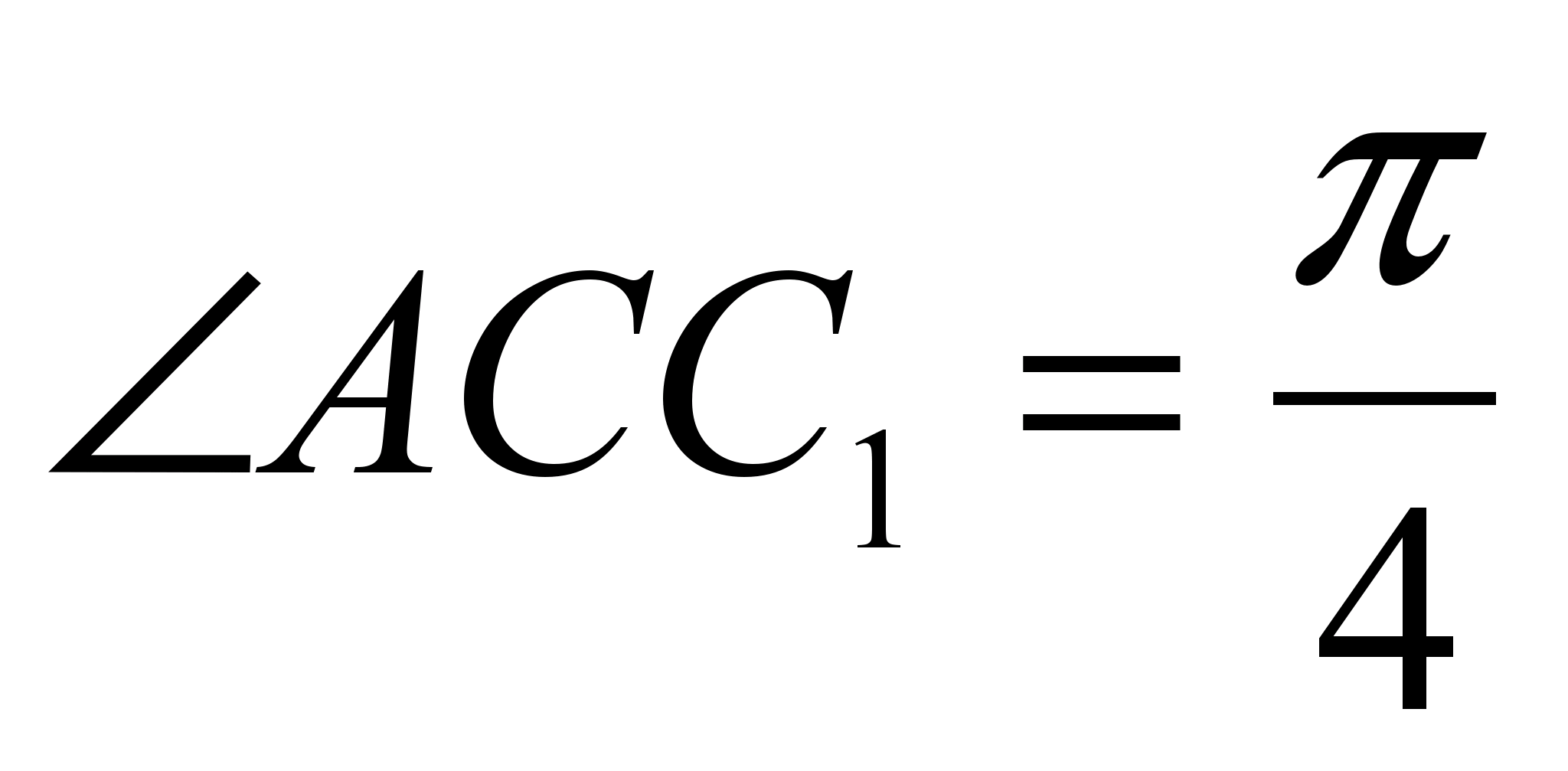 . Найдите площадь
треугольника АВС.
. Найдите площадь
треугольника АВС.
-
Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.
-
Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.
Задачи для самостоятельного решения
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
О т в е т: 8.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
О т в е т: 3.
3. Две медианы равнобедренного
треугольника взаимно перпендикулярны. Боковая сторона
равна ![]() . Найдите площадь
треугольника.
. Найдите площадь
треугольника.
О т в е т: 3.
4. В
треугольнике АВС медианы АD и ВE перпендикулярны, ![]() ,
, ![]() . Чему равен квадрат третьей
стороны?
. Чему равен квадрат третьей
стороны?
О т в е т: 5.
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
О т в е т: 288.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
О т в е т: 14.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
О т в е т: 10.
8. Найдите площадь
треугольника, если две его стороны равны 1
и ![]() , а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т:
, а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т: ![]() .
.
Задачи для самостоятельного решения
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
О т в е т: 8.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
О т в е т: 3.
3. Две медианы равнобедренного
треугольника взаимно перпендикулярны. Боковая сторона
равна ![]() . Найдите площадь
треугольника.
. Найдите площадь
треугольника.
О т в е т: 3.
4. В
треугольнике АВС медианы АD и ВE перпендикулярны, ![]() ,
, ![]() . Чему равен квадрат третьей
стороны?
. Чему равен квадрат третьей
стороны?
О т в е т: 5.
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
О т в е т: 288.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
О т в е т: 14.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
О т в е т: 10.
8. Найдите площадь
треугольника, если две его стороны равны 1
и ![]() , а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т:
, а медиана третьей стороны
равна 2. (Указание – достроить до параллелограмма). О т в е
т: ![]() .
.
Теорема
(Свойство медиан треугольника)
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
 Дано: ABC, AA1, BB1, CC1
— медианы
Дано: ABC, AA1, BB1, CC1
— медианы
Доказать:
![]()
![]()
Доказательство:
 1) Пусть M —
середина отрезка AO, N — середина
BO
1) Пусть M —
середина отрезка AO, N — середина
BO
(то есть AM=OM, BN=ON).
2) Соединим точки M, N, A1 и B1 отрезками.
Тогда MN — средняя линия треугольника AOB и
![]()
3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.
Следовательно, A1B1 — средняя линия треугольника ABC и
![]()
4) Имеем:
![]()
Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).
По свойству диагоналей параллелограмма
![]()
Таким образом,
![]()
![]()
![]()
из чего следует, что
![]()
5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.
Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.
Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.
Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:
![]()
Что и требовалось доказать.

шағым қалдыра аласыз




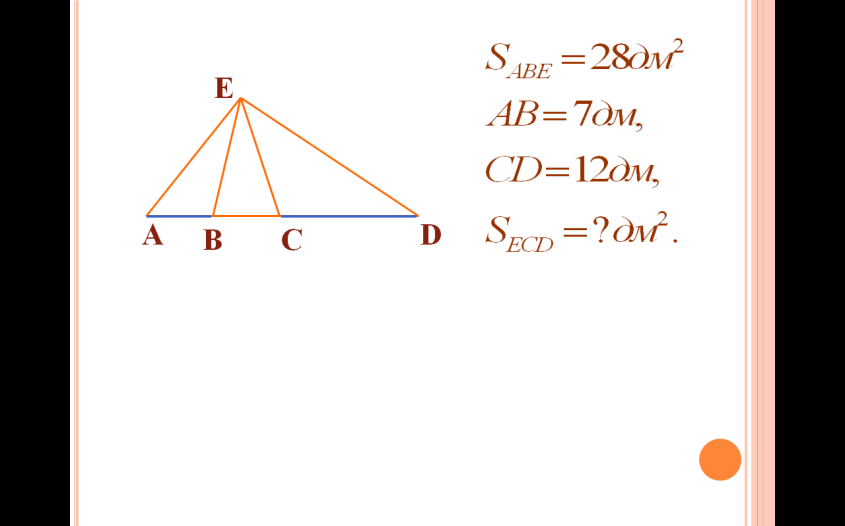
 V.
V.












