|
Тема урока |
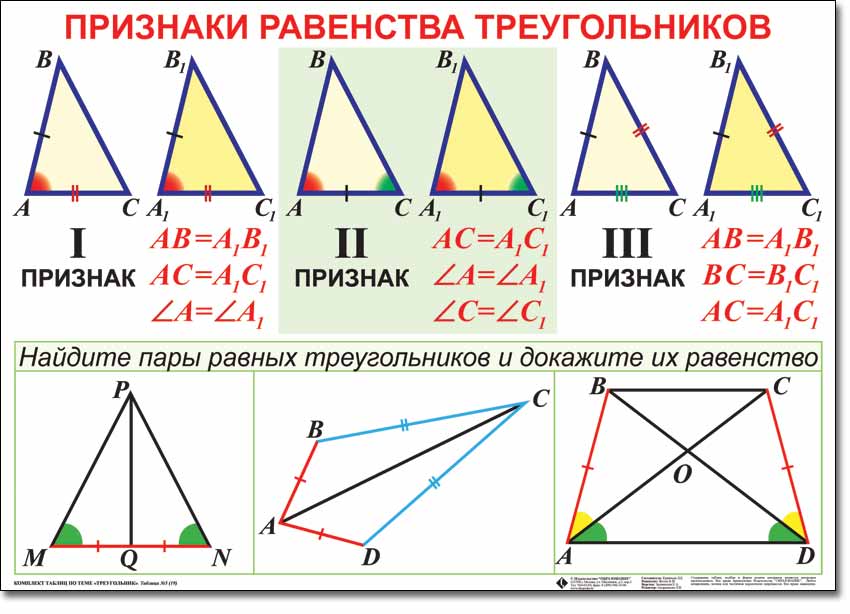
Признаки равенства треугольников |
|
Цели обучения, достигаемые на этом уроке |
7.1.1.21 знать и доказывать признаки равенства треугольников; 7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на доказательство |
|
Цель урока |
Все учащиеся смогут распознавать признаки равенства треугольников Большинство учащихся смогут применять признаки равенства треугольников при решении задач на вычисление и на доказательство Некоторые учащиеся смогут доказывать признаки равенства треугольников |
Ход урока
|
Запланированные этапы урока |
Виды упражнений, запланированных на урок: |
Ресурсы |
|
Начало урока |
Психологический настрой «Все в твоих руках» Притча «Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: «Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая? А сам думает: «Скажет живая - я ее умертвлю, скажет мертвая-выпущу». Мудрец подумав, ответил: «Все в твоих руках». А означает, что результат сегодняшнего урока в ваших руках. Исторический факт Для казахстанцев новый дворец-своеобразный символ межнациональной и межконфессиональной стабильности, дружбы народов, которая является важнейшим достоянием страны. Четыре стороны пирамиды олицетворяют четыре стихии: землю, воду, воздух и огонь. Внутренние проекции символизируют свет, тепло и жизнь. Для закрепления пирамиды Астаны нужно установить 4 металлические трубы. Один конец каждой трубы должен крепиться на высоте 62 м, а другой конец с вершиной основания со сторонами 62 м. Данная пирамида имеет форму треугольника. Актуализация опорных знаний: Стратегия «Внешний и внутренний круг» Ученики создают внешний и внутренний круг, двигаясь по часовой стрелке, отвечают на вопросы Объясните, какая фигура называется треугольником. Что такое периметр треугольника? Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Какой треугольник называется равнобедренным? Какой треугольник называется равносторонним? Данная стратегия позволит определить скорость мышления у учащихся Формативное оценивание: Уточняющий вопрос Деление на группы «Атомы и молекулы» Данная стратегия направлена на развитие коммуникативных навыков |
слайд
Слайд |
|
Середина урока |
Проблемный вопрос: Достаточно ли иметь три пары соответственных элементов, для того, чтобы сделать вывод о равенстве данных треугольников. -Каким способом мы сможем ответить на свой вопрос? Попробуем доказать. Стратегия «Составление кластера» Работа с учебником для самостоятельного изучения нового материала, составляют кластер. 1 группа: Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2 группа: Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 3 группа: Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
После того, как группа составит кластер, работы выващиваются на доску, и идет защита своей работы. Данная стратегия направлена на критическое мышление детей. Дескрипторы: Учащиеся понимают задание Учащиеся могут с помощью символов кратко записать теорему Делают вывод Заслушиваются и анализируются ответы групп. Оценивание: «Две звезды и одно пожелание». (Оценивание 1-2-3-1). Способы дифференциации «Темп» Задание 1. Равны ли треугольники, если АВ=DE? AC=EF и угол A равен углу Е.
А В D E Дескриптор: Определяет равенство треугольников. Задание 2. ВН перпендикулярна АС и АН=СН=2 см, АВ=5 см. Найдите ВС.
А Н С Дескриптор: Находит сторону треугольника Задание 3. Три деревни А,В,С расположены так, что деревня В находится в 15 км к югу от А, а деревня С-в 7 км к северо-востоку от В. Три другие деревни M, N и K расположены так, что деревня N находится в 15 км к западу от М, а деревня К-в 7 км к северо-западу от М. Сравните расстояние между деревнями А, С и N,K. Дескриптор: Сравнивает расстояние между сторонами. Оценивание: проверяют самостоятельно по ответам на слайде. Этап первичного закрепления умений и навыков. Стратегия «Джигсо» Способ дифференциации «Темп» 1 группа:
А)На рисунке
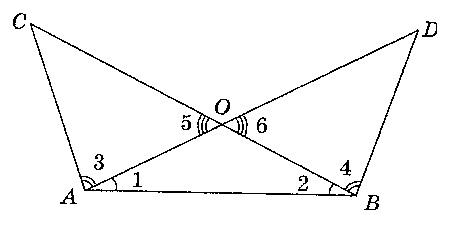
Дескрипторы: Учащейся доказывает равенство треугольников Учащейся доказывает равенство углов Учащейся доказывает равенство сторон Б)На сторонах треугольника CAD отмечены точки В и Е так, что точка В лежит на отрезке АС, а точка Е-на отрезке AD. AC=AD и AB=AE. А)Постройте чертеж по условию задачи В)Докажите, что ∠CBD=∠DEC. Дескрипторы: Выполняет построение чертежа по условию задачи Применяет признаки равенства треугольников Доказывает равенство углов 2 группа: Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. А)докажите, что треугольники АВС и EBD равны
Б)найдите углы А и С треугольника АВС,
если в треугольнике BDE
∠D=47 Дескрипторы: Выполняет построение чертежа по условию задачи Применяет признаки равенства треугольников Доказывает равенство треугольников Находит градусные меры углов 3 группа:
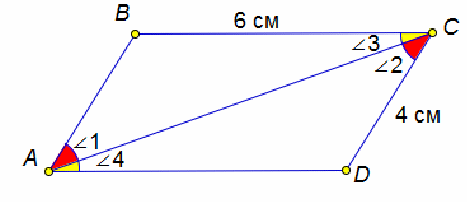
На рисунке ∠1=∠2,
∠3=∠4. Найдите периметр четырёхугольника ABCD.
Дескрипторы: Применяет признаки равенства треугольников Доказывает равенство треугольников Доказывает равенство сторон Находит периметр фигуры Данная стратегия развивает умение анализировать задание совместно с другими, вести исследовательскую работу в группе, доступно передавать информацию другому человеку. Оценивание: «Светофор» Физминутка
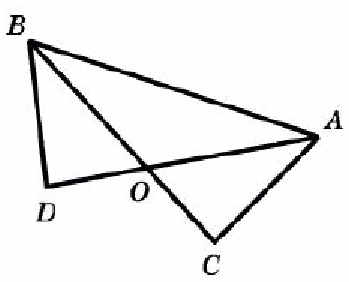
Способ дифференциации «Заключение» Решите задачу разными способами: На рисунке изображены два равных треугольника: АВС=ВАD. Докажите, что АОС= ВОD.
Дескрипторы: Учащиеся понимают условие задачи Записывают краткое условие задачи Применяют признаки равенства треугольников при решении задач Оценивание: «Уточняющий вопрос» |
Учебник Геометрия 7 класс (В.А.Смирнов, Е.А.Туяков) А3, маркеры
\
Сборник формативного оценивания. Слайд /library/nestandartnij_urok_matematiki_v_7_klasse_priznaki__181341.html |
|
Конец урока |
Стратегия «Да-Нетка» . Игровое поле – прямоугольник с числами от 1 до 8. Раздается каждому ученику. Если ребенок согласен с утверждением, то квадратик игрового поля с номером утверждения остается незакрашенным. Если же считает, что ложное, то закрашивает (ошибку зачеркнуть). В результате выполнения всех 8 заданий получается картинка. 1.Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. 2. В равнобедренном треугольнике две стороны равны. 3. В равнобедренном треугольнике все углы равны. 4. В равностороннем треугольнике боковые стороны равны. 5. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. 6. В любом треугольнике все стороны равны. 7. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 8. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Формативное оценивание: плюс-минус Рефлексия Паутина: ученики встают в круг и по очереди получают клубок с нитью, и отвечают на вопросы :Теперь я могу…? Было трудно…? У меня получилось…? Было интересно…? После передают клубок, а нить оставляют себе и окончанию последнего ученика распутывают клубок, в обратном порядке выражая тем самым, пожелания к следующему уроку. Образуется паутина обратной связи с учителем |
Карточки, клубок ниток |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Үшбұрыштардың теңдік белгілері, 7 сынып
Үшбұрыштардың теңдік белгілері, 7 сынып
|
Тема урока |
Признаки равенства треугольников |
|
Цели обучения, достигаемые на этом уроке |
7.1.1.21 знать и доказывать признаки равенства треугольников; 7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на доказательство |
|
Цель урока |
Все учащиеся смогут распознавать признаки равенства треугольников Большинство учащихся смогут применять признаки равенства треугольников при решении задач на вычисление и на доказательство Некоторые учащиеся смогут доказывать признаки равенства треугольников |
Ход урока
|
Запланированные этапы урока |
Виды упражнений, запланированных на урок: |
Ресурсы |
|
Начало урока |
Психологический настрой «Все в твоих руках» Притча «Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: «Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая? А сам думает: «Скажет живая - я ее умертвлю, скажет мертвая-выпущу». Мудрец подумав, ответил: «Все в твоих руках». А означает, что результат сегодняшнего урока в ваших руках. Исторический факт Для казахстанцев новый дворец-своеобразный символ межнациональной и межконфессиональной стабильности, дружбы народов, которая является важнейшим достоянием страны. Четыре стороны пирамиды олицетворяют четыре стихии: землю, воду, воздух и огонь. Внутренние проекции символизируют свет, тепло и жизнь. Для закрепления пирамиды Астаны нужно установить 4 металлические трубы. Один конец каждой трубы должен крепиться на высоте 62 м, а другой конец с вершиной основания со сторонами 62 м. Данная пирамида имеет форму треугольника. Актуализация опорных знаний: Стратегия «Внешний и внутренний круг» Ученики создают внешний и внутренний круг, двигаясь по часовой стрелке, отвечают на вопросы Объясните, какая фигура называется треугольником. Что такое периметр треугольника? Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Какой треугольник называется равнобедренным? Какой треугольник называется равносторонним? Данная стратегия позволит определить скорость мышления у учащихся Формативное оценивание: Уточняющий вопрос Деление на группы «Атомы и молекулы» Данная стратегия направлена на развитие коммуникативных навыков |
слайд
Слайд |
|
Середина урока |
Проблемный вопрос: Достаточно ли иметь три пары соответственных элементов, для того, чтобы сделать вывод о равенстве данных треугольников. -Каким способом мы сможем ответить на свой вопрос? Попробуем доказать. Стратегия «Составление кластера» Работа с учебником для самостоятельного изучения нового материала, составляют кластер. 1 группа: Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2 группа: Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 3 группа: Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
После того, как группа составит кластер, работы выващиваются на доску, и идет защита своей работы. Данная стратегия направлена на критическое мышление детей. Дескрипторы: Учащиеся понимают задание Учащиеся могут с помощью символов кратко записать теорему Делают вывод Заслушиваются и анализируются ответы групп. Оценивание: «Две звезды и одно пожелание». (Оценивание 1-2-3-1). Способы дифференциации «Темп» Задание 1. Равны ли треугольники, если АВ=DE? AC=EF и угол A равен углу Е.
А В D E Дескриптор: Определяет равенство треугольников. Задание 2. ВН перпендикулярна АС и АН=СН=2 см, АВ=5 см. Найдите ВС.
А Н С Дескриптор: Находит сторону треугольника Задание 3. Три деревни А,В,С расположены так, что деревня В находится в 15 км к югу от А, а деревня С-в 7 км к северо-востоку от В. Три другие деревни M, N и K расположены так, что деревня N находится в 15 км к западу от М, а деревня К-в 7 км к северо-западу от М. Сравните расстояние между деревнями А, С и N,K. Дескриптор: Сравнивает расстояние между сторонами. Оценивание: проверяют самостоятельно по ответам на слайде. Этап первичного закрепления умений и навыков. Стратегия «Джигсо» Способ дифференциации «Темп» 1 группа:
А)На рисунке
Дескрипторы: Учащейся доказывает равенство треугольников Учащейся доказывает равенство углов Учащейся доказывает равенство сторон Б)На сторонах треугольника CAD отмечены точки В и Е так, что точка В лежит на отрезке АС, а точка Е-на отрезке AD. AC=AD и AB=AE. А)Постройте чертеж по условию задачи В)Докажите, что ∠CBD=∠DEC. Дескрипторы: Выполняет построение чертежа по условию задачи Применяет признаки равенства треугольников Доказывает равенство углов 2 группа: Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. А)докажите, что треугольники АВС и EBD равны
Б)найдите углы А и С треугольника АВС,
если в треугольнике BDE
∠D=47 Дескрипторы: Выполняет построение чертежа по условию задачи Применяет признаки равенства треугольников Доказывает равенство треугольников Находит градусные меры углов 3 группа:
На рисунке ∠1=∠2,
∠3=∠4. Найдите периметр четырёхугольника ABCD.
Дескрипторы: Применяет признаки равенства треугольников Доказывает равенство треугольников Доказывает равенство сторон Находит периметр фигуры Данная стратегия развивает умение анализировать задание совместно с другими, вести исследовательскую работу в группе, доступно передавать информацию другому человеку. Оценивание: «Светофор» Физминутка
Способ дифференциации «Заключение» Решите задачу разными способами: На рисунке изображены два равных треугольника: АВС=ВАD. Докажите, что АОС= ВОD.
Дескрипторы: Учащиеся понимают условие задачи Записывают краткое условие задачи Применяют признаки равенства треугольников при решении задач Оценивание: «Уточняющий вопрос» |
Учебник Геометрия 7 класс (В.А.Смирнов, Е.А.Туяков) А3, маркеры
\
Сборник формативного оценивания. Слайд /library/nestandartnij_urok_matematiki_v_7_klasse_priznaki__181341.html |
|
Конец урока |
Стратегия «Да-Нетка» . Игровое поле – прямоугольник с числами от 1 до 8. Раздается каждому ученику. Если ребенок согласен с утверждением, то квадратик игрового поля с номером утверждения остается незакрашенным. Если же считает, что ложное, то закрашивает (ошибку зачеркнуть). В результате выполнения всех 8 заданий получается картинка. 1.Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. 2. В равнобедренном треугольнике две стороны равны. 3. В равнобедренном треугольнике все углы равны. 4. В равностороннем треугольнике боковые стороны равны. 5. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. 6. В любом треугольнике все стороны равны. 7. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 8. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Формативное оценивание: плюс-минус Рефлексия Паутина: ученики встают в круг и по очереди получают клубок с нитью, и отвечают на вопросы :Теперь я могу…? Было трудно…? У меня получилось…? Было интересно…? После передают клубок, а нить оставляют себе и окончанию последнего ученика распутывают клубок, в обратном порядке выражая тем самым, пожелания к следующему уроку. Образуется паутина обратной связи с учителем |
Карточки, клубок ниток |

шағым қалдыра аласыз



 С
С  В
В
 ∠
∠