
Дисциплина: Математика
Курс 1. Семестр 1
Преподаватель:
Дата:
№40
Тема: «Вогнутость и выпуклость графика функции. Точки перегиба»
Здравствуйте уважаемые студенты
Мы с вами рассмотрелир найбольшее и найменьшее значение функции, сегодня продолжаем эту тему: рассмотрим вогнутость и выпуклость графика функции и точки перегиба.
Опр.1. Точки перегиба График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
Опр. 2. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Рассмотрим график
функции ![]() , которая непрерывна на всей числовой прямой:
, которая непрерывна на всей числовой прямой:

Его легко построить с помощью геометрических
преобразований,
и, наверное, многие читатели в курсе, как он получен
из кубической параболы.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции
является выпуклым на некотором интервале, если он
расположен не ниже любой хорды данного интервала. Подопытная
линия выпукла на ![]() , и, очевидно, что здесь любая часть графика
расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных
отрезка.
, и, очевидно, что здесь любая часть графика
расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных
отрезка.
График функции
являются вогнутым на интервале, если он
расположен не выше любой хорды этого интервала. В
рассматриваемом примере пациент вогнут на
промежутке ![]() . Пара коричневых отрезков убедительно
демонстрирует, что тут и любой кусок графика расположен ПОД
своей хордой.
. Пара коричневых отрезков убедительно
демонстрирует, что тут и любой кусок графика расположен ПОД
своей хордой.
Точка графика, в которой он меняет выпуклость на
вогнутость или вогнутость на выпуклость,
называется точкой
перегиба. У
нас она в единственном экземпляре (первый случай), причём, на
практике под точкой перегиба можно подразумевать как зелёную
точку ![]() , принадлежащую самой линии, так и «иксовое»
значение
, принадлежащую самой линии, так и «иксовое»
значение ![]() .
.
Второй подход к определению выпуклости/вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не ниже любой касательной на этом интервале.
Гипербола ![]() вогнута на
интервале
вогнута на
интервале ![]() и выпукла
на
и выпукла
на ![]() :
:

При переходе через начало координат вогнутость меняется на
выпуклость, однако точку ![]() НЕ
СЧИТАЮТ точкой перегиба, так
как функция
НЕ
СЧИТАЮТ точкой перегиба, так
как функция ![]() не
определена в ней. Более строгие утверждения и теоремы
по теме можно найти в учебнике, а мы переходим к насыщенной практической
части:
не
определена в ней. Более строгие утверждения и теоремы
по теме можно найти в учебнике, а мы переходим к насыщенной практической
части:
Как найти интервалы выпуклости, интервалы
вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на экстремум.
Выпуклость/вогнутость графика характеризует вторая производная функции.
Пусть функция ![]() дважды дифференцируема на некотором
интервале. Тогда:
дважды дифференцируема на некотором
интервале. Тогда:
– если вторая
производная ![]() на интервале, то график
функции
на интервале, то график
функции ![]() является выпуклым на данном
интервале;
является выпуклым на данном
интервале;
– если вторая
производная ![]() на интервале, то график
функции
на интервале, то график
функции ![]() является вогнутым на данном
интервале.
является вогнутым на данном
интервале.
На счёт знаков второй производной по просторам
учебных заведений гуляет доисторическая ассоциация: «–» показывает,
что «в график функции нельзя налить воду» (выпуклость),
а «+» – «даёт такую возможность» (вогнутость).
Необходимое условие перегиба
Если в точке ![]() есть перегиб графика
функции
есть перегиб графика
функции ![]() ,
то:
,
то:
![]() либо значения
либо значения ![]() не
существует (разберём,
читайте!).
не
существует (разберём,
читайте!).
Данная фраза подразумевает, что
функция ![]() непрерывна в точке
непрерывна в точке ![]() и в
случае
и в
случае ![]() – дважды дифференцируема в некоторой
её окрестности.
– дважды дифференцируема в некоторой
её окрестности.
Необходимость условия говорит о том, что обратное
справедливо не всегда. То есть из
равенства ![]() (либо небытия
значения
(либо небытия
значения ![]() ) ещё не
следует существования перегиба графика
функции
) ещё не
следует существования перегиба графика
функции ![]() в точке
в точке ![]() . Но и в той, и в другой
ситуации
. Но и в той, и в другой
ситуации ![]() называют критической точкой второй
производной.
называют критической точкой второй
производной.
Достаточное условие перегиба
Если вторая
производная ![]() при переходе через
точку
при переходе через
точку ![]() меняет знак, то в данной точке
существует перегиб графика функции
меняет знак, то в данной точке
существует перегиб графика функции ![]()
Точек перегиба (встретился уже пример) может не
быть вовсе, и в этом смысле показательны некоторые элементарные
образцы. Проанализируем вторую производную
функции ![]() :
: ![]()
Получена положительная функция-константа,
то есть для любого значения
«икс» ![]() .
Факты, лежащие на поверхности:
парабола
.
Факты, лежащие на поверхности:
парабола ![]() вогнута на всей области
определения,
точки перегиба отсутствуют. Легко заметить, что отрицательный
коэффициент при
вогнута на всей области
определения,
точки перегиба отсутствуют. Легко заметить, что отрицательный
коэффициент при ![]() «переворачивает» параболу и делает её
выпуклой (о чём нам сообщит вторая производная – отрицательная
функция-константа).
«переворачивает» параболу и делает её
выпуклой (о чём нам сообщит вторая производная – отрицательная
функция-константа).
Экспоненциальная
функция ![]() также вогнута
на
также вогнута
на ![]() :
:
![]()
![]() для любого значения «икс». Точек перегиба у
графика
для любого значения «икс». Точек перегиба у
графика ![]() , разумеется, нет.
, разумеется, нет.
Исследуем на выпуклость/вогнутость график
логарифмической функции ![]() :
:
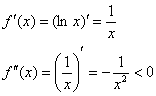
Таким образом, ветка логарифма является выпуклой
на интервале ![]() . Вторая
производная
. Вторая
производная ![]() определена и на
промежутке
определена и на
промежутке ![]() , но рассматривать
его НЕЛЬЗЯ, поскольку данный интервал не входит
в область
определения функции
, но рассматривать
его НЕЛЬЗЯ, поскольку данный интервал не входит
в область
определения функции ![]() .
Требование очевидно – коль скоро там нет графика логарифма, то ни о
какой выпуклости/вогнутости/перегибах речи, естественно, не
заходит.
.
Требование очевидно – коль скоро там нет графика логарифма, то ни о
какой выпуклости/вогнутости/перегибах речи, естественно, не
заходит.
Как видите, всё действительно очень напоминает
историю с возрастанием, убыванием и
экстремумами функции.
Похож и сам алгоритм исследования графика
функции ![]() на выпуклость, вогнутость и наличие
перегибов:
на выпуклость, вогнутость и наличие
перегибов:
1) На первом шаге
находим область определения
функции ![]() и точки
разрыва.
и точки
разрыва.
2)
Разыскиваем критические значения. Для этого берём вторую
производную ![]() и решаем
уравнение
и решаем
уравнение ![]() . Точки, в которых не существует 2-й производной,
но которые входят в область определения самой функции – тоже
считаются критическими!
. Точки, в которых не существует 2-й производной,
но которые входят в область определения самой функции – тоже
считаются критическими!
3) Отмечаем на числовой прямой все найденные точки разрыва и критические точки (ни тех, ни других может не оказаться – тогда чертить ничего не надо (как и в слишком простом случае), достаточно ограничиться письменным комментарием).
Методом
интервалов определяем
знаки ![]() на полученных интервалах. Как только что
пояснялось, рассматривать следует только те промежутки, которые входят
в
область определения функции
на полученных интервалах. Как только что
пояснялось, рассматривать следует только те промежутки, которые входят
в
область определения функции ![]() . Делаем выводы о выпуклости/вогнутости и точках
перегиба графика функции
. Делаем выводы о выпуклости/вогнутости и точках
перегиба графика функции ![]() . Даём ответ.
. Даём ответ.
Попытайтесь устно применить алгоритм для
функций ![]() . Во втором случае, кстати, пример, когда в
критической точке не существует перегиба графика. Впрочем, начнём с
ненамного более сложных заданий:
. Во втором случае, кстати, пример, когда в
критической точке не существует перегиба графика. Впрочем, начнём с
ненамного более сложных заданий:
Пример
1Найти интервалы выпуклости, вогнутости и точки
перегиба графика
![]()
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Очень
хорошо.
2)
Найдём вторую производную. Можно предварительно выполнить
возведение в куб, но значительно выгоднее
использовать правило дифференцирование сложной
функции:
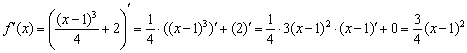
Заметьте, что ![]() , а
значит, функция является неубывающей. Хоть это и не относится к заданию, но на
такие факты всегда желательно обращать внимание.
, а
значит, функция является неубывающей. Хоть это и не относится к заданию, но на
такие факты всегда желательно обращать внимание.
![]()
Найдём критические точки второй
производной: 
![]() – критическая
точка
– критическая
точка
3)
Проверим выполнение достаточного условия перегиба. Определим знаки
второй производной на полученных
интервалах ![]() .
.
Внимание! Сейчас работаем со второй производной (а не с функцией!)
Используем метод интервалов. Повторим его ещё разок.
Выберем наиболее выгодную
точку ![]() интервала
интервала ![]() и вычислим в ней значение второй
производной:
и вычислим в ней значение второй
производной:
![]() ,
следовательно,
,
следовательно, ![]() в любой точке
интервала
в любой точке
интервала ![]() .
.
Из
интервала ![]() возьмём
значение
возьмём
значение ![]() и проведём аналогичное
действие:
и проведём аналогичное
действие:
![]() , а значит,
, а значит, ![]() и на всём
интервале
и на всём
интервале ![]() .
.
В
результате получены следующие знаки второй
производной:

Таким образом, график САМОЙ
ФУНКЦИИ ![]() является выпуклым на
интервале
является выпуклым на
интервале ![]() и вогнутым
на
и вогнутым
на ![]() . При переходе
через
. При переходе
через ![]() вторая производная меняет знак, поэтому в
данной точке существует перегиб графика.
вторая производная меняет знак, поэтому в
данной точке существует перегиб графика.
Найдём
ординату: ![]()
Ответ: график функции выпукл на
интервале ![]() и вогнут
на
и вогнут
на ![]() , в точке
, в точке ![]() существует перегиб
графика.
существует перегиб
графика.
Как
вариант, пойдёт и запись «…в
точке ![]() существует перегиб
графика».
существует перегиб
графика».
Пример 2
Найти интервалы выпуклости, вогнутости и точки
перегиба графика
![]()
Решение:
1) Функция определена и непрерывна
на ![]() .
.
2)
Найдём критические точки второй
производной:
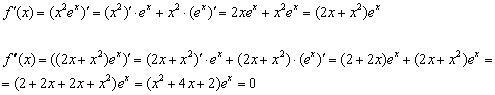
Так
как ![]() , то корни могут появиться только
из решения квадратного
уравнения:
, то корни могут появиться только
из решения квадратного
уравнения:
![]()
Дискриминант положителен, и на подходе две
критические точки:
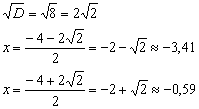
Как и в ситуации с экстремумами функции, критические точки рациональнее не нумеровать подстрочными индексами. Ну а то, что они получились с радикалами – обычное дело.
3)
Определим знаки второй производной. Можно использовать
стандартный метод
интервалов, но здесь ![]() , и учитывая,
что
, и учитывая,
что ![]() – парабола, ветви которой направлены вверх,
получаем:
– парабола, ветви которой направлены вверх,
получаем:

Таким образом, график функции ![]() является выпуклым на
интервале
является выпуклым на
интервале ![]() и вогнутым
на
и вогнутым
на ![]() . В обеих критических точках существуют перегибы
графика (так как 2-я производная при переходе через них меняет
знак).
. В обеих критических точках существуют перегибы
графика (так как 2-я производная при переходе через них меняет
знак).
Найдём ординаты данных
точек:

(в целях вычислений подставлять, конечно,
удобнее приближенные значения)
Ответ: график функции выпуклый на
интервале ![]() и вогнутый
на
и вогнутый
на ![]() . В точках
. В точках ![]() существуют перегибы
графика.
существуют перегибы
графика.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Вогнутость и выпуклость графика функции. Точки перегиба
Вогнутость и выпуклость графика функции. Точки перегиба
Дисциплина: Математика
Курс 1. Семестр 1
Преподаватель:
Дата:
№40
Тема: «Вогнутость и выпуклость графика функции. Точки перегиба»
Здравствуйте уважаемые студенты
Мы с вами рассмотрелир найбольшее и найменьшее значение функции, сегодня продолжаем эту тему: рассмотрим вогнутость и выпуклость графика функции и точки перегиба.
Опр.1. Точки перегиба График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
Опр. 2. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Рассмотрим график
функции ![]() , которая непрерывна на всей числовой прямой:
, которая непрерывна на всей числовой прямой:

Его легко построить с помощью геометрических
преобразований,
и, наверное, многие читатели в курсе, как он получен
из кубической параболы.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции
является выпуклым на некотором интервале, если он
расположен не ниже любой хорды данного интервала. Подопытная
линия выпукла на ![]() , и, очевидно, что здесь любая часть графика
расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных
отрезка.
, и, очевидно, что здесь любая часть графика
расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных
отрезка.
График функции
являются вогнутым на интервале, если он
расположен не выше любой хорды этого интервала. В
рассматриваемом примере пациент вогнут на
промежутке ![]() . Пара коричневых отрезков убедительно
демонстрирует, что тут и любой кусок графика расположен ПОД
своей хордой.
. Пара коричневых отрезков убедительно
демонстрирует, что тут и любой кусок графика расположен ПОД
своей хордой.
Точка графика, в которой он меняет выпуклость на
вогнутость или вогнутость на выпуклость,
называется точкой
перегиба. У
нас она в единственном экземпляре (первый случай), причём, на
практике под точкой перегиба можно подразумевать как зелёную
точку ![]() , принадлежащую самой линии, так и «иксовое»
значение
, принадлежащую самой линии, так и «иксовое»
значение ![]() .
.
Второй подход к определению выпуклости/вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не ниже любой касательной на этом интервале.
Гипербола ![]() вогнута на
интервале
вогнута на
интервале ![]() и выпукла
на
и выпукла
на ![]() :
:

При переходе через начало координат вогнутость меняется на
выпуклость, однако точку ![]() НЕ
СЧИТАЮТ точкой перегиба, так
как функция
НЕ
СЧИТАЮТ точкой перегиба, так
как функция ![]() не
определена в ней. Более строгие утверждения и теоремы
по теме можно найти в учебнике, а мы переходим к насыщенной практической
части:
не
определена в ней. Более строгие утверждения и теоремы
по теме можно найти в учебнике, а мы переходим к насыщенной практической
части:
Как найти интервалы выпуклости, интервалы
вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на экстремум.
Выпуклость/вогнутость графика характеризует вторая производная функции.
Пусть функция ![]() дважды дифференцируема на некотором
интервале. Тогда:
дважды дифференцируема на некотором
интервале. Тогда:
– если вторая
производная ![]() на интервале, то график
функции
на интервале, то график
функции ![]() является выпуклым на данном
интервале;
является выпуклым на данном
интервале;
– если вторая
производная ![]() на интервале, то график
функции
на интервале, то график
функции ![]() является вогнутым на данном
интервале.
является вогнутым на данном
интервале.
На счёт знаков второй производной по просторам
учебных заведений гуляет доисторическая ассоциация: «–» показывает,
что «в график функции нельзя налить воду» (выпуклость),
а «+» – «даёт такую возможность» (вогнутость).
Необходимое условие перегиба
Если в точке ![]() есть перегиб графика
функции
есть перегиб графика
функции ![]() ,
то:
,
то:
![]() либо значения
либо значения ![]() не
существует (разберём,
читайте!).
не
существует (разберём,
читайте!).
Данная фраза подразумевает, что
функция ![]() непрерывна в точке
непрерывна в точке ![]() и в
случае
и в
случае ![]() – дважды дифференцируема в некоторой
её окрестности.
– дважды дифференцируема в некоторой
её окрестности.
Необходимость условия говорит о том, что обратное
справедливо не всегда. То есть из
равенства ![]() (либо небытия
значения
(либо небытия
значения ![]() ) ещё не
следует существования перегиба графика
функции
) ещё не
следует существования перегиба графика
функции ![]() в точке
в точке ![]() . Но и в той, и в другой
ситуации
. Но и в той, и в другой
ситуации ![]() называют критической точкой второй
производной.
называют критической точкой второй
производной.
Достаточное условие перегиба
Если вторая
производная ![]() при переходе через
точку
при переходе через
точку ![]() меняет знак, то в данной точке
существует перегиб графика функции
меняет знак, то в данной точке
существует перегиб графика функции ![]()
Точек перегиба (встретился уже пример) может не
быть вовсе, и в этом смысле показательны некоторые элементарные
образцы. Проанализируем вторую производную
функции ![]() :
: ![]()
Получена положительная функция-константа,
то есть для любого значения
«икс» ![]() .
Факты, лежащие на поверхности:
парабола
.
Факты, лежащие на поверхности:
парабола ![]() вогнута на всей области
определения,
точки перегиба отсутствуют. Легко заметить, что отрицательный
коэффициент при
вогнута на всей области
определения,
точки перегиба отсутствуют. Легко заметить, что отрицательный
коэффициент при ![]() «переворачивает» параболу и делает её
выпуклой (о чём нам сообщит вторая производная – отрицательная
функция-константа).
«переворачивает» параболу и делает её
выпуклой (о чём нам сообщит вторая производная – отрицательная
функция-константа).
Экспоненциальная
функция ![]() также вогнута
на
также вогнута
на ![]() :
:
![]()
![]() для любого значения «икс». Точек перегиба у
графика
для любого значения «икс». Точек перегиба у
графика ![]() , разумеется, нет.
, разумеется, нет.
Исследуем на выпуклость/вогнутость график
логарифмической функции ![]() :
:
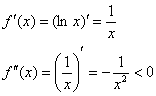
Таким образом, ветка логарифма является выпуклой
на интервале ![]() . Вторая
производная
. Вторая
производная ![]() определена и на
промежутке
определена и на
промежутке ![]() , но рассматривать
его НЕЛЬЗЯ, поскольку данный интервал не входит
в область
определения функции
, но рассматривать
его НЕЛЬЗЯ, поскольку данный интервал не входит
в область
определения функции ![]() .
Требование очевидно – коль скоро там нет графика логарифма, то ни о
какой выпуклости/вогнутости/перегибах речи, естественно, не
заходит.
.
Требование очевидно – коль скоро там нет графика логарифма, то ни о
какой выпуклости/вогнутости/перегибах речи, естественно, не
заходит.
Как видите, всё действительно очень напоминает
историю с возрастанием, убыванием и
экстремумами функции.
Похож и сам алгоритм исследования графика
функции ![]() на выпуклость, вогнутость и наличие
перегибов:
на выпуклость, вогнутость и наличие
перегибов:
1) На первом шаге
находим область определения
функции ![]() и точки
разрыва.
и точки
разрыва.
2)
Разыскиваем критические значения. Для этого берём вторую
производную ![]() и решаем
уравнение
и решаем
уравнение ![]() . Точки, в которых не существует 2-й производной,
но которые входят в область определения самой функции – тоже
считаются критическими!
. Точки, в которых не существует 2-й производной,
но которые входят в область определения самой функции – тоже
считаются критическими!
3) Отмечаем на числовой прямой все найденные точки разрыва и критические точки (ни тех, ни других может не оказаться – тогда чертить ничего не надо (как и в слишком простом случае), достаточно ограничиться письменным комментарием).
Методом
интервалов определяем
знаки ![]() на полученных интервалах. Как только что
пояснялось, рассматривать следует только те промежутки, которые входят
в
область определения функции
на полученных интервалах. Как только что
пояснялось, рассматривать следует только те промежутки, которые входят
в
область определения функции ![]() . Делаем выводы о выпуклости/вогнутости и точках
перегиба графика функции
. Делаем выводы о выпуклости/вогнутости и точках
перегиба графика функции ![]() . Даём ответ.
. Даём ответ.
Попытайтесь устно применить алгоритм для
функций ![]() . Во втором случае, кстати, пример, когда в
критической точке не существует перегиба графика. Впрочем, начнём с
ненамного более сложных заданий:
. Во втором случае, кстати, пример, когда в
критической точке не существует перегиба графика. Впрочем, начнём с
ненамного более сложных заданий:
Пример
1Найти интервалы выпуклости, вогнутости и точки
перегиба графика
![]()
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Очень
хорошо.
2)
Найдём вторую производную. Можно предварительно выполнить
возведение в куб, но значительно выгоднее
использовать правило дифференцирование сложной
функции:
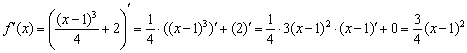
Заметьте, что ![]() , а
значит, функция является неубывающей. Хоть это и не относится к заданию, но на
такие факты всегда желательно обращать внимание.
, а
значит, функция является неубывающей. Хоть это и не относится к заданию, но на
такие факты всегда желательно обращать внимание.
![]()
Найдём критические точки второй
производной: 
![]() – критическая
точка
– критическая
точка
3)
Проверим выполнение достаточного условия перегиба. Определим знаки
второй производной на полученных
интервалах ![]() .
.
Внимание! Сейчас работаем со второй производной (а не с функцией!)
Используем метод интервалов. Повторим его ещё разок.
Выберем наиболее выгодную
точку ![]() интервала
интервала ![]() и вычислим в ней значение второй
производной:
и вычислим в ней значение второй
производной:
![]() ,
следовательно,
,
следовательно, ![]() в любой точке
интервала
в любой точке
интервала ![]() .
.
Из
интервала ![]() возьмём
значение
возьмём
значение ![]() и проведём аналогичное
действие:
и проведём аналогичное
действие:
![]() , а значит,
, а значит, ![]() и на всём
интервале
и на всём
интервале ![]() .
.
В
результате получены следующие знаки второй
производной:

Таким образом, график САМОЙ
ФУНКЦИИ ![]() является выпуклым на
интервале
является выпуклым на
интервале ![]() и вогнутым
на
и вогнутым
на ![]() . При переходе
через
. При переходе
через ![]() вторая производная меняет знак, поэтому в
данной точке существует перегиб графика.
вторая производная меняет знак, поэтому в
данной точке существует перегиб графика.
Найдём
ординату: ![]()
Ответ: график функции выпукл на
интервале ![]() и вогнут
на
и вогнут
на ![]() , в точке
, в точке ![]() существует перегиб
графика.
существует перегиб
графика.
Как
вариант, пойдёт и запись «…в
точке ![]() существует перегиб
графика».
существует перегиб
графика».
Пример 2
Найти интервалы выпуклости, вогнутости и точки
перегиба графика
![]()
Решение:
1) Функция определена и непрерывна
на ![]() .
.
2)
Найдём критические точки второй
производной:
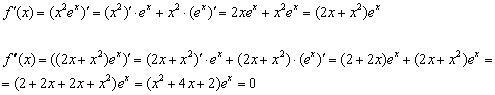
Так
как ![]() , то корни могут появиться только
из решения квадратного
уравнения:
, то корни могут появиться только
из решения квадратного
уравнения:
![]()
Дискриминант положителен, и на подходе две
критические точки:
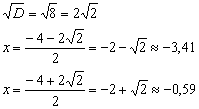
Как и в ситуации с экстремумами функции, критические точки рациональнее не нумеровать подстрочными индексами. Ну а то, что они получились с радикалами – обычное дело.
3)
Определим знаки второй производной. Можно использовать
стандартный метод
интервалов, но здесь ![]() , и учитывая,
что
, и учитывая,
что ![]() – парабола, ветви которой направлены вверх,
получаем:
– парабола, ветви которой направлены вверх,
получаем:

Таким образом, график функции ![]() является выпуклым на
интервале
является выпуклым на
интервале ![]() и вогнутым
на
и вогнутым
на ![]() . В обеих критических точках существуют перегибы
графика (так как 2-я производная при переходе через них меняет
знак).
. В обеих критических точках существуют перегибы
графика (так как 2-я производная при переходе через них меняет
знак).
Найдём ординаты данных
точек:

(в целях вычислений подставлять, конечно,
удобнее приближенные значения)
Ответ: график функции выпуклый на
интервале ![]() и вогнутый
на
и вогнутый
на ![]() . В точках
. В точках ![]() существуют перегибы
графика.
существуют перегибы
графика.

шағым қалдыра аласыз















