
ДИНАМИКА
Материалдық нүкте динамикасы
Динамиканың негізгі аксиомалары (заңдары) алғаш рет И.Ньютон тұжырымдаған.
1) Бірінші аксиома - инерция заңы (Галилей, 1636 ж.).
Егер материалдық нүктеге ешбір күш әсер етпесе, онда ол өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайды.
2) Екінші аксиома – динамиканың негізгі заңы (И.Ньютон, 1687 ж.). Материалдық нүктеге әсер етуші күш осы нүкте үдеуімен бағытталады және шамасы үдеуге:
![]() .
.
3) Үшінші аксиома – әсер және кері әсер теңдігінің заңы.
4) Күштер суперпозиция аксиомасы: егер материалдық нүктеге бір уақытта бірнеше күш әсер етсе, онда олар бір күшке, яғни осы күштердің геометриялық қосындысына тең болатын тең әсер күшіне эквивалент болады
![]() .
.
Динамиканың есептерін шығару үшін материалдық нүкте қозғалысының дифференциалдық теңдеулері құрылады.
Материалдық нүкте қозғалысының ИСЖ-дегі дифференциалдық теңдеулері:
- нүкте қозғалысының векторлық тәсілмен берілген кезде:
![]() ,
,
- нүкте қозғалысының координаталық тәсілмен берілген кезде:
![]() ,
, ![]() ,
,
![]()
- нүкте қозғалысының табиғи тәсілмен берілген кезде:
![]() ,
, ![]() , 0 =
, 0 =
![]() .
.
Нүкте және нүктелер жүйесі динамикасында келесі негізгі екі есеп қарастырылады:
1) бірінші есеп - нүктенің берілген қозғалыс заңы мен массасы бойынша оған әсер ететін күшті анықтау керек;
2) кері есеп - нүктеге әсер етуші күш пен нүктенің массасын біле отырып, оның кинематикалық сипаттамаларын анықтау (үдеуін, жылдамдығын, қозғалыс заңын және т. б.).
Материалдық нүкте динамикасының жалпы теоремалары.
Материалдық нүкте мен механикалық жүйенің қозғалыс мөлшері
Материалдық нүкте қозғалысының мөлшері деп бағыты жылдамдықпен бағыттас, ал шамасы масса мен жылдамдық модулінің көбейтіндісіне тең векторды айтамыз:
![]()
![]()
Механикалық жүйенің қозғалыс мөлшері – жүйе нүктелерінің қозғалыс мөлшерлерінің векторлық қосындысына тең
![]()
Жүйенің қозғалыс мөлшері жүйенің массасы мен массалар центрінің жылдамдық көбейтіндісіне тең:
![]() ,
,
мұндағы М - жүйе массасы,
бүкіл нүктелерінің массаларының қосындысы, ал
![]() - мехеникалық жүйенің массалар
центрінің жылдамдығы.
- мехеникалық жүйенің массалар
центрінің жылдамдығы.
Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы тероема:
Бірінші түрі (диф. түрдегі жүйенің қозғалыс мөлшерінің өзгеру туралы теорема)
![]()
Жүйенің қозғалыс мөлшерінің уақыт бойынша туындысы жүйегі әсер ететін барлық сыртқы күштердің қосындысына тең.
Екінші түрі (диф. түрдегі нүкте қозғалыс мөлшерінің өзгеруі туралы теорема)
![]() -импульстар
теоремасы
-импульстар
теоремасы
Үшінші түрі (интегралдық түрдегі жүйе қозғалыс мөлшерінің өзгеруі туралы теорема)

Егер k = 1 болса, онда бір материлдық нүкте үшін қозғалыс мөлшерінің өзгеруі туралы теоремасын аламыз:
![]() ,
, ![]() ,
, 
Жүйе үшін қозғалыс мөлшерінің өзгерісі туралы теоремадан төмендегідей бірнеше салдар шығады:
1) Егер жүйеге әсер ететін барлық сыртқы күштердің бас векторы нөлге тең болса, онда материалдық жүйе қозғалысының мөлшері векторының шамасы да, бағыты да өзгермейді.
2) Егер жүйеге әсер ететін барлық сыртқы күштердің бас векторының белгілі бір қозғалмайтын өстегі проекциясы нөлге тең болса, онда материалдық жүйе қозғалысы мөлшерінің векторының осы өстегі проекциясы тұрақты.
3) Ішкі күштер материалдық жүйе қозғалысы мөлшерінің өзгерісіне тікелей әсер етеді.
Механикалық жүйе массалары центрінің қозғалысы туралы теорема
Механикалық жүйенің массалар центрінің қозғалыс заңын біле отырып, бүкіл механикалық жүйе қалай қозғалатынын айтуға болады.
Теорема: механикалық жүйенің массалар центрі материялдық нүкте сияқты қозғалады. Бұл нүктенің массасы тұтас жүйенің массасына тең, ал оған әсер етуші күш сыртқы күштердің бас векторына тең.
M![]()
Бұл векторлық теңдеудің екі жағын координаттық өстерге проекцияласақ механикалық жүйенің массалар центрінің қозғалысының дифференциалдық теңдеуін аламыз:
M![]() ;
M
;
M![]() ;
M
;
M![]()
Қозғалыс мөлшерінің моменті
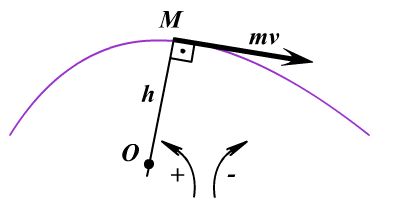
Нүктеге және өске қатысты күш моментін статика бөлімінде қарастырғанбыз. Нүктеге, центрге, өске қатысты материалдық нүктенің қозғалыс мөлшерінің моментін де сол сияқты анықтайды. Мысалы, қандайда бір О нүктесіне қатысты материалдық нүктенің қозғалыс мөлшерінің моментін анықтау үшін, О нүктесінен қозғалыс мөлшерінің сызығына перпендикуляр түсіріп, ұзындығын анықтап, есептейміз
М0(m![]() ) =
± mv.h
) =
± mv.h
Тұрақты өстен айналатын қатты дененің кин. моменті оның осы өске қатысты инерция моменті мен бұрыштық жылдамдығының көбейтіндісіне тең
Kz = Jzw
мұндағы Jz – айналу өсіне қатысты дененің өстік инерция моменті.
Материалдық дене нүктелерінің механикалық жүйесінің z өсіне қатысты инерция моменті деп жүйенеің барлық нүктелерінің массаларының, берілген z өсінен қашықтығының квадрат көбейтіндісінің қосындысына тең скаляр шаманы айтады
Jz
= ![]()
Қандай да болмасын бір өске қатысты дененің инерция моменті (Штейнер теоремасы бойынша) оның массалар центрі арқылы өтетін параллель өске қатысты инерция моменті мен дене массасы және өстердің арақашықтығының квадратының көбейтіндісімен қосындысына тең болады
Jzz =Jzc + мd2
мұндағы d - өстер арасының арақашықтығы.
Механикалық жүйенің кез келген жылжымайтын О центріне және z өсіне қатысты кинетикалық моментінің өзгеруі туралы теорема келесі түрде жазылады:
![]()
![]()
Сол сияқты механикалық жүйенің кинетикалық моментінің өзгеруі туралы теорема жүйенің массалар центріне және центрлік өстерге қатысты болады:
![]()
![]() .
.
Теорема: Жүйенің кез келген қозғалмайтын центрге қатысты кинетикалық моментінен уақыт бойынша алынған бірінші туынды барлық сыртқы күштердің сол центрге қатысты бас моментіне тең.
Дербес жағдайда ретінде қозғалмайтын центрге қатысты механикалық жүйенің кинетикалық моментінің сақталу заңын алуға болады.
Қозғалмайтын центрге қатысты механикалық жүйенің кинетикалық моменті уақыт бойынша өзгермейді, егер осы центрге қатысты жүйенің нүктелеріне түсірілген сыртқы күштер моменттерінің қосындысы нөлге тең болса.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Материалдық нүкте динамикасы
Материалдық нүкте динамикасы
ДИНАМИКА
Материалдық нүкте динамикасы
Динамиканың негізгі аксиомалары (заңдары) алғаш рет И.Ньютон тұжырымдаған.
1) Бірінші аксиома - инерция заңы (Галилей, 1636 ж.).
Егер материалдық нүктеге ешбір күш әсер етпесе, онда ол өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайды.
2) Екінші аксиома – динамиканың негізгі заңы (И.Ньютон, 1687 ж.). Материалдық нүктеге әсер етуші күш осы нүкте үдеуімен бағытталады және шамасы үдеуге:
![]() .
.
3) Үшінші аксиома – әсер және кері әсер теңдігінің заңы.
4) Күштер суперпозиция аксиомасы: егер материалдық нүктеге бір уақытта бірнеше күш әсер етсе, онда олар бір күшке, яғни осы күштердің геометриялық қосындысына тең болатын тең әсер күшіне эквивалент болады
![]() .
.
Динамиканың есептерін шығару үшін материалдық нүкте қозғалысының дифференциалдық теңдеулері құрылады.
Материалдық нүкте қозғалысының ИСЖ-дегі дифференциалдық теңдеулері:
- нүкте қозғалысының векторлық тәсілмен берілген кезде:
![]() ,
,
- нүкте қозғалысының координаталық тәсілмен берілген кезде:
![]() ,
, ![]() ,
,
![]()
- нүкте қозғалысының табиғи тәсілмен берілген кезде:
![]() ,
, ![]() , 0 =
, 0 =
![]() .
.
Нүкте және нүктелер жүйесі динамикасында келесі негізгі екі есеп қарастырылады:
1) бірінші есеп - нүктенің берілген қозғалыс заңы мен массасы бойынша оған әсер ететін күшті анықтау керек;
2) кері есеп - нүктеге әсер етуші күш пен нүктенің массасын біле отырып, оның кинематикалық сипаттамаларын анықтау (үдеуін, жылдамдығын, қозғалыс заңын және т. б.).
Материалдық нүкте динамикасының жалпы теоремалары.
Материалдық нүкте мен механикалық жүйенің қозғалыс мөлшері
Материалдық нүкте қозғалысының мөлшері деп бағыты жылдамдықпен бағыттас, ал шамасы масса мен жылдамдық модулінің көбейтіндісіне тең векторды айтамыз:
![]()
![]()
Механикалық жүйенің қозғалыс мөлшері – жүйе нүктелерінің қозғалыс мөлшерлерінің векторлық қосындысына тең
![]()
Жүйенің қозғалыс мөлшері жүйенің массасы мен массалар центрінің жылдамдық көбейтіндісіне тең:
![]() ,
,
мұндағы М - жүйе массасы,
бүкіл нүктелерінің массаларының қосындысы, ал
![]() - мехеникалық жүйенің массалар
центрінің жылдамдығы.
- мехеникалық жүйенің массалар
центрінің жылдамдығы.
Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы тероема:
Бірінші түрі (диф. түрдегі жүйенің қозғалыс мөлшерінің өзгеру туралы теорема)
![]()
Жүйенің қозғалыс мөлшерінің уақыт бойынша туындысы жүйегі әсер ететін барлық сыртқы күштердің қосындысына тең.
Екінші түрі (диф. түрдегі нүкте қозғалыс мөлшерінің өзгеруі туралы теорема)
![]() -импульстар
теоремасы
-импульстар
теоремасы
Үшінші түрі (интегралдық түрдегі жүйе қозғалыс мөлшерінің өзгеруі туралы теорема)

Егер k = 1 болса, онда бір материлдық нүкте үшін қозғалыс мөлшерінің өзгеруі туралы теоремасын аламыз:
![]() ,
, ![]() ,
, 
Жүйе үшін қозғалыс мөлшерінің өзгерісі туралы теоремадан төмендегідей бірнеше салдар шығады:
1) Егер жүйеге әсер ететін барлық сыртқы күштердің бас векторы нөлге тең болса, онда материалдық жүйе қозғалысының мөлшері векторының шамасы да, бағыты да өзгермейді.
2) Егер жүйеге әсер ететін барлық сыртқы күштердің бас векторының белгілі бір қозғалмайтын өстегі проекциясы нөлге тең болса, онда материалдық жүйе қозғалысы мөлшерінің векторының осы өстегі проекциясы тұрақты.
3) Ішкі күштер материалдық жүйе қозғалысы мөлшерінің өзгерісіне тікелей әсер етеді.
Механикалық жүйе массалары центрінің қозғалысы туралы теорема
Механикалық жүйенің массалар центрінің қозғалыс заңын біле отырып, бүкіл механикалық жүйе қалай қозғалатынын айтуға болады.
Теорема: механикалық жүйенің массалар центрі материялдық нүкте сияқты қозғалады. Бұл нүктенің массасы тұтас жүйенің массасына тең, ал оған әсер етуші күш сыртқы күштердің бас векторына тең.
M![]()
Бұл векторлық теңдеудің екі жағын координаттық өстерге проекцияласақ механикалық жүйенің массалар центрінің қозғалысының дифференциалдық теңдеуін аламыз:
M![]() ;
M
;
M![]() ;
M
;
M![]()
Қозғалыс мөлшерінің моменті
Нүктеге және өске қатысты күш моментін статика бөлімінде қарастырғанбыз. Нүктеге, центрге, өске қатысты материалдық нүктенің қозғалыс мөлшерінің моментін де сол сияқты анықтайды. Мысалы, қандайда бір О нүктесіне қатысты материалдық нүктенің қозғалыс мөлшерінің моментін анықтау үшін, О нүктесінен қозғалыс мөлшерінің сызығына перпендикуляр түсіріп, ұзындығын анықтап, есептейміз
М0(m![]() ) =
± mv.h
) =
± mv.h

Тұрақты өстен айналатын қатты дененің кин. моменті оның осы өске қатысты инерция моменті мен бұрыштық жылдамдығының көбейтіндісіне тең
Kz = Jzw
мұндағы Jz – айналу өсіне қатысты дененің өстік инерция моменті.
Материалдық дене нүктелерінің механикалық жүйесінің z өсіне қатысты инерция моменті деп жүйенеің барлық нүктелерінің массаларының, берілген z өсінен қашықтығының квадрат көбейтіндісінің қосындысына тең скаляр шаманы айтады
Jz
= ![]()
Қандай да болмасын бір өске қатысты дененің инерция моменті (Штейнер теоремасы бойынша) оның массалар центрі арқылы өтетін параллель өске қатысты инерция моменті мен дене массасы және өстердің арақашықтығының квадратының көбейтіндісімен қосындысына тең болады
Jzz =Jzc + мd2
мұндағы d - өстер арасының арақашықтығы.
Механикалық жүйенің кез келген жылжымайтын О центріне және z өсіне қатысты кинетикалық моментінің өзгеруі туралы теорема келесі түрде жазылады:
![]()
![]()
Сол сияқты механикалық жүйенің кинетикалық моментінің өзгеруі туралы теорема жүйенің массалар центріне және центрлік өстерге қатысты болады:
![]()
![]() .
.
Теорема: Жүйенің кез келген қозғалмайтын центрге қатысты кинетикалық моментінен уақыт бойынша алынған бірінші туынды барлық сыртқы күштердің сол центрге қатысты бас моментіне тең.
Дербес жағдайда ретінде қозғалмайтын центрге қатысты механикалық жүйенің кинетикалық моментінің сақталу заңын алуға болады.
Қозғалмайтын центрге қатысты механикалық жүйенің кинетикалық моменті уақыт бойынша өзгермейді, егер осы центрге қатысты жүйенің нүктелеріне түсірілген сыртқы күштер моменттерінің қосындысы нөлге тең болса.

шағым қалдыра аласыз















