
НАВЬЕ — СТОКС ТЕҢДЕУЛЕРІНІҢ ШЕШІМДЕРІН ҚҰРУ ӘДІСІ
Қойшыбай Бекнұр Ерболатұлы
Информатика БББ 3 курс студенті, Астана халықаралық университеті, Астана, Қазақстан
Аңдатпа. Мақалада тұтқыр сығылмайтын сұйықтықтың қозғалысы үшін Навье — Стокс теңдеулері қарастырылады. Теңдеулердің бірінші интегралына негізделген шешімдерді аналитикалық құру процедурасы және ішінара туындылардағы риккати теңдеуі ұсынылады. Практикалық қызығушылық тудыратын кейбір жаңа шешімдер жасалды.
Түйін сөздер: Жартылай туынды, Дифференциалдық теңдеу, қозғалыс, сұйықтықтар, интеграл, тұтқырлық
Кіріспе
Навье — Стокс теңдеулері-тұтқырлық болған кезде сұйық және газ тәрізді орталардың қозғалысын сипаттайтын сызықтық емес дифференциалдық теңдеулердің белгілі түрі. Олар тек математикалық қызығушылық тудырады және практикалық есептерге көптеген қосымшалары бар.
Тұтқыр сығылмайтын сұйықтықтың тұрақты қозғалысының 2D қарапайым жағдайы үшін Навье-Стокс теңдеулерінің өлшемсіз нұсқасы келесі түрде ұсынылуы мүмкін:
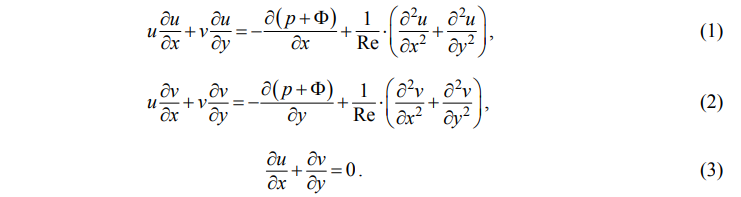
Мұнда u, v, p — негізгі белгісіз, жылдамдық пен қысым; F — сыртқы күштердің потенциалы, берілген функция; Re — Рейнольдс саны, оң параметр.
Навье — Стокс теңдеулерінің айрықша ерекшелігі - зерттеу мен шешуді едәуір қиындататын мүшелердің болуы.
Бүгінгі таңда көптеген мәселелер жеткілікті зерттелмеген және қосымша зерттеуді қажет етеді. Шешудің жалпы әдісі жоқ және Навье - Стокс теңдеулерін де, олар үшін шекаралық және бастапқы есептерді де шешудің жалпы тәсілі жоқ. Болмыс мәселесін түпкілікті шешу жоқ [6, 7]. Шешімнің тегістігінің қасиеттері жеткілікті зерттелмеген, re-дегі шешімнің асимптотикасы туралы нақты түсінік жоқ .
Навье — Стокс теңдеулерімен байланысты шешілмеген математикалық мәселелер көп. Олардың күрделілігі бағаланады. Клэй математикалық институты (Clay Mathematical Institute, USA) Навье — Стокс теңдеулерін зерттеуді үшінші мыңжылдықтың жеті негізгі мәселелерінің бірі ретінде анықтады [8].
Барлық қиындықтарға қарамастан, Навье — Стокс теңдеулері қарқынды зерттелуде. Және теңдеулерді жалпы зерттеуді азаптау орын алды.
Атап айтқанда, жұмыстарда [3, 4] сығылмайтын сұйықтық жағдайында Навье - Стокс теңдеулері интегралға мүмкіндік беретіндігі көрсетілген. Бұл нәтиже жалпы жағдайда, шекаралық және бастапқы шарттар, аймақтың сипаты, Рейнольдс санының мәні және басқа да жеке болжамдар туралы қосымша болжамдарсыз орын алады.
Әрі қарай интеграциялау
Кейбір жағдайларда бірінші интегралды білдіретін қатынастар қайта біріктіруге мүмкіндік береді. Атап айтқанда, бұл тұтқыр сығылмайтын сұйықтықтың тұрақты қозғалысының 2D жағдайына қатысты.
Осы жағдай үшін шешімдерді одан әрі интеграциялау және құру жолдарын талдауға тырысайық.
Көрсетілген жағдайға сәйкес келетін (1)–(2) теңдеулердің бірінші интегралы үш қатынасты білдіреді. Олар негізгі белгісіздерді байланыстырады u, v, p, байланысты белгісіз жар 2 және бір айнымалының ерікті аддитивті функциялары [3].
Өлшемсіз айнымалыларда бұл қатынастарды келесі түрде ұсынуға болады
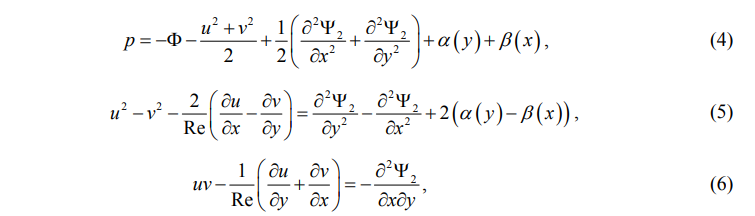
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
НАВЬЕ — СТОКС ТЕҢДЕУЛЕРІНІҢ ШЕШІМДЕРІН ҚҰРУ ӘДІСІ
НАВЬЕ — СТОКС ТЕҢДЕУЛЕРІНІҢ ШЕШІМДЕРІН ҚҰРУ ӘДІСІ
НАВЬЕ — СТОКС ТЕҢДЕУЛЕРІНІҢ ШЕШІМДЕРІН ҚҰРУ ӘДІСІ
Қойшыбай Бекнұр Ерболатұлы
Информатика БББ 3 курс студенті, Астана халықаралық университеті, Астана, Қазақстан
Аңдатпа. Мақалада тұтқыр сығылмайтын сұйықтықтың қозғалысы үшін Навье — Стокс теңдеулері қарастырылады. Теңдеулердің бірінші интегралына негізделген шешімдерді аналитикалық құру процедурасы және ішінара туындылардағы риккати теңдеуі ұсынылады. Практикалық қызығушылық тудыратын кейбір жаңа шешімдер жасалды.
Түйін сөздер: Жартылай туынды, Дифференциалдық теңдеу, қозғалыс, сұйықтықтар, интеграл, тұтқырлық
Кіріспе
Навье — Стокс теңдеулері-тұтқырлық болған кезде сұйық және газ тәрізді орталардың қозғалысын сипаттайтын сызықтық емес дифференциалдық теңдеулердің белгілі түрі. Олар тек математикалық қызығушылық тудырады және практикалық есептерге көптеген қосымшалары бар.
Тұтқыр сығылмайтын сұйықтықтың тұрақты қозғалысының 2D қарапайым жағдайы үшін Навье-Стокс теңдеулерінің өлшемсіз нұсқасы келесі түрде ұсынылуы мүмкін:
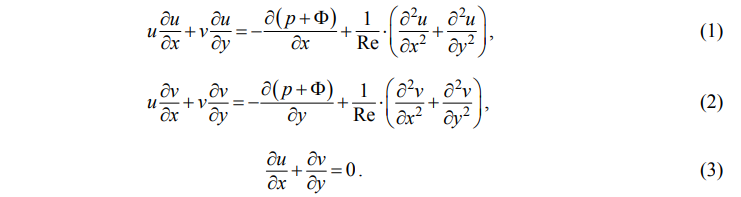
Мұнда u, v, p — негізгі белгісіз, жылдамдық пен қысым; F — сыртқы күштердің потенциалы, берілген функция; Re — Рейнольдс саны, оң параметр.
Навье — Стокс теңдеулерінің айрықша ерекшелігі - зерттеу мен шешуді едәуір қиындататын мүшелердің болуы.
Бүгінгі таңда көптеген мәселелер жеткілікті зерттелмеген және қосымша зерттеуді қажет етеді. Шешудің жалпы әдісі жоқ және Навье - Стокс теңдеулерін де, олар үшін шекаралық және бастапқы есептерді де шешудің жалпы тәсілі жоқ. Болмыс мәселесін түпкілікті шешу жоқ [6, 7]. Шешімнің тегістігінің қасиеттері жеткілікті зерттелмеген, re-дегі шешімнің асимптотикасы туралы нақты түсінік жоқ .
Навье — Стокс теңдеулерімен байланысты шешілмеген математикалық мәселелер көп. Олардың күрделілігі бағаланады. Клэй математикалық институты (Clay Mathematical Institute, USA) Навье — Стокс теңдеулерін зерттеуді үшінші мыңжылдықтың жеті негізгі мәселелерінің бірі ретінде анықтады [8].
Барлық қиындықтарға қарамастан, Навье — Стокс теңдеулері қарқынды зерттелуде. Және теңдеулерді жалпы зерттеуді азаптау орын алды.
Атап айтқанда, жұмыстарда [3, 4] сығылмайтын сұйықтық жағдайында Навье - Стокс теңдеулері интегралға мүмкіндік беретіндігі көрсетілген. Бұл нәтиже жалпы жағдайда, шекаралық және бастапқы шарттар, аймақтың сипаты, Рейнольдс санының мәні және басқа да жеке болжамдар туралы қосымша болжамдарсыз орын алады.
Әрі қарай интеграциялау
Кейбір жағдайларда бірінші интегралды білдіретін қатынастар қайта біріктіруге мүмкіндік береді. Атап айтқанда, бұл тұтқыр сығылмайтын сұйықтықтың тұрақты қозғалысының 2D жағдайына қатысты.
Осы жағдай үшін шешімдерді одан әрі интеграциялау және құру жолдарын талдауға тырысайық.
Көрсетілген жағдайға сәйкес келетін (1)–(2) теңдеулердің бірінші интегралы үш қатынасты білдіреді. Олар негізгі белгісіздерді байланыстырады u, v, p, байланысты белгісіз жар 2 және бір айнымалының ерікті аддитивті функциялары [3].
Өлшемсіз айнымалыларда бұл қатынастарды келесі түрде ұсынуға болады
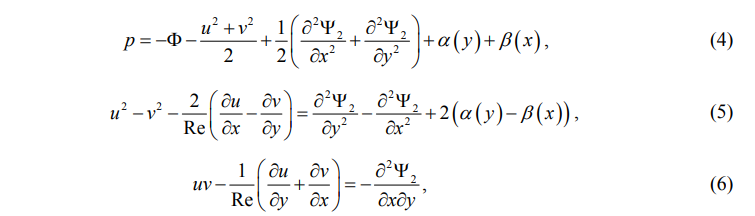

шағым қалдыра аласыз















