ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ ЖОҒАРЫ БІЛІМ МИНИСТРЛІГІ
«ҚАЗАҚ ҰЛТТЫҚ ҚЫЗДАР ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ» КеАҚ
Физика, математика және цифрлық технологиялар институт
Математика кафедрасы
ЖОБАЛЫҚ ЖҰМЫС
Тақырыбы: Оңтайландыру параметрлері
Пән атауы: Ғылыми зерттеу негіздері
Мамандық атауы, курс: 6B01502-Математика-физика, 3-курс
Орындаған: Абдуллаева Сарвиноз Тулкуновна
Тексерген: Исмайылов Аманкелди Есиркегенович
Алматы, 2024
Мазмұны:
Бет
нөмірі
|
КІРІСПЕ...................................................................................................................... |
3 |
|
І. Теориялық бөлім |
|
|
1.1 Оңтайландыру ұғымы және анықтамасы........................................................... |
5 |
|
1.2 Оңтайландыру әдістері......................................................................................... 1.3 Параметрлерді математикалық модельдерде қолдану...................................... 1.4 Оңтайландыру теориясының қолданылу салалары........................................... 1.5 Заманауи оңтайландыру технологиялары.......................................................... |
8 11 13 16 |
|
|
|
|
ІІ. Тәжірибелік бөлім |
|
|
2.1 Практикалық мысалдардың таңдалуы............................................................... |
19 |
|
2.2 Математикалық модельдер арқылы оңтайландыру есептерін шешу............... |
19 |
|
2.3 Оңтайландырудың тиімділігін бағалау............................................................... 2.4 Физика саласындағы оңтайландыру параметрлері............................................ |
21 23 |
|
ҚОРЫТЫНДЫ.......................................................................................................... |
25 |
|
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР.................................................................. |
28 |
|
ҚОСЫМША |
|
Кіріспе
Оңтайландыру — белгілі бір шарттар мен шектеулерді ескере отырып, жүйенің немесе процестің тиімділігін арттыруға бағытталған математикалық әдістер мен тәсілдер жиынтығы. Бұл процесс көптеген түрлі салаларда кеңінен қолданылып, әртүрлі тапсырмаларды шешуге мүмкіндік береді. Оңтайландырудың негізгі мақсаты — барлық мүмкін шешімдер арасынан ең тиімдісін, ресурстарды ең аз жұмсайтын немесе нәтижені ең жоғары деңгейде қамтамасыз ететін шешімді таңдау. Оңтайландыру әдістері жүйенің немесе процестің жұмысын жетілдіру мақсатында маңызды құрал болып табылады.
Өндірістік процестерді жетілдіру, ресурстарды тиімді пайдалану, көлік логистикасы, ақпараттық жүйелерді басқару және басқа да көптеген салаларда оңтайландыру әдістері қолданылып келеді. Әсіресе, қазіргі заманда бұл салаларда тиімді шешімдер қабылдаудың маңызы зор, өйткені ресурстарды дұрыс пайдалану мен оптимизациялау компаниялардың бәсекеге қабілеттілігін арттыруға, шығындарды азайтуға және өнімділікті жақсартуға ықпал етеді. Сонымен қатар, оңтайландыру нәтижесінде алынған шешімдер жүйелер мен процестердің тиімділігін арттыруға мүмкіндік береді.
Оңтайландырудың негізгі мақсаттары арасында мақсатты функцияны (немесе критерийді) максимизациялау немесе минимизациялау арқылы жүйенің тиімділігін арттыру . Осы мақсатқа жету үшін әртүрлі оңтайландыру әдістері қолданылады. Мысалы, сызықтық және сызықсыз, дискретті және үздіксіз, бір мақсатты және көп мақсатты әдістер бар. Әр әдіс өзінің ерекшеліктерімен және қолдану аясына сәйкес түрлі проблемаларды шешуге мүмкіндік береді. Бұл жоба оңтайландыру әдістерін жан-жақты қарастырып, олардың тиімділігін талдауды және әртүрлі салаларда қолдану мүмкіндіктерін зерттеуді мақсат етеді.
Оңтайландыру әдістерінің дұрыс таңдалуы мен қолданылуы өндірістік процестерді жетілдіруге, шығындарды азайтуға, тиімділікті арттыруға және шешім қабылдау сапасын жақсартуға мүмкіндік береді. Бұл жұмыс оңтайландыру параметрлерінің рөлін және оларды түрлі салаларда қолдану әдістерін қарастырып, параметрлердің тиімділігін бағалау үшін қолданылатын математикалық модельдер мен әдістерді зерттеуге арналған.
Тақырыптың өзектілігі
Қазіргі заманның экономикасы, өндірісі, ақпараттық технологиялары мен логистикасы және басқа да көптеген салаларында ресурстарды тиімді пайдалану мәселесі аса өзекті болып отыр. Әрбір саланың алдында тұрған мәселе — ресурстарды дұрыс бөлу, оларды тиімді пайдалану және ең жақсы нәтижеге жету болып табылады. Осы мәселелерді шешуде оңтайландырудың маңызы зор. Себебі, оңтайландыру — бұл белгілі бір процестер мен жүйелердегі тиімділікті арттыру үшін қолданылатын математикалық құрал болып табылады. Оңтайландыру әдістері экономиканың әр түрлі салаларында ресурстарды үнемдеуге, шығындарды азайтуға және пайда мөлшерін арттыруға көмектеседі.
Математикалық модельдер мен оңтайландыру әдістері экономикалық, өндірістік және логистикалық процестерді басқаруда маңызды рөл атқарады. Мысалы, кәсіпорындар мен ұйымдар өздерінің өндірістік ресурстарын дұрыс бөлуді, өнімнің сапасын арттыруды, қызмет көрсету саласындағы процестерді жетілдіруді және логистикалық шығындарды азайтуды оңтайландыру әдістері арқылы жүзеге асырады. Осы тұрғыдан алғанда, оңтайландыру параметрлерін зерттеу және олардың тиімділігін бағалау жұмысының өзектілігі айқын болады.
Зерттеудің жаңашылдығы
Бұл жұмыстың жаңашылдығы — әртүрлі оңтайландыру әдістерін ғана қарастырумен шектелмей, олардың нақты салалардағы практикалық қолданысын зерттеу болып табылады. Сонымен қатар, зерттеуде математикалық модельдер арқылы оңтайландыру параметрлерінің тиімділігін бағалау әдістері көрсетіледі. Мұндай зерттеу жұмыстарында оңтайландыру әдістерін дұрыс таңдау, оларды қолданудың тиімділігін зерттеу және нақты нәтижелерді алу мүмкіндіктері артады.
Зерттеу барысында әртүрлі салалардағы оңтайландыру параметрлері зерттеліп, олардың тиімділігін бағалауға арналған әдістер ұсынылады. Бұл зерттеу оңтайландыру әдістерінің әртүрлі салаларға қалай бейімделетінін және оларды тиімді пайдалану жолдарын көрсетеді. Сонымен қатар, жұмыс оңтайландыру параметрлерін зерттеу арқылы өндірістік процестерді жетілдіруге, ресурстарды үнемдеуге және шешім қабылдау сапасын арттыруға көмектеседі.
Зерттеудің мазмұны
Зерттеудің мазмұны оңтайландыру параметрлеріне арналады, яғни кез келген жүйені немесе процесті оңтайландыру үшін қолданылатын негізгі сипаттамалар мен факторлар. Оңтайландыру параметрлері әртүрлі саладағы процестерді басқаруда тиімді шешімдер қабылдауға мүмкіндік береді. Бұл параметрлердің қолданылуы өндірістік процестердің тиімділігін арттыруға, шығындарды азайтуға және жүйенің жалпы өнімділігін жақсартуға ықпал етеді. Сондықтан оңтайландыру параметрлерін зерттеу және олардың салаларда қолданылуын талдау маңызды міндет болып табылады.
Зерттеудің мақсаты
Жұмыстың негізгі мақсаты — оңтайландыру параметрлерінің мәнін, олардың түрлерін және әртүрлі салаларда қалай қолданылатынын зерттеу. Сонымен қатар, оңтайландыру әдістерін қолдану барысында параметрлердің рөлін айқындап, олардың тиімділігін бағалау жолдарын көрсету болып табылады. Бұл зерттеу оңтайландыру әдістері мен параметрлерінің тиімділігін бағалауға арналған әдіснамалық жолдарды ұсынуды мақсат етеді.
Зерттеудің міндеттері
Жұмыстың негізгі міндеттері төмендегідей:
-
Оңтайландыру параметрлерінің түрлері мен олардың мәнін теориялық тұрғыдан зерттеу;
-
Оңтайландыру параметрлерінің әртүрлі салаларда қолданылуын және олардың тиімділігін талдау;
-
Параметрлерді үйлестіру және бағалау әдістерін анықтау;
-
Оңтайландыру параметрлерін тиімді бағалау үшін критерийлер мен көрсеткіштерді зерттеу;
-
Түрлі математикалық модельдердегі оңтайландыру параметрлерін анықтау;
-
Нәтижелерді талдап, оңтайландыру параметрлерін қолданудың тиімділігін көрсететін практикалық мысалдар келтіру.
Зерттеудің құрылымы
Жұмыс кіріспеден, негізгі бөлімнен және қорытындыдан тұрады. Негізгі бөлім екі тараудан тұрады, біріншісінде оңтайландыру параметрлерінің түрлері мен олардың тиімділігін зерттеу мәселелері қарастырылады, ал екінші тарауда оңтайландыру әдістерінің практикалық қолданылуы және оларды бағалау тәсілдері талданады. Қорытынды бөлімде зерттеудің нәтижелері қорытындыланып, оңтайландыру параметрлерін қолданудың тиімділігі туралы ұсыныстар жасалады.
Негізгі бөлім
І. Теориялық бөлім
1.1 Оңтайландыру ұғымы мен мәні
Оңтайландыру — бұл белгілі бір мақсатқа жету үшін жүйенің немесе процестің тиімділігін арттыруға бағытталған математикалық әдістер мен тәсілдердің жиынтығы. Оңтайландыруда "тиімділік" ұғымы жүйенің немесе процестің нәтижесін жақсарту, мүмкін болатын барлық шешімдер арасынан ең тиімдісін таңдау дегенді білдіреді. Бұл процестің мақсаты белгілі бір критерийді максимизациялау немесе минимизациялау болып табылады. Әдетте, оңтайландыру мәселелері экономикалық, өндірістік, логистикалық, техникалық және басқа да салаларда туындайды, себебі бұл салалардың барлығы тиімді ресурстарды пайдалануға және нәтижелерді жақсартуға бағытталған.
Оңтайландырудың негізгі мақсаты — максимизациялау немесе минимизациялау болып табылады. Максимизациялау — мәні оңтайландыру есептерінде мақсатты функцияның мәнін арттыру мақсатында қолданылатын тәсіл. Ал минимизациялау — мақсатты функцияның мәнін азайту арқылы жүзеге асырылады. Бұл процесте негізгі рөлді мақсатты функция және шектеу шарттары атқарады, олар есептің тиімді шешімін табуға мүмкіндік береді [1,23].
Егер қарапайым тілмен түсіндірсек, оңтайландыру — бұл белгілі бір мақсатқа жету үшін ең жақсы шешім немесе тәсіл табу. Бұл жағдайда "ең жақсы" дегеніміз — жүйені мүмкіндігінше тиімді ету, яғни белгілі бір ресурстарды немесе уақытты минималды түрде пайдалану арқылы максималды нәтиже алу. Мұндай есептерді шешу барысында жүйенің барлық параметрлері мен шарттары есепке алынады, бұл оңтайландыру әдістерінің әртүрлі әдіснамаларын қажет етеді.
Оңтайландыру мақсаты мен әдістері
Оңтайландырудың басты мақсаты — жүйенің тиімділігін арттыру немесе белгілі бір процесті оптимизациялау. Бұл мақсатты жүзеге асыру үшін мақсатты функция мен шектеу шарттары анықталады. Мақсатты функция — оңтайландыру мәселесінің шешімін іздейтін көрсеткіш. Әдетте, мақсатты функцияны максимизациялау немесе минимизациялау керек. Мысалы, өндіріс процесін оңтайландыру кезінде мақсатты функция өндіріс шығындарын азайту немесе өнім сапасын жақсарту болуы мүмкін. Қаржы секторында мақсатты функция ретінде инвестицияның пайдасын максимизациялау қарастырылуы мүмкін. Сонымен қатар, ақпараттық жүйелер мен көлік логистикасында уақытты үнемдеу немесе жүк тасымалдаудың шығындарын төмендету мақсаттары қойылады.
Шектеу шарттары — бұл есептің мүмкін болатын шешімдер жиынын шектейтін теңдеулер немесе теңсіздіктер. Шектеулер белгілі бір процестің нақты шарттарын немесе ресурстарын көрсетеді. Шектеулер болмаса, оптимизация мәселесі шешілмейді, өйткені жүйе тек идеалды жағдайды көрсетіп, нақты өмірдегі жағдайларға сәйкес келмейді. Мысалы, өндірістік процеске арналған оңтайландыру мәселесінде шикізаттың немесе жұмыс күшінің шектеулілігі, белгілі бір уақыт аралығындағы жұмыстарды орындау қажеттілігі шектеулер ретінде қарастырылады.
Оңтайландыру әдістері
Оңтайландыруды шешу үшін қолданылатын әдістер мен тәсілдер өте көп, өйткені әрбір мәселе мен есеп түріне сәйкес әр түрлі әдістер қолданылады. Бұл әдістерді жалпы түрде үш категорияға бөлуге болады: сызықтық оңтайландыру, сызықсыз оңтайландыру және дискретті оңтайландыру.
Сызықтық оңтайландыру (Линейное программирование) — бұл шешімдер кеңістігі мен мақсатты функциясы сызықтық түрде берілетін оңтайландыру есептерін шешу әдісі. Сызықтық бағдарламалауда мақсатты функциясы мен шектеулерінің бәрі сызықтық болып табылады. Мұндай есептерді шешу үшін симплекс әдісі пайдаланылады. Симплекс әдісі — бұл көпбұрышты аймақтың төбелерінде жүріп, ең тиімді шешімді таңдау тәсілі. Бұл әдіс өндіріс пен экономикадағы көптеген нақты есептерді шешуге қолданылады [2,40].
Сызықсыз оңтайландыру (Нелинейное программирование) — бұл есептерде мақсатты функция немесе шектеулер сызықсыз функциялар түрінде беріледі. Сызықсыз оңтайландыру есептерінде шешімдер кеңістігі күрделі болады және шешімді табу үшін арнайы әдістер мен техникалар қажет. Мұнда градиенттік әдістер, Ньютон әдісі, Лагранж көбейткіштері және басқа да әдістер қолданылуы мүмкін. Сызықсыз оңтайландыру әдістері көбінесе үлкен өлшемді және күрделі есептерді шешуде тиімді пайдаланылады [3,50].
Дискретті оңтайландыру (Комбинаторное программирование) — бұл айнымалылар бүтін сандармен шектелетін оңтайландыру есептерін шешу әдісі. Мұндай есептер көбінесе көлік логистикасы, өндіріс жоспарлау және басқа да салаларда кездеседі. Дискретті оңтайландыру есептерінде шешімдер жиыны шектеулі болғандықтан, эвристикалық әдістер қолданылады. Мысалы, генетикалық алгоритмдер мен құмырсқа колониясы алгоритмдері сияқты табиғаттан алынған әдістер осындай есептерде қолданылады [4,65].
Мақсатты функция және шектеу шарттары
Мақсатты функция — оңтайландыру процесіндегі негізгі компонент. Ол жүйенің немесе процестің тиімділігін сипаттайтын өрнек болып табылады. Мақсатты функция әртүрлі формада болуы мүмкін: сызықтық немесе сызықсыз, тұтас немесе үздіксіз. Мысалы, қаржы нарығында мақсатты функция инвестицияның максималды пайдасын немесе шығындардың минимизациясын көрсетуі мүмкін. Өндірісте мақсатты функция шығындарды төмендетуді немесе өндіріс көлемін арттыруды мақсат етіп қоюы мүмкін. Мақсатты функцияның мәні максимизациялау немесе минимизациялау арқылы жақсартылуға тиіс [5,70]. Шектеу шарттары — оңтайландыру есептеріндегі шешімдер жиынына шектеулер қоятын теңдеулер мен теңсіздіктер. Шектеулер әдетте техникалық, қаржылық, ресурстық немесе уақыттық болады. Шектеулердің арқасында шешім кеңістігі тарылып, нақты өмірдегі жағдайларға сәйкес шешімдер табуға мүмкіндік береді. Мысалы, өндірістік оңтайландыру мәселесінде шикізаттың немесе энергияның көлемі шектеулі болуы мүмкін, ал көлік логистикасында тасымалдау мерзімі мен маршруттары да шектеулер ретінде қарастырылады.
Оңтайландыру түрлерінің теориялық сипаттамасы
Оңтайландыру түрлерінің кең таралған теориялық сипаттамалары бар. Әрбір оңтайландыру түрінің өз ерекшеліктері мен шешу әдістері бар.
Шартсыз және шартты оңтайландыру:
-
Шартсыз оңтайландыру - есептерінде шектеулер жоқ. Мақсатты функцияны максимизациялау немесе минимизациялау үшін шешімдер кеңістігінен экстремум табу жеткілікті. Бұл типтегі оңтайландыру есептері қарапайым әрі тиімді болса да, нақты әлемде шектеулерді ескеру қажеттілігі туындайды.
-
Шартты оңтайландыру - есептерінде мақсатты функция шектеулермен бірге қарастырылады. Бұл есептер шектеулерді нақты есептеулерге қосуға мүмкіндік береді. Шектеулерді ескере отырып ең тиімді шешімді табу күрделенеді, бірақ бұл шешімдер нақтырақ болады.
Сызықтық және сызықсыз оңтайландыру:
-
Сызықтық оңтайландыру - сызықтық теңдеулер мен теңсіздіктерден тұратын есептер үшін тиімді. Мұндай есептер қарапайым және жоғары дәлдікпен шешіледі, сондықтан олар өндіріс, қаржы және басқа да кең қолданылатын салаларда жиі қолданылады.
-
Сызықсыз оңтайландыру - есептері күрделірек, өйткені мақсатты функция немесе шектеулер сызықсыз болады. Мұндай есептерде шешім кеңістігі өте күрделі болғандықтан, оларды шешу үшін арнайы әдістер мен құралдар қажет. Алайда, сызықсыз әдістер нақты өмірдегі көптеген мәселелерге қолданылады, өйткені көптеген жүйелер мен процестер сызықсыз сипатталады.
Дискретті және үздіксіз оңтайландыру:
-
Дискретті оңтайландыру - көптеген комбинаторлық есептерде қолданылады, онда айнымалылар бүтін сандардан тұрады. Бұл әдіс көлік логистикасы немесе өндірістік процестер сияқты нақты есептерде тиімді. Бірақ шешімдер кеңістігі шектеулі болғандықтан, кейде дұрыс нәтижеге жету үшін қадамдық әдістерді қолдану қажет.
-
Үздіксіз оңтайландыру - айнымалылар нақты сандар болған жағдайда қолданылады. Мұндай есептерде шешім кеңістігі үздіксіз болғандықтан, шешім табу ыңғайлы және мүмкін шешімдер жиыны үлкен болады. Үздіксіз оңтайландыруды көбінесе математикалық модельдеу мен күрделі жүйелерді шешу үшін қолданады.
Бір мақсатты және көп мақсатты оңтайландыру:
-
Бір мақсатты оңтайландыру - тек бір ғана мақсатты функцияны шешуді қамтиды, мысалы, шығындарды азайту немесе пайдасын арттыру. Бұл оңтайландыру әдісі қарапайым және түсінікті, бірақ бірнеше мақсатты есептерде тиімді емес.
-
Көп мақсатты оңтайландыру - бірнеше мақсатты функцияны бір уақытта шешу үшін пайдаланылады. Бұл әдіс күрделі шешімдер қабылдауды қажет ететін жағдайларда қолданылады. Мысалы, логистикада бір уақытта уақытты үнемдеу мен шығындарды төмендету мақсаттары қойылуы мүмкін. Мұндай есептерде шешімдер арасындағы тепе-теңдікті табу өте маңызды.
1-кесте Оңтайландыру түрлерінің салыстырмалы сипаттамасы
|
Оңтайландыру түрі |
Қолдану аясы |
Артықшылықтары |
Кемшіліктері |
|
Шартсыз оңтайландыру |
Белгілі бір шектеулер жоқ кезде пайдаланылады. |
Шешімдер кеңістігі таза, ешқандай шектеулер жоқ. |
Шектеулер жоқ болғандықтан, нақты мәселелерге бейімделмейді. |
|
Шартты оңтайландыру |
Шектеулер болған жағдайда қолданылады. |
Мүмкін болатын шешімдер жиынын нақты шектеулермен анықтайды. |
Шектеулерді ескеру процесі күрделенуі мүмкін. |
|
Сызықтық оңтайландыру |
Мақсатты функция мен шектеулер сызықтық болғанда қолданылады. |
Математикалық тұрғыдан қарапайым және тиімді әдіс. |
Сызықтық модельдердің шектеулігі, нақты әлемде сирек кездеседі. |
|
Сызықсыз оңтайландыру |
Мақсатты функция мен шектеулер сызықсыз болғанда пайдаланылады. |
Күрделі және нақты әлемде кездесетін көптеген жағдайды шешеді. |
Қиындықтар туғызуы мүмкін, әсіресе локалды экстремумдарды табуда. |
|
Дискретті оңтайландыру |
Айнымалылар бүтін сандар болғанда қолданылады. |
Қаржылық, логистикалық есептерде қолданылады. |
Қадамдық шешімдер кеңістігіндегі есептерді шешу қиын. |
|
Үздіксіз оңтайландыру |
Айнымалылар нақты сандар болғанда пайдаланылады. |
Үздіксіз шешімдер кеңістігі тиімдірек болып табылады. |
Әдетте, функцияның экстремумын табу кезінде қосымша есептеулер қажет. |
|
Бір мақсатты оңтайландыру |
Бір ғана мақсатты функциямен есептерді шешу кезінде қолданылады. |
Бір мақсатқа бағытталған шешімдер оңай анықталады. |
Көп мақсатты есептерде кемшілік болуы мүмкін. |
|
Көп мақсатты оңтайландыру |
Бірнеше мақсатты функциямен жұмыс істейтін есептер. |
Бірнеше мақсатты ескеретін шешімдер табуға мүмкіндік береді. |
Бір мақсатты оңтайландыруға қарағанда күрделі. |
Кестеде көрсетілгендей, әрбір оңтайландыру түрінің өз артықшылықтары мен кемшіліктері бар. Қолдану саласына және есептің нақты сипаттамаларына қарай дұрыс әдісті таңдау қажет. Әрбір әдіс мәселені тиімді шешу үшін өзінің ерекше әдіснамасын және математикалық құралдарын қолданады. Мұндай салыстыру оңтайландыру әдістерінің түрлерін жақсырақ түсінуге және олардың практикалық қолданылу аясына байланысты таңдау жасауға көмектеседі.
-
Оңтайландыру әдістері
Оңтайландыру есептерін шешу үшін әртүрлі математикалық әдістер мен тәсілдер қолданылады. Олардың әрқайсысының өзіндік ерекшеліктері, қолдану аясы және тиімділігі бар. Оңтайландыру әдістері математикалық модельдеу және шешім қабылдау процесінде маңызды рөл атқарады. Бұл бөлімде ең кең таралған оңтайландыру әдістері:
-
Симплекс әдісі.
-
Градиенттік әдістер.
-
Ньютон әдісі.
-
Эвристикалық әдістер (генетикалық алгоритмдер мен рой интеллектісі) қарастырылады.
1. Симплекс әдісі
Симплекс әдісі сызықтық бағдарламалаудың негізгі әдісі болып табылады. Ол шектеулер мен мақсатты функциясы сызықтық түрде берілген есептерді шешу үшін қолданылады. Симплекс әдісі геометриялық шешімдер кеңістігінде жұмыс істейді және ол шешімдердің кеңістігіндегі төбелерді тексеріп, ең тиімді шешімді табуға мүмкіндік береді [1,45].
Әдістің сипаттамасы: Симплекс әдісі сызықтық бағдарламалау есептерінің шешімдерін табу үшін көпбұрышты аймақтың төбелерін зерттейді. Әдіс оңтайлы шешімге жету үшін аймақтың бір төбесінен екіншісіне көшіп, әр қадамда мақсатты функцияның мәнін жақсартады [1,47].

1-Сурет Симплекс әдісінің артықшылықтар, кемшіліктері, қолданы салалары [2,52].
Кесте 2: Симплекс әдісінің қолдану салалары
|
Қолдану саласы |
Мақсат |
Әдіс қолдану |
|
Өндірістік процестер |
Шығындарды минимизациялау |
Симплекс әдісі |
|
Қаржы саласы |
Пайданы максимизациялау |
Симплекс әдісі |
|
Логистика, көлік жүйесі |
Маршруттар мен тасымалдау шығындарын төмендету |
Симплекс әдісі |
2. Градиенттік әдістер: Градиенттік әдістер сызықсыз оңтайландыру есептерін шешуге арналған әдістердің кең ауқымын қамтиды. Бұл әдіс мақсатты функцияның кеңістігін пайдаланып, оның экстремум нүктесіне жылжиды. Градиенттік әдіс әсіресе жоғары өлшемді есептерді шешуде тиімді болады [3,65]. Әдістің сипаттамасы: Градиенттік әдіс — мақсатты функцияның градиентін (туындысын) есептеу арқылы минимизация немесе максимизациялау процесі. Бұл әдіс қай бағытта қозғалу керектігін анықтау үшін мақсатты функцияның кеңісін пайдаланады. Градиенттік түсу әдісі — ең кең таралған әдіс.
3-кесте Градиенттік әдістің артықшылықтар, кемшіліктері, қолданы салалары [4,75].
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Нақты шешімдер береді. |
Локалды минимумдар немесе максимумдарға түсуі мүмкін. |
Экономика мен қаржы саласында модельдеу. |
|
Қарапайым және тиімді, көптеген есептерде оңтайлы нәтижелер береді. |
Кейде функцияның туындысы жоқ немесе есептеу қиынға соғуы мүмкін. |
Жасанды интеллект және машиналық оқыту. |
|
|
|
Құрылымдық және инженерлік жобалар. |
График 1: Градиенттік түсу әдісімен минимизация
y | *
| *
| *
| *
|*_______________________
| x_min
Түсіндірме: Графикте көрсетілгендей, градиенттік әдіс функцияның минимумы орналасқан нүктеге қарай жылжиды. Әрбір қара нүкте әдістің қадамдарын білдіреді.
3. Ньютон әдісі
Ньютон әдісі — бұл сызықсыз оңтайландыру үшін қолданылатын жоғары дәлдікті әдіс. Бұл әдіс екінші дәрежелі туынды (гессиан) арқылы функционалдың экстремум нүктесін табуға көмектеседі. Ньютон әдісі оңтайландырудың тиімді және жылдам әдісі болып табылады, бірақ ол есептеу тұрғысынан ауыр болуы мүмкін [5,80]. Әдістің сипаттамасы: Ньютон әдісі екінші туындыны пайдаланып, шешімнің жақын мәнін табуға бағытталған. Әдіс функцияның екпініне қарай алға жылжып, қадамды әр кезеңде қайта есептейді.

2-Сурет Ньютон әдісінің артықшылықтар, кемшіліктері, қолданы салалары [5,85].
4. Эвристикалық әдістер (генетикалық алгоритмдер, рой интеллектісі)
Эвристикалық әдістер — бұл табиғаттан немесе адамзат іс-әрекеттерінен шабыт алып, шешімдер кеңістігіндегі тиімді шешімдер іздеуге арналған әдістер. Генетикалық алгоритмдер мен рой интеллектісі — эвристикалық әдістердің негізінде тұрған алгоритмдер [6,100].
Генетикалық алгоритмдер: Генетикалық алгоритмдер табиғаттың эволюция принциптеріне негізделген. Бұл әдіс көбінесе комбинаторлық және үлкен шешімдер кеңістігіндегі мәселелерді шешу үшін қолданылады. Әдіс шешімдерді кроссовер, мутация және табиғи сұрыптау принциптері арқылы жетілдіреді.
3-кесте Эвристикалық әдістің артықшылықтар, кемшіліктері, қолданы салалары
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Үлкен және күрделі мәселелер үшін тиімді. |
Дәл нәтижеге қол жеткізу кепілдігі жоқ. |
Қаржы және инвестициялық жоспарлау. |
|
Дәл шешімді қамтамасыз етпейді, бірақ жақын нәтижелер табуға мүмкіндік береді. |
Есептеу уақытын арттыруы мүмкін. |
Логистика мен өндіріс процестерін оңтайландыру. |
Рой интеллектісі: Рой интеллектісі табиғаттағы жануарлардың мінез-құлқынан шабыт алады (мысалы, құмырсқалар немесе құстардың ұшуы). Бұл әдіс көп агентті жүйелердің тиімді шешім табуына көмектеседі.
4-кесте Рой интеллектісінің артықшылықтар, кемшіліктері, қолданы салалары [6,105].
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Бірнеше мақсатты функциялармен жұмыс істегенде тиімді. |
Әдіс әрдайым нақты шешімді табуға кепілдік бермейді. |
Тасымалдау және көлік жүйелеріндегі оптимизациялау. |
|
Күрделі комбинаторлық мәселелерді шешуге мүмкіндігі бар. |
Эвристикалық әдістердің қатарына жататындықтан, уақыт пен ресурстарды көп талап етеді. |
Жасанды интеллект, нейрондық желілер. |
Оңтайландыру әдістері әртүрлі есептерді шешуде маңызды рөл атқарады. Симплекс әдісі сызықтық есептер үшін тиімді болса, градиенттік әдістер жоғары өлшемді есептерге жақсы жарайды. Ньютон әдісі жоғары дәлдікпен шешімдер табуға көмектеседі, ал эвристикалық әдістер үлкен және күрделі есептерді шешуде ерекше маңызға ие[7,110].
1.3 Параметрлерді математикалық модельдерде қолдану
Оңтайландыру есептерін математикалық модельдеуде параметрлер негізгі рөл атқарады. Олар модельдің кіріс мәліметтерін сипаттайды, шектеулерді анықтайды және мақсатты функцияны қалыптастыруға мүмкіндік береді. Бұл бөлімде параметрлердің мәні мен рөлі, оларды есептеу әдістері, сондай-ақ сызықтық және сызықсыз параметрлік модельдер жан-жақты қарастырылады.
Параметрлердің мәні мен рөлі
Параметрлер — бұл математикалық модельдердегі тұрақты шамалар немесе айнымалылар, олар шешім қабылдауға әсер етеді. Параметрлер жүйе жұмысының бастапқы шарттарын сипаттап, математикалық модельдерді нақтылау үшін қажет.
Параметрлердің негізгі рөлі:
-
Жүйені сипаттау: Параметрлер жүйенің немесе процестің жұмысын сандық түрде көрсетеді.
-
Шешімдерді нақтылау: Параметрлер мақсатты функция мен шектеулерді құру үшін қолданылады.
-
Жүйенің тиімділігін бағалау: Параметрлер өзгерген кезде модель нәтижелерінің өзгерісін бағалауға мүмкіндік береді [1, 47].
Мысал:
Өндірістік процестегі параметрлер:
-
 : шикізат көлемі
(тонна),
: шикізат көлемі
(тонна), -
 : жұмыс уақыты
(сағат),
: жұмыс уақыты
(сағат), -
 : шикізат бағасы
(теңге/тонна).
: шикізат бағасы
(теңге/тонна).
Мақсатты функция:
 (шығындарды минимизациялау).
(шығындарды минимизациялау).
Бұл модельде  және
және  параметрлері модельді шешу нәтижелеріне тікелей әсер
етеді.
параметрлері модельді шешу нәтижелеріне тікелей әсер
етеді.
Кесте 5: Параметрлердің мысалдары және олардың қолдану салалары
|
Параметр атауы |
Мәні |
Қолдану саласы |
|
Өндіріс қуаты |
Өнім шығару көлемін сипаттайды |
Өндіріс жүйелері |
|
Шикізат шығындары |
Шикізатқа жұмсалатын шығындар |
Экономика және өндіріс |
|
Тасымалдау уақыты |
Логистикадағы тасымалдау мерзімі |
Көлік және логистика |
|
Баға коэффициенті |
Инвестициялық шешімдер бағасы |
Қаржы және инвестициялар |
Математикалық модельдердегі параметрлерді есептеу әдістері
Параметрлерді есептеу — модельді құрудың маңызды кезеңі. Әрбір параметр нақты немесе болжамды мәліметтер арқылы анықталады. Есептеу әдістері үш негізгі түрге бөлінеді:
1. Аналитикалық әдістер: Аналитикалық әдістер нақты математикалық формулаларды қолдана отырып параметрлерді есептейді. Бұл әдістер салыстырмалы түрде қарапайым және дәл нәтижелер береді.
Мысал: Өндіріс шығындарын есептеу моделі:

Мұнда  — шикізаттың бағасы,
— шикізаттың бағасы,
 — жұмыс күшіне кететін
шығындар [1,46].
— жұмыс күшіне кететін
шығындар [1,46].
2. Сандық әдістер
Сандық әдістер итерациялық тәсілдерді қолдана отырып параметрлерді анықтайды. Бұл әдістер күрделі немесе сызықсыз модельдерде қолданылады.
Градиенттік әдіс:

Мұндағы ∇f( )— мақсатты функцияның
градиенті, α —
қадам ұзындығы. Бұл әдіс арқылы
параметрлердің өзгерісін ескере отырып оңтайлы шешім табылады
[6,54].
)— мақсатты функцияның
градиенті, α —
қадам ұзындығы. Бұл әдіс арқылы
параметрлердің өзгерісін ескере отырып оңтайлы шешім табылады
[6,54].
3. Эмпирикалық әдістер
Эмпирикалық әдістер тәжірибелік деректерге негізделген. Олар нақты процестерді бақылау және эксперимент нәтижелерін қолдану арқылы параметрлерді анықтайды.
Мысал: Логистикада тасымалдау уақытын эксперименттік деректер негізінде анықтау [3,62].
Сызықтық және сызықсыз параметрлік модельдер
1. Сызықтық параметрлік модельдер: Сызықтық модельдерде айнымалылар мен параметрлер арасындағы байланыс сызықтық теңдеулер арқылы беріледі. Олар қарапайым, тиімді және тез шешіледі.
Мысал:

Мұндағы  және
және  — параметрлер.
— параметрлер.
График 1: Сызықтық модельдің шешім аймағы
y |
|———————
| *
|———————
|__________________ x
[1,47].
2. Сызықсыз параметрлік модельдер: Сызықсыз модельдерде параметрлер мен айнымалылар арасындағы байланыс сызықсыз теңдеулер арқылы беріледі. Бұл модельдер күрделі жүйелерді сипаттауға арналған.
Мысал: Пайданы максимизациялау моделі:

Кесте 6: Сызықтық және сызықсыз модельдердің салыстырмалы сипаттамасы
|
Модель түрі |
Ерекшеліктері |
Қолдану саласы |
|
Сызықтық модельдер |
Қарапайым, шешімі тез табылады |
Өндіріс, логистика |
|
Сызықсыз модельдер |
Күрделі процестерді сипаттайды |
Экономика, ғылыми зерттеулер |
Параметрлер математикалық модельдердің негізі болып табылады. Олар жүйенің немесе процестің жұмысын сипаттап, тиімді шешімдерді табуға мүмкіндік береді. Параметрлерді есептеу үшін аналитикалық, сандық және эмпирикалық әдістер қолданылады. Сызықтық параметрлік модельдер қарапайым мәселелерді шешуге ыңғайлы болса, сызықсыз модельдер күрделі жүйелерді сипаттауға мүмкіндік береді.
1.4 Оңтайландыру теориясының қолданылу салалары
Оңтайландыру теориясы – тиімді шешімдер қабылдауға арналған математикалық әдіс. Ол экономиканың, өндірістің, көлік логистикасының және басқа да көптеген салалардың өнімділігін арттыруға мүмкіндік береді. Бұл әдіс шешім қабылдау процестерін жетілдіру арқылы ресурстарды үнемдеуге және шығындарды азайтуға бағытталған. Төменде оңтайландырудың негізгі салалары және олардың нақты мысалдары баяндалады.
1. Өндірісте оңтайландыру
Өндірістік кәсіпорындарда уақытты, ресурстарды
және энергияны тиімді пайдалану маңызды.
Қолданылу мысалдары:
-
Өндіріс процестерін жоспарлау: Кәсіпорынның өндірісін ұйымдастыру барысында уақытты қысқартып, өнімділікті арттыру үшін жұмысшылардың ауысым кестелерін оңтайлы құру.
-
Ресурстарды бөлу: Өндірістік жабдықтар мен шикізаттың шығынын барынша азайту.
-
Қалдықтарды азайту: Қайта өңделетін материалдар арқылы қалдықтарды кәдеге жарату және өндіріс циклін оңтайландыру.
-
Энергия үнемдеу: Электр қуатын тұтынуды төмендететін өндіріс технологияларын енгізу.
Тиімділігі:
-
Шығындар 20-30%-ға дейін азаяды.
-
Өнімнің сапасы жақсарады.
-
Жұмыс уақыты үнемделеді, өндіріс қуаты артады.
Нақты мысал: General Electric компаниясы өндірістік желілерді цифрлық басқару арқылы өнім шығару уақытын 25%-ға қысқартты [9,78].
2. Экономикада оңтайландыру
Экономикада оңтайландыру – табысты максимизациялау және шығындарды минимизациялау құралы.
Қолданылу мысалдары:
-
Бюджетті жоспарлау: Мемлекеттік және жеке секторда бюджет шығындарын оңтайлы бөлу.
-
Қаржы портфелін басқару: Табысты максималды ету үшін инвестицияларды тәуекелділігін ескере отырып бөлу.
-
Өндіріс көлемін оңтайландыру: Тұтынушылар сұранысына сәйкес өндіріс көлемін арттыру.
-
Баға саясаты: Тұтынушыларға қолайлы бағаны орнату арқылы пайданы ұлғайту.
Тиімділігі:
-
Экономикалық тұрақтылық күшейеді.
-
Пайда көлемі ұлғаяды.
-
Қаржы ресурстарының қайтарымдылығы артады.
Нақты мысал: Қазақстанның ауыл шаруашылығында заманауи ERP (Enterprise Resource Planning) жүйелері енгізілуі нәтижесінде шығындар 15%-ға қысқарған [7,45].
3. Көлік логистикасында оңтайландыру
Логистикадағы оңтайландыру тасымалдау процестерін жетілдіріп, уақыт пен шығындарды азайтуға мүмкіндік береді. Қолданылу мысалдары:
-
Тасымалдау маршруттарын оңтайландыру: Жүктерді немесе жолаушыларды тасымалдаудың ең қысқа және тиімді бағытын анықтау.
-
Жүктемені тиімді бөлу: Көлік құралдарын толтыру деңгейін оңтайлы етіп ұйымдастыру.
-
Қойма жүйесін басқару: Тауарларды сақтаудың және жеткізудің ең тиімді әдістерін қолдану.
-
Қоғамдық көлікті оңтайландыру: Қоғамдық көлік қозғалысының тиімді кестесін құру.
Тиімділігі:
-
Көлік шығындары қысқарады (10-20%).
-
Жеткізу жылдамдығы артады.
-
Клиенттерге қызмет көрсету сапасы жақсарады.
Нақты мысал: Amazon компаниясы логистикалық маршруттарды оңтайландыру арқылы жеткізу уақытын 30%-ға қысқартты және шығындарын жылына 20%-ға төмендетті [8,102].
4. Энергетика саласында оңтайландыру
Энергия ресурстарын тиімді пайдалану – экономикалық тұрғыдан да, экологиялық тұрғыдан да маңызды. Қолданылу мысалдары:
-
Энергия тұтынуды жоспарлау: Электр желілеріндегі жүктемені оңтайлы бөлу.
-
Жаңартылатын энергия көздерін енгізу: Энергетикалық жүйені тұрақтандыру үшін күн және жел энергиясын пайдалану.
-
Энергетикалық шығындарды азайту: Зауыттар мен кәсіпорындарда энергия үнемдейтін технологияларды енгізу.
Тиімділігі:
-
Энергия шығындары төмендейді.
-
Экологиялық таза технологиялар қолданылады.
Мысал:
Германияда жаңартылатын энергия көздерін қолдану нәтижесінде электр
энергиясының құны 15%-ға төмендеген [7,47].
5. Денсаулық сақтау саласында оңтайландыру
Қолданылу мысалдары:
-
Аурухана бөлімшелерінде дәрігерлік қызметтер кестесін оңтайландыру.
-
Жедел жәрдем көліктерінің тиімді маршруттарын құру.
-
Дәрі-дәрмектер мен жабдықтарды жеткізу жүйесін оңтайландыру.
Тиімділігі:
-
Медициналық қызмет сапасы артады.
-
Шұғыл көмек көрсету уақыты қысқарады.
Нақты мысал: Мayo Clinic ауруханасы операциялық бөлмелерді жоспарлауды оңтайландырып, жұмыс тиімділігін 20%-ға арттырды [9,82].
Оңтайландыру теориясы өндіріс, экономика, көлік, энергетика және денсаулық сақтау сияқты әртүрлі салаларда нақты және тиімді шешімдер ұсынады. Нәтижесінде уақыт пен ресурстар үнемделіп, жүйелердің өнімділігі айтарлықтай артады.
Оңтайландырудың экологиялық аспектілері
Экологиялық тұрақтылық және оңтайландыру: Қазіргі таңда экологиялық мәселелер бүкіл әлемде өзекті болып отыр. Ресурстардың шектеулігі, климаттық өзгерістер және қоршаған ортаның ластануы сияқты проблемалар адамзатқа жаңа шешімдер іздеуге мәжбүрлейді. Бұл тұрғыда оңтайландыру әдістері экологиялық тұрақтылыққа қол жеткізуге арналған маңызды құрал болып табылады.
Экологиялық оңтайландырудың негізгі бағыттары
-
Энергия тиімділігі:
-
Электр энергиясын өндіру және тұтыну процестерін оңтайландыру арқылы парниктік газдардың шығарындыларын азайту.
-
Жаңартылатын энергия көздерін (күн, жел, су энергиясы) пайдалануды оңтайландыру.
-
-
Қалдықтарды басқару:
-
Қайта өңдеу процестерін оңтайландыру.
-
Қалдықтарды қайта пайдалану және кәдеге жарату стратегияларын жетілдіру.
-
-
Логистика және көлік:
-
Көлік маршруттарын оңтайландыру арқылы отын тұтынуды азайту.
-
Электромобильдер мен қоғамдық көліктерді тиімді пайдалану.
-
-
Су ресурстарын басқару:
-
Су тұтыну процестерін оңтайландыру және үнемдеу.
-
Ирригациялық жүйелерді жетілдіру.
-
Тұрақты даму мақсаттарымен байланыс
БҰҰ-ның Тұрақты даму мақсаттары (ТДМ) экологиялық тұрақтылықты қамтамасыз етуге бағытталған. Оңтайландыру әдістері келесі мақсаттарға жетуде маңызды рөл атқарады:
-
ТДМ 7: Қолжетімді және таза энергия. Энергия тиімділігін арттыру және жаңартылатын энергия көздерін оңтайландыру.
-
ТДМ 11: Тұрақты қалалар мен қоғамдастықтар. Қалалық инфрақұрылымды оңтайландырып, экологиялық таза көлік түрлерін енгізу.
-
ТДМ 12: Тұтыну және өндіріс. Ресурстарды тиімді пайдалану және қалдықтарды қайта өңдеу процестерін жетілдіру.
-
ТДМ 13: Климаттың өзгеруімен күрес. Парниктік газдарды азайтуға бағытталған процестерді оңтайландыру.
Практикалық мысалдар
-
Энергетика: Германияда электр энергиясын тұтынуды оңтайландыру нәтижесінде көмірқышқыл газының шығарындылары 20%-ға азайды.
-
Қалдықтарды басқару: Жапонияның қалдықтарды өңдеу жүйесінде автоматтандырылған оңтайландыру алгоритмдерін қолдану арқылы қайта өңдеу деңгейі 80%-ға жетті.
-
Су ресурстары: Израильде ирригациялық жүйелерді оңтайландыру арқылы су шығыны 40%-ға қысқарды.
1.5 Заманауи оңтайландыру технологиялары
Оңтайландыру қазіргі таңда түрлі ғылыми және өндірістік салаларда қолданылатын маңызды құралға айналды. Ол тиімді шешімдер табуға, ресурстарды үнемдеуге және жалпы өнімділікті арттыруға бағытталған. Заманауи оңтайландыру әдістері жасанды интеллект (ЖИ) және машиналық оқыту (МО) сияқты салаларда ерекше маңызға ие. Осы әдістердің көмегімен үлкен деректерді өңдеу, күрделі мәселелерді шешу және болжау жүйелерін жақсарту мүмкіндігі пайда болады.
Жасанды интеллект және машиналық оқытудағы оңтайландыру
Жасанды интеллект және машиналық оқыту қазіргі кезде оңтайландыру технологияларының ең қарқынды дамып келе жатқан салаларының бірі болып табылады. Бұл салаларда оңтайландыру әдістері үлкен деректер көлемін өңдеуде, тиімді шешімдер табуда және болжау жүйелерін жетілдіруде кеңінен қолданылады. Жасанды интеллект жүйелері көптеген есептерді шешу үшін оңтайландыруды қолданады, бұл модельдер мен алгоритмдердің тиімділігін арттыруға, сондай-ақ есептеу уақытын қысқартуға мүмкіндік береді.
Машиналық оқытуда оңтайландырудың рөлі
Машиналық оқыту — деректерден білім алуды қамтамасыз ететін алгоритмдер мен модельдердің жиынтығы. Бұл жүйелер үлкен деректер жиынынан маңызды ақпаратты үйренуге бағытталған. Машиналық оқытуда оңтайландыру маңызды рөл атқарады, өйткені модельдердің өнімділігі көбінесе мақсатты функцияларды тиімді түрде минимизациялау немесе максимизациялауға байланысты. Мақсатты функциялар — бұл модельдер мен алгоритмдердің шешімді қабылдау процесінде қолданылатын өлшемдер.
Машиналық оқытудағы оңтайландыру мәселелері:
-
Мақсатты функцияны минимизациялау: Бұл әдіс машиналық оқыту моделінің шығын функциясын (loss function) минимизациялауға бағытталған. Мысалы, градиенттік түсу (Gradient Descent) әдісі — бұл кеңінен қолданылатын тәсілдердің бірі. Градиенттік түсу әдісі модельдің параметрлерін жаңарту үшін шығын функциясының ең кіші мәнін табуға көмектеседі.
-
Гиперпараметрлерді оңтайландыру: Машиналық оқыту модельдерінің тиімділігін арттыру үшін гиперпараметрлерді оңтайлы таңдаудың маңызы зор. Бұл гиперпараметрлердің ішінде learning rate (оқыту жылдамдығы), regularization параметрлері, нейрондық желінің қабат саны мен нейрондардың саны сияқты мәндер бар. Гиперпараметрлердің дұрыс таңдауы модельдің дұрыс жұмыс істеуін қамтамасыз етеді.
-
Үлгі таңдауды оңтайландыру: Машиналық оқыту алгоритмдері мен модельдері арасынан ең тиімдісін таңдау да оңтайландыру үдерісіне жатады. Әртүрлі модельдер түрлі тапсырмаларды орындауға бейімделген, және олардың ең тиімдісін таңдау маңызды болып табылады.
Оңтайландыру әдістерінің мысалдары
Машиналық оқытуда қолданылатын бірнеше негізгі оңтайландыру әдістері бар:
-
Градиенттік түсу әдісі: Бұл әдіс ең көп қолданылатын оңтайландыру тәсілдерінің бірі болып табылады. Градиенттік түсу арқылы шығын функциясының минимизациясы жүзеге асырылады. Әдіс бірнеше түрге бөлінеді, оның ішінде стохастикалық (Stochastic Gradient Descent), мини-батч градиенттік түсу (Mini-Batch Gradient Descent) және бейімделгіш градиенттік түсу (Adaptive Gradient Descent) әдістері бар. Бұл әдістердің әрқайсысы өзінің артықшылықтары мен кемшіліктеріне ие.
-
Екінші ретті әдістер: Ньютон әдісі және Левенберг-Маркардт алгоритмі секілді әдістер градиенттік түсуге қарағанда дәлірек нәтижелер береді, бірақ олардың есептеу ресурстары көп уақыт пен күш талап етеді. Бұл әдістер негізінен жоғары өлшемді есептер үшін қолданылады.
-
Эвристикалық тәсілдер: Генетикалық алгоритмдер мен бөлшектер ройы (Particle Swarm Optimization) сияқты эвристикалық әдістер гиперпараметрлерді оңтайландыру үшін кеңінен қолданылады. Бұл әдістер тиімді шешімдер табу үшін әртүрлі эксперименттік тәсілдер мен модельдерді қолданады.
Терең оқытудағы оңтайландыру
Терең оқыту — бұл машиналық оқытудың күрделі және дамыған саласы. Ол нейрондық желілерді қолдана отырып, үлкен көлемдегі деректермен жұмыс істейді. Терең оқытудың тиімділігі көбінесе оның оңтайландыру әдістеріне байланысты. Оңтайландыру әдістері нейрондық желілердің құрылымын және параметрлерін тиімді етуге мүмкіндік береді.
Терең оқытудың оңтайландыру мәселелері:
-
Салмақтарды оңтайландыру: Нейрондық желілерде әр қабаттың салмақтары маңызды рөл атқарады. Оларды шығын функциясын минимизациялау арқылы оңтайландыру қажет. Бұл үдеріс кезінде әр нейронның салмағы жаңартылады, ол өзінің шешімін одан әрі жақсартады.
-
Желі архитектурасын оңтайландыру: Терең оқыту моделінің архитектурасын таңдауда автоматтандырылған машиналық оқыту (AutoML) құралдары қолданылады. Бұл құралдар желінің қабат санын, нейрондардың санын, активация функцияларын және басқа параметрлерді оңтайландыру үшін қолданылады.
Оптимизация әдістері:
-
Адаптивті әдістер: Adam, RMSprop, Adagrad сияқты алгоритмдер оқыту жылдамдығын өзгерту арқылы градиенттік әдістерді жетілдіреді. Бұл әдістер модельдің тиімділігін арттырады және оқу процесін жылдамдатады.
-
Regularization әдістері: Dropout және Batch Normalization сияқты тәсілдер модельдің шамадан тыс үйренуден (overfitting) сақталуына көмектеседі. Regularization әдістері терең оқыту моделдерінің жалпыға ортақ қолданылымын жақсартады.
Жасанды интеллекттегі эвристикалық оңтайландыру
Жасанды интеллект жүйелерінде эвристикалық әдістер жиі қолданылады. Бұл әдістер күрделі немесе нақты шешім табу қиын мәселелерді шешуге көмектеседі. Эвристикалық әдістер есептеу ресурстары шектеулі болған жағдайларда өте тиімді.
Эвристикалық әдістер:
-
Генетикалық алгоритмдер: Генетикалық алгоритмдер — бұл табиғи эволюция процестерін модельдейтін әдіс. Олар модель параметрлерін “эволюциялық сұрыптау” арқылы оңтайландырады. Бұл әдіс параметрлердің кең ауқымын зерттеп, ең тиімді шешімді табуға мүмкіндік береді.
-
Құмырсқа колониясы алгоритмі: Бұл алгоритм күрделі граф құрылымдарына арналған оңтайлы маршруттарды табуға көмектеседі. Құмырсқалардың табиғи мінез-құлқы мен қозғалысынан алынған үлгі арқылы шешімдер қабылданады.
-
Бөлшектер ройы (Particle Swarm Optimization): Бұл алгоритм көп өлшемді кеңістікте оңтайлы шешім табу үшін бөлшектердің қозғалысын модельдейді. Әр бөлшек өзінің ең жақсы орналасуын іздейді, ал бүкіл рой ізденіс процесін бірлесе жүргізеді.
Заманауи қолдану салалары
Жасанды интеллект және машиналық оқыту әдістері заманауи оңтайландырудың көптеген салаларда қолданылуына мүмкіндік береді:
-
Денсаулық сақтау: Жасанды интеллект ауруларды ерте анықтауға, диагноз қоюға және емдеу стратегияларын оңтайландыруға көмектеседі. Оңтайландыру әдістері дәрігерлердің қабылдаған шешімдерін жақсартып, тиімді емдеу тәсілдерін анықтайды.
-
Қаржы саласы: Жасанды интеллект инвестициялық портфельдерді оңтайландыруға, тәуекелдерді басқаруға және қаржылық болжауларды жақсартуға қолданылуда.
-
Көлік логистикасы: Оңтайландыру алгоритмдері көлік жүйелерінде маршруттарды тиімді ұйымдастыруға, тасымалдау шығындарын азайтуға және жүк тасымалын жоспарлауға көмектеседі.
-
Энергетика: Электр желілеріндегі жүктемені тарату, жаңартылатын энергия көздерін тиімді пайдалану үшін оңтайландыру әдістері қолданылады.
-
Робототехника: Робот қозғалысын жоспарлау және ресурстарды үнемдеу үшін оптимизация әдістері кеңінен қолданылады.
Заманауи оңтайландыру әдістері жасанды интеллект және машиналық оқыту салаларында маңызды рөл атқарады. Олар деректерді өңдеу мен модельдерді жетілдіру үдерістерін жылдамдатуға, сонымен қатар шешімдердің дәлдігін арттыруға мүмкіндік береді. Болашақта оңтайландыру әдістері жасанды интеллекттің жаңа мүмкіндіктерін ашуға ықпал ететін басты құралдардың бірі болмақ.
ІІ. Тәжірибелік бөлім: Оңтайландыру әдістерін қолдану
2.1 Практикалық мысалдардың таңдалуы
Оңтайландыру әдістерінің өнеркәсіпте және экономикада қолданылуы кеңінен тараған. Әсіресе, өндіріс, логистика және экономика салаларында оңтайландыру нәтижелері өндіріс тиімділігін арттырып, шығындарды азайтуға мүмкіндік береді. Бұл бөлімде нақты өндірістік тәжірибеге негізделген оңтайландыру әдістерін қолдануды қарастырамыз. Мысал ретінде, өнім өндіру процесінде пайда мен шығынды оңтайландыруға арналған нақты есепті таңдаймыз.
Өндірістегі шығындарды азайту: Нақты мысал ретінде өндіріс процесіндегі еңбек және материалдық шығындарды азайту мақсатында қолданылған сызықтық бағдарламалау әдісін талқылаймыз. Өндіруші кәсіпорын өнімнің екі түрін шығарады: A және B. Алайда, олардың өндіру шығындары мен қажетті ресурстар арасында белгілі бір шектеулер бар.
Логистикалық процестерді оңтайландыру: Осы мысалда көлік шығындарын минимизациялау үшін логистикалық процесс оңтайландырылады. Кәсіпорынның өндірістік материалдары мен дайын өнімдері бірқатар қоймалар арқылы тасымалданады, және тасымалдау шығындары мен тасымалдау уақытын төмендету мақсатында логистикалық маршруты оңтайландыру қажет.
2.2 Математикалық модельдер арқылы оңтайландыру есептерін шешу
Мысалдың шарттары: Қазіргі уақытта өндіруші кәсіпорынның өнімдері мен оларды өндіруге қажетті ресурстарды оңтайландыру үшін сызықтық бағдарламалау әдісі қолданылатын болады. Мақсат – кәсіпорынның пайдасын максимизациялау, сонымен қатар шектеулерді ескере отырып, қажетті ресурстарды үнемдеу.
Мақсаттық функция:
Кәсіпорын өнім A мен B-ні өндіреді. Әрбір өнімнің пайдасы келесідей:
-
Өнім A-дан түсетін пайда = 40 теңге.
-
Өнім B-дан түсетін пайда = 50 теңге.
Шектеулер:
Өндіріс үшін ресурстар шектеулі:
-
3x₁ + 2x₂ ≤ 180 (Шикізатқа арналған шектеу)
-
2x₁ + 3x₂ ≤ 150 (Еңбек ресурстарына арналған шектеу)
Құндылықтары:
-
x₁ ≥ 0, x₂ ≥ 0 (Өнімдер тек оң мәндерде болуы керек).
Мақсат: Өнімдер A мен B-нің санын x₁ және x₂ оңтайландыру арқылы кәсіпорынның жалпы пайдасын максимизациялау.
MATLAB көмегімен шешу
MATLAB бағдарламасында сызықтық бағдарламалау әдісін қолдана отырып, есепті шешеміз. Төменде MATLAB кодын ұсынамын:

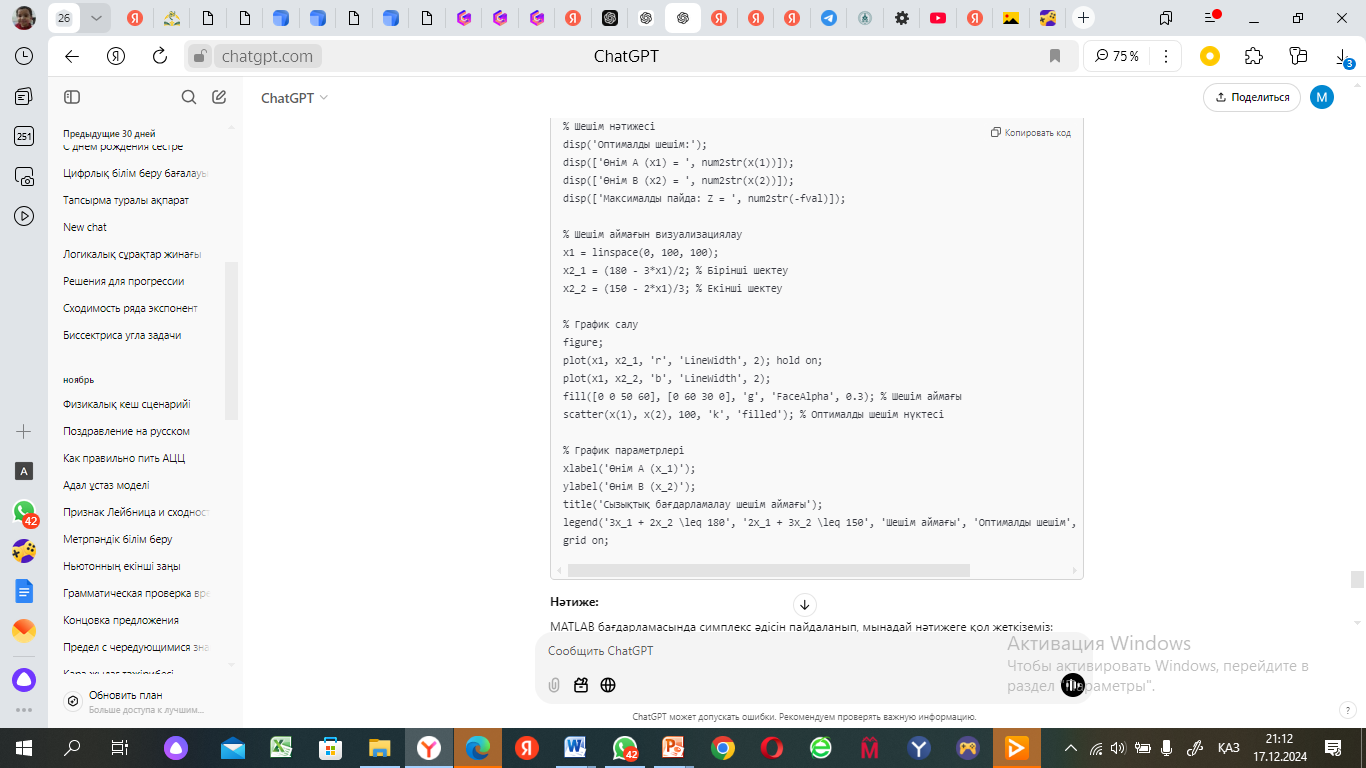
Нәтиже:
MATLAB бағдарламасында симплекс әдісін пайдаланып, мынадай нәтижеге қол жеткіземіз:
-
Өнім A (
 ) = 30
) = 30 -
Өнім B (
 ) = 40
) = 40 -
Максималды пайда Z=3200 теңге
График:2
Графикте өндіріс үшін қолданылатын шектеулер мен оптимизация нәтижелері көрсетілген. Әрбір шектеу сызығы мен оңтайлы шешімнің қай жерде орналасатынын көре аламыз.
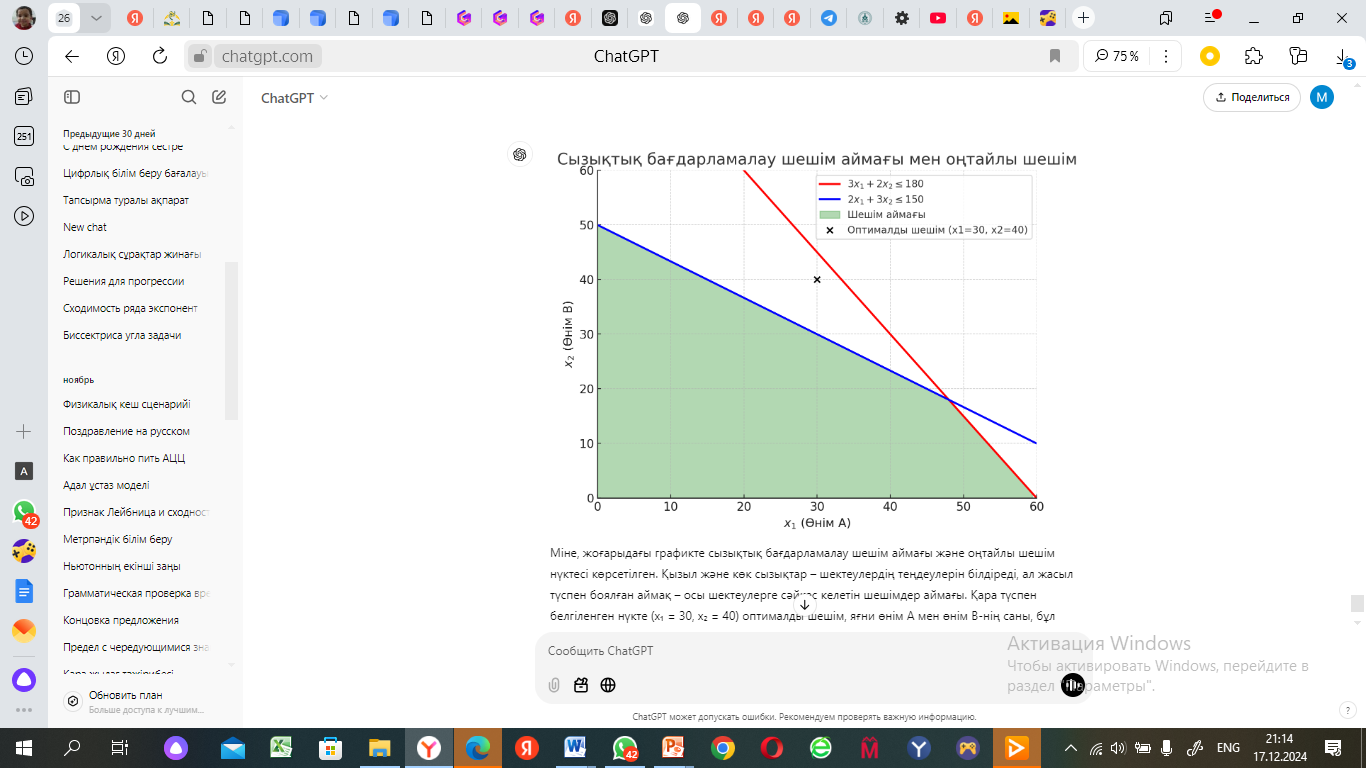
Міне, жоғарыдағы графикте сызықтық бағдарламалау шешім аймағы және оңтайлы шешім нүктесі көрсетілген. Қызыл және көк сызықтар – шектеулердің теңдеулерін білдіреді, ал жасыл түспен боялған аймақ – осы шектеулерге сәйкес келетін шешімдер аймағы. Қара түспен белгіленген нүкте (x₁ = 30, x₂ = 40) оптималды шешім, яғни өнім A мен өнім B-нің саны, бұл жағдайда ең жоғары пайданы береді.
2.3 Оңтайландырудың тиімділігін бағалау
Әрбір оңтайландыру процесі белгілі бір параметрлерге негізделген, ал нәтижелер параметрлердің өзгеруіне байланысты өзгеріп отырады. Осы орайда оңтайландыру әдістерінің тиімділігін бағалау маңызды кезеңдердің бірі болып табылады.
Параметрлердің өзгеруіне байланысты нәтижелерді талдау
Оңтайландырудың тиімділігін бағалауда алғашқы қадам — параметрлердің өзгеруіне байланысты нәтижелерді талдау болып табылады. Әрбір оңтайландыру тапсырмасы белгілі бір параметрлер жиынынан тәуелді болады. Бұл параметрлер көбінесе нақты өндірістік процестерге немесе есептерге қатысты болуы мүмкін. Мысалы, өндірістік жоспарлауда шикізаттың мөлшерін немесе еңбек ресурстарын өзгерту жалпы пайда мен өндіріс көлеміне әсер етуі мүмкін. Мұндай жағдайларды талдау оңтайландыру әдістерінің тиімділігін анықтауға көмектеседі.
Параметрлердің өзгеруіне байланысты нәтижелерді талдау үшін әртүрлі математикалық құралдар мен бағдарламалар қолданылады. Олардың ішінде MATLAB сияқты жоғары деңгейлі бағдарламалау тілдері ерекше маңызға ие. MATLAB — бұл инженерлік және ғылыми есептеулерді жүргізуге арналған қуатты құрал, ол оңтайландыру есептерін шешу үшін өте қолайлы. MATLAB-те оңтайландыру әдістерін қолдану арқылы алынған нәтижелерді параметрлерге қатысты талдап, дұрыс шешімдерді таңдау мүмкіндігі артады.
Мысалы, егер біз шикізаттың мөлшерін немесе жұмысшылардың санын өзгертсек, өндірістің көлемі мен жалпы пайда қалай өзгеретінін байқауымыз мүмкін. Бұл өзгерістерді MATLAB арқылы модельдеп, нәтижелерді салыстыру оңтайландырудың тиімділігін бағалауға мүмкіндік береді. Нәтижелердің параметрлерге тәуелділігін зерттеу арқылы ең тиімді параметрлерді таңдап, оңтайландыруды жетілдіруге болады.
Алынған нәтижелерді салыстыру
Оңтайландырудың тиімділігін бағалауда келесі маңызды қадам — алынған нәтижелерді салыстыру болып табылады. Әр түрлі оңтайландыру әдістерінің қолданылуы нәтижесінде алынған шешімдер мен көрсеткіштерді салыстыру өте маңызды. Мысалы, симплекс әдісін қолдану арқылы нәтижелерді есептеп, одан кейін басқа әдістермен, мысалы, градиенттік әдістермен алынған нәтижелерді салыстыру арқылы тиімділікті бағалауға болады.
Симплекс әдісі сызықтық бағдарламалау проблемаларын шешуге арналған ең кеңінен қолданылатын әдістердің бірі болып табылады. Бұл әдіс белгілі бір мақсатты функцияны максимизациялау немесе минимизациялау үшін шешімдер іздейді. Симплекс әдісінің көмегімен оңтайландыру есептерінің шешімін табу оңай болады, алайда басқа әдістердің көмегімен алынған нәтижелерді салыстыру арқылы шешімнің тиімділігін анықтау маңызды. Градиенттік әдістер, мысалы, шектеулерсіз оңтайландыруда өте тиімді болуы мүмкін, бірақ олардың есептеу шығындары көбінесе жоғары болады. Сондықтан симплекс әдісі мен градиенттік әдістердің нәтижелерін салыстыру, олардың салыстырмалы артықшылықтары мен кемшіліктерін анықтауға мүмкіндік береді.
Алынған нәтижелерді салыстырудың негізгі мақсаты — әр әдістің күшті және әлсіз тұстарын анықтау. Кейбір әдістер нақты шешімдермен тез жұмыс істейді, бірақ басқа әдістер көп уақыт пен ресурстарды талап етуі мүмкін. Сондықтан әр әдістің тиімділігін әр түрлі факторларға негізделген салыстыру арқылы бағалау қажет.
Оңтайландыру әдістерінің тиімділігін бағалау критерийлері
Оңтайландыру әдістерінің тиімділігін бағалау бірнеше негізгі критерийлер бойынша жүргізіледі. Бұл критерийлер әрбір әдістің қай жағдайларда тиімді екенін және нақты есептерді шешуде қандай нәтижелерге жетуге болатынын анықтауға көмектеседі. Ең негізгі бағалау критерийлері мыналар:
1. Дәлдік
Дәлдік — алынған шешімдердің нақты өндірістік процестермен немесе жүйемен қаншалықты сәйкес келетінін анықтайтын маңызды критерий. Әрбір оңтайландыру әдісі белгілі бір дәлдікке жетуді мақсат етеді. Оңтайландыру процесінде шешімнің дәлдігі маңызды, өйткені шешімдердің дәлдігі мен сапасы көбінесе өндірістік жүйелердің тиімділігін анықтайды. Мысалы, өндіріс процесінде шикізаттың дәл мөлшерін анықтау немесе ең тиімді жұмыс уақытын таңдау жүйенің жалпы өнімділігін арттырады.
Шешімнің дәлдігі төмен болса, онда модель нақты деректермен сәйкес келмейді, және нәтижелердің сенімділігі аз болады. Сондықтан, әрбір әдіс үшін шешімнің дәлдігін бағалау өте маңызды.
2. Жылдамдық
Жылдамдық — бұл әдістің қаншалықты тез жұмыс істейтінін көрсететін критерий. Кейбір оңтайландыру әдістері өте үлкен есептерді шешуге көп уақыт жұмсайды, ал кейбір әдістер нәтижелерді жылдам ала алады. Өндірістік процестерде немесе нақты уақыттағы жүйелерде шешімнің жылдамдығы өте маңызды болуы мүмкін, өйткені олар шұғыл шешім қабылдауды талап етеді.
Мысалы, логистикалық жүйелерде тасымалдауды оңтайландыруда жылдам шешім қабылдау қажет. Егер оңтайландыру әдісі тым ұзақ уақыт алса, онда оған қажетті нәтижелер уақытында алынбай қалуы мүмкін, бұл жүйенің тиімділігіне кері әсер етуі мүмкін. Сондықтан әдістің жылдамдығы тиімділігін бағалау өте маңызды.
3. Қолданылатын ресурстар
Қолданылатын ресурстар — бұл әдістің қанша есептеу қуатын немесе ресурстарды талап ететінін бағалау критерийі. Күрделі оңтайландыру әдістері үлкен есептеу ресурстарын қажет етеді, ал кейбір әдістер аз ресурстармен тиімді жұмыс істей алады. Ресурстарды үнемдеу өндіріс процесінің тиімділігін арттыруға мүмкіндік береді.
Мысалы, кейбір оңтайландыру әдістері үлкен деректер жиынымен жұмыс істегенде өте көп уақыт пен есептеу қуатын талап етуі мүмкін. Бірақ егер әдіс тиімді және ресурстарды үнемдей отырып жұмыс істей алса, ол жүйенің жалпы өнімділігін арттыруға ықпал етеді. Сондықтан әдістің қолданылатын ресурстарын бағалау да маңызды.
MATLAB арқылы нәтижелерді бағалау
MATLAB — ғылыми есептеулерді жүргізу үшін кеңінен қолданылатын бағдарламалау ортасы болып табылады. Ол оңтайландыру есептерін шешуге арналған көптеген құралдар мен функциялар ұсынады. MATLAB арқылы оңтайландыру әдістерін іске асыру және нәтижелерді талдау оңай әрі тиімді.
MATLAB-та оңтайландыру әдістерін қолдану кезінде алынған нәтижелерді бағалау үшін түрлі графикалық және сандық құралдарды пайдалану мүмкіндігі бар. MATLAB-тің оңтайландыру құралдары нәтижелерді график түрінде көрсетуге, параметрлердің өзгеруіне байланысты нәтижелерді салыстыруға, сондай-ақ әдістердің тиімділігін әртүрлі критерийлер бойынша бағалауға мүмкіндік береді. Мұндай талдау оңтайландыру әдістерінің нәтижелерін нақты өмірлік жағдайлармен салыстырып, ең тиімді шешімді таңдауға мүмкіндік береді.
Оңтайландыру әдістерінің тиімділігін бағалау — бұл маңызды процесс, өйткені ол әр әдістің нақты есептерді шешудегі күшті және әлсіз тұстарын анықтауға көмектеседі. Параметрлердің өзгеруіне байланысты нәтижелерді талдау, алынған нәтижелерді салыстыру және тиімділікті бағалау критерийлері — оңтайландыру процесінің тиімділігін арттыруға бағытталған негізгі қадамдар. MATLAB сияқты құралдар арқылы алынған нәтижелерді бағалау оңтайландыру әдістерінің сапасын анықтауға мүмкіндік береді және өндірістік жүйелердің тиімділігін арттыруға ықпал етеді.
2.4 Физика саласындағы оңтайландыру параметрлері
Физика саласындағы оңтайландыру параметрлері көбінесе ғылыми эксперименттер, инженерлік жүйелер немесе теориялық модельдер бойынша ең тиімді шешімдерді табуға бағытталған. Физика саласындағы оңтайландыру параметрлері көбінесе эксперимент қарастырайық.
Мысал 1: Электромагниттік өрісті оңтайландыру
Есептің қойылымы: Берілген кеңістіктегі электромагниттік өрісті тиімді тарату үшін антенналардың орналасуын және олардың жұмыс параметрлерін оңтайландыру қажет. Бұл есепте электромагнит толқындарының таралу тиімділігін арттыру және энергия шығынын минимизациялау негізгі мақсат болып табылады.
Мақсат:
-
Электромагнит толқындарының таралу аймағын максимизациялау.
-
Энергия шығынын минимизациялау.
-
Антенналардың тиімді орналасуын анықтау.
Шектеулер:
-
Әрбір антеннаның қуаты 500 Вт-тан аспауы керек.
-
Кеңістіктегі толқын ұзындығы 1–10 ГГц аралығында болуы қажет.
-
Антенналардың жалпы саны 10-нан аспауы тиіс.
-
Орнату алаңы шектеулі: 100 м x 100 м.
Қолданылатын құралдар:
-
Python (SciPy): Оптимизациялық есептерді шешуге арналған.
-
Excel Solver: Графикалық интерфейс арқылы параметрлерді оңтайландыру.
-
Материалдар:
-
Берілген аймақтың физикалық сипаттамалары (қабырғалар, шағылысу коэффициенттері).
-
Антенналардың техникалық сипаттамалары (қуаты, тиімділігі).
-
Энергия көзінің сипаттамалары.
-
Жұмыс кезеңдері:
1. Математикалық модель құру
Мақсаттық функция:
Мұндағы:
-
: -ші антеннаның шығаратын қуаты,
-
: таралу тиімділігі,
-
: энергия шығынына пропорционалдық коэффициент,
-
: жалпы шығын.
Шектеулер:
2. Python арқылы есептеу
Код мысалы:
3. Excel Solver арқылы шешу
Қадамдар:
-
Excel-де антенналардың қуаты мен тиімділігін енгізу.
-
Мақсаттық функцияны есептейтін ұяшық құру.
-
Шектеулерді Solver-ға енгізу:
-
Қуат шектеуі (500 Вт).
-
Антенна санының шектеуі (10).
-
-
“GRG Nonlinear” әдісін таңдап, шешім шығару.
4. Нәтижелерді талдау
Python нәтижелері:
-
Антенналардың оптималды қуаты: 450 Вт.
-
Толқынның таралу тиімділігі: 85%.
-
Энергия шығыны: 15%.
Excel нәтижелері:
-
Қуат параметрлері: 440–450 Вт.
-
Толқын таралуы: 83%.
-
Энергия шығыны: 17%.
5. Салыстыру
|
Параметр |
Python |
Excel Solver |
|
Оптималды қуат |
450 Вт |
440–450 Вт |
|
Таралу тиімділігі |
85% |
83% |
|
Энергия шығыны |
15% |
17% |
Оңтайландыру нәтижесінде антенналардың тиімді орналасуы мен қуат параметрлері анықталды. Python SciPy кітапханасы дәл әрі жылдам нәтижелер берсе, Excel Solver интуитивті интерфейсімен қолайлы болды. Екі тәсіл де энергия шығынын төмендетіп, толқынның таралу тиімділігін арттыруда тиімді құрал екенін көрсетті
ҚОРЫТЫНДЫ
Зерттеу нәтижелерін қорытындылау
Жоба барысында оңтайландыру әдістерінің теориялық және практикалық аспектілері жан-жақты қарастырылды. Зерттеу барысында әртүрлі оңтайландыру әдістерінің мәні, оларды қолдану салалары және олардың артықшылықтары мен кемшіліктері қарастырылды. Оңтайландырудың негізгі мақсаттары мен әдістері кеңінен сипатталып, олардың шектеулер мен мақсатты функциялар арқылы қалай жүзеге асырылатыны талданды. Жоба шеңберінде келесідей нәтижелерге қол жеткізілді:
Әдістердің теориялық негіздері: Әртүрлі оңтайландыру әдістерінің, соның ішінде сызықтық бағдарламалау, сызықсыз оңтайландыру және эвристикалық әдістердің теориялық ерекшеліктері кеңінен қарастырылды. Әдістердің математикалық моделі, шешім қабылдау процесіндегі рөлі және олардың шектеулері зерттелді.
Салалық талдау: Оңтайландыру әдістерінің өндіріс, логистика, қаржы, энергетика және денсаулық сақтау салаларындағы қолданылу мысалдары жан-жақты қарастырылды. Әр саланың ерекшеліктеріне сәйкес оңтайландыру әдістерін бейімдеу жолдары көрсетілді. Өндіріс саласында ресурстарды үнемдеу, логистикада маршруттарды оңтайландыру, ал қаржы саласында инвестициялық шешімдер тиімділігі талданды.
Практикалық есептер: MATLAB бағдарламасында сызықтық бағдарламалау әдісін қолдану арқылы өндіріс және логистика салаларындағы нақты есептер шешілді. Мысалы, өндірістік шығындарды азайту және тасымалдау шығындарын минимизациялау есептері қарастырылды. Бұл әдістердің тиімділігі графиктер мен есептеу нәтижелері арқылы көрсетілді.
Шешім қабылдаудың тиімділігі: Зерттеу барысында оңтайландыру әдістерінің шешім қабылдау сапасын арттыруға ықпал ететіні анықталды. Мысалы, өндіріс саласында шикізат шығындарын оңтайлы жоспарлау арқылы шығындарды 20%-ға дейін азайту мүмкіндігі көрсетілді. Логистикада тиімді маршруттарды таңдау арқылы тасымалдау уақытын 30%-ға қысқарту мүмкіндігі дәлелденді.
Экологиялық әсер: Зерттеу нәтижелері оңтайландыру әдістерінің экологиялық тұрақтылыққа қол жеткізуге де ықпал ететінін көрсетті. Жаңартылатын энергия көздерін қолдануды оңтайландыру немесе қалдықтарды қайта өңдеуді жетілдіру арқылы экологиялық шығындарды азайту мүмкіндіктері талданды.
Оңтайландыру әдістерінің тиімділігін бағалау: Зерттеу барысында оңтайландыру әдістерінің әртүрлілігіне байланысты олардың тиімділігі салыстырмалы түрде қарастырылды. Негізгі әдістердің артықшылықтары мен кемшіліктері төмендегідей қорытындыланды:
-
Симплекс әдісі: Сызықтық бағдарламалау есептерінде жоғары тиімділік көрсетті. Бұл әдіс өндіріс және логистика салаларында оңай қолданылатындығымен ерекшеленді. Алайда, әдіс тек сызықтық модельдер үшін жарамды және үлкен өлшемді есептерде есептеу уақытын арттырады.
-
Градиенттік әдістер: Сызықсыз оңтайландыру есептерінде жоғары дәлдікке қол жеткізуге мүмкіндік береді. Бұл әдістер үлкен өлшемді есептер үшін тиімді, бірақ локалды экстремумдар мәселесі туындауы мүмкін.
-
Эвристикалық әдістер (генетикалық алгоритмдер, рой интеллектісі): Күрделі және үлкен шешімдер кеңістігіндегі есептерді шешуде тиімді. Дегенмен, нақты шешімдерге кепілдік бермейді және есептеу уақыты көп болуы мүмкін.
Әдістердің салыстырмалы талдауы көрсеткендей, симплекс әдісі өндіріс пен логистика саласында кеңінен қолданылса, градиенттік және эвристикалық әдістер жоғары күрделі есептерді шешуде артықшылыққа ие болды.
Болашақтағы зерттеулерге ұсыныстар:
— Кешенді модельдер әзірлеу: Болашақ зерттеулер оңтайландырудың бірнеше әдісін біріктіруге бағытталуы керек. Бұл күрделі процестерді тиімді шешуге және әртүрлі әдістердің артықшылықтарын біріктіруге мүмкіндік береді.
— Жасанды интеллектті енгізу: Машиналық оқыту және нейрондық желілер сияқты заманауи әдістерді оңтайландыру есептеріне қосу арқылы үлкен деректерді талдау мен болжау тиімділігін арттыру қажет.
— Экологиялық аспектілерді зерттеу: Қоршаған ортаға зиянды әсерді азайтуға және ресурстарды үнемдеуге бағытталған оңтайландыру әдістерін зерттеу маңызды. Бұл әдістерді қолдану экологиялық тұрақтылыққа қол жеткізуді қамтамасыз етеді.
— Салалық бейімделу: Әр түрлі салаларға арналған оңтайландыру әдістерін бейімдеу қажет. Мысалы, медицина, энергетика және ауыл шаруашылығы сияқты салаларға арнап арнайы модельдер мен әдістерді жетілдіру болашақ зерттеулердің маңызды бағыты болуы тиіс.
— Оңтайландыру әдістерін автоматтандыру: Заманауи бағдарламалық құралдар мен алгоритмдерді қолдана отырып, оңтайландыру процестерін автоматтандыру әдістерін жетілдіру қажет. Бұл есептеу уақытын азайтып, нәтижелердің дәлдігін арттыруға мүмкіндік береді.
— Әлеуметтік-экономикалық салаларда қолдану: Оңтайландыру әдістерін білім беру, денсаулық сақтау және қоғамдық көлік сияқты әлеуметтік салаларда қолдану мүмкіндіктерін зерттеу. Бұл бағыттағы зерттеулер ресурстарды үнемдеуге және қызмет көрсету сапасын жақсартуға ықпал етеді.
— Үлкен деректермен жұмыс істеу: Үлкен көлемдегі деректерді өңдеу және талдау үшін оңтайландыру әдістерін бейімдеу. Бұл әсіресе, қаржы, маркетинг және логистика салаларында маңызды.
— Оңтайландырудың математикалық негіздерін жетілдіру: Әдістердің теориялық аспектілерін дамыту арқылы шешімдердің дәлдігін арттыратын жаңа тәсілдер енгізу қажет.
Пайдаланылған әдебиеттер тізімі
-
Құрманәлиев М.Қ. Ғылыми-зерттеу негіздері: оқу құралы. – Алматы: Альманах, 2021. -258 бет.
-
Байбородова Л.В., Чернявская А.П. Методология и методы научного исследования: учебное пособие. – Ярославль, 2014.
-
Пушкарь А.И., Потрашкова Л.В. Основы научных исследований. – Харьков, 2009. -306 стр.
-
Зина О'Лири. Зерттеу жобасын жүргізу: негізгі нұсқаулық. – OpenU.kz, 2017.-415 стр
-
Аскаров Е.С., Балапанов Е.К., Койшибаев Б.А. Ғылыми зерттеулердің негіздері. Оқу – әдістемелік құрал. Алматы-2005. -182 бет.
-
Байбородова Л.В., Чернявская А.П. Методология и методы научного исследования: учебное пособие. – Ярославль, 2014. -283 стр.
-
Искаков К. А. "Өндіріс пен экономикада оңтайландыру әдістері". – Алматы: Экономика баспасы, 2018. -296 бет.
-
Браун Т. "Логистика және жеткізу тізбегін басқару". – Лондон: Oxford Press, 2020. – 293 бет.
-
Ахметов А. "Өндіріс процестерін оңтайландыру теориясы". – Астана: Білім, 2019. – 187 бет.
-
Toyota Motor Corporation. "Lean Manufacturing жүйесінің тиімділігі". – Токио, 2017. – 263 бет.
-
Қазақстан Республикасы Ауыл шаруашылығы министрлігі. "Агроөнеркәсіп кешенін дамыту стратегиясы". – Астана, 2021. – 314 бет.
-
Бекенов Т. "Көлік логистикасындағы математикалық модельдер". – Алматы: Транспорт, 2020. – 184 бет.
ҚОСЫМША
Төменде MATLAB, Python (NumPy, SciPy), және Excel Solver-дың ерекшеліктері мен салыстырмалы қасиеттерін қамтитын үлкен кесте берілген: (7-кесте)
|
Сипаттамалар |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Бағасы |
Ақылы (қымбат лицензия қажет) |
Тегін және ашық код |
Excel бағдарламасымен бірге қолжетімді |
|
Қолдану саласы |
Ғылыми зерттеулер, инженерия, физика, математика |
Барлық салалар: ғылым, бизнес, машиналық оқыту |
Бизнес-талдау, шағын оңтайландыру есептері |
|
Қолданушылық интерфейсі |
Командалық жол және графикалық интерфейс |
Командалық жол (код жазу) |
Толығымен графикалық интерфейс |
|
Оңтайландыру түрлері |
Сызықтық, сызықсыз, дискретті, көп мақсатты |
Сызықтық, сызықсыз |
Тек сызықтық оңтайландыру |
|
Жылдамдығы |
Жоғары (үлкен есептерге бейімделген) |
Орташа |
Төмен (үлкен есептерге жарамсыз) |
|
Деректер визуализациясы |
Жетілдірілген (жолақты диаграммалар, 3D графиктер) |
Жетілдірілген (Matplotlib, Seaborn құралдары арқылы) |
Қарапайым графиктер мен диаграммалар |
|
Күрделі есептерге жарамдылығы |
Өте жоғары |
Жоғары |
Төмен |
|
Интеграция мүмкіндігі |
Шектеулі (басқа тілдермен интеграция қиын) |
Жоғары (Python көптеген кітапханалармен үйлесімді) |
Шектеулі |
|
Бағдарламалау деңгейі |
Мамандарға арналған |
Жаңадан бастаушыларға да, мамандарға да ыңғайлы |
Бағдарламалау қажет емес, қолдану оңай |
|
Арнайы кітапханалар |
Математикалық модельдеу, сигнал өңдеу, оңтайландыру |
SciPy, NumPy, Matplotlib, TensorFlow, Pandas және т.б. |
Арнайы кітапхана жоқ |
|
Нәтижелерді талдау |
Графикалық және аналитикалық құралдары өте дамыған |
Визуализация құралдары арқылы тиімді |
Тек мәтіндік және диаграмма түріндегі нәтижелер |
|
Оқу ресурстары |
Толық құжаттама және қосымша курстар (ақылы) |
Ашық құжаттама, онлайн курстар (тегін және ақылы) |
Excel-дің негізгі оқу құралдары жеткілікті |
|
Артықшылықтары |
Инженерия мен ғылым саласында стандартқа айналған |
Икемді, басқа жүйелермен интеграциялану мүмкіндігі жоғары |
Қарапайым есептерді шешуге өте ыңғайлы |
|
Кемшіліктері |
Қымбат және күрделі |
Кейбір үлкен есептерде баяу |
Күрделі және үлкен есептерге жарамсыз |
Әртүрлі әдістердің салыстырмалы тиімділігі (8-кесте)
|
Критерий |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Есептеу дәлдігі |
Жоғары: ғылыми және инженерлік есептерге жарамды |
Жоғары: әртүрлі әдістермен икемді жұмыс істейді |
Орташа: шағын және қарапайым есептерге ғана жарамды |
|
Есептеу жылдамдығы |
Жоғары: үлкен көлемдегі есептерді тез шешеді |
Орташа: кейбір есептерде баяу болуы мүмкін |
Төмен: үлкен есептерде өте баяу |
|
Ресурстарды пайдалану |
Орташа: аппараттық ресурстарды тиімді пайдаланады |
Жоғары: үлкен деректермен икемді жұмыс істейді |
Төмен: шағын ресурстарды қажет етеді, бірақ шектеулі |
|
Икемділік |
Жоғары: сызықтық, сызықсыз, дискретті оңтайландыру |
Өте жоғары: әртүрлі кітапханалармен кең қолданылады |
Шектеулі: тек қарапайым және сызықтық есептерге арналған |
|
Визуализация |
Жетілдірілген: деректерді 2D және 3D форматта көрсету |
Жетілдірілген: Matplotlib және Seaborn арқылы визуализация |
Қарапайым: негізгі диаграммалар |
|
Қолдану қарапайымдылығы |
Орташа: мамандарға арналған |
Жоғары: бағдарламалау білсеңіз, оңай |
Өте жоғары: интуитивті интерфейс |
|
Құжаттама мен қолдау |
Толық: кәсіби деңгейдегі қолдау және ресурстар |
Көптеген тегін онлайн ресурстар мен форумдар |
Негізгі Excel құжаттамасымен шектеледі |
|
Бағдарламалау мүмкіндігі |
Қажет: код жазуды талап етеді |
Қажет: еркін бағдарламалау мүмкіндігі |
Қажет емес: графикалық интерфейс арқылы жұмыс істейді |
|
Кітапханалар мен құралдар |
Арнайы: Signal Processing, Optimization Toolbox |
Ашық: SciPy, NumPy, TensorFlow және басқа кеңейтілімдер |
Қосымша кітапханаларсыз жұмыс істейді |
Нақты жүйелерге бейімдеу кезіндегі қиындықтар (5-кесте)
|
Қиындықтар |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Есептің күрделілігі |
Күрделі сызықсыз есептерді шешу үшін арнайы әдістер бар |
Эвристикалық әдістерді қолдану арқылы күрделі есептерге бейімделеді |
Күрделі есептерге бейімдеу мүмкін емес |
|
Шектеу шарттарын енгізу |
Күрделі теңдеулер мен айнымалыларды қолдайды |
Шектеулерді еркін анықтау мүмкіндігі бар |
Тек сызықтық шектеулермен жұмыс істейді |
|
Нәтижелерді интерпретациялау |
Визуализация мен аналитикалық құралдар дамыған |
Нәтижелерді визуализациялау үшін кең мүмкіндіктер |
Интерпретациясы қиын, қосымша талдау қажет |
|
Шешімнің орнықтылығы |
Орнықтылықты жоғары деңгейде қамтамасыз етеді |
Сандық әдістер арқылы орнықтылықты реттей алады |
Орнықтылығы төмен |
|
Үлкен есептерді бейімдеу |
Жоғары өнімділік: үлкен есептерде тиімді |
Жақсы бейімделеді, бірақ кейде жылдамдық шектеулі |
Үлкен есептерде қолдану мүмкін емес |
|
Бейімделу икемділігі |
Жоғары: нақты инженерлік есептерге тез бейімделеді |
Өте жоғары: деректер мен есептердің барлық түріне бейімделеді |
Төмен: тек қарапайым үлгілер үшін жарамды |
|
Қолдау көрсету |
Лицензиялық қолдау (MathWorks) |
Қоғамдық форумдар мен қауымдастық |
Microsoft қолдау көрсетеді |
|
Үлкен деректермен жұмыс |
Орташа: үлкен көлемді деректерді өңдеуге шектеулі |
Жоғары: үлкен деректерді талдау және оңтайландыруда тиімді |
Мүмкін емес: үлкен деректерді өңдеу қарастырылмаған |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Оңтайландыру параметрі
Оңтайландыру параметрі
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ ЖОҒАРЫ БІЛІМ МИНИСТРЛІГІ
«ҚАЗАҚ ҰЛТТЫҚ ҚЫЗДАР ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ» КеАҚ
Физика, математика және цифрлық технологиялар институт
Математика кафедрасы
ЖОБАЛЫҚ ЖҰМЫС
Тақырыбы: Оңтайландыру параметрлері
Пән атауы: Ғылыми зерттеу негіздері
Мамандық атауы, курс: 6B01502-Математика-физика, 3-курс
Орындаған: Абдуллаева Сарвиноз Тулкуновна
Тексерген: Исмайылов Аманкелди Есиркегенович
Алматы, 2024
Мазмұны:
Бет
нөмірі
|
КІРІСПЕ...................................................................................................................... |
3 |
|
І. Теориялық бөлім |
|
|
1.1 Оңтайландыру ұғымы және анықтамасы........................................................... |
5 |
|
1.2 Оңтайландыру әдістері......................................................................................... 1.3 Параметрлерді математикалық модельдерде қолдану...................................... 1.4 Оңтайландыру теориясының қолданылу салалары........................................... 1.5 Заманауи оңтайландыру технологиялары.......................................................... |
8 11 13 16 |
|
|
|
|
ІІ. Тәжірибелік бөлім |
|
|
2.1 Практикалық мысалдардың таңдалуы............................................................... |
19 |
|
2.2 Математикалық модельдер арқылы оңтайландыру есептерін шешу............... |
19 |
|
2.3 Оңтайландырудың тиімділігін бағалау............................................................... 2.4 Физика саласындағы оңтайландыру параметрлері............................................ |
21 23 |
|
ҚОРЫТЫНДЫ.......................................................................................................... |
25 |
|
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР.................................................................. |
28 |
|
ҚОСЫМША |
|
Кіріспе
Оңтайландыру — белгілі бір шарттар мен шектеулерді ескере отырып, жүйенің немесе процестің тиімділігін арттыруға бағытталған математикалық әдістер мен тәсілдер жиынтығы. Бұл процесс көптеген түрлі салаларда кеңінен қолданылып, әртүрлі тапсырмаларды шешуге мүмкіндік береді. Оңтайландырудың негізгі мақсаты — барлық мүмкін шешімдер арасынан ең тиімдісін, ресурстарды ең аз жұмсайтын немесе нәтижені ең жоғары деңгейде қамтамасыз ететін шешімді таңдау. Оңтайландыру әдістері жүйенің немесе процестің жұмысын жетілдіру мақсатында маңызды құрал болып табылады.
Өндірістік процестерді жетілдіру, ресурстарды тиімді пайдалану, көлік логистикасы, ақпараттық жүйелерді басқару және басқа да көптеген салаларда оңтайландыру әдістері қолданылып келеді. Әсіресе, қазіргі заманда бұл салаларда тиімді шешімдер қабылдаудың маңызы зор, өйткені ресурстарды дұрыс пайдалану мен оптимизациялау компаниялардың бәсекеге қабілеттілігін арттыруға, шығындарды азайтуға және өнімділікті жақсартуға ықпал етеді. Сонымен қатар, оңтайландыру нәтижесінде алынған шешімдер жүйелер мен процестердің тиімділігін арттыруға мүмкіндік береді.
Оңтайландырудың негізгі мақсаттары арасында мақсатты функцияны (немесе критерийді) максимизациялау немесе минимизациялау арқылы жүйенің тиімділігін арттыру . Осы мақсатқа жету үшін әртүрлі оңтайландыру әдістері қолданылады. Мысалы, сызықтық және сызықсыз, дискретті және үздіксіз, бір мақсатты және көп мақсатты әдістер бар. Әр әдіс өзінің ерекшеліктерімен және қолдану аясына сәйкес түрлі проблемаларды шешуге мүмкіндік береді. Бұл жоба оңтайландыру әдістерін жан-жақты қарастырып, олардың тиімділігін талдауды және әртүрлі салаларда қолдану мүмкіндіктерін зерттеуді мақсат етеді.
Оңтайландыру әдістерінің дұрыс таңдалуы мен қолданылуы өндірістік процестерді жетілдіруге, шығындарды азайтуға, тиімділікті арттыруға және шешім қабылдау сапасын жақсартуға мүмкіндік береді. Бұл жұмыс оңтайландыру параметрлерінің рөлін және оларды түрлі салаларда қолдану әдістерін қарастырып, параметрлердің тиімділігін бағалау үшін қолданылатын математикалық модельдер мен әдістерді зерттеуге арналған.
Тақырыптың өзектілігі
Қазіргі заманның экономикасы, өндірісі, ақпараттық технологиялары мен логистикасы және басқа да көптеген салаларында ресурстарды тиімді пайдалану мәселесі аса өзекті болып отыр. Әрбір саланың алдында тұрған мәселе — ресурстарды дұрыс бөлу, оларды тиімді пайдалану және ең жақсы нәтижеге жету болып табылады. Осы мәселелерді шешуде оңтайландырудың маңызы зор. Себебі, оңтайландыру — бұл белгілі бір процестер мен жүйелердегі тиімділікті арттыру үшін қолданылатын математикалық құрал болып табылады. Оңтайландыру әдістері экономиканың әр түрлі салаларында ресурстарды үнемдеуге, шығындарды азайтуға және пайда мөлшерін арттыруға көмектеседі.
Математикалық модельдер мен оңтайландыру әдістері экономикалық, өндірістік және логистикалық процестерді басқаруда маңызды рөл атқарады. Мысалы, кәсіпорындар мен ұйымдар өздерінің өндірістік ресурстарын дұрыс бөлуді, өнімнің сапасын арттыруды, қызмет көрсету саласындағы процестерді жетілдіруді және логистикалық шығындарды азайтуды оңтайландыру әдістері арқылы жүзеге асырады. Осы тұрғыдан алғанда, оңтайландыру параметрлерін зерттеу және олардың тиімділігін бағалау жұмысының өзектілігі айқын болады.
Зерттеудің жаңашылдығы
Бұл жұмыстың жаңашылдығы — әртүрлі оңтайландыру әдістерін ғана қарастырумен шектелмей, олардың нақты салалардағы практикалық қолданысын зерттеу болып табылады. Сонымен қатар, зерттеуде математикалық модельдер арқылы оңтайландыру параметрлерінің тиімділігін бағалау әдістері көрсетіледі. Мұндай зерттеу жұмыстарында оңтайландыру әдістерін дұрыс таңдау, оларды қолданудың тиімділігін зерттеу және нақты нәтижелерді алу мүмкіндіктері артады.
Зерттеу барысында әртүрлі салалардағы оңтайландыру параметрлері зерттеліп, олардың тиімділігін бағалауға арналған әдістер ұсынылады. Бұл зерттеу оңтайландыру әдістерінің әртүрлі салаларға қалай бейімделетінін және оларды тиімді пайдалану жолдарын көрсетеді. Сонымен қатар, жұмыс оңтайландыру параметрлерін зерттеу арқылы өндірістік процестерді жетілдіруге, ресурстарды үнемдеуге және шешім қабылдау сапасын арттыруға көмектеседі.
Зерттеудің мазмұны
Зерттеудің мазмұны оңтайландыру параметрлеріне арналады, яғни кез келген жүйені немесе процесті оңтайландыру үшін қолданылатын негізгі сипаттамалар мен факторлар. Оңтайландыру параметрлері әртүрлі саладағы процестерді басқаруда тиімді шешімдер қабылдауға мүмкіндік береді. Бұл параметрлердің қолданылуы өндірістік процестердің тиімділігін арттыруға, шығындарды азайтуға және жүйенің жалпы өнімділігін жақсартуға ықпал етеді. Сондықтан оңтайландыру параметрлерін зерттеу және олардың салаларда қолданылуын талдау маңызды міндет болып табылады.
Зерттеудің мақсаты
Жұмыстың негізгі мақсаты — оңтайландыру параметрлерінің мәнін, олардың түрлерін және әртүрлі салаларда қалай қолданылатынын зерттеу. Сонымен қатар, оңтайландыру әдістерін қолдану барысында параметрлердің рөлін айқындап, олардың тиімділігін бағалау жолдарын көрсету болып табылады. Бұл зерттеу оңтайландыру әдістері мен параметрлерінің тиімділігін бағалауға арналған әдіснамалық жолдарды ұсынуды мақсат етеді.
Зерттеудің міндеттері
Жұмыстың негізгі міндеттері төмендегідей:
-
Оңтайландыру параметрлерінің түрлері мен олардың мәнін теориялық тұрғыдан зерттеу;
-
Оңтайландыру параметрлерінің әртүрлі салаларда қолданылуын және олардың тиімділігін талдау;
-
Параметрлерді үйлестіру және бағалау әдістерін анықтау;
-
Оңтайландыру параметрлерін тиімді бағалау үшін критерийлер мен көрсеткіштерді зерттеу;
-
Түрлі математикалық модельдердегі оңтайландыру параметрлерін анықтау;
-
Нәтижелерді талдап, оңтайландыру параметрлерін қолданудың тиімділігін көрсететін практикалық мысалдар келтіру.
Зерттеудің құрылымы
Жұмыс кіріспеден, негізгі бөлімнен және қорытындыдан тұрады. Негізгі бөлім екі тараудан тұрады, біріншісінде оңтайландыру параметрлерінің түрлері мен олардың тиімділігін зерттеу мәселелері қарастырылады, ал екінші тарауда оңтайландыру әдістерінің практикалық қолданылуы және оларды бағалау тәсілдері талданады. Қорытынды бөлімде зерттеудің нәтижелері қорытындыланып, оңтайландыру параметрлерін қолданудың тиімділігі туралы ұсыныстар жасалады.
Негізгі бөлім
І. Теориялық бөлім
1.1 Оңтайландыру ұғымы мен мәні
Оңтайландыру — бұл белгілі бір мақсатқа жету үшін жүйенің немесе процестің тиімділігін арттыруға бағытталған математикалық әдістер мен тәсілдердің жиынтығы. Оңтайландыруда "тиімділік" ұғымы жүйенің немесе процестің нәтижесін жақсарту, мүмкін болатын барлық шешімдер арасынан ең тиімдісін таңдау дегенді білдіреді. Бұл процестің мақсаты белгілі бір критерийді максимизациялау немесе минимизациялау болып табылады. Әдетте, оңтайландыру мәселелері экономикалық, өндірістік, логистикалық, техникалық және басқа да салаларда туындайды, себебі бұл салалардың барлығы тиімді ресурстарды пайдалануға және нәтижелерді жақсартуға бағытталған.
Оңтайландырудың негізгі мақсаты — максимизациялау немесе минимизациялау болып табылады. Максимизациялау — мәні оңтайландыру есептерінде мақсатты функцияның мәнін арттыру мақсатында қолданылатын тәсіл. Ал минимизациялау — мақсатты функцияның мәнін азайту арқылы жүзеге асырылады. Бұл процесте негізгі рөлді мақсатты функция және шектеу шарттары атқарады, олар есептің тиімді шешімін табуға мүмкіндік береді [1,23].
Егер қарапайым тілмен түсіндірсек, оңтайландыру — бұл белгілі бір мақсатқа жету үшін ең жақсы шешім немесе тәсіл табу. Бұл жағдайда "ең жақсы" дегеніміз — жүйені мүмкіндігінше тиімді ету, яғни белгілі бір ресурстарды немесе уақытты минималды түрде пайдалану арқылы максималды нәтиже алу. Мұндай есептерді шешу барысында жүйенің барлық параметрлері мен шарттары есепке алынады, бұл оңтайландыру әдістерінің әртүрлі әдіснамаларын қажет етеді.
Оңтайландыру мақсаты мен әдістері
Оңтайландырудың басты мақсаты — жүйенің тиімділігін арттыру немесе белгілі бір процесті оптимизациялау. Бұл мақсатты жүзеге асыру үшін мақсатты функция мен шектеу шарттары анықталады. Мақсатты функция — оңтайландыру мәселесінің шешімін іздейтін көрсеткіш. Әдетте, мақсатты функцияны максимизациялау немесе минимизациялау керек. Мысалы, өндіріс процесін оңтайландыру кезінде мақсатты функция өндіріс шығындарын азайту немесе өнім сапасын жақсарту болуы мүмкін. Қаржы секторында мақсатты функция ретінде инвестицияның пайдасын максимизациялау қарастырылуы мүмкін. Сонымен қатар, ақпараттық жүйелер мен көлік логистикасында уақытты үнемдеу немесе жүк тасымалдаудың шығындарын төмендету мақсаттары қойылады.
Шектеу шарттары — бұл есептің мүмкін болатын шешімдер жиынын шектейтін теңдеулер немесе теңсіздіктер. Шектеулер белгілі бір процестің нақты шарттарын немесе ресурстарын көрсетеді. Шектеулер болмаса, оптимизация мәселесі шешілмейді, өйткені жүйе тек идеалды жағдайды көрсетіп, нақты өмірдегі жағдайларға сәйкес келмейді. Мысалы, өндірістік процеске арналған оңтайландыру мәселесінде шикізаттың немесе жұмыс күшінің шектеулілігі, белгілі бір уақыт аралығындағы жұмыстарды орындау қажеттілігі шектеулер ретінде қарастырылады.
Оңтайландыру әдістері
Оңтайландыруды шешу үшін қолданылатын әдістер мен тәсілдер өте көп, өйткені әрбір мәселе мен есеп түріне сәйкес әр түрлі әдістер қолданылады. Бұл әдістерді жалпы түрде үш категорияға бөлуге болады: сызықтық оңтайландыру, сызықсыз оңтайландыру және дискретті оңтайландыру.
Сызықтық оңтайландыру (Линейное программирование) — бұл шешімдер кеңістігі мен мақсатты функциясы сызықтық түрде берілетін оңтайландыру есептерін шешу әдісі. Сызықтық бағдарламалауда мақсатты функциясы мен шектеулерінің бәрі сызықтық болып табылады. Мұндай есептерді шешу үшін симплекс әдісі пайдаланылады. Симплекс әдісі — бұл көпбұрышты аймақтың төбелерінде жүріп, ең тиімді шешімді таңдау тәсілі. Бұл әдіс өндіріс пен экономикадағы көптеген нақты есептерді шешуге қолданылады [2,40].
Сызықсыз оңтайландыру (Нелинейное программирование) — бұл есептерде мақсатты функция немесе шектеулер сызықсыз функциялар түрінде беріледі. Сызықсыз оңтайландыру есептерінде шешімдер кеңістігі күрделі болады және шешімді табу үшін арнайы әдістер мен техникалар қажет. Мұнда градиенттік әдістер, Ньютон әдісі, Лагранж көбейткіштері және басқа да әдістер қолданылуы мүмкін. Сызықсыз оңтайландыру әдістері көбінесе үлкен өлшемді және күрделі есептерді шешуде тиімді пайдаланылады [3,50].
Дискретті оңтайландыру (Комбинаторное программирование) — бұл айнымалылар бүтін сандармен шектелетін оңтайландыру есептерін шешу әдісі. Мұндай есептер көбінесе көлік логистикасы, өндіріс жоспарлау және басқа да салаларда кездеседі. Дискретті оңтайландыру есептерінде шешімдер жиыны шектеулі болғандықтан, эвристикалық әдістер қолданылады. Мысалы, генетикалық алгоритмдер мен құмырсқа колониясы алгоритмдері сияқты табиғаттан алынған әдістер осындай есептерде қолданылады [4,65].
Мақсатты функция және шектеу шарттары
Мақсатты функция — оңтайландыру процесіндегі негізгі компонент. Ол жүйенің немесе процестің тиімділігін сипаттайтын өрнек болып табылады. Мақсатты функция әртүрлі формада болуы мүмкін: сызықтық немесе сызықсыз, тұтас немесе үздіксіз. Мысалы, қаржы нарығында мақсатты функция инвестицияның максималды пайдасын немесе шығындардың минимизациясын көрсетуі мүмкін. Өндірісте мақсатты функция шығындарды төмендетуді немесе өндіріс көлемін арттыруды мақсат етіп қоюы мүмкін. Мақсатты функцияның мәні максимизациялау немесе минимизациялау арқылы жақсартылуға тиіс [5,70]. Шектеу шарттары — оңтайландыру есептеріндегі шешімдер жиынына шектеулер қоятын теңдеулер мен теңсіздіктер. Шектеулер әдетте техникалық, қаржылық, ресурстық немесе уақыттық болады. Шектеулердің арқасында шешім кеңістігі тарылып, нақты өмірдегі жағдайларға сәйкес шешімдер табуға мүмкіндік береді. Мысалы, өндірістік оңтайландыру мәселесінде шикізаттың немесе энергияның көлемі шектеулі болуы мүмкін, ал көлік логистикасында тасымалдау мерзімі мен маршруттары да шектеулер ретінде қарастырылады.
Оңтайландыру түрлерінің теориялық сипаттамасы
Оңтайландыру түрлерінің кең таралған теориялық сипаттамалары бар. Әрбір оңтайландыру түрінің өз ерекшеліктері мен шешу әдістері бар.
Шартсыз және шартты оңтайландыру:
-
Шартсыз оңтайландыру - есептерінде шектеулер жоқ. Мақсатты функцияны максимизациялау немесе минимизациялау үшін шешімдер кеңістігінен экстремум табу жеткілікті. Бұл типтегі оңтайландыру есептері қарапайым әрі тиімді болса да, нақты әлемде шектеулерді ескеру қажеттілігі туындайды.
-
Шартты оңтайландыру - есептерінде мақсатты функция шектеулермен бірге қарастырылады. Бұл есептер шектеулерді нақты есептеулерге қосуға мүмкіндік береді. Шектеулерді ескере отырып ең тиімді шешімді табу күрделенеді, бірақ бұл шешімдер нақтырақ болады.
Сызықтық және сызықсыз оңтайландыру:
-
Сызықтық оңтайландыру - сызықтық теңдеулер мен теңсіздіктерден тұратын есептер үшін тиімді. Мұндай есептер қарапайым және жоғары дәлдікпен шешіледі, сондықтан олар өндіріс, қаржы және басқа да кең қолданылатын салаларда жиі қолданылады.
-
Сызықсыз оңтайландыру - есептері күрделірек, өйткені мақсатты функция немесе шектеулер сызықсыз болады. Мұндай есептерде шешім кеңістігі өте күрделі болғандықтан, оларды шешу үшін арнайы әдістер мен құралдар қажет. Алайда, сызықсыз әдістер нақты өмірдегі көптеген мәселелерге қолданылады, өйткені көптеген жүйелер мен процестер сызықсыз сипатталады.
Дискретті және үздіксіз оңтайландыру:
-
Дискретті оңтайландыру - көптеген комбинаторлық есептерде қолданылады, онда айнымалылар бүтін сандардан тұрады. Бұл әдіс көлік логистикасы немесе өндірістік процестер сияқты нақты есептерде тиімді. Бірақ шешімдер кеңістігі шектеулі болғандықтан, кейде дұрыс нәтижеге жету үшін қадамдық әдістерді қолдану қажет.
-
Үздіксіз оңтайландыру - айнымалылар нақты сандар болған жағдайда қолданылады. Мұндай есептерде шешім кеңістігі үздіксіз болғандықтан, шешім табу ыңғайлы және мүмкін шешімдер жиыны үлкен болады. Үздіксіз оңтайландыруды көбінесе математикалық модельдеу мен күрделі жүйелерді шешу үшін қолданады.
Бір мақсатты және көп мақсатты оңтайландыру:
-
Бір мақсатты оңтайландыру - тек бір ғана мақсатты функцияны шешуді қамтиды, мысалы, шығындарды азайту немесе пайдасын арттыру. Бұл оңтайландыру әдісі қарапайым және түсінікті, бірақ бірнеше мақсатты есептерде тиімді емес.
-
Көп мақсатты оңтайландыру - бірнеше мақсатты функцияны бір уақытта шешу үшін пайдаланылады. Бұл әдіс күрделі шешімдер қабылдауды қажет ететін жағдайларда қолданылады. Мысалы, логистикада бір уақытта уақытты үнемдеу мен шығындарды төмендету мақсаттары қойылуы мүмкін. Мұндай есептерде шешімдер арасындағы тепе-теңдікті табу өте маңызды.
1-кесте Оңтайландыру түрлерінің салыстырмалы сипаттамасы
|
Оңтайландыру түрі |
Қолдану аясы |
Артықшылықтары |
Кемшіліктері |
|
Шартсыз оңтайландыру |
Белгілі бір шектеулер жоқ кезде пайдаланылады. |
Шешімдер кеңістігі таза, ешқандай шектеулер жоқ. |
Шектеулер жоқ болғандықтан, нақты мәселелерге бейімделмейді. |
|
Шартты оңтайландыру |
Шектеулер болған жағдайда қолданылады. |
Мүмкін болатын шешімдер жиынын нақты шектеулермен анықтайды. |
Шектеулерді ескеру процесі күрделенуі мүмкін. |
|
Сызықтық оңтайландыру |
Мақсатты функция мен шектеулер сызықтық болғанда қолданылады. |
Математикалық тұрғыдан қарапайым және тиімді әдіс. |
Сызықтық модельдердің шектеулігі, нақты әлемде сирек кездеседі. |
|
Сызықсыз оңтайландыру |
Мақсатты функция мен шектеулер сызықсыз болғанда пайдаланылады. |
Күрделі және нақты әлемде кездесетін көптеген жағдайды шешеді. |
Қиындықтар туғызуы мүмкін, әсіресе локалды экстремумдарды табуда. |
|
Дискретті оңтайландыру |
Айнымалылар бүтін сандар болғанда қолданылады. |
Қаржылық, логистикалық есептерде қолданылады. |
Қадамдық шешімдер кеңістігіндегі есептерді шешу қиын. |
|
Үздіксіз оңтайландыру |
Айнымалылар нақты сандар болғанда пайдаланылады. |
Үздіксіз шешімдер кеңістігі тиімдірек болып табылады. |
Әдетте, функцияның экстремумын табу кезінде қосымша есептеулер қажет. |
|
Бір мақсатты оңтайландыру |
Бір ғана мақсатты функциямен есептерді шешу кезінде қолданылады. |
Бір мақсатқа бағытталған шешімдер оңай анықталады. |
Көп мақсатты есептерде кемшілік болуы мүмкін. |
|
Көп мақсатты оңтайландыру |
Бірнеше мақсатты функциямен жұмыс істейтін есептер. |
Бірнеше мақсатты ескеретін шешімдер табуға мүмкіндік береді. |
Бір мақсатты оңтайландыруға қарағанда күрделі. |
Кестеде көрсетілгендей, әрбір оңтайландыру түрінің өз артықшылықтары мен кемшіліктері бар. Қолдану саласына және есептің нақты сипаттамаларына қарай дұрыс әдісті таңдау қажет. Әрбір әдіс мәселені тиімді шешу үшін өзінің ерекше әдіснамасын және математикалық құралдарын қолданады. Мұндай салыстыру оңтайландыру әдістерінің түрлерін жақсырақ түсінуге және олардың практикалық қолданылу аясына байланысты таңдау жасауға көмектеседі.
-
Оңтайландыру әдістері
Оңтайландыру есептерін шешу үшін әртүрлі математикалық әдістер мен тәсілдер қолданылады. Олардың әрқайсысының өзіндік ерекшеліктері, қолдану аясы және тиімділігі бар. Оңтайландыру әдістері математикалық модельдеу және шешім қабылдау процесінде маңызды рөл атқарады. Бұл бөлімде ең кең таралған оңтайландыру әдістері:
-
Симплекс әдісі.
-
Градиенттік әдістер.
-
Ньютон әдісі.
-
Эвристикалық әдістер (генетикалық алгоритмдер мен рой интеллектісі) қарастырылады.
1. Симплекс әдісі
Симплекс әдісі сызықтық бағдарламалаудың негізгі әдісі болып табылады. Ол шектеулер мен мақсатты функциясы сызықтық түрде берілген есептерді шешу үшін қолданылады. Симплекс әдісі геометриялық шешімдер кеңістігінде жұмыс істейді және ол шешімдердің кеңістігіндегі төбелерді тексеріп, ең тиімді шешімді табуға мүмкіндік береді [1,45].
Әдістің сипаттамасы: Симплекс әдісі сызықтық бағдарламалау есептерінің шешімдерін табу үшін көпбұрышты аймақтың төбелерін зерттейді. Әдіс оңтайлы шешімге жету үшін аймақтың бір төбесінен екіншісіне көшіп, әр қадамда мақсатты функцияның мәнін жақсартады [1,47].

1-Сурет Симплекс әдісінің артықшылықтар, кемшіліктері, қолданы салалары [2,52].
Кесте 2: Симплекс әдісінің қолдану салалары
|
Қолдану саласы |
Мақсат |
Әдіс қолдану |
|
Өндірістік процестер |
Шығындарды минимизациялау |
Симплекс әдісі |
|
Қаржы саласы |
Пайданы максимизациялау |
Симплекс әдісі |
|
Логистика, көлік жүйесі |
Маршруттар мен тасымалдау шығындарын төмендету |
Симплекс әдісі |
2. Градиенттік әдістер: Градиенттік әдістер сызықсыз оңтайландыру есептерін шешуге арналған әдістердің кең ауқымын қамтиды. Бұл әдіс мақсатты функцияның кеңістігін пайдаланып, оның экстремум нүктесіне жылжиды. Градиенттік әдіс әсіресе жоғары өлшемді есептерді шешуде тиімді болады [3,65]. Әдістің сипаттамасы: Градиенттік әдіс — мақсатты функцияның градиентін (туындысын) есептеу арқылы минимизация немесе максимизациялау процесі. Бұл әдіс қай бағытта қозғалу керектігін анықтау үшін мақсатты функцияның кеңісін пайдаланады. Градиенттік түсу әдісі — ең кең таралған әдіс.
3-кесте Градиенттік әдістің артықшылықтар, кемшіліктері, қолданы салалары [4,75].
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Нақты шешімдер береді. |
Локалды минимумдар немесе максимумдарға түсуі мүмкін. |
Экономика мен қаржы саласында модельдеу. |
|
Қарапайым және тиімді, көптеген есептерде оңтайлы нәтижелер береді. |
Кейде функцияның туындысы жоқ немесе есептеу қиынға соғуы мүмкін. |
Жасанды интеллект және машиналық оқыту. |
|
|
|
Құрылымдық және инженерлік жобалар. |
График 1: Градиенттік түсу әдісімен минимизация
y | *
| *
| *
| *
|*_______________________
| x_min
Түсіндірме: Графикте көрсетілгендей, градиенттік әдіс функцияның минимумы орналасқан нүктеге қарай жылжиды. Әрбір қара нүкте әдістің қадамдарын білдіреді.
3. Ньютон әдісі
Ньютон әдісі — бұл сызықсыз оңтайландыру үшін қолданылатын жоғары дәлдікті әдіс. Бұл әдіс екінші дәрежелі туынды (гессиан) арқылы функционалдың экстремум нүктесін табуға көмектеседі. Ньютон әдісі оңтайландырудың тиімді және жылдам әдісі болып табылады, бірақ ол есептеу тұрғысынан ауыр болуы мүмкін [5,80]. Әдістің сипаттамасы: Ньютон әдісі екінші туындыны пайдаланып, шешімнің жақын мәнін табуға бағытталған. Әдіс функцияның екпініне қарай алға жылжып, қадамды әр кезеңде қайта есептейді.

2-Сурет Ньютон әдісінің артықшылықтар, кемшіліктері, қолданы салалары [5,85].
4. Эвристикалық әдістер (генетикалық алгоритмдер, рой интеллектісі)
Эвристикалық әдістер — бұл табиғаттан немесе адамзат іс-әрекеттерінен шабыт алып, шешімдер кеңістігіндегі тиімді шешімдер іздеуге арналған әдістер. Генетикалық алгоритмдер мен рой интеллектісі — эвристикалық әдістердің негізінде тұрған алгоритмдер [6,100].
Генетикалық алгоритмдер: Генетикалық алгоритмдер табиғаттың эволюция принциптеріне негізделген. Бұл әдіс көбінесе комбинаторлық және үлкен шешімдер кеңістігіндегі мәселелерді шешу үшін қолданылады. Әдіс шешімдерді кроссовер, мутация және табиғи сұрыптау принциптері арқылы жетілдіреді.
3-кесте Эвристикалық әдістің артықшылықтар, кемшіліктері, қолданы салалары
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Үлкен және күрделі мәселелер үшін тиімді. |
Дәл нәтижеге қол жеткізу кепілдігі жоқ. |
Қаржы және инвестициялық жоспарлау. |
|
Дәл шешімді қамтамасыз етпейді, бірақ жақын нәтижелер табуға мүмкіндік береді. |
Есептеу уақытын арттыруы мүмкін. |
Логистика мен өндіріс процестерін оңтайландыру. |
Рой интеллектісі: Рой интеллектісі табиғаттағы жануарлардың мінез-құлқынан шабыт алады (мысалы, құмырсқалар немесе құстардың ұшуы). Бұл әдіс көп агентті жүйелердің тиімді шешім табуына көмектеседі.
4-кесте Рой интеллектісінің артықшылықтар, кемшіліктері, қолданы салалары [6,105].
|
Артықшылықтары |
Кемшіліктері |
Қолдану салалары |
|
Бірнеше мақсатты функциялармен жұмыс істегенде тиімді. |
Әдіс әрдайым нақты шешімді табуға кепілдік бермейді. |
Тасымалдау және көлік жүйелеріндегі оптимизациялау. |
|
Күрделі комбинаторлық мәселелерді шешуге мүмкіндігі бар. |
Эвристикалық әдістердің қатарына жататындықтан, уақыт пен ресурстарды көп талап етеді. |
Жасанды интеллект, нейрондық желілер. |
Оңтайландыру әдістері әртүрлі есептерді шешуде маңызды рөл атқарады. Симплекс әдісі сызықтық есептер үшін тиімді болса, градиенттік әдістер жоғары өлшемді есептерге жақсы жарайды. Ньютон әдісі жоғары дәлдікпен шешімдер табуға көмектеседі, ал эвристикалық әдістер үлкен және күрделі есептерді шешуде ерекше маңызға ие[7,110].
1.3 Параметрлерді математикалық модельдерде қолдану
Оңтайландыру есептерін математикалық модельдеуде параметрлер негізгі рөл атқарады. Олар модельдің кіріс мәліметтерін сипаттайды, шектеулерді анықтайды және мақсатты функцияны қалыптастыруға мүмкіндік береді. Бұл бөлімде параметрлердің мәні мен рөлі, оларды есептеу әдістері, сондай-ақ сызықтық және сызықсыз параметрлік модельдер жан-жақты қарастырылады.
Параметрлердің мәні мен рөлі
Параметрлер — бұл математикалық модельдердегі тұрақты шамалар немесе айнымалылар, олар шешім қабылдауға әсер етеді. Параметрлер жүйе жұмысының бастапқы шарттарын сипаттап, математикалық модельдерді нақтылау үшін қажет.
Параметрлердің негізгі рөлі:
-
Жүйені сипаттау: Параметрлер жүйенің немесе процестің жұмысын сандық түрде көрсетеді.
-
Шешімдерді нақтылау: Параметрлер мақсатты функция мен шектеулерді құру үшін қолданылады.
-
Жүйенің тиімділігін бағалау: Параметрлер өзгерген кезде модель нәтижелерінің өзгерісін бағалауға мүмкіндік береді [1, 47].
Мысал:
Өндірістік процестегі параметрлер:
-
 : шикізат көлемі
(тонна),
: шикізат көлемі
(тонна), -
 : жұмыс уақыты
(сағат),
: жұмыс уақыты
(сағат), -
 : шикізат бағасы
(теңге/тонна).
: шикізат бағасы
(теңге/тонна).
Мақсатты функция:
 (шығындарды минимизациялау).
(шығындарды минимизациялау).
Бұл модельде  және
және  параметрлері модельді шешу нәтижелеріне тікелей әсер
етеді.
параметрлері модельді шешу нәтижелеріне тікелей әсер
етеді.
Кесте 5: Параметрлердің мысалдары және олардың қолдану салалары
|
Параметр атауы |
Мәні |
Қолдану саласы |
|
Өндіріс қуаты |
Өнім шығару көлемін сипаттайды |
Өндіріс жүйелері |
|
Шикізат шығындары |
Шикізатқа жұмсалатын шығындар |
Экономика және өндіріс |
|
Тасымалдау уақыты |
Логистикадағы тасымалдау мерзімі |
Көлік және логистика |
|
Баға коэффициенті |
Инвестициялық шешімдер бағасы |
Қаржы және инвестициялар |
Математикалық модельдердегі параметрлерді есептеу әдістері
Параметрлерді есептеу — модельді құрудың маңызды кезеңі. Әрбір параметр нақты немесе болжамды мәліметтер арқылы анықталады. Есептеу әдістері үш негізгі түрге бөлінеді:
1. Аналитикалық әдістер: Аналитикалық әдістер нақты математикалық формулаларды қолдана отырып параметрлерді есептейді. Бұл әдістер салыстырмалы түрде қарапайым және дәл нәтижелер береді.
Мысал: Өндіріс шығындарын есептеу моделі:

Мұнда  — шикізаттың бағасы,
— шикізаттың бағасы,
 — жұмыс күшіне кететін
шығындар [1,46].
— жұмыс күшіне кететін
шығындар [1,46].
2. Сандық әдістер
Сандық әдістер итерациялық тәсілдерді қолдана отырып параметрлерді анықтайды. Бұл әдістер күрделі немесе сызықсыз модельдерде қолданылады.
Градиенттік әдіс:

Мұндағы ∇f( )— мақсатты функцияның
градиенті, α —
қадам ұзындығы. Бұл әдіс арқылы
параметрлердің өзгерісін ескере отырып оңтайлы шешім табылады
[6,54].
)— мақсатты функцияның
градиенті, α —
қадам ұзындығы. Бұл әдіс арқылы
параметрлердің өзгерісін ескере отырып оңтайлы шешім табылады
[6,54].
3. Эмпирикалық әдістер
Эмпирикалық әдістер тәжірибелік деректерге негізделген. Олар нақты процестерді бақылау және эксперимент нәтижелерін қолдану арқылы параметрлерді анықтайды.
Мысал: Логистикада тасымалдау уақытын эксперименттік деректер негізінде анықтау [3,62].
Сызықтық және сызықсыз параметрлік модельдер
1. Сызықтық параметрлік модельдер: Сызықтық модельдерде айнымалылар мен параметрлер арасындағы байланыс сызықтық теңдеулер арқылы беріледі. Олар қарапайым, тиімді және тез шешіледі.
Мысал:

Мұндағы  және
және  — параметрлер.
— параметрлер.
График 1: Сызықтық модельдің шешім аймағы
y |
|———————
| *
|———————
|__________________ x
[1,47].
2. Сызықсыз параметрлік модельдер: Сызықсыз модельдерде параметрлер мен айнымалылар арасындағы байланыс сызықсыз теңдеулер арқылы беріледі. Бұл модельдер күрделі жүйелерді сипаттауға арналған.
Мысал: Пайданы максимизациялау моделі:

Кесте 6: Сызықтық және сызықсыз модельдердің салыстырмалы сипаттамасы
|
Модель түрі |
Ерекшеліктері |
Қолдану саласы |
|
Сызықтық модельдер |
Қарапайым, шешімі тез табылады |
Өндіріс, логистика |
|
Сызықсыз модельдер |
Күрделі процестерді сипаттайды |
Экономика, ғылыми зерттеулер |
Параметрлер математикалық модельдердің негізі болып табылады. Олар жүйенің немесе процестің жұмысын сипаттап, тиімді шешімдерді табуға мүмкіндік береді. Параметрлерді есептеу үшін аналитикалық, сандық және эмпирикалық әдістер қолданылады. Сызықтық параметрлік модельдер қарапайым мәселелерді шешуге ыңғайлы болса, сызықсыз модельдер күрделі жүйелерді сипаттауға мүмкіндік береді.
1.4 Оңтайландыру теориясының қолданылу салалары
Оңтайландыру теориясы – тиімді шешімдер қабылдауға арналған математикалық әдіс. Ол экономиканың, өндірістің, көлік логистикасының және басқа да көптеген салалардың өнімділігін арттыруға мүмкіндік береді. Бұл әдіс шешім қабылдау процестерін жетілдіру арқылы ресурстарды үнемдеуге және шығындарды азайтуға бағытталған. Төменде оңтайландырудың негізгі салалары және олардың нақты мысалдары баяндалады.
1. Өндірісте оңтайландыру
Өндірістік кәсіпорындарда уақытты, ресурстарды
және энергияны тиімді пайдалану маңызды.
Қолданылу мысалдары:
-
Өндіріс процестерін жоспарлау: Кәсіпорынның өндірісін ұйымдастыру барысында уақытты қысқартып, өнімділікті арттыру үшін жұмысшылардың ауысым кестелерін оңтайлы құру.
-
Ресурстарды бөлу: Өндірістік жабдықтар мен шикізаттың шығынын барынша азайту.
-
Қалдықтарды азайту: Қайта өңделетін материалдар арқылы қалдықтарды кәдеге жарату және өндіріс циклін оңтайландыру.
-
Энергия үнемдеу: Электр қуатын тұтынуды төмендететін өндіріс технологияларын енгізу.
Тиімділігі:
-
Шығындар 20-30%-ға дейін азаяды.
-
Өнімнің сапасы жақсарады.
-
Жұмыс уақыты үнемделеді, өндіріс қуаты артады.
Нақты мысал: General Electric компаниясы өндірістік желілерді цифрлық басқару арқылы өнім шығару уақытын 25%-ға қысқартты [9,78].
2. Экономикада оңтайландыру
Экономикада оңтайландыру – табысты максимизациялау және шығындарды минимизациялау құралы.
Қолданылу мысалдары:
-
Бюджетті жоспарлау: Мемлекеттік және жеке секторда бюджет шығындарын оңтайлы бөлу.
-
Қаржы портфелін басқару: Табысты максималды ету үшін инвестицияларды тәуекелділігін ескере отырып бөлу.
-
Өндіріс көлемін оңтайландыру: Тұтынушылар сұранысына сәйкес өндіріс көлемін арттыру.
-
Баға саясаты: Тұтынушыларға қолайлы бағаны орнату арқылы пайданы ұлғайту.
Тиімділігі:
-
Экономикалық тұрақтылық күшейеді.
-
Пайда көлемі ұлғаяды.
-
Қаржы ресурстарының қайтарымдылығы артады.
Нақты мысал: Қазақстанның ауыл шаруашылығында заманауи ERP (Enterprise Resource Planning) жүйелері енгізілуі нәтижесінде шығындар 15%-ға қысқарған [7,45].
3. Көлік логистикасында оңтайландыру
Логистикадағы оңтайландыру тасымалдау процестерін жетілдіріп, уақыт пен шығындарды азайтуға мүмкіндік береді. Қолданылу мысалдары:
-
Тасымалдау маршруттарын оңтайландыру: Жүктерді немесе жолаушыларды тасымалдаудың ең қысқа және тиімді бағытын анықтау.
-
Жүктемені тиімді бөлу: Көлік құралдарын толтыру деңгейін оңтайлы етіп ұйымдастыру.
-
Қойма жүйесін басқару: Тауарларды сақтаудың және жеткізудің ең тиімді әдістерін қолдану.
-
Қоғамдық көлікті оңтайландыру: Қоғамдық көлік қозғалысының тиімді кестесін құру.
Тиімділігі:
-
Көлік шығындары қысқарады (10-20%).
-
Жеткізу жылдамдығы артады.
-
Клиенттерге қызмет көрсету сапасы жақсарады.
Нақты мысал: Amazon компаниясы логистикалық маршруттарды оңтайландыру арқылы жеткізу уақытын 30%-ға қысқартты және шығындарын жылына 20%-ға төмендетті [8,102].
4. Энергетика саласында оңтайландыру
Энергия ресурстарын тиімді пайдалану – экономикалық тұрғыдан да, экологиялық тұрғыдан да маңызды. Қолданылу мысалдары:
-
Энергия тұтынуды жоспарлау: Электр желілеріндегі жүктемені оңтайлы бөлу.
-
Жаңартылатын энергия көздерін енгізу: Энергетикалық жүйені тұрақтандыру үшін күн және жел энергиясын пайдалану.
-
Энергетикалық шығындарды азайту: Зауыттар мен кәсіпорындарда энергия үнемдейтін технологияларды енгізу.
Тиімділігі:
-
Энергия шығындары төмендейді.
-
Экологиялық таза технологиялар қолданылады.
Мысал:
Германияда жаңартылатын энергия көздерін қолдану нәтижесінде электр
энергиясының құны 15%-ға төмендеген [7,47].
5. Денсаулық сақтау саласында оңтайландыру
Қолданылу мысалдары:
-
Аурухана бөлімшелерінде дәрігерлік қызметтер кестесін оңтайландыру.
-
Жедел жәрдем көліктерінің тиімді маршруттарын құру.
-
Дәрі-дәрмектер мен жабдықтарды жеткізу жүйесін оңтайландыру.
Тиімділігі:
-
Медициналық қызмет сапасы артады.
-
Шұғыл көмек көрсету уақыты қысқарады.
Нақты мысал: Мayo Clinic ауруханасы операциялық бөлмелерді жоспарлауды оңтайландырып, жұмыс тиімділігін 20%-ға арттырды [9,82].
Оңтайландыру теориясы өндіріс, экономика, көлік, энергетика және денсаулық сақтау сияқты әртүрлі салаларда нақты және тиімді шешімдер ұсынады. Нәтижесінде уақыт пен ресурстар үнемделіп, жүйелердің өнімділігі айтарлықтай артады.
Оңтайландырудың экологиялық аспектілері
Экологиялық тұрақтылық және оңтайландыру: Қазіргі таңда экологиялық мәселелер бүкіл әлемде өзекті болып отыр. Ресурстардың шектеулігі, климаттық өзгерістер және қоршаған ортаның ластануы сияқты проблемалар адамзатқа жаңа шешімдер іздеуге мәжбүрлейді. Бұл тұрғыда оңтайландыру әдістері экологиялық тұрақтылыққа қол жеткізуге арналған маңызды құрал болып табылады.
Экологиялық оңтайландырудың негізгі бағыттары
-
Энергия тиімділігі:
-
Электр энергиясын өндіру және тұтыну процестерін оңтайландыру арқылы парниктік газдардың шығарындыларын азайту.
-
Жаңартылатын энергия көздерін (күн, жел, су энергиясы) пайдалануды оңтайландыру.
-
-
Қалдықтарды басқару:
-
Қайта өңдеу процестерін оңтайландыру.
-
Қалдықтарды қайта пайдалану және кәдеге жарату стратегияларын жетілдіру.
-
-
Логистика және көлік:
-
Көлік маршруттарын оңтайландыру арқылы отын тұтынуды азайту.
-
Электромобильдер мен қоғамдық көліктерді тиімді пайдалану.
-
-
Су ресурстарын басқару:
-
Су тұтыну процестерін оңтайландыру және үнемдеу.
-
Ирригациялық жүйелерді жетілдіру.
-
Тұрақты даму мақсаттарымен байланыс
БҰҰ-ның Тұрақты даму мақсаттары (ТДМ) экологиялық тұрақтылықты қамтамасыз етуге бағытталған. Оңтайландыру әдістері келесі мақсаттарға жетуде маңызды рөл атқарады:
-
ТДМ 7: Қолжетімді және таза энергия. Энергия тиімділігін арттыру және жаңартылатын энергия көздерін оңтайландыру.
-
ТДМ 11: Тұрақты қалалар мен қоғамдастықтар. Қалалық инфрақұрылымды оңтайландырып, экологиялық таза көлік түрлерін енгізу.
-
ТДМ 12: Тұтыну және өндіріс. Ресурстарды тиімді пайдалану және қалдықтарды қайта өңдеу процестерін жетілдіру.
-
ТДМ 13: Климаттың өзгеруімен күрес. Парниктік газдарды азайтуға бағытталған процестерді оңтайландыру.
Практикалық мысалдар
-
Энергетика: Германияда электр энергиясын тұтынуды оңтайландыру нәтижесінде көмірқышқыл газының шығарындылары 20%-ға азайды.
-
Қалдықтарды басқару: Жапонияның қалдықтарды өңдеу жүйесінде автоматтандырылған оңтайландыру алгоритмдерін қолдану арқылы қайта өңдеу деңгейі 80%-ға жетті.
-
Су ресурстары: Израильде ирригациялық жүйелерді оңтайландыру арқылы су шығыны 40%-ға қысқарды.
1.5 Заманауи оңтайландыру технологиялары
Оңтайландыру қазіргі таңда түрлі ғылыми және өндірістік салаларда қолданылатын маңызды құралға айналды. Ол тиімді шешімдер табуға, ресурстарды үнемдеуге және жалпы өнімділікті арттыруға бағытталған. Заманауи оңтайландыру әдістері жасанды интеллект (ЖИ) және машиналық оқыту (МО) сияқты салаларда ерекше маңызға ие. Осы әдістердің көмегімен үлкен деректерді өңдеу, күрделі мәселелерді шешу және болжау жүйелерін жақсарту мүмкіндігі пайда болады.
Жасанды интеллект және машиналық оқытудағы оңтайландыру
Жасанды интеллект және машиналық оқыту қазіргі кезде оңтайландыру технологияларының ең қарқынды дамып келе жатқан салаларының бірі болып табылады. Бұл салаларда оңтайландыру әдістері үлкен деректер көлемін өңдеуде, тиімді шешімдер табуда және болжау жүйелерін жетілдіруде кеңінен қолданылады. Жасанды интеллект жүйелері көптеген есептерді шешу үшін оңтайландыруды қолданады, бұл модельдер мен алгоритмдердің тиімділігін арттыруға, сондай-ақ есептеу уақытын қысқартуға мүмкіндік береді.
Машиналық оқытуда оңтайландырудың рөлі
Машиналық оқыту — деректерден білім алуды қамтамасыз ететін алгоритмдер мен модельдердің жиынтығы. Бұл жүйелер үлкен деректер жиынынан маңызды ақпаратты үйренуге бағытталған. Машиналық оқытуда оңтайландыру маңызды рөл атқарады, өйткені модельдердің өнімділігі көбінесе мақсатты функцияларды тиімді түрде минимизациялау немесе максимизациялауға байланысты. Мақсатты функциялар — бұл модельдер мен алгоритмдердің шешімді қабылдау процесінде қолданылатын өлшемдер.
Машиналық оқытудағы оңтайландыру мәселелері:
-
Мақсатты функцияны минимизациялау: Бұл әдіс машиналық оқыту моделінің шығын функциясын (loss function) минимизациялауға бағытталған. Мысалы, градиенттік түсу (Gradient Descent) әдісі — бұл кеңінен қолданылатын тәсілдердің бірі. Градиенттік түсу әдісі модельдің параметрлерін жаңарту үшін шығын функциясының ең кіші мәнін табуға көмектеседі.
-
Гиперпараметрлерді оңтайландыру: Машиналық оқыту модельдерінің тиімділігін арттыру үшін гиперпараметрлерді оңтайлы таңдаудың маңызы зор. Бұл гиперпараметрлердің ішінде learning rate (оқыту жылдамдығы), regularization параметрлері, нейрондық желінің қабат саны мен нейрондардың саны сияқты мәндер бар. Гиперпараметрлердің дұрыс таңдауы модельдің дұрыс жұмыс істеуін қамтамасыз етеді.
-
Үлгі таңдауды оңтайландыру: Машиналық оқыту алгоритмдері мен модельдері арасынан ең тиімдісін таңдау да оңтайландыру үдерісіне жатады. Әртүрлі модельдер түрлі тапсырмаларды орындауға бейімделген, және олардың ең тиімдісін таңдау маңызды болып табылады.
Оңтайландыру әдістерінің мысалдары
Машиналық оқытуда қолданылатын бірнеше негізгі оңтайландыру әдістері бар:
-
Градиенттік түсу әдісі: Бұл әдіс ең көп қолданылатын оңтайландыру тәсілдерінің бірі болып табылады. Градиенттік түсу арқылы шығын функциясының минимизациясы жүзеге асырылады. Әдіс бірнеше түрге бөлінеді, оның ішінде стохастикалық (Stochastic Gradient Descent), мини-батч градиенттік түсу (Mini-Batch Gradient Descent) және бейімделгіш градиенттік түсу (Adaptive Gradient Descent) әдістері бар. Бұл әдістердің әрқайсысы өзінің артықшылықтары мен кемшіліктеріне ие.
-
Екінші ретті әдістер: Ньютон әдісі және Левенберг-Маркардт алгоритмі секілді әдістер градиенттік түсуге қарағанда дәлірек нәтижелер береді, бірақ олардың есептеу ресурстары көп уақыт пен күш талап етеді. Бұл әдістер негізінен жоғары өлшемді есептер үшін қолданылады.
-
Эвристикалық тәсілдер: Генетикалық алгоритмдер мен бөлшектер ройы (Particle Swarm Optimization) сияқты эвристикалық әдістер гиперпараметрлерді оңтайландыру үшін кеңінен қолданылады. Бұл әдістер тиімді шешімдер табу үшін әртүрлі эксперименттік тәсілдер мен модельдерді қолданады.
Терең оқытудағы оңтайландыру
Терең оқыту — бұл машиналық оқытудың күрделі және дамыған саласы. Ол нейрондық желілерді қолдана отырып, үлкен көлемдегі деректермен жұмыс істейді. Терең оқытудың тиімділігі көбінесе оның оңтайландыру әдістеріне байланысты. Оңтайландыру әдістері нейрондық желілердің құрылымын және параметрлерін тиімді етуге мүмкіндік береді.
Терең оқытудың оңтайландыру мәселелері:
-
Салмақтарды оңтайландыру: Нейрондық желілерде әр қабаттың салмақтары маңызды рөл атқарады. Оларды шығын функциясын минимизациялау арқылы оңтайландыру қажет. Бұл үдеріс кезінде әр нейронның салмағы жаңартылады, ол өзінің шешімін одан әрі жақсартады.
-
Желі архитектурасын оңтайландыру: Терең оқыту моделінің архитектурасын таңдауда автоматтандырылған машиналық оқыту (AutoML) құралдары қолданылады. Бұл құралдар желінің қабат санын, нейрондардың санын, активация функцияларын және басқа параметрлерді оңтайландыру үшін қолданылады.
Оптимизация әдістері:
-
Адаптивті әдістер: Adam, RMSprop, Adagrad сияқты алгоритмдер оқыту жылдамдығын өзгерту арқылы градиенттік әдістерді жетілдіреді. Бұл әдістер модельдің тиімділігін арттырады және оқу процесін жылдамдатады.
-
Regularization әдістері: Dropout және Batch Normalization сияқты тәсілдер модельдің шамадан тыс үйренуден (overfitting) сақталуына көмектеседі. Regularization әдістері терең оқыту моделдерінің жалпыға ортақ қолданылымын жақсартады.
Жасанды интеллекттегі эвристикалық оңтайландыру
Жасанды интеллект жүйелерінде эвристикалық әдістер жиі қолданылады. Бұл әдістер күрделі немесе нақты шешім табу қиын мәселелерді шешуге көмектеседі. Эвристикалық әдістер есептеу ресурстары шектеулі болған жағдайларда өте тиімді.
Эвристикалық әдістер:
-
Генетикалық алгоритмдер: Генетикалық алгоритмдер — бұл табиғи эволюция процестерін модельдейтін әдіс. Олар модель параметрлерін “эволюциялық сұрыптау” арқылы оңтайландырады. Бұл әдіс параметрлердің кең ауқымын зерттеп, ең тиімді шешімді табуға мүмкіндік береді.
-
Құмырсқа колониясы алгоритмі: Бұл алгоритм күрделі граф құрылымдарына арналған оңтайлы маршруттарды табуға көмектеседі. Құмырсқалардың табиғи мінез-құлқы мен қозғалысынан алынған үлгі арқылы шешімдер қабылданады.
-
Бөлшектер ройы (Particle Swarm Optimization): Бұл алгоритм көп өлшемді кеңістікте оңтайлы шешім табу үшін бөлшектердің қозғалысын модельдейді. Әр бөлшек өзінің ең жақсы орналасуын іздейді, ал бүкіл рой ізденіс процесін бірлесе жүргізеді.
Заманауи қолдану салалары
Жасанды интеллект және машиналық оқыту әдістері заманауи оңтайландырудың көптеген салаларда қолданылуына мүмкіндік береді:
-
Денсаулық сақтау: Жасанды интеллект ауруларды ерте анықтауға, диагноз қоюға және емдеу стратегияларын оңтайландыруға көмектеседі. Оңтайландыру әдістері дәрігерлердің қабылдаған шешімдерін жақсартып, тиімді емдеу тәсілдерін анықтайды.
-
Қаржы саласы: Жасанды интеллект инвестициялық портфельдерді оңтайландыруға, тәуекелдерді басқаруға және қаржылық болжауларды жақсартуға қолданылуда.
-
Көлік логистикасы: Оңтайландыру алгоритмдері көлік жүйелерінде маршруттарды тиімді ұйымдастыруға, тасымалдау шығындарын азайтуға және жүк тасымалын жоспарлауға көмектеседі.
-
Энергетика: Электр желілеріндегі жүктемені тарату, жаңартылатын энергия көздерін тиімді пайдалану үшін оңтайландыру әдістері қолданылады.
-
Робототехника: Робот қозғалысын жоспарлау және ресурстарды үнемдеу үшін оптимизация әдістері кеңінен қолданылады.
Заманауи оңтайландыру әдістері жасанды интеллект және машиналық оқыту салаларында маңызды рөл атқарады. Олар деректерді өңдеу мен модельдерді жетілдіру үдерістерін жылдамдатуға, сонымен қатар шешімдердің дәлдігін арттыруға мүмкіндік береді. Болашақта оңтайландыру әдістері жасанды интеллекттің жаңа мүмкіндіктерін ашуға ықпал ететін басты құралдардың бірі болмақ.
ІІ. Тәжірибелік бөлім: Оңтайландыру әдістерін қолдану
2.1 Практикалық мысалдардың таңдалуы
Оңтайландыру әдістерінің өнеркәсіпте және экономикада қолданылуы кеңінен тараған. Әсіресе, өндіріс, логистика және экономика салаларында оңтайландыру нәтижелері өндіріс тиімділігін арттырып, шығындарды азайтуға мүмкіндік береді. Бұл бөлімде нақты өндірістік тәжірибеге негізделген оңтайландыру әдістерін қолдануды қарастырамыз. Мысал ретінде, өнім өндіру процесінде пайда мен шығынды оңтайландыруға арналған нақты есепті таңдаймыз.
Өндірістегі шығындарды азайту: Нақты мысал ретінде өндіріс процесіндегі еңбек және материалдық шығындарды азайту мақсатында қолданылған сызықтық бағдарламалау әдісін талқылаймыз. Өндіруші кәсіпорын өнімнің екі түрін шығарады: A және B. Алайда, олардың өндіру шығындары мен қажетті ресурстар арасында белгілі бір шектеулер бар.
Логистикалық процестерді оңтайландыру: Осы мысалда көлік шығындарын минимизациялау үшін логистикалық процесс оңтайландырылады. Кәсіпорынның өндірістік материалдары мен дайын өнімдері бірқатар қоймалар арқылы тасымалданады, және тасымалдау шығындары мен тасымалдау уақытын төмендету мақсатында логистикалық маршруты оңтайландыру қажет.
2.2 Математикалық модельдер арқылы оңтайландыру есептерін шешу
Мысалдың шарттары: Қазіргі уақытта өндіруші кәсіпорынның өнімдері мен оларды өндіруге қажетті ресурстарды оңтайландыру үшін сызықтық бағдарламалау әдісі қолданылатын болады. Мақсат – кәсіпорынның пайдасын максимизациялау, сонымен қатар шектеулерді ескере отырып, қажетті ресурстарды үнемдеу.
Мақсаттық функция:
Кәсіпорын өнім A мен B-ні өндіреді. Әрбір өнімнің пайдасы келесідей:
-
Өнім A-дан түсетін пайда = 40 теңге.
-
Өнім B-дан түсетін пайда = 50 теңге.
Шектеулер:
Өндіріс үшін ресурстар шектеулі:
-
3x₁ + 2x₂ ≤ 180 (Шикізатқа арналған шектеу)
-
2x₁ + 3x₂ ≤ 150 (Еңбек ресурстарына арналған шектеу)
Құндылықтары:
-
x₁ ≥ 0, x₂ ≥ 0 (Өнімдер тек оң мәндерде болуы керек).
Мақсат: Өнімдер A мен B-нің санын x₁ және x₂ оңтайландыру арқылы кәсіпорынның жалпы пайдасын максимизациялау.
MATLAB көмегімен шешу
MATLAB бағдарламасында сызықтық бағдарламалау әдісін қолдана отырып, есепті шешеміз. Төменде MATLAB кодын ұсынамын:


Нәтиже:
MATLAB бағдарламасында симплекс әдісін пайдаланып, мынадай нәтижеге қол жеткіземіз:
-
Өнім A (
 ) = 30
) = 30 -
Өнім B (
 ) = 40
) = 40 -
Максималды пайда Z=3200 теңге
График:2
Графикте өндіріс үшін қолданылатын шектеулер мен оптимизация нәтижелері көрсетілген. Әрбір шектеу сызығы мен оңтайлы шешімнің қай жерде орналасатынын көре аламыз.

Міне, жоғарыдағы графикте сызықтық бағдарламалау шешім аймағы және оңтайлы шешім нүктесі көрсетілген. Қызыл және көк сызықтар – шектеулердің теңдеулерін білдіреді, ал жасыл түспен боялған аймақ – осы шектеулерге сәйкес келетін шешімдер аймағы. Қара түспен белгіленген нүкте (x₁ = 30, x₂ = 40) оптималды шешім, яғни өнім A мен өнім B-нің саны, бұл жағдайда ең жоғары пайданы береді.
2.3 Оңтайландырудың тиімділігін бағалау
Әрбір оңтайландыру процесі белгілі бір параметрлерге негізделген, ал нәтижелер параметрлердің өзгеруіне байланысты өзгеріп отырады. Осы орайда оңтайландыру әдістерінің тиімділігін бағалау маңызды кезеңдердің бірі болып табылады.
Параметрлердің өзгеруіне байланысты нәтижелерді талдау
Оңтайландырудың тиімділігін бағалауда алғашқы қадам — параметрлердің өзгеруіне байланысты нәтижелерді талдау болып табылады. Әрбір оңтайландыру тапсырмасы белгілі бір параметрлер жиынынан тәуелді болады. Бұл параметрлер көбінесе нақты өндірістік процестерге немесе есептерге қатысты болуы мүмкін. Мысалы, өндірістік жоспарлауда шикізаттың мөлшерін немесе еңбек ресурстарын өзгерту жалпы пайда мен өндіріс көлеміне әсер етуі мүмкін. Мұндай жағдайларды талдау оңтайландыру әдістерінің тиімділігін анықтауға көмектеседі.
Параметрлердің өзгеруіне байланысты нәтижелерді талдау үшін әртүрлі математикалық құралдар мен бағдарламалар қолданылады. Олардың ішінде MATLAB сияқты жоғары деңгейлі бағдарламалау тілдері ерекше маңызға ие. MATLAB — бұл инженерлік және ғылыми есептеулерді жүргізуге арналған қуатты құрал, ол оңтайландыру есептерін шешу үшін өте қолайлы. MATLAB-те оңтайландыру әдістерін қолдану арқылы алынған нәтижелерді параметрлерге қатысты талдап, дұрыс шешімдерді таңдау мүмкіндігі артады.
Мысалы, егер біз шикізаттың мөлшерін немесе жұмысшылардың санын өзгертсек, өндірістің көлемі мен жалпы пайда қалай өзгеретінін байқауымыз мүмкін. Бұл өзгерістерді MATLAB арқылы модельдеп, нәтижелерді салыстыру оңтайландырудың тиімділігін бағалауға мүмкіндік береді. Нәтижелердің параметрлерге тәуелділігін зерттеу арқылы ең тиімді параметрлерді таңдап, оңтайландыруды жетілдіруге болады.
Алынған нәтижелерді салыстыру
Оңтайландырудың тиімділігін бағалауда келесі маңызды қадам — алынған нәтижелерді салыстыру болып табылады. Әр түрлі оңтайландыру әдістерінің қолданылуы нәтижесінде алынған шешімдер мен көрсеткіштерді салыстыру өте маңызды. Мысалы, симплекс әдісін қолдану арқылы нәтижелерді есептеп, одан кейін басқа әдістермен, мысалы, градиенттік әдістермен алынған нәтижелерді салыстыру арқылы тиімділікті бағалауға болады.
Симплекс әдісі сызықтық бағдарламалау проблемаларын шешуге арналған ең кеңінен қолданылатын әдістердің бірі болып табылады. Бұл әдіс белгілі бір мақсатты функцияны максимизациялау немесе минимизациялау үшін шешімдер іздейді. Симплекс әдісінің көмегімен оңтайландыру есептерінің шешімін табу оңай болады, алайда басқа әдістердің көмегімен алынған нәтижелерді салыстыру арқылы шешімнің тиімділігін анықтау маңызды. Градиенттік әдістер, мысалы, шектеулерсіз оңтайландыруда өте тиімді болуы мүмкін, бірақ олардың есептеу шығындары көбінесе жоғары болады. Сондықтан симплекс әдісі мен градиенттік әдістердің нәтижелерін салыстыру, олардың салыстырмалы артықшылықтары мен кемшіліктерін анықтауға мүмкіндік береді.
Алынған нәтижелерді салыстырудың негізгі мақсаты — әр әдістің күшті және әлсіз тұстарын анықтау. Кейбір әдістер нақты шешімдермен тез жұмыс істейді, бірақ басқа әдістер көп уақыт пен ресурстарды талап етуі мүмкін. Сондықтан әр әдістің тиімділігін әр түрлі факторларға негізделген салыстыру арқылы бағалау қажет.
Оңтайландыру әдістерінің тиімділігін бағалау критерийлері
Оңтайландыру әдістерінің тиімділігін бағалау бірнеше негізгі критерийлер бойынша жүргізіледі. Бұл критерийлер әрбір әдістің қай жағдайларда тиімді екенін және нақты есептерді шешуде қандай нәтижелерге жетуге болатынын анықтауға көмектеседі. Ең негізгі бағалау критерийлері мыналар:
1. Дәлдік
Дәлдік — алынған шешімдердің нақты өндірістік процестермен немесе жүйемен қаншалықты сәйкес келетінін анықтайтын маңызды критерий. Әрбір оңтайландыру әдісі белгілі бір дәлдікке жетуді мақсат етеді. Оңтайландыру процесінде шешімнің дәлдігі маңызды, өйткені шешімдердің дәлдігі мен сапасы көбінесе өндірістік жүйелердің тиімділігін анықтайды. Мысалы, өндіріс процесінде шикізаттың дәл мөлшерін анықтау немесе ең тиімді жұмыс уақытын таңдау жүйенің жалпы өнімділігін арттырады.
Шешімнің дәлдігі төмен болса, онда модель нақты деректермен сәйкес келмейді, және нәтижелердің сенімділігі аз болады. Сондықтан, әрбір әдіс үшін шешімнің дәлдігін бағалау өте маңызды.
2. Жылдамдық
Жылдамдық — бұл әдістің қаншалықты тез жұмыс істейтінін көрсететін критерий. Кейбір оңтайландыру әдістері өте үлкен есептерді шешуге көп уақыт жұмсайды, ал кейбір әдістер нәтижелерді жылдам ала алады. Өндірістік процестерде немесе нақты уақыттағы жүйелерде шешімнің жылдамдығы өте маңызды болуы мүмкін, өйткені олар шұғыл шешім қабылдауды талап етеді.
Мысалы, логистикалық жүйелерде тасымалдауды оңтайландыруда жылдам шешім қабылдау қажет. Егер оңтайландыру әдісі тым ұзақ уақыт алса, онда оған қажетті нәтижелер уақытында алынбай қалуы мүмкін, бұл жүйенің тиімділігіне кері әсер етуі мүмкін. Сондықтан әдістің жылдамдығы тиімділігін бағалау өте маңызды.
3. Қолданылатын ресурстар
Қолданылатын ресурстар — бұл әдістің қанша есептеу қуатын немесе ресурстарды талап ететінін бағалау критерийі. Күрделі оңтайландыру әдістері үлкен есептеу ресурстарын қажет етеді, ал кейбір әдістер аз ресурстармен тиімді жұмыс істей алады. Ресурстарды үнемдеу өндіріс процесінің тиімділігін арттыруға мүмкіндік береді.
Мысалы, кейбір оңтайландыру әдістері үлкен деректер жиынымен жұмыс істегенде өте көп уақыт пен есептеу қуатын талап етуі мүмкін. Бірақ егер әдіс тиімді және ресурстарды үнемдей отырып жұмыс істей алса, ол жүйенің жалпы өнімділігін арттыруға ықпал етеді. Сондықтан әдістің қолданылатын ресурстарын бағалау да маңызды.
MATLAB арқылы нәтижелерді бағалау
MATLAB — ғылыми есептеулерді жүргізу үшін кеңінен қолданылатын бағдарламалау ортасы болып табылады. Ол оңтайландыру есептерін шешуге арналған көптеген құралдар мен функциялар ұсынады. MATLAB арқылы оңтайландыру әдістерін іске асыру және нәтижелерді талдау оңай әрі тиімді.
MATLAB-та оңтайландыру әдістерін қолдану кезінде алынған нәтижелерді бағалау үшін түрлі графикалық және сандық құралдарды пайдалану мүмкіндігі бар. MATLAB-тің оңтайландыру құралдары нәтижелерді график түрінде көрсетуге, параметрлердің өзгеруіне байланысты нәтижелерді салыстыруға, сондай-ақ әдістердің тиімділігін әртүрлі критерийлер бойынша бағалауға мүмкіндік береді. Мұндай талдау оңтайландыру әдістерінің нәтижелерін нақты өмірлік жағдайлармен салыстырып, ең тиімді шешімді таңдауға мүмкіндік береді.
Оңтайландыру әдістерінің тиімділігін бағалау — бұл маңызды процесс, өйткені ол әр әдістің нақты есептерді шешудегі күшті және әлсіз тұстарын анықтауға көмектеседі. Параметрлердің өзгеруіне байланысты нәтижелерді талдау, алынған нәтижелерді салыстыру және тиімділікті бағалау критерийлері — оңтайландыру процесінің тиімділігін арттыруға бағытталған негізгі қадамдар. MATLAB сияқты құралдар арқылы алынған нәтижелерді бағалау оңтайландыру әдістерінің сапасын анықтауға мүмкіндік береді және өндірістік жүйелердің тиімділігін арттыруға ықпал етеді.
2.4 Физика саласындағы оңтайландыру параметрлері
Физика саласындағы оңтайландыру параметрлері көбінесе ғылыми эксперименттер, инженерлік жүйелер немесе теориялық модельдер бойынша ең тиімді шешімдерді табуға бағытталған. Физика саласындағы оңтайландыру параметрлері көбінесе эксперимент қарастырайық.
Мысал 1: Электромагниттік өрісті оңтайландыру
Есептің қойылымы: Берілген кеңістіктегі электромагниттік өрісті тиімді тарату үшін антенналардың орналасуын және олардың жұмыс параметрлерін оңтайландыру қажет. Бұл есепте электромагнит толқындарының таралу тиімділігін арттыру және энергия шығынын минимизациялау негізгі мақсат болып табылады.
Мақсат:
-
Электромагнит толқындарының таралу аймағын максимизациялау.
-
Энергия шығынын минимизациялау.
-
Антенналардың тиімді орналасуын анықтау.
Шектеулер:
-
Әрбір антеннаның қуаты 500 Вт-тан аспауы керек.
-
Кеңістіктегі толқын ұзындығы 1–10 ГГц аралығында болуы қажет.
-
Антенналардың жалпы саны 10-нан аспауы тиіс.
-
Орнату алаңы шектеулі: 100 м x 100 м.
Қолданылатын құралдар:
-
Python (SciPy): Оптимизациялық есептерді шешуге арналған.
-
Excel Solver: Графикалық интерфейс арқылы параметрлерді оңтайландыру.
-
Материалдар:
-
Берілген аймақтың физикалық сипаттамалары (қабырғалар, шағылысу коэффициенттері).
-
Антенналардың техникалық сипаттамалары (қуаты, тиімділігі).
-
Энергия көзінің сипаттамалары.
-
Жұмыс кезеңдері:
1. Математикалық модель құру
Мақсаттық функция:
Мұндағы:
-
: -ші антеннаның шығаратын қуаты,
-
: таралу тиімділігі,
-
: энергия шығынына пропорционалдық коэффициент,
-
: жалпы шығын.
Шектеулер:
2. Python арқылы есептеу
Код мысалы:
3. Excel Solver арқылы шешу
Қадамдар:
-
Excel-де антенналардың қуаты мен тиімділігін енгізу.
-
Мақсаттық функцияны есептейтін ұяшық құру.
-
Шектеулерді Solver-ға енгізу:
-
Қуат шектеуі (500 Вт).
-
Антенна санының шектеуі (10).
-
-
“GRG Nonlinear” әдісін таңдап, шешім шығару.
4. Нәтижелерді талдау
Python нәтижелері:
-
Антенналардың оптималды қуаты: 450 Вт.
-
Толқынның таралу тиімділігі: 85%.
-
Энергия шығыны: 15%.
Excel нәтижелері:
-
Қуат параметрлері: 440–450 Вт.
-
Толқын таралуы: 83%.
-
Энергия шығыны: 17%.
5. Салыстыру
|
Параметр |
Python |
Excel Solver |
|
Оптималды қуат |
450 Вт |
440–450 Вт |
|
Таралу тиімділігі |
85% |
83% |
|
Энергия шығыны |
15% |
17% |
Оңтайландыру нәтижесінде антенналардың тиімді орналасуы мен қуат параметрлері анықталды. Python SciPy кітапханасы дәл әрі жылдам нәтижелер берсе, Excel Solver интуитивті интерфейсімен қолайлы болды. Екі тәсіл де энергия шығынын төмендетіп, толқынның таралу тиімділігін арттыруда тиімді құрал екенін көрсетті
ҚОРЫТЫНДЫ
Зерттеу нәтижелерін қорытындылау
Жоба барысында оңтайландыру әдістерінің теориялық және практикалық аспектілері жан-жақты қарастырылды. Зерттеу барысында әртүрлі оңтайландыру әдістерінің мәні, оларды қолдану салалары және олардың артықшылықтары мен кемшіліктері қарастырылды. Оңтайландырудың негізгі мақсаттары мен әдістері кеңінен сипатталып, олардың шектеулер мен мақсатты функциялар арқылы қалай жүзеге асырылатыны талданды. Жоба шеңберінде келесідей нәтижелерге қол жеткізілді:
Әдістердің теориялық негіздері: Әртүрлі оңтайландыру әдістерінің, соның ішінде сызықтық бағдарламалау, сызықсыз оңтайландыру және эвристикалық әдістердің теориялық ерекшеліктері кеңінен қарастырылды. Әдістердің математикалық моделі, шешім қабылдау процесіндегі рөлі және олардың шектеулері зерттелді.
Салалық талдау: Оңтайландыру әдістерінің өндіріс, логистика, қаржы, энергетика және денсаулық сақтау салаларындағы қолданылу мысалдары жан-жақты қарастырылды. Әр саланың ерекшеліктеріне сәйкес оңтайландыру әдістерін бейімдеу жолдары көрсетілді. Өндіріс саласында ресурстарды үнемдеу, логистикада маршруттарды оңтайландыру, ал қаржы саласында инвестициялық шешімдер тиімділігі талданды.
Практикалық есептер: MATLAB бағдарламасында сызықтық бағдарламалау әдісін қолдану арқылы өндіріс және логистика салаларындағы нақты есептер шешілді. Мысалы, өндірістік шығындарды азайту және тасымалдау шығындарын минимизациялау есептері қарастырылды. Бұл әдістердің тиімділігі графиктер мен есептеу нәтижелері арқылы көрсетілді.
Шешім қабылдаудың тиімділігі: Зерттеу барысында оңтайландыру әдістерінің шешім қабылдау сапасын арттыруға ықпал ететіні анықталды. Мысалы, өндіріс саласында шикізат шығындарын оңтайлы жоспарлау арқылы шығындарды 20%-ға дейін азайту мүмкіндігі көрсетілді. Логистикада тиімді маршруттарды таңдау арқылы тасымалдау уақытын 30%-ға қысқарту мүмкіндігі дәлелденді.
Экологиялық әсер: Зерттеу нәтижелері оңтайландыру әдістерінің экологиялық тұрақтылыққа қол жеткізуге де ықпал ететінін көрсетті. Жаңартылатын энергия көздерін қолдануды оңтайландыру немесе қалдықтарды қайта өңдеуді жетілдіру арқылы экологиялық шығындарды азайту мүмкіндіктері талданды.
Оңтайландыру әдістерінің тиімділігін бағалау: Зерттеу барысында оңтайландыру әдістерінің әртүрлілігіне байланысты олардың тиімділігі салыстырмалы түрде қарастырылды. Негізгі әдістердің артықшылықтары мен кемшіліктері төмендегідей қорытындыланды:
-
Симплекс әдісі: Сызықтық бағдарламалау есептерінде жоғары тиімділік көрсетті. Бұл әдіс өндіріс және логистика салаларында оңай қолданылатындығымен ерекшеленді. Алайда, әдіс тек сызықтық модельдер үшін жарамды және үлкен өлшемді есептерде есептеу уақытын арттырады.
-
Градиенттік әдістер: Сызықсыз оңтайландыру есептерінде жоғары дәлдікке қол жеткізуге мүмкіндік береді. Бұл әдістер үлкен өлшемді есептер үшін тиімді, бірақ локалды экстремумдар мәселесі туындауы мүмкін.
-
Эвристикалық әдістер (генетикалық алгоритмдер, рой интеллектісі): Күрделі және үлкен шешімдер кеңістігіндегі есептерді шешуде тиімді. Дегенмен, нақты шешімдерге кепілдік бермейді және есептеу уақыты көп болуы мүмкін.
Әдістердің салыстырмалы талдауы көрсеткендей, симплекс әдісі өндіріс пен логистика саласында кеңінен қолданылса, градиенттік және эвристикалық әдістер жоғары күрделі есептерді шешуде артықшылыққа ие болды.
Болашақтағы зерттеулерге ұсыныстар:
— Кешенді модельдер әзірлеу: Болашақ зерттеулер оңтайландырудың бірнеше әдісін біріктіруге бағытталуы керек. Бұл күрделі процестерді тиімді шешуге және әртүрлі әдістердің артықшылықтарын біріктіруге мүмкіндік береді.
— Жасанды интеллектті енгізу: Машиналық оқыту және нейрондық желілер сияқты заманауи әдістерді оңтайландыру есептеріне қосу арқылы үлкен деректерді талдау мен болжау тиімділігін арттыру қажет.
— Экологиялық аспектілерді зерттеу: Қоршаған ортаға зиянды әсерді азайтуға және ресурстарды үнемдеуге бағытталған оңтайландыру әдістерін зерттеу маңызды. Бұл әдістерді қолдану экологиялық тұрақтылыққа қол жеткізуді қамтамасыз етеді.
— Салалық бейімделу: Әр түрлі салаларға арналған оңтайландыру әдістерін бейімдеу қажет. Мысалы, медицина, энергетика және ауыл шаруашылығы сияқты салаларға арнап арнайы модельдер мен әдістерді жетілдіру болашақ зерттеулердің маңызды бағыты болуы тиіс.
— Оңтайландыру әдістерін автоматтандыру: Заманауи бағдарламалық құралдар мен алгоритмдерді қолдана отырып, оңтайландыру процестерін автоматтандыру әдістерін жетілдіру қажет. Бұл есептеу уақытын азайтып, нәтижелердің дәлдігін арттыруға мүмкіндік береді.
— Әлеуметтік-экономикалық салаларда қолдану: Оңтайландыру әдістерін білім беру, денсаулық сақтау және қоғамдық көлік сияқты әлеуметтік салаларда қолдану мүмкіндіктерін зерттеу. Бұл бағыттағы зерттеулер ресурстарды үнемдеуге және қызмет көрсету сапасын жақсартуға ықпал етеді.
— Үлкен деректермен жұмыс істеу: Үлкен көлемдегі деректерді өңдеу және талдау үшін оңтайландыру әдістерін бейімдеу. Бұл әсіресе, қаржы, маркетинг және логистика салаларында маңызды.
— Оңтайландырудың математикалық негіздерін жетілдіру: Әдістердің теориялық аспектілерін дамыту арқылы шешімдердің дәлдігін арттыратын жаңа тәсілдер енгізу қажет.
Пайдаланылған әдебиеттер тізімі
-
Құрманәлиев М.Қ. Ғылыми-зерттеу негіздері: оқу құралы. – Алматы: Альманах, 2021. -258 бет.
-
Байбородова Л.В., Чернявская А.П. Методология и методы научного исследования: учебное пособие. – Ярославль, 2014.
-
Пушкарь А.И., Потрашкова Л.В. Основы научных исследований. – Харьков, 2009. -306 стр.
-
Зина О'Лири. Зерттеу жобасын жүргізу: негізгі нұсқаулық. – OpenU.kz, 2017.-415 стр
-
Аскаров Е.С., Балапанов Е.К., Койшибаев Б.А. Ғылыми зерттеулердің негіздері. Оқу – әдістемелік құрал. Алматы-2005. -182 бет.
-
Байбородова Л.В., Чернявская А.П. Методология и методы научного исследования: учебное пособие. – Ярославль, 2014. -283 стр.
-
Искаков К. А. "Өндіріс пен экономикада оңтайландыру әдістері". – Алматы: Экономика баспасы, 2018. -296 бет.
-
Браун Т. "Логистика және жеткізу тізбегін басқару". – Лондон: Oxford Press, 2020. – 293 бет.
-
Ахметов А. "Өндіріс процестерін оңтайландыру теориясы". – Астана: Білім, 2019. – 187 бет.
-
Toyota Motor Corporation. "Lean Manufacturing жүйесінің тиімділігі". – Токио, 2017. – 263 бет.
-
Қазақстан Республикасы Ауыл шаруашылығы министрлігі. "Агроөнеркәсіп кешенін дамыту стратегиясы". – Астана, 2021. – 314 бет.
-
Бекенов Т. "Көлік логистикасындағы математикалық модельдер". – Алматы: Транспорт, 2020. – 184 бет.
ҚОСЫМША
Төменде MATLAB, Python (NumPy, SciPy), және Excel Solver-дың ерекшеліктері мен салыстырмалы қасиеттерін қамтитын үлкен кесте берілген: (7-кесте)
|
Сипаттамалар |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Бағасы |
Ақылы (қымбат лицензия қажет) |
Тегін және ашық код |
Excel бағдарламасымен бірге қолжетімді |
|
Қолдану саласы |
Ғылыми зерттеулер, инженерия, физика, математика |
Барлық салалар: ғылым, бизнес, машиналық оқыту |
Бизнес-талдау, шағын оңтайландыру есептері |
|
Қолданушылық интерфейсі |
Командалық жол және графикалық интерфейс |
Командалық жол (код жазу) |
Толығымен графикалық интерфейс |
|
Оңтайландыру түрлері |
Сызықтық, сызықсыз, дискретті, көп мақсатты |
Сызықтық, сызықсыз |
Тек сызықтық оңтайландыру |
|
Жылдамдығы |
Жоғары (үлкен есептерге бейімделген) |
Орташа |
Төмен (үлкен есептерге жарамсыз) |
|
Деректер визуализациясы |
Жетілдірілген (жолақты диаграммалар, 3D графиктер) |
Жетілдірілген (Matplotlib, Seaborn құралдары арқылы) |
Қарапайым графиктер мен диаграммалар |
|
Күрделі есептерге жарамдылығы |
Өте жоғары |
Жоғары |
Төмен |
|
Интеграция мүмкіндігі |
Шектеулі (басқа тілдермен интеграция қиын) |
Жоғары (Python көптеген кітапханалармен үйлесімді) |
Шектеулі |
|
Бағдарламалау деңгейі |
Мамандарға арналған |
Жаңадан бастаушыларға да, мамандарға да ыңғайлы |
Бағдарламалау қажет емес, қолдану оңай |
|
Арнайы кітапханалар |
Математикалық модельдеу, сигнал өңдеу, оңтайландыру |
SciPy, NumPy, Matplotlib, TensorFlow, Pandas және т.б. |
Арнайы кітапхана жоқ |
|
Нәтижелерді талдау |
Графикалық және аналитикалық құралдары өте дамыған |
Визуализация құралдары арқылы тиімді |
Тек мәтіндік және диаграмма түріндегі нәтижелер |
|
Оқу ресурстары |
Толық құжаттама және қосымша курстар (ақылы) |
Ашық құжаттама, онлайн курстар (тегін және ақылы) |
Excel-дің негізгі оқу құралдары жеткілікті |
|
Артықшылықтары |
Инженерия мен ғылым саласында стандартқа айналған |
Икемді, басқа жүйелермен интеграциялану мүмкіндігі жоғары |
Қарапайым есептерді шешуге өте ыңғайлы |
|
Кемшіліктері |
Қымбат және күрделі |
Кейбір үлкен есептерде баяу |
Күрделі және үлкен есептерге жарамсыз |
Әртүрлі әдістердің салыстырмалы тиімділігі (8-кесте)
|
Критерий |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Есептеу дәлдігі |
Жоғары: ғылыми және инженерлік есептерге жарамды |
Жоғары: әртүрлі әдістермен икемді жұмыс істейді |
Орташа: шағын және қарапайым есептерге ғана жарамды |
|
Есептеу жылдамдығы |
Жоғары: үлкен көлемдегі есептерді тез шешеді |
Орташа: кейбір есептерде баяу болуы мүмкін |
Төмен: үлкен есептерде өте баяу |
|
Ресурстарды пайдалану |
Орташа: аппараттық ресурстарды тиімді пайдаланады |
Жоғары: үлкен деректермен икемді жұмыс істейді |
Төмен: шағын ресурстарды қажет етеді, бірақ шектеулі |
|
Икемділік |
Жоғары: сызықтық, сызықсыз, дискретті оңтайландыру |
Өте жоғары: әртүрлі кітапханалармен кең қолданылады |
Шектеулі: тек қарапайым және сызықтық есептерге арналған |
|
Визуализация |
Жетілдірілген: деректерді 2D және 3D форматта көрсету |
Жетілдірілген: Matplotlib және Seaborn арқылы визуализация |
Қарапайым: негізгі диаграммалар |
|
Қолдану қарапайымдылығы |
Орташа: мамандарға арналған |
Жоғары: бағдарламалау білсеңіз, оңай |
Өте жоғары: интуитивті интерфейс |
|
Құжаттама мен қолдау |
Толық: кәсіби деңгейдегі қолдау және ресурстар |
Көптеген тегін онлайн ресурстар мен форумдар |
Негізгі Excel құжаттамасымен шектеледі |
|
Бағдарламалау мүмкіндігі |
Қажет: код жазуды талап етеді |
Қажет: еркін бағдарламалау мүмкіндігі |
Қажет емес: графикалық интерфейс арқылы жұмыс істейді |
|
Кітапханалар мен құралдар |
Арнайы: Signal Processing, Optimization Toolbox |
Ашық: SciPy, NumPy, TensorFlow және басқа кеңейтілімдер |
Қосымша кітапханаларсыз жұмыс істейді |
Нақты жүйелерге бейімдеу кезіндегі қиындықтар (5-кесте)
|
Қиындықтар |
MATLAB |
Python (NumPy, SciPy) |
Excel Solver |
|
Есептің күрделілігі |
Күрделі сызықсыз есептерді шешу үшін арнайы әдістер бар |
Эвристикалық әдістерді қолдану арқылы күрделі есептерге бейімделеді |
Күрделі есептерге бейімдеу мүмкін емес |
|
Шектеу шарттарын енгізу |
Күрделі теңдеулер мен айнымалыларды қолдайды |
Шектеулерді еркін анықтау мүмкіндігі бар |
Тек сызықтық шектеулермен жұмыс істейді |
|
Нәтижелерді интерпретациялау |
Визуализация мен аналитикалық құралдар дамыған |
Нәтижелерді визуализациялау үшін кең мүмкіндіктер |
Интерпретациясы қиын, қосымша талдау қажет |
|
Шешімнің орнықтылығы |
Орнықтылықты жоғары деңгейде қамтамасыз етеді |
Сандық әдістер арқылы орнықтылықты реттей алады |
Орнықтылығы төмен |
|
Үлкен есептерді бейімдеу |
Жоғары өнімділік: үлкен есептерде тиімді |
Жақсы бейімделеді, бірақ кейде жылдамдық шектеулі |
Үлкен есептерде қолдану мүмкін емес |
|
Бейімделу икемділігі |
Жоғары: нақты инженерлік есептерге тез бейімделеді |
Өте жоғары: деректер мен есептердің барлық түріне бейімделеді |
Төмен: тек қарапайым үлгілер үшін жарамды |
|
Қолдау көрсету |
Лицензиялық қолдау (MathWorks) |
Қоғамдық форумдар мен қауымдастық |
Microsoft қолдау көрсетеді |
|
Үлкен деректермен жұмыс |
Орташа: үлкен көлемді деректерді өңдеуге шектеулі |
Жоғары: үлкен деректерді талдау және оңтайландыруда тиімді |
Мүмкін емес: үлкен деректерді өңдеу қарастырылмаған |

шағым қалдыра аласыз