ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ
Цели: доказать признаки параллелограмма и рассмотреть решение задач.
Ход урока
I. Проверка домашнего задания.
1. Ответить на вопросы учащихся по домашнему заданию.
2. Выполнить задания (устно):
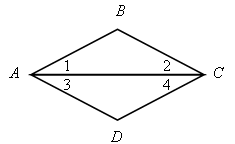
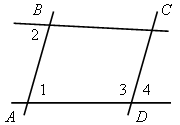
1) На рисунке а)
![]() 1 =
1 = ![]() 4,
4, ![]() 2 =
2 = ![]() 3. является ли четырехугольник АВСD параллелограммом?
3. является ли четырехугольник АВСD параллелограммом?
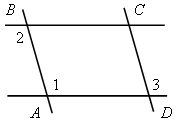
2) На рисунке б)
![]() 1 =
1 = ![]() 2 =
2 = ![]() 3. Докажите, что четырехугольник
АВСD
– параллелограмм.
3. Докажите, что четырехугольник
АВСD
– параллелограмм.
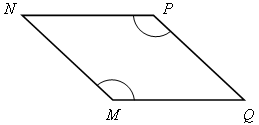
3) На рисунке в)
ММ ||
РQ,
![]() М =
М = ![]() Р. Докажите, что МNPO – параллелограмм.
Р. Докажите, что МNPO – параллелограмм.
4) Является ли
четырехугольник АВСD, изображенный на рисунке г), параллелограммом,
если а) ![]() 1 = 70°;
1 = 70°; ![]() 3 = 110°;
3 = 110°; ![]() 2 +
2 + ![]() 3 = 180°;
3 = 180°;
б) ![]() 1 =
1 = ![]() 2,
2, ![]() 2 ≠
2 ≠![]() 4?
4?
а) б)
в) г)
3. Анализ самостоятельной работы.
II. Изучение нового материала.
1. Перед тем как приступить к изучению признаков параллелограмма, следует напомнить учащимся, что означает слово «признак» и что такое обратная теорема.
2. Предложить учащимся самим сформулировать теоремы, обратные утверждениям о свойствах параллелограмма.
3. Подчеркнуть, что некоторое утверждение верно, но отсюда еще не следует, что верно и обратное ему утверждение.
4. Доказательство признаков можно провести силами учащихся.
III. Закрепление изученного материала.
Решить задачи №№ 379, 382.
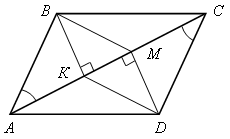
№ 379.
Решение
|
|
1) Так как ВK
2) Прямоугольные
треугольники АВK и СDМ равны по острому углу и гипотенузе
( |
3) Тогда ВK = DМ.
4) Четырехугольник
ВМDK
является параллелограммом,
так как
ВK || DМ, ВK = DМ.
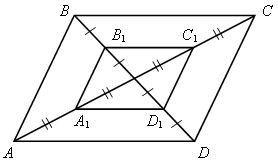
№ 382.
Решение
|
|
1) По свойству параллелограмма АО = ОС, ВО = ОD. 2) По условию ВВ1 = В1О = ОD1 = 3) Четырехугольник А1В1С1D1 – параллелограмм, так как его диагонали пересекаются и точкой пересечения делятся пополам. |
IV. Итоги урока.
Если в задаче необходимо доказать, что АВСD – параллелограмм, то применяют один из признаков:
|
АВ || СD и ВС || СD |
|
АВСD – параллелограмм |
|
АВ || СD и АВ = СD |
|
АВСD – параллелограмм |
|
АВ = СD и АD = ВС |
|
АВСD – параллелограмм |
|
АО = ОС и ВО = ОD |
|
АВСD – параллелограмм |
Домашнее задание: вопросы 6–9, с. 114; №№ 380, 373, 377, 384.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ
ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ
ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ
Цели: доказать признаки параллелограмма и рассмотреть решение задач.
Ход урока
I. Проверка домашнего задания.
1. Ответить на вопросы учащихся по домашнему заданию.
2. Выполнить задания (устно):
1) На рисунке а)
![]() 1 =
1 = ![]() 4,
4, ![]() 2 =
2 = ![]() 3. является ли четырехугольник АВСD параллелограммом?
3. является ли четырехугольник АВСD параллелограммом?
2) На рисунке б)
![]() 1 =
1 = ![]() 2 =
2 = ![]() 3. Докажите, что четырехугольник
АВСD
– параллелограмм.
3. Докажите, что четырехугольник
АВСD
– параллелограмм.
3) На рисунке в)
ММ ||
РQ,
![]() М =
М = ![]() Р. Докажите, что МNPO – параллелограмм.
Р. Докажите, что МNPO – параллелограмм.
4) Является ли
четырехугольник АВСD, изображенный на рисунке г), параллелограммом,
если а) ![]() 1 = 70°;
1 = 70°; ![]() 3 = 110°;
3 = 110°; ![]() 2 +
2 + ![]() 3 = 180°;
3 = 180°;
б) ![]() 1 =
1 = ![]() 2,
2, ![]() 2 ≠
2 ≠![]() 4?
4?


а) б)


в) г)
3. Анализ самостоятельной работы.
II. Изучение нового материала.
1. Перед тем как приступить к изучению признаков параллелограмма, следует напомнить учащимся, что означает слово «признак» и что такое обратная теорема.
2. Предложить учащимся самим сформулировать теоремы, обратные утверждениям о свойствах параллелограмма.
3. Подчеркнуть, что некоторое утверждение верно, но отсюда еще не следует, что верно и обратное ему утверждение.
4. Доказательство признаков можно провести силами учащихся.
III. Закрепление изученного материала.
Решить задачи №№ 379, 382.
№ 379.
Решение
|
|
1) Так как ВK
2) Прямоугольные
треугольники АВK и СDМ равны по острому углу и гипотенузе
( |
3) Тогда ВK = DМ.
4) Четырехугольник
ВМDK
является параллелограммом,
так как
ВK || DМ, ВK = DМ.
№ 382.
Решение
|
|
1) По свойству параллелограмма АО = ОС, ВО = ОD. 2) По условию ВВ1 = В1О = ОD1 = 3) Четырехугольник А1В1С1D1 – параллелограмм, так как его диагонали пересекаются и точкой пересечения делятся пополам. |
IV. Итоги урока.
Если в задаче необходимо доказать, что АВСD – параллелограмм, то применяют один из признаков:
|
АВ || СD и ВС || СD |
|
АВСD – параллелограмм |
|
АВ || СD и АВ = СD |
|
АВСD – параллелограмм |
|
АВ = СD и АD = ВС |
|
АВСD – параллелограмм |
|
АО = ОС и ВО = ОD |
|
АВСD – параллелограмм |
Домашнее задание: вопросы 6–9, с. 114; №№ 380, 373, 377, 384.

шағым қалдыра аласыз